Stagnation-point flow over a permeable stretching/shrinking sheet in a copper-water nanofluid

Abstract

An analysis is carried out to study the heat transfer characteristics of steady two-dimensional stagnation-point flow of a copper (Cu)-water nanofluid over a permeable stretching/shrinking sheet. The stretching/shrinking velocity and the ambient fluid velocity are assumed to vary linearly with the distance from the stagnation-point. Results for the skin friction coefficient, local Nusselt number, velocity as well as the temperature profiles are presented for different values of the governing parameters. It is found that dual solutions exist for the shrinking case, while for the stretching case, the solution is unique. The results indicate that the inclusion of nanoparticles into the base fluid produces an increase in the skin friction coefficient and the heat transfer rate at the surface. Moreover, suction increases the surface shear stress and in consequence increases the heat transfer rate at the fluid-solid interface.

MSC: 34B15, 76D10.

1 Introduction

Nanofluids are the suspension of metallic, nonmetallic or polymeric nano-sized powders in base liquid which are employed to increase the heat transfer rate in various applications. The term nanofluid, first introduced by Choi [1], refers to the fluids with suspended nanoparticles. Most of the convectional heat transfer fluids such as water, ethylene glycol and mineral oils have low thermal conductivity and thus are inadequate to meet the requirements of today’s cooling rate. An innovative way of improving the thermal conductivities of such fluids is to suspend small solid particles in the base fluids to form slurries. An industrial application test was carried out by Liu et al. [2] and Ahuja [3], in which the effect of particle volumetric loading, size and flow rate on the slurry pressure drop and heat transfer behavior was investigated (Xuan and Li [4]). Experimental results by Eastman et al. [5] showed that an increase in thermal conductivity of approximately 60% is obtained for the nanofluid consisting of water and 5% volume fraction of CuO nanoparticles. The procedure for preparing a nanofluid is given in the paper by Xuan and Li [4].

Many of the publications on nanofluids are about understanding of their behaviors so that they can be utilized where straight heat transfer enhancement is paramount as in many industrial applications, nuclear reactors, transportation, electronics as well as biomedicine and food (see Ding et al. [6]). Nanofluid is a smart fluid, where the heat transfer capabilities can be reduced or enhanced at will. These fluids enhance thermal conductivity of the base fluid enormously, which is beyond the explanation of any existing theory. They are also very stable and have no additional problems, such as sedimentation, erosion, additional pressure drop and non-Newtonian behavior, due to the tiny size of nanoelements and the low volume fraction of nanoelements required for conductivity enhancement. Much attention has been paid in the past to this new type of composite material because of its enhanced properties and behavior associated with heat transfer, mass transfer, wetting and spreading as well as antimicrobial activities, and the number of publications related to nanofluids increases in an exponential manner. The enhanced thermal behavior of nanofluids could provide a basis for an enormous innovation for heat transfer intensification, which is of major importance to a number of industrial sectors including transportation, power generation, micro-manufacturing, thermal therapy for cancer treatment, chemical and metallurgical sectors, as well as heating, cooling, ventilation and air-conditioning. Nanofluids are also important for the production of nanostructured materials, for the engineering of complex fluids, as well as for cleaning oil from surfaces due to their excellent wetting and spreading behavior (Ding et al. [6]).

There are some nanofluid models available in the literature. Among the popular models are the model proposed by Buongiorno [7] and Tiwari and Das [8]. Buongiorno [7] noted that the nanoparticle absolute velocity can be viewed as the sum of the base fluid velocity and a relative velocity (that he calls the slip velocity). He considered in turn seven slip mechanisms: inertia, Brownian diffusion, thermophoresis, diffusiophoresis, Magnus effect, fluid drainage and gravity settling (Nield and Kuznetsov [9]). The nanofluid mathematical model proposed by Buongiorno [7] was very recently used by several researchers such as, among others, Nield and Kuznetsov [9, 10], Kuznetsov and Nield [11, 12], Khan and Pop [13], Khan and Aziz [14], Makinde and Aziz [15], Bachok et al. [16, 17], etc. On the other hand, the Tiwari and Das model analyzes the behavior of nanofluids taking into account the solid volume fraction of the nanofluid. In the present paper, we study the flow and heat transfer characteristics near a stagnation region of a permeable stretching/shrinking sheet immersed in a Cu-water nanofluid using the Tiwari and Das model. It is worth mentioning that this model was recently employed in Refs. [18–33], and the flow over a shrinking sheet was considered in Refs. [34–44]. The velocity distribution of the two-dimensional stagnation flow was first analyzed by Hiemenz (see White [45]) who discovered that this flow can be analyzed exactly by the Navier-Stokes equations. Homann (see White [45]) extended this problem to the axisymmetric stagnation flow and found that the solution differs a little from the plane flow, where the displacement and boundary layer thicknesses are slightly smaller and the wall shear stress is slightly larger. On the other hand, the temperature distributions of the Hiemenz and Homann flows were given by Goldstein [46] and Sibulkin [47], respectively. The governing partial differential equations are first transformed into a system of ordinary differential equations before being solved numerically. We study the effects of suction and injection at the boundary. Suction or injection of a fluid through the bounding surface, as, for example, in mass transfer cooling, can significantly change the flow field and, as a consequence, affect the heat transfer rate at the surface. In general, suction tends to increase the skin friction and heat transfer coefficients, whereas injection acts in the opposite manner (Al-Sanea [48]). Injection of fluid through a porous bounding heated or cooled wall is of general interest in practical problems involving film cooling, control of boundary layer, etc. This can lead to enhance heating (or cooling) of the system and can help to delay the transition from laminar flow (see Chaudhary and Merkin [49]). We mention to this end that studies of the boundary layer flows of a Newtonian (or regular) fluid past a permeable static or moving flat plate have been done by Merkin [50], Weidman et al. [51], Ishak et al. [52], Zheng et al. [53] and Zhu et al. [54, 55], while Bachok et al. [32] have considered the boundary layers over a permeable moving surface in a nanofluid.

2 Mathematical formulation

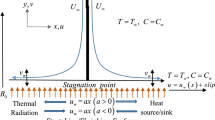
Consider a stagnation flow of an incompressible nanofluid over a stretching/shrinking surface located at $y=0$ with a fixed stagnation point at $x=0$. The stretching/shrinking velocity $U_w(x)$ and the ambient fluid velocity $U_{\mathrm{\infty }}(x)$ are assumed to vary linearly from the stagnation point, i.e., $U_w(x)=ax$ and $U_{\mathrm{\infty }}(x)=bx$, where a and b are constant with $b>0$. We note that $a>0$ and $a<0$ correspond to stretching and shrinking sheets, respectively. The simplified two-dimensional equations governing the flow in the boundary layer of a steady, laminar, and incompressible nanofluid are (see Ahmad et al. [26])

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0,$$

(1)

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=U_{\mathrm{\infty }}\frac{d{U}_{\mathrm{\infty }}}{dx}+\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^{2}u}{\partial y^2},$$

(2)

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial y^2}$$

(3)

subject to the boundary conditions

$$\begin{array}{r}u=U_w,v=V_w,T=T_w\text{at }y=0,\\ u\to U_{\mathrm{\infty }},T\to T_{\mathrm{\infty }}\text{as }y\to \mathrm{\infty },\end{array}$$

(4)

where u and v are the velocity components along the x- and y-axes, respectively, $V_w$ is the mass transfer velocity, T is the temperature of the nanofluid, $T_w$ is the surface temperature, $T_{\mathrm{\infty }}$ is the ambient temperature, ${\mu }_{nf}$ is the viscosity of the nanofluid, ${\alpha }_{nf}$ is the thermal diffusivity of the nanofluid and ${\rho }_{nf}$ is the density of the nanofluid, which are given by (Oztop and Abu-Nada [28])

$$\begin{array}{r}{\alpha }_{nf}=\frac{k_{nf}}{{(\rho C_p)}_{nf}},{\rho }_{nf}=(1-\phi ){\rho }_f+\phi {\rho }_s,{\mu }_{nf}=\frac{{\mu }_f}{{(1-\phi )}^{2.5}},\\ {(\rho C_p)}_{nf}=(1-\phi ){(\rho C_p)}_f+\phi {(\rho C_p)}_s,\frac{k_{nf}}{k_f}=\frac{(k_s+2k_f)-2\phi (k_f-k_s)}{(k_s+2k_f)+\phi (k_f-k_s)}.\end{array}$$

(5)

Here, φ is the nanoparticle volume fraction, ${(\rho C_p)}_{nf}$ is the heat capacity of the nanofluid, $k_{nf}$ is the thermal conductivity of the nanofluid, $k_f$ and $k_s$ are the thermal conductivities of the fluid and of the solid fractions, respectively, and ${\rho }_f$ and ${\rho }_s$ are the densities of the fluid and of the solid fractions, respectively. It should be mentioned that the use of the above expression for $k_{nf}$ is restricted to spherical nanoparticles where it does not account for other shapes of nanoparticles (Abu-Nada [18]). Also, the viscosity of the nanofluid ${\mu }_{nf}$ has been approximated by Brinkman [56] as viscosity of a base fluid ${\mu }_f$ containing dilute suspension of fine spherical particles.

The governing Eqs. (1)-(3) subject to the boundary conditions (4) can be expressed in a simpler form by introducing the following transformation:

$$\eta ={\left(\frac{U_{\mathrm{\infty }}}{{\nu }_{f}x}\right)}^{1/2}y,\psi ={({\nu }_{f}x{U}_{\mathrm{\infty }})}^{1/2}f(\eta ),\theta (\eta )=\frac{T-T_{\mathrm{\infty }}}{T_w-T_{\mathrm{\infty }}},$$

(6)

where η is the similarity variable and ψ is the stream function defined as $u=\partial \psi /\partial y$ and $v=-\partial \psi /\partial x$, which identically satisfies Eq. (1). Employing the similarity variables (6), Eqs. (2) and (3) reduce to the following ordinary differential equations:

$$\frac{1}{{(1-\phi )}^{2.5}(1-\phi +\phi {\rho }_s/{\rho }_f)}{f}^{‴}+f{f}^{″}-f^{\mathrm{\prime }2}+1=0,$$

(7)

$$\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{[1-\phi +\phi {(\rho C_p)}_s/{(\rho C_p)}_f]}{\theta }^{″}+f{\theta }^{\prime }=0$$

(8)

subjected to the boundary conditions (4) which become

$$\begin{array}{r}f(0)=S,f^{\prime }(0)=\epsilon ,\theta (0)=1,\\ f^{\prime }(\eta )\to 1,\theta (\eta )\to 0\text{as }\eta \to \mathrm{\infty }.\end{array}$$

(9)

In the above equations, primes denote differentiation with respect to η, Pr is the Prandtl number, S is the suction/injection parameter and ε is the stretching/shrinking parameter defined respectively as

$$\mathrm{Pr}={\nu }_f/{\alpha }_f,S=-V_w/{({\nu }_{f}b)}^{1/2},\epsilon =\frac{a}{b}$$

(10)

with $\epsilon >0$ for stretching and $\epsilon <0$ for shrinking.

The physical quantities of interest are the skin friction coefficient $C_f$ and the local Nusselt number ${\mathrm{Nu}}_x$, which are defined as

$$C_f=\frac{{\tau }_w}{{\rho }_f{U}_{\mathrm{\infty }}^2},{\mathrm{Nu}}_x=\frac{x{q}_w}{k_f(T_w-T_{\mathrm{\infty }})},$$

(11)

where the surface shear stress ${\tau }_w$ and the surface heat flux $q_w$ are given by

$${\tau }_w={\mu }_{nf}{\left(\frac{\partial u}{\partial y}\right)}_{y=0},q_w=-k_{nf}{\left(\frac{\partial T}{\partial y}\right)}_{y=0},$$

(12)

with ${\mu }_{nf}$ and $k_{nf}$ being the dynamic viscosity and thermal conductivity of the nanofluids, respectively. Using the similarity variables (6), we obtain

$$C_f{\mathrm{Re}}_x^{1/2}=\frac{1}{{(1-\phi )}^{2.5}}{f}^{″}(0),$$

(13)

$${\mathrm{Nu}}_x/{\mathrm{Re}}_x^{1/2}=-\frac{k_{nf}}{k_f}{\theta }^{\prime }(0),$$

(14)

where ${\mathrm{Re}}_x=U_{\mathrm{\infty }}x/{\nu }_f$ is the local Reynolds number.

3 Numerical scheme

The nonlinear differential equations (7) and (8) along with the boundary conditions (9) form a two-point boundary value problem (BVP) and are solved using a shooting method, by converting them into an initial value problem (IVP). This method is very well described in the recent papers by Bhattacharyya and Layek [57] and Bhattacharyya et al. [58]. In this method, we choose suitable finite values of η, say ${\eta }_{\mathrm{\infty }}$, which depend on the values of the parameters considered. First, the system of equations (7) and (8) is reduced to a first-order system (by introducing new variables) as follows:

$$f^{\prime }=p,p^{\prime }=q,\frac{1}{{(1-\phi )}^{2.5}(1-\phi +\phi {\rho }_s/{\rho }_f)}{q}^{\prime }+fq-p^2+1=0,$$

(15)

$${\theta }^{\prime }=r,\frac{1}{\mathrm{Pr}}\frac{k_{nf}/k_f}{[1-\phi +\phi {(\rho C_p)}_s/{(\rho C_p)}_f]}{r}^{\prime }+fr=0$$

(16)

with the boundary conditions

$$\begin{array}{r}f(0)=S,p(0)=\epsilon ,\theta (0)=1,\\ p({\eta }_{\mathrm{\infty }})=1,\theta ({\eta }_{\mathrm{\infty }})=0.\end{array}$$

(17)

Now we have a set of ‘partial’ initial conditions

$$f(0)=S,p(0)=\epsilon ,q(0)=?,\theta (0)=1,r(0)=?.$$

(18)

As we notice, we do not have the values of $q(0)$ and $r(0)$. To solve Eqs. (15) and (16) as an IVP, we need the values of $q(0)$ and $r(0)$, i.e., $f^{″}(0)$ and ${\theta }^{\prime }(0)$. We guess these values and apply the Runge-Kutta-Fehlberg method, then see if this guess matches the boundary conditions at the very end. Varying the initial slopes gives rise to a set of profiles which suggest the trajectory of a projectile ‘shot’ from the initial point. That initial slope is sought which results in the trajectory ‘hitting’ the target, that is, the final value (Bailey et al. [59]).

To determine either the solution obtained is valid or not, it is necessary to check the velocity and the temperature profiles. The correct profiles must satisfy the boundary conditions at $\eta ={\eta }_{\mathrm{\infty }}$ asymptotically. This procedure is repeated for other guessing values of $q(0)$ and $r(0)$ for the same values of parameters. If a different solution is obtained and the profiles satisfy the far field boundary conditions asymptotically but with different boundary layer thickness, then this solution is also a solution to the boundary-value problem (second solution).

4 Results and discussion

We have considered one type of nanoparticle, namely, copper (Cu), with water as the base fluid. The effects of the solid volume fraction of nanoparticles φ, the stretching/shrinking parameter ε and the suction/injection parameter S are analyzed. Following Oztop and Abu-Nada [28], Abu-Nada and Oztop [29] and Khanafer et al. [60], the value of the Prandtl number Pr is taken as 6.2 (for water) and the volume fraction of nanoparticles is from 0 to 0.2 ($0\le \phi \le 0.2$) in which $\phi =0$ corresponds to the regular (Newtonian) fluid. The thermophysical properties of the base fluid (water) and the nanoparticles are given in Table 1. The numerical results are presented in Figures 1-6.

Figure 1

Variation of ${\mathit{f}}^{\mathbf{″}}\mathbf{(}\mathbf{0}\mathbf{)}$ with ε for different values of S when $\mathit{\phi }\mathbf{=}\mathbf{0.1}$ .

Figure 2

Variation of $\mathbf{-}{\mathit{\theta }}^{\mathbf{\prime }}\mathbf{(}\mathbf{0}\mathbf{)}$ with ε for different values of S when $\mathit{\phi }\mathbf{=}\mathbf{0.1}$ and $\mathbf{Pr}\mathbf{=}\mathbf{6.2}$ .

Figure 3

Variation of the skin friction coefficient with φ for different values of S when $\mathit{\epsilon }\mathbf{=}\mathbf{0.5}$ .

Figure 4

Variation of the local Nusselt number with φ for different values of S when $\mathit{\epsilon }\mathbf{=}\mathbf{0.5}$ and $\mathbf{Pr}\mathbf{=}\mathbf{6.2}$ .

Figure 5

Velocity profiles for different values of ϕ when $\mathit{\epsilon }\mathbf{=}\mathbf{-}\mathbf{1.3}$ and $\mathit{S}\mathbf{=}\mathbf{0.3}$ .

Figure 6

Temperature profiles for different values of ϕ when$\mathit{\epsilon }\mathbf{=}\mathbf{-}\mathbf{1.3}$,$\mathit{S}\mathbf{=}\mathbf{0.3}$and$\mathbf{Pr}\mathbf{=}\mathbf{6.2}$. Solid line for first solution and dash line for second solution.

Table 1 Thermophysical properties of fluid and nanoparticles (Oztop and Abu-Nada [28])

Solving Eqs. (7) and (8) subject to the boundary conditions (9), it was found that dual solutions exist, which were obtained by setting different initial guesses for the missing values of $f^{″}(0)$ and ${\theta }^{\prime }(0)$, where all profiles satisfy the far fields boundary conditions (9) asymptotically but with different shapes. The variations of $f^{″}(0)$ and $-{\theta }^{\prime }(0)$ with ε are shown in Figures 1 and 2 for some values of the suction/injection parameter S. These figures show that there are regions of unique solutions for $\epsilon \ge -1$, dual (upper and lower branches) solutions for ${\epsilon }_c\le \epsilon <-1$ and no solutions for $\epsilon <{\epsilon }_c<0$, where ${\epsilon }_c$ is the critical value of ε ($<{\epsilon }_c<0$) beyond which Eqs. (7) and (8) have no solutions. Based on our computation, the critical values of ε, say ${\epsilon }_c$, are −1.1098, −1.2465 and −1.4311 for $S=-0.3$, $S=0$ and $S=0.3$, respectively. Thus, from this observation, the value of $|{\epsilon }_c|$ increases as S increases. Hence, suction widens the range of ε for which the solution exists, while injection acts in the opposite manner. Further, it should be mentioned that similar to other studies where dual solutions exist, we postulate that upper branch (the first) solutions of Eqs. (7) and (8) are stable and physically realizable, while the lower branch (the second) solutions are not. The procedure for showing this has been described by Merkin [50], Weidman et al. [51] and very recently by Postelnicu and Pop [61], so that we will not repeat it here.

Figures 3 and 4 illustrate the variations of the skin friction coefficient $C_f{\mathrm{Re}}_x^{1/2}$ and the local Nusselt number ${\mathrm{Nu}}_x{\mathrm{Re}}_x^{-1/2}$ given by Eqs. (13) and (14) with the nanoparticle volume fraction parameter φ for three different values of S with $\epsilon =0.5$ (stretching sheet). These figures show that these quantities increase almost linearly with φ. The presence of the nanoparticles in the fluids increases appreciably the effective thermal conductivity of the fluid and consequently enhances the heat transfer characteristics, as seen in Figure 4. Nanofluids have a distinctive characteristics, which is quite different from those of traditional solid-liquid mixtures in which millimeter and/or micrometer-sized particles are involved. Such particles can clot equipment and can increase pressure drop due to settling effects. Moreover, they settle rapidly, creating substantial additional pressure (Khanafer et al. [60]). Figure 3 also shows that the effect of suction ($S>0$) is to increase the skin friction coefficient, and in consequence it increases the local Nusselt number, as presented in Figure 4.

The samples of velocity and temperature profiles for some values of parameters are presented in Figures 5 and 6. These profiles have essentially the same form as in the case of regular fluid ($\phi =0$). The terms first solution and second solution refer to the curves shown in Figures 1 and 2, where the first solution has larger values of $f^{″}(0)$ and $-{\theta }^{\prime }(0)$ compared to the second solution. Figures 5 and 6 show that the far field boundary conditions (9) are satisfied asymptotically, thus support the validity of the numerical results, besides supporting the existence of the dual solutions presented in Figures 1 and 2.

5 Conclusions

We have numerically studied the existence of dual similarity solutions in boundary layer flow over a stretching/shrinking sheet immersed in a nanofluid with suction and injection effects. Discussions were carried out for the effects of suction/injection parameter S, the nanoparticle volume fraction φ and the stretching/shrinking parameter ε on the skin friction coefficient and the local Nusselt number. It was found that dual solutions exist for the shrinking case, while for the stretching case, the solution is unique. The results indicate that the inclusion of nanoparticles into the base fluid produced an increase in the skin friction coefficient and the local Nusselt number. Moreover, these quantities increase with suction but decrease with injection.