Abstract
In this paper, we develop a Jacobi-Gauss-Lobatto collocation method for solving the nonlinear fractional Langevin equation with three-point boundary conditions. The fractional derivative is described in the Caputo sense. The shifted Jacobi-Gauss-Lobatto points are used as collocation nodes. The main characteristic behind the Jacobi-Gauss-Lobatto collocation approach is that it reduces such a problem to those of solving a system of algebraic equations. This system is written in a compact matrix form. Through several numerical examples, we evaluate the accuracy and performance of the proposed method. The method is easy to implement and yields very accurate results.
Similar content being viewed by others
1 Introduction
Many practical problems arising in science and engineering require solving initial and boundary value problems of fractional order differential equations (FDEs), see [1, 2] and references therein. Several methods have also been proposed in the literature to solve FDEs (see, for instance, [3–7]). Spectral methods are relatively new approaches to provide an accurate approximation to FDEs (see, for instance, [8–11]).
In this work, we propose the shifted Jacobi-Gauss-Lobatto collocation (SJ-GL-C) method to solve numerically the following nonlinear Langevin equation involving two fractional orders in different intervals:
subject to the three-point boundary conditions
where denotes the Caputo fractional derivative of order ν for , λ is a real number, , , are given constants and f is a given nonlinear source function.
The existence and uniqueness of solution of Langevin equation involving two fractional orders in different intervals () have been studied in [12], and for other choices of ν and μ, see [13, 14].
Fractional Langevin equation is one of the basic equations in the theory of the evolution of physical phenomena in fluctuating environments and provides a more flexible model for fractal processes as compared with the usual ordinary Langevin equation. Moreover, fractional generalized Langevin equation with external force is used to model single-file diffusion. This equation has been the focus of many studies, see, for instance, [15–18].
Due to high order accuracy, spectral methods have gained increasing popularity for several decades, especially in the field of computational fluid dynamics (see, e.g., [19] and the references therein). Collocation methods have become increasingly popular for solving differential equations; also, they are very useful in providing highly accurate solutions to nonlinear differential equations [20–22]. Bhrawy and Alofi [20] proposed the spectral shifted Jacobi-Gauss collocation method to find the solution of the Lane-Emden type equation. Moreover, Doha et al. [23] developed the shifted Jacobi-Gauss collocation method for solving nonlinear high-order multi-point boundary value problems. To the best of our knowledge, there are no results on Jacobi-Gauss-Lobatto collocation method for three-point nonlinear Langevin equation arising in mathematical physics. This partially motivated our interest in such a method.
The advantage of using Jacobi polynomials for solving differential equations is obtaining the solution in terms of the Jacobi parameters α and β (see [24–27]). Some special cases of Jacobi parameters α and β are used for numerically solving various types of differential equations (see [28–31]).
The main concern of this paper is to extend the application of collocation method to solve the three-point nonlinear Langevin equation involving two fractional orders in different intervals. It would be very useful to carry out a systematic study on Jacobi-Gauss-Lobatto collocation method with general indexes (). The fractional Langevin equation is collocated only at points; for suitable collocation points, we use the nodes of the shifted Jacobi-Gauss-Lobatto interpolation (). These equations together with the three-point boundary conditions generate nonlinear algebraic equations which can be solved using Newton’s iterative method. Finally, the accuracy of the proposed method is demonstrated by test problems.
The remainder of the paper is organized as follows. In the next section, we introduce some notations and summarize a few mathematical facts used in the remainder of the paper. In Section 3, the way of constructing the Gauss-Lobatto collocation technique for fractional Langevin equation is described using the shifted Jacobi polynomials; and in Section 4 the proposed method is applied to some types of Langevin equations. Finally, some concluding remarks are given in Section 5.
2 Preliminaries
In this section, we give some definitions and properties of the fractional calculus (see, e.g., [1, 2, 32]) and Jacobi polynomials (see, e.g., [33–35]).
Definition 2.1 The Riemann-Liouville fractional integral operator of order μ () is defined as
Definition 2.2 The Caputo fractional derivative of order μ is defined as
where m is an integer number and is the classical differential operator of order m.
For the Caputo derivative, we have
We use the ceiling function to denote the smallest integer greater than or equal to μ and the floor function to denote the largest integer less than or equal to μ. Also and . Recall that for , the Caputo differential operator coincides with the usual differential operator of an integer order.
Let , and be the standard Jacobi polynomial of degree k. We have that
Besides,
Let , then we define the weighted space as usual, equipped with the following inner product and norm:
The set of Jacobi polynomials forms a complete -orthogonal system, and
Let , then the shifted Jacobi polynomial of degree k on the interval is defined by .
By virtue of (6), we have that
Next, let , then we define the weighted space in the usual way, with the following inner product and norm:
The set of shifted Jacobi polynomials is a complete -orthogonal system. Moreover, due to (8), we have
For one recovers the shifted ultraspherical polynomials (symmetric shifted Jacobi polynomials) and for , , the shifted Chebyshev of the first and second kinds and shifted Legendre polynomials respectively; and for the nonsymmetric shifted Jacobi polynomials, the two important special cases (shifted Chebyshev polynomials of the third and fourth kinds) are also recovered.
3 Shifted Jacobi-Gauss-Lobatto collocation method
In this section, we derive the SJ-GL-C method to solve numerically the following model problem:
subject to the three-point boundary conditions
where denotes the Caputo fractional derivative of order ν for λ is a real number, are given constants and is a given nonlinear source function. For the existence and uniqueness of solution of (11)-(12), see [12].
The choice of collocation points is important for the convergence and efficiency of the collocation method. For boundary value problems, the Gauss-Lobatto points are commonly used. It should be noted that for a differential equation with the singularity at in the interval one is unable to apply the collocation method with Jacobi-Gauss-Lobatto points because the two assigned abscissas 0 and L are necessary to use as a two points from the collocation nodes. Also, a Jacobi-Gauss-Radau nodes with the fixed node cannot be used in this case. In fact, we use the collocation method with Jacobi-Gauss-Lobatto nodes to treat the nonlinear Langevin differential equation; i.e., we collocate this equation only at the Jacobi-Gauss-Lobatto points . These equations together with three-point boundary conditions generate nonlinear algebraic equations which can be solved.
Let us first introduce some basic notation that will be used in the sequel. We set
We next recall the Jacobi-Gauss-Lobatto interpolation. For any positive integer N, stands for the set of all algebraic polynomials of degree at most N. If we denote by , , and , (), to the nodes and Christoffel numbers of the standard (shifted) Jacobi-Gauss-Lobatto quadratures on the intervals , respectively. Then one can easily show that

For any ,
We introduce the following discrete inner product and norm:
where and are the nodes and the corresponding weights of the shifted Jacobi-Gauss-quadrature formula on the interval respectively.
Due to (14), we have
Thus, for any , the norms and coincide.
Associating with this quadrature rule, we denote by the shifted Jacobi-Gauss interpolation,
The shifted Jacobi-Gauss collocation method for solving (11)-(12) is to seek , such that
We now derive an efficient algorithm for solving (17)-(18). Let
We first approximate , , as Eq. (19). By substituting these approximations in Eq. (11), we get
Here, the fractional derivative of order μ in the Caputo sense for the shifted Jacobi polynomials expanded in terms of shifted Jacobi polynomials themselves can be represented formally in the following theorem.
Theorem 3.1 Letbe a shifted Jacobi polynomial of degree j, then the fractional derivative of order ν in the Caputo sense foris given by
where
Proof This theorem can be easily proved (see Doha et al. [36]).
In practice, only the first -terms shifted Jacobi polynomials are considered, with the aid of Theorem 3.1 (Eq. (21)), we obtain from (20) that
Also, by substituting Eq. (19) in Eq. (12) we obtain
To find the solution , we first collocate Eq. (22) at the shifted Jacobi-Gauss-Lobatto notes, yields
Next, Eq. (23), after using (9) and (6), can be written as
The scheme (24)-(25) can be rewritten as a compact matrix form. To do this, we introduce the matrix A with the entries as follows:
Also, we define the matrix B with the entries:
and the matrix C with the entries:
Further, let , and
where is the k th component of C a. Then we obtain from (24)-(25) that
or equivalently
Finally, from (26), we obtain nonlinear algebraic equations which can be solved for the unknown coefficients by using any standard iteration technique, like Newton’s iteration method. Consequently, given in Eq. (19) can be evaluated. □
Remark 3.2 In actual computation for fixed μ, ν and λ, it is required to compute only once. This allows us to save a significant amount of computational time.
4 Numerical results
To illustrate the effectiveness of the proposed method in the present paper, two test examples are carried out in this section. Comparison of the results obtained by various choices of Jacobi parameters α and β reveal that the present method is very effective and convenient for all choices of α and β.
We consider the following two examples.
Example 1 Consider the nonlinear fractional Langevin equation
subject to three-point boundary conditions:
The analytic solution for this problem is not known. In Table 1 we introduce the approximate solution for (27)-(28) using SJ-GL-C method at and . The approximate solutions at and a few collocation points of this problem are depicted in Figure 1. The approximate solution at agrees very well with the approximate solution at ; this means the numerical solution converges fast as N increases.
Example 2 In this example we consider the following nonlinear fractional Langevin differential equation
subject to the following three-point boundary conditions:
where
The exact solution of this problem is .
Numerical results are obtained for different choices of ν, μ, α, β, and N. In Tables 2 and 3 we introduce the maximum absolute error, using the shifted Jacobi collocation method based on Gauss-Lobatto points, with two choices of α, β, and various choices of ν, μ, and N.
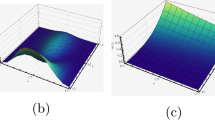
The approximate solutions are evaluated for , , and . The results of the numerical simulations are plotted in Figure 2. In Figure 3, we plotted the approximate solutions at fixed , and various choices of with and . It is evident from Figure 2 and Figure 3 that, as ν and μ approach close to 2 and 1, the numerical solution by shifted Jacobi-Gauss-Lobatto collocation method with for fractional order differential equation approaches to the solution of integer order differential equation.
In the case of , with , and , the results of the numerical simulations are shown in Figure 4. In Figure 5, we plotted the approximate solutions for , with , and . In fact, the approximate solutions obtained by the present method at , with are shown in Figure 4 and Figure 5 to make it easier to show that; as ν and μ approach to their integer values, the solution of fractional order Langevin equation approaches to the solution of integer order Langevin differential equation.
5 Conclusion
An efficient and accurate numerical scheme based on the Jacobi-Gauss-Lobatto collocation spectral method is proposed for solving the nonlinear fractional Langevin equation. The problem is reduced to the solution of nonlinear algebraic equations. Numerical examples were given to demonstrate the validity and applicability of the method. The results show that the SJ-GL-C method is simple and accurate. In fact, by selecting a few collocation points, excellent numerical results are obtained.
References
Magin RL: Fractional Calculus in Bioengineering. Begell House Publishers, New York; 2006.
Das S: Functional Fractional Calculus for System Identification and Controls. Springer, New York; 2008.
Jafari H, Yousefi SA, Firoozjaee MA, Momanic S, Khalique CM: Application of Legendre wavelets for solving fractional differential equations. Comput. Math. Appl. 2011, 62: 1038-1045. 10.1016/j.camwa.2011.04.024
Bhrawy AH, Alofi AS: The operational matrix of fractional integration for shifted Chebyshev polynomials. Appl. Math. Lett. 2012.
Lotfi A, Dehghan M, Yousefi SA: A numerical technique for solving fractional optimal control problems. Comput. Math. Appl. 2011, 62: 1055-1067. 10.1016/j.camwa.2011.03.044
Lakestani M, Dehghan M, Irandoust-pakchin S: The construction of operational matrix of fractional derivatives using B-spline functions. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 1149-1162. 10.1016/j.cnsns.2011.07.018
Pedas A, Tamme E: Piecewise polynomial collocation for linear boundary value problems of fractional differential equations. J. Comput. Appl. Math. 2012.
Bhrawy AH, Alofi AS, Ezz-Eldien SS: A quadrature tau method for variable coefficients fractional differential equations. Appl. Math. Lett. 2011, 24: 2146-2152. 10.1016/j.aml.2011.06.016
Bhrawy AH, Alshomrani M: A shifted Legendre spectral method for fractional-order multi-point boundary value problems. Adv. Differ. Equ. 2012., 2012:
Doha EH, Bhrawy AH, Ezz-Eldien SS: Efficient Chebyshev spectral methods for solving multi-term fractional orders differential equations. Appl. Math. Model. 2011, 35: 5662-5672. 10.1016/j.apm.2011.05.011
Doha EH, Bhrawy AH, Ezz-Eldien SS: A Chebyshev spectral method based on operational matrix for initial and boundary value problems of fractional order. Comput. Math. Appl. 2011, 62: 2364-2373. 10.1016/j.camwa.2011.07.024
Ahmad B, Nieto JJ, Alsaedi A, El-Shahed M: A study of nonlinear Langevin equation involving two fractional orders in different intervals. Nonlinear Anal., Real World Appl. 2012, 13: 599-606. 10.1016/j.nonrwa.2011.07.052
Ahmad B, Nieto JJ: Solvability of nonlinear Langevin equation involving two fractional orders with Dirichlet boundary conditions. Int. J. Differ. Equ. 2010., 2010:
Chen A, Chen Y: Existence of solutions to nonlinear Langevin equation involving two fractional orders with boundary value conditions. Bound. Value Probl. 2011., 2011:
Fa KS: Fractional Langevin equation and Riemann-Liouville fractional derivative. Eur. Phys. J. E 2007, 24: 139-143. 10.1140/epje/i2007-10224-2
Picozzi S, West B: Fractional Langevin model of memory in financial markets. Phys. Rev. E 2002, 66: 46-118.
Lim SC, Li M, Teo LP: Langevin equation with two fractional orders. Phys. Lett. A 2008, 372: 6309-6320. 10.1016/j.physleta.2008.08.045
Eab CH, Lim SC: Fractional generalized Langevin equation approach to single-file diffusion. Physica A 2010, 389: 2510-2521. 10.1016/j.physa.2010.02.041
Canuto C, Hussaini MY, Quarteroni A, Zang TA: Spectral Methods in Fluid Dynamics. Springer, New York; 1988.
Bhrawy AH, Alofi AS: A Jacobi-Gauss collocation method for solving nonlinear Lane-Emden type equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 62-70. 10.1016/j.cnsns.2011.04.025
Guo B-Y, Yan J-P: Legendre-Gauss collocation method for initial value problems of second order ordinary differential equations. Appl. Numer. Math. 2009, 59: 1386-1408. 10.1016/j.apnum.2008.08.007
Saadatmandi A, Dehghan M: The use of sinc-collocation method for solving multi-point boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 593-601. 10.1016/j.cnsns.2011.06.018
Doha EH, Bhrawy AH, Hafez RM: On shifted Jacobi spectral method for high-order multi-point boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 3802-3810. 10.1016/j.cnsns.2012.02.027
Doha EH, Bhrawy AH: Efficient spectral-Galerkin algorithms for direct solution of fourth-order differential equations using Jacobi polynomials. Appl. Numer. Math. 2008, 58: 1224-1244. 10.1016/j.apnum.2007.07.001
Doha EH, Bhrawy AH: A Jacobi spectral Galerkin method for the integrated forms of fourth-order elliptic differential equations. Numer. Methods Partial Differ. Equ. 2009, 25: 712-739. 10.1002/num.20369
El-Kady M: Jacobi discrete approximation for solving optimal control problems. J. Korean Math. Soc. 2012, 49: 99-112.
Doha EH, Abd-Elhameed WM, Youssri YH: Efficient spectral-Petrov-Galerkin methods for the integrated forms of third- and fifth-order elliptic differential equations using general parameters generalized Jacobi polynomials. Appl. Math. Comput. 2012, 218: 7727-7740. 10.1016/j.amc.2012.01.031
Xie, Z, Wang, L-L, Zhao, X: On exponential convergence of Gegenbauer interpolation and spectral differentiation. Math. Comput. (2012, in press)
Liu F, Ye X, Wang X: Efficient Chebyshev spectral method for solving linear elliptic PDEs using quasi-inverse technique. Numer. Math. Theor. Meth. Appl. 2011, 4: 197-215.
Zhu L, Fan Q: Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet. Commun. Nonlinear Sci. Numer. Simul. 2012, 17: 2333-2341. 10.1016/j.cnsns.2011.10.014
Doha EH, Bhrawy AH: An efficient direct solver for multidimensional elliptic Robin boundary value problems using a Legendre spectral-Galerkin method. Comput. Math. Appl. 2012.
Podlubny I: Fractional Differential Equations. Academic Press, San Diego; 1999.
Szegö G: Orthogonal Polynomials. 1985.
Doha EH: On the coefficients of differentiated expansions and derivatives of Jacobi polynomials. J. Phys. A, Math. Gen. 2002, 35: 3467-3478. 10.1088/0305-4470/35/15/308
Doha EH: On the construction of recurrence relations for the expansion and connection coefficients in series of Jacobi polynomials. J. Phys. A, Math. Gen. 2004, 37: 657-675. 10.1088/0305-4470/37/3/010
Doha EH, Bhrawy AH, Ezz-Eldien SS: A new Jacobi operational matrix: an application for solving fractional differential equations. Appl. Math. Model. 2012.
Acknowledgements
This study was supported by the Deanship of Scientific Research of King Abdulaziz University. The authors would like to thank the editor and the reviewers for their constructive comments and suggestions to improve the quality of the article.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors have equal contributions to each part of this article. All the authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bhrawy, A.H., Alghamdi, M.A. A shifted Jacobi-Gauss-Lobatto collocation method for solving nonlinear fractional Langevin equation involving two fractional orders in different intervals. Bound Value Probl 2012, 62 (2012). https://doi.org/10.1186/1687-2770-2012-62
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-2770-2012-62