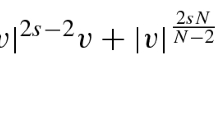Multiple positive solutions for semilinear elliptic systems involving subcritical nonlinearities in ${\mathbb{R}}^N$

Abstract

In this paper, we investigate the effect of the coefficient $f(x)$ of the subcritical nonlinearity. Under some assumptions, for sufficiently small $\epsilon ,\lambda ,\mu >0$, there are at least k (≥1) positive solutions of the semilinear elliptic systems

$$\{\begin{array}{c}-{\epsilon }^2\mathrm{\Delta }\overline{u}+\overline{u}=\lambda g(x)|\overline{u}{|}^{q-2}\overline{u}+\frac{\alpha }{\alpha +\beta }f(x)|\overline{u}{|}^{\alpha -2}\overline{u}|\overline{v}{|}^{\beta }\text{in }{\mathbb{R}}^N;\hfill \\ -{\epsilon }^2\mathrm{\Delta }\overline{v}+\overline{v}=\mu h(x)|\overline{v}{|}^{q-2}\overline{v}+\frac{\beta }{\alpha +\beta }f(x)|\overline{u}{|}^{\alpha }|\overline{v}{|}^{\beta -2}\overline{v}\text{in }{\mathbb{R}}^N;\hfill \\ \overline{u},\overline{v}\in H^1({\mathbb{R}}^N),\hfill \end{array}$$

where $\alpha >1$, $\beta >1$, $2<q<p=\alpha +\beta <2^{\ast }=2N/(N-2)$ for $N\ge 3$.

MSC:35J20, 35J25, 35J65.

1 Introduction

For $N\ge 3$, $\alpha >1$, $\beta >1$ and $2<q<p=\alpha +\beta <2^{\ast }=2N/(N-2)$, we consider the semilinear elliptic systems

where $\epsilon ,\lambda ,\mu >0$.

Let f, g and h satisfy the following conditions:

(A1) f is a positive continuous function in ${\mathbb{R}}^N$ and ${lim}_{|x|\to \mathrm{\infty }}f(x)=f_{\mathrm{\infty }}>0$.

(A2) there exist k points $a^1,a^2,\dots ,a^k$ in ${\mathbb{R}}^N$ such that

$$f\left(a^i\right)=\underset{x\in {\mathbb{R}}^N}{max}f(x)=1\text{for }1\le i\le k,$$

and $f_{\mathrm{\infty }}<1$.

(A3) $g,h\in L^m({\mathbb{R}}^N)\cap L^{\mathrm{\infty }}({\mathbb{R}}^N)$ where $m=(\alpha +\beta )/(\alpha +\beta -q)$, and $g,h\gneqq 0$.

In [1], if Ω is a smooth and bounded domain in ${\mathbb{R}}^N$ ($N\le 3$), they considered the following system:

$$\{\begin{array}{c}{\epsilon }^2\mathrm{\Delta }\overline{u}-{\lambda }_1\overline{u}={\mu }_1{\overline{u}}^3+\beta \overline{u}{\overline{v}}^2\text{in }\mathrm{\Omega };\hfill \\ {\epsilon }^2\mathrm{\Delta }\overline{v}-{\lambda }_2\overline{v}={\mu }_2{\overline{v}}^3+\beta {\overline{u}}^2\overline{v}\text{in }\mathrm{\Omega };\hfill \\ \overline{u}>0,\overline{v}>0,\hfill \end{array}$$

and proved the existence of a least energy solution in Ω for sufficiently small $\epsilon >0$ and $\beta \in (-\mathrm{\infty },{\beta }_0)$. Lin and Wei also showed that this system has a least energy solution in ${\mathbb{R}}^N$ for $\epsilon =1$ and $\beta \in (0,{\beta }_0)$. In this paper, we study the effect of $f(z)$ of (${\overline{E}}_{\epsilon ,\lambda ,\mu }$). Recently, many authors [2–5] considered the elliptic systems with subcritical or critical exponents, and they proved the existence of a least energy positive solution or the existence of at least two positive solutions for these problems. In this paper, we construct the k compact Palais-Smale sequences which are suitably localized in correspondence of k maximum points of f. Then we could show that under some assumptions (A1)-(A3), for sufficiently small $\epsilon ,\lambda ,\mu >0$, there are at least k (≥1) positive solutions of the elliptic system ($E_{\epsilon ,\lambda ,\mu }$). By the change of variables

$$x=\epsilon z,u(z)=\overline{u}(\epsilon z)\text{and}v(z)=\overline{v}(\epsilon z),$$

System (${\overline{E}}_{\epsilon ,\lambda ,\mu }$) is transformed to

Let $H=H^1({\mathbb{R}}^N)\times H^1({\mathbb{R}}^N)$ be the space with the standard norm

$${\parallel (u,v)\parallel }_H={[{\int }_{{\mathbb{R}}^N}(|\mathrm{\nabla }u{|}^2+u^2)dz+{\int }_{{\mathbb{R}}^N}(|\mathrm{\nabla }v{|}^2+v^2)dz]}^{1/2}.$$

Associated with the problem ($E_{\epsilon ,\lambda ,\mu }$), we consider the $C^1$-functional $J_{\epsilon ,\lambda ,\mu }$, for $(u,v)\in H$,

$$\begin{array}{rcl}{J}_{\epsilon ,\lambda ,\mu }(u,v)& =& \frac{1}{2}{\parallel (u,v)\parallel }_H^2-\frac{1}{\alpha +\beta }{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\\ -\frac{1}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz.\end{array}$$

Actually, the weak solution $(u,v)\in H$ of ($E_{\epsilon ,\lambda ,\mu }$) is the critical point of the functional $J_{\epsilon ,\lambda ,\mu }$, that is, $(u,v)\in H$ satisfies

for any $({\phi }_1,{\phi }_2)\in H$.

We consider the Nehari manifold

$${\mathbf{M}}_{\epsilon ,\lambda ,\mu }=\{(u,v)\in H\mathrm{\setminus }\{(0,0)\}|〈J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u,v),(u,v)〉=0\},$$

(1.1)

where

$$〈J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u,v),(u,v)〉={\parallel (u,v)\parallel }_H^2-{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz-{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz.$$

The Nehari manifold ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ contains all nontrivial weak solutions of ($E_{\epsilon ,\lambda ,\mu }$).

Let

$$S_{\alpha ,\beta }=\underset{u,v\in H^1({\mathbb{R}}^N)\mathrm{\setminus }\{(0)\}}{inf}\frac{{\parallel (u,v)\parallel }_H^2}{{({\int }_{{\mathbb{R}}^N}|u{|}^{\alpha }|v{|}^{\beta }dz)}^{2/(\alpha +\beta )}},$$

(1.2)

then by [[2], Theorem 5], we have

$$S_{\alpha ,\beta }=[{\left(\frac{\alpha }{\beta }\right)}^{\frac{\beta }{\alpha +\beta }}+{\left(\frac{\beta }{\alpha }\right)}^{\frac{\alpha }{\alpha +\beta }}]S_p,$$

where $p=\alpha +\beta$ and $S_p$ is the best Sobolev constant defined by

$$S_p=\underset{u\in H^1({\mathbb{R}}^N)\mathrm{\setminus }\{0\}}{inf}\frac{{\int }_{{\mathbb{R}}^N}(|\mathrm{\nabla }u{|}^2+u^2)dz}{{({\int }_{{\mathbb{R}}^N}|u{|}^{p}dz)}^{2/p}}.$$

For the semilinear elliptic systems ($\lambda =\mu =0$)

we define the energy functional $I_{\epsilon }(u,v)=\frac{1}{2}{\parallel (u,v)\parallel }_H^2-\frac{1}{\alpha +\beta }{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz$, and

$${\mathbf{N}}_{\epsilon }=\{(u,v)\in H\mathrm{\setminus }\{(0,0)\}|〈I_{\epsilon }^{\mathrm{\prime }}(u,v),(u,v)〉=0\}.$$

If $f\equiv {max}_{z\in {\mathbb{R}}^N}f(z)$ (=1), then we define $I_{max}(u,v)=\frac{1}{2}{\parallel (u,v)\parallel }_H^2-\frac{1}{\alpha +\beta }{\int }_{{\mathbb{R}}^N}|u{|}^{\alpha }|v{|}^{\beta }dz$ and

$${\theta }_{max}=\underset{(u,v)\in {\mathbf{N}}_{max}}{inf}{I}_{max}(u,v),$$

where ${\mathbf{N}}_{max}=\{(u,v)\in H\mathrm{\setminus }\{(0,0)\}|〈I_{max}^{\mathrm{\prime }}(u,v),(u,v)〉=0\}$.

It is well known that this problem

has the unique, radially symmetric and positive ground state solution $w\in H^1({\mathbb{R}}^N)$. Define ${\overline{I}}_{max}(u)=\frac{1}{2}{\int }_{{\mathbb{R}}^N}(|\mathrm{\nabla }u{|}^2+u^2)dz-\frac{1}{p}{\int }_{{\mathbb{R}}^N}|u{|}^{p}dz$ and ${\overline{\theta }}_{max}={inf}_{u\in {\overline{\mathbf{N}}}_{max}}{\overline{I}}_{max}(u)$, where

$${\overline{\mathbf{N}}}_{max}=\{u\in H^1\left({\mathbb{R}}^N\right)\mathrm{\setminus }\{0\}|〈{\overline{I}}_{max}^{\mathrm{\prime }}(u),u〉=0\}.$$

Moreover, we have that

$${\overline{\theta }}_{max}=\frac{p-2}{2p}{S}_p^{\frac{p}{p-2}}>0.\text{(See Wang [6, Theorems 4.12 and 4.13].)}$$

This paper is organized as follows. First of all, we study the argument of the Nehari manifold ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$. Next, we prove that the existence of a positive solution $(u_0,v_0)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ of ($E_{\epsilon ,\lambda ,\mu }$). Finally, in Section 4, we show that the condition (A2) affects the number of positive solutions of ($E_{\epsilon ,\lambda ,\mu }$); that is, there are at least k critical points $(u_i,v_i)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ of $J_{\epsilon ,\lambda ,\mu }$ such that $J_{\epsilon ,\lambda ,\mu }(u_i,v_i)={\beta }_{\epsilon ,\lambda ,\mu }^i$ ((PS)-value) for $1\le i\le k$.

Theorem 1.1 ($E_{\epsilon ,\lambda ,\mu }$) has at least one positive solution $(u_0,v_0)$, that is, (${\overline{E}}_{\epsilon ,\lambda ,\mu }$) admits at least one positive solution.

Theorem 1.2 There exist two positive numbers ${\epsilon }_0$ and ${\mathrm{\Lambda }}^{\ast }$ such that ($E_{\epsilon ,\lambda ,\mu }$) has at least k positive solutions for any $0<\epsilon <{\epsilon }_0$ and $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$, that is, (${\overline{E}}_{\epsilon ,\lambda ,\mu }$) admits at least k positive solutions.

2 Preliminaries

By studying the argument of Han [[7], Lemma 2.1], we obtain the following lemma.

Lemma 2.1 Let $\mathrm{\Omega }\subset {\mathbb{R}}^N$ (possibly unbounded) be a smooth domain. If $u_n\rightharpoonup u$, $v_n\rightharpoonup v$ weakly in $H_0^1(\mathrm{\Omega })$, and $u_n\to u$, $v_n\to v$ almost everywhere in Ω, then

$$\underset{n\to \mathrm{\infty }}{lim}{\int }_{\mathrm{\Omega }}|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz=\underset{n\to \mathrm{\infty }}{lim}{\int }_{\mathrm{\Omega }}|u_n{|}^{\alpha }|v_n{|}^{\beta }dz-{\int }_{\mathrm{\Omega }}|u{|}^{\alpha }|v{|}^{\beta }dz.$$

Note that $J_{\epsilon ,\lambda ,\mu }$ is not bounded from below in H. From the following lemma, we have that $J_{\epsilon ,\lambda ,\mu }$ is bounded from below on ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$.

Lemma 2.2 The energy functional $J_{\epsilon ,\lambda ,\mu }$ is bounded from below on ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$.

Proof For $(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$, by (1.1), we obtain that

$$J_{\epsilon ,\lambda ,\mu }(u,v)=(\frac{1}{2}-\frac{1}{q}){\parallel (u,v)\parallel }_H^2+(\frac{1}{q}-\frac{1}{p}){\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz>0,$$

where $p=\alpha +\beta$. Hence, we have that $J_{\epsilon ,\lambda ,\mu }$ is bounded from below on ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$. □

We define

$${\theta }_{\epsilon ,\lambda ,\mu }=\underset{(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }}{inf}{J}_{\epsilon ,\lambda ,\mu }(u,v).$$

Lemma 2.3 (i) There exist positive numbers σ and $d_0$ such that $J_{\epsilon ,\lambda ,\mu }(u,v)\ge d_0$ for ${\parallel (u,v)\parallel }_H=\sigma$;

• (ii) There exists $(\overline{u},\overline{v})\in H\mathrm{\setminus }\{(0,0)\}$ such that ${\parallel (\overline{u},\overline{v})\parallel }_H>\sigma$ and $J_{\epsilon ,\lambda ,\mu }(\overline{u},\overline{v})<0$.

Proof (i) By (1.2), the Hölder inequality ($p_1=\frac{p}{p-q}$, $p_2=\frac{p}{q}$) and the Sobolev embedding theorem, we have that

$$\begin{array}{rcl}{J}_{\epsilon ,\lambda ,\mu }(u,v)& =& \frac{1}{2}{\parallel (u,v)\parallel }_H^2-\frac{1}{p}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\\ -\frac{1}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz\\ \ge & \frac{1}{2}{\parallel (u,v)\parallel }_H^2-\frac{1}{p}{S}_{\alpha ,\beta }^{-p/2}{\parallel (u,v)\parallel }_H^p\\ -\frac{1}{q}Max{S}_p^{-\frac{q}{2}}(\lambda +\mu ){\parallel (u,v)\parallel }_H^q,\end{array}$$

where $p=\alpha +\beta$ and $Max=max\{{\parallel g\parallel }_m,{\parallel h\parallel }_m\}$. Hence, there exist positive σ and $d_0$ such that $J_{\epsilon ,\lambda ,\mu }(u,v)\ge d_0$ for ${\parallel (u,v)\parallel }_H=\sigma$.

• (ii) For any $(u,v)\in H\mathrm{\setminus }\{(0,0)\}$, since

  $$\begin{array}{rcl}{J}_{\epsilon ,\lambda ,\mu }(tu,tv)& =& \frac{t^2}{2}{\parallel (u,v)\parallel }_H^2-\frac{t^p}{p}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\\ -\frac{t^q}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz,\end{array}$$

then ${lim}_{t\to \mathrm{\infty }}{J}_{\epsilon ,\lambda ,\mu }(tu,tv)=-\mathrm{\infty }$. Fix some $(u,v)\in H\mathrm{\setminus }\{(0,0)\}$, there exists $\overline{t}>0$ such that ${\parallel (\overline{t}u,\overline{t}v)\parallel }_H>\sigma$ and $J_{\epsilon ,\lambda ,\mu }(\overline{t}u,\overline{t}v)<0$. Let $(\overline{u},\overline{v})=(\overline{t}u,\overline{t}v)$. □

Define

$$\psi (u,v)=〈J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u,v),(u,v)〉.$$

Then for $(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$, we obtain that

$$\begin{array}{rcl}〈{\psi }^{\mathrm{\prime }}(u,v),(u,v)〉& =& 2{\parallel (u,v)\parallel }_H^2-p{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\\ -q{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz\\ =& (p-q){\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz-(p-2){\parallel (u,v)\parallel }_H^2\end{array}$$

(2.1)

$$=(2-q){\parallel (u,v)\parallel }_H^2+(q-p){\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz<0.$$

(2.2)

Lemma 2.4 For each $(u,v)\in H\mathrm{\setminus }\{(0,0)\}$, there exists a unique positive number $t_{u,v}$ such that $(t_{u,v}u,t_{u,v}v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ and $J_{\epsilon ,\lambda ,\mu }(t_{u,v}u,t_{u,v}v)={sup}_{t\ge 0}{J}_{\epsilon ,\lambda ,\mu }(tu,tv)$.

Proof Fixed $(u,v)\in H\mathrm{\setminus }\{(0,0)\}$, we consider

$$\begin{array}{rl}R(t)& =J_{\epsilon ,\lambda ,\mu }(tu,tv)\\ =\frac{t^2}{2}{\parallel (u,v)\parallel }_H^2-\frac{t^p}{p}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz-\frac{t^q}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz.\end{array}$$

Since $R(0)=0$, ${lim}_{t\to \mathrm{\infty }}R(t)=-\mathrm{\infty }$, by Lemma 2.3(i), then ${sup}_{t\ge 0}R(t)$ is achieved at some $t_{u,v}>0$. Moreover, we have that $R^{\mathrm{\prime }}(t_{u,v})=0$, that is, $(t_{u,v}u,t_{u,v}v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$. Next, we claim that $t_{u,v}$ is a unique positive number such that $R^{\mathrm{\prime }}(t_{u,v})=0$. Consider

$$r(t)={\parallel (u,v)\parallel }_H^2-t^{p-2}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz-t^{q-2}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz,$$

then $R^{\mathrm{\prime }}(t)=tr(t)$. Since $r(0)={\parallel (u,v)\parallel }_H^2>0$,

$$\begin{array}{rcl}{r}^{\mathrm{\prime }}(t)& =& -(p-2)t^{p-3}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\\ -(q-2)t^{q-3}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz<0,\end{array}$$

there exists a unique positive number ${\overline{t}}_{u,v}$ such that $r({\overline{t}}_{u,v})=0$. It follows that $R^{\mathrm{\prime }}({\overline{t}}_{u,v})=0$. Hence, ${\overline{t}}_{u,v}=t_{u,v}$. □

Remark 2.5 By Lemma 2.3(i) and Lemma 2.4, then ${\theta }_{\epsilon ,\lambda ,\mu }\ge d_0>0$ for some constant $d_0$.

Lemma 2.6 Let $(u_0,v_0)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ satisfy

$$J_{\epsilon ,\lambda ,\mu }(u_0,v_0)=\underset{(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }}{min}{J}_{\epsilon ,\lambda ,\mu }(u,v)={\theta }_{\epsilon ,\lambda ,\mu },$$

then $(u_0,v_0)$ is a solution of ($E_{\epsilon ,\lambda ,\mu }$).

Proof By (2.2), $〈{\psi }^{\mathrm{\prime }}(u,v),(u,v)〉<0$ for $(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$. Since $J_{\epsilon ,\lambda ,\mu }(u_0,v_0)={min}_{(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }}{J}_{\epsilon ,\lambda ,\mu }(u,v)$, by the Lagrange multiplier theorem, there is $\tau \in \mathbb{R}$ such that $J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u_0,v_0)=\tau {\psi }^{\mathrm{\prime }}(u_0,v_0)$ in $H^{-1}$. Then we have

$$0=〈J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u_0,v_0),(u_0,v_0)〉=\tau 〈{\psi }^{\mathrm{\prime }}(u_0,v_0),(u_0,v_0)〉.$$

It follows that $\tau =0$ and $J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u_0,v_0)=0$ in $H^{-1}$. Therefore, $(u_0,v_0)$ is a nontrivial solution of ($E_{\epsilon ,\lambda ,\mu }$) and $J_{\epsilon ,\lambda ,\mu }(u_0,v_0)={\theta }_{\epsilon ,\lambda ,\mu }$. □

3 (PS) _γ -condition in H for $J_{\epsilon ,\lambda ,\mu }$

First of all, we define the Palais-Smale (denoted by (PS)) sequence and (PS)-condition in H for some functional J.

Definition 3.1 (i) For $\gamma \in \mathbb{R}$, a sequence $\{(u_n,v_n)\}$ is a (PS) _γ -sequence in H for J if $J(u_n,v_n)=\gamma +o_n(1)$ and $J^{\mathrm{\prime }}(u_n,v_n)=o_n(1)$ strongly in $H^{-1}$ as $n\to \mathrm{\infty }$, where $H^{-1}$ is the dual space of H;

• (ii) J satisfies the (PS) _γ -condition in H if every (PS) _γ -sequence in H for J contains a convergent subsequence.

Applying Ekeland’s variational principle and using the same argument as in Cao-Zhou [8] or Tarantello [9], we have the following lemma.

Lemma 3.2 (i) There exists a (PS)-sequence $\{(u_n,v_n)\}$ in ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ for $J_{\epsilon ,\lambda ,\mu }$.

In order to prove the existence of positive solutions, we want to prove that $J_{\epsilon ,\lambda ,\mu }$ satisfies the (PS) _γ -condition in H for $\gamma \in (0,\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}})$.

Lemma 3.3 $J_{\epsilon ,\lambda ,\mu }$ satisfies the (PS) _γ -condition in H for $\gamma \in (0,\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}})$.

Proof Let $\{(u_n,v_n)\}$ be a (PS) _γ -sequence in H for $J_{\epsilon ,\lambda ,\mu }$ such that $J_{\epsilon ,\lambda ,\mu }(u_n,v_n)=\gamma +o_n(1)$ and $J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u_n,v_n)=o_n(1)$ in $H^{-1}$. Then

$$\begin{array}{rl}\gamma +c_n+\frac{d_n{\parallel (u_n,v_n)\parallel }_H}{q}& \ge J_{\epsilon ,\lambda ,\mu }(u_n,v_n)-\frac{1}{q}〈J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u_n,v_n),(u_n,v_n)〉\\ =(\frac{1}{2}-\frac{1}{q}){\parallel (u_n,v_n)\parallel }_H^2+(\frac{1}{q}-\frac{1}{p}){\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n{|}^{\alpha }|v_n{|}^{\beta }dz\\ \ge \frac{q-2}{2q}{\parallel (u_n,v_n)\parallel }_H^2,\end{array}$$

where $c_n=o_n(1)$, $d_n=o_n(1)$ as $n\to \mathrm{\infty }$. It follows that $\{(u_n,v_n)\}$ is bounded in H. Hence, there exist a subsequence $\{(u_n,v_n)\}$ and $(u,v)\in H$ such that

Moreover, we have that $J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u,v)=0$ in $H^{-1}$. We use the Brézis-Lieb lemma to obtain (3.1) and (3.2) as follows:

(3.1)

(3.2)

Next, we claim that

$${\int }_{{\mathbb{R}}^N}g(\epsilon z)|u_n-u{|}^{q}dz\to 0\text{as }n\to \mathrm{\infty }$$

(3.3)

and

$${\int }_{{\mathbb{R}}^N}h(\epsilon z)|v_n-v{|}^{q}dz\to 0\text{as }n\to \mathrm{\infty }.$$

(3.4)

Since $g\in L^m({\mathbb{R}}^N)$, where $m=p/(p-q)$, then for any $\sigma >0$, there exists $r>0$ such that ${\int }_{{[B_r^N(0)]}^c}g{(\epsilon z)}^{\frac{p}{p-q}}dz<\sigma$. By the Hölder inequality and the Sobolev embedding theorem, we get

Similarly, ${\int }_{{\mathbb{R}}^N}h(\epsilon z)|v_n-v{|}^{q}dz\to 0$ as $n\to \mathrm{\infty }$. By (A1) and $u_n\to u$, $v_n\to v$ strongly in $L_{\mathrm{loc}}^p({\mathbb{R}}^N)$, we have that

$${\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz={\int }_{{\mathbb{R}}^N}{f}_{\mathrm{\infty }}|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz=o_n(1).$$

(3.5)

Let $p_n=(u_n-u,v_n-v)$. By (3.1)-(3.4) and Lemma 2.1, we deduce that

$$\begin{array}{rcl}{\parallel p_n\parallel }_H^2& =& ({\parallel u_n\parallel }_H^2+{\parallel v_n\parallel }_H^2)-({\parallel u\parallel }_H^2+{\parallel v\parallel }_H^2)+o_n(1)\\ =& {\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n{|}^{\alpha }|v_n{|}^{\beta }dz+{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u_n{|}^q+\mu h(\epsilon z)|v_n{|}^q)dz\\ -{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz-{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz+o_n(1)\\ =& {\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz+o_n(1),\end{array}$$

and

$$\frac{1}{2}{\parallel p_n\parallel }_H^2-\frac{1}{\alpha +\beta }{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz=\gamma -J_{\epsilon ,\lambda ,\mu }(u,v)+o_n(1).$$

(3.6)

We may assume that

$${\parallel p_n\parallel }_H^2\to l\text{and}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz\to l\text{as }n\to \mathrm{\infty }.$$

(3.7)

Recall that

$$S_{\alpha ,\beta }=\underset{u,v\in H^1({\mathbb{R}}^N)\mathrm{\setminus }\{(0)\}}{inf}\frac{{\parallel (u,v)\parallel }_H^2}{{({\int }_{{\mathbb{R}}^N}|u{|}^{\alpha }|v{|}^{\beta }dz)}^{2/p}},\text{where }p=\alpha +\beta .$$

If $l>0$, by (3.5), then

$$\begin{array}{rcl}{S}_{\alpha ,\beta }{l}^{\frac{2}{p}}& =& S_{\alpha ,\beta }{({\int }_{{\mathbb{R}}^N}f(\epsilon z)|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz)}^{2/p}+o_n(1)\\ =& S_{\alpha ,\beta }{({\int }_{{\mathbb{R}}^N}{f}_{\mathrm{\infty }}|u_n-u{|}^{\alpha }|v_n-v{|}^{\beta }dz)}^{2/p}+o_n(1)\\ \le & {(f_{\mathrm{\infty }})}^{2/p}{\parallel p_n\parallel }_H^2+o_n(1)={(f_{\mathrm{\infty }})}^{2/p}l.\end{array}$$

This implies $l\ge {(S_{\alpha ,\beta })}^{p/(p-2)}/{(f_{\mathrm{\infty }})}^{2/(p-2)}$. By (3.6) and (3.7), we obtain that

$$\gamma =(\frac{1}{2}-\frac{1}{p})l+J_{\epsilon ,\lambda ,\mu }(u,v)\ge \frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}},$$

which is a contradiction. Hence, $l=0$, that is, $(u_n,v_n)\to (u,v)$ strongly in H. □

4 Existence of k solutions

Let $w\in H^1({\mathbb{R}}^N)$ be the unique, radially symmetric and positive ground state solution of equation (E 0) in ${\mathbb{R}}^N$. Recall the facts (or see Bahri-Li [10], Bahri-Lions [11], Gidas-Ni-Nirenberg [12] and Kwong [13]):

• (i) $w\in L^{\mathrm{\infty }}({\mathbb{R}}^N)\cap C_{\mathrm{loc}}^{2,\theta }({\mathbb{R}}^N)$ for some $0<\theta <1$ and ${lim}_{|z|\to \mathrm{\infty }}w(z)=0$;

• (ii) for any $\epsilon >0$, there exist positive numbers $C_1$, $C_2^{\epsilon }$ and $C_3^{\epsilon }$ such that for all $z\in {\mathbb{R}}^N$

  $$C_2^{\epsilon }exp(-(1+\epsilon )|z|)\le w(z)\le C_{1}exp(-|z|)$$

and

$$|\mathrm{\nabla }w(z)|\le C_3^{\epsilon }exp(-(1-\epsilon )|z|).$$

By Lien-Tzeng-Wang [14], then

$$S_p=\frac{{\int }_{{\mathbb{R}}^N}(|\mathrm{\nabla }w{|}^2+w^2)dz}{{({\int }_{{\mathbb{R}}^N}{w}^{p}dz)}^{2/p}}.$$

(4.1)

For $1\le i\le k$, we define

$$w_{\epsilon }^i(z)=w(z-\frac{a^i}{\epsilon }),\text{where }f\left(a^i\right)=\underset{z\in {\mathbb{R}}^N}{max}f(z)=1.$$

Clearly, $w_{\epsilon }^i(z)\in H^1({\mathbb{R}}^N)$.

First of all, we want to prove that

$$\underset{\epsilon \to 0^{+}}{lim}\underset{t\ge 0}{sup}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\text{uniformly in }i.$$

Lemma 4.1 For $\lambda >0$ and $\mu >0$, then

$$\underset{\epsilon \to 0^{+}}{lim}\underset{t\ge 0}{sup}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\mathit{\text{uniformly in}}i.$$

Moreover, we have that

$$0<{\theta }_{\epsilon ,\lambda ,\mu }\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}.$$

Proof Part I: Since $J_{\epsilon ,\lambda ,\mu }$ is continuous in H, $J_{\epsilon ,\lambda ,\mu }(0,0)=0$, and $\{(\sqrt{\alpha }{w}_{\epsilon }^i,\sqrt{\beta }{w}_{\epsilon }^i)\}$ is uniformly bounded in H for any $\epsilon >0$ and $1\le i\le k$, then there exists $t_0>0$ such that for $0\le t<t_0$ and any $\epsilon >0$,

$$J_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)<\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\text{uniformly in }i.$$

From (A1), we have that ${inf}_{z\in {\mathbb{R}}^N}f(z)>0$. Then

$$\begin{array}{rcl}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)& \le & \frac{t^2}{2}{\parallel (\sqrt{\alpha }w,\sqrt{\beta }w)\parallel }_H^2\\ -\frac{t^{\alpha +\beta }}{\alpha +\beta }(\underset{z\in {\mathbb{R}}^N}{inf}f(z)){\int }_{{\mathbb{R}}^N}|\sqrt{\alpha }w{|}^{\alpha }|\sqrt{\beta }w{|}^{\beta }dz\\ \to & -\mathrm{\infty }\text{as }t\to \mathrm{\infty }.\end{array}$$

It follows that there exists $t_1>0$ such that for $t>t_1$ and any $\epsilon >0$,

$$J_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)<\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\text{uniformly in }i.$$

From now on, we only need to show that

$$\underset{\epsilon \to 0^{+}}{lim}\underset{t_0\le t\le t_1}{sup}{J}_{\epsilon ,\lambda ,\mu }\left(t{w}_{\epsilon }^i\right)\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\text{uniformly in }i.$$

Since

$$\underset{t\ge 0}{sup}(\frac{t^2}{2}a-\frac{t^{\alpha +\beta }}{\alpha +\beta }b)=\frac{\alpha +\beta -2}{2(\alpha +\beta )}{\left(\frac{a}{b^{\frac{2}{\alpha +\beta }}}\right)}^{\frac{\alpha +\beta }{\alpha +\beta -2}},\text{where }a,b>0,$$

and by (4.1), then

(4.2)

For $t_0\le t\le t_1$, by (4.2), we have that

$$\begin{array}{rcl}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)& =& \frac{t^2}{2}{\parallel (\sqrt{\alpha }{w}_{\epsilon }^i,\sqrt{\beta }{w}_{\epsilon }^i)\parallel }_H^2-\frac{t^{\alpha +\beta }}{\alpha +\beta }{\int }_{{\mathbb{R}}^N}f(\epsilon z)\left|\sqrt{\alpha }{w}_{\epsilon }^i{|}^{\alpha }\right|\sqrt{\beta }{w}_{\epsilon }^i{|}^{\beta }dz\\ -\frac{t^q}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|\sqrt{\alpha }{w}_{\epsilon }^i{|}^q+\mu h(\epsilon z)\left|\sqrt{\beta }{w}_{\epsilon }^i{|}^q\right)dz\\ \le & \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\\ +\frac{t_1^p}{p}{\int }_{{\mathbb{R}}^N}(1-f(\epsilon z))\left|\sqrt{\alpha }{w}_{\epsilon }^i{|}^{\alpha }\right|\sqrt{\alpha }{w}_{\epsilon }^i{|}^{\beta }dz.\end{array}$$

Since

then

$$\underset{\epsilon \to 0^{+}}{lim}\underset{t_0\le t\le t_1}{sup}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)},$$

that is, for $\lambda >0$ and $\mu >0$,

$$\underset{\epsilon \to 0^{+}}{lim}\underset{t\ge 0}{sup}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\text{uniformly in }i.$$

Part II: By Lemma 2.4, there is a number $t_{\epsilon }^i>0$ such that $(t_{\epsilon }^i\sqrt{\alpha }{w}_{\epsilon }^i,t_{\epsilon }^i\sqrt{\beta }{w}_{\epsilon }^i)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$, where $1\le i\le k$. Hence, from the result of Part I, we have that for $\lambda >0$ and $\mu >0$,

$$0<{\theta }_{\epsilon ,\lambda ,\mu }\le \underset{\epsilon \to 0^{+}}{lim}\underset{t\ge 0}{sup}{J}_{\epsilon ,\lambda ,\mu }(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}.$$

 □

Proof of Theorem 1.1 By Lemma 3.2, there exists a (PS)-sequence $\{(u_n,v_n)\}$ in ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ for $J_{\epsilon ,\lambda ,\mu }$. Since $0<{\theta }_{\epsilon ,\lambda ,\mu }\le \frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}<\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}}$ for $\lambda >0$ and $\mu >0$, by Lemma 3.3, there exist a subsequence $\{(u_n,v_n)\}$ and $(u_0,v_0)\in H$ such that $(u_n,v_n)\to (u_0,v_0)$ strongly in H. It is easy to check that $(u_0,v_0)$ is a nontrivial solution of ($E_{\epsilon ,\lambda ,\mu }$) and $J_{\epsilon ,\lambda ,\mu }(u_0,v_0)={\theta }_{\epsilon ,\lambda ,\mu }$. Since $J_{\epsilon ,\lambda ,\mu }(u_0,v_0)=J_{\lambda ,\mu }(|u_0|,|v_0|)$ and $(|u_0|,|v_0|)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$, by Lemma 2.6, we may assume that $u_0\ge 0$, $v_0\ge 0$. Applying the maximum principle, $u_0>0$ and $v_0>0$ in Ω. □

Choosing $0<{\rho }_0<1$ such that

$$\overline{B_{{\rho }_0}^N\left(a^i\right)}\cap \overline{B_{{\rho }_0}^N\left(a^j\right)}=\mathrm{\varnothing }\text{for }i\ne j\text{ and }1\le i,j\le k,$$

where $\overline{B_{{\rho }_0}^N(a^i)}=\{z\in {\mathbb{R}}^N||z-a^i|\le {\rho }_0\}$ and $f(a^i)={max}_{z\in {\mathbb{R}}^N}f(z)=1$, define $\mathbf{K}=\{a^i|1\le i\le k\}$ and ${\mathbf{K}}_{{\rho }_0/2}={\bigcup }_{i=1}^k\overline{B_{{\rho }_0/2}^N(a^i)}$. Suppose ${\bigcup }_{i=1}^k\overline{B_{{\rho }_0}^N(a^i)}\subset B_{r_0}^N(0)$ for some $r_0>0$. Let $Q_{\epsilon }$ be given by

$$Q_{\epsilon }(u,v)=\frac{{\int }_{{\mathbb{R}}^N}\chi (\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz}{{\int }_{{\mathbb{R}}^N}|u{|}^{\alpha }|v{|}^{\beta }dz},$$

where $\chi :{\mathbb{R}}^N\to {\mathbb{R}}^N$, $\chi (z)=z$ for $|z|\le r_0$ and $\chi (z)=r_{0}z/|z|$ for $|z|>r_0$.

For each $1\le i\le k$, we define

By Lemma 2.4, there exists $t_{\epsilon }^i>0$ such that $(t_{\epsilon }^i\sqrt{\alpha }{w}_{\epsilon }^i,t_{\epsilon }^i\sqrt{\beta }{w}_{\epsilon }^i)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ for each $1\le i\le k$. Then we have the following result.

Lemma 4.2 There exists ${\epsilon }_1>0$ such that if $\epsilon \in (0,{\epsilon }_1)$, then $Q_{\epsilon }(t_{\epsilon }^i\sqrt{\alpha }{w}_{\epsilon }^i,t_{\epsilon }^i\sqrt{\beta }{w}_{\epsilon }^i)\in {\mathbf{K}}_{{\rho }_0/2}$ for each $1\le i\le k$.

Proof Since

$$\begin{array}{rcl}{Q}_{\epsilon }(t_{\epsilon }^i\sqrt{\alpha }{w}_{\epsilon }^i,t_{\epsilon }^i\sqrt{\beta }{w}_{\epsilon }^i)& =& \frac{{\int }_{{\mathbb{R}}^N}\chi (\epsilon z)|w(z-\frac{a^i}{\epsilon }){|}^{p}dz}{{\int }_{{\mathbb{R}}^N}|w(z-\frac{a^i}{\epsilon }){|}^{p}dz}\\ =& \frac{{\int }_{{\mathbb{R}}^N}\chi (\epsilon z+a^i)|w(z){|}^{p}dz}{{\int }_{{\mathbb{R}}^N}|w(z){|}^{p}dz}\\ \to & a^i\text{as }\epsilon \to 0^{+},\end{array}$$

there exists ${\epsilon }_1>0$ such that

$$Q_{\epsilon }(t_{\epsilon }^i\sqrt{\alpha }{w}_{\epsilon }^i,t_{\epsilon }^i\sqrt{\beta }{w}_{\epsilon }^i)\in {\mathbf{K}}_{{\rho }_0/2}\text{for any }\epsilon \in (0,{\epsilon }_1)\text{ and each }1\le i\le k.$$

 □

We need the following lemmas to prove that ${\beta }_{\lambda ,\mu }^i<{\tilde{\beta }}_{\lambda ,\mu }^i$ for sufficiently small ε, λ, μ.

Lemma 4.3 ${\theta }_{max}=\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}$.

Proof From Part I of Lemma 4.1, we obtain ${sup}_{t\ge 0}{I}_{max}(t\sqrt{\alpha }{w}_{\epsilon }^i,t\sqrt{\beta }{w}_{\epsilon }^i)=\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}$ uniformly in i. Similarly to Lemma 2.4, there is a sequence $\{s_{max}^i\}\subset {\mathbb{R}}^{+}$ such that $(s_{max}^i\sqrt{\alpha }{w}_{\epsilon }^i,s_{max}^i\sqrt{\beta }{w}_{\epsilon }^i)\in {\mathbf{N}}_{max}$ and

$${\theta }_{max}\le I_{max}(s_{max}^i\sqrt{\alpha }{u}_{\epsilon }^i,s_{max}^i\sqrt{\beta }{u}_{\epsilon }^i)=\underset{t\ge 0}{sup}{J}_{max}(t\sqrt{\alpha }{u}_{\epsilon }^i,t\sqrt{\beta }{u}_{\epsilon }^i)=\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}.$$

Let $\{(u_n,v_n)\}\subset {\mathbf{N}}_{max}$ be a minimizing sequence of ${\theta }_{max}$ for $I_{max}$. It follows that ${\parallel (u_n,v_n)\parallel }_H^2={\int }_{{\mathbb{R}}^N}|u_n{|}^{\alpha }|v_n{|}^{\beta }dz$ and

$$\begin{array}{rcl}{\theta }_{max}& =& \frac{1}{2}{\parallel (u_n,v_n)\parallel }_H^2-\frac{1}{p}{\int }_{{\mathbb{R}}^N}|u_n{|}^{\alpha }|v_n{|}^{\beta }dz+o_n(1)\\ =& \frac{p-2}{2p}{\parallel (u_n,v_n)\parallel }_H^2+o_n(1).\end{array}$$

We may assume that ${\parallel (u_n,v_n)\parallel }_H^2\to l$ and ${\int }_{{\mathbb{R}}^N}|u_n{|}^{\alpha }|v_n{|}^{\beta }dz\to l$ as $n\to \mathrm{\infty }$, where $l=\frac{2p}{p-2}{\theta }_{max}>0$. By the definition of $S_{\alpha ,\beta }$, then $S_{\alpha ,\beta }{l}^{\frac{2}{p}}\le l$. We can deduce that $S_{\alpha ,\beta }\le l^{\frac{p-2}{p}}={(\frac{2p}{p-2}{\theta }_{max})}^{\frac{p-2}{p}}$, that is, $\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}\le {\theta }_{max}$. □

Lemma 4.4 There exists a number ${\delta }_0>0$ such that if $(u,v)\in {\mathbf{N}}_{\epsilon }$ and $I_{\epsilon }(u,v)\le {\theta }_{max}+{\delta }_0$, then $Q_{\epsilon }(u,v)\in {\mathbf{K}}_{{\rho }_0/2}$ for any $0<\epsilon <{\epsilon }_1$.

Proof On the contrary, there exist the sequences $\{{\epsilon }_n\}\subset {\mathbb{R}}^{+}$ and $\{(u_n,v_n)\}\subset {\mathbf{N}}_{{\epsilon }_n}$ such that ${\epsilon }_n\to 0$, $I_{{\epsilon }_n}(u_n,v_n)={\theta }_{max}\text{(}>0\text{)}+o_n(1)$ as $n\to \mathrm{\infty }$ and $Q_{{\epsilon }_n}(u_n,v_n)\notin {\mathbf{K}}_{{\rho }_0/2}$ for all $n\in \mathbb{N}$. It is easy to check that $\{(u_n,v_n)\}$ is bounded in H. Suppose that ${\int }_{{\mathbb{R}}^N}|u_n{|}^{\alpha }|v_n{|}^{\beta }dz\to 0$ as $n\to \mathrm{\infty }$. Since

$${\parallel (u_n,v_n)\parallel }_H^2={\int }_{{\mathbb{R}}^N}f({\epsilon }_{n}z)|u_n{|}^{\alpha }|v_n{|}^{\beta }dz\text{for each }n\in \mathbb{N},$$

then

$${\theta }_{max}+o_n(1)=I_{{\epsilon }_n}(u_n,v_n)=(\frac{1}{2}-\frac{1}{p}){\int }_{{\mathbb{R}}^N}f({\epsilon }_{n}z)|u_n{|}^{\alpha }|v_n{|}^{\beta }dz\le o_n(1),$$

which is a contradiction. Thus, ${\int }_{{\mathbb{R}}^N}|u_n{|}^{\alpha }|v_n{|}^{\beta }dz\nrightarrow 0$ as $n\to \mathrm{\infty }$. Similarly to the concentration-compactness principle (see Lions [15, 16] or Wang [[6], Lemma 2.16]), then there exist a constant $c_0>0$ and a sequence $\{\widetilde{z_n}\}\subset {\mathbb{R}}^N$ such that

$${\int }_{B^N(\widetilde{z_n};1)}|u_n{|}^{\frac{\alpha l}{p}}|v_n{|}^{\frac{\beta l}{p}}dz\ge c_0>0,$$

(4.3)

where $2<l<p=\alpha +\beta <2^{\ast }$ and $p=l(1-t)+2^{\ast }t$ for some $t\in ((N-2)/N,1)$. Let $(\widetilde{u_n}(z),\widetilde{v_n}(z))=(u_n(z+\widetilde{z_n}),v_n(z+\widetilde{z_n}))$. Then there are a subsequence $\{(\widetilde{u_n},\widetilde{v_n})\}$ and $(\tilde{u},\tilde{v})\in H$ such that $\widetilde{u_n}\rightharpoonup \tilde{u}$ and $\widetilde{v_n}\rightharpoonup \tilde{v}$ weakly in $H^1({\mathbb{R}}^N)$. Using the similar computation of Lemma 2.4, there is a sequence $\{s_{max}^n\}\subset {\mathbb{R}}^{+}$ such that $(s_{max}^n\widetilde{u_n},s_{max}^n\widetilde{v_n})\in {\mathbf{N}}_{max}$ and

$$\begin{array}{rcl}0& <& {\theta }_{max}\le I_{max}(s_{max}^n\widetilde{u_n},s_{max}^n\widetilde{v_n})=I_{max}(s_{max}^n{u}_n,s_{max}^n{v}_n)\\ \le & I_{{\epsilon }_n}(s_{max}^n{u}_n,s_{max}^n{v}_n)\le I_{{\epsilon }_n}(u_n,v_n)={\theta }_{max}+o_n(1)\text{as }n\to \mathrm{\infty }.\end{array}$$

We deduce that a subsequence $\{s_{max}^n\}$ satisfies $s_{max}^n\to s_0>0$. Then there are a subsequence $\{(s_{max}^n\widetilde{u_n},s_{max}^n\widetilde{v_n})\}$ and $(s_0\tilde{u},s_0\tilde{v})\in H$ such that $s_{max}^n\widetilde{u_n}\rightharpoonup s_0\tilde{u}$ and $s_{max}^n\widetilde{v_n}\rightharpoonup s_0\tilde{v}$ weakly in $H^1({\mathbb{R}}^N)$. By (4.3), then $\tilde{u}\ne 0$ and $\tilde{v}\ne 0$. Applying Ekeland’s variational principle, there exists a (PS)-sequence $\{(U_n,V_n)\}$ for $I_{max}$ and ${\parallel (U_n-s_{max}^n\widetilde{u_n},V_n-s_{max}^n\widetilde{v_n})\parallel }_H=o_n(1)$. Similarly to the proof of Lemma 3.3, there exist a subsequence $\{(U_n,V_n)\}$ and $(U_0,V_0)\in H$ such that $U_n\to U_0$, $V_n\to V_0$ strongly in $H^1({\mathbb{R}}^N)$ and $I_{max}(U_0,V_0)={\theta }_{max}$. Now, we want to show that there exists a subsequence $\{z_n\}=\{{\epsilon }_n\widetilde{z_n}\}$ such that $z_n\to z_0\in \mathbf{K}$.

• (i) Claim that the sequence $\{z_n\}$ is bounded in ${\mathbb{R}}^N$. On the contrary, assume that $|z_n|\to \mathrm{\infty }$, then

  $$\begin{array}{rl}{\theta }_{max}& =I_{max}(U_0,V_0)<\frac{1}{2}{\parallel (U_0,V_0)\parallel }_H^2-\frac{1}{p}{\int }_{{\mathbb{R}}^N}{f}_{\mathrm{\infty }}|U_0{|}^{\alpha }|V_0{|}^{\beta }dz\\ \le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}[\frac{{(s_{max}^n)}^2}{2}{\parallel (\widetilde{u_n},\widetilde{v_n})\parallel }_H^2-\frac{{(s_{max}^n)}^p}{p}{\int }_{{\mathbb{R}}^N}f({\epsilon }_{n}z+z_n)|\widetilde{u_n}{|}^{\alpha }|\widetilde{v_n}{|}^{\beta }dz]\\ =\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}[\frac{{(s_{max}^n)}^2}{2}{\parallel (u_n,v_n)\parallel }_H^2-\frac{{(s_{max}^n)}^p}{p}{\int }_{{\mathbb{R}}^N}f({\epsilon }_{n}z)|u_n{|}^{\alpha }|v_n{|}^{\beta }dz]\\ =\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}{I}_{{\epsilon }_n}(s_{max}^n{u}_n,s_{max}^n{v}_n)\le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}{I}_{{\epsilon }_n}(u_n,v_n)={\theta }_{max},\end{array}$$

which is a contradiction.

• (ii) Claim that $z_0\in \mathbf{K}.$ On the contrary, assume that $z_0\notin \mathbf{K}$, that is, $f(z_0)<1={max}_{z\in {\mathbb{R}}^N}f(z)$. Then use the argument of (i) to obtain that

  $$\begin{array}{rl}{\theta }_{max}& =I_{max}(U_0,V_0)\le I_{max}(s_0{U}_0,s_0{V}_0)\\ <\frac{{(s_0)}^2}{2}{\parallel (U_0,V_0)\parallel }_H^2-\frac{{(s_0)}^p}{p}{\int }_{{\mathbb{R}}^N}f(z_0)|U_0{|}^{\alpha }|V_0{|}^{\beta }dz\\ \le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}[\frac{{(s_{max}^n)}^2}{2}{\parallel (\widetilde{u_n},\widetilde{v_n})\parallel }_H^2-\frac{{(s_{max}^n)}^p}{p}{\int }_{{\mathbb{R}}^N}f({\epsilon }_{n}z+z_n)|\widetilde{u_n}{|}^{\alpha }|\widetilde{v_n}{|}^{\beta }dz]\\ \le {\theta }_{max},\end{array}$$

which is a contradiction.

Since ${\parallel (U_n-s_{max}^n\widetilde{u_n},V_n-s_{max}^n\widetilde{v_n})\parallel }_H=o_n(1)$ and $U_n\to U_0$, $V_n\to V_0$ strongly in $H^1({\mathbb{R}}^N)$, we have that

$$\begin{array}{rl}{Q}_{{\epsilon }_n}(u_n,v_n)& =\frac{{\int }_{{\mathbb{R}}^N}\chi ({\epsilon }_{n}z)|\widetilde{u_n}(z-\widetilde{z_n}){|}^{\alpha }|\widetilde{v_n}(z-\widetilde{z_n}){|}^{\beta }dz}{{\int }_{{\mathbb{R}}^N}|\widetilde{u_n}(z-\widetilde{z_n}){|}^{\alpha }|\widetilde{v_n}(z-\widetilde{z_n}){|}^{\beta }dz}\\ =\frac{{\int }_{{\mathbb{R}}^N}\chi ({\epsilon }_{n}z+{\epsilon }_n\widetilde{z_n})|U_0{|}^{\alpha }|V_0{|}^{\beta }dz}{{\int }_{{\mathbb{R}}^N}|U_0{|}^{\alpha }|V_0{|}^{\beta }dz}\to z_0\in {\mathbf{K}}_{{\rho }_0/2}\text{as }n\to \mathrm{\infty },\end{array}$$

which is a contradiction.

Hence, there exists ${\delta }_0>0$ such that if $(u,v)\in {\mathbf{N}}_{\epsilon }$ and $I_{\epsilon }(u,v)\le {\theta }_{max}+{\delta }_0$, then $Q_{\epsilon }(u,v)\in {\mathbf{K}}_{{\rho }_0/2}$ for any $0<\epsilon <{\epsilon }_1$. □

Lemma 4.5 If $(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ and $J_{\epsilon ,\lambda ,\mu }(u,v)\le {\theta }_{max}+{\delta }_0/2$, then there exists a number ${\mathrm{\Lambda }}^{\ast }>0$ such that $Q_{\epsilon }(u,v)\in {\mathbf{K}}_{{\rho }_0/2}$ for any $0<\epsilon <{\epsilon }_1$ and $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$.

Proof Using the similar computation in Lemma 2.4, we obtain that there is the unique positive number

$$s_{\epsilon }={\left(\frac{{\parallel (u,v)\parallel }_H^2}{{\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz}\right)}^{1/(p-2)}$$

such that $(s_{\epsilon }u,s_{\epsilon }v)\in {\mathbf{N}}_{\epsilon }$. We want to show that there exists ${\mathrm{\Lambda }}_0>0$ such that if $0<\lambda +\mu <{\mathrm{\Lambda }}_0$, then $s_{\epsilon }<c$ for some constant $c>0$ (independent of u and v). First, for $(u,v)\in {\mathbf{M}}_{\epsilon ,\lambda ,\mu }$,

$$0<d_0\le {\theta }_{\epsilon ,\lambda ,\mu }\le J_{\epsilon ,\lambda ,\mu }(u,v)\le {\theta }_{max}+{\delta }_0/2.$$

Since $〈J_{\epsilon ,\lambda ,\mu }^{\mathrm{\prime }}(u,v),(u,v)〉=0$, then

$$\begin{array}{rl}{\theta }_{max}+{\delta }_0/2& \ge J_{\epsilon ,\lambda ,\mu }(u,v)\\ =(\frac{1}{2}-\frac{1}{q}){\parallel (u,v)\parallel }_H^2+(\frac{1}{q}-\frac{1}{p}){\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\\ \ge \frac{q-2}{2q}{\parallel (u,v)\parallel }_H^2,\text{that is,}{\parallel (u,v)\parallel }_H^2\le c_1=\frac{2q}{q-2}({\theta }_{max}+{\delta }_0/2),\end{array}$$

(4.4)

and

$$\begin{array}{rl}{d}_0& \le J_{\epsilon ,\lambda ,\mu }(u,v)\\ =(\frac{1}{2}-\frac{1}{p}){\parallel (u,v)\parallel }_H^2-(\frac{1}{q}-\frac{1}{p}){\int }_{\mathrm{\Omega }}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz\\ \le \frac{p-2}{2p}{\parallel (u,v)\parallel }_H^2,\text{that is,}{\parallel (u,v)\parallel }_H^2\ge c_2=\frac{2p}{p-2}{d}_0.\end{array}$$

(4.5)

Moreover, we have that

$$\begin{array}{rl}{\int }_{\mathrm{\Omega }}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz& ={\parallel (u,v)\parallel }_H^2-{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz\\ \ge c_2-Max{S}_p^{-\frac{q}{2}}(\lambda +\mu )c_1^{q/2},\end{array}$$

where $Max=max\{{\parallel g\parallel }_m,{\parallel h\parallel }_m\}$. It follows that there exists ${\mathrm{\Lambda }}_0>0$ such that for $0<\lambda +\mu <{\mathrm{\Lambda }}_0$

$${\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz\ge c_2-Max{S}_p^{-\frac{q}{2}}(\lambda +\mu ){(c_1)}^{q/2}>0.$$

(4.6)

Hence, by (4.4), (4.5) and (4.6), $s_{\epsilon }<c$ for some constant $c>0$ (independent of u and v) for $0<\lambda +\mu <{\mathrm{\Lambda }}_0$. Now, we obtain that

$$\begin{array}{rcl}{\theta }_{max}+{\delta }_0/2& \ge & J_{\epsilon ,\lambda ,\mu }(u,v)=\underset{t\ge 0}{sup}{J}_{\epsilon ,\lambda ,\mu }(tu,tv)\ge J_{\epsilon ,\lambda ,\mu }(s_{\epsilon }u,s_{\epsilon }v)\\ =& \frac{1}{2}{\parallel (s_{\epsilon }u,s_{\epsilon }v)\parallel }_H^2-\frac{1}{p}{\int }_{{\mathbb{R}}^N}f(\epsilon z)|s_{\epsilon }u{|}^{\alpha }|s_{\epsilon }v{|}^{\beta }dz\\ -\frac{1}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|s_{\epsilon }u{|}^q+\mu h(\epsilon z)|s_{\epsilon }v{|}^q)dz\\ \ge & I_{\epsilon }(s_{\epsilon }u,s_{\epsilon }v)-\frac{1}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|s_{\epsilon }u{|}^q+\mu h(\epsilon z)|s_{\epsilon }v{|}^q)dz.\end{array}$$

From the above inequality, we deduce that for any $0<\epsilon <{\epsilon }_1$ and $0<\lambda +\mu <{\mathrm{\Lambda }}_0$,

$$\begin{array}{rl}{I}_{\epsilon }(s_{\epsilon }u,s_{\epsilon }v)& \le {\theta }_{max}+{\delta }_0/2+\frac{1}{q}{\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|s_{\epsilon }u{|}^q+\mu h(\epsilon z)|s_{\epsilon }v{|}^q)dz\\ \le {\theta }_{max}+{\delta }_0/2+Max(\lambda +\mu )S_p^{-\frac{q}{2}}{\parallel (s_{\epsilon }u,s_{\epsilon }v)\parallel }_H^q\\ <{\theta }_{max}+{\delta }_0/2+Max{S}_p^{-\frac{q}{2}}(\lambda +\mu )c^q{(c_1)}^{q/2}.\end{array}$$

Hence, there exists ${\mathrm{\Lambda }}^{\ast }\in (0,{\mathrm{\Lambda }}_0)$ such that for $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$,

$$I_{\epsilon }(s_{\epsilon }u,s_{\epsilon }v)\le {\theta }_{max}+{\delta }_0,\text{where }(s_{\epsilon }u,s_{\epsilon }v)\in {\mathbf{N}}_{\epsilon }.$$

By Lemma 4.4, we obtain

$$Q_{\epsilon }(s_{\epsilon }u,s_{\epsilon }v)=\frac{{\int }_{{\mathbb{R}}^N}\chi (\epsilon z)|s_{\epsilon }u{|}^{\alpha }|s_{\epsilon }v{|}^{\beta }dz}{{\int }_{{\mathbb{R}}^N}|s_{\epsilon }u{|}^{\alpha }|s_{\epsilon }v{|}^{\beta }dz}\in {\mathbf{K}}_{{\rho }_0/2},$$

or $Q_{\epsilon }(u,v)\in {\mathbf{K}}_{{\rho }_0/2}$ for any $0<\epsilon <{\epsilon }_0$ and $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$. □

Since $f_{\mathrm{\infty }}<1$, then by Lemma 4.3,

$${\theta }_{max}=\frac{p-2}{2p}{(S_{\alpha ,\beta })}^{p/(p-2)}<\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}}.$$

(4.7)

By Lemmas 4.1, 4.2 and (4.7), for any $0<\epsilon <{\epsilon }_0$ ($<{\epsilon }_1$) and $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$,

$${\beta }_{\epsilon ,\lambda ,\mu }^i\le J_{\epsilon ,\lambda ,\mu }(t_{\epsilon }^i\sqrt{\alpha }{w}_{\epsilon }^i,t_{\epsilon }^i\sqrt{\beta }{w}_{\epsilon }^i)<\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}}.$$

(4.8)

Applying above Lemma 4.5, we get that

$${\tilde{\beta }}_{\epsilon ,\lambda ,\mu }^i\ge {\theta }_{max}+{\delta }_0/2\text{for any }0<\epsilon <{\epsilon }_0\text{ and }0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }.$$

(4.9)

For each $1\le i\le k$, by (4.8) and (4.9), we obtain that

$${\beta }_{\epsilon ,\lambda ,\mu }^i<{\tilde{\beta }}_{\epsilon ,\lambda ,\mu }^i\text{for any }0<\epsilon <{\epsilon }_0\text{ and }0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }.$$

It follows that

$${\beta }_{\epsilon ,\lambda ,\mu }^i=\underset{(u,v)\in O_{\epsilon ,\lambda ,\mu }^i\cup \partial O_{\epsilon ,\lambda ,\mu }^i}{inf}{J}_{\epsilon ,\lambda ,\mu }(u,v)\text{for any }0<\epsilon <{\epsilon }_0\text{ and }0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }.$$

Then applying Ekeland’s variational principle and using the standard computation, we have the following lemma.

Lemma 4.6 For each $1\le i\le k$, there is a ${\text{(}\mathit{\text{PS}}\text{)}}_{{\beta }_{\epsilon ,\lambda ,\mu }^i}$-sequence $\{(u_n,v_n)\}\subset O_{\epsilon ,\lambda ,\mu }^i$ in H for $J_{\epsilon ,\lambda ,\mu }$.

Proof See Cao-Zhou [8]. □

Proof of Theorem 1.2 For any $0<\epsilon <{\epsilon }_0$ and $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$, by Lemma 4.6, there is a ${(\text{PS})}_{{\beta }_{\epsilon ,\lambda ,\mu }^i}$-sequence $\{(u_n,v_n)\}\subset O_{\epsilon ,\lambda ,\mu }^i$ for $J_{\epsilon ,\lambda ,\mu }$ where $1\le i\le k$. By (4.8), we obtain that

$${\beta }_{\epsilon ,\lambda ,\mu }^i<\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}}.$$

Since $J_{\epsilon ,\lambda ,\mu }$ satisfies the (PS) _γ -condition for $\gamma \in (-\mathrm{\infty },\frac{p-2}{2p}\frac{{(S_{\alpha ,\beta })}^{p/(p-2)}}{{(f_{\mathrm{\infty }})}^{2/(p-2)}})$, then $J_{\epsilon ,\lambda ,\mu }$ has at least k critical points in ${\mathbf{M}}_{\epsilon ,\lambda ,\mu }$ for any $0<\epsilon <{\epsilon }_0$ and $0<\lambda +\mu <{\mathrm{\Lambda }}^{\ast }$. Set $u_{+}=max\{u,0\}$ and $v_{+}=max\{v,0\}$. Replace the terms ${\int }_{{\mathbb{R}}^N}f(\epsilon z)|u{|}^{\alpha }|v{|}^{\beta }dz$ and ${\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)|u{|}^q+\mu h(\epsilon z)|v{|}^q)dz$ of the functional $J_{\epsilon ,\lambda ,\mu }$ by ${\int }_{{\mathbb{R}}^N}f(\epsilon z)u_{+}^{\alpha }{v}_{+}^{\beta }dz$ and ${\int }_{{\mathbb{R}}^N}(\lambda g(\epsilon z)u_{+}^q+\mu h(\epsilon z)v_{+}^q)dz$, respectively. It follows that ($E_{\epsilon ,\lambda ,\mu }$) has k nonnegative solutions. Applying the maximum principle, ($E_{\epsilon ,\lambda ,\mu }$) admits at least k positive solutions. □