An efficient computer application of the sinc-Galerkin approximation for nonlinear boundary value problems

Abstract

A powerful technique based on the sinc-Galerkin method is presented for obtaining numerical solutions of second-order nonlinear Dirichlet-type boundary value problems (BVPs). The method is based on approximating functions and their derivatives by using the Whittaker cardinal function. Without any numerical integration, the differential equation is reduced to a system of algebraic equations via new accurate explicit approximations of the inner products; therefore, the evaluation is based on solving a matrix system. The solution is obtained by constructing the nonlinear (or linear) matrix system using Maple and the accuracy is compared with the Newton method. The main aspect of the technique presented here is that the obtained solution is valid for various boundary conditions in both linear and nonlinear equations and it is not affected by any singularities that can occur in variable coefficients or a nonlinear part of the equation. This is a powerful side of the method when being compared to other models.

1 Introduction

We present here the sinc-Galerkin approximation technique using Maple to solve systems of nonlinear BVPs such as

$$\begin{array}{r}P(x)y^{″}+Q(x)y^{\prime }+R(x)NL(y)=F(x),\\ y(a)=0,y(b)=0,\end{array}$$

(1.1)

where NL is the nonlinear part of Eq. (1.1) which can take any form of nonlinearity, and we investigate the approximate solution on some closed interval $[a,b]$ in R.

We start by casting a given linear or nonlinear BVP into a sinc-Galerkin form accurate to the order $O(N^{1/2}{e}^{-{(\pi d\alpha N)}^{1/2}})$ [1]. This discretization yields a set of linear or nonlinear algebraic equations that include all unknown coefficients. These equations are expressed in a nonlinear or linear matrix form depending on (1.1). If the equation is linear, the LU decomposition method can be used to find unknown coefficients. However, if it is not linear, the coefficients can be found by the Newton interpolation method for nonlinear equation systems by using Maple. The methodology is illustrated on nonlinear ordinary differential equations with Dirichlet-type boundaries. Once the solution is obtained, we compare its accuracy with the Newton method as a graphical and numerical simulation by using Maple.

We start with some literature on the sinc-Galerkin methods. The sinc methods were introduced in [2] and expanded in [1] by Frank Stenger. Sinc functions were first analyzed in [3] and [4]. An extensive research of sinc methods for two-point boundary value problems can be found in [5, 6]. In [7, 8] parabolic and hyperbolic problems are discussed in detail. Some kind of singular elliptic problems are solved in [9], and the symmetric sinc-Galerkin method is introduced in [10]. The sinc domain decomposition is presented in [11–14]. Also, iterative methods for symmetric sinc-Galerkin systems are given in [15–17]. Sinc methods are studied thoroughly in [18]. Applications of sinc methods can also be found in [19–21]. The article [22] summarizes the results that are obtained by sinc numerical methods of computation. In [14] a numerical solution of the Volterra integro-differential equation by means of the sinc collocation method is considered. The paper [1] illustrates the application of a sinc-Galerkin method to the approximate solution of linear and nonlinear second-order ordinary differential equations and to the approximate solution of some linear elliptic and parabolic partial differential equations in the plane. The fully sinc-Galerkin method is developed for a family of complex-valued partial differential equations with time-dependent boundary conditions [19]. In [23] some novel procedures of using sinc methods to compute the solutions of three types of medical problems are illustrated. In [24], the sinc-based algorithm is used to solve a nonlinear set of partial differential equations. A new sinc-Galerkin method is developed for approximating the solution of convection diffusion equations with mixed boundary conditions on half-infinite intervals in [25]. The work which is presented in [26] deals with the sinc-Galerkin method for solving nonlinear fourth-order differential equations with homogeneous and nonhomogeneous boundary conditions. In [27], the sinc methods are used to solve second-order ordinary differential equations with homogeneous Dirichlet-type boundary conditions. In the paper given in [28], the sinc-Galerkin method is applied to solving Troesch’s problem. The properties of the sinc procedure are utilized to reduce the computation of Troesch’s equation to nonlinear equations with unknown coefficients.

2 Sinc basis functions

Let C denote the set of all complex numbers, and for all $z\in C$ define the sine cardinal or sinc function by

$$sinc(z)=\{\begin{array}{cc}\frac{sin(\pi z)}{\pi z},\hfill & y\ne 0,\hfill \\ 1,\hfill & y=0.\hfill \end{array}$$

(2.1)

For $h>0$, the translated sinc function with evenly spaced nodes is given by

$$sinc(k,h)(z)=\{\begin{array}{cc}\frac{sin(\pi \frac{z-kh}{h})}{\pi \frac{z-kh}{h}},\hfill & z\ne kh,\hfill \\ 1,\hfill & z=kh.\hfill \end{array}$$

(2.2)

For various values of k, the sinc basis function $S(k,\pi /4)(x)$ on the whole real line, $-\mathrm{\infty }<x<\mathrm{\infty }$, is illustrated in Figure 1. For various values of h, the central function $S(0,h)(x)$ is illustrated in Figure 2.

Figure 1

The basis functions $\mathit{S}\mathbf{(}\mathit{k}\mathbf{,}\mathit{h}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{)}$ for $\mathit{k}\mathbf{=}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{0}\mathbf{,}\mathbf{1}$ with $\mathit{h}\mathbf{=}\mathit{\pi }\mathbf{/}\mathbf{4}$ .

Figure 2

Central sinc basis function $\mathit{S}\mathbf{(}\mathbf{0}\mathbf{,}\mathit{h}\mathbf{)}\mathbf{(}\mathit{x}\mathbf{)}$ for $\mathit{h}\mathbf{=}\mathit{\pi }\mathbf{/}\mathbf{2}\mathbf{,}\mathit{\pi }\mathbf{/}\mathbf{4}\mathbf{,}\mathit{\pi }\mathbf{/}\mathbf{8}$ .

If a function $f(x)$ is defined over the real line, then for $h>0$ the series

$$C(f,h)(x)=\sum _{k=-\mathrm{\infty }}^{\mathrm{\infty }}f(kh)sinc\left(\frac{x-kh}{h}\right)$$

(2.3)

is called the Whittaker cardinal expansion of f whenever this series converges. The infinite strip Ds of the complex w plane, where $d>0$, is given by

$$Ds\equiv \{w=u+iv:|v|<d\le \frac{\pi }{2}\}.$$

(2.4)

In general, approximations can be constructed for infinite, semi-infinite, and finite intervals. Define the function

$$w=\varphi (z)=ln\left(\frac{z}{1-z}\right)$$

(2.5)

which is a conformal mapping from $D_E$, the eye-shaped domain in the z-plane, onto the infinite strip $D_S$, where

$$D_E=z=\{x+iy:|arg\left(\frac{z}{1-z}\right)|<d\le \frac{\pi }{2}\}.$$

(2.6)

This is shown in Figure 3.

Figure 3

The relationship between the eye-shaped domain ${\mathit{D}}_{\mathit{E}}$ and the infinite strip ${\mathit{D}}_{\mathit{S}}$ .

For the sinc-Galerkin method, the basis functions are derived from the composite translated sinc functions:

$$S_h(z)=S(k,h)(z)=sinc\left(\frac{\varphi (z)-kh}{h}\right)$$

(2.7)

for $z\in D_E$. These are shown in Figure 4 for real values of x. The function $z={\varphi }^{-1}(w)=\frac{e^w}{1+e^w}$ is an inverse mapping of $w=\varphi (z)$. We may define the range of ${\varphi }^{-1}$ on the real line as

$$\mathrm{\Gamma }=\{{\varphi }^{-1}(u)\in D_E:-\mathrm{\infty }<u<\mathrm{\infty }\}.$$

(2.8)

For the evenly spaced nodes ${\{kh\}}_{k=-\mathrm{\infty }}^{\mathrm{\infty }}$ on the real line, the image which corresponds to these nodes is denoted by

$$x_k={\varphi }^{-1}(kh)=\frac{e^{kh}}{1+e^{kh}}.$$

(2.9)

A list of conformal mappings may be found in Table 2.1 [6].

Figure 4

Three adjacent members $\mathit{S}\mathbf{(}\mathit{k}\mathbf{,}\mathit{h}\mathbf{)}\mathbf{\circ }\mathit{\varphi }\mathbf{(}\mathit{x}\mathbf{)}$ when $\mathit{k}\mathbf{=}\mathbf{-}\mathbf{1}\mathbf{,}\mathbf{0}\mathbf{,}\mathbf{1}$ and $\mathit{h}\mathbf{=}\frac{\mathit{\pi }}{\mathbf{8}}$ of the mapped sinc basis on the interval $\mathbf{(}\mathbf{0}\mathbf{,}\mathbf{1}\mathbf{)}$ .

Definition 2.1 Let $D_E$ be a simply connected domain in the complex plane C, and let $\partial D_E$ denote the boundary of $D_E$. Let a, b be points on $\partial D_E$ and ϕ be a conformal map $D_E$ onto $D_S$ such that $\varphi (a)=-\mathrm{\infty }$ and $\varphi (b)=-\mathrm{\infty }$. If the inverse map of ϕ is denoted by φ, define

$$\mathrm{\Gamma }=\{{\varphi }^{-1}(u)\in D_E:-\mathrm{\infty }<u<\mathrm{\infty }\}$$

(2.10)

and $z_k=\phi (kh)$, $k=\mp 1,\mp 2,\dots$ .

We can use Table 1 to choose convenient conformal map according to boundary conditions.

Table 1 Conformal mappings and nodes for several subintervals of R

Definition 2.2 Let $B(D_E)$ be the class of functions F that are analytic in $D_E$ and satisfy

$${\int }_{\psi (L+u)}|F(z)|dz\to 0,\text{as }u=\mp \mathrm{\infty },$$

(2.11)

where

$$L=\{iy:|y|<d\le \frac{\pi }{2}\}$$

(2.12)

and on the boundary of $D_E$ it satisfies

$$T(F)={\int }_{\partial D_E}|F(z)dz|<\mathrm{\infty }.$$

(2.13)

The proof of following theorems can be found in [1].

Theorem 2.1 Let Γ be $(0,1)$, $F\in B(D_E)$, then for $h>0$ sufficiently small,

$${\int }_{\mathrm{\Gamma }}F(z)dz-h\sum _{j=-\mathrm{\infty }}^{\mathrm{\infty }}\frac{F(z_j)}{{\varphi }^{\prime }(z_j)}=\frac{i}{2}{\int }_{\partial D}\frac{F(z)k(\varphi ,h)(z)}{sin(\pi \varphi (z)/h)}dz\equiv I_F,$$

(2.14)

where

$$|k(\varphi ,h){|}_{z\in \partial D}=|e^{[\frac{i\pi \varphi (z)}{h}sgn(Im\varphi (z))]}{|}_{z\in \partial D}=e^{\frac{-\pi d}{h}}.$$

(2.15)

For the sinc-Galerkin method, the infinite quadrature rule must be truncated to a finite sum. The following theorem indicates the conditions under which an exponential convergence results.

Theorem 2.2 If there exist positive constants α, β and C such that

$$\left|\frac{F(x)}{{\varphi }^{\prime }(x)}\right|\le C\{\begin{array}{cc}{e}^{-\alpha |\varphi (x)|},\hfill & x\in \psi ((-\mathrm{\infty },\mathrm{\infty })),\hfill \\ e^{-\beta |\varphi (x)|},\hfill & x\in \psi ((0,\mathrm{\infty })),\hfill \end{array}$$

(2.16)

then the error bound for the quadrature rule (2.14) is given by

$$|{\int }_{\mathrm{\Gamma }}F(x)dx-h\sum _{j=-N}^N\frac{F(x_j)}{{\varphi }^{\prime }(x_j)}|\le C(\frac{e^{-\alpha Nh}}{\alpha }+\frac{e^{-\beta Nh}}{\beta })+|I_F|.$$

(2.17)

The infinite sum in (2.14) is truncated with the use of (2.16) to arrive at (2.17).

Making the selections

(2.18)

(2.19)

where $〚\cdot 〛$ is an integer part of the statement and N is the integer value which specifies the grid size, then

$${\int }_{\mathrm{\Gamma }}F(x)dx=h\sum _{j=-N}^N\frac{F(x_j)}{{\varphi }^{\prime }(x_j)}+O\left(e^{-{(\pi \alpha dN)}^{1/2}}\right).$$

(2.20)

We used Theorems 2.1 and 2.2 to approximate the integrals that arise in the formulation of the discrete systems corresponding to the second-order boundary value problem.

Theorem 2.3 Let ϕ be a conformal one-to-one map of the simply connected domain $D_E$ onto $D_S$. Then

(2.21)

(2.22)

(2.23)

3 Convergence analysis

Consider the following problem:

$$P(x)y^{″}+Q(x)y^{\prime }+R(x)NL(y)=F(x)$$

(3.1)

with Dirichlet-type boundary condition

$$y(a)=0,y(b)=0,$$

(3.2)

where P, Q, R, and F are analytic on D. We consider sinc approximation by the formula

(3.3)

(3.4)

The unknown coefficients $c_k$ in Eq. (3.3) are determined by orthogonalizing the residual with respect to the sinc basis functions. The Galerkin method enables us to determine the $c_k$ coefficients by solving the nonlinear system of equations

$$〈NL{y}_N-F,S(k,h)\circ \varphi (x)〉=0,k=-N,-N+1,\dots ,N-1,N.$$

(3.5)

Let $f_1$ and $f_2$ be analytic functions on D. The inner product in (3.5) is defined as follows:

$$〈f_1,f_2〉={\int }_{\mathrm{\Gamma }}w(x)f_1(x)f_2(x)dx,$$

(3.6)

where w is the weight function. For the second-order problems, it is convenient to take [1]

$$w(x)=\frac{1}{{\varphi }^{\prime }(x)}.$$

(3.7)

For Eq. (3.1), we use the notations (2.21)-(2.23) together with the inner product given in (3.5) [1] to get the following approximation formulas:

(3.8)

(3.9)

(3.10)

(3.11)

where $w_k=w(x_k)$ etc. The choices $h={(\pi d/\alpha N)}^{1/2}$ and $w(x)=1/{\varphi }^{\prime }(x)$ yield $O(N^{1/2}{e}^{-{(\pi d\alpha N)}^{1/2}})$ [1] accuracy for each of the approximations in (3.8)-(3.11).

Using (3.5), (3.8)-(3.11), we obtain a nonlinear system of equations for $2N+1$ numbers $c_k$.

The nonlinear system with $2N+1$ unknowns given in (3.5) can be expressed by means of matrices. Let $m=2N+1$ and let $S_m$, $c_m$, $NL(c_m)$ be column vectors defined by

$$S_m(x)=\left(\begin{array}{c}{S}_{-N}\\ S_{-N+1}\\ ⋮\\ S_N\end{array}\right),c_m=\left(\begin{array}{c}{c}_{-N}\\ c_{-N+1}\\ ⋮\\ c_N\end{array}\right),NL(c_m)=\left(\begin{array}{c}NL(c_{-N})\\ NL(c_{-N+1})\\ ⋮\\ NL(c_N)\end{array}\right).$$

(3.12)

Let $A_m(y)$ denote a diagonal matrix whose diagonal elements are $y(x_{-N}),y(x_{-N+1}),\dots ,y(x_N)$ and non-diagonal elements are zero, and also let $I_m^{(0)}$, $I_m^{(1)}$ and $I_m^{(2)}$ denote the matrices

(3.13)

(3.14)

(3.15)

With these notations, the discrete system in (3.5) takes the form:

(3.16)

Theorem 3.1 Let c, $NL(c)$ be an m-vector whose jth component is $c_j$ and $NL(c_j)$ then the system (3.16) yields the following matrix system whose dimensions are $(2N+1)\times (2N+1)$:

$${\mathrm{\Phi }}_1\cdot c+{\mathrm{\Phi }}_2\cdot NL(c)=A_m\frac{Fw}{{\varphi }^{\prime }}.$$

(3.17)

Now we have a nonlinear system with $(2N+1)$ equations in the $(2N+1)$ unknown coefficients. If we solve (3.17) with the Newton method (for nonlinear equation systems) by using Maple, we can obtain $c_j$ coefficients for the approximate sinc-Galerkin solution

$$y(x)\approx y_N(x)=\sum _{k=-N}^N{c}_{k}S(k,h)\circ \varphi (x).$$

(3.18)

4 Examples

In this section, three examples are given to illustrate the performance of the sinc-Galerkin method by solving nonlinear Dirichlet-type boundary value problems. Each of these problems have been chosen to simulate how the solutions change in different zero boundary intervals. In the following examples, the discrete sinc system defined by (3.18) is used to compute the coefficients $c_j$; $j=-N,\dots ,N$. The computations are done by the algorithm which we developed for sinc-Galerkin method by using Maple. The algorithm automatically compares the sinc-method to the Newton method. The following examples show that the sinc-Galerkin method is a very efficient and powerful tool for nonlinear Dirichlet-type boundary value problems.

Example 4.1 Consider the following nonlinear Dirichlet-type boundary value problem on the interval $[-1,1]$:

$$\begin{array}{r}\frac{d^2}{d{x}^2}y(x)+5\frac{d}{dx}y(x)+xy(x)sin(y(x))=-{\mathrm{e}}^{x^3}tan\left(x^2\right)+2x^2,\\ y(-1)=0,y(1)=0.\end{array}$$

(4.1)

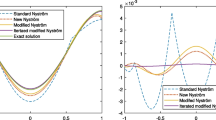
We choose the weight function according to [1], $\varphi (x)=ln(\frac{x+1}{1-x})$, $w(x)=\frac{1}{{\varphi }^{\prime }(x)}$ and by taking $d=\pi /2$, $h=\frac{2}{\sqrt{N}}$, $x_k=\frac{-1+e^{kh}}{1+e^{kh}}$ for $N=2,4,8,48$, the solutions presented in Figure 5 and Table 2.

Figure 5

The red-colored curve displays the Newton solution and the green one is an approximate solution of Eq. ( 4.1 ).

Table 2 The numerical results for the approximate solutions obtained by sinc-Galerkin in comparison with the Newton solutions of Eq. ( 4.1 ) for $\mathit{N}\mathbf{=}\mathbf{48}$

Example 4.2 Let us have the following form of nonlinear Dirichlet-type boundary value problem on the interval $[-1,1]$:

$$\begin{array}{r}{\mathrm{e}}^{-x}\frac{d^2}{d{x}^2}y(x)+x\frac{d}{dx}y(x)+x^3{\mathrm{e}}^{-y(x)}=cos(\pi x),\\ y(-1)=0,y(1)=0,\end{array}$$

(4.2)

where $\varphi (x)=ln(\frac{x+1}{1-x})$, $w(x)=\frac{1}{{\varphi }^{\prime }(x)}$ and by taking $d=\pi /2$, $h=\frac{2}{\sqrt{N}}$, $x_k=\frac{-1+e^{kh}}{1+e^{kh}}$ for $N=2,4,8,32$ we get the solutions presented in Figure 6 and Table 3.

Figure 6

The red-colored curve displays the Newton solution and the green one is an approximate solution of Eq. ( 4.2 ).

Table 3 The numerical results for the approximate solutions obtained by sinc-Galerkin in comparison with the exact solutions of Eq. ( 4.2 ) for $\mathit{N}\mathbf{=}\mathbf{32}$

Example 4.3 In this case, we take the problem to be given on the interval $[4,5]$

$$\begin{array}{r}\frac{d^2}{d{x}^2}y(x)+\frac{d}{dx}y(x)-\frac{{\mathrm{e}}^{-sin(y(x))}{(y(x))}^2}{1+y(x)}=cos\left(\pi x^2\right)x,\\ y(4)=0,y(5)=0,\end{array}$$

(4.3)

where we chose $\varphi (x)=ln(\frac{x-4}{5-x})$, $w(x)=\frac{1}{{\varphi }^{\prime }(x)}$ and by taking $d=\pi /2$, $h=\frac{2}{\sqrt{N}}$ , $x_k=\frac{4+5e^{kh}}{1+e^{kh}}$ for $N=16,24,32,48$ we get the results presented in Figure 7 and Table 4.

Figure 7

The red-colored curve displays the Newton solution and the green one is an approximate solution of Eq. ( 4.3 ).

Table 4 The numerical results for the approximate solutions obtained by sinc-Galerkin in comparison with the Newton solutions of Eq. ( 4.3 ) for $\mathit{N}\mathbf{=}\mathbf{48}$

5 Discussion

A new efficient computer application of sinc-Galerkin method has been presented for nonlinear BVPs. The main advantage of our technique compared to other methods (e.g., Newton’s method) is that the solution is independent of the singularity conditions and valid for Dirichlet-type boundary conditions. The order of accuracy used in this paper is $O(N^{1/2}{e}^{-{(\pi d\alpha N)}^{1/2}})$. We have used different N node points for all figures presented in this paper. Even though the numerical solution looks complex for even $N>30$ node points, Maple handles it very well. In the Appendix, a useful Maple program is given to explain the technique and to show how the same solution can be used for different boundary conditions. By using the same program, substituting N and other parameters (like equations, boundaries), different solutions and graphics can be produced. The total time taken on a 3.5 GHz Pentium I7 processor with 8 Core and 8 GB RAM for producing figures and numerical results is less than 20 seconds.

6 Conclusion

In this study, the sinc-Galerkin method has been employed to find the solutions of second-order nonlinear Dirichlet-type boundary value problems on some closed real interval and the method has been compared to the Newton method. Our main purpose is to find the solution of boundary value problems which arise from the singular problems for which the Newton method does not converge at singular points. The powerful side of our method is that it can easily compute solutions even if the equation has singularities. The Newton method can fail when computing some complicated forms of governing equations; on the other hand, our method can easily handle this situation. The examples show that the accuracy improves by increasing the number of sinc grid points N. The method presented here is simple and gives a numerical solution, which is valid for various boundary conditions. We have developed a very efficient algorithm to solve second-order nonlinear Dirichlet-type boundary value problems with sinc-Galerkin method in Maple Computer Algebra System. Several nonlinear BVPs have been solved by using our technique in less than 20 seconds. All computations and graphical representations have been prepared automatically by our algorithm.

Appendix: A computer application of numeric solutions for nonlinear boundary value problems (NBVPs)

We demonstrate below how to solve and simulate for a nonlinear BVP. For example, the following Maple code computes and simulates Example 4.3.

Set all parameters as default values

> restart:

For drawing approximation graphics, we must type the following line

> with(plots):

A user has to specify with (linalg) for linear algebra operations in Maple

> with(linalg):

A user can define the grid point size N for sinc-Galerkin approximation

> N:=48:

The boundary conditions are given as Eq. (4.3).

> a:=4:

> b:=5:

> Boundaries:=y(a)=0,y(b)=0;

$$Boundaries:=y(a)=0,y(b)=0.$$

P, Q and R are the variable coefficients of Eq. (1.1). In Maple for Eq. (4.3) they are defined as follows:

> P(x):=1;

$$P(x):=1.$$

> Q(x):=1;

$$Q(x):=1.$$

> R(x):=1;

$$R(x):=1.$$

F is right side of Eq. (4.3)

> F(x):=cos(Pi*x^2)*x;

$$F(x):=cos\left(\pi x^2\right)x.$$

We can write a nonlinear part of Eq. (1.1) as follows. User can define any form of nonlinearity in this section.

> NLPart:=-exp(-sin(y(x)))*y(x)^2/(1+y(x));

$$NL(y(x))=NLPart:=-\frac{{\mathrm{e}}^{-sin(y(x))}{(y(x))}^2}{1+y(x)}.$$

The main form of Eq. (1.1)

> Equation:=P(x)*diff(y(x),x$2)+Q(x)*diff(y(x),x$1)+R(x)*NLPart=F(x);

$$\frac{d^2}{d{x}^2}y(x)+\frac{d}{dx}y(x)-\frac{{\mathrm{e}}^{-sin(y(x))}{(y(x))}^2}{1+y(x)}=cos\left(\pi x^2\right)x.$$

If the user needs, the main equation can be written in the latex format

In order to compare our method with the Newton interpolation (for nonlinear ODE) method, we first solve Eq. (4.3) numerically as follows:

Prepare the plot of the Newton solution

> PlotNewtonSolution:=odeplot(NewtonSolution,a....b):

To define $I_m^{(0)}=[{\delta }_{jk}^{(0)}]$, $I_m^{(1)}=[{\delta }_{jk}^{(1)}]$ and $I_m^{(2)}=[{\delta }_{jk}^{(2)}]$ matrices given in Eqs. (3.13)-(3.15), we use piecewise functions in Maple in the following way:

> delta[0]:=unapply(piecewise(j=k,1,j<>k,0),j,k):

> delta[1]:=unapply(piecewise(j=k,0,j<>k,((-1)^(k-j))/(k-j)),j,k):

> delta[2]:=unapply(piecewise(j=k,(-Pi^2)/3,j<>k,-2*(-1)^(k-j)/(k-j)^2),j,k):

The parameters for sinc-approximation given [1]

> d:=Pi/2:

> h:=2/sqrt(N):

The evenly spaced nodes given (2.9) and Table 1 are defined as follows:

> xk:=unapply((a+b*exp(k*h))/(1+exp(k*h)),k);

$$x_k:=k\mapsto \frac{4+5{\mathrm{e}}^{kh}}{1+{\mathrm{e}}^{kh}}.$$

The conformal map in Table 1 for sinc-Galerkin method and its derivatives is computed as follows:

> phi:=unapply(log((x-a)/(b-x)),x);

$$\varphi (x):=x\mapsto ln\left(\frac{x-4}{5-x}\right).$$

> Dphi:=unapply(simplify(diff(phi(x),x)),x):

> D2phi:=unapply(simplify(diff(phi(x),x$2)),x):

The weight function and its derivatives are computed for using an inner product to discretization Eq. (4.3)

> w:=unapply(1/Dphi(x),x):

> Dw:=unapply(simplify(diff(w(x),x$1)),x):

> D2w:=unapply(simplify(diff(w(x),x$2)),x):

By using sinc-discretization in (3.16), the matrix system with $(2N+1)\times (2N+1)$ dimensions defined in (3.17) is obtained by the following iteration:

If we want to obtain solutions of linear BVPs, we can use the following lines. They can reduce time complexity. Here, the linear solution is given as a comment (“#”).

> #for Linear system

> #vars:=seq(c[i],i=-N..N):

> #A,b:=LinearAlgebra[GenerateMatrix](evalf(MatrixSystem),[vars]):

> #c:=linsolve(A,b);

In this paper, we want to solve nonlinear problems. Then we use fsolve function given by Maple to find unknown $c_j$ coefficients (3.17)-(3.18) from nonlinear matrix systems. This function can solve any nonlinear systems by using the Newton method (for nonlinear equation systems).

> c:=fsolve(evalf(MatrixSystem)):

Finally, we have unknown $c_j$ coefficients for the approximate sinc-Galerkin solution (3.18)

We define plot of Eq. (4.3) obtained by the sinc-Galerkin solution

> Sinc-GalerkinPlot:=plot({ApproximateSol(x)},x=a..b,color=green,thickness=1):

Simulation: Figure 5, Figure 6, and Figure 7 are obtained as

Enter the number of digits here

> Digits := 15:

Tables 2, 3, and 4 are obtained by the following code: