Abstract
In this paper, we investigate the dynamics of a discrete-time predator-prey system of Holling-III type in the closed first quadrant . Firstly, the existence and stability of fixed points of the system is discussed. Secondly, it is shown that the system undergoes a flip bifurcation and a Neimark-Sacker bifurcation in the interior of by using bifurcation theory. Finally, numerical simulations including bifurcation diagrams, phase portraits, and maximum Lyapunov exponents are presented not only to explain our results with the theoretical analysis, but also to exhibit the complex dynamical behaviors, such as the period-6, -7, -9, -15, -16, -22, -23, -32, -35 orbits, a cascade of period-doubling bifurcations in period-2, -4, -8, -16 orbits, quasi-periodic orbits, and chaotic sets.
MSC: 37G05, 37G35, 39A28, 39A33.
Similar content being viewed by others
1 Introduction
The Lotka-Volterra prey-predator model has become one of the fundamental population models since the theoretical works going back to Lotka (1925) [1] and Volterra (1926) [2] in the last century. Holling (1965) [3] introduced three kinds of functional responses for different species to model the phenomena of predation. Qualitative analyses of more realistic prey-predator models can be found in [4–11]. Recently, there is a growing evidence showing that the dynamics of the discrete-time prey-predator models can present a much richer set of patterns than those observed in continuous-time models [12–23].
In this paper, we consider the predator-prey system of Holling-III type that is given in [24] as follows:
where and denote prey and predator densities, respectively; r, K, α, β, d, γ are positive constants that stand for prey intrinsic growth rate, carrying capacity, conversion rate, half capturing saturation, the death rate of the predator, the harvesting rate of the predator, respectively. The predator-prey system (1) assumes that the prey grows logistically with intrinsic growth rate r and carrying capacity K in the absence of predation. The predator consumes the prey according to the Holling type-III functional response and contributes to its growth with rate . In [24], Wang et al. presented a bifurcation analysis by choosing the death rate and the harvesting rate of the predator as the bifurcation parameters and proved that system (1) can undergo the Bogdanov-Takens bifurcation.
Applying the forward Euler scheme to system (1), we obtain the discrete-time predator-prey system of Holling-III type as follows:
where δ is the step size. In this paper, we investigate this version as a discrete-time dynamical system in the interior of the first quadrant by using the normal form theory of the discrete system (see Section 4 in [25]; see also [26–28]), and we prove that this discrete model possesses the flip bifurcation and the Neimark-Sacker bifurcation.
This paper is organized as follows. In Section 2, we discuss the existence and stability of fixed points for system (2) in the closed first quadrant . In Section 3, we show that there exist some values of the parameters such that (2) undergoes the flip bifurcation and the Neimark-Sacker bifurcation in the interior of . In Section 4, we present the numerical simulations, which not only illustrate our results with the theoretical analysis, but which also exhibit the complex dynamical behaviors such as the period-6, -7, -9, -15, -16, -22, -23, -32, -35 orbits, a cascade of period-doubling bifurcations in period-2, -4, -8, -16 orbits, quasi-periodic orbits, and chaotic sets. The Lyapunov exponents are computed numerically to further confirm the dynamical behaviors. A brief discussion is given in Section 5.
2 The existence and stability of fixed points
It is clear that the fixed points of (2) satisfy the following equations:
Next, we consider the existence of the positive fixed points of system (2). Suppose that is a positive fixed point of map (2). Then and are positive solutions of the following equations:
From Eq. (4), we can see that is the root in the interval of the following equation:
Let
Using the Cardano formula (see [[29], p.106]), we have the following results.
Lemma 2.1
-
(i)
If , then system (2) has one unique positive fixed point , where .
-
(ii)
If and , then system (2) has two different fixed points, and , where is a real root of double multiplicity and is another real root of (5), respectively. Here and .
-
(iii)
If , then system (2) has three different fixed points, , and , where (), and .
Now we study the stability of the fixed points for (2). The Jacobian matrix J of system (2) evaluated at the fixed point is given by
where
and the characteristic equation of the Jacobian matrix J can be written as
where
Using the Schur-Cohn criterion [30], we can show the stability of the fixed points as follows.
Lemma 2.2 The positive fixed point of system (2) is stable if one of the following conditions holds:
-
(1)
and ;
-
(2)
and ,
where
3 Flip bifurcation and Neimark-Sacker bifurcation
In this section, we choose the parameter δ as a bifurcation parameter to study the flip bifurcation and the Neimark-Sacker bifurcation of by using bifurcation theory in (see Section 4 in [25]; see also [26–28]).
We first discuss the flip bifurcation of (2) at . Suppose that , i.e.,
If
or
then the eigenvalues of the positive fixed point are , .
The condition leads to
Let , , , we transform the fixed point of system (2) into the origin, then system (2) becomes
where
and . It follows that
and .
We know that A has the simple eigenvalue , and the corresponding eigenspace is one-dimensional and spanned by an eigenvector such that . Let be the adjoint eigenvector, that is, . By direct calculation we obtain
In order to normalize p with respect to q, we denote
where
It is easy to see , where means the standard scalar product in : .
Following the algorithms given in [25], the sign of the critical normal form coefficient , which determines the direction of the flip bifurcation, is given by the following formula:
From the above analysis and the theorem in [25–28], we have the following result.
Theorem 3.1 Suppose that is the positive fixed point. If the conditions (9), (10) hold and , then system (2) undergoes a flip bifurcation at the fixed point when the parameter δ varies in a small neighborhood of . Moreover, if (respectively, ), then the period-2 orbits that bifurcate from are stable (respectively, unstable).
In Section 4 we will give some values of the parameters such that , thus the flip bifurcation occurs as δ varies (see Figure 1).
We next discuss the existence of a Neimark-Sacker bifurcation by using the Neimark-Sacker theorem in [25–28].
The eigenvalues of the characteristic (8) are
where
The eigenvalues are complex conjugate for , which leads to , i.e.,
Let
we have .
For , the eigenvalues of the matrix associated with the linearization of the map (11) at are conjugate with modulus 1, and they are written as
and , .
In addition, if , which leads to
then we have for .
Let be an eigenvector of corresponding to the eigenvalue such that
Also let be an eigenvector of the transposed matrix corresponding to its eigenvalue, that is, ,
By direct calculation we obtain
In order to normalize p with respect to q, we denote
where
It is easy to see that , where means the standard scalar product in : .
Any vector can be represented for δ near as
for some complex z. Obviously, . Thus, system (11) can be transformed for δ near into the following form:
where can be written as ( is a smooth function with ) and g is a complex-valued smooth function of z, , and δ, whose Taylor expression with respect to contains quadratic and higher-order terms:
with , . By (13) and the formulas
we can calculate the coefficient via
where .
For the above argument and the theorem in [25–28], we have the following result.
Theorem 3.2 Suppose that is the positive fixed point. If (respectively, >0) the Neimark-Sacker bifurcation of system (2) at is supercritical (respectively, subcritical) and there exists a unique closed invariant curve bifurcation from for , which is asymptotically stable (respectively, unstable).
In Section 4 we will choose some values of the parameters so as to show the process of a Neimark-Sacker bifurcation for system (2) in Figure 2 by numerical simulation.
4 Numerical simulations
In this section, we present the bifurcation diagrams, phase portraits, and maximum Lyapunov exponents for system (2) to explain the above theoretical analysis and show the new interesting complex dynamical behaviors by using numerical simulations. The bifurcation parameters are considered in the following three cases:
-
(1)
Varying δ in the range , and fixing , , , , , .
-
(2)
Varying δ in the range , and fixing , , , , , .
-
(3)
Varying r in the range , and fixing , , , , , .
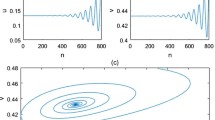
Case (1). The bifurcation diagrams of system (2) in the and plane for , , , , , are given in Figure 1(a) and (b), respectively. From Figure 1(a) and (b), we can see that the flip bifurcation emerges from the fixed point at with . We also observe that there is a cascade of period-doubling bifurcations in period-2, -4, -8, -16 orbits. The maximum Lyapunov exponents corresponding to Figure 1(a) and (b) are calculated and plotted in Figure 1(c), confirming the existence of the chaotic regions and period orbits in the parametric space.
Case (2). The bifurcation diagrams of system (2) in the and plane for , , , , , are given in Figure 2(a) and (b), respectively. After calculation for the positive fixed point of system (2), the Neimark-Sacker bifurcation emerges from the fixed point at , and its eigenvalues are . For , we have , , , , , , . It shows the correctness of Theorem 3.2.
From Figure 2(a) and (b), we observe that the fixed point of system (2) is stable for , loses its stability at , and an invariant circle appears when the parameter δ exceeds 1.
The maximum Lyapunov exponents corresponding to Figure 2(a) and (b) are calculated and plotted in Figure 2(c), confirming the existence of the chaotic regions and period orbits in the parametric space. Figure 3(a) and (b) show the local amplification corresponding to Figure 2(a) for and , respectively. From Figure 3(c) and (d), we observe that some Lyapunov exponents are bigger than 0, some are smaller than 0, so there exist stable fixed points or stable period windows in the chaotic region. In general the positive Lyapunov exponent is considered to be one of the characteristics implying the existence of chaos [31, 32].
The phase portraits which are associated with Figure 2(a) and (b) are revealed in Figure 4, which clearly depicts the process of how a smooth invariant circle bifurcates from the stable fixed point . When δ exceeds 1 there appears a circle curve enclosing the fixed point , and its radius becomes larger with respect to the growth of δ. When δ increases at certain values, for example, at , the circle disappears and a period-7 orbit appears. From Figure 4, we observe that there are period-7, -9, -15, -22 orbits, quasi-periodic orbits, and attracting chaotic sets.
Phase portraits for various values of δ corresponding to Figure 1 (a).
Case (3). The bifurcation diagrams of system (2) in the and plane for , , , , , are given in Figure 5(a) and (b), respectively. After calculation for the positive fixed point of system (2), the Neimark-Sacker bifurcation emerges from the fixed point at . From Figure 5(a) and (b), we observe that the fixed point of map (2) is stable for , loses its stability at , and an invariant circle appears when the parameter r exceeds 2.
The maximum Lyapunov exponents corresponding to Figure 5(a) and (b) are calculated and plotted in Figure 5(c). For , some Lyapunov exponents are bigger than 0, some are smaller than 0, which implies that there exist stable fixed points or stable period windows in the chaotic region.
The phase portraits which are associated with Figure 5(a) and (b) are revealed in Figure 6. From Figure 6, we observe that there are period-6, -16, -23, -32, -35 orbits, quasi-periodic orbits, and attracting chaotic sets.
Phase portraits for various values of r corresponding to Figure 5 (a) and (b).
5 Conclusion
In this paper, we investigate the complex behaviors of the discrete-time predator-prey system of Holling-III type obtained by the Euler method in the closed first quadrant , and we show that system (2) can undergo a flip bifurcation and a Neimark-Sacker bifurcation in the interior of . Moreover, system (2) displays very interesting dynamical behaviors, including period-6, -7, -9, -15, -16, -22, -23, -32, -35 orbits, a cascade of period-doubling bifurcations in period-2, -4, -8, -16 orbits, an invariant cycle, quasi-periodic orbits, and chaotic sets. These results reveal far richer dynamics of the discrete-time models compared to the continuous-time models.
References
Lotka AJ: Elements of Mathematical Biology. Dover, New York; 1956.
Volterra V V. In Opere Matematiche: Memorie e Note. Acc. Naz. dei Lincei, Roma; 1962.
Holling CS: The functional response of predator to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 1965, 45: 1–60.
Collings JB: Bifurcation and stability analysis of a temperature-dependent mite predator-prey interaction model incorporating a prey refuge. Bull. Math. Biol. 1995, 57: 63–76. 10.1007/BF02458316
Collings JB, Wollking DJ: A global analysis of a temperature-dependent model system for a mite predator-prey interaction. SIAM J. Appl. Math. 1990, 50: 1348–1372. 10.1137/0150081
Freedman HI, Mathsen RM: Persistence in predator-prey systems with ratio-dependent predator influence. Bull. Math. Biol. 1993, 55: 817–827. 10.1007/BF02460674
Hastings A: Multiple limit cycles in predator-prey models. J. Math. Biol. 1981, 11: 51–63. 10.1007/BF00275824
Lindström T: Qualitative analysis of a predator-prey systems with limit cycles. J. Math. Biol. 1993, 31: 541–561. 10.1007/BF00161198
Murray JD: Mathematical Biology: I. An Introduction. 3rd edition. Springer, New York; 2002.
Ruan S, Xiao D: Global analysis in a predator-prey system with nonmonotonic functional response. SIAM J. Appl. Math. 2001, 61: 1445–1472. 10.1137/S0036139999361896
Sáez E, González-Olivares E: Dynamics of a predator-prey model. SIAM J. Appl. Math. 1999, 59: 1867–1878. 10.1137/S0036139997318457
Agiza HN, Elabbasy EM, El-Metwally H, Elsadany AA: Chaotic dynamics of a discrete prey-predator model with Holling type II. Nonlinear Anal., Real World Appl. 2009, 10: 116–129. 10.1016/j.nonrwa.2007.08.029
Beddington JR, Free CA, Lawton JH: Dynamic complexity in predator-prey models framed in difference equations. Nature 1975, 255: 58–60. 10.1038/255058a0
Danca M, Codreanu S, Bako B: Detailed analysis of a nonlinear prey-predator model. J. Biol. Phys. 1997, 23: 11–20. 10.1023/A:1004918920121
Hadeler KP, Gerstmann I: The discrete Rosenzweig model. Math. Biosci. 1990, 98: 49–72. 10.1016/0025-5564(90)90011-M
He ZM, Lai X: Bifurcations and chaotic behavior of a discrete-time predator-prey system. Nonlinear Anal., Real World Appl. 2011, 12: 403–417. 10.1016/j.nonrwa.2010.06.026
Jing ZJ, Yang J: Bifurcation and chaos in discrete-time predator-prey system. Chaos Solitons Fractals 2006, 27: 259–277. 10.1016/j.chaos.2005.03.040
Jing ZJ, Jia ZY, Wang RQ: Chaos behavior in the discrete BVP oscillator. Int. J. Bifurc. Chaos 2002, 12(3):619–627. 10.1142/S0218127402004577
Johnson P, Burke M: An investigation of the global properties of a two-dimensional competing species model. Discrete Contin. Dyn. Syst., Ser. B 2008, 10: 109–128.
Liu X, Xiao D: Complex dynamics behaviors of a discrete-time predator-prey system. Chaos Solitons Fractals 2007, 32: 80–94. 10.1016/j.chaos.2005.10.081
Lopez-Ruiz R, Fournier-Prunaret R: Indirect Allee effect, bistability and chaotic oscillations in a predator-prey discrete model of logistic type. Chaos Solitons Fractals 2005, 24: 85–101. 10.1016/j.chaos.2004.07.018
Summers D, Cranford JG, Healey BP: Chaos in periodically forced discrete-time ecosystem models. Chaos Solitons Fractals 2000, 11: 2331–2342. 10.1016/S0960-0779(99)00154-X
Xiao YN, Cheng DZ, Tang SY: Dynamic complexities in predator-prey ecosystem models with age-structure for predator. Chaos Solitons Fractals 2002, 14: 1403–1411. 10.1016/S0960-0779(02)00061-9
Wang LL, Fan YH, Li WT: Multiple bifurcations in a predator-prey system with monotonic functional response. Appl. Math. Comput. 2006, 172: 1103–1120. 10.1016/j.amc.2005.03.010
Kuznetsov YK: Elements of Applied Bifurcation Theory. 3rd edition. Springer, New York; 1998.
Guckenheimer J, Holmes P: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York; 1983.
Robinson C: Dynamical Systems, Stability, Symbolic Dynamics and Chaos. 2nd edition. CRC Press, Boca Raton; 1999.
Wiggins S: Introduction to Applied Nonlinear Dynamical Systems and Chaos. 2nd edition. Springer, New York; 2003.
Polyanin AD, Chernoutsan AI: A Concise Handbook of Mathematics, Physics, and Engineering Science. CRC Press, New York; 2011.
Elaydi SN: An Introduction to Difference Equations. 3rd edition. Springer, New York; 2005.
Alligood KT, Sauer TD, Yorke JA: Chaos - An Introduction to Dynamical Systems. Springer, New York; 1996.
Ott E: Chaos in Dynamical Systems. 2nd edition. Cambridge University Press, Cambridge; 2002.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, Z., Li, B. Complex dynamic behavior of a discrete-time predator-prey system of Holling-III type. Adv Differ Equ 2014, 180 (2014). https://doi.org/10.1186/1687-1847-2014-180
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2014-180