Abstract
In this paper, we investigate the dynamics of a discrete-time predator-prey system with simplified Monod-Haldane functional response. The existence and local stability of positive fixed point of the discrete dynamical system is analyzed algebraically. It is shown that the system undergoes a flip bifurcation and a Neimark-Sacker bifurcation in the interior of \(\mathbb {R}^{2}_{+}\) by using bifurcation theory. Numerical simulation results not only show the consistence with the theoretical analysis but also display new and interesting dynamical behaviors, including phase portraits, period-11 orbits, attracting invariant circle, cascade of period-doubling bifurcation from period-11 leading to chaos, quasi-periodic orbits, and the sudden disappearance of the chaotic dynamics and attracting chaotic set. The Lyapunov exponents are numerically computed to characterize the complexity of the dynamical behaviors.
Similar content being viewed by others
1 Introduction
It is well known the Lotka-Voltera predator-prey model is one of the fundamental population models; a predator-prey interaction has been described first by two pioneers Lotka [1] and Voltera [2] in two independent works. After them, more realistic predator-prey model were introduced by Holling suggesting three types of functional responses for different species to model the phenomena of predation [3]. Qualitative analyses of predator-prey models describe by set of differential equations were studied by many authors [4–8]. Another possible way to understand a predator-prey interaction is by using discrete-time models. In recent years, many authors [4, 5, 9–17] have suggested that discrete-time models governed by difference equations are more appropriate than the continuous ones, especially when the populations have non-overlapping generations. These models are more reasonable, showing that the dynamics of the discrete-time predator-prey models can present a much richer set of patterns than those observed in continuous-time models and lead to unpredictable dynamic behaviors from a biological point of view. However, there are few articles discussing the dynamical behaviors of predator-prey models, which include bifurcations and chaos phenomena for the discrete-time models. Hence, the discrete version has been an important subject of study in diverse phenomenology from the mathematical point of view. The authors [13, 15–17] obtained the flip bifurcation and Hopf bifurcation by using the center manifold theorem and bifurcation theory, while in [9–11], the authors only showed the flip bifurcation and Hopf bifurcation by using numerical simulations. But in [18–21], the authors showed that the system undergoes a flip bifurcation and/or a Neimark-Sacker (NS) bifurcation by using bifurcation theory. Many important and interesting research works on bifurcation theory can be found in [19, 22] and the references cited therein.
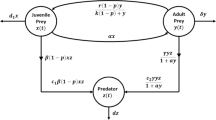
In this paper, we consider a generalized Gauss-type predator-prey interaction [23] when the prey exhibits group defense that can be modeled by the following system of ordinary differential equations:
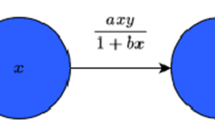
where x and y are functions of time representing population densities of prey and predator, respectively; \(K>0\) is the carrying capacity of the prey and \(d>0\) is the death rate of the predator. The function \(g(x,K)\) represents the specific growth rate of the prey in the absence of predator. A prototype is the logistic growth, \(g(x,K)=r(1-\frac{x}{K})\), with intrinsic growth rate r. The function \(p(x)\) denotes the predator response function and we assume it is of the simplified Monod-Haldane form, \(p(x)=\frac{mx}{\beta+x^{2}}\). The rate of conversion of prey to predator is described by \(q(x)\). In Gauss’ model, \(q(x)=cp(x)\) for some positive constant c.
Without loss of generality, by scaling the parameters, we first write system (1) in the specific form [7]
where r, K, d, α, and β are positive parameters. Applying the forward Euler scheme to system (2), we obtain the discrete-time predator–prey system as follows:
where δ is the step size. In this paper, we only restrict our attention to investigate this version as a discrete-time dynamical system in the closed first quadrant \(\mathbb {R}^{2}_{+}\) by using bifurcation theory and center manifold theory (see Section 4, [24]). We rigorously prove that this discrete model possesses the flip bifurcation and the NS bifurcation, respectively. Meanwhile, numerical simulations are presented not only to illustrate our results with the theoretical analysis, but also to exhibit the complex dynamical behaviors such as the cascade periodic-doubling bifurcation in periods 11-orbits, quasi-periodic orbits and chaotic sets. These results reveal a far richer dynamics of the discrete model compared with the continuous model. In particular; we observe that when the prey shows chaotic dynamics, the predator can tend to extinction or to a stable equilibrium. The computations of the Lyapunov exponents confirm the dynamical behaviors. The analysis and results in this paper are interesting in mathematics and biology.
This paper is organized as follows. In Section 2, we discuss the existence and local stability of positive fixed point for system (3) in \(\mathbb {R}^{2}_{+}\). In Section 3, we show that there exist some values of the parameters such that (3) undergoes the flip bifurcation and the NS bifurcation in the interior of \(\mathbb {R}^{2}_{+}\). In Section 4, we present the numerical simulations including the bifurcation diagrams, the phase portraits at neighborhood of critical values and the maximum Lyapunov exponents corresponding to the bifurcation diagrams. Finally a short discussion is given in Section 5.
2 Existence and stability of fixed points
In this section, we first determine the existence of the fixed points of system (3), then investigate their stability by the eigenvalues for the Jacobian matrix of (3) at the fixed point.
It is clear that the fixed points of (3) satisfy the following equations:
The fixed point of the greatest interest would be a fixed point interior to the first quadrant, so we seek conditions for such a fixed point to exist. From system (4), we can see that if there is an interior fixed point, then the equation
has positive roots, say \(x^{*}\). Therefore, the first condition is that
To determine the y value of the fixed point, we merely solve
for y at the root \(x^{*}\) and get
To ensure that \(y^{*}>0\), however, we must make a second assumption:
By a simple algebraic computation, it is straightforward to obtain the following results:
Lemma 2.1
(i) For all permissible parameter values, system (3) has two fixed points, \(E_{0}(0,0)\) and \(E_{1}(K,0)\);
(ii) if \(\tilde{\Delta}=0\) and \(\frac{\alpha}{2d}< K\), then system (3) has a unique positive fixed point, \(E_{2}(x_{0}^{*}, y_{0}^{*})\), where
(iii) if \(\tilde{\Delta}>0\), then system (3) has at most two positive fixed points, \(E_{2}(x_{1}^{*}, y_{1}^{*})\), \(E_{2}(x_{2}^{*}, y_{2}^{*})\), where
More precisely, there are three possibilities.
-
(iii.a)
When \(K\le x_{1}^{*}\), then system (3) has no positive fixed points;
-
(iii.b)
when \(x_{1}^{*}< K< x_{2}^{*}\), then system (3) has one positive fixed points \(E_{2}(x_{1}^{*}, y_{1}^{*})\);
-
(iii.c)
when \(x_{1}^{*}< x_{2}^{*}< K\), then system (3) has two positive fixed points \(E_{2}(x_{1}^{*}, y_{1}^{*})\) and \(E_{2}(x_{2}^{*}, y_{2}^{*})\).
Biologically, the condition \(\tilde{\Delta}>0\) is necessary for the persistence of the ecosystem. If \(\tilde{\Delta}<0\), the predator species goes extinct. Mathematically, \(\tilde{\Delta}=0\) is a saddle-node bifurcation surface. When the parameters pass from one side of the surface to the other side, the number of fixed points of the system changes. Figure 1 shows the distribution of the fixed points in the space \((\alpha, \beta, d)\). There is at most two positive fixed point in the region (I), and on the surface \(\mathcal {C}\) and no positive fixed point in the region (II) for any choice of K such that \(x^{*}< K\), where surface \(\mathcal{C}= \{(\alpha, \beta , d): \alpha^{2}-4d^{2}\beta=0 \}\).
Distribution of fixed point of map ( 3 ).
Now we investigate the stability of the fixed points for (3). The Jacobian matrix of system (3) at a fixed point \(\bar {E}(\bar{x}, \bar{y})\) is
where
The characteristic equation associated with (5) is
where λ is the eigenvalue of (5) and
Hence system (3) is a dissipative dynamical system if and only if
a conservative dynamical system if and only if
and an non-dissipating dynamical system otherwise.
In the following we deduce the local dynamics of the positive fixed point \(E_{2}(x^{*}, y^{*})\) only (we left the others). Note that the local stability of the fixed point \((x^{*}, y^{*})\) is determined by the modules of eigenvalues of the characteristic equation at the fixed point.
The Jacobian matrix due to the linearization of (3) evaluated at \(E_{2}\) is given by
and the corresponding characteristic equation of (9) can be written as
where \(a_{1}\), \(b_{1}\), \(a_{2}\), \(b_{2}\) in (9) and trJ, detJ in (10) are determined by (6) and (8) with x̄ and ȳ replaced by \(x^{*} \) and \(y^{*}\), respectively. Therefore, the eigenvalues of (10) are
where
For \(\Delta<0\), i.e., \((\operatorname{tr}J)^{2}-4 \operatorname{det}J<0\), the eigenvalues \(\lambda_{1,2}\) given by (11) are complex, and these can be written as
where
Using Jury’s criterion [25], we have necessary and sufficient condition for local stability of the fixed point \(E_{2}\), which are given in the following proposition.
Proposition 2.2
Let \(E_{2}\) be a positive fixed point of (3). Then
-
(i)
it is a sink if one of the following conditions holds:
-
(i.1)
\(\Delta\geq0\) and \(\delta<\frac {-(a_{1}+b_{2})-\sqrt{\Delta}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(i.2)
\(\Delta<0\) and \(\delta<-\frac{a_{1}+b_{2}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(i.1)
-
(ii)
it is a source if one of the following conditions holds:
-
(ii.1)
\(\Delta\geq0\) and \(\delta>\frac {-(a_{1}+b_{2})+\sqrt{\Delta}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(ii.2)
\(\Delta<0\) and \(\delta>-\frac{a_{1}+b_{2}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(ii.1)
-
(iii)
it is non-hyperbolic if one of the following conditions holds:
-
(iii.1)
\(\Delta\geq0\) and \(\delta=\frac {-(a_{1}+b_{2}) \pm\sqrt{\Delta}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(iii.2)
\(\Delta<0\) and \(\delta=-\frac{a_{1}+b_{2}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(iii.1)
-
(iv)
it is a saddle for the other values of parameters except those values in (i)-(iii).
Following Jury’s criterion, we can see that one of the eigenvalues of \(J(E_{2})\) is −1 and the others are neither 1 nor −1 if the term (iii.1) of Proposition 2.2 holds. Therefore, there may be a flip bifurcation of the fixed point \(E_{2}\) if δ varies in the small neighborhood of \(FB1_{E_{2}}\) or \(FB2_{E_{2}}\) where
or
Also when the term (iii.2) of Proposition 2.2 holds, we see that the eigenvalues of \(J(E_{2})\) are a pair of conjugate complex numbers with module one. The conditions in the term (iii.2) of Proposition 2.2 can be written as the following set:
and if the parameter δ varies in the small neighborhood of \(NSB_{E_{2}}\), then the NS bifurcation will appear.
The next result is obtained from the above analysis to study the bifurcation of system (3).
Proposition 2.3
The positive fixed point \(E_{2}\) loses its stability:
-
(i)
via a flip point when \(\Delta\geq0\) and \(\delta=\frac{-(a_{1}+b_{2}) \pm\sqrt{\Delta}}{a_{1} b_{2}+a_{2} b_{1}}\);
-
(ii)
via a Neimark-Sacker point when \(\Delta<0\) and \(\delta=-\frac{a_{1}+b_{2}}{a_{1} b_{2}+a_{2} b_{1}}\).
3 Bifurcation analysis
In this section, we choose the parameter δ as a bifurcation parameter to study the flip bifurcation and the Neimark-Sacker bifurcation of \(E_{2}\), respectively, by using bifurcation theory in (see Section 4 in [24]; see also [26–28]).
We first discuss the flip bifurcation of (3) at \(E_{2}\). Suppose that \(\Delta>0\), i.e.,
If
or
then the eigenvalues of (9) given by (11) are
The condition \(|\lambda_{2}(\delta_{F})|\ne1\) leads to
Let \(\tilde{x}=x-x^{*}\), \(\tilde{y}=y-y^{*}\), and \(A(\delta)=J(x^{*}, y^{*})\), we transform the fixed point \((x^{*}, y^{*})\) of system (3) into the origin, then system (3) becomes
where
and \(X=(\tilde{x}, \tilde{y})^{T}\). It follows that
and \(\delta=\delta_{F}\).
Therefore, \(B(x, y) = \bigl({\scriptsize\begin{matrix}{} B_{1}(x, y) \cr B_{2}(x, y) \end{matrix}} \bigr) \) and \(C(x, y, u) = \bigl({\scriptsize\begin{matrix}{} C_{1}(x, y, u) \cr C_{2}(x, y, u)\end{matrix}} \bigr) \) are symmetric multilinear vector functions of \(x, y, u \in \mathbb {R}^{2}\).
We know that A has simple eigenvalue \(\lambda_{1}(\delta_{F})=-1\), and the corresponding eigenspace \(E^{c}\) is one-dimensional and spanned by an eigenvector \(q \in \mathbb {R}^{2}\) such that \(A(\delta_{F})q=-q\). Let \(p \in \mathbb {R}^{2}\) be the adjoint eigenvector, that is, \(A^{T}(\delta_{F})p=-p\). By direct calculation we obtain
In order to normalize p with respect to q, we denote
where
It is easy to see \(\langle p, q \rangle=1\), where \(\langle\cdot , \cdot \rangle\) means the standard scalar product in \(\mathbb {R}^{2}: \langle p, q \rangle=p_{1} q_{2} + p_{2} q_{1}\).
Following the algorithms given in [24], the sign of the critical normal form coefficient \(c(\delta_{F})\), which determines the direction of the flip bifurcation, is given by the following formula:
From the above analysis and the theorem in [24, 26–28], we have the following result.
Theorem 3.1
Suppose that \(E_{2}(x^{*}, y^{*})\) is the positive fixed point. If the conditions (13) and (14) hold and \(c(\delta_{F})\ne0\), then system (3) undergoes a flip bifurcation at the fixed point \(E_{2}(x^{*}, y^{*})\) when the parameter δ varies in a small neighborhood of \(\delta_{F}\). Moreover, if \(c(\delta_{F})>0\) (resp., \(c(\delta_{F})<0\)), then the period-2 orbits that bifurcate from \(E_{2}(x^{*}, y^{*})\) are stable (resp., unstable).
We next discuss the existence of a Neimark-Sacker bifurcation by using the NS theorem in [24, 26–28].
It is clear that, for the complex eigenvalues given by (12), the condition is \((\operatorname{tr}J)^{2}-4 \operatorname{det}J<0\), which leads to \(\Delta<0\), i.e.,
Let
then we have \(\operatorname{det}J(\delta_{NS})=1\).
For \(\delta= \delta_{NS}\), the eigenvalues of the matrix associated with the linearization of the map (15) at \((\tilde{x}, \tilde {y}) = (0, 0)\) are conjugate with modulus 1, and they are written as
and
In addition, if \(\operatorname{tr}J(\delta_{NS}) \ne0, -1\),
which obviously satisfies
Let \(q \in \mathbb {C}^{2}\) be an eigenvector of \(A(\delta_{NS})\) corresponding to the eigenvalue \(\lambda(\delta_{NS})\) such that
Also let \(p \in \mathbb {C}^{2}\) be an eigenvector of the transposed matrix \(A^{T}(\delta_{NS})\) corresponding to its eigenvalue, that is, \(\bar {\lambda}(\delta_{NS})\),
By direct calculation we obtain
In order to normalize p with respect to q, we denote
where
It is easy to see \(\langle p, q \rangle=1\), where \(\langle\cdot , \cdot \rangle\) means the standard scalar product in \(\mathbb {C}^{2}: \langle p, q \rangle=\bar{p_{1}} q_{2} + \bar{p_{2}} q_{1}\).
Any vector \(X \in \mathbb {R}^{2}\) can be represented for δ near \(\delta _{NS}\) as \(X = zq + \bar{z}\bar{q}\), for some complex z. Indeed, the explicit formula to determine z is \(z = \langle p, X \rangle\). Thus, system (15) can be transformed for sufficiently small \(|\delta |\) (near \(\delta_{NS}\)) into the following form:
where \(\lambda(\delta)\) can be written as \(\lambda(\delta) = (1+\varphi (\delta)) e^{i \theta(\delta)}\) (where \(\varphi(\delta)\) is a smooth function with \(\varphi(\delta_{NS}) = 0\)) and g is a complex-valued smooth function of z, z̄, and δ, whose Taylor expression with respect to \((z, \bar{z})\) contains quadratic and higher-order terms:
By symmetric multilinear vector functions, the Taylor coefficients \(g_{kl}\) can be expressed by the formulas
and the coefficient \(a(\delta_{NS})\), which determines the direction of the appearance of the invariant curve in a generic system exhibiting the NS bifurcation, can be computed via
where \(e^{i \theta(\delta_{NS})} = \lambda(\delta_{NS})\).
Clearly, (20) and (21) demonstrate that the transversal condition and the nondegenerate condition of system (3) are satisfied. So, summarizing the above discussions, we obtain the following conclusion.
Theorem 3.2
Suppose that \(E_{2}(x^{*}, y^{*})\) is the positive fixed point. If \(a(\delta _{NS}) \ne0\), then system (3) undergoes a Neimark-Sacker bifurcation at the fixed point \(E_{2}\) when the parameter δ varies in the small neighborhood of \(NSB_{E_{2}}\). Moreover, if \(a(\delta_{NS}) < 0\) (resp., >0), then the NS bifurcation of system (3) at \(\delta= \delta_{NS}\) is supercritical (resp., subcritical) and there exists a unique closed invariant curve bifurcation from \(E_{2}\) for \(\delta= \delta_{NS}\), which is attracting (resp., repelling).
In Section 4, we will choose some values of the parameters so as to show the process of a NS bifurcation for system (3) in Figures 2 and 3 resp. by numerical simulation. Here one example, which illustrates Theorem 3.1, is given below.
Bifurcation diagrams and maximum Lyapunov exponent for system ( 3 ) around \(\pmb{E_{2}}\) . (a) Neimark-Sacker bifurcation diagram of system (3) in \((\delta-x-y)\) space, (b)-(c) NS bifurcation diagrams in \((\delta-x)\) and \((\delta-y)\) planes, (d) maximum Lyapunov exponents corresponding to (b)-(c), (e) maximum Lyapunov exponents are superimposed on bifurcation diagrams, (f) local amplification corresponding to (b) for \(\delta\in[1.26141, 1.6309]\). The initial value is \((x_{0}, y_{0}) = (0.29, 1.62)\).
Example 3.1
Consider system (3) with \(r = 2\), \(K = 1.2\), \(d = 0.25\), \(\alpha= 0.75\), \(\beta= 2\), \(\delta= \delta_{F} = 1.40356\). Then \((r, K, d, \alpha, \beta, \delta) \in FB1_{E_{2}}\) and there is a unique positive fixed point \((1, 1)\) with multipliers \(\lambda_{1}=-1\), \(\lambda _{2}=0.972639\), and \(c(\delta_{F}) = -23.9313\). Hence, according to Theorem 3.1, the flip bifurcation emerges from the fixed point \((1, 1)\) at \(\delta= \delta_{F}\).
4 Numerical simulations
In this section, by using numeral simulation, we give the bifurcation diagrams, phase portraits and Lyapunov exponents of system (3) to confirm the previous analytic results and show some new interesting complex dynamical behaviors existing in system (3). It is known that maximum Lyapunov exponents quantify the exponential divergence of initially close state-space trajectories and frequently are employed to identify chaotic behavior. Since the dynamics of discrete prey-predator model with Holling type I, II, and III functional response has been examined by many researchers, we will now mainly focus our attention on the effect of simplified Monod-Haldane functional response. Based on the previous analysis, we choose the parameter δ as a bifurcation parameter (varied parameter) and the other model parameters are taken as fixed parameters, unless otherwise stated; to study the flip bifurcation and the Neimark-Sacker bifurcation, respectively, for the unique positive fixed point, one can consider the initial condition \((x_{0}, y_{0})\) situated in the basin of attraction of fixed point. Without loss of generality, the bifurcation parameters are considered in the following cases:
Case (i) varying δ in range \(0.5 \le\delta\le1.74\), and fixing \(r = 2\), \(K = 1.2\), \(d = 0.25\), \(\alpha= 0.9\), \(\beta= 1\);
Case (ii) varying β in range \(0.7 \le\beta\le1.25\), and fixing \(r = 2\), \(K = 1.2\), \(d = 0.25\), \(\alpha= 0.9\), \(\delta= 0.816737\).
For case (i): The bifurcation diagrams of system (3) in the \((\delta-x-y)\) space, the \((\delta-x)\) plane and the \((\delta-y)\) plane are given in Figure 2(a)-(b)-(c). After calculation for the fixed point \(E_{2}\) of map (3), the NS bifurcation emerges from the fixed point \((0.303337, 1.63195)\) at \(\delta= \delta_{NS} = 0.816737\) and \((r, K, d, \alpha, \beta, \delta) \in NSB_{E_{2}}\). It shows the correctness of Proposition 2.2. For \(\delta= \delta _{NS}\), we have λ, \(\bar{\lambda} = 0.89639 \pm0.443267 i\), \(|\lambda| = 1\), \(|\bar{\lambda}| = 1\), \(\frac{d|\lambda(\delta)|}{d\delta }|_{\delta= \delta_{NS}} = 0.126859>0\), \(\lambda_{NS} (a_{1} + b_{2}) = -0.20722 \ne-2, -3\), \(g_{20} = 0.288682 + 0.020187 i\), \(g_{11} = 0.24234 - 0.138155 i\), \(g_{02} = -0.503202 + 0.679727 i\), \(g_{21} = 0.058348 - 0.248692 i\), and \(a(\delta_{NS}) = -0.174522\). Therefore, the NS bifurcation is supercritical and it shows the correctness of Theorem 3.2.
From Figure 2(b)-(c), we observe that the fixed point \(E_{2}\) of map (3) is stable for \(\delta< 0.816737\) and loses its stability at \(\delta= 0.816737\) and an invariant circle appears when the parameter δ exceeds 0.816737, we also observe that there are period-doubling phenomenons. The maximum Lyapunov exponents corresponding to Figure 2(b)-(c) are computed and plotted in Figure 2(d), confirming the existence of the chaotic regions and period orbits in the parametric space. From Figure 2(d), we observe that some Lyapunov exponents are bigger than 0, some are smaller than 0, so there exist stable fixed points or stable period windows in the chaotic region. In general the positive Lyapunov exponent is considered to be one of the characteristics implying the existence of chaos. The bifurcation diagrams for x and y together with maximum Lyapunov exponents is presented in Figure 2(e). Figure 2(f) is the local amplification corresponding to Figure 2(b) for \(\delta\in[1.2614, 1.6309]\).
The phase portraits which are associated with Figure 2(a) are disposed in Figure 4, which clearly depicts the process of how a smooth invariant circle bifurcates from the stable fixed point \((0.303337, 1.63195)\). When δ exceeds 0.816737, there appears a circular curve enclosing the fixed point \(E_{2}\), and its radius becomes larger with respect to the growth of δ. When δ increases at certain values, for example, at \(\delta= 1.3\), the circle disappears and a period-11 orbits appears. As δ is increased further, however, the phase portrait starts to fold. We see that the circle, after being stretched, shrunk and folded, creates new phenomena due to the breakdown of the closed curve (see at \(\delta= 1.37 \)). For further increasing δ, we obtain the multiple invariant closed curves brought about by a NS bifurcation of iterates of the model (3), quasi-periodic orbits and attracting chaotic sets. We see that for \(\delta= 1.63\) and \(\delta= 1.74\), where the strange attractors are produced by the breaking of the invariant circles, the values of maximal Lyapunov exponent are positive, confirming the existence of the chaotic sets. In addition, in system (3) fully developed chaos occurs when \(\delta= 1.74\).
Phase portraits for various values of δ corresponding to Figure 2 (a).
For case (ii): Figure 3 demonstrates the dynamic behavior of the model (3) when the parameter β varies. The bifurcation diagram for system (3) is plotted as a function of the control parameter β. It turns out that the fixed point \(E_{2}\) of map (3) loses its stability through a NS bifurcation, when β varies around 1. As β decreases the behavior of this model becomes very complicated, including the NS bifurcation and many chaotic bands. The sign of the maximal Lyapunov exponent confirms the existence of the strange attractor.
In order to observe the complex dynamics, we can vary more parameters of system (3). Since the values of the Lyapunov exponents quantify the chaotic behavior of the discrete system or at least the sensitive dependence on the initial conditions, so we compute the maximum Lyapunov exponents of system (3) and study the dependence of these Lyapunov exponents on the two real parameters δ and β. The signs of the maximum Lyapunov exponents of system (3) for parameters \(\delta\in[0.5, 1.1]\), \(\beta \in[0.8, 1.25]\), and \(\delta\in[1.1, 1.74]\), \(\beta\in[1.0, 1.25]\), respectively, and fixing other parameters as in case (ii), are plotted in Figure 5. A blue color represents a negative Lyapunov exponent and a red color represents a positive Lyapunov exponent. Here it is easy to see for which choice of parameters system (3) is showing chaotic motion, and for which one is system (3) exhibiting periodic or quasi-periodic movement. For instance, the chaotic situation is on Figure 4 for values of parameters \(\delta= 1.63\), \(\beta= 1\), and the non-chaotic situation is for values of the parameters \(\delta= 0.785\), \(\beta= 1\), which are consistent with the signs in Figure 5. It shows that the dynamics of system (3) is chaotic for small values of the parameter β.
Sign of maximum Lyapunov exponent for system ( 3 ) around \(\pmb{E_{2}}\) . (a) Sign of maximum Lyapunov exponents of system (3) covering \(\delta\in[0.5, 1.1]\), \(\beta\in [0.8, 1.25]\), and \(r = 2\), \(K = 1.2\), \(d = 0.25\), \(\alpha= 0.9\). (b) Sign of maximum Lyapunov exponents covering \(\delta\in[1.1, 1.74]\), \(\beta \in[1.0, 1.25]\) (red ‘*’ = positive, blue ‘o’ = negative). The initial value is \((x_{0}, y_{0}) = (0.29, 1.62)\).
4.1 Sensitive dependence on initial conditions
To demonstrate the sensitivity to initial conditions of the model (3), two perturbed trajectories are represented in Figure 6. At the beginning, the two trajectories are overlapped and are indistinguishable; but after a number of iterations, the difference between them builds up rapidly. Figure 6 shows a sensitive dependence on the initial conditions for x- and y-coordinate of the two trajectories for the model (3), which is plotted against the number of iterations. The initial perturbation of two trajectories for x-coordinate is \(1 \times 10^{-3}\), while the other coordinate is kept to have the same value. For this case the two trajectories with initial points \((x_{0}, y_{0}) = (0.227, 4.585)\) and \((x_{0}+0.001, y_{0})\) are computed and plotted in Figure 6(a), respectively.
Sensitive dependence on the initial conditions for system ( 3 ). (a) The two trajectories for x-coordinate, plotted against number of iterations, red for \((x_{0}, y_{0})\); blue for \((x_{0}+0.001, y_{0})\). (b) The two trajectories for y-coordinate, plotted against number of iterations, red for \((x_{0}, y_{0})\); blue for \((x_{0}, y_{0}+0.001)\). The parameter values are \(r = 5.5\), \(K = 0.771525\), \(d = 0.3\), \(\alpha= 1.65\), \(\beta= 1.3\), \(\delta= 1.565\). The initial value is \((x_{0}, y_{0}) = (0.227, 4.585)\).
Also, a sensitive dependence on the initial conditions of two trajectories for y-coordinate of the model (3) is plotted in Figure 6(b). The initial conditions of two trajectories for y-coordinate differ by \(1 \times10^{-3}\), while the other coordinate is kept at the same value. In Figure 6, it is shown that the trajectories of system (3) sensitively depend on the initial conditions, i.e. complex dynamic behavior occurs with initial perturbation.
5 Discussions
In this paper, we investigated the behaviors of the discrete-time predator-prey system (3) involving group defense with simplified Monod-Haldane functional response and showed that it has a complex dynamics in the closed first quadrant \(\mathbb {R}^{2}_{+}\). We showed that the unique positive fixed point of (3) can undergo a flip bifurcation and a NS bifurcation under certain parametric conditions. Some other basic dynamical properties of system (3) have been analyzed by means of bifurcation diagrams, phase portraits, Lyapunov exponents, and the sensitive dependence on the initial conditions. More precisely, as the parameters vary, system (3) exhibits a variety of dynamical behaviors, including period-11 orbits, an invariant cycle, a cascade of period-doubling, quasi-periodic orbits, and chaotic sets, which imply that the predators and prey can coexist in the stable period-n orbits and invariant cycle. Finally, simulation works showed that in certain regions of the parameter space, the model (3) had a great sensitivity to the choice of the initial conditions and parameter values. These results reveal a far richer dynamics of the discrete model compared to the continuous model.
References
Lotka, AJ: Elements of Mathematical Biology. Williams & Wilkins, Baltimore (1925)
Volterra, V: Variazioni e fluttuazioni del numero di’individui in specie animali conviventi. Mem. R. Accad. Naz. Dei Lincei, Ser. VI 2, 31-113 (1926)
Holling, CS: The functional response of predator to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 45, 1-60 (1965)
Brauer, F, Castillo-Chavez, C: Mathematical Models in Population Biology and Epidemiology. Springer, New York (2001)
Murry, JD: Mathematical Biology. Springer, New York (1989)
Rosenzweig, ML, MacArthur, RH: Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 209-223 (1963)
Ruan, S, Xiao, D: Global analysis in a predator-prey system with nonmonotonic functional response. SIAM J. Appl. Math. 61(4), 1445-1472 (2001)
Zhu, H, Campbell, SA, Wolkowicz, GSK: Bifurcation analysis of a predator-prey system with nonmonotonic functional response. SIAM J. Appl. Math. 63, 636-682 (2002)
Agiza, HN, Elabbasy, EM, El-Metwally, H, Elasdany, AA: Chaotic dynamics of a discrete prey-predator model with Holling type II. Nonlinear Anal., Real World Appl. 10, 116-129 (2009)
Danca, M, Codreanu, S, Bakó, B: Detailed analysis of a nonlinear prey predator model. J. Biol. Phys. 23, 11-20 (1997)
Elsadany, AA, El-Metwally, HA, Elabbasy, EM, Agiza, HN: Chaos and bifurcation of a nonlinear discrete prey-predator system. Comput. Ecol. Softw. 2(3), 69-180 (2012)
Hasan, KA, Hama, MF: Complex dynamics behaviors of a discrete prey-predator model with Beddington-DeAngelis functional response. Int. J. Contemp. Math. Sci. 7(45), 2179-2195 (2012)
He, ZM, Lai, X: Bifurcation and chaotic behavior of a discrete-time predator-prey system. Nonlinear Anal., Real World Appl. 12, 403-417 (2011)
He, ZM, Li, B: Complex dynamic behavior of a discrete-time predator-prey system of Holling-III type. Adv. Differ. Equ. 2014, 180 (2014)
Hu, ZY, Teng, ZD, Zhang, L: Stability and bifurcation analysis of a discrete predator-prey model with nonmonotonic functional response. Nonlinear Anal., Real World Appl. 12, 2356-2377 (2011)
Jing, ZJ, Yang, J: Bifurcation and chaos discrete-time predator-prey system. Chaos Solitons Fractals 27, 259-277 (2006)
Liu, XL, Xiao, DM: Complex dynamic behaviors of a discrete-time predator-prey system. Chaos Solitons Fractals 32, 80-94 (2007)
Ghaziani, RK: Dynamics and bifurcations of a Lotka-Volterra population model. Iran. J. Sci. Technol., Trans. A, Sci. 38A3, 265-279 (2014)
Li, B, He, Z: Bifurcations and chaos in a two-dimensional discrete Hindmarsh-Rose model. Nonlinear Dyn. 76, 697-715 (2014)
Rana, SMS: Bifurcation and complex dynamics of a discrete-time predator-prey system. Comput. Ecol. Softw. 5(2), 187-200 (2015)
Wang, C, Li, X: Stability and Neimark-Sacker bifurcation of a semi-discrete population model. J. Appl. Anal. Comput. 4(4), 419-435 (2014)
Li, B, He, Z: 1:2 and 1:4 resonances in a two-dimensional discrete Hindmarsh-Rose model. Nonlinear Dyn. 796, 705-720 (2015)
Freedman, HI, Wolkowicz, GSK: Predator-prey systems with group defense: the paradox of enrichment revisited. Bull. Math. Biol. 48, 493-508 (1986)
Kuzenetsov, YA: Elements of Applied Bifurcation Theory, 2nd edn. Springer, New York (1998)
Elaydi, SN: An Introduction to Difference Equations. Springer, New York (1996)
Guckenheimer, J, Holmes, P: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)
Robinson, C: Dynamical Systems: Stability, Symbolic Dynamics, and Chaos, 2nd edn. CRC Press, Boca Raton (1999)
Winggins, S: Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York (2003)
Acknowledgements
The author would like to thank the editor and the referees for their valuable comments and suggestions which led to the improvement of the paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that there is no competing interest regarding the publication of this paper.
Author’s contributions
The author carried out the proof of the main results and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rana, S.M.S. Bifurcation and complex dynamics of a discrete-time predator-prey system with simplified Monod-Haldane functional response. Adv Differ Equ 2015, 345 (2015). https://doi.org/10.1186/s13662-015-0680-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-015-0680-7