Almost periodic solutions for neutral delay Hopfield neural networks with time-varying delays in the leakage term on time scales

Abstract

In this paper, a class of neutral delay Hopfield neural networks with time-varying delays in the leakage term on time scales is considered. By utilizing the exponential dichotomy of linear dynamic equations on time scales, Banach’s fixed point theorem and the theory of calculus on time scales, some sufficient conditions are obtained for the existence and exponential stability of almost periodic solutions for this class of neural networks. Finally, a numerical example illustrates the feasibility of our results and also shows that the continuous-time neural network and the discrete-time analogue have the same dynamical behaviors. The results of this paper are completely new and complementary to the previously known results even when the time scale $\mathbb{T}=\mathbb{R}\text{ or }\mathbb{Z}$.

1 Introduction

The dynamical properties for delayed Hopfield neural networks have been extensively studied since they can be applied into pattern recognition, image processing, speed detection of moving objects, optimization problems and many other fields. Besides, due to the finite speed of information processing, the existence of time delays frequently causes oscillation, divergence, or instability in neural networks. Therefore, it is of prime importance to consider the delay effects on the stability of neural networks. Up to now, neural networks with various types of delay have been widely investigated by many authors [1–20].

However, so far, very little attention has been paid to neural networks with time delay in the leakage (or ‘forgetting’) term [21–35]. Such time delays in the leakage terms are difficult to handle and have been rarely considered in the literature. In fact, the leakage term has a great impact on the dynamical behavior of neural networks. Also, recently, another type of time delays, namely, neutral-type time delays which always appear in the study of automatic control, population dynamics and vibrating masses attached to an elastic bar, etc., has drawn much research attention. So far there have been only a few papers that have taken neutral-type phenomenon into account in delayed neural networks [33–43].

In fact, both continuous and discrete systems are very important in implementation and applications. But it is troublesome to study the existence of almost periodic solutions for continuous and discrete systems respectively. Therefore, it is meaningful to study that on time scales which can unify the continuous and discrete situations (see [44–50]).

To the best of our knowledge, up to now, there have been no papers published on the existence and stability of almost periodic solutions to neutral-type delay neural networks with time-varying delays in the leakage term on time scales. Thus, it is important and, in effect, necessary to study the existence of almost periodic solutions for neutral-type neural networks with time-varying delay in the leakage term on time scales.

Motivated by above, in this paper, we propose the following neutral delay Hopfield neural networks with time-varying delays in the leakage term on time scale :

$$\begin{array}{rcl}{x}_i^{\mathrm{\Delta }}(t)& =& -c_i(t)x_i(t-{\eta }_i(t))+\sum _{j=1}^n{a}_{ij}(t)f_j\left(x_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))\mathrm{\Delta }s+\sum _{j=1}^n{b}_{ij}(t)g_j\left(x_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(x_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s+I_i(t),i=1,2,\dots ,n,\end{array}$$

(1.1)

where is an almost periodic time scale that will be defined in the next section, $x_i(t)$ denotes the potential (or voltage) of cell i at time t, $c_i(t)>0$ represents the rate at which the i th unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at time t, $a_{ij}(t)$, $b_{ij}(t)$, $d_{ij}(t)$ and $e_{ij}(t)$ represent the delayed strengths of connectivity and neutral delayed strengths of connectivity between cell i and j at time t, respectively, ${\theta }_{ij}(\cdot )$ and ${\xi }_{ij}(\cdot )$ are the kernel functions determining the distributed delays, $f_j$, $g_j$, $h_j$ and $k_j$ are the activation functions in system (1.1), $I_i(t)$ is an external input on the i th unit at time t, ${\tau }_{ij}(t)\ge 0$ and ${\sigma }_{ij}(t)\ge 0$ correspond to the transmission delays of the i th unit along the axon of the j th unit at time t.

If $\mathbb{T}=\mathbb{R}$, then system (1.1) is reduced to the following continuous-time neutral delay Hopfield neural network:

$$\begin{array}{rcl}{x}_i^{\prime }(t)& =& -c_i(t)x_i(t-{\eta }_i(t))+\sum _{j=1}^n{a}_{ij}(t)f_j\left(x_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))\mathrm{d}s+\sum _{j=1}^n{b}_{ij}(t)g_j\left(x_j^{\prime }(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(x_j^{\prime }(s))\mathrm{d}s+I_i(t),i=1,2,\dots ,n,\end{array}$$

(1.2)

and if $\mathbb{T}=\mathbb{Z}$, then system (1.1) is reduced to the discrete-time neutral delay Hopfield neural network

$$\begin{array}{rcl}\mathrm{\Delta }{x}_i(t)& =& -c_i(t)x_i(t-{\eta }_i(t))+\sum _{j=1}^n{a}_{ij}(t)f_j\left(x_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{d}_{ij}(t)\sum _{s=t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))+\sum _{j=1}^n{b}_{ij}(t)g_j\left(\mathrm{\Delta }{x}_j(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^n{e}_{ij}(t)\sum _{s=t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(\mathrm{\Delta }{x}_j(s))+I_i(t),i=1,2,\dots ,n,\end{array}$$

(1.3)

where $t\in \mathbb{Z}$ and $\mathrm{\Delta }x(t)=x(t+1)-x(t)$. When ${\eta }_i(t)\equiv 0$, $d_{ij}(t)\equiv 0$, $e_{ij}(t)\equiv 0$, $i,j=1,2,\dots ,n$, Bai [37] and Xiao [38] studied the almost periodicity of (1.2), respectively. However, even when ${\eta }_i(t)\equiv 0$, $i=1,2,\dots ,n$, the almost periodicity to (1.3), the discrete-time analogue of (1.2), has been not studied yet.

For convenience, for any almost periodic function $f(t)$ defined on , we define $f^{-}={inf}_{i\in \mathbb{T}}|f(t)|$, $f^{+}={sup}_{\in \mathbb{T}}|f(t)|$.

The initial condition associated with system (1.1) is of the form

$$x_i(t)={\phi }_i(t),x_i^{\mathrm{\Delta }}(t)={\phi }_i^{\mathrm{\Delta }}(t),t\in {[-\iota ,0]}_{\mathbb{T}},i=1,2,\dots ,n,$$

where ${\phi }_i(\cdot )$ denotes a real-value bounded Δ-differentiable function defined on ${[-\iota ,0]}_{\mathbb{T}}$ and $\iota ={max}_{1\le i,j\le n}\{{\eta }_i^{+},{\tau }_{ij}^{+},{\sigma }_{ij}^{+},{\delta }_{ij}^{+},{\zeta }_{ij}^{+}\}$.

Throughout this paper, we assume that:

(H₁) $c_i(t)>0$ with $-c_i\in {\mathcal{R}}^{+}$, ${\eta }_i(t)\ge 0$, ${\tau }_{ij}(t)\ge 0$, ${\sigma }_{ij}(t)\ge 0$, ${\delta }_{ij}(t)\ge 0$, ${\zeta }_{ij}(t)\ge 0$, $a_{ij}(t)$, $b_{ij}(t)$, $d_{ij}(t)$, $e_{ij}(t)$ and $I_i(t)$ are all almost periodic functions on , $t-{\eta }_i(t)\in \mathbb{T}$, $t-{\tau }_{ij}(t)\in \mathbb{T}$, $t-{\sigma }_{ij}(t)\in \mathbb{T}$, $t-{\delta }_{ij}(t)\in \mathbb{T}$, $t-{\zeta }_{ij}(t)\in \mathbb{T}$ for $t\in \mathbb{T}$, $i,j=1,2,\dots ,n$.

(H₂) There exist positive constants $L_i>0$, $l_i>0$, $L_i^h>0$, $l_i^k>0$ such that for $i=1,2,\dots ,n$,

$$\begin{array}{c}|f_i(x)-f_i(y)|\le L_i|x-y|,|g_i(x)-g_i(y)|\le l_i|x-y|,\hfill \\ |h_i(x)-h_i(y)|\le L_i^h|x-y|,|k_i(x)-k_i(y)|\le l_i^k|x-y|,\hfill \end{array}$$

where $x,y\in \mathbb{R}$ and $f_i(0)=g_i(0)=h_i(0)=k_i(0)=0$.

(H₃) For $i,j=1,2,\dots ,n$, the delay kernels ${\theta }_{ij},{\xi }_{ij}:\mathbb{T}\to \mathbb{R}$ are continuous and integrable with

$$0\le {\int }_{t-{\delta }_{ij}^{+}}^t|{\theta }_{ij}(s)|\mathrm{\Delta }s\le {\overline{\theta }}_{ij},0\le {\int }_{t-{\zeta }_{ij}^{+}}^t|{\xi }_{ij}(s)|\mathrm{\Delta }s\le {\overline{\xi }}_{ij}.$$

Our main purpose of this paper is to study the existence and global exponential stability of the almost periodic solution to (1.1). Our results of this paper are completely new and complementary to the previously known results even when the time scale $\mathbb{T}=\mathbb{R}\text{ or }\mathbb{Z}$. The organization of the rest of this paper is as follows. In Section 2, we introduce some definitions and make some preparations for later sections. In Section 3 and Section 4, by utilizing Banach’s fixed point theorem and the theory of calculus on time scales, we present some sufficient conditions which guarantee the existence of a unique globally exponentially stable almost periodic solution for system (1.1). In Section 5, we present examples to illustrate the feasibility and effectiveness of our results obtained in previous sections. We draw a conclusion in Section 6.

2 Preliminaries

In this section, we shall first recall some basic definitions and lemmas which will be useful for the proof of our main results.

Let be a nonempty closed subset (time scale) of ℝ. The forward and backward jump operators $\sigma ,\rho :\mathbb{T}\to \mathbb{T}$ and the graininess $\mu :\mathbb{T}\to {\mathbb{R}}^{+}$ are defined, respectively, by

$$\sigma (t)=inf\{s\in \mathbb{T}:s>t\},\rho (t)=sup\{s\in \mathbb{T}:s<t\}\text{and}\mu (t)=\sigma (t)-t.$$

A point $t\in \mathbb{T}$ is called left-dense if $t>inf\mathbb{T}$ and $\rho (t)=t$, left-scattered if $\rho (t)<t$, right-dense if $t<sup\mathbb{T}$ and $\sigma (t)=t$, and right-scattered if $\sigma (t)>t$. If has a left-scattered maximum m, then ${\mathbb{T}}^k=\mathbb{T}\setminus \{m\}$; otherwise ${\mathbb{T}}^k=\mathbb{T}$. If has a right-scattered minimum m, then ${\mathbb{T}}_k=\mathbb{T}\setminus \{m\}$; otherwise ${\mathbb{T}}_k=\mathbb{T}$.

A function $f:\mathbb{T}\to \mathbb{R}$ is right-dense continuous provided it is continuous at right-dense point in and its left-side limits exist at left-dense points in . If f is continuous at each right-dense point and each left-dense point, then f is said to be a continuous function on .

For $y:\mathbb{T}\to \mathbb{R}$ and $t\in {\mathbb{T}}^k$, we define the delta derivative of $y(t)$, $y^{\mathrm{\Delta }}(t)$, to be the number (if it exists) with the property that for a given $\epsilon >0$, there exists a neighborhood U of t such that

$$|[y(\sigma (t))-y(s)]-y^{\mathrm{\Delta }}(t)[\sigma (t)-s]|<\epsilon |\sigma (t)-s|$$

for all $s\in U$.

If y is continuous, then y is right-dense continuous, and if y is delta differentiable at t, then y is continuous at t.

Let y be right-dense continuous. If $Y^{\mathrm{\Delta }}(t)=y(t)$, then we define the delta integral by

$${\int }_a^{t}y(s)\mathrm{\Delta }s=Y(t)-Y(a).$$

A function $r:\mathbb{T}\to \mathbb{R}$ is called regressive if

$$1+\mu (t)r(t)\ne 0$$

for all $t\in {\mathbb{T}}^k$. The set of all regressive and rd-continuous functions $r:\mathbb{T}\to \mathbb{R}$ will be denoted by $\mathcal{R}=\mathcal{R}(\mathbb{T})=\mathcal{R}(\mathbb{T},\mathbb{R})$. We define the set ${\mathcal{R}}^{+}={\mathcal{R}}^{+}(\mathbb{T},\mathbb{R})=\{r\in \mathcal{R}:1+\mu (t)r(t)>0,\mathrm{\forall }t\in \mathbb{T}\}$.

If r is a regressive function, then the generalized exponential function $e_r$ is defined by

$$e_r(t,s)=exp\left\{{\int }_s^t{\xi }_{\mu (\tau )}(r(\tau ))\mathrm{\Delta }\tau \right\}\text{for }s,t\in \mathbb{T},$$

with the cylinder transformation

$${\xi }_h(z)=\{\begin{array}{ll}\frac{Log(1+hz)}{h}& \text{if }h\ne 0,\\ z& \text{if }h=0.\end{array}$$

Let $p,q:\mathbb{T}\to \mathbb{R}$ be two regressive functions, we define

$$p\oplus q:=p+q+\mu pq,\ominus p:=-\frac{p}{1+\mu p},p\ominus q:=p\oplus (\ominus q).$$

Then the generalized exponential function has the following properties.

Definition 2.1 [51]

Let $p,q:\mathbb{T}\to \mathbb{R}$ be two regressive functions, define

$$p\oplus q=p+q+\mu pq,\ominus p=-\frac{p}{1+\mu p},p\ominus q=p\oplus (\ominus q).$$

Lemma 2.1 [51]

Assume that $p,q:\mathbb{T}\to \mathbb{R}$ are two regressive functions, then

• (1) $e_0(t,s)\equiv 1$ and $e_p(t,t)\equiv 1$;

• (2) $e_p(\sigma (t),s)=(1+\mu (t)p(t))e_p(t,s)$;

• (3) $e_p(t,s)=\frac{1}{e_p(s,t)}=e_{\ominus p}(s,t)$;

• (4) $e_p(t,s)e_p(s,r)=e_p(t,r)$;

• (5) ${(e_{\ominus p}(t,s))}^{\mathrm{\Delta }}=(\ominus p)(t)e_{\ominus p}(t,s)$;

• (6) if $a,b,c\in \mathbb{T}$, then ${\int }_a^{b}p(t)e_p(c,\sigma (t))\mathrm{\Delta }t=e_p(c,a)-e_p(c,b)$.

Definition 2.2 [51]

Assume that $f:\mathbb{T}\to \mathbb{R}$ is a function and let $t\in {\mathbb{T}}^k$. Then we define $f^{\mathrm{\Delta }}(t)$ to be the number (provided it exists) with the property that given any $\epsilon >0$, there is a neighborhood U of t (i.e., $U=(t-\delta ,t+\delta )\cap \mathbb{T}$ for some $\delta >0$) such that

$$|[f(\sigma (t))-f(s)]-f^{\mathrm{\Delta }}(t)[\sigma (t)-s]|\le \epsilon |\sigma (t)-s|$$

for all $s\in U$. We call $f^{\mathrm{\Delta }}(t)$ the delta (or Hilger) derivative of f at t. Moreover, we say that f is delta (or Hilger) differentiable (or, in short, differentiable) on ${\mathbb{T}}^k$ provided $f^{\mathrm{\Delta }}(t)$ exists for all $t\in {\mathbb{T}}^k$. The function $f^{\mathrm{\Delta }}:{\mathbb{T}}^k\to \mathbb{R}$ is then called the (delta) derivative of f on ${\mathbb{T}}^k$.

Definition 2.3 [52]

A time scale is called an almost periodic time scale if

$$\mathrm{\Pi }:=\{\tau \in \mathbb{R}:t\pm \tau \in \mathbb{T},\mathrm{\forall }t\in \mathbb{T}\}\ne \{0\}.$$

Definition 2.4 [52]

Let be an almost periodic time scale. A function $f\in C(\mathbb{T},{\mathbb{E}}^n)$ is called an almost periodic function if the ε-translation set of

$$E(\epsilon ,f)=\{\tau \in \mathrm{\Pi }:|f(t+\tau )-f(t)|<\epsilon ,\mathrm{\forall }t\in \mathbb{T}\}$$

is a relatively dense set in for all $\epsilon >0$; that is, for any given $\epsilon >0$, there exists a constant $l(\epsilon )>0$ such that each interval of length $l(\epsilon )$ contains a $\tau (\epsilon )\in E(\epsilon ,f)$ such that

$$|f(t+\tau )-f(t)|<\epsilon ,\mathrm{\forall }t\in \mathbb{T}.$$

τ is called the ε-translation number of f and $l(\epsilon )$ is called the inclusion length of $T(\epsilon ,f)$.

Definition 2.5 [52]

Let $A(t)$ be an $n\times n$ rd-continuous matrix on , the linear system

$$x^{\mathrm{\Delta }}(t)=A(t)x(t),t\in \mathbb{T}$$

(2.1)

is said to admit an exponential dichotomy on if there exist positive constants k, α, projection P and the fundamental solution matrix $X(t)$ of (2.1), satisfying

$$\begin{array}{c}{\parallel X(t)P{X}^{-1}(\sigma (s))\parallel }_0\le k{e}_{\ominus \alpha }(t,\sigma (s)),s,t\in \mathbb{T},t\ge \sigma (s),\hfill \\ {\parallel X(t)(I-P)X^{-1}(\sigma (s))\parallel }_0\le k{e}_{\ominus \alpha }(\sigma (s),t),s,t\in \mathbb{T},t\le \sigma (s),\hfill \end{array}$$

where ${\parallel \cdot \parallel }_0$ is a matrix norm on (say, for example, if $A={(a_{ij})}_{n\times m}$, then we can take ${\parallel A\parallel }_0={({\sum }_{i=1}^n{\sum }_{j=1}^m{|a_{ij}|}^2)}^{\frac{1}{2}}$).

Consider the following almost periodic system:

$$x^{\mathrm{\Delta }}(t)=A(t)x(t)+f(t),t\in \mathbb{T},$$

(2.2)

where $A(t)$ is an almost periodic matrix function, $f(t)$ is an almost periodic vector function.

Lemma 2.2 [52]

If the linear system (2.1) admits exponential dichotomy, then system (2.2) has a unique almost periodic solution

$$x(t)={\int }_{-\mathrm{\infty }}^{t}X(t)P{X}^{-1}(\sigma (s))f(s)\mathrm{\Delta }s-{\int }_t^{+\mathrm{\infty }}X(t)(I-P)X^{-1}(\sigma (s))f(s)\mathrm{\Delta }s,$$

where $X(t)$ is the fundamental solution matrix of (2.1).

Lemma 2.3 [53]

Let $c_i(t)$ be an almost periodic function on , where $c_i(t)>0$, $-c_i(t)\in {\mathcal{R}}^{+}$, $i=1,2,\dots ,n$, $\mathrm{\forall }t\in \mathbb{T}$ and ${min}_{1\le i\le n}\{{inf}_{t\in \mathbb{T}}{c}_i(t)\}=\tilde{m}>0$, then the linear system

$$x^{\mathrm{\Delta }}(t)=\mathrm{diag}(-c_1(t),-c_2(t),\dots ,-c_n(t))x(t)$$

(2.3)

admits an exponential dichotomy on .

One can easily prove the following.

Lemma 2.4 Suppose that $f(t)$ is an rd-continuous function and $c(t)$ is a positive rd-continuous function satisfying $-c(t)\in {\mathcal{R}}^{+}$. Let

$$g(t)={\int }_{t_0}^t{e}_{-c}(t,\sigma (s))f(s)\mathrm{\Delta }s,$$

where $t_0\in \mathbb{T}$, then

$$g^{\mathrm{\Delta }}(t)=f(t)+{\int }_{t_0}^t[-c(t)e_{-c}(t,\sigma (s))f(s)]\mathrm{\Delta }s.$$

3 Existence of almost periodic solutions

Let $\mathit{AP}(\mathbb{T})=\{x(t)\in C(\mathbb{T},\mathbb{R}):x(t)\text{ is a real-valued, almost periodic function on }\mathbb{T}\}$, $\mathbb{Y}=\{x(t)\in C^1(\mathbb{T},\mathbb{R}):x(t),x^{\mathrm{\Delta }}(t)\in \mathit{AP}(\mathbb{T})\}$ and

$$\mathbb{X}=\{\phi ={({\phi }_1(t),{\phi }_2(t),\dots ,{\phi }_n(t))}^T:{\phi }_i(t)\in \mathbb{Y},i=1,2,\dots ,n\}.$$

For $\mathrm{\forall }\phi \in \mathbb{X}$, if we define induced modulus ${\parallel \phi \parallel }_{\mathbb{X}}=max\{{\parallel \phi \parallel }_0,{\parallel {\phi }^{\mathrm{\Delta }}\parallel }_0\}$, where

$${\parallel \phi \parallel }_0=\underset{t\in \mathbb{T}}{sup}{\parallel \phi (t)\parallel }_0,{\parallel \phi (t)\parallel }_0=\underset{1\le i\le n}{max}|{\phi }_i(t)|$$

and ${\phi }^{\mathrm{\Delta }}(t)={({\phi }_1^{\mathrm{\Delta }}(t),{\phi }_2^{\mathrm{\Delta }}(t),\dots ,{\phi }_n^{\mathrm{\Delta }}(t))}^T$, then is a Banach space.

Theorem 3.1 Assume that (H₁)-(H₃) and

(H₄) $r={max}_{1\le i\le n}max\{\frac{1}{c_i^{-}},1+\frac{c_i^{+}}{c_i^{-}}\}(c_i^{+}{\eta }_i^{+}+{\sum }_{j=1}^n{a}_{ij}^{+}{L}_j+{\sum }_{j=i}^n{b}_{ij}^{+}{l}_j+{\sum }_{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+{\sum }_{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})<1$

hold, then there exists exactly one almost periodic solution of system (1.1) in the region ${\mathbb{X}}_0=\{\varphi (t)\mid {\parallel \varphi -{\varphi }_0\parallel }_{\mathbb{X}}\le \frac{rR}{1-r}\}$, where

$$\begin{array}{c}R=\underset{1\le i\le n}{max}max\{\frac{I_i^{+}}{c_i^{-}},I_i^{+}(1+\frac{c_i^{+}}{c_i^{-}})\},\hfill \\ {\varphi }_0={({\int }_{-\mathrm{\infty }}^t{I}_1(s)e_{-c_1}(t,\sigma (s))\mathrm{\Delta }s,\dots ,{\int }_{-\mathrm{\infty }}^t{I}_n(s)e_{-c_n}(t,\sigma (s))\mathrm{\Delta }s)}^T.\hfill \end{array}$$

Proof Rewrite (1.1) in the form

$$\begin{array}{rcl}{x}_i^{\mathrm{\Delta }}(t)& =& -c_i(t)x_i(t)+c_i(t){\int }_{t-{\eta }_i(t)}^t{x}_i^{\mathrm{\Delta }}(s)\mathrm{\Delta }s+\sum _{j=1}^n{a}_{ij}(t)f_j\left(x_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))\mathrm{\Delta }s+\sum _{j=1}^n{b}_{ij}(t)g_j\left(x_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(x_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s+I_i(t),i=1,2,\dots ,n.\end{array}$$

For any $\varphi \in \mathbb{X}$, we consider the following system:

$$\begin{array}{rcl}{x}_i^{\mathrm{\Delta }}(t)& =& -c_i(t)x_i(t)+c_i(t){\int }_{t-{\eta }_i(t)}^t{\varphi }_i^{\mathrm{\Delta }}(s)\mathrm{\Delta }s+\sum _{j=1}^n{a}_{ij}(t)f_j\left({\varphi }_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j({\varphi }_j(s))\mathrm{\Delta }s+\sum _{j=1}^n{b}_{ij}(t)g_j\left({\varphi }_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j({\varphi }_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s+I_i(t),i=1,2,\dots ,n.\end{array}$$

(3.1)

Since ${min}_{1\le i\le n}\{{inf}_{t\in \mathbb{T}}{c}_i(t)\}>0$, it follows from Lemma 2.2 and Lemma 2.3 that system (3.1) has a unique almost periodic solution which can be expressed as follows:

$$x^{\varphi }(t)={(x_1^{\varphi }(t),x_2^{\varphi }(t),\dots ,x_n^{\varphi }(t))}^T,$$

where

$$\begin{array}{rcl}{x}_i^{\varphi }(t)& =& {\int }_{-\mathrm{\infty }}^t{e}_{-c_i}(t,\sigma (s))[c_i(s){\int }_{s-{\eta }_i(s)}^s{\varphi }_i^{\mathrm{\Delta }}(u)\mathrm{\Delta }u+\sum _{j=1}^n{a}_{ij}(s)f_j\left({\varphi }_j(s-{\tau }_{ij}(s))\right)\\ +\sum _{j=1}^n{d}_{ij}(s){\int }_{s-{\delta }_{ij}(s)}^s{\theta }_{ij}(u)h_j({\varphi }_j(u))\mathrm{\Delta }u+\sum _{j=1}^n{b}_{ij}(s)g_j\left({\varphi }_j^{\mathrm{\Delta }}(s-{\sigma }_{ij}(s))\right)\\ +\sum _{j=1}^n{e}_{ij}(s){\int }_{s-{\zeta }_{ij}(s)}^s{\xi }_{ij}(u)k_j({\varphi }_j^{\mathrm{\Delta }}(u))\mathrm{\Delta }u+I_i(s)]\mathrm{\Delta }s,i=1,2,\dots ,n.\end{array}$$

Now, we define a mapping $T:{\mathbb{X}}_0\to {\mathbb{X}}_0$ by $(T\varphi )(t)=x^{\varphi }(t)$, $\mathrm{\forall }\varphi \in {\mathbb{X}}_0$.

By the definition of ${\parallel \cdot \parallel }_{\mathbb{X}}$, we have

$$\begin{array}{rcl}{\parallel {\varphi }_0\parallel }_{\mathbb{X}}& =& max\{{\parallel {\varphi }_0\parallel }_0,{\parallel {\varphi }_0^{\mathrm{\Delta }}\parallel }_0\}\\ =& max\left\{\underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}\right|{\int }_{-\mathrm{\infty }}^t{I}_i(s)e_{-c_i}(t,\sigma (s))\mathrm{\Delta }s|,\\ \underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}|I_i(t)-{\int }_{-\mathrm{\infty }}^t{c}_i(t)I_i(s)e_{-c_i}(t,\sigma (s))\mathrm{\Delta }s|\}\\ \le & max\{\underset{1\le i\le n}{max}\left\{\frac{I_i^{+}}{c_i^{-}}\right\},\underset{1\le i\le n}{max}\left\{I_i^{+}(1+\frac{c_i^{+}}{c_i^{-}})\right\}\}=R.\end{array}$$

(3.2)

Hence, for any $\varphi \in {\mathbb{X}}_0=\{\varphi \mid \varphi \in \mathbb{X},{\parallel \varphi -{\varphi }_0\parallel }_{\mathbb{X}}\le \frac{rR}{1-r}\}$, one has

$${\parallel \varphi \parallel }_{\mathbb{X}}\le {\parallel {\varphi }_0\parallel }_{\mathbb{X}}+{\parallel \varphi -{\varphi }_0\parallel }_{\mathbb{X}}\le R+\frac{rR}{1-r}=\frac{R}{1-r}.$$

Next, we will show that $T({\mathbb{X}}_0)\subset {\mathbb{X}}_0$. In fact, for any $\varphi \in {\mathbb{X}}_0$, we have

$$\begin{array}{c}{\parallel T\varphi -{\varphi }_0\parallel }_0\hfill \\ =\underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}\left\{\right|{\int }_{-\mathrm{\infty }}^t{e}_{-c_i}(t,\sigma (s))[c_i(s){\int }_{s-{\eta }_i(s)}^s{\varphi }_i^{\mathrm{\Delta }}(u)\mathrm{\Delta }u\hfill \\ +\sum _{j=1}^n{d}_{ij}(s){\int }_{s-{\delta }_{ij}(s)}^s{\theta }_{ij}(u)h_j({\varphi }_j(u))\mathrm{\Delta }u+\sum _{j=1}^n{b}_{ij}(s)g_j\left({\varphi }_j^{\mathrm{\Delta }}(s-{\sigma }_{ij}(s))\right)\hfill \\ +\sum _{j=1}^n{e}_{ij}(s){\int }_{s-{\zeta }_{ij}(s)}^s{\xi }_{ij}(u)k_j({\varphi }_j^{\mathrm{\Delta }}(u))\mathrm{\Delta }u\left]\mathrm{\Delta }s\right|\}\hfill \\ \le \underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}\left\{{\int }_{-\mathrm{\infty }}^t{e}_{-c_i}(t,\sigma (s))\right[c_i^{+}{\parallel {\varphi }^{\mathrm{\Delta }}\parallel }_0{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j{\parallel \varphi \parallel }_0+\sum _{j=1}^n{b}_{ij}^{+}{l}_j{\parallel {\varphi }^{\mathrm{\Delta }}\parallel }_0\hfill \\ +\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}{\parallel \varphi \parallel }_0+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}{\parallel {\varphi }^{\mathrm{\Delta }}\parallel }_0\left]\mathrm{\Delta }s\right\}\hfill \\ \le \underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}\left\{{\int }_{-\mathrm{\infty }}^t{e}_{-c_i}(t,\sigma (s))\right(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j\hfill \\ +\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}\left){\parallel \varphi \parallel }_{\mathbb{X}}\mathrm{\Delta }s\right\}\hfill \\ \le \underset{1\le i\le n}{max}\left\{\frac{1}{c_i^{-}}(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})\right\}{\parallel \varphi \parallel }_{\mathbb{X}}\hfill \end{array}$$

and

$$\begin{array}{c}{\parallel {(T\varphi -{\varphi }_0)}^{\mathrm{\Delta }}\parallel }_0\hfill \\ =\underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}\left\{\right|c_i(t){\int }_{t-{\eta }_i(t)}^t{\varphi }^{\mathrm{\Delta }}(u)\mathrm{\Delta }u+\sum _{j=1}^n{a}_{ij}(t)f_j\left({\varphi }_j(t-{\tau }_{ij}(t))\right)\hfill \\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))\mathrm{\Delta }s+\sum _{j=1}^n{b}_{ij}(t)g_j\left(x_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\hfill \\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(x_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s\hfill \\ -{\int }_{-\mathrm{\infty }}^t{c}_i(t)e_{-c_i}(t,\sigma (s))[c_i(s){\int }_{s-{\eta }_i(s)}^s{\varphi }_i^{\mathrm{\Delta }}(u)\mathrm{\Delta }u\hfill \\ +\sum _{j=1}^n{a}_{ij}(s)f_j\left({\varphi }_j(s-{\tau }_{ij}(s))\right)+\sum _{j=1}^n{d}_{ij}(s){\int }_{s-{\delta }_{ij}(s)}^s{\theta }_{ij}(u)h_j({\varphi }_j(u))\mathrm{\Delta }u\hfill \\ +\sum _{j=1}^n{b}_{ij}(s)g_j\left({\varphi }_j^{\mathrm{\Delta }}(s-{\sigma }_{ij}(s))\right)+\sum _{j=1}^n{e}_{ij}(s){\int }_{s-{\zeta }_{ij}(s)}^s{\xi }_{ij}(u)k_j({\varphi }_j^{\mathrm{\Delta }}(u))\mathrm{\Delta }u\left]\mathrm{\Delta }s\right|\}\hfill \\ \le \underset{t\in \mathbb{T}}{sup}\underset{1\le i\le n}{max}\{(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}){\parallel \varphi \parallel }_X\hfill \\ +c_i^{+}{\int }_{-\mathrm{\infty }}^t{e}_{-c_i}(t,\sigma (s))(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j\hfill \\ +\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}\left){\parallel \varphi \parallel }_X\mathrm{\Delta }s\right\}\hfill \\ \le \underset{1\le i\le n}{max}\left\{(1+\frac{c_i^{+}}{c_i^{-}})(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})\right\}{\parallel \varphi \parallel }_X.\hfill \end{array}$$

Thus, we obtain

$$\begin{array}{c}{\parallel T\varphi -{\varphi }_0\parallel }_{\mathbb{X}}\hfill \\ =max\{{\parallel T\varphi -{\varphi }_0\parallel }_0,{\parallel {(T\varphi -{\varphi }_0)}^{\mathrm{\Delta }}\parallel }_0\}\hfill \\ \le \underset{1\le i\le n}{max}max\{\frac{1}{c_i^{-}},1+\frac{c_i^{+}}{c_i^{-}}\}\hfill \\ \times (c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}){\parallel \varphi \parallel }_{\mathbb{X}}\hfill \\ =r{\parallel \varphi \parallel }_{\mathbb{X}}\le \frac{rR}{1-r},\hfill \end{array}$$

which implies $(T\varphi )\in {\mathbb{X}}_0$, so the mapping T is a self-mapping from ${\mathbb{X}}_0$ to ${\mathbb{X}}_0$.

Finally, we prove that T is a contraction mapping. Taking $\varphi ,\psi \in {\mathbb{X}}_0$, we have that

$$\begin{array}{c}{\parallel T\varphi -T\psi \parallel }_0\hfill \\ \le \underset{1\le i\le n}{max}\left\{\frac{1}{c_i^{-}}(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})\right\}{\parallel \varphi -\psi \parallel }_{\mathbb{X}}\hfill \\ \le r{\parallel \varphi -\psi \parallel }_{\mathbb{X}}\hfill \end{array}$$

and

$$\begin{array}{c}{\parallel {(T\varphi -T\psi )}^{\mathrm{\Delta }}\parallel }_0\hfill \\ \le \underset{1\le i\le n}{max}\left\{(1+\frac{c_i^{+}}{c_i^{-}})(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})\right\}\hfill \\ \times {\parallel \varphi -\psi \parallel }_{\mathbb{X}}\hfill \\ \le r{\parallel \varphi -\psi \parallel }_{\mathbb{X}}.\hfill \end{array}$$

Noticing that $r<1$, it means that T is a contraction mapping. Thus, there exists a unique fixed point $\varphi \in {\mathbb{X}}_0$ such that $T\varphi =\varphi$. Then system (1.1) has a unique almost periodic solution in the region ${\mathbb{X}}_0=\{\varphi (t)\in \mathbb{X}\mid \parallel \varphi -{\varphi }_0\parallel \le \frac{rR}{1-r}\}$. This completes the proof. □

4 Exponential stability of the almost periodic solution

Definition 4.1 The almost periodic solution $\overline{x}(t)={({\overline{x}}_1(t),{\overline{x}}_2(t),\dots ,{\overline{x}}_n(t))}^T$ of system (1.1) with initial value $\overline{\phi }(t)={({\overline{\phi }}_1(t),{\overline{\phi }}_2(t),\dots ,{\overline{\phi }}_n(t))}^T$ is said to be globally exponentially stable. If there exist positive constants λ with $\ominus \lambda \in {\mathcal{R}}^{+}$ and $M>1$ such that every solution $x(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T$ of system (1.1) with initial value $\phi (t)={({\phi }_1(t),{\phi }_2(t),\dots ,{\phi }_n(t))}^T$ satisfies

$${\parallel x(t)-\overline{x}(t)\parallel }_1\le M{e}_{\ominus \lambda }(t,t_0){\parallel \psi \parallel }_{\mathbb{X}},\mathrm{\forall }t\in {[-\iota ,+\mathrm{\infty })}_{\mathbb{T}},t\ge t_0,$$

where

$$\begin{array}{c}{\parallel x(t)-\overline{x}(t)\parallel }_1=max\{{\parallel x(t)-\overline{x}(t)\parallel }_0,{\parallel {(x(t)-\overline{x}(t))}^{\mathrm{\Delta }}\parallel }_0\},\hfill \\ {\parallel \psi \parallel }_X=max\left\{\underset{t\in {[-\iota ,0]}_{\mathbb{T}}}{sup}\underset{1\le i\le n}{max}\right|{\phi }_i(t)-\overline{{\phi }_i}(t)|,\underset{t\in {[-\iota ,0]}_{\mathbb{T}}}{sup}\underset{1\le i\le n}{max}|{\phi }_i^{\mathrm{\Delta }}(t)-{(\overline{{\phi }_i})}^{\mathrm{\Delta }}(t)\left|\right\},\hfill \end{array}$$

and $t_0\in {[-\iota ,0]}_{\mathbb{T}}$.

Theorem 4.1 Assume that (H₁)-(H₄) hold, then system (1.1) has a unique almost periodic solution which is globally exponentially stable.

Proof From Theorem 3.1, we see that system (1.1) has at least one almost periodic solution $\overline{x}(t)={({\overline{x}}_1(t),{\overline{x}}_2(t),\dots ,{\overline{x}}_n(t))}^T$. Suppose that $x(t)={(x_1(t),x_2(t),\dots ,x_n(t))}^T$ is an arbitrary solution. Set $y_i(t)=x_i(t)-{\overline{x}}_i(t)$, $i=1,2,\dots ,n$, then it follows from system (1.1) that

$$\begin{array}{rcl}{y}_i^{\mathrm{\Delta }}(t)& =& x_i^{\mathrm{\Delta }}(t)-{\overline{x}}_i^{\mathrm{\Delta }}(t)\\ =& -c_i(t)x_i(t-{\eta }_i(t))+\sum _{j=1}^n{a}_{ij}(t)f_j\left(x_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))\mathrm{\Delta }s+\sum _{j=1}^n{b}_{ij}(t)g_j\left(x_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(x_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s+c_i(t){\overline{x}}_i(t-{\eta }_i(t))\\ -\sum _{j=1}^n{a}_{ij}(t)f_j\left({\overline{x}}_j(t-{\tau }_{ij}(t))\right)-\sum _{j=1}^n{b}_{ij}(t)g_j\left({\overline{x}}_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\\ -\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j({\overline{x}}_j(s))\mathrm{\Delta }s-\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j({\overline{x}}_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s\\ =& -c_i(t)y_i(t-{\eta }_i(t))+\sum _{j=1}^n{a}_{ij}(t)[f_j\left(x_j(t-{\tau }_{ij}(t))\right)-f_j\left({\overline{x}}_j(t-{\tau }_{ij}(t))\right)]\\ +\sum _{j=1}^n{b}_{ij}(t)[g_j\left(x_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)-g_j\left({\overline{x}}_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)]\\ +\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)[h_j(x_j(s))-h_j({\overline{x}}_j(s))]\mathrm{\Delta }s\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)[k_j(x_j^{\mathrm{\Delta }}(s))-k_j({\overline{x}}_j^{\mathrm{\Delta }}(s))]\mathrm{\Delta }s\\ =& -c_i(t)y_i(t-{\eta }_i(t))+\sum _{j=1}^n{a}_{ij}(t)F_j\left(y_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{b}_{ij}(t)G_j\left(y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)+\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)H_j(y_j(s))\mathrm{\Delta }s\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)K_j(y_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s,\end{array}$$

(4.1)

where $i=1,2,\dots ,n$ and for $i,j=1,2,\dots ,n$,

$$\begin{array}{c}{F}_j\left(y_j(t-{\tau }_{ij}(t))\right)=f_j(y_j(t-{\tau }_{ij}(t))+{\overline{x}}_j(t-{\tau }_{ij}(t)))-f_j\left({\overline{x}}_j(t-{\tau }_{ij}(t))\right),\hfill \\ g_j\left(y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)=g_j(y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))+{\overline{x}}_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t)))-g_j\left({\overline{x}}_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right),\hfill \\ H_j(y_j(s))=h_j(x_j(s))-h_j({\overline{x}}_j(s)),K_j(y_j^{\mathrm{\Delta }}(s))=k_j(x_j^{\mathrm{\Delta }}(s))-k_j({\overline{x}}_j^{\mathrm{\Delta }}(s)).\hfill \end{array}$$

From (H₂) we have that for $i,j=1,2,\dots ,n$,

$$\begin{array}{c}\left|F_j\left(y_j(t-{\tau }_{ij}(t))\right)\right|\le L_j\left|y_j(t-{\tau }_{ij}(t))\right|,\hfill \\ \left|G_j\left(y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\right|\le l_j\left|y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right|\hfill \end{array}$$

and

$$\begin{array}{c}\left|H_j(y_j(s))\right|\le L_j^h|y_j(s)|,\hfill \\ \left|K_j(y_j^{\mathrm{\Delta }}(s))\right|\le l_j^k|y_j^{\mathrm{\Delta }}(s)|.\hfill \end{array}$$

The initial condition of (4.1) is

$${\psi }_i(t)={\phi }_i(t)-{\overline{\phi }}_i(t),{\psi }_i^{\mathrm{\Delta }}(t)={\phi }_i^{\mathrm{\Delta }}(t)-{\overline{\phi }}_i^{\mathrm{\Delta }}(t),t\in {[-\iota ,0]}_{\mathbb{T}},i=1,2,\dots ,n.$$

Let ${\mathrm{\Theta }}_i$ and ${\mathrm{\Lambda }}_i$ be defined by

$$\begin{array}{rcl}{\mathrm{\Theta }}_i(\omega )& =& c_i^{-}-\omega -exp(\omega \underset{s\in \mathbb{T}}{sup}\mu (s))(c_i^{+}{\eta }_i^{+}exp\left(\omega {\eta }_i^{+}\right)\\ +\sum _{j=1}^n{a}_{ij}^{+}{L}_{j}exp\left(\omega {\tau }_{ij}^{+}\right)+\sum _{j=1}^n{b}_{ij}^{+}{l}_{j}exp\left(\omega {\sigma }_{ij}^{+}\right)\\ +\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}exp(\omega )+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}exp(\omega )),i=1,2,\dots ,n\end{array}$$

and

$$\begin{array}{rcl}{\mathrm{\Lambda }}_i(\omega )& =& c_i^{-}-\omega -(c_i^{+}exp(\omega \underset{s\in \mathbb{T}}{sup}\mu (s))+c_i^{-}-\omega )(c_i^{+}{\eta }_i^{+}exp\left(\omega {\eta }_i^{+}\right)\\ +\sum _{j=1}^n{a}_{ij}^{+}{L}_{j}exp\left(\omega {\tau }_{ij}^{+}\right)+\sum _{j=1}^n{b}_{ij}^{+}{l}_{j}exp\left(\omega {\sigma }_{ij}^{+}\right)\\ +\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}exp(\omega )+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}exp(\omega )),i=1,2,\dots ,n.\end{array}$$

By (H₃), for $i=1,2,\dots ,n$, we get

$${\mathrm{\Theta }}_i(0)=c_i^{-}-(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})>0$$

and

$${\mathrm{\Lambda }}_i(0)=c_i^{-}-(c_i^{+}+c_i^{-})(c_i^{+}{\eta }_i^{+}+\sum _{j=1}^n{a}_{ij}^{+}{L}_j+\sum _{j=1}^n{b}_{ij}^{+}{l}_j+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij})>0.$$

Since ${\mathrm{\Theta }}_i$, ${\mathrm{\Lambda }}_i$ are continuous on $[0,+\mathrm{\infty })$ and ${\mathrm{\Theta }}_i(\omega )$, ${\mathrm{\Theta }}_i(\omega )\to -\mathrm{\infty }$, as $\omega \to +\mathrm{\infty }$, so there exist ${\omega }_i,{\omega }_i^{\ast }>0$ such that ${\mathrm{\Theta }}_i({\omega }_i)={\mathrm{\Lambda }}_i({\omega }_i^{\ast })=0$ and ${\mathrm{\Theta }}_i(\omega )>0$ for $\omega \in (0,{\omega }_i)$, ${\mathrm{\Lambda }}_i(\omega )>0$ for $\omega \in (0,{\omega }_i^{\ast })$, $i=1,2,\dots ,n$.

By choosing $a=min\{{\omega }_1,{\omega }_2,\dots ,{\omega }_n,{\omega }_1^{\ast },{\omega }_2^{\ast },\dots ,{\omega }_n^{\ast }\}$, we have ${\mathrm{\Theta }}_i(a)\ge 0$, ${\mathrm{\Lambda }}_i(a)\ge 0$, $i=1,2,\dots ,n$. So, we can choose a positive constant $0<\lambda <min\{a,{min}_{1\le i\le n}\{c_i^{-}\}\}$ such that

$${\mathrm{\Theta }}_i(\lambda )>0,{\mathrm{\Lambda }}_i(\lambda )>0,i=1,2,\dots ,n,$$

which implies that

$$\begin{array}{c}\frac{exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_i^{-}-\lambda }(c_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+\sum _{j=1}^n{a}_{ij}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)+\sum _{j=1}^n{b}_{ij}^{+}{l}_{j}exp\left(\lambda {\sigma }_{ij}^{+}\right)\hfill \\ +\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}exp(\lambda )+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}exp(\lambda ))<1\hfill \end{array}$$

(4.2)

and

$$\begin{array}{c}(1+\frac{c_i^{+}exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_i^{-}-\lambda })(c_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+\sum _{j=1}^n{a}_{ij}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)\hfill \\ +\sum _{j=1}^n{b}_{ij}^{+}{l}_{j}exp\left(\lambda {\sigma }_{ij}^{+}\right)+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}exp(\lambda )+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}exp(\lambda ))<1,\hfill \end{array}$$

(4.3)

where $i=1,2,\dots ,n$. Let

$$M=\underset{1\le i\le n}{max}\left\{\frac{c_i^{-}}{c_i^{+}{\eta }_i^{+}+{\sum }_{j=1}^n{a}_{ij}^{+}{L}_j+{\sum }_{j=1}^n{b}_{ij}^{+}{l}_j+{\sum }_{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}+{\sum }_{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}}\right\},$$

by (H₃) we have $M>1$. Thus

$$\begin{array}{rcl}\frac{1}{M}& <& \frac{exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_i^{-}-\lambda }(c_i^{+}{\eta }_i^{+}exp\left(\lambda {\eta }_i^{+}\right)+\sum _{j=1}^n{a}_{ij}^{+}{L}_{j}exp\left(\lambda {\tau }_{ij}^{+}\right)\\ +\sum _{j=1}^n{b}_{ij}^{+}{l}_{j}exp\left(\lambda {\sigma }_{ij}^{+}\right)+\sum _{j=1}^n{d}_{ij}^{+}{L}_j^h{\overline{\theta }}_{ij}exp(\lambda )+\sum _{j=1}^n{e}_{ij}^{+}{l}_j^k{\overline{\xi }}_{ij}exp(\lambda )).\end{array}$$

Rewrite (4.1) in the form

$$\begin{array}{rcl}{y}_i^{\mathrm{\Delta }}(t)+c_i(t)y_i(t)& =& c_i(t){\int }_{t-{\eta }_i(t)}^t{y}_i^{\mathrm{\Delta }}(s)\mathrm{\Delta }s+\sum _{j=1}^n{a}_{ij}(t)F_j\left(y_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{b}_{ij}(t)G_j\left(y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)+\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)H_j(y_j(s))\mathrm{\Delta }s\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)K_j(y_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s,i=1,2,\dots ,n.\end{array}$$

(4.4)

Multiplying the both sides of (4.4) by $e_{-c_i}(t,\sigma (s))$ and integrating over ${[t_0,t]}_{\mathbb{T}}$, we get

$$\begin{array}{rcl}{y}_i(t)& =& y_i(t_0)e_{-c_i}(t,t_0)+{\int }_{t_0}^t{e}_{-c_i}(t,\sigma (s))\{c_i(s){\int }_{s-{\eta }_i(s)}^s{y}_i^{\mathrm{\Delta }}(s)\mathrm{\Delta }s\\ +\sum _{j=1}^n{a}_{ij}(s)F_j\left(y_j(s-{\tau }_{ij}(s))\right)+\sum _{j=1}^n{b}_{ij}(s)G_j\left(y_j^{\mathrm{\Delta }}(s-{\sigma }_{ij}(s))\right)\\ +\sum _{j=1}^n{d}_{ij}(s){\int }_{s-{\delta }_{ij}(s)}^s{\theta }_{ij}(u)H_j(y_j(u))\mathrm{\Delta }u\\ +\sum _{j=1}^n{e}_{ij}(s){\int }_{s-{\zeta }_{ij}(s)}^s{\xi }_{ij}(u)K_j(y_j^{\mathrm{\Delta }}(u))\mathrm{\Delta }u\}\mathrm{\Delta }s,i=1,2,\dots ,n.\end{array}$$

(4.5)

It is easy to see that

$${\parallel y(t)\parallel }_1={\parallel \psi (t)\parallel }_1\le {\parallel \psi \parallel }_{\mathbb{X}}\le M{e}_{\ominus \lambda }(t,t_0){\parallel \psi \parallel }_{\mathbb{X}},\mathrm{\forall }t\in {[-\iota ,0]}_{\mathbb{T}}.$$

We claim that

$${\parallel y(t)\parallel }_1\le M{e}_{\ominus \lambda }(t,t_0){\parallel \psi \parallel }_{\mathbb{X}},\mathrm{\forall }t\in {(0,+\mathrm{\infty })}_{\mathbb{T}}.$$

(4.6)

To prove (4.6), we first show that for any $p>1$, the following inequality holds:

$${\parallel y(t)\parallel }_1<pM{e}_{\ominus \lambda }(t,t_0){\parallel \psi \parallel }_{\mathbb{X}},\mathrm{\forall }t\in {(0,+\mathrm{\infty })}_{\mathbb{T}}.$$

(4.7)

If (4.7) is not true, then there must be some $t_1\in {(0,+\mathrm{\infty })}_{\mathbb{T}}$ and some $i_1,i_2\in \{1,2,\dots ,n\}$ such that

$$\begin{array}{rcl}{\parallel y(t_1)\parallel }_1& =& max\{{\parallel y(t_1)\parallel }_0,{\parallel y^{\mathrm{\Delta }}(t_1)\parallel }_0\}=max\left\{\right|y_{i_1}(t_1)|,|y_{i_2}^{\mathrm{\Delta }}(t_1)\left|\right\}\\ \ge & pM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\end{array}$$

and

$${\parallel y(t)\parallel }_1\le pM{e}_{\ominus \lambda }(t,t_0){\parallel \psi \parallel }_{\mathbb{X}},t\in {[-\iota ,t_1]}_{\mathbb{T}}.$$

Therefore, there must exist a constant $c\ge 1$ such that

$$\begin{array}{rcl}{\parallel y(t_1)\parallel }_1& =& max\{{\parallel y(t_1)\parallel }_0,{\parallel y^{\mathrm{\Delta }}(t_1)\parallel }_0\}=max\left\{\right|y_{i_1}(t_1)|,|y_{i_2}^{\mathrm{\Delta }}(t_1)\left|\right\}\\ =& cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\end{array}$$

(4.8)

and

$${\parallel y(t)\parallel }_1\le cpM{e}_{\ominus \lambda }(t,t_0){\parallel \psi \parallel }_{\mathbb{X}},t\in {[-\iota ,t_1]}_{\mathbb{T}}.$$

(4.9)

By (4.5), (4.8), (4.9) and (H₁)-(H₃), we obtain

$$\begin{array}{rcl}|y_{i_1}(t_1)|& \le & {\parallel \psi \parallel }_X{e}_{-c_{i_1}}(t_1,t_0)+cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}{\int }_{t_0}^{t_1}{e}_{-c_{i_1}}(t_1,\sigma (s))e_{\lambda }(t_1,\sigma (s))\\ \times \{c_{i_1}^{+}{\int }_{s-{\eta }_{i_1}(s)}^s{e}_{\lambda }(\sigma (s),\theta )\mathrm{\Delta }\theta +\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_j{e}_{\lambda }(\sigma (s),s-{\tau }_{i_{1}j}(s))\\ +\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_j{e}_{\lambda }(\sigma (s),s-{\sigma }_{i_{1}j}(s))+\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}{e}_{\lambda }(\sigma (s),s)\\ +\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}{e}_{\lambda }(\sigma (s),s)\}\mathrm{\Delta }s\\ \le & {\parallel \psi \parallel }_X{e}_{-c_{i_1}}(t_1,t_0)+cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}{\int }_{t_0}^{t_1}{e}_{-c_{i_1}\oplus \lambda }(t_1,\sigma (s))\\ \times \{c_{i_1}^{+}{\eta }_{i_1}^{+}{e}_{\lambda }(\sigma (s),s-{\eta }_{i_1}(s))+\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_j{e}_{\lambda }(\sigma (s),s-{\tau }_{i_{1}j}(s))\\ +\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_j{e}_{\lambda }(\sigma (s),s-{\sigma }_{i_{1}j}(s))+\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}{e}_{\lambda }(\sigma (s),s)\\ +\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}{e}_{\lambda }(\sigma (s),s)\}\mathrm{\Delta }s\\ \le & {\parallel \psi \parallel }_X{e}_{-c_{i_1}}(t_1,t_0)+cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}{\int }_{t_0}^{t_1}{e}_{-c_{i_1}\oplus \lambda }(t_1,\sigma (s))\\ \times \{c_{i_1}^{+}{\eta }_{i_1}^{+}exp\left[\lambda ({\eta }_{i_1}^{+}+\underset{s\in \mathbb{T}}{sup}\mu (s))\right]+\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_{j}exp\left[\lambda ({\tau }_{i_{1}j}^{+}+\underset{s\in \mathbb{T}}{sup}\mu (s))\right]\\ +\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_{j}exp\left[\lambda ({\sigma }_{i_{1}j}^{+}+\underset{s\in \mathbb{T}}{sup}\mu (s))\right]+\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s))\\ +\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s))\}\mathrm{\Delta }s\\ =& cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\{\frac{1}{pM}{e}_{-c_{i_1}\oplus \lambda }(t_1,t_0)\\ +exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s))[c_{i_1}^{+}{\eta }_{i_1}^{+}exp\left(\lambda {\eta }_{i_1}^{+}\right)+\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{1}j}^{+}\right)\\ +\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{1}j}^{+}\right)+\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}+\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}]\\ \times {\int }_{t_0}^{t_1}{e}_{-c_{i_1}\oplus \lambda }(t_1,\sigma (s))\mathrm{\Delta }s\}\\ <& cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\{\frac{1}{M}{e}_{-(c_{i_1}^{-}-\lambda )}(t_1,t_0)+exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s))[c_{i_1}^{+}{\eta }_{i_1}^{+}exp\left(\lambda {\eta }_{i_1}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{1}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{1}j}^{+}\right)+\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}+\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}]\\ \times \frac{1}{-(c_{i_1}^{-}-\lambda )}{\int }_{t_0}^{t_1}-(c_{i_1}^{-}-\lambda )e_{-(c_{i_1}^{-}-\lambda )}(t_1,\sigma (s))\mathrm{\Delta }s\}\\ \le & cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\left\{\right[\frac{1}{M}-\frac{exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_{i_1}^{-}-\lambda }(c_{i_1}^{+}{\eta }_{i_1}^{+}exp\left(\lambda {\eta }_{i_1}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{1}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{1}j}^{+}\right)+\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}\\ +\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}\left)\right]e_{-(c_{i_1}^{-}-\lambda )}(t_1,t_0)+\frac{exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_{i_1}^{-}-\lambda }(c_{i_1}^{+}{\eta }_{i_1}^{+}exp\left(\lambda {\eta }_{i_1}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{1}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{1}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{1}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{1}j}^{+}\right)\\ +\sum _{j=1}^n{d}_{i_{1}j}^{+}{L}_j^h{\overline{\theta }}_{i_{1}j}exp(\lambda )+\sum _{j=1}^n{e}_{i_{1}j}^{+}{l}_j^k{\overline{\xi }}_{i_{1}j}exp(\lambda )\left)\right\}\\ <& cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}.\end{array}$$

(4.10)

By Lemma 2.4 and (4.5), we have, for $i=1,2,\dots ,n$,

$$\begin{array}{rcl}{y}_i^{\mathrm{\Delta }}(t)& =& -c_i(t)y_i(t_0)e_{-c_i}(t,t_0)+(c_i(t){\int }_{t-{\eta }_i(t)}^t{y}_i^{\mathrm{\Delta }}(s)\mathrm{\Delta }s+\sum _{j=1}^n{a}_{ij}(t)F_j\left(y_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^n{b}_{ij}(t)G_j\left(y_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right))+\sum _{j=1}^n{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)H_j(y_j(s))\mathrm{\Delta }s\\ +\sum _{j=1}^n{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)K_j(y_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s\\ +{\int }_{t_0}^t-c_i(t)e_{-c_i}(t,\sigma (s))\{c_i(s){\int }_{s-{\eta }_i(s)}^s{y}_i^{\mathrm{\Delta }}(u)\mathrm{\Delta }u+\sum _{j=1}^n{a}_{ij}(s)F_j\left(y_j(s-{\tau }_{ij}(s))\right)\\ +\sum _{j=1}^n{b}_{ij}(s)G_j\left(y_j^{\mathrm{\Delta }}(s-{\sigma }_{ij}(s))\right)+\sum _{j=1}^n{d}_{ij}(s){\int }_{s-{\delta }_{ij}(s)}^s{\theta }_{ij}(u)H_j(y_j(u))\mathrm{\Delta }u\\ +\sum _{j=1}^n{e}_{ij}(s){\int }_{s-{\zeta }_{ij}(s)}^s{\xi }_{ij}(u)K_j(y_j^{\mathrm{\Delta }}(u))\mathrm{\Delta }u\}\mathrm{\Delta }s.\end{array}$$

(4.11)

Thus, it follows from (4.8), (4.9) and (4.11) that

$$\begin{array}{rcl}|y_{i_2}^{\mathrm{\Delta }}(t_1)|& \le & c_{i_2}^{+}{e}_{-c_{i_2}}(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}+cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_X(c_{i_2}^{+}{\int }_{t_1-{\eta }_{i_2}(t_1)}^{t_1}{e}_{\lambda }(t_1,\theta )\mathrm{\Delta }\theta \\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_j{e}_{\lambda }(t_1,t_1-{\tau }_{i_{2}j}(t_1))+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_j{e}_{\lambda }(t_1,t_1-{\sigma }_{i_{2}j}(t_1))\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}{e}_{\lambda }(t_1,t_1)+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}{e}_{\lambda }(t_1,t_1))\\ +c_{i_2}^{+}cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}{\int }_{t_0}^{t_1}{e}_{-c_{i_2}}(t_1,\sigma (s))e_{\lambda }(t_1,\sigma (s))\\ \times \{c_{i_2}^{+}{\int }_{s-{\eta }_{i_2}(s)}^s{e}_{\lambda }(\sigma (s),\theta )\mathrm{\Delta }\theta \\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_j{e}_{\lambda }(\sigma (s),s-{\tau }_{i_{2}j}(s))+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_j{e}_{\lambda }(\sigma (s),s-{\sigma }_{i_{2}j}(s))\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}{e}_{\lambda }(\sigma (s),s)+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}{e}_{\lambda }(\sigma (s),s)\}\mathrm{\Delta }s\\ \le & c_{i_2}^{+}{e}_{-c_{i_2}}(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}+cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}(c_{i_2}^{+}{\eta }_{i_2}^{+}{e}_{\lambda }(t_1,t_1-{\eta }_{i_2}(t_1))\\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_j{e}_{\lambda }(t_1,t_1-{\tau }_{i_{2}j}(t_1))+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_j{e}_{\lambda }(t_1,t_1-{\sigma }_{i_{2}j}(t_1))\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j})+c_{i_2}^{+}cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}{\int }_{t_0}^{t_1}{e}_{-c_{i_2}\oplus \lambda }(t_1,\sigma (s))\\ \times \{c_{i_2}^{+}{\eta }_{i_2}^{+}{e}_{\lambda }(\sigma (s),s-{\eta }_{i_2}(s))+\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_j{e}_{\lambda }(\sigma (s),s-{\tau }_{i_{2}j}(s))\\ +\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_j{e}_{\lambda }(\sigma (s),s-{\sigma }_{i_{2}j}(s))+\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}{e}_{\lambda }(\sigma (s),s)\\ +\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}{e}_{\lambda }(\sigma (s),s)\}\mathrm{\Delta }s\\ \le & c_{i_2}^{+}{e}_{-c_{i_2}}(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}+cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}(c_{i_2}^{+}{\eta }_{i_2}^{+}exp\left(\lambda {\eta }_{i_2}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{2}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{2}j}^{+}\right)\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}exp(\lambda )+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}exp(\lambda ))\\ \times (1+c_{i_2}^{+}exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s)){\int }_{t_0}^{t_1}{e}_{-c_{i_2}\oplus \lambda }(t_1,\sigma (s))\mathrm{\Delta }s)\\ <& cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\{\frac{c_{i_2}^{+}}{M}{e}_{-c_{i_2}\oplus \lambda }(t_1,t_0)+(c_{i_2}^{+}{\eta }_{i_2}^{+}exp\left(\lambda {\eta }_{i_2}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{2}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{2}j}^{+}\right)\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}exp(\lambda )+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}exp(\lambda ))\\ \times (1+c_{i_2}^{+}exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s)){\int }_{t_0}^{t_1}{e}_{-c_{i_2}\oplus \lambda }(t_1,\sigma (s))\mathrm{\Delta }s)\}\\ \le & cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\{\frac{c_{i_2}^{+}}{M}{e}_{-(c_{i_2}^{-}-\lambda )}(t_1,t_0)+(c_{i_2}^{+}{\eta }_{i_2}^{+}exp\left(\lambda {\eta }_{i_2}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{2}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{2}j}^{+}\right)\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}exp(\lambda )+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}exp(\lambda ))\\ \times (1+c_{i_2}^{+}exp(\lambda \underset{s\in \mathbb{T}}{sup}\mu (s))\frac{1}{-(c_{i_2}^{-}-\lambda )}(e_{-(c_{i_2}^{-}-\lambda )}(t_1,t_0)-1))\}\\ \le & cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}\left\{\right[\frac{1}{M}-\frac{exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_{i_2}^{-}-\lambda }(c_{i_2}^{+}{\eta }_{i_2}^{+}exp\left(\lambda {\eta }_{i_2}^{+}\right)\\ +\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{2}j}^{+}\right)+\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{2}j}^{+}\right)\\ +\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}exp(\lambda )+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}exp(\lambda )\left)\right]c_{i_2}^{+}{e}_{-(c_{i_2}^{-}-\lambda )}(t_1,t_0)\\ +(1+\frac{c_{i_2}^{+}exp(\lambda {sup}_{s\in \mathbb{T}}\mu (s))}{c_{i_2}^{-}-\lambda })(c_{i_2}^{+}{\eta }_{i_2}^{+}exp\left(\lambda {\eta }_{i_2}^{+}\right)+\sum _{j=1}^n{a}_{i_{2}j}^{+}{L}_{j}exp\left(\lambda {\tau }_{i_{2}j}^{+}\right)\\ +\sum _{j=1}^n{b}_{i_{2}j}^{+}{l}_{j}exp\left(\lambda {\sigma }_{i_{2}j}^{+}\right)+\sum _{j=1}^n{d}_{i_{2}j}^{+}{L}_j^h{\overline{\theta }}_{i_{2}j}exp(\lambda )+\sum _{j=1}^n{e}_{i_{2}j}^{+}{l}_j^k{\overline{\xi }}_{i_{2}j}exp(\lambda )\left)\right\}\\ <& cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}}.\end{array}$$

(4.12)

In view of (4.10) and (4.12), we get

$${\parallel y(t_1)\parallel }_1<cpM{e}_{\ominus \lambda }(t_1,t_0){\parallel \psi \parallel }_{\mathbb{X}},$$

which contradicts (4.8), and so (4.7) holds. Letting $p\to 1$, then (4.6) holds. Hence, the almost periodic solution of system (1.1) is globally exponentially stable. This completes the proof. □

Remark 4.1 When $\mathbb{T}=\mathbb{R}$, ${\eta }_i(t)=d_{ij}(t)=e_{ij}(t)\equiv 0$, $i=1,2,\dots ,n$, Theorem 3.1 and Theorem 4.1 are reduced to Theorem 2.3 and Theorem 3.1 in [37], respectively.

Remark 4.2 According to Theorem 3.1 and Theorem 4.1, we see that the existence and exponential stability of almost periodic solutions for system (1.1) only depend on time delays ${\eta }_i$ (the delays in the leakage term) and do not depend on time delays ${\tau }_{ij}$ and ${\sigma }_{ij}$.

5 An example

In this section, we give an example to illustrate the feasibility and effectiveness of our results obtained in Sections 3 and 4.

Example 5.1 Let $n=3$. Consider the following neutral Hopfield neural network on time scale :

$$\begin{array}{rcl}{x}_i^{\mathrm{\Delta }}(t)& =& -c_i(t)x_i(t-{\eta }_i(t))+\sum _{j=1}^3{a}_{ij}(t)f_j\left(x_j(t-{\tau }_{ij}(t))\right)\\ +\sum _{j=1}^3{d}_{ij}(t){\int }_{t-{\delta }_{ij}(t)}^t{\theta }_{ij}(s)h_j(x_j(s))\mathrm{\Delta }s+\sum _{j=1}^3{b}_{ij}(t)g_j\left(x_j^{\mathrm{\Delta }}(t-{\sigma }_{ij}(t))\right)\\ +\sum _{j=1}^3{e}_{ij}(t){\int }_{t-{\zeta }_{ij}(t)}^t{\xi }_{ij}(s)k_j(x_j^{\mathrm{\Delta }}(s))\mathrm{\Delta }s+I_i(t),\end{array}$$

(5.1)

where $i=1,2,3$ and the coefficients are as follows:

$$\begin{array}{c}{c}_1(t)=0.5+0.1|sint|,c_2(t)=0.6+0.3|cos\sqrt{2}t|,c_3(t)=0.8+0.1|sin2t|,\hfill \\ {\eta }_1(t)=\frac{1+|sin\sqrt{2}t|}{200},{\eta }_2(t)=\frac{1.8+0.2|cos\sqrt{2}t|}{100},{\eta }_3(t)=\frac{2.5+0.5|sin2t|}{200},\hfill \\ {(a_{ij}(t))}_{3\times 3}=\left(\begin{array}{ccc}0.08|sint|& 0.15|cos\sqrt{2}t|& 0.06|cost|\\ 0.15|cost|& 0.12|cos\sqrt{2}t|& 0.04|sin\sqrt{2}t|\\ 0.10|sint|& 0.08|sin\sqrt{2}t|& 0.09|sint|\end{array}\right),\hfill \\ {(b_{ij}(t))}_{3\times 3}=\left(\begin{array}{ccc}0.10|sint|& 0.06|sin\sqrt{2}t|& 0.05|cost|\\ 0.06|sint|& 0.03|cos\sqrt{2}t|& 0.08|sin\sqrt{2}t|\\ 0.12|cost|& 0.04|sin\sqrt{2}t|& 0.07|sint|\end{array}\right),\hfill \\ {(d_{ij}(t))}_{3\times 3}=\left(\begin{array}{ccc}0.02|cost|& 0.15|sin\sqrt{2}t|& 0.01|cost|\\ 0.05|sint|& 0.12|cos\sqrt{2}t|& 0.03|sin\sqrt{2}t|\\ 0.03|sint|& 0.08|cos\sqrt{2}t|& 0.01|sint|\end{array}\right),\hfill \\ {(e_{ij}(t))}_{3\times 3}=\left(\begin{array}{ccc}0.02|cost|& 0.01|sin\sqrt{2}t|& 0.05|cost|\\ 0.01|sint|& 0.03|cos\sqrt{2}t|& 0.04|cos\sqrt{2}t|\\ 0.02|cost|& 0.04|sin\sqrt{2}t|& 0.01|sint|\end{array}\right),\hfill \\ f_1(x)=0.2|x|,f_2(x)=0.4|sinx|,f_3(x)=|x|,\hfill \\ g_1(x)=0.3|cosx|,g_2(x)=0.1|x|,g_3(x)=0.5|sinx|,\hfill \\ h_1(x)=0.1|x|,h_2(x)=0.4|sinx|,h_3(x)=0.2|x|,\hfill \\ k_1(x)=0.3|cosx|,k_2(x)=k_3(x)=0.2|x|,\hfill \\ {\theta }_{ij}(u)=exp(-2u),{\xi }_{ij}(u)=exp(-4u),\hfill \\ {\delta }_{ij}(t)=0.001|sint|,{\zeta }_{ij}(t)=0.002|cost|,i,j=1,2,3.\hfill \end{array}$$

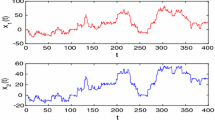
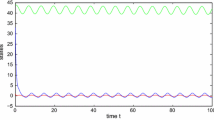
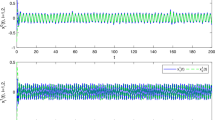
Take ${\tau }_{ij}>0$, ${\sigma }_{ij}>0$, $I_i(t)$ ($i,j=1,2,3$) to be arbitrary almost periodic functions. If $\mathbb{T}=\mathbb{R}$, then $\mu (t)=0$ and if $\mathbb{T}=\mathbb{Z}$, then $\mu (t)=1$. By calculating, we can easily check, for above two cases, that $-c_i\in {\mathcal{R}}^{+}$, $r\approx 0.7961<1$. By Theorem 3.1 and Theorem 4.1, we know that system (5.1) has a unique almost periodic solution that is globally exponentially stable. This shows that the almost periodicity of system (5.1) does not depend on time scale . In particular, the continuous-time neural network and the discrete-time analogue described by (5.1) have the same dynamical behaviors (see Figures 1-4).

Figure 1

Continuous situation ${\mathit{x}}_{\mathbf{1}}$ , ${\mathit{x}}_{\mathbf{2}}$ , ${\mathit{x}}_{\mathbf{3}}$ with time t .

Figure 2

Continuous situation ${\mathit{x}}_{\mathbf{1}}$ , ${\mathit{x}}_{\mathbf{2}}$ , ${\mathit{x}}_{\mathbf{3}}$ .

Figure 3

Discrete situation ${\mathit{x}}_{\mathbf{1}}$ , ${\mathit{x}}_{\mathbf{2}}$ , ${\mathit{x}}_{\mathbf{3}}$ with time t .

Figure 4

Discrete situation ${\mathit{x}}_{\mathbf{1}}$ , ${\mathit{x}}_{\mathbf{2}}$ , ${\mathit{x}}_{\mathbf{3}}$ .

6 Conclusion

In this paper, a class of neutral delay Hopfield neural networks with neutral time-varying delays in the leakage term on time scales is investigated. For the model, we have given some sufficient conditions ensuring the existence and global exponential stability of almost periodic solutions by using the exponential dichotomy of linear dynamic equations on time scales, Banach’s fixed point theorem and the theory of calculus on time scales. These obtained results are new and complement previously known results. Furthermore, a simple example is given to demonstrate the effectiveness of our results and the example also shows that the continuous-time neural network and the discrete-time analogue have the same dynamical behaviors.