Weighted pseudo almost periodic solutions for Clifford-valued neutral-type neural networks with leakage delays on time scales

Abstract

In this paper, we consider a class of Clifford-valued neutral-type neural networks with leakage delays on time scales. We do not decompose the networks under consideration into real-valued systems, but we directly study the Clifford-valued networks. We first establish the existence of weighted pseudo almost periodic solutions of this class of neural networks by the theory of calculus on time scales and the Banach fixed point theorem. Then, we study the global exponential stability of weighted pseudo almost periodic solutions of this class of neural networks by using inequality techniques and the proof by contradiction. Finally, we give an example to illustrate the feasibility of the obtained results.

1 Introduction

After nearly half a century of development, neural network theory has been widely and successfully applied in many research fields, such as associative memory, pattern recognition, automatic control, signal processing, auxiliary decision-making, artificial intelligence, and so on [1–6]. With the development of artificial intelligence technology, the integration of neural network and fuzzy logic, expert system, genetic algorithm, wavelet, chaos, rough set, fractal, evidence theory, grey system, and other technologies has become an important development trend of intelligent technology, which has a good development prospect. Although neural networks have been widely used in many fields, their development is not very mature, and there are still some problems to be further studied. For example, the basic theoretical framework of neural computing and the research of physiological level still need to be in-depth, the research of new models and structures, the better combination of neural network technology and other technologies, etc.

As far as the new neural network models are concerned, Clifford-valued neural networks, which are neural networks whose state variables and connection weights are all Clifford numbers, were first proposed in the reference [7]. They include real-valued neural networks, complex-valued neural networks, and quaternion-valued neural networks as their special cases, and they have more advantages than real-valued networks (see [8]). Recently, more and more attention has been paid to the study of Clifford-valued neural networks [9–13]. However, because Clifford-valued neural networks are a kind of multi-dimensional neural networks, and the multiplication of Clifford numbers does not satisfy the commutativity law, it is more difficult to study the dynamics of Clifford-valued neural networks than that of real-valued and complex-valued neural networks. Nevertheless, it is well known that the dynamics of neural networks is of great significance to the design and implementation of neural networks. Recently, in [12–14], by decomposing Clifford-valued systems into real-valued systems, the stability of the equilibrium, anti-periodicity, and $S^{P}$-almost periodicity of three types of Clifford-valued neural networks have been studied, respectively. At present, it is rare to study the dynamics of Clifford-valued neural networks by direct method, that is, not decomposing the Clifford-valued neural networks into real-value systems [15, 16]. In particular, until now, no paper has been published on the dynamics of Clifford-valued neural networks on time scales by direct method.

On the one hand, time delays are inevitable in real systems, and the existence of time delays may change the dynamic behavior of systems. The three types of time delays usually considered in neural network systems are transmission delay, leakage delay, and neutral-type delay. Therefore, neural network models with these types of delays are widely studied [17–21].

On the other hand, as we all know, the continuous-time systems and the discrete-time systems have the same importance in theory and practice, and the discrete-time systems are more convenient for computer processing than the continuous-time ones. So it is necessary to study the continuous-time systems and the discrete-time systems at the same time. The time scale calculus theory can unify the research of continuous analysis and discrete analysis, so the study of neural networks on time scales has important theoretical and practical significance.

In addition, in the design, implementation, and application of neural networks, the existence and stability of periodic solutions, almost periodic solutions, pseudo almost periodic solutions, and almost automorphic solutions of non-autonomous neural networks are of equal importance to the existence and stability of equilibrium solutions of autonomous neural networks. The weighted pseudo almost periodicity is the generalization of almost periodicity and pseudo almost periodicity, so it is of great theoretical significance and practical value to study the existence and stability of weighted pseudo almost periodic solutions of neural networks [22–24].

Based on the above discussion, one can see that studying Clifford-valued neural networks on time scales cannot only unify the research of real-valued neural networks, complex-valued neural networks, and quaternion-valued neural networks, but also unify the research of continuous-time neural networks and discrete-time neural networks. At the same time, the weighted pseudo almost periodic oscillation is one of the important dynamic behaviors of neural networks. Therefore, the main purpose of this paper is to study the existence and global exponential stability of weighted pseudo almost periodic solutions for a class of Clifford-valued neutral-type neural networks with leakage delays on time scales by direct method. The results of this paper are new. The method can be used to study the existence and stability of almost periodic function solutions of other types of neural networks on time scales.

This paper is organized as follows: In Sect. 2, we introduce some definitions, preliminary lemmas and give a model description. In Sect. 3, we study the existence and global exponential stability of weighted pseudo almost periodic solutions for a class of Clifford-valued neural networks on time scales. In Sect. 4, we investigate the global exponential stability of weighted pseudo almost periodic solutions of this class of neural networks. In Sect. 5, we give an example to demonstrate the feasibility of our results. This paper ends with a brief conclusion in Sect. 6.

2 Preliminaries and model description

The real Clifford algebra over $\mathbb{R}^{m}$ is defined as

$$ \mathcal{A}= \biggl\{ \sum_{A\subseteq \varOmega }x^{A}e_{A}, x^{A}\in \mathbb{R} \biggr\} , $$

where $\varOmega =\{\emptyset , 1,2,\ldots ,A,\ldots ,12\cdots m\}$, $e_{A}=e_{\iota _{1}}e_{\iota _{2}}\cdots e_{\iota _{\nu }}$ with $A=\iota _{1}\iota _{2}\cdots \iota _{\nu }, 1\leq \iota _{1}<\iota _{2}< \cdots <\iota _{\nu }\leq m$. Moreover, $e_{\emptyset }=e_{0}=1$ and $e_{\iota }, \iota =1,2,\ldots ,m$, are called Clifford generators and satisfy the following relations:

$$\begin{aligned} \textstyle\begin{cases} e_{0}^{2}=1, \qquad e_{0}e_{i}=e_{i}e_{0}=e_{i}, & i = 1, 2,\ldots ,m, \\ e_{i}^{2}=1,& i=1,2,\ldots ,s, \\ e_{i}^{2}=-1, & i = s+1, s+2,\ldots ,m, \\ e_{i}e_{j}+e_{j}e_{i}=0, &i\neq j. \end{cases}\displaystyle \end{aligned}$$

For $x=\sum_{A}x^{A}\in \mathcal{A}$, we define $\|x\|_{\mathcal{A}}=\max_{A\in \varOmega }\{|x^{A}|\}$, and for $x=(x_{1},x_{2},\ldots ,x_{n})^{T}\in \mathcal{A}^{n}$, we define $\|x\|_{\mathcal{A}^{n}}=\max_{1\leq p\leq n}\{\|x_{p}\|_{ \mathcal{A}}\}$, then $(\mathcal{A},\|\cdot \|_{\mathcal{A}})$ and $(\mathcal{A}^{n},\|\cdot \|_{\mathcal{A}^{n}})$ are Banach spaces. For more information about Clifford algebra, we refer the reader to [25].

A time scale $\mathbb{T}$ is an arbitrary nonempty closed subset of the real set $\mathbb{R}$. We use $\rho (t)$ and $\nu (t)$ to denote the backward jump operator and the graininess function of $\mathbb{T}$, respectively.

Definition 2.1

([26])

Assume that $f:\mathbb{T} \rightarrow \mathbb{R}$ is a function, and let $t\in \mathbb{T}_{{k}}$. Then we define $f^{\nabla }(t)$ to be the number (provided it exists) with the property that given any $\varepsilon >0$, there is a neighborhood U of t (i.e., $U=(t-\delta ,t+\delta )\cap \mathbb{T}$ for some $\delta >0$) such that

$$ \bigl\vert f\bigl(\rho (t)\bigr)-f(s)-f^{\nabla }(t) \bigl(\rho (t)-s \bigr) \bigr\vert \leq \varepsilon \bigl\vert \rho (t)-s \bigr\vert $$

for all $s\in U$. We call $f^{\nabla }(t)$ the nabla derivative of f at t.

The derivative of function $z=\sum_{A}z^{A}e_{A}:\mathbb{T}\rightarrow \mathcal{A}$ is given by $z^{\nabla }(t)=\sum_{A}(z^{A})^{\nabla }(t)e_{A}$, where $z^{A}:\mathbb{T}\rightarrow \mathbb{R}$.

Let $\mathcal{R}_{\nu }=\{f: \mathbb{T}\rightarrow \mathbb{R}: 1-\nu (t)r(t) \neq 0, \forall t\in \mathbb{T}_{k}\}$ and $\mathcal{R}_{\nu }^{+}=\{r\in \mathcal{R}_{\nu }:1-\nu (t)r(t)>0, \forall t\in \mathbb{T}\}$. Then, for $p \in \mathcal{R}_{\nu }$, we define the nabla exponential function by

$$ \hat{e}_{p}(t,s) =\exp \biggl( \int _{s}^{t}\widehat{\xi }_{\nu (\tau )} \bigl(p( \tau ) \bigr)\nabla \tau \biggr) \quad\text{for } t,s\in \mathbb{T}, $$

where

$$ \hat{\xi }_{h}(z)=\textstyle\begin{cases} -\frac{\operatorname{Log}(1-hz)}{h} &\text{if } h\neq 0, \\ z &\text{if } h=0. \end{cases} $$

For $p,q\in \mathcal{R}_{\nu }$, we define a circle plus addition by $(p \oplus _{\nu } q)(t)= p(t)+q(t)-\nu (t) p(t)q(t)$ for all $t \in \mathbb{T}_{k}$. For $p\in \mathcal{R}_{\nu }$, we define a circle minus p by $\ominus _{\nu } p=-\frac{p}{1-\nu p}$. For the basic theory and notation of the time scale theory, we refer the reader to [26, 27].

Definition 2.2

([28])

A time scale $\mathbb{T}$ is called an almost periodic time scale if

$$\begin{aligned} \varPi:=\{\tau \in \mathbb{R}:t\pm \tau \in \mathbb{T}, \forall t\in \mathbb{T} \}\neq \{0\}. \end{aligned}$$

Remark 2.1

Obviously, if $\mathbb{T}$ is called an almost periodic time scale, then $\inf \mathbb{T}=-\infty$ and $\sup \mathbb{T}=+\infty$.

Lemma 2.1

Let$t\in \mathbb{T}$, where$\mathbb{T}$is an almost periodic time scale. Iftis left-dense, then for every$h\in \varPi$, $t+h$is also left-dense. Similarly, iftis left-scattered, then for every$h\in \varPi$, $t+h$is also left-scattered.

Proof

If t is left-dense, then there exists $\{s_{n}\}\subset \mathbb{T}$ such that

$$ \lim_{n\rightarrow \infty }s_{n}=t \quad\text{and}\quad s_{n}< t. $$

Since $\mathbb{T}$ is an almost periodic time scale, we have

$$ s_{n}+h\in \mathbb{T} \quad\text{and}\quad s_{n}+h< t+h $$

for each $h\in \varPi$. Thus, we obtain that

$$ \lim_{n\rightarrow \infty }s_{n}+h=t+h, $$

so $\rho (t+h)=t+h$. Consequently, $t+h$ is left-dense.

Now, we shall show that if t is left-scattered, then $t+h$ is also left-dense. Otherwise, there exists $h\in \varPi$ such that $t+h$ is left-dense. Then there exists $\{s_{n}+h\}\subset \mathbb{T}$ such that

$$ \lim_{n\rightarrow \infty }s_{n}+h=t+h \quad\text{and}\quad s_{n}+h< t+h. $$

Hence,

$$ \lim_{n\rightarrow \infty }s_{n}=t \quad\text{and}\quad s_{n}< t. $$

Since $\mathbb{T}$ is an almost periodic time scale, we have $\{s_{n}\}\subset \mathbb{T}$. That is, $\rho (t)=t$, which contradicts the fact that t is left-scattered. Hence, $t+h$ is also left-scattered for every $h\in \varPi$. The proof is complete. □

Lemma 2.2

Let$\mathbb{T}$be an almost periodic time scale and$h\in \varPi$, then for each$t\in \mathbb{T}$,

$$\begin{aligned} \rho (t)+h=\rho (t+h) \quad\textit{and} \quad \rho (t)-h=\rho (t-h). \end{aligned}$$

(1)

Proof

If t is left-dense, then, by Lemma 2.1, it is obvious that (1) holds.

If t is left-scattered, then, by Lemma 2.1, for each $h\in \varPi$, $t+h$ is also left-scattered. Hence, for each $h\in \varPi$, $\rho (t+h)< t+h$. That is,

$$\begin{aligned} \rho (t+h)-h< t \quad\text{for each } h\in \varPi. \end{aligned}$$

(2)

Since $\mathbb{T}$ is an almost periodic time scale and $h\in \varPi$, we have that $\rho (t+h)-h\in \mathbb{T}$. According to (2) and the definition of the backward jump operator, for each $h\in \varPi$, we have $\rho (t)\geq \rho (t+h)-h$. Hence,

$$\begin{aligned} \rho (t+h)\leq \rho (t)+h \quad \text{for each } h\in \varPi. \end{aligned}$$

(3)

On the other hand, since t is left-scattered, $\rho (t)< t$. Hence,

$$\begin{aligned} \rho (t)+h< t+h. \end{aligned}$$

(4)

Since $h\in \varPi$, $\rho (t)+h\in \mathbb{T}$. By (4) and the definition of the backward jump operator, we obtain that

$$\begin{aligned} \rho (t)+h\leq \rho (t+h) \quad\text{for each } h \in \varPi. \end{aligned}$$

(5)

By (3) and (5), we obtain that the first equality of (1) holds. Similarly, one can prove that the second equality of (1) also holds. The proof is complete. □

In the following, we always assume that $\mathbb{T}$ is an almost periodic time scale.

Lemma 2.3

If$-a\in \mathcal{R}^{+}_{\nu }$and$t,s\in \mathbb{T}$, $\tau \in \varPi$, then$\hat{e}_{-a}(t+\tau ,\rho (s+\tau ))-\hat{e}_{-a}(t,\rho (s)) =\int ^{t}_{ \rho (s)}\hat{e}_{-a}(t,\rho (\theta )) (a(\theta )-a(\theta + \tau ) )\hat{e}_{-a}(\theta +\tau ,\rho (s+\tau ))\nabla \theta$.

Proof

From $(\hat{e}_{-a}(t,s))^{\nabla }=-a(t)\hat{e}_{-a}(t,s)$ it follows that

$$\begin{aligned} &\bigl(\hat{e}_{-a}\bigl(t+\tau ,\sigma (s+ \tau )\bigr)\bigr)^{\nabla }+a(t)\hat{e}_{-a}\bigl(t+ \tau ,\rho (s+ \tau )\bigr) \\ &\quad =\bigl(a(t)-a(t+\tau )\bigr)\hat{e}_{-a}\bigl(t+\tau ,\rho (s+\tau ) \bigr). \end{aligned}$$

(6)

Multiplying both sides of (6) by $\hat{e}_{-a}(\rho (s),\rho (t))$ and integrating over $[\rho (s),t]_{\mathbb{T}}$, we obtain

$$\begin{aligned} & \int ^{t}_{\rho (s)}e_{-a}\bigl(\rho (s),\rho ( \theta )\bigr) \bigl(a(\theta )-a( \theta +\tau )\bigr) \hat{e}_{-a} \bigl(\theta +\tau ,\rho (s+\tau )\bigr)\nabla \theta \\ &\quad= \int ^{t}_{\rho (s)}\bigl(\hat{e}_{-a}\bigl( \theta +\tau ,\rho (s+\tau )\bigr)\bigr)^{ \nabla } \hat{e}_{-a} \bigl(\rho (s),\rho (\theta )\bigr)\nabla \theta \\ &\qquad{}+ \int ^{t}_{\rho (s)}a(\theta )\hat{e}_{-a}\bigl( \theta +\tau ,\rho (s+ \tau )\bigr) \hat{e}_{-a}\bigl(\rho (s),\rho ( \theta )\bigr)\nabla \theta. \end{aligned}$$

Noting that $[\hat{e}_{p}(c,\cdot ) ]^{\nabla }=-p [e_{p}(c,\cdot ) ]^{\rho }$ and by Lemma 2.2, $\rho (t+\tau )=\rho (t)+\tau$, we have

$$\begin{aligned} & \int ^{t}_{\rho (s)}e_{-a}\bigl(\rho (s),\rho ( \theta )\bigr) \bigl(a(\theta )-a( \theta +\tau )\bigr) \hat{e}_{-a} \bigl(\theta +\tau ,\rho (s+\tau )\bigr)\nabla \theta \\ &\quad= \int ^{t}_{\rho (s)} \bigl(\bigl(\hat{e}_{-a} \bigl(\theta +\tau ,\rho (s+\tau )\bigr)\bigr)^{ \nabla } \hat{e}_{-a}\bigl(\rho (s),\rho (\theta )\bigr) \\ &\qquad{}+\hat{e}_{-a}\bigl(\theta +\tau ,\rho (s+\tau )\bigr) \bigl( \hat{e}_{-a}\bigl(\rho (s), \theta \bigr)\bigr)^{\nabla } \bigr) \nabla \theta \\ &\quad= \int ^{t}_{\rho (s)} \bigl(\hat{e}_{-a}\bigl( \theta +\tau ,\rho (s+\tau )\bigr) \hat{e}_{-a}\bigl(\rho (s),\theta \bigr) \bigr)^{\nabla }\nabla \theta \\ &\quad=\hat{e}_{-a}\bigl(t+\tau ,\rho (s+\tau )\bigr)\hat{e}_{-a} \bigl(\rho (s),t\bigr)- \hat{e}_{-a}\bigl(\rho (s)+\tau ,\rho (s+\tau ) \bigr) \hat{e}_{-a}\bigl(\rho (s), \rho (s)\bigr) \\ &\quad=\hat{e}_{-a}\bigl(t+\tau ,\rho (s+\tau )\bigr)\hat{e}_{-a} \bigl(\rho (s),t\bigr)-1. \end{aligned}$$

(7)

Multiplying both sides of (7) by $\hat{e}_{-a}(t,\rho (s))$, we obtain

$$\begin{aligned} &\hat{e}_{-a}\bigl(t+\tau ,\rho (s+\tau )\bigr)-\hat{e}_{-a} \bigl(t,\rho (s)\bigr) \\ &\quad= \int ^{t}_{\rho (s)}\hat{e}_{-a}\bigl(t,\rho (s) \bigr)\hat{e}_{-a}\bigl(\rho (s), \rho (\theta )\bigr) \bigl(a(\theta )-a(\theta +\tau ) \bigr)\hat{e}_{-a}\bigl( \theta +\tau ,\rho (s+\tau )\bigr)\nabla \theta \\ &\quad= \int ^{t}_{\rho (s)}\hat{e}_{-a}\bigl(t,\rho ( \theta )\bigr) \bigl(a(\theta )-a( \theta +\tau ) \bigr)\hat{e}_{-a} \bigl(\theta +\tau ,\rho (s+\tau )\bigr)\nabla \theta. \end{aligned}$$

The proof is complete. □

In the sequel, we denote by $BC(\mathbb{T},\mathcal{A}^{n})$ the set of all bounded continuous functions from $\mathbb{T}$ to $\mathcal{A}^{n}$ and by $C^{1}_{\nabla }(\mathbb{T},\mathcal{A}^{n})$ the set of all functions from $\mathbb{T}$ to $\mathcal{A}^{n}$ with continuous ∇-derivatives. Obviously, $BC(\mathbb{T},\mathcal{A}^{n})$ with the norm $\|x\|_{\infty }=\sup_{t\in \mathbb{T}}\|x(t)\|_{\mathcal{A}^{n}}$ is a Banach space.

Similar to Definition 3.9 in [28], we give the following definition.

Definition 2.3

A function $f \in BC(\mathbb{T},\mathcal{A}^{n})$ is called almost periodic on $\mathbb{T}$ if the ε-translation set of

$$\begin{aligned} E\{\varepsilon ,f\}=\bigl\{ {\tau \in \varPi: \bigl\Vert f(t+\tau )-f(t) \bigr\Vert _{\mathcal{A}^{n}}< \varepsilon , \forall t\in \mathbb{T}}\bigr\} \end{aligned}$$

is a relatively dense set in $\mathbb{R}$ for all $\varepsilon >0$; that is, for any given $\varepsilon >0$, there exists a constant $l(\varepsilon )>0$ such that each interval of length $l(\varepsilon )$ contains at least one $\tau (\varepsilon )\in E\{\varepsilon ,f\}$ such that

$$\begin{aligned} \bigl\Vert f(t+\tau )-f(t) \bigr\Vert _{\mathcal{A}^{n}}< \varepsilon , \quad\forall t \in \mathbb{T}. \end{aligned}$$

We denote by $AP(\mathbb{T},\mathcal{A}^{n})$ the set of all almost periodic functions defined on $\mathbb{T}$.

Similar to the proofs of the corresponding results in [28], one can easily prove the following.

Lemma 2.4

If$f,g\in AP(\mathbb{T},\mathcal{A})$, then$f+g,fg\in AP(\mathbb{T},\mathcal{A})$.

Lemma 2.5

If$f\in C(\mathcal{A},\mathcal{A})$satisfies the Lipschitz condition, $x\in AP(\mathbb{T},\mathcal{A})$, then$f(x(\cdot ))\in AP(\mathbb{T},\mathcal{A})$.

Lemma 2.6

If$x\in AP(\mathbb{T},\mathcal{A})$and$\tau \in AP(\mathbb{T},\mathcal{A})$, then$x(\cdot -\tau (\cdot ))\in AP(\mathbb{T},\mathcal{A})$.

Lemma 2.7

([29])

Let$f_{i}\in AP(\mathbb{T},\mathbb{X}_{i})$, where$\mathbb{X}_{i}$is a Banach space, $i = 1,\ldots , n$. Then, for every$\varepsilon >0$, all the functions$f_{1}, f_{2}, \ldots , f_{n}$have a common set ofε-almost periods.

Let $\mathbb{U}$ be the set of all functions $\varsigma:\mathbb{T}\rightarrow (0,+\infty )$ that are locally ∇-integrable over $\mathbb{T}$ such that $\varsigma >0$ almost everywhere. From now on, for $\varsigma \in \mathbb{U}$ and $r\in \mathbb{T}$ with $r>0$, we denote

$$ u(r,\varsigma ):= \int ^{r}_{-r}\varsigma (t)\nabla t. $$

The space of weights $\mathbb{U}_{\infty }$ is defined by

$$ \mathbb{U}_{\infty }:= \Bigl\{ \varsigma \in \mathbb{U}:\inf _{t \in \mathbb{T}}\varsigma (t)=\varsigma _{0}>0, \lim _{r \rightarrow +\infty } u(r,\varsigma )=+\infty \Bigr\} . $$

Noting that $\lim_{r\rightarrow +\infty }u(r,1)=+\infty$, $\mathbb{U}_{\infty }\neq \emptyset$.

Fix $\varsigma \in \mathbb{U}_{\infty }$, set

$$\begin{aligned} &PAP_{0}\bigl(\mathbb{T},\mathcal{A}^{n},\varsigma \bigr)= \biggl\{ h\in BC\bigl( \mathbb{T},\mathcal{A}^{n}\bigr):\lim _{r\rightarrow +\infty } \frac{1}{u(r,\varsigma )} \int ^{r}_{-r} \bigl\Vert h(t) \bigr\Vert _{\mathcal{A}^{n}} \varsigma (t)\nabla t=0 \biggr\} . \end{aligned}$$

Similar to Definition 3.1 in [30], we introduce the following definition.

Definition 2.4

Fix $\varsigma \in \mathbb{U}_{\infty }$. A function $f\in BC(\mathbb{T},\mathcal{A}^{n})$ is called weighted pseudo almost periodic if $f=g+h$, where $g\in AP(\mathbb{T},\mathcal{A}^{n})$ and $h\in PAP_{0}(\mathbb{T},\mathcal{A}^{n},\varsigma )$.

We denote by $PAP(\mathbb{T},\mathcal{A}^{n},\varsigma )$ the set of all weighted pseudo almost periodic functions from $\mathbb{T}$ to $\mathcal{A}^{n}$.

Denote

$$\begin{aligned} \mathbb{H}_{\infty }={}& \biggl\{ \varsigma \in \mathbb{U}_{\infty }: \lim \sup_{t\rightarrow \infty } \frac{\varsigma (t+\theta (t))}{\varsigma (t)}< +\infty \text{ and } \\ & \lim \sup_{r\rightarrow +\infty } \frac{u(r+\overline{\theta },\varsigma )}{u(r,\varsigma )}< +\infty , \forall \theta \in BC(\mathbb{T},\varPi ) \biggr\} , \end{aligned}$$

where $\overline{\theta }=\sup_{t\in \mathbb{T}}\theta (t)$.

Lemma 2.8

Let$\varsigma \in \mathbb{H}_{\infty }$. If$x\in PAP(\mathbb{T},\mathcal{A},\varsigma )$, $\theta \in C^{1}_{\nabla }(\mathbb{T},\varPi )\cap AP(\mathbb{T},\varPi )$, and$\alpha:=\inf_{t\in \mathbb{T}}(1-\theta ^{\nabla }(t))>0$, then$x(\cdot -\theta (\cdot ))\in PAP(\mathbb{T},\mathcal{A},\varsigma )$.

Proof

Since $x\in PAP(\mathbb{T},\mathcal{A},\varsigma )$, by Definition 2.4, we have $x=x_{1}+x_{0}$, where $x_{1}\in AP(\mathbb{T},\mathcal{A})$ and $x_{0}\in PAP_{0}(\mathbb{T},\mathcal{A},\varsigma )$. Then we have

$$ x\bigl(t-\theta (t)\bigr)=x_{1}\bigl(t-\theta (t) \bigr)+x_{0}\bigl(t-\theta (t)\bigr). $$

By Lemma 2.6, we get $x_{1}\in AP(\mathbb{T},\mathcal{A})$. Now, we will show that $x_{0}\in PAP_{0}(\mathbb{T},\mathcal{A},\varsigma )$. In fact,

$$\begin{aligned} 0\leq{}& \lim_{r\rightarrow \infty }\frac{1}{u(r,\varsigma )} \int ^{r}_{-r} \varsigma (t) \bigl\Vert x_{0}\bigl(t-\theta (t)\bigr) \bigr\Vert _{\mathcal{A}}\nabla t \\ ={}&\lim_{r\rightarrow \infty }\frac{1}{u(r,\varsigma )} \int ^{r- \theta (t)}_{-r-\theta (t)}\varsigma \bigl(s+\theta (t)\bigr) \frac{1}{1-\theta ^{\nabla }(t)} \bigl\Vert x_{0}(s) \bigr\Vert _{\mathcal{A}} \nabla s \\ \leq {}&\lim_{r\rightarrow \infty }\frac{1}{\alpha } \frac{1}{u(r,\varsigma )} \int ^{r+\overline{\theta }}_{-r- \overline{\theta }} \frac{\varsigma (s+\theta (s))}{\varsigma (s)} \varsigma (s) \bigl\Vert x_{0}(u) \bigr\Vert _{\mathcal{A}} \nabla s \\ \leq{} &\frac{1}{\alpha }\lim_{s\rightarrow \infty }\sup \frac{\varsigma (s+\theta (s))}{\varsigma (s)} \lim _{r\rightarrow \infty }\sup \frac{u(r+\overline{\theta },\varsigma )}{u(r,\varsigma )} \\ &{}\times \lim_{r\rightarrow \infty } \frac{1}{u(r+\overline{\theta },\varsigma )} \int ^{r+ \overline{\theta }}_{-r-\overline{\theta }} \varsigma (s) \bigl\Vert x_{0}(s) \bigr\Vert _{ \mathcal{A}}\nabla s=0, \end{aligned}$$

which implies that $x_{0}(\cdot -\theta (\cdot ))\in PAP_{0}(\mathbb{T},\mathcal{A}, \varsigma )$. Therefore, $x(\cdot -\theta (\cdot ))\in PAP(\mathbb{T},\mathcal{A},\varsigma )$. The proof is completed. □

Similar to the proofs of the corresponding results in [30], it is not difficult to prove the following three lemmas.

Lemma 2.9

Let$\varsigma \in \mathbb{H}_{\infty }$. If$\alpha \in \mathbb{R}$, $f,g\in PAP(\mathbb{T},\mathcal{A},\varsigma )$, then$\alpha f, f+g,fg\in PAP(\mathbb{T},\mathcal{A},\varsigma )$.

Lemma 2.10

Let$\varsigma \in \mathbb{H}_{\infty }$. If$f \in C(\mathcal{A},\mathcal{A})$satisfies the Lipschitz condition and$\varphi \in PAP(\mathbb{T},\mathcal{A},\varsigma )$, then$f(x(\cdot ))\in PAP(\mathbb{T},\mathcal{A},\varsigma )$.

Lemma 2.11

If$\varsigma \in \mathbb{H}_{\infty }$, then$(PAP(\mathbb{T},\mathcal{A},\varsigma ),\|\cdot \|_{\infty })$is a Banach space.

In this paper, we consider the following Clifford-valued neutral-type neural networks with leakage delays on time scale $\mathbb{T}$:

$$\begin{aligned} x^{\nabla }_{i}(t) ={}&{-}a_{i}(t)x_{i} \bigl(t-\delta _{i}(t)\bigr)+\sum_{j=1}^{n}b_{ij}(t)f_{j} \bigl(x_{j}\bigl(t- \eta _{ij}(t)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}c_{ij}(t)g_{j} \bigl(x^{\nabla }_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr)+u_{i}(t),\quad t\in \mathbb{T}, \end{aligned}$$

(8)

where $i \in \{1,2,\ldots ,n\}=:I$; n corresponds to the number of units in the neural network; $x_{i}(t)\in \mathcal{A}$ is the state vector of the ith unit at time t; $a_{i}(t)>0$ represents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs; $b_{ij}(t)$, $c_{ij}(t)\in \mathcal{A}$ are the delay connection weight and the neutral delay connection weight from neuron j to neuron i at time t, respectively; $\delta _{i}(t)\geq 0$ denotes the leakage delay at time t and satisfies $t-\delta _{i}(t)\in \mathbb{T}$ for $t\in \mathbb{T}$, $\eta _{ij}(t),\tau _{ij}(t)\geq 0$ correspond to the transmission delays at time t and satisfy $t-\eta _{ij}(t)$ and $t-\tau _{ij}(t) \in \mathbb{T}$ for $t\in \mathbb{T}$; $u_{i}(t)\in \mathcal{A}$ is the external input at time t; $f_{j},g_{j}:\mathcal{A}\rightarrow \mathcal{A}$ are the activation functions of signal transmission.

For convenience, we introduce the following notation:

$$\begin{aligned} & a^{-}_{i}=\inf_{t\in \mathbb{T}}a_{i}(t),\qquad a^{+}_{i}= \sup_{t\in \mathbb{T}}a_{i}(t),\qquad b^{+}_{ij}=\sup_{t\in \mathbb{T}} \bigl\Vert b_{ij}(t) \bigr\Vert _{\mathcal{A}}, \\ &c^{+}_{ij}=\sup_{t\in \mathbb{T}} \bigl\Vert c_{ij}(t) \bigr\Vert _{ \mathcal{A}}, \qquad u^{+}_{i}= \sup_{t\in \mathbb{T}} \bigl\Vert u_{i}(t) \bigr\Vert _{\mathcal{A}}, \qquad \delta ^{+}_{i}=\sup_{t\in \mathbb{T}} \delta _{i}(t), \\ &\eta ^{+}_{ij}=\sup_{t\in \mathbb{T}}\eta _{ij}(t), \qquad \tau ^{+}_{ij}= \sup_{t\in \mathbb{T}} \tau _{ij}(t), \qquad \vartheta =\max_{1\leq i,j\leq n} \bigl\{ \delta ^{+}_{i},\eta ^{+}_{ij},\tau ^{+}_{ij} \bigr\} . \end{aligned}$$

The initial values of system (8) are as follows:

$$\begin{aligned} x_{i}(s)=\varphi _{i}(s),\qquad x^{\nabla }_{i}(s)= \varphi ^{\nabla }_{i}(s) \in \mathcal{A},\quad s\in [t_{0}- \vartheta ,t_{0}]_{\mathbb{T}}, i \in I, \end{aligned}$$

where $\varphi _{i}:[t_{0}-\vartheta ,t_{0}]_{\mathbb{T}}\rightarrow \mathcal{A}$ is a bounded and ∇-differentiable function.

Throughout this paper, we assume that the following conditions hold:

$(\mathrm{A}_{1})$:

For $i,j\in I$, $a_{i}\in AP(\mathbb{R},\mathbb{R}^{+})$ with $-a_{i}\in \mathcal{R}_{\nu }^{+}$, $\delta _{i},\tau _{ij}, \eta _{ij}\in C^{1}(\mathbb{R},\varPi )\cap AP( \mathbb{R},\mathbb{R}^{+})$ with $\inf_{t\in \mathbb{R}} \{(1-\delta ^{\nabla }_{i}(t)),(1- \tau ^{\nabla }_{ij}(t)),(1-\eta ^{\nabla }_{ij}(t)) \}>0$, $b_{ij}$, $c_{ij}\in PAP(\mathbb{T},\mathcal{A},\varsigma )$ and $u_{i}\in PAP(\mathbb{T},\mathcal{A},\varsigma )$.

$(\mathrm{A}_{2})$:

There exist positive constant numbers $L^{f}_{j},L^{g}_{j}$ such that, for any $u,v\in \mathcal{A}$ and $j\in I$,

$$\begin{aligned} \bigl\Vert f_{j}(u)-f_{j}(v) \bigr\Vert _{\mathcal{A}}\leq L^{f}_{j} \Vert u-v \Vert _{\mathcal{A}}, \qquad \bigl\Vert g_{j}(u)-g_{j}(v) \bigr\Vert _{\mathcal{A}}\leq L^{g}_{j} \Vert u-v \Vert _{ \mathcal{A}}. \end{aligned}$$

$(\mathrm{A}_{3})$:

There exists a positive constant ϒ such that

$$\begin{aligned} \max_{i\in I} \biggl\{ \frac{P_{i}}{a^{-}_{i}},P_{i} \biggl(1 + \frac{a^{+}_{i}}{a^{-}_{i}} \biggr) \biggr\} \leq \varUpsilon\quad \text{and}\quad \max _{i\in I} \biggl\{ \frac{Q_{i}}{a^{-}_{i}}, Q_{i} \biggl(1+ \frac{a^{+}_{i}}{a^{-}_{i}} \biggr) \biggr\} =:\kappa < 1, \end{aligned}$$

where

$$\begin{aligned} &P_{i}=a^{+}_{i}\delta ^{+}_{i} \varUpsilon + \sum_{j=1}^{n}b^{+}_{ij} \bigl(L^{f}_{j}\varUpsilon + \bigl\Vert f(0) \bigr\Vert _{\mathcal{A}} \bigr) +\sum_{j=1}^{n}c^{+}_{ij} \bigl(L^{g}_{j}\varUpsilon + \bigl\Vert g(0) \bigr\Vert _{\mathcal{A}} \bigr)+u^{+}_{i}, \\ &Q_{i}=a^{+}_{i}\delta ^{+}_{i}+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} +\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j},\quad i\in I. \end{aligned}$$

3 The existence of weighted pseudo almost periodic solutions

Let $\mathbb{E}= \{\varphi \in C^{1}_{\nabla }(\mathbb{T},\mathcal{A}^{n}): \varphi ,\varphi ^{\nabla }\in PAP(\mathbb{T},\mathcal{A}^{n}, \varsigma ) \}$ with the norm

$$ \Vert \varphi \Vert _{\mathbb{E}}=\max \bigl\{ \Vert \varphi \Vert _{\infty }, \bigl\Vert \varphi ^{\nabla } \bigr\Vert _{\infty } \bigr\} , $$

then $\mathbb{E}$ is a Banach space.

Theorem 3.1

Let$\varsigma \in H_{\infty }$. Assume that$(\mathrm{A}_{1})$–$(\mathrm{A}_{3})$hold. Then system (8) has a unique weighted pseudo almost periodic solution in$\mathbb{E}_{0}=\{\varphi \in \mathbb{E}:\|\varphi \|_{\mathbb{E}} \leq \varUpsilon \}$, whereϒis mentioned in$(\mathrm{A}_{3})$.

Proof

Firstly, it is easy to see that if $x=(x_{1},x_{2},\ldots ,x_{n})^{T}\in BC(\mathbb{T},\mathcal{A}^{n})$ is a solution of the following system

$$\begin{aligned} x_{i}(t)={}& \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)}x^{\nabla }_{i}(u) \nabla u+\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl(x_{j}\bigl(s- \eta _{ij}(s)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}c_{ij}(s)g_{j} \bigl(x^{\nabla }_{j}\bigl(s-\tau _{ij}(s)\bigr) \bigr)+u_{i}(s) \Biggr)\nabla s,\quad i\in I, \end{aligned}$$

then x is also a solution of system (8).

Secondly, we define a mapping $\varPhi:\mathbb{E}\rightarrow BC(\mathbb{T},\mathcal{A}^{n})$ by

$$ \varPhi \varphi =(\varPhi _{1}\varphi ,\varPhi _{2}\varphi ,\ldots ,\varPhi _{n} \varphi )^{T}, $$

where $\varphi \in \mathbb{E}$, $i\in I$,

$$\begin{aligned} (\varPhi _{i}\varphi ) (t)={}& \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)}\varphi ^{\nabla }_{i}(u) \nabla u+\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl(\varphi _{j}\bigl(s-\eta _{ij}(s)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}c_{ij}(s)g_{j} \bigl(\varphi ^{\nabla }_{j}\bigl(s- \tau _{ij}(s)\bigr) \bigr)+u_{i}(s) \Biggr)\nabla s. \end{aligned}$$

We will prove that Φ maps $\mathbb{E}$ into itself. To this end, let

$$\begin{aligned} \varGamma _{i}(s)={}&a_{i}(s) \int ^{s}_{s-\delta _{i}(s)}\varphi ^{ \nabla }_{i}(u) \nabla u+\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl( \varphi _{j}\bigl(s-\eta _{ij}(s)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}c_{ij}(s) g_{j}\bigl(\varphi ^{\nabla }_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr)+u_{i}(s),\quad i\in I. \end{aligned}$$

By Lemmas 2.8 and 2.9, we find that $\varGamma _{i}\in PAP(\mathbb{T},\mathcal{A},\varsigma ), i\in I$. Let $\varGamma _{i}=\varGamma ^{1}_{i}+\varGamma ^{0}_{i}$, where $\varGamma ^{1}_{i}\in AP(\mathbb{T},\mathcal{A})$, $\varGamma ^{0}_{i}\in PAP_{0}(\mathbb{T},\mathcal{A},\varsigma )$, then we have

$$\begin{aligned} (\varPhi _{i}\varphi ) (t)&= \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \varGamma ^{1}_{i}(s)\Delta s+ \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t, \rho (s)\bigr)\varGamma ^{0}_{i}(s)\nabla s \\ &:=F^{1}_{i}(t)+F^{0}_{i}(t),\quad i\in I. \end{aligned}$$

We will prove that $F^{1}_{i}\in AP(\mathbb{T},\mathcal{A})$ and $F^{0}_{i}\in PAP_{0}(\mathbb{T},\mathcal{A},\varsigma )$ for $i\in I$.

In fact, since $a_{i}\in AP(\mathbb{T},\mathbb{R}), \varGamma ^{1}_{i}\in AP(\mathbb{T}, \mathcal{A})$, by Lemma 2.7, for every $\varepsilon >0$, there exists $\xi \in \varPi$ such that

$$\begin{aligned} \bigl\vert a_{i}(t+\xi )-a_{i}(t) \bigr\vert < \varepsilon , \qquad\bigl\Vert \varGamma ^{1}_{i}(t+\xi )- \varGamma ^{1}_{i}(t) \bigr\Vert _{\mathcal{A}}< \varepsilon ,\quad t\in \mathbb{T}, i \in I. \end{aligned}$$

Hence, from the definition of $F^{1}_{i}$ and Lemma 2.3, we have

$$\begin{aligned} & \bigl\Vert F^{1}_{i}(t+\xi )-F^{1}_{i}(t) \bigr\Vert _{\mathcal{A}} \\ &\quad= \biggl\Vert \int _{-\infty }^{t+\xi }\hat{e}_{-a_{i}}\bigl(t+\xi , \rho (s)\bigr) \varGamma ^{1}_{i}(s)\nabla s- \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t, \rho (s)\bigr) \varGamma ^{1}_{i}(s)\nabla s \biggr\Vert _{\mathcal{A}} \\ &\quad= \biggl\Vert \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t+\xi , \rho (s+\xi )\bigr) \varGamma ^{1}_{i}(s+\xi )\nabla s- \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t, \rho (s)\bigr) \varGamma ^{1}_{i}(s)\nabla s \biggr\Vert _{\mathcal{A}} \\ &\quad\leq \biggl\Vert \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t+\xi , \rho (s+ \xi )\bigr) \varGamma ^{1}_{i}(s+\xi )\nabla s- \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t+ \xi , \rho (s+\xi )\bigr) \varGamma ^{1}_{i}(s)\nabla s \biggr\Vert _{\mathcal{A}} \\ &\qquad{}+ \biggl\Vert \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t+\xi , \rho (s+\xi )\bigr) \varGamma ^{1}_{i}(s)\nabla s- \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t, \rho (s)\bigr) \varGamma ^{1}_{i}(s)\nabla s \biggr\Vert _{\mathcal{A}} \\ &\quad\leq \int _{-\infty }^{t} \bigl\vert \hat{e}_{-a_{i}} \bigl(t+\xi ,\rho (s+\xi )\bigr) \bigr\vert \bigl\Vert \varGamma ^{1}_{i}(s+\xi )-\varGamma ^{1}_{i}(s) \bigr\Vert _{ \mathcal{A}}\nabla s \\ &\qquad{}+ \int _{-\infty }^{t} \bigl\vert \hat{e}_{-a_{i}} \bigl(t+\xi ,\rho (s+\xi )\bigr) - \hat{e}_{-a_{i}}\bigl(t,\rho (s)\bigr) \bigr\vert \bigl\Vert \varGamma ^{1}_{i}(s) \bigr\Vert _{ \mathcal{A}}\nabla s \\ &\quad\leq \frac{\varepsilon }{a^{-}_{i}}+\sup_{t\in \mathbb{T}} \bigl\{ \varGamma _{i}^{1}(t)\bigr\} \int _{-\infty }^{t} \bigl\vert \hat{e}_{-a_{i}} \bigl(t+ \xi ,\rho (s+\xi )\bigr) -\hat{e}_{-a_{i}}\bigl(t,\rho (s)\bigr) \bigr\vert \nabla s \\ &\quad\leq \frac{\varepsilon }{a^{-}_{i}} +\sup_{t\in \mathbb{T}} \bigl\{ \varGamma _{i}^{1}(t)\bigr\} \int _{-\infty }^{t} \biggl\vert \int ^{\rho (s)}_{t} \hat{e}_{-a_{i}}\bigl(t,\rho ( \theta )\bigr) \bigl(a_{i}(\theta +\xi ) -a_{i}( \theta ) \bigr)\nabla \theta \biggr\vert \nabla s \\ &\quad\leq \frac{\varepsilon }{(a_{i}^{-})^{2}} \Bigl(a^{-}_{i}+ \sup _{t\in \mathbb{T}}\bigl\{ \varGamma _{i}^{1}(t)\bigr\} \Bigr), \quad i\in I, \end{aligned}$$

which implies that $F^{1}_{i}\in AP(\mathbb{T},\mathcal{A})$ for all $i\in I$.

Since $\varGamma ^{0}_{i}\in PAP_{0}(\mathbb{T},\mathcal{A},\varsigma ), i\in I$ and by Lebesgue’s dominated convergence theorem, we have

$$\begin{aligned} &\lim_{r\rightarrow \infty }\frac{1}{u(r,\varsigma )} \int ^{r}_{-r} \varsigma (s) \bigl\Vert F^{0}_{i}(s) \bigr\Vert _{\mathcal{A}}\Delta s \\ &\quad=\lim_{r\rightarrow \infty }\frac{1}{u(r,\varsigma )} \int ^{r}_{-r} \biggl\Vert \int _{-\infty }^{s}\hat{e}_{-a_{i}}\bigl(s,\rho ( \theta )\bigr)\varGamma ^{0}_{i}( \theta )\nabla \theta \biggr\Vert _{\mathcal{A}}\nabla s \\ &\quad\leq \lim_{r\rightarrow \infty }\frac{1}{u(r,\varsigma )} \int _{- \infty }^{s}\hat{e}_{-a_{i}}\bigl(s,\rho ( \theta )\bigr) \biggl( \int ^{r}_{-r} \bigl\Vert \varGamma ^{0}_{i}(\theta ) \bigr\Vert _{\mathcal{A}}\nabla \theta \biggr)\nabla s,\quad i\in I, r\in \varPi , \end{aligned}$$

which implies that $F^{0}_{i}\in PAP_{0}(\mathbb{T},\mathcal{A},\varsigma )$ for all $i\in I$. Therefore, $\varPhi _{i}\varphi \in PAP(\mathbb{T},\mathcal{A},\varsigma )$, $i\in I$. Moreover, noting that for $i\in I$,

$$\begin{aligned} &(\varPhi _{i}\varphi )^{\nabla }(t) \\ &\quad=\varGamma _{i}(t)-a_{i}(t) \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t, \rho (s)\bigr) \varGamma _{i}(s)\nabla s \\ &\quad= -a_{i}(t) (\varPhi _{i}\varphi ) (t)+\varGamma _{i}(t), \end{aligned}$$

$a_{i}\in AP(\mathbb{T},\mathbb{R})$, and $\varPhi _{i}\varphi , \varGamma _{i} \in PAP(\mathbb{T},\mathcal{A}, \varsigma )$, we can conclude that $\varPhi _{i}^{\nabla }\varphi \in PAP(\mathbb{T},\mathcal{A},\varsigma )$ for $i\in I$.

Thirdly, we will prove that Φ is a self-mapping defined on $\mathbb{E}_{0}$. In fact, for each $\varphi \in \mathbb{E}_{0}$, we have

$$\begin{aligned} &\sup_{t\in \mathbb{T}} \bigl\Vert (\varPhi \varphi ) (t) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad=\max_{i\in I} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl\Vert \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)}\varphi ^{\nabla }_{i}(u) \nabla u \\ &\qquad{}+\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl(\varphi _{j}\bigl(s-\eta _{ij}(s)\bigr)\bigr)+ \sum _{j=1}^{n}c_{ij}(s) g_{j}\bigl(\varphi ^{\nabla }_{j}\bigl(s-\tau _{ij}(s)\bigr)\bigr)+u_{i}(s) \Biggr)\nabla s \Biggr\Vert _{\mathcal{A}} \Biggr\} \\ &\quad\leq \max_{i\in I} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl[ \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \Biggl(a^{+}_{i} \delta ^{+}_{i} \bigl\Vert \varphi ^{\nabla }_{i}(s) \bigr\Vert _{\mathcal{A}} +\sum_{j=1}^{n}b^{+}_{ij} \bigl(L^{f}_{j} \bigl\Vert \varphi _{j} \bigl(s-\tau _{ij}(s)\bigr) \bigr\Vert _{\mathcal{A}} \\ &\qquad{}+ \bigl\Vert f(0) \bigr\Vert _{\mathcal{A}} \bigr)+\sum _{j=1}^{n}c^{+}_{ij} \bigl( L^{g}_{j} \bigl\Vert \varphi ^{\nabla }_{j} \bigl(s-\tau _{ij}(s)\bigr) \bigr\Vert _{\mathcal{A}}+ \bigl\Vert g(0) \bigr\Vert _{ \mathcal{A}} \bigr) +u^{+}_{i} \Biggr) \nabla s \Biggr] \Biggr\} \\ &\quad\leq \max_{i\in I} \Biggl\{ \frac{1}{a^{-}_{i}} \Biggl(a^{+}_{i} \delta ^{+}_{i} \varUpsilon + \sum_{j=1}^{n}b^{+}_{ij} \bigl(L^{f}_{j} \varUpsilon + \bigl\Vert f(0) \bigr\Vert _{\mathcal{A}} \bigr) +\sum_{j=1}^{n}c^{+}_{ij} \bigl(L^{g}_{j}\varUpsilon + \bigl\Vert g(0) \bigr\Vert _{\mathcal{A}} \bigr)+u^{+}_{i} \Biggr) \Biggr\} \\ &\quad\leq \max_{i\in I} \biggl\{ \frac{P_{i}}{a^{-}_{i}} \biggr\} \end{aligned}$$

and

$$\begin{aligned} &\sup_{t\in \mathbb{T}} \bigl\Vert (\varPhi \varphi )^{\nabla }(t) \bigr\Vert _{ \mathcal{A}^{n}} \\ &\quad=\max_{i\in I} \biggl\{ \sup_{t\in \mathbb{T}} \biggl\Vert \varGamma _{i}(t)-a_{i}(t) \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t, \rho (s)\bigr) \varGamma _{i}(s)\nabla s \biggr\Vert _{\mathcal{A}} \biggr\} \\ &\quad\leq \max_{i\in I} \Biggl\{ P_{i}+\frac{a^{+}_{i}}{a^{-}_{i}} \Biggl(a^{+}_{i}\delta ^{+}_{i} \varUpsilon + \sum_{j=1}^{n}b^{+}_{ij} \bigl(L^{f}_{j}\varUpsilon + \bigl\Vert f(0) \bigr\Vert _{\mathcal{A}} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij} \bigl(L^{g}_{j}\varUpsilon + \bigl\Vert g(0) \bigr\Vert _{\mathcal{A}} \bigr)+u^{+}_{i} \Biggr) \Biggr\} \\ &\quad\leq \max_{i\in I} \biggl\{ P_{i}+ \frac{a^{+}_{i}P_{i}}{a^{-}_{i}} \biggr\} . \end{aligned}$$

Hence, in view of $(\mathrm{A}_{3})$, we have $\|\varPhi \varphi \|_{\mathbb{E}}\leq \varUpsilon$, that is, $\varPhi (\mathbb{E}_{0})\subset \mathbb{E}_{0}$.

Finally, we shall prove that Φ is a contraction mapping. In fact, for any $\varphi =(\varphi _{1},\varphi _{2},\ldots , \varphi _{n})^{T}$, $\psi =(\psi _{1},\psi _{2},\ldots ,\psi _{n})^{T}\in \mathbb{E}_{0}$, we have

$$\begin{aligned} &\sup_{t\in \mathbb{T}} \bigl\Vert (\varPhi \varphi ) (t)-(\varPhi \psi ) (t) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad=\max_{i\in I} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl\Vert \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)} \bigl(\varphi ^{\nabla }_{i}(u)- \psi ^{ \nabla }_{i}(u) \bigr)\nabla u \\ &\qquad{}+\sum_{j=1}^{n}b_{ij}(s) \bigl(f_{j}\bigl(\varphi _{j}\bigl(s-\tau _{ij}(s) \bigr)\bigr)-f_{j}\bigl( \psi _{j}\bigl(s-\eta _{ij}(s)\bigr)\bigr) \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}(s) \bigl(g_{j}\bigl(\varphi ^{\nabla }_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr)-g_{j}\bigl(\psi ^{\nabla }_{j} \bigl(s-\tau _{ij}(s)\bigr)\bigr) \bigr) \Biggr)\nabla s \Biggr\Vert _{\mathcal{A}} \Biggr\} \\ &\quad\leq \max_{i\in I} \Biggl\{ \frac{1}{a^{-}_{i}} \Biggl(a^{+}_{i} \delta ^{+}_{i}+\sum _{j=1}^{n}b^{+}_{ij}L^{f}_{j} +\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \Biggr) \Biggr\} \Vert \varphi -\psi \Vert _{ \mathbb{E}} \\ &\quad=\max_{i\in I} \biggl\{ \frac{Q_{i}}{a^{-}_{i}} \biggr\} \Vert \varphi -\psi \Vert _{\mathbb{E}} \end{aligned}$$

and

$$\begin{aligned} &\sup_{t\in \mathbb{T}} \bigl\Vert (\varPhi \varphi )^{\nabla }(t)-( \varPhi \psi )^{\nabla }(t) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad=\max_{i\in I} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl\Vert a_{i}(t) \int ^{t}_{t-\delta _{i}(t)} \bigl(\varphi ^{\nabla }_{i}(u)- \psi ^{\nabla }_{i}(u) \bigr)\nabla u+\sum _{j=1}^{n}b_{ij}(t) \bigl(f_{j} \bigl(\varphi _{j}\bigl(t-\tau _{ij}(t)\bigr)\bigr) \\ &\qquad{}-f_{j}\bigl(\psi _{j}\bigl(t-\eta _{ij}(t) \bigr)\bigr) \bigr)+\sum_{j=1}^{n}c_{ij}(t) \bigl(g_{j}\bigl(\varphi ^{\nabla }_{j}\bigl(t-\tau _{ij}(t)\bigr)\bigr)-g_{j}\bigl(\psi ^{ \nabla }_{j} \bigl(t-\tau _{ij}(t)\bigr)\bigr) \bigr) \\ &\qquad{}-a_{i}(t) \int _{-\infty }^{t}\hat{e}_{-a_{i}}\bigl(t,\rho (s) \bigr) \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)} \bigl(\varphi ^{\nabla }_{i}(u)- \psi ^{ \nabla }_{i}(u) \bigr)\nabla u \\ &\qquad{}+\sum_{j=1}^{n}b_{ij}(s) \bigl(f_{j}\bigl(\varphi _{j}\bigl(s-\tau _{ij}(s) \bigr)\bigr)-f_{j}\bigl( \psi _{j}\bigl(s-\eta _{ij}(s)\bigr)\bigr) \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}(s) \bigl(g_{j}\bigl(\varphi ^{\nabla }_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr)-g_{j}\bigl(\psi ^{\nabla }_{j} \bigl(s-\tau _{ij}(s)\bigr)\bigr) \bigr) \Biggr)\nabla s \Biggr\Vert _{\mathcal{A}} \Biggr\} \\ &\quad=\max_{i\in I} \biggl\{ Q_{i}+ \frac{a^{+}_{i}Q_{i}}{a^{-}_{i}} \biggr\} \Vert \varphi -\psi \Vert _{\mathbb{E}}. \end{aligned}$$

By $(\mathrm{A}_{3})$, we have

$$\begin{aligned} \Vert \varPhi \varphi -\varPhi \psi \Vert _{\mathbb{E}}\leq \kappa \Vert \varphi -\psi \Vert _{\mathbb{E}}. \end{aligned}$$

Hence, Φ is a contraction mapping. Therefore, system (8) has a unique weighted pseudo almost periodic in the set $\mathbb{E}_{0}=\{\varphi \in \mathbb{E}_{0}:\|\varphi \|_{\mathbb{E}} \leq \varUpsilon \}$. This completes the proof of Theorem 3.1. □

4 The stability of weighted pseudo almost periodic solutions

In this section, we study the global exponential stability of the unique weighted pseudo almost periodic solution of system (8) by using the proof by contradiction and the technique of inequalities.

Definition 4.1

A solution x with the initial value φ of system (8) is called globally exponentially stable if there exist positive constants λ with $\ominus _{\nu }\lambda \in \mathcal{R}_{\nu }^{+}$ and $\tilde{C}>1$ such that for each solution y with the initial value ψ satisfies

$$\begin{aligned} \bigl\Vert x(t)-y(t) \bigr\Vert _{1}\leq \tilde{C} \hat{e}_{\ominus _{\nu }\lambda }(t,t_{0}) \Vert \zeta \Vert _{0},\quad \forall t\in (t_{0},+\infty )_{\mathbb{T}}, \end{aligned}$$

where

$$\begin{aligned} &\bigl\Vert x(t)-y(t) \bigr\Vert _{1}=\max \bigl\{ \bigl\Vert x(t)-y(t) \bigr\Vert _{\mathcal{A}^{n}}, \bigl\Vert x^{\nabla }(t)-y^{ \nabla }(t) \bigr\Vert _{\mathcal{A}^{n}}\bigr\} , \\ &\Vert \zeta \Vert _{0}=\max \Bigl\{ \sup_{s\in [t_{0}-\vartheta ,t_{0}]_{ \mathbb{T}}} \bigl\Vert \varphi (s)-\psi (s) \bigr\Vert _{\mathcal{A}^{n}}, \sup _{s \in [t_{0}-\vartheta ,t_{0}]_{\mathbb{T}}} \bigl\Vert \varphi ^{\nabla }(s)- \psi ^{\nabla }(s) \bigr\Vert _{\mathcal{A}^{n}} \Bigr\} . \end{aligned}$$

Theorem 4.1

Let conditions$(\mathrm{A}_{1})$–$(\mathrm{A}_{3})$hold, then system (8) has a unique weighted pseudo almost periodic solution that is globally exponentially stable.

Proof

According to Theorem 3.1, system (8) has a weighted pseudo almost periodic solution $x=(x_{1},x_{2},\ldots ,x_{n})^{T}$. Assume that its initial value is $\varphi =(\varphi _{1},\varphi _{2},\ldots ,\varphi _{n})^{T}$. Suppose that $y=(y_{1},y_{2},\ldots ,y_{n})^{T}$ is an arbitrary solution of system (8) with the initial value $\psi =(\psi _{1},\psi _{2},\ldots ,\psi _{n})^{T}$. Then, by (8), we have

$$\begin{aligned} &\bigl(x_{i}(t)-y_{i}(t) \bigr)^{\nabla } \\ &\quad=-a_{i}(t) \bigl(x_{i}(t)-y_{i}(t) \bigr)+a_{i}(t) \int ^{t}_{t-\delta _{i}(t)} \bigl(x^{\nabla }_{i}(u) -y^{\nabla }_{i}(u) \bigr)\nabla u \\ &\qquad{}+\sum_{j=1}^{n}b_{ij}(t) \bigl(f_{j}\bigl(x_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr)-f_{j}\bigl(y_{j}\bigl(t- \eta _{ij}(t) \bigr)\bigr) \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}(t) \bigl(g_{j}\bigl(x^{\nabla }_{j}\bigl(t- \tau _{ij}(t)\bigr)\bigr)-g_{j}\bigl(y^{\nabla }_{j} \bigl(t-\tau _{ij}(t)\bigr)\bigr) \bigr),\quad i \in I. \end{aligned}$$

(9)

Multiplying both sides of (9) by $\hat{e}_{-a_{i}}(t_{0},\rho (t))$ and integrating over $[t_{0},t]_{\mathbb{T}}$, we obtain

$$\begin{aligned} &x_{i}(t)-y_{i}(t) \\ &\quad=\bigl(x_{i}(t_{0})-y_{i}(t_{0}) \bigr)\hat{e}_{-a_{i}}(t,t_{0}) + \int _{t_{0}}^{t} \hat{e}_{-a_{i}}\bigl(t,\rho (s)\bigr) \\ &\qquad{}\times \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)} \bigl(x^{\nabla }_{i}(u) -y^{\nabla }_{i}(u) \bigr)\nabla u \\ &\qquad{}+\sum_{j=1}^{n}b_{ij}(s) \bigl(f_{j}\bigl(x_{j}\bigl(s-\tau _{ij}(s)\bigr) \bigr)-f_{j}\bigl(y_{j}\bigl(s- \eta _{ij}(s) \bigr)\bigr) \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}(s) \bigl(g_{j}\bigl(x^{\nabla }_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr)-g_{j}\bigl(y^{\nabla }_{j} \bigl(s-\tau _{ij}(s)\bigr)\bigr) \bigr) \Biggr) \nabla s,\quad i\in I. \end{aligned}$$

(10)

Denote

$$\begin{aligned} \varTheta _{i}(\omega )={}&a^{-}_{i}-\omega - \exp \Bigl(\omega \sup_{s \in \mathbb{T}}\mu (s) \Bigr) \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl( \omega \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\omega \eta ^{+}_{ij} \bigr) \\ &{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\omega \tau ^{+}_{ij} \bigr) \Biggr) \end{aligned}$$

and

$$\begin{aligned} \varTheta ^{\ast }_{i}(\omega )={}&a^{-}_{i}- \omega - \Bigl(a^{+}_{i}\exp \Bigl(\omega \sup _{s\in \mathbb{T}}\nu (s) \Bigr)+a^{-}_{i} \Bigr) \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl(\omega \delta ^{+}_{i} \bigr) \\ &{}+\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\omega \eta ^{+}_{ij} \bigr)+\sum _{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\omega \tau ^{+}_{ij} \bigr) \Biggr),\quad i\in I. \end{aligned}$$

Then, by ($\mathrm{A}_{3}$), for $i\in I$, we have

$$\begin{aligned} \varTheta _{i}(0)=a^{-}_{i}-Q_{i}>0 \end{aligned}$$

and

$$\begin{aligned} \varTheta ^{\ast }_{i}(0)=a^{-}_{i}- \bigl(a^{-}_{i}+a^{+}_{i} \bigr)Q_{i}>0,\quad i \in I. \end{aligned}$$

Because $\varTheta _{i}$ and $\varTheta ^{\ast }_{i}$ are continuous on $[0,+\infty )$ and $\varTheta _{i}(\omega ), \varTheta ^{\ast }_{i}(\omega ) \rightarrow - \infty$, as $\omega \rightarrow +\infty$, so there exist $\xi _{i}$, $\xi ^{\ast }_{i}$ such that $\varTheta _{i}(\xi _{i})=\varTheta ^{\ast }_{i}(\xi ^{\ast }_{i})=0$ and $\varTheta _{i}(\omega )>0$ for $\omega \in (0,\xi _{i})$, $\varTheta ^{\ast }_{i}(\omega )>0$ for $\omega \in (0,\xi ^{\ast }_{i})$, $i\in I$. Let $c=\min_{i\in I}\{\xi _{i},\xi ^{\ast }_{i}\}$, we have $\varTheta _{i}(c)\geq 0$, $\varTheta ^{\ast }_{i}(c)\geq 0$, $i\in I$. Hence, we can take a positive constant $0<\lambda <\min \{c,\min_{i\in I}\{a^{-}_{i}\} \}$ with $\ominus _{\nu }\lambda \in \mathcal{R}_{\nu }^{+}$ such that

$$\begin{aligned} \varTheta _{i}(\lambda )>0, \qquad \varTheta ^{\ast }_{i}( \lambda )>0, \quad i \in I, \end{aligned}$$

which imply that

$$\begin{aligned} &\frac{\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \Biggl(a^{+}_{i}\delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\quad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr)< 1 \end{aligned}$$

and

$$\begin{aligned} & \biggl(1+ \frac{a^{+}_{i}\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \biggr) \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\quad {}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr)< 1, \quad i\in I. \end{aligned}$$

Denote $\tilde{C}=\max_{ i\in I} \{\frac{a^{-}_{i}}{Q_{i}} \}$, then by ($\mathrm{A}_{3}$) we have $\tilde{C}>1$. Hence,

$$\begin{aligned} \frac{1}{\tilde{C}}< {}&\frac{\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr),\quad i\in I. \end{aligned}$$

Since $\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0})>1$ for $t\in [t_{0}-\vartheta ,t_{0}]_{\mathbb{T}}$, it is easy to see that

$$\begin{aligned} \bigl\Vert x(t)-y(t) \bigr\Vert _{1}\leq \tilde{C} \hat{e}_{\ominus _{\nu }\lambda }(t,t_{0}) \Vert \zeta \Vert _{0},\quad \forall t\in [t_{0}-\vartheta ,t_{0}]_{ \mathbb{T}}. \end{aligned}$$

We claim that

$$\begin{aligned} \bigl\Vert x(t)-y(t) \bigr\Vert _{1} \leq \tilde{C}\hat{e}_{\ominus _{\nu }\lambda }(t,t_{0}) \Vert \zeta \Vert _{0}, \quad \forall t\in (t_{0},+\infty )_{\mathbb{T}}. \end{aligned}$$

(11)

To prove that (11) holds, we first show that, for any ${\varrho }>1$, the following inequality holds:

$$\begin{aligned} \bigl\Vert x(t)-y(t) \bigr\Vert _{1}< { \varrho }\tilde{C}\hat{e}_{\ominus _{\nu } \lambda }(t,t_{0}) \Vert \zeta \Vert _{0},\quad \forall t\in (t_{0},+ \infty )_{\mathbb{T}}, \end{aligned}$$

(12)

that is, for $i\in I$,

$$\begin{aligned} \bigl\Vert x_{i}(t)-y_{i}(t) \bigr\Vert _{\mathcal{A}}< {\varrho }\tilde{C}\hat{e}_{ \ominus _{\nu }\lambda }(t,t_{0}) \Vert \zeta \Vert _{0}, \quad\forall t \in (t_{0},+\infty )_{\mathbb{T}}. \end{aligned}$$

(13)

In fact, if (13) is not true, then there exist some $i\in I$ and $t_{1}\in (t_{0},+\infty )_{\mathbb{T}}$ such that

$$\begin{aligned} \bigl\Vert x_{i}(t_{1})-y_{i}(t_{1}) \bigr\Vert _{\mathcal{A}}\geq {\varrho }\tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \end{aligned}$$

and

$$\begin{aligned} \bigl\Vert x_{i}(t)-y_{i}(t) \bigr\Vert _{\mathcal{A}}< {\varrho }\tilde{C} \Vert \zeta \Vert _{0} \hat{e}_{\ominus _{\nu }\lambda }(t,t_{0}),\quad t\in (t_{0},t_{1})_{ \mathbb{T}}. \end{aligned}$$

Hence, one can choose a constant $c\geq 1$ such that

$$\begin{aligned} \bigl\Vert x_{i}(t_{1})-y_{i}(t_{1}) \bigr\Vert _{\mathcal{A}}= c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \end{aligned}$$

(14)

and

$$\begin{aligned} \bigl\Vert x_{i}(t)-y_{i}(t) \bigr\Vert _{\mathcal{A}}< c\varrho \tilde{C} \Vert \zeta \Vert _{0} \hat{e}_{\ominus _{\nu }\lambda }(t,t_{0}),\quad t\in (t_{0},t_{1})_{ \mathbb{T}}. \end{aligned}$$

(15)

By (10), (14), (15), and $\tilde{C}>1$, we have

$$\begin{aligned} & \bigl\Vert x_{i}(t_{1})-y_{i}(t_{1}) \bigr\Vert _{\mathcal{A}} \\ &\quad= \Biggl\Vert \bigl(x_{i}(t_{0})-y_{i}(t_{0}) \bigr)\hat{e}_{-a_{i}}(t_{1},t_{0})+ \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}} \bigl(t_{1},\rho (s)\bigr) \\ &\qquad{}\times \Biggl(a_{i}(s) \int ^{s}_{s-\delta _{i}(s)} \bigl(x^{\nabla }_{i}(u) -y^{\nabla }_{i}(u) \bigr)\nabla u+ \\ &\qquad{}\times \sum_{j=1}^{n}b_{ij}(s) \bigl(f_{j}\bigl(x_{j}\bigl(s-\tau _{ij}(s)\bigr) \bigr)-f_{j}\bigl(y_{j}\bigl(s- \eta _{ij}(s) \bigr)\bigr) \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c_{ij}(s) \bigl(g_{j}\bigl(x^{\nabla }_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr)-g_{j}\bigl(y^{\nabla }_{j} \bigl(s-\tau _{ij}(s)\bigr)\bigr) \bigr) \Biggr) \nabla s \Biggr\Vert _{\mathcal{A}} \\ &\quad< \bigl\Vert x_{i}(t_{0})-y_{i}(t_{0}) \bigr\Vert _{\mathcal{A}}\hat{e}_{-a_{i}}(t_{1},t_{0})+c \varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}} \bigl(t_{1},\rho (s)\bigr) \\ &\qquad{}\times \hat{e}_{\lambda }\bigl(t_{1},\rho (s)\bigr) \Biggl(a^{+}_{i} \int ^{s}_{s- \delta _{i}(s)}\hat{e}_{\lambda }\bigl(\rho (s),u \bigr)\nabla u+\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \hat{e}_{\lambda }\bigl(\rho (s),s-\eta _{ij}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \hat{e}_{\lambda }\bigl( \rho (s),s-\tau _{ij}(s)\bigr) \Biggr) \nabla s \\ &\quad= \bigl\Vert x_{i}(t_{0})-y_{i}(t_{0}) \bigr\Vert _{\mathcal{A}}\hat{e}_{-a_{i}}(t_{1},t_{0})+c \varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}\oplus _{\nu }\lambda } \bigl(t_{1}, \rho (s)\bigr) \\ &\qquad{}\times \Biggl(a^{+}_{i} \delta ^{+}_{i} \hat{e}_{\lambda }\bigl(\rho (s),s- \delta _{i}(s)\bigr)+ \sum _{j=1}^{n}b^{+}_{ij}L^{f}_{j} \hat{e}_{ \lambda }\bigl(\rho (s),s-\eta _{ij}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \hat{e}_{\lambda }\bigl( \rho (s),s-\tau _{ij}(s)\bigr) \Biggr) \nabla s \\ &\quad\leq \bigl\Vert x_{i}(t_{0})-y_{i}(t_{0}) \bigr\Vert _{\mathcal{A}}\hat{e}_{-a_{i}}(t_{1},t_{0})+c \varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}\oplus _{\nu }\lambda } \bigl(t_{1}, \rho (s)\bigr) \\ &\qquad{}\times \Biggl(a^{+}_{i}\delta ^{+}_{i} \exp \Bigl(\lambda \Bigl(\delta ^{+}_{i}+ \sup _{s\in \mathbb{T}}\nu (s)\Bigr) \Bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \Bigl(\lambda \Bigl(\eta ^{+}_{ij}+ \sup _{s\in \mathbb{T}}\nu (s)\Bigr) \Bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \Bigl(\lambda \Bigl( \tau ^{+}_{ij}+ \sup _{s\in \mathbb{T}}\nu (s)\Bigr) \Bigr) \Biggr)\nabla s \\ &\quad\leq \Biggl\{ \frac{\hat{e}_{-a_{i}\oplus _{\nu } \lambda }(t_{1},t_{0})}{c\varrho \tilde{C}}+ \exp \Bigl(\lambda \sup _{s\in \mathbb{T}}\nu (s) \Bigr) \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}\oplus _{\nu }\lambda } \bigl(t_{1}, \rho (s)\bigr)\nabla s \Biggr\} c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{ \ominus _{\nu }\lambda }(t_{1},t_{0}) \\ &\quad \leq \Biggl\{ \frac{\hat{e}_{-a_{i}\oplus _{\nu } \lambda }(t_{1},t_{0})}{c\varrho \tilde{C}}+ \exp \Bigl(\lambda \sup _{s\in \mathbb{T}}\nu (s) \Bigr) \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \frac{1-\hat{e}_{-a_{i}\oplus _{\nu }\lambda }(t_{1},t_{0})}{a^{-}_{i}-\lambda } \Biggr\} c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu } \lambda }(t_{1},t_{0}) \\ &\quad< \Biggl\{ \Biggl[\frac{1}{ \tilde{C}}- \frac{\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \Biggl(a^{+}_{i} \delta ^{+}_{i} \exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \Biggr] \hat{e}_{-a_{i}\oplus _{\nu }\lambda }(t_{1},t_{0}) + \frac{\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \Biggl(a^{+}_{i}\delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) +\sum _{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \Biggr\} c \varrho \tilde{C} \Vert \zeta \Vert _{0} \hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \\ &\quad < c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}). \end{aligned}$$

Similarly, in view of (10), we have

$$\begin{aligned} & \bigl\Vert x^{\nabla }_{i}(t_{1})-y^{\nabla }_{i}(t_{1}) \bigr\Vert _{\mathcal{A}} \\ &\quad < a^{+}_{i} \Vert \zeta \Vert _{0} \hat{e}_{-a_{i}}(t_{1},t_{0})+c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \Biggl(a^{+}_{i} \int ^{t_{1}}_{t_{1}-\delta _{i}(t_{1})}\hat{e}_{ \lambda }(t_{1},u) \nabla u \\ &\qquad{}+\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \hat{e}_{\lambda }\bigl(t_{1},t_{1}- \eta _{ij}(t_{1})\bigr) +\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \hat{e}_{\lambda }\bigl(t_{1},t_{1}-\tau _{ij}(t_{1})\bigr) \Biggr) \\ &\qquad{}+a^{+}_{i}c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu } \lambda }(t_{1},t_{0}) \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}\oplus _{ \nu }\lambda } \bigl(t_{1},\rho (s)\bigr) \Biggl(a^{+}_{i} \delta ^{+}_{i}\hat{e}_{ \lambda }\bigl(\rho (s),s-\delta _{i}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \hat{e}_{\lambda }\bigl( \rho (s),s-\eta _{ij}(s)\bigr) +\sum _{j=1}^{n}c^{+}_{ij}L^{g}_{j} \hat{e}_{\lambda }\bigl(\rho (s),s-\tau _{ij}(s)\bigr) \Biggr) \nabla s \\ &\quad\leq a^{+}_{i} \Vert \zeta \Vert _{0} \hat{e}_{-a_{i}}(t_{1},t_{0})+c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}) \\ &\qquad{}\times \Biggl(a^{+}_{i}\delta ^{+}_{i} \exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum _{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \biggl(1+a^{+}_{i}\exp \Bigl(\lambda \sup _{s\in \mathbb{T}} \nu (s) \Bigr) \int _{t_{0}}^{t_{1}}\hat{e}_{-a_{i}\oplus _{\nu } \lambda } \bigl(t_{1},\rho (s)\bigr)\nabla s \biggr) \\ &\quad< \Biggl\{ \Biggl[\frac{1}{ \tilde{C}}- \frac{\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \Biggl(a^{+}_{i} \delta ^{+}_{i}\exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \Biggr] \hat{e}_{-a_{i}\oplus _{\nu }\lambda }(t_{1},t_{0}) + \biggl(1+ \frac{a^{+}_{i}\exp (\lambda \sup_{s\in \mathbb{T}}\nu (s) )}{a^{-}_{i}-\lambda } \biggr) \\ &\qquad{}\times \Biggl(a^{+}_{i}\delta ^{+}_{i} \exp \bigl(\lambda \delta ^{+}_{i} \bigr)+ \sum _{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\lambda \eta ^{+}_{ij} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}c^{+}_{ij}L^{g}_{j} \exp \bigl(\lambda \tau ^{+}_{ij} \bigr) \Biggr) \Biggr\} c \varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{ \nu }\lambda }(t_{1},t_{0}) \\ &\quad < c\varrho \tilde{C} \Vert \zeta \Vert _{0}\hat{e}_{\ominus _{\nu }\lambda }(t_{1},t_{0}), \end{aligned}$$

which contradicts (14), and so (13) holds. Letting ${\varrho }\rightarrow 1$, we obtain that (11) holds. Hence, the weighted pseudo almost periodic solution of system (8) is globally exponentially stable. The proof of Theorem 4.1 is completed. □

5 An example

In this section, we give an example to illustrate the feasibility of our results obtained in this paper.

Example 5.1

In system (8), let $m=3$, $n=2$, the weight $\varrho (t)=e^{-|t|}$, and take the coefficients as follows:

$$\begin{aligned} &f_{j}(x)=g_{j}(x)=\frac{1}{120}e_{0}\sin \bigl(x^{2}+x^{0}\bigr)+ \frac{3}{400}\cos \bigl(x^{1}+x^{12}\bigr)e_{1}+ \frac{1}{150}e_{2}\tanh x^{12} \\ &\phantom{f_{j}(x)=}{}+\frac{1}{130}e_{3}\sin \bigl(x^{13}+x^{1} \bigr)+\frac{\sqrt{3}}{210}e_{12} \sin \sqrt{3}x^{12}+ \frac{3}{500}\cos \bigl(x^{2}+x^{13}\bigr)e_{13} \\ &\phantom{f_{j}(x)=}{}+\frac{1}{185}e_{23}\tanh x^{23}+\frac{1}{150}e_{123} \sin \bigl(x^{123}+x^{3}\bigr), \\ &u_{1}(t)=0.3e_{0}\cos 2t +0.35 e_{1} \cos 3t +0.25e_{2} \sin 4t+0.45 e_{3}\cos \sqrt{3}t \\ &\phantom{u_{1}(t)=}{} + 0.15e_{12}\cos 2t+0.4 e_{13} \cos 2t +0.5 e_{23} \sin \sqrt{2}t +0.2 e_{123}\sin \sqrt{2}t, \\ &u_{2}(t)=0.25 e_{0}\cos 2t +0.3 e_{1}\sin 3t+0.2e_{2}\cos 2t+0.35 e_{3} \sin \sqrt{3}t \\ &\phantom{u_{2}(t)=}{}+0.4 e_{12}\cos 3t+0.3 e_{13}\sin 2t+0.25 e_{23} \sin \sqrt{2}t+ 0.3 e_{123}\sin \sqrt{2}t, \\ &b_{11}(t)=b_{12}(t)=0.001 e_{0}\cos \sqrt{2}t+0.003 e_{1}\sin 3t +0.003 e_{3}\cos \sqrt{3}t \\ &\phantom{b_{11}(t)=}{}+0.0015e_{12}\sin 2t+0.004 e_{13} \cos 4t+0.004 e_{23} \cos \sqrt{5}t +0.001 e_{123}\sin \sqrt{7}t, \\ &b_{21}(t)=b_{22}(t)=0.002 e_{0} \sin 3t +0.003 e_{2} \cos \sqrt{3}t \\ &\phantom{b_{21}(t)=}{}+0.0015e_{12}\cos 2t+0.003 e_{13} \sin 5t +0.001 e_{123}\cos \sqrt{2}t, \\ &c_{11}(t)=c_{22}(t)=0.0015 e_{0}\cos 3t +0.003 e_{3}\sin 9t \\ &\phantom{c_{11}(t)=}{}+0.005e_{12}\cos 2t+0.004 e_{23} \sin \sqrt{2}t +0.001 e_{123}\sin \sqrt{2}t, \\ &c_{12}(t)=c_{21}(t)=0.002 e_{0}\cos 3t +0.003 e_{2}\sin \sqrt{5}t \\ &\phantom{c_{12}(t)=}{}+0.001 e_{3}\sin 2t+0.0015e_{12}\cos 2t+0.004 e_{13} \cos 4t , \\ &a_{1}(t)=0.95-0.01 \sin \sqrt{2}t,\qquad a_{2}(t)=0.9+0.03 \cos 3t. \end{aligned}$$

If $\mathbb{T}=\mathbb{R}$, then we take

$$\begin{aligned} \tau _{ij}(t)=\frac{1}{2} \vert \cos 2t \vert ,\qquad \delta _{i}(t)=\frac{1}{3} \vert \sin 3t \vert ,\qquad \eta _{ij}(t)=\frac{1}{4} \vert \cos \sqrt{2}t \vert ,\quad i,j=1,2, \end{aligned}$$

and if $\mathbb{T}=\mathbb{Z}$, then we take

$$\begin{aligned} \tau _{ij}(t)=2e^{-2 \vert \cos (\pi t+\frac{3\pi }{2}) \vert }, \qquad\delta _{i}(t)= \biggl\vert \cos \biggl(\pi t+\frac{\pi }{2}\biggr) \biggr\vert ,\qquad \eta _{ij}(t)=e^{- \vert \sin 2\pi t \vert },\quad i,j=1,2. \end{aligned}$$

By calculating, we have $a^{-}_{1}=0.94$, $a^{-}_{2}=0.87$, $a^{+}_{1}=0.96$, $a^{+}_{2}=0.93$, $L^{f}_{1}=L^{f}_{2}=L^{g}_{1}=L^{g}_{2}=\frac{1}{70}$, $\|f(\mathrm{0})\|_{\mathcal{A}}=\|g(\mathrm{0})\|_{\mathcal{A}}= \frac{3}{400}$, $b^{+}_{11}=b^{+}_{12}=0.004$, $b^{+}_{21}=b^{+}_{22}=0.003$, $c^{+}_{11}=c^{+}_{22}=0.005$, $c^{+}_{12}=c^{+}_{21}=0.004$, $u^{+}_{1}=0.5$, $u^{+}_{2}=0.4$.

Take $\varUpsilon =3$, for $i,j=1,2$, when $\mathbb{T}=\mathbb{R}$,

$$\begin{aligned} &\delta ^{+}_{i}=\frac{1}{3},\qquad \tau ^{+}_{ij}=\frac{1}{2},\qquad \eta ^{+}_{ij}= \frac{1}{4}, \qquad P_{1}\approx 1.4609,\qquad P_{2} \approx 1.3308, \\ & Q_{1}\approx 0.3202,\qquad Q_{2}\approx 0.3102, \\ &\max \biggl\{ \frac{P_{1}}{a^{-}_{1}}, \frac{P_{2}}{a^{-}_{2}},P_{1} \biggl(1+ \frac{a^{+}_{1}}{a^{-}_{1}} \biggr), P_{2} \biggl(1+\frac{a^{+}_{2}}{a^{-}_{2}} \biggr) \biggr\} \approx \max \{1.5541,1.5297,2.9529,2.7534\} \\ &\quad =2.9529< \varUpsilon =3 \end{aligned}$$

and

$$\begin{aligned} &\max \biggl\{ \frac{Q_{1}}{a^{-}_{1}} , \frac{Q_{2}}{a^{-}_{2}}, Q_{1} \biggl(1+\frac{a^{+}_{1}}{a^{-}_{1}} \biggr), Q_{2} \biggl(1+\frac{a^{+}_{2}}{a^{-}_{2}} \biggr) \biggr\} \\ &\quad \approx \max \{0.3406,0.3566,0.6472,0.6418\}=0.6472=\kappa < 1, \end{aligned}$$

when $\mathbb{T}=\mathbb{Z}$,

$$\begin{aligned} &\delta ^{+}_{i}=0,\qquad \tau ^{+}_{ij}=2,\qquad \eta ^{+}_{ij}=1,\qquad P_{1}\approx 0.8009,\qquad P_{2}\approx 0.4008, \\ & Q_{1}= Q_{2}\approx 0.0002, \\ &\max \biggl\{ \frac{P_{1}}{a^{-}_{1}}, \frac{P_{2}}{a^{-}_{2}},P_{1} \biggl(1+ \frac{a^{+}_{1}}{a^{-}_{1}} \biggr), P_{2} \biggl(1+\frac{a^{+}_{2}}{a^{-}_{2}} \biggr) \biggr\} \approx \max \{0.8520,0.4607,1.6188,0.8292\} \\ &\quad =1.6188< \varUpsilon =3 \end{aligned}$$

and

$$\begin{aligned} &\max \biggl\{ \frac{Q_{1}}{a^{-}_{1}} , \frac{Q_{2}}{a^{-}_{2}}, Q_{1} \biggl(1+\frac{a^{+}_{1}}{a^{-}_{1}} \biggr), Q_{2} \biggl(1+\frac{a^{+}_{2}}{a^{-}_{2}} \biggr) \biggr\} \\ &\quad \approx \max \{0.00021,0.00023,0.00040,0.00041\}=0.00041=\kappa < 1. \end{aligned}$$

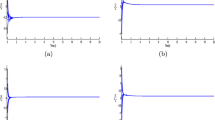
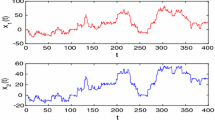
Hence, whether $\mathbb{T}=\mathbb{R}$ or $\mathbb{T}=\mathbb{Z}$, all the conditions of Theorems 3.1 and 4.1 are satisfied. Therefore, system (8) has a weighted pseudo almost periodic solution, which is globally exponentially stable (see Figs. 1–8).

Figure 1

$\mathbb{T}=\mathbb{R}$. Transient states of the solutions $x_{i}^{0}(t)$ and $x_{i}^{1}(t)$ of system (8) with the initial values $x_{i}^{0}(0)=(0.1,-0.2)^{T}, (-0.4,0.3)^{T}, (0.7,-0.8)^{T}$ and $x_{i}^{1}(0)=(-0.3,0.4)^{T}, (0.2,-0.5)^{T}, (-0.1,0.5)^{T}$, $i=1,2$

Figure 2

$\mathbb{T}=\mathbb{R}$. Transient states of the solutions $x_{i}^{2}(t)$ and $x_{i}^{3}(t)$ of system (8) with the initial values $x_{i}^{2}(0)=(-0.2,-0.3)^{T}, (0.1,0.25)^{T}, (0.2,-0.1)^{T}$ and $x_{i}^{3}(0)=(0.1,-0.5)^{T}, (0.5,1)^{T}, (-0.7,-0.3)^{T}$, $i=1,2$

Figure 3

$\mathbb{T}=\mathbb{R}$. Transient states of the solutions $x_{i}^{12}(t)$ and $x_{i}^{13}(t)$ of system (8) with the initial values $x_{i}^{12}(0)=(0.3,-0.4)^{T}, (0.6,0.4)^{T}, (-0.1,-0.7)^{T}$ and $x_{i}^{13}(0)=(-0.1,0.2)^{T}, (-0.5,0.4)^{T}, (-0.2,0.5)^{T}$, $i=1,2$

Figure 4

$\mathbb{T}=\mathbb{R}$. Transient states of the solutions $x_{i}^{23}(t)$ and $x_{i}^{123}(t)$ of system (8) with the initial values $x_{i}^{23}(0)=(0.3,1)^{T}, (-0.7,0.7)^{T}, (-1,-0.3)^{T}$ and $x_{i}^{123}(0)=(0.4,-0.5)^{T}, (0.6,0.2)^{T}, (-0.1,-0.3)^{T}$, $i=1,2$

Figure 5

$\mathbb{T}=\mathbb{Z}$. Transient states of the solutions $x_{i}^{0}(n)$ and $x_{i}^{1}(n)$ of system (8) with the initial values $x_{i}^{0}(0)=(0.2,-0.1)^{T}, (-0.3,0.3)^{T}, (0.5,-0.4)^{T}$ and $x_{i}^{1}(0)=(-0.4,0.2)^{T}, (0.5,-0.5)^{T}, (-0.6,-0.1)^{T}$, $i=1,2$

Figure 6

$\mathbb{T}=\mathbb{Z}$. Transient states of the solutions $x_{i}^{2}(n)$ and $x_{i}^{3}(n)$ of system (8) with the initial values $x_{i}^{2}(0)=(0.2,-0.1)^{T}, (-0.25,0.15)^{T}, (0.1,-0.2)^{T}$ and $x_{i}^{3}(0)=(0.1,0.5)^{T}, (-0.5,-0.2)^{T}, (0.3,-0.4)^{T}$, $i=1,2$

Figure 7

$\mathbb{T}=\mathbb{Z}$. Transient states of the solutions $x_{i}^{12}(n)$ and $x_{i}^{13}(n)$ of system (8) with the initial values $x_{i}^{12}(0)=(0.3,-0.2)^{T}, (-0.6,0.5)^{T}, (-0.1,-0.3)^{T}$ and $x_{i}^{13}(0)=(0.1,0.3)^{T}, (-0.2,-0.15)^{T}, (-0.5,-0.1)^{T}$, $i=1,2$

Figure 8

$\mathbb{T}=\mathbb{Z}$. Transient states of the solutions $x_{i}^{23}(n)$ and $x_{i}^{123}(n)$ of system (8) with the initial values $x_{i}^{23}(0)=(0.2,-0.3)^{T}, (-0.7,-0.5)^{T}, (0.5,0.7)^{T}$ and $x_{i}^{123}(0)=(0.4,0.2)^{T}, (-0.05,-0.3)^{T}, (-0.4,0.25)^{T}$, $i=1,2$

Remark 5.1

There are no existing results that can be applied to Example 5.1.

6 Conclusion

In this paper, we have considered a class of Clifford-valued neutral-type neural networks with leakage delays on time scales. By using the Banach fixed point theorem, the theory of calculus on time scales, inequality techniques, and the proof by contradiction, we have established the existence and exponential stability of weighted pseudo almost periodic solutions for this class of neural networks. An example has been given to show the feasibility of our results. This is the first paper to study the existence and global exponential stability of weighted pseudo almost periodic solutions for Clifford-valued neutral-type neural networks with leakage delays on time scales. The study of Clifford-valued neural networks on time scales cannot only unify the research of real-valued neural networks, complex-valued neural networks, and quaternion-valued neural networks, but also unify the research of continuous-time neural networks and discrete-time neural networks. Our method of this paper can be applied to study other types of the Clifford-valued neural networks on times scales, such as BAM neural networks on time scales, shunting inhibitory cellular neural networks on time scales, high-order Hopfield neural networks, and so on.