The use of generation stochastic models to study an epidemic disease

Abstract

Stochastic models have an important role in modeling and analyzing epidemic diseases for small size population. In this article, we study the generation of stochastic models for epidemic disease susceptible-infective-susceptible model. Here, we use the separation variable method to solve partial differential equation and the new developed modified probability generating function (PGF) of a random process to include a random catastrophe to solve the ordinary differential equations generated from partial differential equation. The results show that the probability function is too sensitive to μ, β and γ parameters.

1 Deterministic susceptible-infective-susceptible model

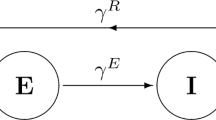
Figure 1 shows a deterministic susceptible-infective-susceptible model for an epidemic disease. In this figure, S is the susceptible population, I is the infective population, $\mu >0$ is the natural death rate, $\gamma >0$ is the removal rate which is a constant. Note that $S,I\ge 0$ because they represent the number of people. The infection rate, λ, depends on the number of partners per individual per unit time ($r>0$) and the transmission probability per partner ($\beta >0$). In this system, the first susceptible population in class S is going to be infected, then infected population in class I is going to be susceptible again. The following system of ODE’s describes this susceptible-infective-susceptible model [1]

$$\{\begin{array}{c}\frac{dS(t)}{dt}=\gamma I(t)-\mu -\lambda S(t),\hfill \\ \frac{dI(t)}{dt}=\lambda S(t)-\mu -\gamma .\hfill \end{array}$$

(1)

Figure 1

A schematic of system (1).

Figure 1 illustrates the system (1). This system is nonlinear due to the form of $\lambda =\beta I$.

2 Generation stochastic susceptible-infective-susceptible model

In this section, we present the state of the generation stochastic [2–5] susceptible-infective-susceptible model. The stochastic susceptible-infective-susceptible model is similar to the deterministic susceptible-infective-susceptible model, for the deterministic model we can find an exact function but for the stochastic model, we cannot obtain an exact function. Figure 2 shows the state diagram for the stochastic [2–5] susceptible-infective-susceptible model [1, 6–10].

Figure 2

Stochastic susceptible-infective-susceptible model state diagram.

At $t_0$, if m is infective and n is susceptible, namely $S(t_0)+I(t_0)=n+m$, then $P_i(t)=P[S(t)=i|S(0)=n]$ is the probability function in the time t and stage i. Here, our goal is to determine $P_i(t)$. Table 1 shows the transition diagram for this model. To determine $P_i(t)$’s, we should create the Kolmogorov equations. From Figure 2, we have

$$P[\text{staying at state }i]=1-(\beta i(m+(n-i))\mathrm{\Delta }t+\mu \mathrm{\Delta }t-\gamma \mathrm{\Delta }t)$$

(2)

and

$$P[\text{moving from state }i\text{ to }i-1]=\beta i(m+(n-i))\mathrm{\Delta }t+\mu \mathrm{\Delta }t-\gamma \mathrm{\Delta }t.$$

(3)

Now, to produce the forward Kolmogorov equations, we have

$$\begin{array}{rcl}{P}_i(t+\mathrm{\Delta }t)& =& P(0\text{ contact during }\mathrm{\Delta }t|S(t)=i)P_i(t)\\ +P(1\text{ contact during }\mathrm{\Delta }t|S(t)=i+1)P_{i+1}(t)\\ =& P(\text{staying at state }i)P_i(t)+P(\text{moving from state }i+1\text{ to }i)P_{i+1}(t)\\ =& (1-(\beta i(m+(n-i))\mathrm{\Delta }t+\mu \mathrm{\Delta }t-\gamma \mathrm{\Delta }t))P_i(t)\\ +(\beta (i+1)(m+(n-i-1))\mathrm{\Delta }t+\mu \mathrm{\Delta }t-\gamma \mathrm{\Delta }t)P_{i+1}(t).\end{array}$$

So,

$$\begin{array}{rcl}{P}_i(t+\mathrm{\Delta }t)-P_i(t)& =& -(\beta i(m+n-i)\mathrm{\Delta }t+\mu \mathrm{\Delta }t-\gamma \mathrm{\Delta }t)P_i(t)\\ +(\beta (i+1)(m+n-i-1)\mathrm{\Delta }t+\mu \mathrm{\Delta }t\\ -\gamma \mathrm{\Delta }t)P_{i+1}(t),\end{array}$$

(4)

then

$$\begin{array}{rcl}\frac{P_i(t+\mathrm{\Delta }t)-P_i(t)}{\mathrm{\Delta }t}& =& -(\beta i(m+n-i)+\mu -\gamma )P_i(t)\\ +(\beta (i+1)(m+n-i-1)+\mu -\gamma )P_{i+1}(t).\end{array}$$

(5)

Having limited from both sides of Eq. (5), when $\mathrm{\Delta }t⟶0$, we have

$$\begin{array}{rcl}{P}_i^{\mathrm{\prime }}(t)& =& \underset{\mathrm{\Delta }t⟶0}{lim}\frac{P_i(t+\mathrm{\Delta }t)-P_i(t)}{\mathrm{\Delta }t}=-(\beta i(m+n-i)+\mu -\gamma )P_i(t)\\ +(\beta (i+1)(m+n-i-1)+\mu -\gamma )P_{i+1}(t).\end{array}$$

(6)

Therefore, the forward Kolmogorov equations for this model will be as follows:

$$\begin{array}{rcl}{P}_i^{\mathrm{\prime }}(t)& =& -(\beta i(m+n-i)+\mu -\gamma )P_i(t)\\ +(\beta (i+1)(m+n-i-1)+\mu -\gamma )P_{i+1}(t).\end{array}$$

(7)

The probabilities function $P_i(t)$ is found from Eq. (7). Also, from probability generating functions (PGFs) and partial differential functions equations (PDEs), the probabilities function $P_i(t)$ can be obtained. Probability generating functions can be written as

$$y(x,t)=\sum _{i=0}^n{P}_i(t)x^i=P_0(t)+P_1(t)x+P_2(t)x^2+\cdots +P_n(t)x^n.$$

(8)

Now, the partial derivative of $y(x,t)$ with respect to t will be $\frac{\partial y}{\partial t}={\sum }_{i=0}^n{P}_i^{\mathrm{\prime }}(t)x^i$, so one can write the partial derivative as follows:

$$\begin{array}{rcl}\frac{\partial y}{\partial t}& =& \sum _{i=0}^n[-(\beta i(m+n-i)+\mu -\gamma )P_i(t)\\ +(\beta (i+1)(m+n-i-1)+\mu -\gamma )P_{i+1}(t)]x^i.\end{array}$$

(9)

Having simplified Eq. (9), we can write

$$\begin{array}{rcl}\frac{\partial y(x,t)}{\partial t}& =& (\mu -\gamma )\cdot \frac{1}{x}+(\gamma -\mu )y(x,t)+\beta (m+n-1)(1-x)\frac{\partial y(x,t)}{\partial x}\\ +\beta x(x-1)\frac{{\partial }^{2}y(x,t)}{\partial x^2}.\end{array}$$

(10)

The separation variable method is employed to solve Eq. (10). If $y(x,t)=X(x)T(t)$, then we have

$$\begin{array}{rcl}\frac{T^{\mathrm{\prime }}(t)}{T(t)}& =& (\gamma -\mu )+(\mu -\gamma )\cdot \frac{1}{x}\cdot \frac{1}{X(x)}+\beta (m+n-1)(1-x)\frac{X^{\mathrm{\prime }}(x)}{X(x)}\\ +\beta x(x-1)\frac{X^{\mathrm{\prime }\mathrm{\prime }}(x)}{X(x)}.\end{array}$$

(11)

Two sides of Eq. (11) are equal, so

$$\begin{array}{rcl}\frac{T^{\mathrm{\prime }}(t)}{T(t)}& =& -c\text{ and }(\gamma -\mu )+(\mu -\gamma )\cdot \frac{1}{x}\cdot \frac{1}{X(x)}+\beta (m+n-1)(1-x)\frac{X^{\mathrm{\prime }}(x)}{X(x)}\\ +\beta x(x-1)\frac{X^{\mathrm{\prime }\mathrm{\prime }}(x)}{X(x)}=-c.\end{array}$$

(12)

To include a random catastrophe presented by Gani and Swift in 2006 [11], we develop the modified probability generating function (PGF) of a random process to solve Eq. (10) as follows:

$$G(x,t)=\sum _{j=0}^n{G}_j(x,t)=\sum _{j=0}^n[e^{-(\mu -\gamma )t}y(x,t)+{\int }_0^t(\mu -\gamma )e^{-(\mu -\gamma )v}y(x,v)dv],$$

(13)

with $\mu -\gamma \ge 0$, here $y(x,t)$ is the answer of Eq. (10) when $\mu =0$, $\gamma =0$. So, we can put $\mu =0$, $\gamma =0$ with $m=1$ in Eq. (12)

$$x(x-1)X^{\mathrm{\prime }\mathrm{\prime }}(x)-n(x-1)X^{\mathrm{\prime }}(x)+(c/\beta )X(x)=0.$$

(14)

This equation was solved by Bailey in 1963 [12]. After having solved Eq. (14) by Maple, we have

$$\begin{array}{rcl}X(x)& =& -C_1{\times }_2{F}_1[-1/2\frac{\sqrt{\beta +2\beta n+n^2\beta -4c}+\sqrt{\beta }(-1+n)}{\sqrt{\beta }},\\ -1/2\frac{-\sqrt{\beta +2\beta n+n^2\beta -4c}+\sqrt{\beta }(-1+n)}{\sqrt{\beta }};-n;x],\end{array}$$

(15)

where ${}_{2}F_1[\cdot ,\cdot ;\cdot ;\cdot ]$ is a hypergeometric function.

Table 1 Transition diagram for the stochastic susceptible-infective-susceptible model

Notation 1 The standard hypergeometric function ${}_{2}F_1[a,b;c;x]$ is as follows:

$${}_{2}F_1[a,b;c;x]=\sum _{i=0}^{\mathrm{\infty }}\frac{{(a)}_i{(b)}_i}{{(c)}_i}\times \frac{x^i}{i!},$$

(16)

where ${(a)}_i=a(a+1)(a+2)(a+3)\cdots (a+i-1)$ with ${(a)}_0=1$ is the Pochhammer symbol. The derivatives of ${}_{2}F_1[a,b;c;x]$ are given by

Also, from equation $\frac{T^{\mathrm{\prime }}(t)}{T(t)}=-c$, we have $T(t)=k_1{e}^{-ct}$. So,

$$\begin{array}{rcl}y(x,t)& =& e^{-ct}\frac{1}{{}_{2}F_1[-1/2\frac{\sqrt{\beta +2\beta n+n^2\beta -4c}+\sqrt{\beta }(-1+n)}{\sqrt{\beta }},-1/2\frac{-\sqrt{\beta +2\beta n+n^2\beta -4c}+\sqrt{\beta }(-1+n)}{\sqrt{\beta }};-n;1]}\\ {\times }_2{F}_1[-1/2\frac{\sqrt{\beta +2\beta n+n^2\beta -4c}+\sqrt{\beta }(-1+n)}{\sqrt{\beta }},\\ -1/2\frac{-\sqrt{\beta +2\beta n+n^2\beta -4c}+\sqrt{\beta }(-1+n)}{\sqrt{\beta }};-n;x].\end{array}$$

(17)

In Eq. (17) we can take $c=j(N+m-j)\beta$; $N=n+ϵ$, here ϵ is so small parameter. Then from Eq. (17) and Eq. (13), one can write

$$G(x,t)=\sum _{j=0}^n[e^{-(\mu -\gamma )t}\times e^{-j(N+m-j)\beta t}\frac{1}{{}_{2}F_1[-j,j-N-1,-N,1]}$$

(18)

$${\times }_2{F}_1[-j,j-N-1,-N,x]+{\int }_0^t(\mu -\gamma )e^{-(\mu -\gamma )v}\times e^{-j(m+N-j)\beta v}$$

(19)

$$\times \frac{1}{{}_{2}F_1[-j,j-N-1,-N,1]}{\times }_2{F}_1[-j,j-N-1,-N,v]dv].$$

(20)

Thus,

$$\begin{array}{rcl}G(x,t)& =& \sum _{j=0}^n{\lambda }_j{\times }_2{F}_1[-j,j-N-1,-N,x]\times [(e^{-[(\mu -\gamma )+j(N+m-j)\beta ]t}\\ +{\int }_0^t(\mu -\gamma )e^{-[(\mu -\gamma )+j(N+m-j)\beta )]v}dv]\\ =& \sum _{j=0}^n{\lambda }_j{\times }_2{F}_1[-j,j-N-1,-N,x]\times [e^{-[(\mu -\gamma )+j(m+N-j)\beta ]t}\\ -\frac{1-{\mathrm{e}}^{(-\mu +\gamma +j\beta N-j^2\beta +j\beta )t}}{-\mu +\gamma +j\beta N-j^2\beta +j\beta }],\end{array}$$

(21)

where

$${\lambda }_j=\frac{{(-1)}^{j}n!(N-2j+1)N!\mathrm{\Gamma }(-N+j-1)}{j!(n-j)!(N-n)!{(-1)}^{n+1}\mathrm{\Gamma }(n-N+j)}.$$

Now, to find $P_0(t),P_1(t),P_2(t),\dots ,P_k(t)$, one can calculate $G(x,t)$ as follows:

$$G(x,t)=\sum _{k=0}^{\mathrm{\infty }}{P}_k(t)x^k=P_0(t)+P_1(t)x+P_2(t)x^2+\cdots .$$

(22)

So,

$$\begin{array}{rcl}{P}_0(t)& =& G(0,t)\\ =& \sum _{j=0}^n{\lambda }_j\times [e^{-[(\mu -\gamma )+j(m+N-j)\beta )]t}\\ -\frac{1-e^{(-\mu +\gamma +j\beta N-j^2\beta +j\beta )t}}{-\mu +\gamma +j\beta N-j^2\beta +j\beta }].\end{array}$$

(23)

Hence, $P_1(t)$ and $P_2(t)$ are obtained as follows:

Therefore,

$$P_k(t)=\frac{d^{k}G(x,t)}{d{x}^k}{|}_{x=0}=\sum _{j=0}^n\frac{1}{k!}\frac{{(-j)}_k{(j-N-1)}_k}{{(-N)}_k}\times {\lambda }_j\times {\mathrm{\Psi }}_j(t),$$

(24)

with

$${\mathrm{\Psi }}_j(t)=[e^{-j\mu t-(n-j)\gamma t-(m+N-j^2)\beta t}-\frac{1-e^{(-\mu +\gamma +j\beta N-j^2\beta +j\beta )t}}{-\mu +\gamma +j\beta N-j^2\beta +j\beta }].$$

(25)

3 Numerical results

Some numerical examples illustrate the behavior of the probability function $P_K(t,\beta ,\mu ,\gamma )$ with the following parameters: $t=1$; $\beta =0.3$; $\mu =0.3$; $\gamma =0.1$.

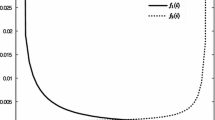
Figure 3(a) and (b) show the behavior of the probability functions, $P_0(t,\beta )$ and $P_8(t,\beta )$ with $\mu =0.3$ and $\gamma =0.1$ when $0<t<5$ and $0<\beta <1$.

Figure 3

Probability function ${\mathit{P}}_{\mathit{k}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{\beta }\mathbf{)}$ with $\mathit{\mu }\mathbf{=}\mathbf{0.3}$ and $\mathit{\gamma }\mathbf{=}\mathbf{0.1}$ , (a): $\mathit{k}\mathbf{=}\mathbf{0}$ and (b): $\mathit{k}\mathbf{=}\mathbf{8}$ .

Figure 3(a) shows that with an increase in t and β, the probability function $P_0(t,\beta )$ increases fast, but in Figure 3(b) $P_8(t,\beta )$ decreases fast.

Figure 4(a) and (b) show the behavior of the probability functions, $P_0(t,\mu )$ and $P_8(t,\mu )$ with $\beta =0.3$ and $\gamma =0.1$ when $0<t<5$ and $0<\mu <1$. Figure 4(a) shows that as t increases, the probability function $P_0(t,\mu )$ increases, but with an increase in μ, the probability function $P_0(t,\mu )$ decreases. Figure 4(b) shows that as t increases, the probability function $P_8(t,\mu )$ decreases, but with an increase in μ, the probability function $P_0(t,\mu )$ increases.

Figure 4

Probability function ${\mathit{P}}_{\mathit{k}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{\mu }\mathbf{)}$ with $\mathit{\beta }\mathbf{=}\mathbf{0.3}$ and $\mathit{\gamma }\mathbf{=}\mathbf{0.1}$ , (a): $\mathit{k}\mathbf{=}\mathbf{0}$ and (b): $\mathit{k}\mathbf{=}\mathbf{8}$ .

Figure 5(a) and (b) display the probability functions, $P_0(t,\gamma )$ and $P_8(t,\gamma )$ with $\beta =0.3$ and $\mu =0.3$. From Figure 5(a) when $0<t<1$ and $0<\gamma <1$, the probability function $P_0(t,\gamma )$ is nearly zero, but for $1<t<5$ as t increases, $P_0(t,\gamma )$ slowly increases, and as γ increases, $P_0(t,\gamma )$ sharply increases. In Figure 5(b), $P_8(t,\gamma )$ is almost constant for $1<t<5$, but with a decrease in γ from 1 to 0, $P_8(t,\gamma )$ increases; also, Figure 5(b) shows the highest value of $P_8(t,\gamma )$ when $0<t<1$ and $0<\gamma <1$.

Figure 5

Probability function ${\mathit{P}}_{\mathit{k}}\mathbf{(}\mathit{t}\mathbf{,}\mathit{\gamma }\mathbf{)}$ with $\mathit{\beta }\mathbf{=}\mathbf{0.3}$ and $\mathit{\mu }\mathbf{=}\mathbf{0.3}$ , (a): $\mathit{k}\mathbf{=}\mathbf{0}$ and (b): $\mathit{k}\mathbf{=}\mathbf{8}$ .

Figure 6(a) and (b) show the probability functions, $P_0(\beta ,\mu )$ and $P_8(\beta ,\mu )$ with $\gamma =0.1$ and $t=1$. Figure 6(a) depicts that for $0<\beta <1$, as μ increases from 0 to 1, the probability function $P_0(\beta ,\mu )$ increases. Figure 6(b) shows that for $0<\mu <1$, with an increase in β and μ, the probability function $P_8(\beta ,\mu )$ increases.

Figure 6

Probability function ${\mathit{P}}_{\mathit{k}}\mathbf{(}\mathit{\beta }\mathbf{,}\mathit{\mu }\mathbf{)}$ with $\mathit{\gamma }\mathbf{=}\mathbf{0.1}$ and $\mathit{t}\mathbf{=}\mathbf{1}$ , (a): $\mathit{k}\mathbf{=}\mathbf{0}$ and (b): $\mathit{k}\mathbf{=}\mathbf{8}$ .

Figure 7(a) and (b) illustrate the probability functions, $P_0(\mu ,\gamma )$ and $P_8(\mu ,\gamma )$ with $\beta =0.3$ and $t=1$. Figure 7(a) shows that the probability function $P_0(\mu ,\gamma )$ decreases with an increase in μ, but inversely it increases with an increase in γ. In Figure 7(a) we observe a separation which means that in the probability function $P_K(\mu ,\gamma )$ we have $\mu \ne \gamma$. Figure 7(b) depicts that the probability function $P_8(\mu ,\gamma )$ increases when μ increases, although it decreases with an increase in γ.

Figure 7

Probability function ${\mathit{P}}_{\mathit{k}}\mathbf{(}\mathit{\mu }\mathbf{,}\mathit{\gamma }\mathbf{)}$ with $\mathit{\beta }\mathbf{=}\mathbf{0.3}$ and $\mathit{t}\mathbf{=}\mathbf{1}$ , (a): $\mathit{k}\mathbf{=}\mathbf{0}$ and (b): $\mathit{k}\mathbf{=}\mathbf{8}$ .

4 Conclusions

We have presented the generation of a stochastic model for the susceptible-infective-susceptible model. The separation variable method has been applied to solve a partial differential equation of this generation. So, two ordinary differential equations have been achieved which relate to the parameter x. To solve this equation, we used the developed modified probability generating function (PGF) of a random process to consider a random catastrophe. Numerical results showed the behavior of the probability function $P_k(t,\beta ,\mu ,\gamma )$ when $0<t<5$ and $0<\beta ,\mu ,\gamma <1$.