Abstract
Numerical solution for the regularized long wave equation is studied by a new conservative Crank-Nicolson finite difference scheme. By the Richardson extrapolation technique, the scheme has the accuracy of without refined mesh. Conservations of discrete mass and discrete energy are discussed, and existence of the numerical solution is proved by the Browder fixed point theorem. Convergence, unconditional stability as well as uniqueness of the solution are also derived using energy method. Numerical examples are carried out to verify the correction of the theory analysis.
MSC:65M06, 65N30.
Similar content being viewed by others
1 Introduction
Consider the initial boundary value problem for the regularized long wave (RLW) equation
with an initial condition
and a boundary condition
where is a given known function. The RLW equation is originally introduced as an alternative to the Korteweg-de Vries (KdV) equation to describe the behavior of the undular bore by Peregrine [1] and plays a very important role in physics media, since it describes phenomena with weak nonlinearity and dispersion waves, including nonlinear transverse waves in shallow water, ion-acoustic and magneto hydrodynamic waves in plasma and phonon packets in nonlinear crystals. When it is used to model waves generated in a shallow water channel, the variables are normalized in the following way: distance x and water elevation u are scaled to the water depth h, and time t is scaled to , where g is the acceleration due to gravity. The physical boundary requires
So, if and , problems (1.1)-(1.3) is in accordance with the Cauchy problem of equation (1.1). The RLW equation has the following conserved laws,
and
where and are two positive constants which relate to the initial condition.
Existence and uniqueness of the solution of the RLW equation are given in [2]. Its analytical solution was found [3] under restricted initial and boundary conditions, and, therefore, it became interesting from a numerical point of view. Some numerical methods for the solution of the RLW equation such as variational iteration method [4, 5], finite-difference method [6–8], Fourier pseudospectral method [9], finite element method [10–13], collocation method [14] and adomian decomposition method [15] have been introduced in many works. In [16], Li and Vu-Quoc pointed out that ‘in some areas, the ability to preserve some invariant properties of the original differential equation is a criterion to judge the success of a numerical simulation.’ Meanwhile, Zhang et al. [17] thought that the conservative difference schemes perform better than the non-conservative ones, and the non-conservative difference schemes may easily show nonlinear ‘blow-up.’ Hence, constructing a conservative difference scheme for the numerical solution of the nonlinear partial differential equation is quite significant. In this paper, coupled with the Richardson extrapolation, a two-level nonlinear Crank-Nicolson finite difference scheme for problems (1.1)-(1.3), which has the accuracy of without refined mesh is proposed. The scheme simulates two conserved quantities (1.5) and (1.6) well, respectively. Moreover, priori estimate, existence and uniqueness of the numerical solutions are discussed. Convergence and unconditional stability of the scheme are also proved.
The outline of the paper is as follows. In Section 2, a nonlinear conservative difference scheme is proposed. In Section 3, we prove the existence of the difference solution by the Browder fixed point theorem. Priori estimate, convergence and stability are proved in Section 4, and numerical experiments to verify the theoretical analysis are reported in Section 5.
2 Nonlinear finite difference scheme
As usual, let be the step size for the spatial grid such that (). Let τ be the step size for the temporal direction (), . Denote and
Define
In the paper, C denotes a general positive constant which may have different values in different occurrences.
Lemma 2.1 For a mesh function , we have
Proof Obviously,
Since , we have . By Cauchy-Schwarz inequality, we get
□
The following Crank-Nicolson conservative difference scheme for problems (1.1)-(1.3) is considered,
From boundary condition (1.3), and physical boundary (1.4), discrete boundary condition (2.3) is reasonable. Based on scheme (2.1)-(2.3), the discrete versions of (1.5) and (1.6) are obtained as follows.
Theorem 2.1 Scheme (2.1)-(2.3) admits the following invariants, i.e.,
for .
Proof Multiplying (2.1) with h, then summing up for j from 1 to , by boundary condition (2.3) and formula of summation by parts [18], we have
By the definition of , (2.4) is obtained from (2.6).
Taking the inner product of (2.1) with , according to boundary condition (2.3), we get
where
and
Since
and
Substituting (2.8)-(2.10) into (2.7), we have
Similarly, by the definition of , (2.5) is obtained from (2.11). □
3 Existence
To prove the existence of solution for scheme (2.1)-(2.3), the following Browder fixed point theorem should be introduced. For the proof, see [19].
Lemma 3.1 Let H be a finite dimensional inner product space. Suppose that is continuous, and there exists an such that for all with . Then there exists such that and .
Theorem 3.1 There exists satisfying difference scheme (2.1)-(2.3).
Proof Use the mathematical induction. Obviously, with condition (2.2), the solution exists for . Suppose that for , satisfy (2.1)-(2.3), then we prove that there exists satisfying (2.1)-(2.3).
Define an operator g on as follows:
Taking the inner product of (3.1) with v, we get
From Lemma 2.1 and Cauchy-Schwarz inequality, we get
Hence, for , when . By Lemma 3.1, there exists which satisfies . Let , and it can be proved easily that is the solution of scheme (2.1)-(2.3). □
4 Priori estimate, convergence and unconditional stability
Let be the solution of problems (1.1)-(1.3) and , then the truncation error of scheme (2.1)-(2.3) is obtained as follows:
According to Taylor expansion, we obtain the following result.
Theorem 4.1 holds as .
Proof Since is the solution of problems (1.1)-(1.3), we have
Firstly, considering the term , by Taylor expansion at the point , we get
It follows from (4.5) and (4.6) that
Similarly, by Taylor expansion, we can obtain the following results, respectively:
and
Thus, by (4.8) and (4.9), we have
By (4.10) and (4.11), we have
Moreover,
Apparently, it follows from (4.7), (4.12), (4.13) and (4.14) that (4.4) holds. □
Lemma 4.1 Suppose that , then the solution of the initial-boundary value problems (1.1)-(1.3) satisfies
Proof It follows from (1.6) that
which yields
By Sobolev inequality, holds. □
Lemma 4.2 Suppose that , then the solution of scheme (2.1)-(2.3) satisfies
for .
Proof It follows from Theorem 2.1 and Lemma 2.1 that
that is,
By discrete Sobolev inequality [18], we have . □
Theorem 4.2 Suppose that , then the solution of difference scheme (2.1)-(2.3) converges to the solution of problems (1.1)-(1.3) with order by the norm.
Proof Letting
and subtracting (2.1)-(2.3) from (4.1)-(4.3), respectively, we have
Computing the inner product of (4.15) with , and using boundary condition (4.17), we get
Similarly to (2.8), we have
According to Lemma 4.1, Lemma 4.2, Theorem 2.1 and Cauchy-Schwartz inequality, we get
and
Substituting (4.19)-(4.22) into (4.18), we get
Letting and summing up (4.23) from 0 to , we have
Noticing
and , from (4.24), we get
By discrete Gronwall inequality [18], we have
Finally, by discrete Sobolev inequality [18], we get
This completes the proof of Theorem 4.2. □
Similarly, we can prove the stability and uniqueness of the difference solution.
Theorem 4.3 Under the conditions of Theorem 4.2, the solution of scheme (2.1)-(2.3) is stable by the norm.
Theorem 4.4 The solution of scheme (2.1)-(2.3) is unique.
5 Numerical experiments
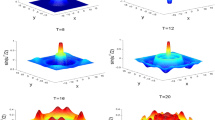
In this section, we compute a numerical example to demonstrate the effectiveness of our difference scheme. The single solitary-wave solution of RLW equation (1.1) is given by
where
and a, δ are constants.
Scheme (2.1)-(2.3) is a nonlinear system of equations which can be solved by the Newton iteration. Take , , and the initial function of problems (1.1)-(1.3) is rewritten as
In the numerical experiments, we take , and . The errors in the sense of -norm and -norm of the numerical solutions under different mesh steps h and τ are listed in Table 1. Table 2 shows that the computational and the theoretical orders of the scheme are very close to each other. Furthermore, since we have shown in Theorem 2.1 that the numerical solution satisfies invariants (2.4) and (2.5), respectively, Table 3 is also presented to show the conservative laws of discrete mass and discrete energy .
From these computational results, the stability and convergence of the scheme are verified, and it shows that our proposed algorithm is effective.
References
Peregrine DH: Long waves on beach. J. Fluid Mech. 1967, 27: 815-827. 10.1017/S0022112067002605
Bona JL, Bryant PJ: A mathematical model for long waves generated by wave makers in nonlinear dispersive systems. Proc. Camb. Philos. Soc. 1973, 73: 391-405. 10.1017/S0305004100076945
Wazwaz AM: Analytic study on nonlinear variants of the RLW and the PHI-four equations. Commun. Nonlinear Sci. Numer. Simul. 2007, 12: 314-327. 10.1016/j.cnsns.2005.03.001
Soliman AA: Numerical simulation of the generalized regularized long wave equation by He’s variational iteration method. Math. Comput. Simul. 2005, 70: 119-124. 10.1016/j.matcom.2005.06.002
Yusufoglu E, Bekir A: Application of the variational iteration method to the regularized long wave equation. Comput. Math. Appl. 2007, 54: 1154-1161. 10.1016/j.camwa.2006.12.073
Chang Q, Wang G, Guo B: Conservative scheme for a model of nonlinear dispersive waves and its solitary waves induced by boundary motion. J. Comput. Phys. 1991, 93: 360-375. 10.1016/0021-9991(91)90189-R
Ramos JI: Explicit finite difference methods for the EW and RLW equations. Appl. Math. Comput. 2006, 179: 622-638. 10.1016/j.amc.2005.12.003
Zhang L, Chang Q: A new finite difference method for regularized long wave equation. J. Numer. Methods Comput. Appl. 2000, 21: 247-254.
Christou MA, Christov CI: Interacting localized waves for the regularized long wave equation via a Galerkin spectral method. Math. Comput. Simul. 2005, 69: 257-268. 10.1016/j.matcom.2005.01.004
Alexender ME, Morris JL: Galerkin method applied to some model equations for nonlinear dispersive waves. J. Comput. Phys. 1979, 30: 428-451. 10.1016/0021-9991(79)90124-4
Esen A, Kutluay S: Application of a lumped Galerkin method to the regularized long wave equation. Appl. Math. Comput. 2006, 174: 833-845. 10.1016/j.amc.2005.05.032
Gu H, Chen N: Least-squares mixed finite element methods for the RLW equations. Numer. Methods Partial Differ. Equ. 2008, 24: 749-758. 10.1002/num.20285
Mei L, Chen Y: Numerical solutions of RLW equation using Galerkin method with extrapolation techniques. Comput. Phys. Commun. 2012, 183: 1609-1616. 10.1016/j.cpc.2012.02.029
Soliman AA, Hussien MH: Collocation solution for RLW equation with septic spline. Appl. Math. Comput. 2005, 161: 623-636. 10.1016/j.amc.2003.12.053
El-Danaf TS, Ramadan MA, Abd Alaal FEI: The use of adomian decomposition method for solving the regularized long-wave equation. Chaos Solitons Fractals 2005, 26: 747-757. 10.1016/j.chaos.2005.02.012
Li S, Vu-Quoc L: Finite difference calculus invariant structure of a class of algorithms for the nonlinear Klein-Gordon equation. SIAM J. Numer. Anal. 1995, 32: 1839-1875. 10.1137/0732083
Zhang F, Victor MP, Luis V: Numerical simulation of nonlinear Schrödinger systems: a new conservative scheme. Appl. Math. Comput. 1995, 71: 165-177. 10.1016/0096-3003(94)00152-T
Zhou Y: Application of Discrete Functional Analysis to the Finite Difference Method. Inter. Acad. Publishers, Beijing; 1990.
Browder FE: Existence and uniqueness theorems for solutions of nonlinear boundary value problems. Proc. Symp. Appl. Math. 1965, 17: 24-49.
Acknowledgements
The authors would like to thank the editor and the anonymous reviewers for their constructive comments and suggestions to improve the quality of the paper. This work is supported by the Scientific Research Fund of Sichuan Provincial Education Department (No. 11ZB009) and the Doctoral Program Research Fund of Southwest University of Science and Technology (No. 11zx7129).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The paper is a joint work of all authors who contributed equally to the final version of the paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zheng, K., Hu, J. High-order conservative Crank-Nicolson scheme for regularized long wave equation. Adv Differ Equ 2013, 287 (2013). https://doi.org/10.1186/1687-1847-2013-287
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2013-287