Global exponential stability of impulsive cellular neural networks with time-varying delays via fixed point theory

Abstract

This work is devoted to studying the application of fixed point theory to the stability analysis of complex neural networks. We employ the new method of contraction mapping principle to investigate the stability of impulsive cellular neural networks with time-varying delays. Some novel and concise sufficient conditions are presented to ensure the existence and uniqueness of a solution and the global exponential stability of the considered system at the same time. These conditions are easily checked and do not require the differentiability of delays.

1 Introduction

Cellular neural networks (CNNs), proposed by Chua and Yang in 1988 [1, 2], have become a hot topic for their numerous successful applications in various fields such as optimization, linear and nonlinear programming, associative memory, pattern recognition and computer vision.

Due to the finite switching speed of neurons and amplifiers in the implementation of neural networks, it turns out that time delays should not be neglected; and therefore, the model of delayed cellular neural networks (DCNNs) is put forward, which is naturally of better realistic significance. In fact, besides delay effects, stochastic and impulsive as well as diffusion effects are also likely to exist in the neural networks. Accordingly, many experts are showing a growing interest in the dynamic behavior research of complex CNNs such as impulsive delayed reaction-diffusion CNNs and stochastic delayed reaction-diffusion CNNs, followed by a mass of achievements [3–9] obtained.

Synthesizing the reported results about the complex CNNs, we find that the existing research skill for dealing with the stability is mainly based on Lyapunov theory. However, we also notice that there are still lots of difficulties in the applications of corresponding theory to the specific problems [10–16]. It is therefore necessary to seek some new techniques to overcome those difficulties.

It is inspiring that in a few recent years, Burton and other authors have applied fixed point theory to investigate the stability of deterministic systems and obtained some more applicable results; for example, see the monograph [17] and the papers [18–29]. In addition, more recently, there have been a few papers where fixed point theory is employed to deal with the stability of stochastic (delayed) differential equations; see [10–16, 30]. Particularly, in [11–13], Luo used fixed point theory to study the exponential stability of mild solutions for stochastic partial differential equations with bounded delays and with infinite delays. In [14, 15], fixed point theory is used to investigate the asymptotic stability in the p th moment of mild solutions to nonlinear impulsive stochastic partial differential equations with bounded delays and with infinite delays. In [16], the exponential stability of stochastic Volterra-Levin equations is studied based on fixed point theory. As is known to all, although Lyapunov functions play an important role in Lyapunov stability theory, it is not easy to find the appropriate Lyapunov functions. This difficulty can be avoided by applying fixed point theory. By means of fixed point theory, refs. [11–16] require no Lyapunov functions for stability analysis, and the delay terms need no differentiability.

Naturally, for the complex CNNs which have great application values, we wonder if fixed point theory can be used to investigate the stability, not just the existence and uniqueness of a solution. With this motivation, in the present paper, we aim to discuss the stability of impulsive CNNs with time-varying delays via fixed point theory. It is worth noting that our research skill is contraction mapping theory which is different from the usual method of Lyapunov theory. We use the fixed point theorem to prove the existence and uniqueness of a solution and the global exponential stability of the considered system all at once. Some new and concise algebraic criteria are provided; moreover, these conditions are easy to verify and do not require even the differentiability of delays, let alone the monotone decreasing behavior of delays.

2 Preliminaries

Let ${\mathrm{R}}^n$ denote the n-dimensional Euclidean space and $\parallel \cdot \parallel$ represent the Euclidean norm. $\mathcal{N}\triangleq \{1,2,\dots ,n\}$, ${\mathrm{R}}_{+}=[0,\mathrm{\infty })$, $C[X,Y]$ corresponds to the space of continuous mappings from the topological space X to the topological space Y.

In this paper, we consider the following impulsive cellular neural network with time-varying delays:

(1)

(2)

where $i\in \mathcal{N}$ and n is the number of neurons in the neural network. $x_i(t)$ corresponds to the state of the i th neuron at time t. $f_j(\cdot ),g_j(\cdot )\in C[\mathrm{R},\mathrm{R}]$, $f_j(x_j(t))$ is the activation function of the j th neuron at time t and $g_j(x_j(t-{\tau }_j(t)))$ represents the activation function of the j th neuron at time $t-{\tau }_j(t)$, where ${\tau }_j(t)\in C[{\mathrm{R}}^{+},{\mathrm{R}}^{+}]$ corresponds to the transmission delay along the axon of the j th neuron and satisfies $0\le {\tau }_j(t)\le \tau$ (τ is a constant). The constant $b_{ij}$ represents the connection weight of the j th neuron on the i th neuron at time t. The constant $c_{ij}$ denotes the connection strength of the j th neuron on the i th neuron at time $t-{\tau }_j(t)$. The constant $a_i>0$ represents the rate with which the i th neuron will reset its potential to the resting state when disconnected from the network and external inputs. The fixed impulsive moments $t_k$ ($k=1,2,\dots$) satisfy $0=t_0<t_1<t_2<\cdots$ , and ${lim}_{k\to \mathrm{\infty }}{t}_k=\mathrm{\infty }$. $x_i(t_k+)$ and $x_i(t_k-)$ stand for the right-hand and left-hand limit of $x_i(t)$ at time $t_k$, respectively. $P_{ik}(x_i(t_k))$ shows the abrupt change of $x_i(t)$ at the impulsive moment $t_k$ and $P_{ik}(\cdot )\in C[\mathrm{R},\mathrm{R}]$.

Throughout this paper, we always assume that $f_i(0)=g_i(0)=P_{ik}(0)=0$ for $i\in \mathcal{N}$ and $k=1,2,\dots$ . Denote by $\mathbf{x}(t)\triangleq \mathbf{x}(t;s,\phi )={(x_1(t;s,{\phi }_1),\dots ,x_n(t;s,{\phi }_n))}^{\mathrm{T}}\in {\mathrm{R}}^n$ the solution to Eqs. (1)-(2) with the initial condition

$$x_i(s)={\phi }_i(s),-\tau \le s\le 0,i\in \mathcal{N},$$

(3)

where $\phi (s)={({\phi }_1(s),\dots ,{\phi }_n(s))}^{\mathrm{T}}\in {\mathrm{R}}^n$ and ${\phi }_i(s)\in C[[-\tau ,0],\mathrm{R}]$.

The solution $\mathbf{x}(t)\triangleq \mathbf{x}(t;s,\phi )\in {\mathrm{R}}^n$ of Eqs. (1)-(3) is, for the time variable t, a piecewise continuous vector-valued function with the first kind discontinuity at the points $t_k$ ($k=1,2,\dots$), where it is left-continuous, i.e., the following relations are valid:

$$x_i(t_k-)=x_i(t_k),x_i(t_k+)=x_i(t_k)+P_{ik}(x_i(t_k)),i\in \mathcal{N},k=1,2,\dots .$$

Definition 2.1 Equations (1)-(2) are said to be globally exponentially stable if for any initial condition $\phi (s)\in C[[-\tau ,0],{\mathrm{R}}^n]$, there exists a pair of positive constants λ and M such that

$$\parallel \mathbf{x}(t;s,\phi )\parallel \le M{\mathrm{e}}^{-\lambda \mathrm{t}},\text{for all }t\ge 0.$$

The consideration of this paper is based on the following fixed point theorem.

Theorem 2.1 [31]

Let ϒ be a contraction operator on a complete metric space Θ, then there exists a unique point $\zeta \in \mathrm{\Theta }$ for which $\mathrm{\Upsilon }(\zeta )=\zeta$.

3 Main results

In this section, we investigate the existence and uniqueness of a solution to Eqs. (1)-(3) and the global exponential stability of Eqs. (1)-(2) by means of the contraction mapping principle. Before proceeding, we introduce some assumptions listed as follows:

(A1) There exist nonnegative constants $l_j$ such that for any $\eta ,\upsilon \in \mathrm{R}$,

$$|f_j(\eta )-f_j(\upsilon )|\le l_j|\eta -\upsilon |,j\in \mathcal{N}.$$

(A2) There exist nonnegative constants $k_j$ such that for any $\eta ,\upsilon \in \mathrm{R}$,

$$|g_j(\eta )-g_j(\upsilon )|\le k_j|\eta -\upsilon |,j\in \mathcal{N}.$$

(A3) There exist nonnegative constants $p_{jk}$ such that for any $\eta ,\upsilon \in \mathrm{R}$,

$$|P_{jk}(\eta )-P_{jk}(\upsilon )|\le p_{jk}|\eta -\upsilon |,j\in \mathcal{N},k=1,2,\dots .$$

Let $\mathcal{H}={\mathcal{H}}_1\times \cdots \times {\mathcal{H}}_n$, and let ${\mathcal{H}}_i$ ($i\in \mathcal{N}$) be the space consisting of functions ${\varphi }_i(t):[-\tau ,\mathrm{\infty })\to \mathrm{R}$, where ${\varphi }_i(t)$ satisfies:

• (1) ${\varphi }_i(t)$ is continuous on $t\ne t_k$ ($k=1,2,\dots$);

• (2) ${lim}_{t\to t_k^{-}}{\varphi }_i(t)$ and ${lim}_{t\to t_k^{+}}{\varphi }_i(t)$ exist; furthermore, ${lim}_{t\to t_k^{-}}{\varphi }_i(t)={\varphi }_i(t_k)$ for $k=1,2,\dots$ ;

• (3) ${\varphi }_i(s)={\phi }_i(s)$ on $s\in [-\tau ,0]$;

• (4) ${\mathrm{e}}^{\alpha t}{\varphi }_i(t)\to 0$ as $t\to \mathrm{\infty }$, where α is a positive constant and satisfies $\alpha <{min}_{i\in \mathcal{N}}\{a_i\}$,

here $t_k$ ($k=1,2,\dots$) and ${\phi }_i(s)$ ($s\in [-\tau ,0]$) are defined as shown in Section 2. Also, ℋ is a complete metric space when it is equipped with a metric defined by

$$d(\overline{\mathbf{q}}(t),\overline{\mathbf{h}}(t))=\sum _{i=1}^n\underset{t\ge -\tau }{sup}|q_i(t)-h_i(t)|,$$

where $\overline{\mathbf{q}}(t)=(q_1(t),\dots ,q_n(t))\in \mathcal{H}$ and $\overline{\mathbf{h}}(t)=(h_1(t),\dots ,h_n(t))\in \mathcal{H}$.

In what follows, we give the main result of this paper.

Theorem 3.1 Assume that the conditions (A1)-(A3) hold. Provided that

• (i) there exists a constant μ such that ${inf}_{k=1,2,\dots }\{t_k-t_{k-1}\}\ge \mu$,

• (ii) there exist constants $p_i$ such that $p_{ik}\le p_i\mu$ for $i\in \mathcal{N}$ and $k=1,2,\dots$ ,

• (iii) $\vartheta \triangleq {\sum }_{i=1}^n\{\frac{1}{a_i}{max}_{j\in \mathcal{N}}|b_{ij}{l}_j|+\frac{1}{a_i}{max}_{j\in \mathcal{N}}|c_{ij}{k}_j|\}+{max}_{i\in \mathcal{N}}\{p_i(\mu +\frac{1}{a_i})\}<1$,

then Eqs. (1)-(2) are globally exponentially stable.

Proof The following proof is based on the contraction mapping principle, which can be divided into three steps.

Step 1. The mapping is needed to be determined. Multiplying both sides of Eq. (1) with ${\mathrm{e}}^{a_{i}t}$ gives, for $t>0$ and $t\ne t_k$,

$$\begin{array}{rcl}{\mathrm{de}}^{a_{i}t}{x}_i(t)& =& {\mathrm{e}}^{a_{i}t}\mathrm{d}{x}_i(t)+a_i{x}_i(t){\mathrm{e}}^{a_{i}t}\mathrm{d}t\\ =& {\mathrm{e}}^{a_{i}t}\{-a_i{x}_i(t)+\sum _{j=1}^n{b}_{ij}{f}_j(x_j(t))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(t-{\tau }_j(t))\right)\}\mathrm{d}t+a_i{x}_i(t){\mathrm{e}}^{a_{i}t}\mathrm{d}t\\ =& {\mathrm{e}}^{a_{i}t}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(t))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(t-{\tau }_j(t))\right)\}\mathrm{d}t,\end{array}$$

which yields, after integrating from $t_{k-1}+\epsilon$ ($\epsilon >0$) to $t\in (t_{k-1},t_k)$ ($k=1,2,\dots$),

$$\begin{array}{rcl}{x}_i(t){\mathrm{e}}^{a_{i}t}& =& x_i(t_{k-1}+\epsilon ){\mathrm{e}}^{a_i(t_{k-1}+\epsilon )}\\ +{\int }_{t_{k-1}+\epsilon }^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s.\end{array}$$

(4)

Letting $\epsilon \to 0$ in (4), we have, for $t\in (t_{k-1},t_k)$ ($k=1,2,\dots$),

$$x_i(t){\mathrm{e}}^{a_{i}t}=x_i(t_{k-1}+){\mathrm{e}}^{a_i{t}_{k-1}}+{\int }_{t_{k-1}}^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s.$$

(5)

Setting $t=t_k-\epsilon$ ($\epsilon >0$) in (5), we get

$$x_i(t_k-\epsilon ){\mathrm{e}}^{a_i(t_k-\epsilon )}=x_i(t_{k-1}+){\mathrm{e}}^{a_i{t}_{k-1}}+{\int }_{t_{k-1}}^{t_k-\epsilon }{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s,$$

which generates by letting $\epsilon \to 0$

$$x_i(t_k-){\mathrm{e}}^{a_i{t}_k}=x_i(t_{k-1}+){\mathrm{e}}^{a_i{t}_{k-1}}+{\int }_{t_{k-1}}^{t_k}{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s.$$

(6)

Noting $x_i(t_k-0)=x_i(t_k)$, (6) can be rearranged as

$$x_i(t_k){\mathrm{e}}^{a_i{t}_k}=x_i(t_{k-1}+){\mathrm{e}}^{a_i{t}_{k-1}}+{\int }_{t_{k-1}}^{t_k}{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s.$$

(7)

Combining (5) and (7), we derive that

$$x_i(t){\mathrm{e}}^{a_{i}t}=x_i(t_{k-1}+){\mathrm{e}}^{a_i{t}_{k-1}}+{\int }_{t_{k-1}}^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s$$

is true for $t\in (t_{k-1},t_k]$ ($k=1,2,\dots$). Further,

$$\begin{array}{rcl}{x}_i(t){\mathrm{e}}^{a_{i}t}& =& \{x_i(t_{k-1})+I_{i(k-1)}(x_i(t_{k-1}))\}{\mathrm{e}}^{a_i{t}_{k-1}}\\ +{\int }_{t_{k-1}}^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s\\ =& x_i(t_{k-1}){\mathrm{e}}^{a_i{t}_{k-1}}+{\int }_{t_{k-1}}^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s\\ +P_{i(k-1)}(x_i(t_{k-1})){\mathrm{e}}^{a_i{t}_{k-1}}\end{array}$$

holds for $t\in (t_{k-1},t_k]$ ($k=1,2,\dots$). Hence,

which produces, for $t>0$,

$$\begin{array}{rcl}{x}_i(t)& =& {\phi }_i(0){\mathrm{e}}^{-a_{i}t}+{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s\\ +{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{P_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\right\}.\end{array}$$

(8)

Noting $x_i(0)={\phi }_i(0)$ in (8), we define the following operator π acting on ℋ for $\overline{\mathbf{x}}(t)=(x_1(t),\dots ,x_n(t))\in \mathcal{H}$:

$$\pi (\overline{\mathbf{x}})(t)=(\pi (x_1)(t),\dots ,\pi (x_n)(t)),$$

where $\pi (x_i)(t):[-\tau ,\mathrm{\infty })\to \mathrm{R}$ ($i\in \mathcal{N}$) obeys the rule as follows:

$$\begin{array}{rcl}\pi (x_i)(t)& =& {\phi }_i(0){\mathrm{e}}^{-a_{i}t}+{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\{\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))+\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\}\mathrm{d}s\\ +{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{P_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\right\}\end{array}$$

(9)

on $t\ge 0$ and $\pi (x_i)(s)={\phi }_i(s)$ on $s\in [-\tau ,0]$.

Step 2. We need to prove $\pi (\mathcal{H})\subset \mathcal{H}$. Choosing $x_i(t)\in {\mathcal{H}}_i$ ($i\in \mathcal{N}$), it is necessary to testify $\pi (x_i)(t)\subset {\mathcal{H}}_i$.

First, since $\pi (x_i)(s)={\phi }_i(s)$ on $s\in [-\tau ,0]$ and ${\phi }_i(s)\in C[[-\tau ,0],\mathrm{R}]$, we immediately know $\pi (x_i)(s)$ is continuous on $s\in [-\tau ,0]$. Then, for a fixed time $t>0$, it follows from (9) that

$$\pi (x_i)(t+r)-\pi (x_i)(t)=Q_1+Q_2+Q_3+Q_4,$$

(10)

where

$$\begin{array}{c}{Q}_1={\phi }_i(0){\mathrm{e}}^{-a_i(t+r)}-{\phi }_i(0){\mathrm{e}}^{-a_{i}t},\hfill \\ Q_2={\mathrm{e}}^{-a_i(t+r)}{\int }_0^{t+r}{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))\mathrm{ds}-{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))\mathrm{ds},\hfill \\ Q_3={\mathrm{e}}^{-a_i(t+r)}{\int }_0^{t+r}{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\mathrm{ds}-{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\mathrm{ds},\hfill \\ Q_4={\mathrm{e}}^{-a_i(t+r)}\sum _{0<t_k<(t+r)}\left\{I_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\right\}-{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{P_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\right\}.\hfill \end{array}$$

Owing to $x_i(t)\in {\mathcal{H}}_i$, we see that $x_i(t)$ is continuous on $t\ne t_k$ ($k=1,2,\dots$). Moreover, as $t=t_k$, ${lim}_{t\to t_k^{-}}{x}_i(t)$ and ${lim}_{t\to t_k^{+}}{x}_i(t)$ exist, in addition, ${lim}_{t\to t_k^{-}}{x}_i(t)=x_i(t_k)$.

Consequently, when $t\ne t_k$ ($k=1,2,\dots$) in (10), it is easy to find that $Q_i\to 0$ as $r\to 0$ for $i=1,\dots ,4$, and so $\pi (x_i)(t)$ is continuous on the fixed time $t\ne t_k$ ($k=1,2,\dots$). On the other hand, as $t=t_k$ ($k=1,2,\dots$) in (10), it is not difficult to find that $Q_i\to 0$ as $r\to 0$ for $i=1,2,3$. Furthermore, if letting $r<0$ be small enough, we have

$$\begin{array}{rcl}{Q}_4& =& {\mathrm{e}}^{-a_i(t_k+r)}\sum _{0<t_m<(t_k+r)}{P}_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}-{\mathrm{e}}^{-a_i{t}_k}\sum _{0<t_m<t_k}{P}_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}\\ =& \{{\mathrm{e}}^{-a_i(t_k+r)}-{\mathrm{e}}^{-a_i{t}_k}\}\sum _{0<t_m<t_k}\left\{P_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}\right\},\end{array}$$

which implies ${lim}_{r\to 0^{-}}{Q}_4=0$. While if letting $r>0$ be small enough, we get

$$\begin{array}{rcl}{Q}_4& =& {\mathrm{e}}^{-a_i(t_k+r)}\sum _{0<t_m<(t_k+r)}{P}_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}-{\mathrm{e}}^{-a_i{t}_k}\sum _{0<t_m<t_k}{P}_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}\\ =& {\mathrm{e}}^{-a_i(t_k+r)}\{\sum _{0<t_m<t_k}\left\{P_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}\right\}+P_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\}\\ -{\mathrm{e}}^{-a_i{t}_k}\sum _{0<t_m<t_k}\left\{P_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}\right\}\\ =& \{{\mathrm{e}}^{-a_i(t_k+r)}-{\mathrm{e}}^{-a_i{t}_k}\}\sum _{0<t_m<t_k}\left\{P_{im}(x_i(t_m)){\mathrm{e}}^{a_i{t}_m}\right\}+{\mathrm{e}}^{-a_i(t_k+r)}{P}_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k},\end{array}$$

which yields ${lim}_{r\to 0^{+}}{Q}_4={\mathrm{e}}^{-a_i{t}_k}{P}_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}$.

According to the above discussion, we see that $\pi (x_i)(t):[-\tau ,\mathrm{\infty })\to \mathrm{R}$ is continuous on $t\ne t_k$ ($k=1,2,\dots$), and for $t=t_k$ ($k=1,2,\dots$), ${lim}_{t\to t_k^{-}}\pi (x_i)(t)$ and ${lim}_{t\to t_k^{+}}\pi (x_i)(t)$ exist; furthermore, ${lim}_{t\to t_k^{-}}\pi (x_i)(t)=\pi (x_i)(t_k)\ne {lim}_{t\to t_k^{+}}\pi (x_i)(t)$.

Next, we will prove ${\mathrm{e}}^{\alpha t}\pi (x_i)(t)\to 0$ as $t\to \mathrm{\infty }$ for $i\in \mathcal{N}$. First of all, it is obvious that ${lim}_{t\to \mathrm{\infty }}{\mathrm{e}}^{-(a_i-\alpha )t}=0$ for $a_i-\alpha >0$. In addition, owing to $x_j(t)\in {\mathcal{H}}_j$ for $j\in \mathcal{N}$, we know ${lim}_{t\to \mathrm{\infty }}{\mathrm{e}}^{\alpha t}{x}_j(t)=0$. Then, for any $\epsilon >0$, there exists a $T_j>0$ such that $s\ge T_j$ implies $|{\mathrm{e}}^{\alpha s}{x}_j(s)|<\epsilon$. Choose $T^{\ast }={max}_{j\in \mathcal{N}}\{T_j\}$. It is derived from (A1) that

$$\begin{array}{c}{\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n\{|b_{ij}{l}_j||x_j(s)\left|\right\}\mathrm{d}s\hfill \\ ={\mathrm{e}}^{-(a_i-\alpha )t}{\int }_0^{T^{\ast }}{\mathrm{e}}^{(a_i-\alpha )s}\sum _{j=1}^n\{|b_{ij}{l}_j|{\mathrm{e}}^{\alpha s}|x_j(s)\left|\right\}\mathrm{d}s\hfill \\ +{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_{T^{\ast }}^t{\mathrm{e}}^{(a_i-\alpha )s}\sum _{j=1}^n\{|b_{ij}{l}_j|{\mathrm{e}}^{\alpha s}|x_j(s)\left|\right\}\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{-(a_i-\alpha )t}\sum _{j=1}^n\{|b_{ij}{l}_j|\underset{s\in [0,T^{\ast }]}{sup}|{\mathrm{e}}^{\alpha s}{x}_j(s)\left|\right\}\left\{{\int }_0^{T^{\ast }}{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{ds}\right\}\hfill \\ +\epsilon \sum _{j=1}^n\{|b_{ij}{l}_j|\}{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_{T^{\ast }}^t{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{-(a_i-\alpha )t}\sum _{j=1}^n\{|b_{ij}{l}_j|\underset{s\in [0,T^{\ast }]}{sup}|{\mathrm{e}}^{\alpha s}{x}_j(s)|\}\left\{{\int }_0^{T^{\ast }}{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{d}s\right\}+\frac{\epsilon }{a_i-\alpha }\sum _{j=1}^n\{|b_{ij}{l}_j|\},\hfill \end{array}$$

which leads to

$${\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{b}_{ij}{f}_j(x_j(s))\mathrm{d}s\to 0\text{as }t\to \mathrm{\infty }\text{ for }i\in \mathcal{N}.$$

(11)

Similarly, for any $\epsilon >0$, since ${lim}_{t\to \mathrm{\infty }}{\mathrm{e}}^{\alpha t}{x}_j(t)=0$, there also exists a $T_j^{\mathrm{\prime }}>0$ such that $s\ge T_j^{\mathrm{\prime }}-\tau$ implies $|{\mathrm{e}}^{\alpha s}{x}_j(s)|<\epsilon$. Select $\hat{T}={max}_{j\in \mathcal{N}}\{T_j^{\mathrm{\prime }}\}$. It follows from (A2) that

$$\begin{array}{c}{\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n\{|c_{ij}{k}_j||x_j(s-{\tau }_j(s))\left|\right\}\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{-(a_i-\alpha )t}{\int }_0^t{\mathrm{e}}^{a_{i}s}{\mathrm{e}}^{-\alpha \{s-\tau \}}\sum _{j=1}^n\{|c_{ij}{k}_j|{\mathrm{e}}^{\alpha [s-{\tau }_j(s)]}|x_j(s-{\tau }_j(s))\left|\right\}\mathrm{d}s\hfill \\ ={\mathrm{e}}^{\alpha \tau }{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_0^{\hat{T}}{\mathrm{e}}^{(a_i-\alpha )s}\sum _{j=1}^n\{|c_{ij}{k}_j|{\mathrm{e}}^{\alpha [s-{\tau }_j(s)]}|x_j(s-{\tau }_j(s))\left|\right\}\mathrm{d}s\hfill \\ +{\mathrm{e}}^{\alpha \tau }{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_{\hat{T}}^t{\mathrm{e}}^{(a_i-\alpha )s}\sum _{j=1}^n\{|c_{ij}{k}_j|{\mathrm{e}}^{\alpha [s-{\tau }_j(s)]}|x_j(s-{\tau }_j(s))\left|\right\}\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{\alpha \tau }\sum _{j=1}^n\{|c_{ij}{k}_j|\underset{s\in [-\tau ,\hat{T}]}{sup}|{\mathrm{e}}^{\alpha s}{x}_j(s)\left|\right\}{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_0^{\hat{T}}{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{d}s\hfill \\ +{\mathrm{e}}^{\alpha \tau }\epsilon \sum _{j=1}^n\{|c_{ij}{k}_j|\}{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_{\hat{T}}^t{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{d}s\hfill \\ \le {\mathrm{e}}^{\alpha \tau }\sum _{j=1}^n\{|c_{ij}{k}_j|\underset{s\in [-\tau ,\hat{T}]}{sup}|{\mathrm{e}}^{\alpha s}{x}_j(s)|\}{\mathrm{e}}^{-(a_i-\alpha )t}{\int }_0^{\hat{T}}{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{d}s+\frac{{\mathrm{e}}^{\alpha \tau }\epsilon }{a_i-\alpha }\sum _{j=1}^n\{|c_{ij}{k}_j|\},\hfill \end{array}$$

which results in

$${\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n{c}_{ij}{g}_j\left(x_j(s-{\tau }_j(s))\right)\mathrm{d}s\to 0\text{as }t\to \mathrm{\infty }\text{ for }i\in \mathcal{N}.$$

(12)

Furthermore, from (A3), we know that $|P_{ik}(x_i(t_k))|\le p_{ik}|x_i(t_k)|$. So,

$${\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{P_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\right\}\le {\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{p_{ik}|x_i(t_k)|{\mathrm{e}}^{a_i{t}_k}\right\}.$$

As $x_i(t)\in {\mathcal{H}}_i$, we have ${lim}_{t\to \mathrm{\infty }}{\mathrm{e}}^{\alpha t}{x}_i(t)=0$. Then, for any $\epsilon >0$, there exists a non-impulsive point $T_i>0$ such that $s\ge T_i$ implies $|{\mathrm{e}}^{\alpha s}{x}_i(s)|<\epsilon$. It then follows from the conditions (i) and (ii) that

$$\begin{array}{c}{\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{p_{ik}\right|x_i(t_k)\left|{\mathrm{e}}^{a_i{t}_k}\right\}\hfill \\ ={\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}\{\sum _{0<t_k<T_i}\left\{p_{ik}\right|x_i(t_k)\left|{\mathrm{e}}^{a_i{t}_k}\right\}+\sum _{T_i<t_k<t}\left\{p_{ik}\right|x_i(t_k)\left|{\mathrm{e}}^{\alpha t_k}{\mathrm{e}}^{(a_i-\alpha )t_k}\right\}\}\hfill \\ \le {\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<T_i}\left\{p_{ik}\right|x_i(t_k)\left|{\mathrm{e}}^{a_i{t}_k}\right\}+{\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}{p}_i\epsilon \sum _{T_i<t_k<t}\left\{\mu {\mathrm{e}}^{(a_i-\alpha )t_k}\right\}\hfill \\ \le {\mathrm{e}}^{-(a_i-\alpha )t}\sum _{0<t_k<T_i}\left\{p_{ik}\right|x_i(t_k)\left|{\mathrm{e}}^{a_i{t}_k}\right\}\hfill \\ +{\mathrm{e}}^{-(a_i-\alpha )t}{p}_i\epsilon \{\sum _{T_i<t_r<t_k}\{{\mathrm{e}}^{(a_i-\alpha )t_r}(t_{r+1}-t_r)\}+\mu {\mathrm{e}}^{(a_i-\alpha )t_k}\}\hfill \\ \le {\mathrm{e}}^{-(a_i-\alpha )t}\sum _{0<t_k<T_i}\left\{p_{ik}\right|x_i(t_k)\left|{\mathrm{e}}^{a_i{t}_k}\right\}+{\mathrm{e}}^{-(a_i-\alpha )t}{p}_i\epsilon {\int }_{T_i}^t{\mathrm{e}}^{(a_i-\alpha )s}\mathrm{d}s+{\mathrm{e}}^{-(a_i-\alpha )t}{p}_i\epsilon \mu {\mathrm{e}}^{(a_i-\alpha )t}\hfill \\ \le {\mathrm{e}}^{-(a_i-\alpha )t}\sum _{0<t_k<T_i}\left\{p_{ik}|x_i(t_k)|{\mathrm{e}}^{a_i{t}_k}\right\}+\frac{p_i\epsilon }{a_i-\alpha }+p_i\epsilon \mu ,\hfill \end{array}$$

which produces

$${\mathrm{e}}^{\alpha t}{\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{P_{ik}(x_i(t_k)){\mathrm{e}}^{a_i{t}_k}\right\}\to 0\text{as }t\to \mathrm{\infty }.$$

(13)

From (11), (12) and (13), we deduce ${\mathrm{e}}^{\alpha t}\pi (x_i)(t)\to 0$ as $t\to \mathrm{\infty }$. We therefore conclude that $\pi (x_i)(t)\subset {\mathcal{H}}_i$ ($i\in \mathcal{N}$), which means $\pi (\mathcal{H})\subset \mathcal{H}$.

Step 3. We need to prove π is contractive. For $\overline{\mathbf{x}}=(x_1(t),\dots ,x_n(t))\in \mathcal{H}$ and $\overline{\mathbf{y}}=(y_1(t),\dots ,y_n(t))\in \mathcal{H}$, we estimate $|\pi (x_i)(t)-\pi (y_i)(t)|\le J_1+J_2+J_3$, where

$$\begin{array}{c}{J}_1={\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n[|b_{ij}||f_j(x_j(s))-f_j(y_j(s))|]\mathrm{d}s,\hfill \\ J_2={\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n[|c_{ij}||g_j\left(x_j(s-{\tau }_j(s))\right)-g_j\left(y_j(s-{\tau }_j(s))\right)|]\mathrm{d}s.\hfill \\ J_3={\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{{\mathrm{e}}^{a_i{t}_k}|P_{ik}(x_i(t_k))-P_{ik}(y_i(t_k))|\right\},\hfill \end{array}$$

Note

$$\begin{array}{rcl}{J}_1& \le & {\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n[|b_{ij}{l}_j||x_j(s)-y_j(s)\left|\right]\mathrm{d}s\\ \le & \underset{j\in \mathcal{N}}{max}|b_{ij}{l}_j|\sum _{j=1}^n\left\{\underset{s\in [0,t]}{sup}\right|x_j(s)-y_j(s)\left|\right\}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\mathrm{d}s\\ \le & \frac{1}{a_i}\underset{j\in \mathcal{N}}{max}|b_{ij}{l}_j|\sum _{j=1}^n\left\{\underset{s\in [0,t]}{sup}|x_j(s)-y_j(s)|\right\},\end{array}$$

(14)

and

$$\begin{array}{rcl}{J}_2& \le & {\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\sum _{j=1}^n[|c_{ij}{k}_j||x_j(s-{\tau }_j(s))-y_j(s-{\tau }_j(s))\left|\right]\mathrm{d}s\\ \le & \underset{j\in \mathcal{N}}{max}|c_{ij}{k}_j|\sum _{j=1}^n\left\{\underset{s\in [-\tau ,t]}{sup}\right|x_j(s)-y_j(s)\left|\right\}{\mathrm{e}}^{-a_{i}t}{\int }_0^t{\mathrm{e}}^{a_{i}s}\mathrm{d}s\\ \le & \frac{1}{a_i}\underset{j\in \mathcal{N}}{max}|c_{ij}{k}_j|\sum _{j=1}^n\left\{\underset{s\in [-\tau ,t]}{sup}|x_j(s)-y_j(s)|\right\},\end{array}$$

(15)

and

$$\begin{array}{rcl}{J}_3& \le & {\mathrm{e}}^{-a_{i}t}\sum _{0<t_k<t}\left\{{\mathrm{e}}^{a_i{t}_k}{p}_{ik}\right|x_i(t_k)-y_i(t_k)\left|\right\}\\ \le & p_i{\mathrm{e}}^{-a_{i}t}\underset{s\in [0,t]}{sup}|x_i(s)-y_i(s)|\sum _{0<t_k<t}\left\{{\mathrm{e}}^{a_i{t}_k}\mu \right\}\\ \le & p_i{\mathrm{e}}^{-a_{i}t}\underset{s\in [0,t]}{sup}|x_i(s)-y_i(s)|\{\sum _{0<t_r<t_k}\{{\mathrm{e}}^{a_i{t}_r}(t_{r+1}-t_r)\}+{\mathrm{e}}^{a_i{t}_k}\mu \}\\ \le & p_i\underset{s\in [0,t]}{sup}|x_i(s)-y_i(s)|{\mathrm{e}}^{-a_{i}t}\{{\int }_0^t{\mathrm{e}}^{a_{i}s}\mathrm{d}s+{\mathrm{e}}^{a_{i}t}\mu \}\\ \le & p_i(\mu +\frac{1}{a_i})\underset{s\in [0,t]}{sup}|x_i(s)-y_i(s)|.\end{array}$$

(16)

It hence follows from (14), (15) and (16) that

$$\begin{array}{rcl}|\pi (x_i)(t)-\pi (y_i)(t)|& \le & \frac{1}{a_i}\underset{j\in \mathcal{N}}{max}|b_{ij}{l}_j|\sum _{j=1}^n\left\{\underset{s\in [0,t]}{sup}|x_j(s)-y_j(s)|\right\}\\ +\frac{1}{a_i}\underset{j\in \mathcal{N}}{max}|c_{ij}{k}_j|\sum _{j=1}^n\left\{\underset{s\in [-\tau ,t]}{sup}\right|x_j(s)-y_j(s)\left|\right\}\\ +p_i(\mu +\frac{1}{a_i})\underset{s\in [0,t]}{sup}|x_i(s)-y_i(s)|,\end{array}$$

which implies

$$\begin{array}{rcl}\underset{t\in [-\tau ,T]}{sup}|\pi (x_i)(t)-\pi (y_i)(t)|& \le & \frac{1}{a_i}\underset{j\in \mathcal{N}}{max}|b_{ij}{l}_j|\sum _{j=1}^n\left\{\underset{s\in [-\tau ,T]}{sup}|x_j(s)-y_j(s)|\right\}\\ +\frac{1}{a_i}\underset{j\in \mathcal{N}}{max}|c_{ij}{k}_j|\sum _{j=1}^n\left\{\underset{s\in [-\tau ,T]}{sup}\right|x_j(s)-y_j(s)\left|\right\}\\ +p_i(\mu +\frac{1}{a_i})\underset{s\in [-\tau ,T]}{sup}|x_i(s)-y_i(s)|.\end{array}$$

Therefore,

$$\sum _{i=1}^n\underset{t\in [-\tau ,T]}{sup}|\pi (x_i)(t)-\pi (y_i)(t)|\le \vartheta \sum _{j=1}^n\left\{\underset{s\in [-\tau ,T]}{sup}|x_j(s)-y_j(s)|\right\}.$$

In view of the condition (iii), we see π is a contraction mapping, and thus there exists a unique fixed point $\overline{\mathbf{x}}(\cdot )$ of π in ℋ, which means ${\overline{\mathbf{x}}}^{\mathrm{T}}(\cdot )$ is the solution to Eqs. (1)-(3) and meets ${\mathrm{e}}^{\alpha t}\parallel {\overline{\mathbf{x}}}^{\mathrm{T}}(\cdot )\parallel \to 0$ as $t\to \mathrm{\infty }$. This completes the proof. □

Theorem 3.2 Assume the conditions (A1)-(A3) hold. Provided that

• (i) ${inf}_{k=1,2,\dots }\{t_k-t_{k-1}\}\ge 1$,

• (ii) there exist constants $p_i$ such that $p_{ik}\le p_i$ for $i\in \mathcal{N}$ and $k=1,2,\dots$ ,

• (iii) ${\sum }_{i=1}^n\{\frac{1}{a_i}{max}_{j\in \mathcal{N}}|b_{ij}{l}_j|+\frac{1}{a_i}{max}_{j\in \mathcal{N}}|c_{ij}{k}_j|\}+{max}_{i\in \mathcal{N}}\{p_i(1+\frac{1}{a_i})\}<1$,

then Eqs. (1)-(2) are globally exponentially stable.

Proof Theorem 3.2 is a direct conclusion by letting $\mu =1$ in Theorem 3.1. □

Remark 3.1 In Theorem 3.1, we see that it is fixed point theory that deals with the existence and uniqueness of a solution and the global exponential stability of impulsive delayed neural networks at the same time, while the Lyapunov method fails to do this.

Remark 3.2 The presented sufficient conditions in Theorems 3.1-3.2 do not require even the differentiability of delays, let alone the monotone decreasing behavior of delays which is necessary in some relevant works.

Remark 3.3 In [4], the abrupt changes are assumed linear with the coefficient $\alpha \in (0,2)$, while in our paper, this restriction is removed and the abrupt changes can be linear and nonlinear. On the other hand, the activation functions in [6] are assumed to satisfy $0\le \frac{f(x)-f(y)}{x-y}\le l$, where f is an activation function. However, in this paper, we relax this restriction and instead suppose an activation function f satisfies $|f(x)-f(y)|\le l|x-y|$.

4 Example

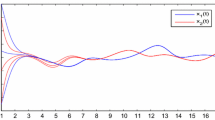
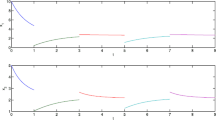
Consider the following two-dimensional impulsive cellular neural network with time-varying delays:

$$\begin{array}{c}\frac{\mathrm{d}{x}_i(t)}{\mathrm{d}t}=-a_i{x}_i(t)+\sum _{j=1}^2{b}_{ij}{f}_j(x_j(t))+\sum _{j=1}^2{c}_{ij}{g}_j\left(x_j(t-{\tau }_j(t))\right),t\ge 0,t\ne t_k,\hfill \\ \mathrm{\Delta }{x}_i(t_k)=x_i(t_k+)-x_i(t_k)=P_{ik}(x_i(t_k)),k=1,2,\dots ,\hfill \end{array}$$

with the initial conditions $x_1(s)=cos(s)$, $x_2(s)=sin(s)$ on $-\tau \le s\le 0$, where $a_1=a_2=7$, $b_{11}=0$, $b_{12}=\frac{1}{7}$, $b_{21}=-\frac{1}{7}$, $b_{22}=-\frac{1}{7}$, $c_{11}=\frac{3}{7}$, $c_{12}=\frac{2}{7}$, $c_{21}=0$, $c_{22}=\frac{1}{7}$, $f_j(s)=g_j(s)=(|s+1|-|s-1|)/2$ ($j=1,2$), $P_{ik}(x_i(t_k))=arctan(0.4x_i(t_k))$ for $i=1,2$ and $k=1,2,\dots$ , $t_k=t_{k-1}+0.5k$ ($k=1,2,\dots$). It is easy to see that $\mu =0.5$ and $l_j=k_j=1$ as well as $p_{ik}=0.4$.

Select $p_i=0.8$ and compute ${\sum }_{i=1}^2\{\frac{1}{a_i}{max}_{j=1,2}|b_{ij}{l}_j|+\frac{1}{a_i}{max}_{j=1,2}|c_{ij}{k}_j|\}+{max}_{i=1,2}\{p_i(\mu +\frac{1}{a_i})\}<1$. From Theorem 3.1, we conclude that this two-dimensional impulsive cellular neural network with time-varying delays is globally exponentially stable.

5 Conclusion

This work aims to seek new methods to study the stability of complex CNNs. From what have been discussed above, we find that the application of fixed point theory to the stability analysis of complex CNNs is successful. We utilize the contraction mapping principle to deal with the existence and uniqueness of a solution and the global exponential stability of the considered system at the same time, for which Lyapunov theory feels helpless. Now that there are different kinds of fixed point theorems and complex neural networks, our future work is to continue the study on the application of fixed point theory to the stability analysis of complex neural networks.