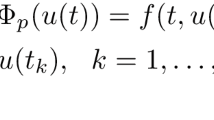Abstract
This paper is concerned with the existence of mild solutions to impulsive differential equations with nonlocal conditions. We firstly establish a property of the measure of noncompactness in the space of piecewise continuous functions. Then, by applying this property and Darbo-Sadovskii’s fixed point theorem, we get the existence results of impulsive differential equations in a unified way under compactness conditions, Lipschitz conditions and mixed-type conditions, respectively.
MSC:34K30, 34G20.
Similar content being viewed by others
1 Introduction
In this paper, we discuss the existence of mild solutions for the following impulsive differential equation with nonlocal conditions:

where is the infinitesimal generator of a strongly continuous semigroup , in a Banach space X, , , , denote the left and right limit of u at , respectively. f, g, are appropriate functions to be specified later.
Impulsive differential equations are recognized as excellent models to study the evolution processes that are subject to sudden changes in their states; see the monographs of Lakshmikantham et al.[1], Benchohra et al.[2]. In recent years impulsive differential equations in Banach spaces have been investigated by many authors; see [3–8] and references therein. Liu [9] discussed the existence and uniqueness of mild solutions for a semilinear impulsive Cauchy problem with Lipschitz impulsive functions. Non-Lipschitzian impulsive equations are considered by Nieto et al.[10]. Cardinali and Rubbioni [11] proved the existence of mild solutions for the impulsive Cauchy problem controlled by a semilinear evolution differential inclusion. In [12], Abada et al. studied the existence of integral solutions for some nondensely defined impulsive semilinear functional differential inclusions.
On the other hand, the study of abstract nonlocal initial value problems was initiated by Byszewski, and the importance of the problem consists in the fact that it is more general and has better effect than the classical initial conditions alone. Therefore, it has been studied extensively under various conditions. Here we mention some results. Byszewski and Lakshmikantham [13], Byszewski [14] obtained the existence and uniqueness of mild solutions and classical solutions in the case that Lipschitz-type conditions are satisfied. In [15], Fu and Ezzinbi studied neutral functional-differential equations with nonlocal conditions. Aizicovici [16], Xue [17, 18] discussed the case when A generates a nonlinear contraction semigroup on X and obtained the existence of integral solutions for nonlinear differential equations. In particular, the measure of noncompactness has been used as an important tool to deal with some similar functional differential and integral equations; see [18–22].
From the viewpoint of theory and practice, it is natural for mathematics to combine impulsive conditions and nonlocal conditions. Recently, the nonlocal impulsive differential problem of type (1.1) has been discussed in the papers of Liang et al.[23] and Fan et al.[24, 25], where a semigroup is supposed to be compact, and g is Lipschitz continuous, compact, and strongly continuous, respectively. Very recently, Zhu et al.[26] obtain the existence results when a nonlocal item g is Lipschitz continuous by using the Hausdorff measure of noncompactness and operator transformation. Compared with the results in [23–25], in this paper we do not require the compactness of the semigroup and Lipschitz continuity of f. More important, by using the property of the measure of noncompactness in given by us (see Lemma 2.7), the impulsive conditions and nonlocal conditions can be considered in a unified way under various conditions, including compactness conditions, Lipschitz conditions and mixed-type conditions. Hence, our results generalize and partially improve the results in [23, 25, 26].
This paper is organized as follows. In Section 2, we present some concepts and facts about the strongly continuous semigroup and the measure of noncompactness. In Section 3, we give four existence theorems of the problem (1.1) by using a condensing operator and the measure of noncompactness. At last, an example of an impulsive partial differential system is given in Section 4.
2 Preliminaries
Let be a real Banach space. We denote by the space of X-valued continuous functions on with the norm and by the space of X-valued Bochner integrable functions on with the norm .
The semigroup is said to be equicontinuous if is equicontinuous at for any bounded subset (cf.[27]). Obviously, if is a compact semigroup, it must be equicontinuous. And the converse of the relation usually is not correct. Throughout this paper, we suppose that
(HA) The semigroup generated by A is equicontinuous. Moreover, there exists a positive number M such that .
For the sake of simplicity, we put ; ; , . In order to define a mild solution of the problem (1.1), we introduce the set . It is easy to verify that is a Banach space with the norm .
Definition 2.1 A function is a mild solution of the problem (1.1) if
for all .
Now, we introduce the Hausdorff measure of noncompactness (in short MNC) defined by
for each bounded subset B in a Banach space X. We recall the following properties of the Hausdorff measure of noncompactness β.
Lemma 2.2 ([28])
Let X be a real Banach space andbe bounded. Then the following properties are satisfied:
-
(1)
B is relatively compact if and only if ;
-
(2)
, where and convB mean the closure and convex hull of B, respectively;
-
(3)
when ;
-
(4)
, where ;
-
(5)
;
-
(6)
for any ;
-
(7)
If the map is Lipschitz continuous with a constant k, then for any bounded subset , where Z is a Banach space.
The map is said to be β-condensing if Q is continuous and bounded, and for any nonprecompact bounded subset , we have , where X is a Banach space.
Lemma 2.3 (See [28], Darbo-Sadovskii)
Ifis bounded, closed, and convex, the continuous mapis β-condensing, then Q has at least one fixed point in D.
In order to remove the strong restriction on the coefficient in Darbo-Sadovskii’s fixed point theorem, Sun and Zhang [29] generalized the definition of a β-condensing operator. At first, we give some notation. Let be closed and convex, the map and . For every , set
where means the closure of convex hull, .
Definition 2.4 Let be closed and convex. The map is said to be β-convex-power condensing if Q is continuous, bounded and there exist , such that for every nonprecompact bounded subset , we have
Obviously, if , then a β-convex-power condensing operator is β-condensing. Thus, the convex-power condensing operator is a generalization of the condensing operator. Now, we give the fixed point theorem about the convex-power condensing operator.
Lemma 2.5 ([29])
Ifis bounded, closed, and convex, the continuous mapis β-convex-power condensing, then Q has at least one fixed point in D.
Now, we give an important property of the Hausdorff MNC in , which is an extension to the property of MNC in and makes us deal with the impulsive differential equations from a unified perspective.
Lemma 2.6 ([28])
Ifis bounded, thenfor all, where. Furthermore, if W is equicontinuous on, thenis continuous onand.
By applying Lemma 2.6, we shall extend the result to the space .
Lemma 2.7 Ifis bounded, thenfor all, where. Furthermore, suppose the following conditions are satisfied:
-
(1)
W is equicontinuous on and each , ;
-
(2)
W is equicontinuous at , .
Then.
Proof For arbitrary , there exists , , such that and
where denotes the diameter of a bounded set. Now, we have for each , and
for . From the above two inequalities, it follows that
By the arbitrariness of ε, we get that for every . Therefore, we have .
Next, if the conditions (1) and (2) are satisfied, it remains to prove that . We denote by the restriction of W on , . That is, for , define that
and obviously is equicontinuous on due to the conditions (1) and (2). Then from Lemma 2.6, we have that
Moreover, we define the map
by , where , , . As Λ is an isometric mapping, noticing the equicontinuity of on , we have that
And from the fact that , for each , we get that . This completes the proof. □
Lemma 2.8 ([28])
Ifis bounded and equicontinuous, thenis continuous and
for all, where.
Lemma 2.9 If the hypothesis (HA) is satisfied, i.e., is equicontinuous, and, then the setis equicontinuous for.
Proof We let and have that

If , then the right-hand side of (2.1) can be made small when h is small independent of u. If , then we can find a small with . Then it follows from (2.1) that

Here, as is equicontinuous for , thus
uniformly for u.
Then from (2.1), (2.2) and the absolute continuity of integrals, we get that is equicontinuous for . □
3 Main results
In this section we give the existence results for the problem (1.1) under different conditions on g and when the semigroup is not compact and f is not compact or Lipschitz continuous, by using Lemma 2.7 and the generalized β-condensing operator. More precisely, Theorem 3.1 is concerned with the case that compactness conditions are satisfied. Theorem 3.4 deals with the case that Lipschitz conditions are satisfied. And mixed-type conditions are considered in Theorem 3.5 and Theorem 3.6.
Let r be a finite positive constant, and set , . We define the solution map by
with

for all . It is easy to see that u is the mild solution of the problem (1.1) if and only if u is a fixed point of the map G.
We list the following hypotheses:
(Hf) satisfies the following conditions:
-
(i)
is continuous for a.e. and is measurable for all . Moreover, for any , there exists a function such that
for a.e. and .
-
(ii)
there exists a constant such that for any bounded set ,
(3.2)
for a.e. .
(Hg1) is continuous and compact.
(HI1) is continuous and compact for .
Theorem 3.1 Assume that the hypotheses (HA), (Hf), (Hg1), (HI1) are satisfied, then the nonlocal impulsive problem (1.1) has at least one mild solution onprovided that there exists a constantsuch that
Proof We will prove that the solution map G has a fixed point by using the fixed point theorem about the β-convex-power condensing operator.
Firstly, we prove that the map G is continuous on . For this purpose, let be a sequence in with in . By the continuity of f with respect to the second argument, we deduce that for each , converges to in X. And we have
Then by the continuity of g, and using the dominated convergence theorem, we get in .
Secondly, we claim that . In fact, for any , from (3.1) and (3.3), we have
for each . It implies that .
Now, we show that is equicontinuous on , and is also equicontinuous at , . Indeed, we only need to prove that is equicontinuous on , as the cases for other subintervals are the same. For , , we have, using the semigroup property,
Thus, is equicontinuous on due to the compactness of g and the strong continuity of . The same idea can be used to prove the equicontinuity of on . That is, for , , we have
which implies the equicontinuity of on due to the compactness of and the strong continuity of . Moreover, from Lemma 2.9, we have that is equicontinuous on . Therefore, we have that the functions in are equicontinuous on each , .
Set , where means the closure of convex hull. It is easy to verify that G maps W into itself and W is equicontiuous on each , . Now, we show that is a convex-power condensing operator. Take , we shall prove that there exists a positive integral such that
for every nonprecompact bounded subset .
From Lemma 2.2 and Lemma 2.8, noticing the compactness of g and , we have
for . Further,
for . We can continue this iterative procedure and get that
for . As is equicontinuous on each , by Lemma 2.7, we have that
By the fact that as , we know that there exists a large enough positive integral such that
which implies that is a convex-power condensing operator. From Lemma 2.5, G has at least one fixed point in W, which is just a mild solution of the nonlocal impulsive problem (1.1). This completes the proof of Theorem 3.1. □
Remark 3.2 By using the method of the measure of noncompactness, we require f to satisfy some proper conditions of MNC, but do not require the compactness of a semigroup . Note that if f is compact or Lipschitz continuous, then the condition (Hf)(ii) is satisfied. And our work improves many previous results, where they need the compactness of or f, or the Lipschitz continuity of f. In the proof, Lemma 2.7 plays an important role for the impulsive differential equations, which provides us with the way to calculate the measure of noncompactness in . The use of noncompact measures in functional differential and integral equations can also be seen in [18–20, 22].
Remark 3.3 When we apply Darbo-Sadovskii’s fixed point theorem to get the fixed point of a map, a strong inequality is needed to guarantee its condensing property. By using the β-convex-power condensing operator developed by Sun et al.[29], we do not impose any restrictions on the coefficient L. This generalized condensing operator also can be seen in Liu et al.[30], where nonlinear Volterra integral equations are discussed.
In the following, by using Lemma 2.7 and Darbo-Sadovskii’s fixed point theorem, we give the existence results of the problem (1.1) under Lipschitz conditions and mixed-type conditions, respectively.
We give the following hypotheses:
(Hg2) is Lipschitz continuous with the Lipschitz constant k.
(HI2) is Lipschitz continuous with the Lipschitz constant ; that is,
for , .
Theorem 3.4 Assume that the hypotheses (HA), (Hf), (Hg2), (HI2) are satisfied, then the nonlocal impulsive problem (1.1) has at least one mild solution onprovided that
and (3.3) are satisfied.
Proof From the proof of Theorem 3.1, we have that the solution operator G is continuous and maps into itself. It remains to show that G is β-condensing in .
By the conditions (Hg2) and (HI2), we get that is Lipschitz continuous with the Lipschitz constant . In fact, for , we have

Thus, from Lemma 2.2(7), we obtain that
For the operator , from Lemma 2.6, Lemma 2.8 and Lemma 2.9, we have
Combining (3.5) and (3.6), we have
From the condition (3.4), , the solution map G is β-condensing in . By Darbo-Sadovskii’s fixed point theorem, G has a fixed point in , which is just a mild solution of the nonlocal impulsive problem (1.1). This completes the proof of Theorem 3.4. □
Among the previous works on nonlocal impulsive differential equations, few are concerned with the mixed-type conditions. Here, by using Lemma 2.7, we can also deal with the mixed-type conditions in a similar way.
Theorem 3.5 Assume that the hypotheses (HA), (Hf), (Hg1), (HI2) are satisfied, then the nonlocal impulsive problem (1.1) has at least one mild solution onprovided that
and (3.3) are satisfied.
Proof We will also use Darbo-Sadovskii’s fixed point theorem to obtain a fixed point of the solution operator G. From the proof of Theorem 3.1, we have that G is continuous and maps into itself.
Subsequently, we show that G is β-condensing in . From the compactness of g and the strong continuity of , we get that is equicontinuous on . Then by Lemma 2.6, we have that
On the other hand, for , we have
Then by Lemma 2.2(7), we obtain that
Combining (3.6), (3.8) and (3.9), we get that
From the condition (3.7), the map G is β-condensing in . So, G has a fixed point in due to Darbo-Sadovskii’s fixed point theorem, which is just a mild solution of the nonlocal impulsive problem (1.1). This completes the proof of Theorem 3.5. □
Theorem 3.6 Assume that the hypotheses (HA), (Hf), (Hg2), (HI1) are satisfied, then the nonlocal impulsive problem (1.1) has at least one mild solution onprovided that
and (3.3) are satisfied.
Proof From the proof of Theorem 3.1, we have that the solution operator G is continuous and maps into itself. In the following, we shall show that G is β-condensing in .
By the Lipschitz continuity of g, we have that for ,
which implies that
Similar to the discussion in Theorem 3.1, from the compactness of and the strong continuity , we get that is equicontinuous on each , . Then by Lemma 2.7, we have that
Combining (3.6), (3.11) and (3.12), we have that
From condition (3.10), the map G is β-condensing in . So, G has a fixed point in due to Darbo-Sadovskii’s fixed point theorem, which is just a mild solution of the nonlocal impulsive problem (1.1). This completes the proof of Theorem 3.6. □
Remark 3.7 With the assumption of compactness on the associated semigroup, the existence of mild solutions to functional differential equations has been discussed in [6, 23–25]. By using the method of the measure of noncompactness, we deal with the four cases of impulsive differential equations in a unified way and get the existence results when the semigroup in not compact.
4 An example
In the application to partial differential equations, such as a class of parabolic equations, the semigroup corresponding to the differential equations is an analytic semigroup. We know that an analytic semigroup or a compact semigroup must be equicontinuous; see Pazy [31]. So, our results can be applied to these problems. If the operator , the corresponding semigroup is equicontinuous on .
We consider the following partial differential system (based on [23]) to illustrate our abstract results:
Take and the operator defined by , with
From Pazy [31], we know that A is the infinitesimal generator of an analytic semigroup , . This implies that A satisfies the condition (HA).
Let , , (), , and for . Now, we define that
-
(1)
, , .
-
(2)
, .
-
(3)
, .
-
(4)
, , .
-
(5)
, , .
Then we obtain that
Case 1. Under the conditions (1) + (3) + (5), the assumptions in Theorem 3.1 are satisfied for large . Therefore, the corresponding system (1.1) has at least a mild solution.
Case 2. Under the conditions (1) + (2) + (4), the assumptions in Theorem 3.4 are satisfied for large . Therefore, the corresponding system (1.1) has at least a mild solution.
Case 3. Under the conditions (1) + (3) + (4), the assumptions in Theorem 3.5 are satisfied for large . Therefore, the corresponding system (1.1) has at least a mild solution.
Case 4. Under the conditions (1) + (2) + (5), the assumptions in Theorem 3.6 are satisfied for large . Therefore, the corresponding system (1.1) has at least a mild solution.
References
Lakshmikantham V, Bainov DD, Simeonov PS: Theory of Impulsive Differential Equations. World Scientific, Singapore; 1989.
Benchohra M, Henderson J, Ntouyas SK: Impulsive Differential Equations and Inclusions. Hindawi Publishing, New York; 2006.
Guo M, Xue X, Li R: Controllability of impulsive evolution inclusions with nonlocal conditions. J. Optim. Theory Appl. 2004, 120: 355–374.
Hernández E, Rabelo M, Henríquez HR: Existence of solutions for impulsive partial neutral functional differential equations. J. Math. Anal. Appl. 2007, 331: 1135–1158. 10.1016/j.jmaa.2006.09.043
Ji S, Wen S: Nonlocal Cauchy problem for impulsive differential equations in Banach spaces. Int. J. Nonlinear Sci. 2010, 10(1):88–95.
Ji S, Li G: Existence results for impulsive differential inclusions with nonlocal conditions. Comput. Math. Appl. 2011, 62: 1908–1915. 10.1016/j.camwa.2011.06.034
Li J, Nieto JJ, Shen J: Impulsive periodic boundary value problems of first-order differential equations. J. Math. Anal. Appl. 2007, 325: 226–236. 10.1016/j.jmaa.2005.04.005
Benchohra M, Henderson J, Ntouyas SK: An existence result for first-order impulsive functional differential equations in Banach spaces. Comput. Math. Appl. 2001, 42: 1303–1310. 10.1016/S0898-1221(01)00241-3
Liu JH: Nonlinear impulsive evolution equations. Dyn. Contin. Discrete Impuls. Syst. 1999, 6: 77–85.
Nieto JJ, Rodriguez-Lopez R: Periodic boundary value problem for non-Lipschitzian impulsive functional differential equations. J. Math. Anal. Appl. 2006, 318: 593–610. 10.1016/j.jmaa.2005.06.014
Cardinali T, Rubbioni P: Impulsive semilinear differential inclusion: topological structure of the solution set and solutions on non-compact domains. Nonlinear Anal. 2008, 14: 73–84.
Abada N, Benchohra M, Hammouche H: Existence and controllability results for nondensely defined impulsive semilinear functional differential inclusions. J. Differ. Equ. 2009, 246: 3834–3863. 10.1016/j.jde.2009.03.004
Byszewski L, Lakshmikantham V: Theorem about the existence and uniqueness of solutions of a nonlocal Cauchy problem in a Banach space. Appl. Anal. 1990, 40: 11–19.
Byszewski L: Theorems about the existence and uniqueness of solutions of a semilinear evolution nonlocal Cauchy problem. J. Math. Anal. Appl. 1991, 162: 494–505. 10.1016/0022-247X(91)90164-U
Fu X, Ezzinbi K: Existence of solutions for neutral functional differential evolution equations with nonlocal conditions. Nonlinear Anal. 2003, 54: 215–227. 10.1016/S0362-546X(03)00047-6
Aizicovici S, McKibben M: Existence results for a class of abstract nonlocal Cauchy problems. Nonlinear Anal. 2000, 39: 649–668. 10.1016/S0362-546X(98)00227-2
Xue X: Nonlinear differential equations with nonlocal conditions in Banach spaces. Nonlinear Anal. 2005, 63: 575–586. 10.1016/j.na.2005.05.019
Xue X: Nonlocal nonlinear differential equations with a measure of noncompactness in Banach spaces. Nonlinear Anal. 2009, 70: 2593–2601. 10.1016/j.na.2008.03.046
Banas J, Zajac T: A new approach to the theory of functional integral equations of fractional order. J. Math. Anal. Appl. 2011, 375: 375–387. 10.1016/j.jmaa.2010.09.004
Cardinali T, Rubbioni P: On the existence of mild solutions of semilinear evolution differential inclusions. J. Math. Anal. Appl. 2005, 308: 620–635. 10.1016/j.jmaa.2004.11.049
Dong Q, Li G: Existence of solutions for semilinear differential equations with nonlocal conditions in Banach spaces. Electron. J. Qual. Theory Differ. Equ. 2009., 2009: Article ID 47
Agarwal RP, Benchohra M, Seba D: On the application of measure of noncompactness to the existence of solutions for fractional differential equations. Results Math. 2009, 55: 221–230. 10.1007/s00025-009-0434-5
Liang J, Liu JH, Xiao TJ: Nonlocal impulsive problems for nonlinear differential equations in Banach spaces. Math. Comput. Model. 2009, 49: 798–804. 10.1016/j.mcm.2008.05.046
Fan Z: Impulsive problems for semilinear differential equations with nonlocal conditions. Nonlinear Anal. 2010, 72: 1104–1109. 10.1016/j.na.2009.07.049
Fan Z, Li G: Existence results for semilinear differential equations with nonlocal and impulsive conditions. J. Funct. Anal. 2010, 258: 1709–1727. 10.1016/j.jfa.2009.10.023
Zhu L, Dong Q, Li G: Impulsive differential equations with nonlocal conditions in general Banach spaces. Adv. Differ. Equ. 2012., 2012: Article ID 10
Barbu V: Nonlinear Semigroups and Differential Equations in Banach Spaces. Noordhoff, Leyden; 1976.
Banas J, Goebel K Lect. Notes Pure Appl. Math. 60. In Measure of Noncompactness in Banach Spaces. Dekker, New York; 1980.
Sun J, Zhang X: The fixed point theorem of convex-power condensing operator and applications to abstract semilinear evolution equations. Acta Math. Sin. Chin. Ser. 2005, 48: 439–446.
Liu LS, Guo F, Wu CX, Wu YH: Existence theorems of global solutions for nonlinear Volterra type integral equations in Banach spaces. J. Math. Anal. Appl. 2005, 309: 638–649. 10.1016/j.jmaa.2004.10.069
Pazy A: Semigroups of Linear Operators and Applications to Partial Differential Equations. Springer, New York; 1983.
Acknowledgements
Research is partially supported by the National Natural Science Foundation of China (11271316), the Postgraduate Innovation Project of Jiangsu Province (No. CXZZ12-0890), the NSF of China (11101353), the first author is also supported by the Youth Teachers Foundation of Huaiyin Institute of Technology (2012).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ji, S., Li, G. A unified approach to nonlocal impulsive differential equations with the measure of noncompactness. Adv Differ Equ 2012, 182 (2012). https://doi.org/10.1186/1687-1847-2012-182
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-182