A new modified generalized Laguerre operational matrix of fractional integration for solving fractional differential equations on the half line

Abstract

In this paper, we derived a new operational matrix of fractional integration of arbitrary order for modified generalized Laguerre polynomials. The fractional integration is described in the Riemann-Liouville sense. This operational matrix is applied together with the modified generalized Laguerre tau method for solving general linear multi-term fractional differential equations (FDEs). Only small dimension of a modified generalized Laguerre operational matrix is needed to obtain a satisfactory result. Illustrative examples reveal that the present method is very effective and convenient for linear multi-term FDEs on a semi-infinite interval.

1 Introduction

Fractional differential equations have drawn the interest of many researchers (see, for instance, [1–4]) due to their important applications in science and engineering. Indeed, we can find numerous applications in viscoelasticity, electrochemistry, control, electromagnetic, porous media, and so forth. In consequence, the subject of fractional differential equations is gaining much importance and attention. For some recent developments on the subject, see [5–13] and the references therein.

Spectral methods employ orthogonal systems as the basis functions and so usually provide accurate numerical results [14–17]. The usual spectral methods are only available for bounded domains for solving FDEs; see [6, 18–20]. However, many problems in science, engineering, and finance are set on unbounded domains. Therefore, it is also interesting to consider spectral tau methods for solving multi-term FDEs on the half line by using the operational matrix of fractional integration of modified Laguerre polynomials.

Some authors developed the Laguerre spectral method for the half line for ordinary, partial, and delay differential equations; see [21–25]. A new family of generalized Laguerre polynomials is introduced in [21], and in [24] Yan and Guo proposed a collocation method for solving initial value problems of second-order ODEs by using modified Laguerre functions.

In the last few years, there has been a growing interest in the use of spectral method for numerical treatments of FDEs in bounded domains. Saadatmandi and Dehghan [18] proposed an operational Legendre tau technique for the numerical solution of multi-term FDEs. The same technique based on the operational matrix of Chebyshev polynomials has been used for the same problem (see [26]). In [27], Doha et al. derived the Jacobi operational matrix of fractional derivatives which was applied together with the spectral tau method for a numerical solution of general linear multi-term fractional differential equations. Bhrawy et al. [20] used a quadrature shifted Legendre tau method for treating multi-term linear FDEs with variable coefficients. Moreover, in [28] the authors developed a Jacobi-Gauss-Lobatto collocation method for solving the nonlinear fractional Langevin equation with three-point boundary conditions.

Recently, El-Danaf et al. [29] investigated the use of spline functions of an integral form to approximate the solution of fractional order differential equations. In [30], Kadem and Baleanu introduced the Chebyshev spectral approach for a fractional radiative transfer equation, in which the multidimensional problem has been transformed into a system of fractional differential equations. Also, the waveform relaxation method in solving fractional differential equations is applied in [31]. A new explicit formula for the integrals of shifted Chebyshev polynomials of any degree for any fractional order in terms of shifted Chebyshev polynomials themselves is derived in [32], and a fast algorithm is developed for the solution of linear multi-order fractional differential equations by considering their integrated forms. Moreover, a new operational Jacobi matrix of fractional integration is investigated in [33] for solving linear FDEs on a bounded domain.

The operational matrix of integer integration has been determined for several types of orthogonal polynomials such as Chebyshev polynomials [34] and Laguerre and Hermite polynomials[35]. Recently, Singh et al. [36] derived the Bernstein operational matrix of integration. More recently, Bhrawy and Alofi [37] proposed the operational Chebyshev matrix of fractional integration in the Riemann-Liouville sense which was applied together with the spectral tau method to solve linear FDEs on a finite interval.

Up to now, and to the best of our knowledge, most of formulae corresponding to those mentioned previously are unknown and are traceless in the literature for fractional integration in the Riemann-Liouville sense. This partially motivates our interest in the operational matrix of fractional integration for modified generalized Laguerre polynomials.

In this paper, we propose a new tau method based on the operational matrix of fractional integration in the Riemann-Liouville sense, in which we take the modified Laguerre functions as the basis functions and approximate the solutions of multi-term FDEs on a semi-infinite interval. Finally, the accuracy of the proposed algorithm is demonstrated by test problems.

The remainder of the paper is organized as follows. The next section is for preliminaries. In Section 3, we derive the modified generalized Laguerre operational matrix of fractional integration. In Section 4, we apply the modified generalized Laguerre operational matrix of fractional integration to solve linear multi-order FDEs. In Section 5, the proposed method is applied to two examples. Also, a conclusion is given in Section 6.

2 Some basic preliminaries

The most used definition of fractional integration is due to Riemann-Liouville, which is as follows:

$$J^{\nu }f(x)=\frac{1}{\mathrm{\Gamma }(\nu )}{\int }_0^x{(x-t)}^{\nu -1}f(t)dt,\nu >0,x>0,\text{and}{J}^{0}f(x)=f(x).$$

(1)

One of the basic properties of the operator $J^{\nu }$ is

$$J^{\nu }{x}^{\beta }=\frac{\mathrm{\Gamma }(\beta +1)}{\mathrm{\Gamma }(\beta +1+\nu )}{x}^{\beta +\nu }.$$

(2)

The next equation defines Riemann-Liouville fractional derivative of order ν

$$D^{\nu }f(x)=\frac{d^m}{d{x}^m}(J^{m-\nu }f(x)),$$

(3)

where $m-1<\nu \le m$, $m\in N$, and m is the smallest integer greater than ν.

If $m-1<\nu \le m$, $m\in N$, then

$$D^{\nu }{J}^{\nu }f(x)=f(x),J^{\nu }{D}^{\nu }f(x)=f(x)-\sum _{i=0}^{m-1}{f}^{(i)}\left(0^{+}\right)\frac{x^i}{i!},x>0.$$

(4)

Now, let $\mathrm{\Lambda }=(0,\mathrm{\infty })$ and $w^{(\alpha ,\beta )}(x)=x^{\alpha }{e}^{-\beta x}$ be a weight function on Λ in the usual sense. Define

$$L_{w^{(\alpha ,\beta )}}^2(\mathrm{\Lambda })=\{v|v\text{ is measurable on }\mathrm{\Lambda }\text{ and }{\parallel v\parallel }_{w^{(\alpha ,\beta )}}<\mathrm{\infty }\},$$

equipped with the following inner product and norm:

$${(u,v)}_{w^{(\alpha ,\beta )}}={\int }_{\mathrm{\Lambda }}u(x)v(x)w^{(\alpha ,\beta )}(x)dx,{\parallel v\parallel }_{w^{(\alpha ,\beta )}}={(u,v)}_{w^{(\alpha ,\beta )}}^{\frac{1}{2}}.$$

Next, let $w^{(\alpha ,\beta )}(x)$ with $\alpha >-1$ and $\beta >0$. The modified generalized Laguerre polynomial of degree i is defined by

$$L_i^{(\alpha ,\beta )}(x)=\frac{1}{i!}{x}^{-\alpha }{e}^{\beta x}{\partial }_x^i\left(x^{i+\alpha }{e}^{-\beta x}\right),i=0,1,\dots .$$

According to (2.2)-(2.4) of [21] for $\alpha >-1$ and $\beta >0$, we have

where $L_0^{(\alpha ,\beta )}(x)=1$ and $L_1^{(\alpha ,\beta )}(x)=-\beta x+\frac{\mathrm{\Gamma }(\alpha +2)}{\mathrm{\Gamma }(\alpha +1)}$.

The set of modified generalized Laguerre polynomials is the $L_{w^{(\alpha ,\beta )}}^2(0,\mathrm{\infty })$-orthogonal system, namely

$${\int }_0^{\mathrm{\infty }}{L}_j^{(\alpha ,\beta )}(x)L_k^{(\alpha ,\beta )}(x)w^{(\alpha ,\beta )}(x)dx=h_k{\delta }_{jk},$$

(5)

where ${\delta }_{jk}$ is the Kronecker function and $h_k=\frac{\mathrm{\Gamma }(k+\alpha +1)}{{\beta }^{\alpha +1}k!}$. The modified generalized Laguerre polynomial on the interval $\mathrm{\Lambda }\equiv (0,\mathrm{\infty })$ is given by

$$L_i^{(\alpha ,\beta )}(x)=\sum _{k=0}^i{(-1)}^k\frac{\mathrm{\Gamma }(i+\alpha +1){\beta }^k}{\mathrm{\Gamma }(k+\alpha +1)(i-k)!k!}{x}^k,i=0,1,\dots .$$

(6)

The special value

$$D^q{L}_i^{(\alpha ,\beta )}(0)=\frac{{(-1)}^q{\beta }^q\mathrm{\Gamma }(i+\alpha +1)}{(i-q)!\mathrm{\Gamma }(q+\alpha +1)},i⩾q,$$

(7)

will be of important use later.

3 Modified generalized Laguerre operational matrix of fractional integration

The main objective of this section is to derive an operational matrix of fractional integration for modified generalized Laguerre polynomials.

Let $u(x)\in L_{w^{(\alpha ,\beta )}}^2(\mathrm{\Lambda })$, then $u(x)$ may be expressed in terms of modified generalized Laguerre polynomials as

$$u(x)=\sum _{j=0}^{\mathrm{\infty }}{a}_j{L}_j^{(\alpha ,\beta )}(x),a_j=\frac{1}{h_k}{\int }_0^{\mathrm{\infty }}u(x)L_j^{(\alpha ,\beta )}(x)w^{(\alpha ,\beta )}(x)dx,j=0,1,\dots .$$

(8)

In practice, only the first $(N+1)$-terms modified generalized Laguerre polynomials are considered. Then we have

$$u_N(x)=\sum _{j=0}^N{a}_j{L}_j^{(\alpha ,\beta )}(x)=C^T\varphi (x),$$

(9)

where the modified generalized Laguerre coefficient vector C and the modified generalized Laguerre vector $\varphi (x)$ are given by

$$C^T=[c_0,c_1,\dots ,c_N],\varphi (x)={[L_0^{(\alpha ,\beta )}(x),L_1^{(\alpha ,\beta )}(x),\dots ,L_N^{(\alpha ,\beta )}(x)]}^T.$$

(10)

Theorem 3.1 Let $\varphi (x)$ be the modified generalized Laguerre vector and $\nu >0$, then

$$J^{\nu }\varphi (x)\simeq {\mathbf{P}}^{(\nu )}\varphi (x),$$

(11)

where ${\mathbf{P}}^{(\nu )}$ is the $(N+1)\times (N+1)$ operational matrix of fractional integration of order ν in the Riemann-Liouville sense and is defined as follows:

$${\mathbf{P}}^{(\nu )}=\left(\begin{array}{ccccc}{\mathrm{\Psi }}_{\nu }(0,0)& {\mathrm{\Psi }}_{\nu }(0,1)& {\mathrm{\Psi }}_{\nu }(0,2)& \cdots & {\mathrm{\Psi }}_{\nu }(0,N)\\ {\mathrm{\Psi }}_{\nu }(1,0)& {\mathrm{\Psi }}_{\nu }(1,1)& {\mathrm{\Psi }}_{\nu }(1,2)& \cdots & {\mathrm{\Psi }}_{\nu }(1,N)\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ {\mathrm{\Psi }}_{\nu }(i,0)& {\mathrm{\Psi }}_{\nu }(i,1)& {\mathrm{\Psi }}_{\nu }(i,2)& \cdots & {\mathrm{\Psi }}_{\nu }(i,N)\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ {\mathrm{\Psi }}_{\nu }(N,0)& {\mathrm{\Psi }}_{\nu }(N,1)& {\mathrm{\Psi }}_{\nu }(N,2)& \cdots & {\mathrm{\Psi }}_{\nu }(N,N)\end{array}\right),$$

(12)

where

$${\mathrm{\Psi }}_{\nu }(i,j)=\sum _{k=0}^i\sum _{r=0}^j\frac{{(-1)}^{k+r}{\beta }^{(-\nu )}j!\mathrm{\Gamma }(i+\alpha +1)\mathrm{\Gamma }(k+\nu +\alpha +r+1)}{(i-k)!(j-r)!r!\mathrm{\Gamma }(k+\nu +1)\mathrm{\Gamma }(k+\alpha +1)\mathrm{\Gamma }(\alpha +r+1)}.$$

Proof Using the analytic form of the modified generalized Laguerre polynomials $L_i^{(\alpha ,\beta )}(x)$ of degree i (6) and (2), then

$$\begin{array}{rcl}{J}^{\nu }{L}_i^{(\alpha ,\beta )}(x)& =& \sum _{k=0}^i{(-1)}^k\frac{{\beta }^k\mathrm{\Gamma }(i+\alpha +1)}{(i-k)!k!\mathrm{\Gamma }(k+\alpha +1)}{J}^{\nu }{x}^k\\ =& \sum _{k=0}^i{(-1)}^k\frac{{\beta }^k\mathrm{\Gamma }(i+\alpha +1)}{(i-k)!\mathrm{\Gamma }(k+\nu +1)\mathrm{\Gamma }(k+\alpha +1)}{x}^{k+\nu },\\ i=0,1,\dots ,N.\end{array}$$

(13)

Now, approximating $x^{k+\nu }$ by $N+1$ terms of modified generalized Laguerre series, we have

$$x^{k+\nu }=\sum _{j=0}^N{c}_j{L}_j^{(\alpha ,\beta )}(x),$$

(14)

where $c_j$ is given from (8) with $u(x)=x^{k+\nu }$, that is,

$$c_j=\sum _{r=0}^j{(-1)}^r\frac{{\beta }^{-k-\nu }j!\mathrm{\Gamma }(k+\nu +\alpha +r+1)}{(j-r)!r!\mathrm{\Gamma }(r+\alpha +1)},j=1,2,\dots ,N.$$

(15)

In virtue of (13) and (14), we get

$$J^{\nu }{L}_i^{(\alpha ,\beta )}(x)=\sum _{j=0}^N{\mathrm{\Psi }}_{\nu }(i,j)L_j^{(\alpha ,\beta )}(x),i=0,1,\dots ,N,$$

(16)

where

$$\begin{array}{rcl}{\mathrm{\Psi }}_{\nu }(i,j)& =& \sum _{k=0}^i\sum _{r=0}^j\frac{{(-1)}^{k+r}{\beta }^{(-\nu )}j!\mathrm{\Gamma }(i+\alpha +1)\mathrm{\Gamma }(k+\nu +\alpha +r+1)}{(i-k)!(j-r)!r!\mathrm{\Gamma }(k+\nu +1)\mathrm{\Gamma }(k+\alpha +1)\mathrm{\Gamma }(\alpha +r+1)},\\ j=1,2,\dots ,N.\end{array}$$

Accordingly, Eq. (16) can be written in a vector form as follows:

$$J^{\nu }{L}_i^{(\alpha ,\beta )}(x)\simeq [{\mathrm{\Psi }}_{\nu }(i,0),{\mathrm{\Psi }}_{\nu }(i,1),{\mathrm{\Psi }}_{\nu }(i,2),\dots ,{\mathrm{\Psi }}_{\nu }(i,N)]\varphi (x),i=0,1,\dots ,N.$$

(17)

Eq. (17) leads to the desired result. □

Corollary 3.2 If we define the q times repeated integration of the modified generalized Laguerre vector $\varphi (x)$ by $J^q\varphi (x)$, and

$$J^q\varphi (x)\simeq {\mathbf{I}}^{(q)}\varphi (x),$$

(18)

then ${\mathbf{I}}^{(q)}={\mathbf{P}}^{(q)}$ is the operational matrix of integration of $\varphi (x)$, where q is an integer value.

4 Modified generalized Laguerre tau method based on operational matrix

Many practical problems are governed by initial value problems of multi-term FDEs. We may decompose such problems to a system of fractional equations of varying orders and then solve them numerically (see [38]). Whereas, for saving work, it seems reasonable to solve them directly.

In this section, the modified generalized Laguerre tau method based on the operational matrix is proposed to numerically solve the FDEs. The basic idea of this technique is as follows: (i) The FDE is converted to a fully integrated form via fractional integration in the Riemann-Liouville sense. (ii) Subsequently, the integrated form equations are approximated by representing them as linear combinations of modified generalized Laguerre polynomials. (iii) Finally, the integrated form equation is converted to an algebraic equation by introducing the operational matrix of fractional integration of the modified generalized Laguerre polynomials.

In order to show the fundamental importance of the modified generalized Laguerre operational matrix of fractional integration, we apply it to solve the following multi-order FDE:

$$D^{\nu }u(x)=\sum _{i=1}^k{\gamma }_j{D}^{{\beta }_i}u(x)+{\gamma }_{k+1}u(x)+f(x),\text{in }\mathrm{\Lambda }=(0,\mathrm{\infty }),$$

(19)

with initial conditions

$$u^{(i)}(0)=d_i,i=0,\dots ,m-1,$$

(20)

where ${\gamma }_i$ ($i=1,\dots ,k+1$) are real constant coefficients, $m-1<\nu \le m$, $0<{\beta }_1<{\beta }_2<\cdots <{\beta }_k<\nu$, and $g(x)$ is a given source function. If we apply the Riemann-Liouville integral of order ν to (19) after making use of (4), we get the integrated form of (19), namely

(21)

where $m_i-1<{\beta }_i\le m_i$, $m_i\in N$. This implies that

(22)

where

$$g(x)=J^{\nu }f(x)+\sum _{j=0}^{m-1}{d}_j\frac{x^j}{j!}+\sum _{i=1}^k{\gamma }_i{J}^{\nu -{\beta }_i}\left(\sum _{j=0}^{m_i-1}{d}_j\frac{x^j}{j!}\right).$$

In order to use the tau method based on the operational matrix of fractional integration for modified generalized Laguerre for solving the fully integrated problem (22) with initial conditions (20), we approximate $u(x)$ and $g(x)$ by the modified generalized Laguerre polynomials as

(23)

(24)

where the vector $G={[g_0,\dots ,g_N]}^T$ is given but $C={[c_0,\dots ,c_N]}^T$ is an unknown vector.

Now, the Riemann-Liouville integral of orders ν and $(\nu -{\beta }_j)$ of the approximate solution (23), after making use of Theorem 3.1 (relation (11)), can be written as

$$J^{\nu }{u}_N(x)\simeq C^T{J}^{\nu }\varphi (x)\simeq C^T{\mathbf{P}}^{(\nu )}\varphi (x),$$

(25)

and

$$J^{\nu -{\beta }_j}{u}_N(x)\simeq C^T{J}^{\nu -{\beta }_j}\varphi (x)\simeq C^T{\mathbf{P}}^{(\nu -{\beta }_j)}\varphi (x),j=1,\dots ,k,$$

(26)

respectively, where ${\mathbf{P}}^{(\nu )}$ is the $(N+1)\times (N+1)$ operational matrix of fractional integration of order ν. Employing Eqs. (23)-(26), the residual $R_N(x)$ for Eq. (22) can be written as

$$R_N(x)=(C^T-C^T\sum _{j=1}^k{\gamma }_j{\mathbf{P}}^{(\nu -{\beta }_j)}-{\gamma }_{k+1}{C}^T{\mathbf{P}}^{(\nu )}-G^T)\varphi (x).$$

(27)

As in a typical tau method, we generate $N-m+1$ linear algebraic equations by applying

$$〈R_N(x),L_j^{(\alpha ,\beta )}(x)〉={\int }_0^{\mathrm{\infty }}{R}_N(x)w^{(\alpha ,\beta )}(x)L_j^{(\alpha ,\beta )}(x)dx=0,j=0,1,\dots ,N-m.$$

(28)

Also, by substituting Eqs. (8) and (23) in Eq. (20), we get

$$u^{(i)}(0)=C^T{\mathbf{D}}^{(i)}\varphi (0)=d_i,i=0,1,\dots ,m-1.$$

(29)

Eqs. (28) and (29) generate $N-m+1$ and m set of linear equations, respectively. These linear equations can be solved for unknown coefficients of the vector C. Consequently, $u_N(x)$ given in Eq. (23) can be calculated, which gives a solution of Eq. (19) with the initial conditions (20).

5 Illustrative examples

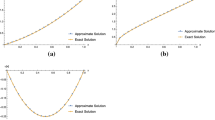
To illustrate the effectiveness of the proposed method in the present paper, some examples are carried out in this section. The results obtained by the present method reveal that it is very effective and convenient for linear FDEs on the half line.

Example 1 Consider the FDE

$$D^{2}u(x)+D^{\frac{3}{2}}u(x)+u(x)=x^2+2+\frac{4x^{\frac{1}{2}}}{\mathrm{\Gamma }(0.5)},u(0)=0,u^{\prime }(0)=0,x\in \mathrm{\Lambda },$$

(30)

whose exact solution is given by $u(x)=x^2$.

If we apply the technique described in Section 4 with $N=2$, then the approximate solution can be written as

$$u_N(x)=\sum _{i=0}^2{c}_i{L}_i^{(\alpha ,\beta )}(x)=C^T\varphi (x),$$

and

Using Eq. (28), we obtain

(31)

Now, by applying Eq. (29), we have

(32)

(33)

Finally, by solving Eqs. (31)-(33), we have the three unknown coefficients with general α and β as follows:

$$c_0=\frac{{\alpha }^2+3\alpha +2}{{\beta }^2},c_1=\frac{-2\alpha -4}{{\beta }^2},c_2=\frac{2}{{\beta }^2}.$$

Thus, we can write

$$u(x)=(c_0,c_1,c_2)\left(\begin{array}{c}{L}_0^{(\alpha ,\beta )}(x)\\ L_1^{(\alpha ,\beta )}(x)\\ L_2^{(\alpha ,\beta )}(x)\end{array}\right)=x^2,$$

which is the exact solution.

The values of $c_0$, $c_1$, $c_2$ with various choices of α and β are listed in Table 1.

Table 1 The values of ${\mathit{c}}_{\mathbf{0}}$ , ${\mathit{c}}_{\mathbf{1}}$ and ${\mathit{c}}_{\mathbf{2}}$ for various choices of α and β for Example 1

Example 2 Consider the following fractional initial value problem:

(34)

whose exact solution is given by $u(x)=x^3$.

If we apply the technique described in Section 4 with $N=3$, then the approximate solution can be written as

$$u_N(x)=\sum _{i=0}^3{c}_i{L}_i^{(\alpha ,\beta )}(x)=C^T\varphi (x),$$

and

$${\mathbf{P}}^{(\frac{5}{2})}=\left(\begin{array}{cccc}{\mathrm{\Psi }}_{\frac{5}{2}}(0,0)& {\mathrm{\Psi }}_{\frac{5}{2}}(0,1)& {\mathrm{\Psi }}_{\frac{5}{2}}(0,2)& {\mathrm{\Psi }}_{\frac{5}{2}}(0,3)\\ {\mathrm{\Psi }}_{\frac{5}{2}}(1,0)& {\mathrm{\Psi }}_{\frac{5}{2}}(1,1)& {\mathrm{\Psi }}_{\frac{5}{2}}(1,2)& {\mathrm{\Psi }}_{\frac{5}{2}}(1,3)\\ {\mathrm{\Psi }}_{\frac{5}{2}}(2,0)& {\mathrm{\Psi }}_{\frac{5}{2}}(2,1)& {\mathrm{\Psi }}_{\frac{5}{2}}(2,2)& {\mathrm{\Psi }}_{\frac{5}{2}}(2,3)\\ {\mathrm{\Psi }}_{\frac{5}{2}}(3,0)& {\mathrm{\Psi }}_{\frac{5}{2}}(3,1)& {\mathrm{\Psi }}_{\frac{5}{2}}(3,2)& {\mathrm{\Psi }}_{\frac{5}{2}}(3,3)\end{array}\right),G=\left(\begin{array}{c}{g}_0\\ g_1\\ g_2\\ g_3\end{array}\right).$$

Using Eq. (28), we obtain

$$\begin{array}{r}3{\mathrm{\Psi }}_{\frac{5}{2}}(0,2)c_0+3{\mathrm{\Psi }}_{\frac{5}{2}}(1,2)c_1+(1+3{\mathrm{\Psi }}_{\frac{5}{2}}(2,2))c_2+3{\mathrm{\Psi }}_{\frac{5}{2}}(3,2)c_3+g_2=0,\\ 3{\mathrm{\Psi }}_{\frac{5}{2}}(0,3)c_0+3{\mathrm{\Psi }}_{\frac{5}{2}}(1,3)c_1+3{\mathrm{\Psi }}_{\frac{5}{2}}(2,3)c_2+(1+3{\mathrm{\Psi }}_{\frac{5}{2}}(3,3))c_3+g_3=0.\end{array}$$

(35)

Now, applying Eq. (29), we get

$$\begin{array}{r}{C}^T\varphi (0)=c_0+\frac{\mathrm{\Gamma }(\alpha +2)}{\mathrm{\Gamma }(\alpha +1)}{c}_1+\frac{\mathrm{\Gamma }(\alpha +3)}{2\mathrm{\Gamma }(\alpha +1)}{c}_2+\frac{\mathrm{\Gamma }(\alpha +4)}{6\mathrm{\Gamma }(\alpha +1)}{c}_3=0,\\ C^T{\mathbf{D}}^{(1)}\varphi (0)=-\beta c_1-\frac{\beta \mathrm{\Gamma }(\alpha +3)}{\mathrm{\Gamma }(\alpha +2)}{c}_2-\frac{\beta \mathrm{\Gamma }(\alpha +4)}{2\mathrm{\Gamma }(\alpha +2)}{c}_3=0.\end{array}$$

(36)

By solving the linear system (35)-(36), we get

Thereby, we can write

$$u_N(x)=\sum _{i=0}^3{c}_i{L}_i^{(\alpha ,\beta )}(x)=x^3.$$

Numerical results will not be presented since the exact solution is obtained. We have presented the values of the four unknown coefficients with various choices of α and β in Table 2.

Table 2 The values of ${\mathit{c}}_{\mathbf{0}}$ , ${\mathit{c}}_{\mathbf{1}}$ , ${\mathit{c}}_{\mathbf{2}}$ and ${\mathit{c}}_{\mathbf{3}}$ for various choices of α and β for Example 2

Example 3 Consider the following fractional initial value problem:

$$D^{\frac{3}{2}}u(x)+3u(x)={\gamma }^{\frac{3}{2}}{e}^{\gamma x}+3e^{\gamma x},u(0)=1,u^{\prime }(0)=\gamma ,x\in (0,20),$$

(37)

whose exact solution is given by $u(x)=e^{\gamma x}$.

Table 3 lists the maximum absolute error of $u-u_N$, using the operational matrix of fractional integration for the modified generalized Laguerre with tau method for $\gamma =0.01$, and various choices of N, α and β. From Table 3, we can achieve a good approximation to the exact solution by using a few terms of modified generalized Laguerre polynomials. Also, the maximum absolute error for $N=10$ and different values of γ, α, and β are shown in Table 4.

Table 3 Maximum absolute error for $\mathit{\gamma }\mathbf{=}\mathbf{0.01}$ and different values of α , β and N for Example 3

Table 4 Maximum absolute error for $\mathit{N}\mathbf{=}\mathbf{10}$ and different values of γ , α , and β for Example 3

6 Conclusion

In this paper, we introduced a general formulation for the modified generalized Laguerre operational matrix of fractional integration. Fractional integration is described in the Riemann-Liouville sense. We have presented an accurate direct solver for the general multi-term linear fractional-order differential equations with initial conditions on a semi-infinite domain by using modified generalized Laguerre tau approximation based on the modified generalized Laguerre operational matrix of fractional integration.

The numerical results given in the previous section demonstrate good accuracy of this algorithm. Moreover, the solutions obtained using the suggested algorithm show that this algorithm with a small number of modified generalized Laguerre polynomials gives a satisfactory result.