Abstract
In this paper, we investigate the Hyers-Ulam stability of the additive-quadratic functional equation () in intuitionistic random normed spaces.
MSC:39B52, 34K36, 46S50, 47S50, 34Fxx.
Similar content being viewed by others
1 Introduction
The concept of stability of a functional equation arises when one replaces a functional equation by an inequality which acts as a perturbation of the equation. The first stability problem concerning group homomorphisms was raised by Ulam [1] in 1940 and affirmatively solved by Hyers [2]. The result of Hyers was generalized by Aoki [3] for approximate additive mappings and by Rassias [4] for approximate linear mappings by allowing the difference Cauchy equation to be controlled by . In 1994, a generalization of the Th.M. Rassias’ theorem was obtained by Gǎvruta [5], who replaced by a general control function . For more details about the results concerning such problems, the reader is referred to [6–16].
The functional equation
is related to a symmetric bi-additive mapping [17, 18]. It is natural that this equation is called a quadratic functional equation. In particular, every solution of the quadratic equation (1.1) is said to be a quadratic mapping. It is well known that a mapping f between real vector spaces is quadratic if and only if there exists a unique symmetric bi-additive mapping such that for all x. The bi-additive mapping is given by . The Hyers-Ulam stability problem for the quadratic functional equation was solved by Skof [19]. In [20], Czerwik proved the Hyers-Ulam stability of the function equation (1.1).
Eshaghi Gordji and Khodaei [21] have established the general solution and investigated the Hyers-Ulam stability for a mixed type of cubic, quadratic and additive functional equation
in quasi-Banach spaces, where k is a nonzero integer with . Obviously, the function is a solution of the functional equation (1.2). Interesting new results concerning mixed functional equations have recently been obtained by Najati et al. [22–24], Jun and Kim [25, 26] as well as for the fuzzy stability of a mixed-type functional equation by Park et al. [27–29].
The stability of the mixed functional equation
was investigated by Najati and Rassias [23].
The theory of random normed spaces (RN-spaces) is important as a generalization of the deterministic result of linear normed spaces and also in the study of random operator equations. The RN-spaces may also provide us with the appropriate tools to study the geometry of nuclear physics and have important application in quantum particle physics. The Hyers-Ulam stability of different functional equations in random normed spaces and RN-spaces has been recently studied in Alsina [30], Eshaghi Gordji et al. [31, 32], Miheţ and Radu [33–35], Miheţ, Saadati and Vaezpour [36, 37], and Saadati et al. [38]. Recently, Zhang et al. [39] investigated the intuitionistic random stability problems for the cubic functional equation.
In this paper, we prove the Hyers-Ulam stability of the additive and quadratic functional equation (1.3) in intuitionistic random spaces.
2 Preliminaries
We start our work with the following notion of intuitionistic random normed spaces. In the sequel, we adopt the usual terminology, notations and conventions of the theory of intuitionistic Menger probabilistic normed spaces as in [33] and [40–44].
A measure distribution function is a function  , which is left continuous on
, which is left continuous on  , non-decreasing,
, non-decreasing,  and
and  .
.
We denote by D the family of all measure distribution functions, and by H a special element of D defined by
If X is a nonempty set, then is called a probabilistic measure on X and is denoted by .
A non-measure distribution function is a function  , which is right continuous on
, which is right continuous on  , non-increasing,
, non-increasing,  and
and  .
.
We denote by B the family of all non-measure distribution functions, and by G a special element of B defined by
If X is a nonempty set, then is called a probabilistic non-measure on X and is denoted by .
Consider the set and the operation defined by
Then is a complete lattice.
We denote the units by and . Classically, for all , a triangular norm on [0,1] is defined as an increasing, commutative, associative mapping satisfying , and a triangular conorm is defined as an increasing, commutative, associative mapping satisfying .
By use of the lattice , these definitions can be straightforwardly extended.
Definition 2.2 [46]
A triangular norm (t-norm) on is a mapping satisfying the following conditions:
-
(i)
, (boundary condition);
-
(ii)
, (commutativity);
-
(iii)
, (associativity);
-
(iv)
, , (monotonicity).
If is an Abelian topological monoid with unit , then ϒ is said to be a continuous t-norm.
Definition 2.3 [46]
A continuous t-norm ϒ on is said to be continuous t-representable if there exist a continuous t-norm ∗ and a continuous t-conorm ⋄ on [0,1] such that
Typical examples of continuous t-representable are and for all , .
Now, we define a sequence recursively by as
for all and .
Recall that if ϒ is a t-norm and is a given sequence of numbers in , is defined recurrently by
for all . is defined as .
A negator on is any decreasing mapping satisfying and . If for all , then ℵ is called an involutive negator. A negator on [0,1] is a decreasing mapping satisfying and . denotes the standard negator on defined by for all .
Definition 2.4 [39]. Let μ and ν be measure and non-measure distribution functions from to such that for all and all . The triple is said to be an intuitionistic random normed space (briefly IRN-space) if X is a vector space, ϒ is a continuous t-representable, and is a mapping such that the following conditions hold for all and all :
() ;
() if and only if ;
() for all ;
() .
In this case, is called an intuitionistic random norm. Here, .
Every normed space defines an IRN-space , where for all and for all , . This space is called the induced IRN-space.
Definition 2.5 Let be an IRN-space.
-
(1)
A sequence in X is said to be convergent to x in X if, as for every .
-
(2)
A sequence in X is called Cauchy if, for every and , there exists
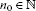 such that for every , where is a standard negator.
such that for every , where is a standard negator. -
(3)
An IRN-space is said to be complete if and only if every Cauchy sequence in X is convergent to a point in X.
From now on, let X be a linear space and be a complete IRN-space.
For convenience, we use the following abbreviation for a given mapping :
for all , where is a fixed integer.
3 Results in intuitionistic random spaces
In the following theorem, we prove the Hyers-Ulam stability of the functional equation (1.3) in IRN-spaces for quadratic mappings.
Theorem 3.1 Let ( is denoted by , is denoted by and is denoted by ) be mappings such that
for all and all , and
for all and all . Suppose that an even mapping with satisfies the inequality
for all and all . Then there exists a unique quadratic mapping such that
for all and all , where
Proof Letting and () in (3.3) and using the evenness of f, we get

for all and all . Interchanging with in (3.6) and using the evenness of f, we get

for all and all . It follows from (3.6) and (3.7) that

for all and all . Setting , and () in (3.3) and using the evenness of f, we get

for all and all . So it follows from (3.8) and (3.9) that

for all and all . So

for all and all . Putting and () in (3.3), we obtain
for all and all . It follows from (3.11) and (3.12) that

for all and all . Letting in (3.9) and replacing by in the obtained inequality, we get
for all and all . It follows from (3.11) and (3.14) that

for all and all . Applying (3.13) and (3.15), we get

for all and all . Setting and () in (3.3), we obtain
for all and all . It follows from (3.16) and (3.17) that

for all and all . It follows from (3.5) that
for all and all , which implies that
for all , all and all  . It follows from (3.19) and () that
. It follows from (3.19) and () that
and

for all and all . Thus
for all and all . In order to prove the convergence of the sequence , we replace x with in (3.20) to find that
for all and all . Since the right-hand side of the inequality (3.21) tends to as and m tend to infinity, the sequence is a Cauchy sequence. Therefore, one can define the mapping by for all . Now, if we replace with in (3.3) respectively, then
for all and all . By letting in (3.22), we find that for all , which implies . Thus Q satisfies (1.3). Hence the mapping is quadratic.
To prove (3.4), take the limit as in (3.20).
Finally, to prove the uniqueness of the quadratic mapping Q subject to (3.4), let us assume that there exists a quadratic mapping which satisfies (3.4). Since and for all and  , from (3.4) and (3.2) it follows that
, from (3.4) and (3.2) it follows that

for all and all . By letting in (3.23), we find that . □
Corollary 3.2 Let be an IRN-space and let be a complete IRN-space. If is a mapping such that
for all and all , and
for all and all , then there exists a unique quadratic mapping such that
for all and all , where
Proof Let . Then the corollary follows immediately from Theorem 3.1. □
Now, we prove the Hyers-Ulam stability of the functional equation (1.3) in IRN-spaces for additive mappings.
Theorem 3.3 Let be mappings such that
for all and all , and
for all and all . Suppose that an odd mapping satisfies (3.3) for all and all . Then there exists a unique additive mapping such that
for all and all , where
Proof Letting and () in (3.3) and using the oddness of f, we get

for all and all . Interchanging with in (3.27) and using the oddness of f, we get

for all and all . It follows from (3.27) and (3.28) that

for all and all . Setting , and () in (3.3) and using the oddness of f, we get

for all and all . It follows from (3.29) and (3.30) that

for all and all . Putting and () in (3.3), we obtain

for all and all . It follows from (3.31) and (3.32) that

for all and all . Replacing and by and in (3.33), respectively, we obtain

for all and all . Therefore,
for all and all , which implies that
for all , and  . It follows from (3.35) and () that
. It follows from (3.35) and () that
and

for all and all . Thus
for all and all . In order to prove the convergence of the sequence , we replace x with in (3.36) to find that
for all and all . Since the right-hand side of the inequality (3.37) tends to as and m tend to infinity, the sequence is a Cauchy sequence. Therefore, one can define the mapping by for all . Now, if we replace with in (3.3) respectively, then
for all and all . By letting in (3.38), we find that for all , which implies . Thus A satisfies (1.3). Hence the mapping is additive. To prove (3.26), take the limit as in (3.36).
The rest of the proof is similar to the proof of Theorem 3.1. □
Corollary 3.4 Let be an IRN-space and let be a complete IRN-space. If is a mapping such that
for all and all , and
for all and all , then there exists a unique additive mapping such that
for all and all , where
The main result of this paper is the following:
Theorem 3.5 Let be mappings satisfying (3.24) and (3.25) for all and all . Suppose that a mapping with satisfies (3.3) for all and all . Then there exist an additive mapping and a quadratic mapping satisfying (1.3) and

Proof Let for all . Then , and
for all and all . By Theorem 3.1, there exists a quadratic mapping such that
for all and all .
On the other hand, let for all . Then , . By Theorem 3.3, there exists an additive mapping such that
for all and all . Hence (3.39) follows from (3.40) and (3.41). □
Corollary 3.6 Let be an IRN-space and let be a complete IRN-space. If is a mapping such that
for all and all , and
for all and all , then there exist an additive mapping and a quadratic mapping such that

for all and all .
Now, we give an example to validate the result of quadratic mappings as follows:
Example Let be a Banach space, an IRN-space in which
and let be a complete IRN-space for all . Define a mapping by , where is a unit vector in X. A straightforward computation shows that, for all ,
and
Therefore, all the conditions of Theorem 3.1 hold, and so there exists a unique quadratic mapping such that .
References
Ulam SM: A Collection of the Mathematical Problems. Interscience, New York; 1960.
Hyers DH: On the stability of the linear functional equation. Proc. Natl. Acad. Sci. USA 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 1950, 2: 64–66. 10.2969/jmsj/00210064
Rassias TM: On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 1978, 72: 297–300. 10.1090/S0002-9939-1978-0507327-1
Găvruta P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. J. Math. Anal. Appl. 1994, 184: 431–436. 10.1006/jmaa.1994.1211
Gajda Z: On stability of additive mappings. Int. J. Math. Math. Sci. 1991, 14: 431–434. 10.1155/S016117129100056X
Jung S: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor; 2001.
Jung S: On the Hyers-Ulam stability of the functional equations that have the quadratic property. J. Math. Anal. Appl. 1998, 222: 126–137. 10.1006/jmaa.1998.5916
Khodaei H, Rassias TM: Approximately generalized additive functions in several variables. Int. J. Nonlinear Anal. Appl 2010, 1: 22–41.
Bae J, Park W: A functional equation having monomials as solutions. Appl. Math. Comput. 2010, 216: 87–94. 10.1016/j.amc.2010.01.006
Rassias JM: On approximation of approximately linear mappings by linear mappings. J. Funct. Anal. 1982, 46: 126–130. 10.1016/0022-1236(82)90048-9
Rassias JM: Solution of a problem of Ulam. J. Approx. Theory 1989, 57: 268–273. 10.1016/0021-9045(89)90041-5
Rassias TM: New characterization of inner product spaces. Bull. Sci. Math. 1984, 108: 95–99.
Rassias TM: On the stability of functional equations in Banach spaces. J. Math. Anal. Appl. 2000, 251: 264–284. 10.1006/jmaa.2000.7046
Rassias TM: On the stability of functional equations and a problem of Ulam. Acta Appl. Math. 2000, 62: 23–130. 10.1023/A:1006499223572
Rassias TM, Šemrl P: On the Hyers-Ulam stability of linear mappings. J. Math. Anal. Appl. 1993, 173: 325–338. 10.1006/jmaa.1993.1070
Aczel J, Dhombres J: Functional Equations in Several Variables. Cambridge University Press, Cambridge; 1989.
Kannappan P: Quadratic functional equation and inner product spaces. Results Math. 1995, 27: 368–372.
Skof F: Proprietàlocalie approssimazione di operatori. Rend. Semin. Mat. Fis. Milano 1983, 53: 113–129. 10.1007/BF02924890
Czerwik S: On the stability of the quadratic mapping in normed spaces. Abh. Math. Semin. Univ. Hamb. 1992, 62: 59–64. 10.1007/BF02941618
Eshaghi Gordji M, Khodaei H: Solution and stability of generalized mixed type cubic, quadratic and additive functional equation in quasi-Banach spaces. Nonlinear Anal., Theory Methods Appl. 2009, 71: 5629–5643. 10.1016/j.na.2009.04.052
Najati A, Moghimi MB: Stability of a functional equation deriving from quadratic and additive function in quasi-Banach spaces. J. Math. Anal. Appl. 2008, 337: 399–415. 10.1016/j.jmaa.2007.03.104
Najati A, Rassias TM: Stability of a mixed functional equation in several variables on Banach modules. Nonlinear Anal., Theory Methods Appl. 2010, 72: 1755–1767. 10.1016/j.na.2009.09.017
Najati A, Zamani Eskandani G: Stability of a mixed additive and cubic functional equation in quasi-Banach spaces. J. Math. Anal. Appl. 2008, 342: 1318–1331. 10.1016/j.jmaa.2007.12.039
Jun K, Kim H: Ulam stability problem for a mixed type of cubic and additive functional equation. Bull. Belg. Math. Soc. Simon Stevin 2006, 13: 271–285.
Kim H: On the stability problem for a mixed type of quartic and quadratic functional equation. J. Math. Anal. Appl. 2006, 324: 358–372. 10.1016/j.jmaa.2005.11.053
Lee J, Kim J, Park C: A fixed point approach to the stability of an additive-quadratic-cubic-quartic functional equation. Fixed Point Theory Appl. 2010., 2010: Article ID 185780
Park C: A fixed point approach to the fuzzy stability of an additive-quadratic-cubic functional equation. Fixed Point Theory Appl. 2009., 2009: Article ID 918785
Park C: Fuzzy stability of a functional equation associated with inner product spaces. Fuzzy Sets Syst. 2009, 160: 1632–1642. 10.1016/j.fss.2008.11.027
Alsina C: On the stability of a functional equation arising in probabilistic normed spaces. 5. In General Inequalities. Birkhäuser, Basel; 1987:263–271.
Eshaghi Gordji M, Ghaemi MB, Majani H: Generalized Hyers-Ulam-Rassias theorem in Menger probabilistic normed spaces. Discrete Dyn. Nat. Soc. 2010., 2010: Article ID 162371
Eshaghi Gordji M, Ghaemi MB, Majani H, Park C: Generalized Ulam-Hyers stability of Jensen functional equation in Šerstnev PN-spaces. J. Inequal. Appl. 2010., 2010: Article ID 868193
Miheţ D, Radu V: On the stability of the additive Cauchy functional equation in random normed spaces. J. Math. Anal. Appl. 2008, 343: 567–572. 10.1016/j.jmaa.2008.01.100
Miheţ D: The probabilistic stability for a functional equation in a single variable. Acta Math. Hung. 2009, 123: 249–256. 10.1007/s10474-008-8101-y
Miheţ D: The fixed point method for fuzzy stability of the Jensen functional equation. Fuzzy Sets Syst. 2009, 160: 1663–1667. 10.1016/j.fss.2008.06.014
Miheţ D, Saadati R, Vaezpour SM: The stability of the quartic functional equation in random normed spaces. Acta Appl. Math. 2010, 110: 797–803. 10.1007/s10440-009-9476-7
Miheţ D, Saadati R, Vaezpour SM: The stability of an additive functional equation in Menger probabilistic φ -normed spaces. Math. Slovaca 2011, 61: 817–826. 10.2478/s12175-011-0049-7
Saadati R, Vaezpour SM, Cho Y: A note to paper “On the stability of cubic mappings and quartic mappings in random normed spaces”. J. Inequal. Appl. 2009., 2009: Article ID 214530
Zhang SS, Rassias JM, Saadati R: Stability of a cubic functional equation in intuitionistic random normed spaces. Appl. Math. Mech.-Engl. Ed. 2010, 31: 21–26. 10.1007/s10483-010-0103-6
Chang SS, Cho Y, Kang S: Nonlinear Operator Theory in Probabilistic Metric Spaces. Nova Science Publishers, New York; 2001.
Hadžić O, Pap E: Fixed Point Theory in PM-Spaces. Kluwer Academic, Amsterdam; 2001.
Kutukcu S, Tuna A, Yakut AT: Generalized contraction mapping principle in intuitionistic Menger spaces and application to differential equations. Appl. Math. Mech.-Engl. Ed. 2007, 28: 799–809. 10.1007/s10483-007-0610-z
Schweizer B, Sklar A: Probabilistic Metric Spaces. Elsevier, Amsterdam; 1983.
Šerstnev AN: On the notion of a random normed space. Dokl. Akad. Nauk SSSR 1963, 149: 280–283. in Russian
Atanassov KT: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20: 87–96. 10.1016/S0165-0114(86)80034-3
Deschrijver G, Kerre EE: On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst. 2003, 133: 227–235. 10.1016/S0165-0114(02)00127-6
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors conceived of the study, participated in its design and coordination, drafted the manuscript, participated in the sequence alignment, and read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Park, C., Eshaghi Gordji, M., Ghanifard, M. et al. Intuitionistic random almost additive-quadratic mappings. Adv Differ Equ 2012, 152 (2012). https://doi.org/10.1186/1687-1847-2012-152
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-152




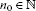 such that for every , where is a standard negator.
such that for every , where is a standard negator.