Approximate solutions to variational inequality over the fixed point set of a strongly nonexpansive mapping

Abstract

Variational inequality problems over fixed point sets of nonexpansive mappings include many practical problems in engineering and applied mathematics, and a number of iterative methods have been presented to solve them. In this paper, we discuss a variational inequality problem for a monotone, hemicontinuous operator over the fixed point set of a strongly nonexpansive mapping on a real Hilbert space. We then present an iterative algorithm, which uses the strongly nonexpansive mapping at each iteration, for solving the problem. We show that the algorithm potentially converges in the fixed point set faster than algorithms using firmly nonexpansive mappings. We also prove that, under certain assumptions, the algorithm with slowly diminishing step-size sequences converges to a solution to the problem in the sense of the weak topology of a Hilbert space. Numerical results demonstrate that the algorithm converges to a solution to a concrete variational inequality problem faster than the previous algorithm.

MSC:47H06, 47J20, 47J25.

1 Introduction

The paper presents an iterative algorithm for the variational inequality problem [1–8] for a monotone, hemicontinuous operator A over a nonempty, closed convex subset C of a real Hilbert space H with inner product $〈\cdot ,\cdot 〉$ and its induced norm $\parallel \cdot \parallel$,

$$\text{find }z\in C\text{ such that }〈y-z,Az〉\ge 0\text{ for all }y\in C.$$

(1)

Problem (1) can be solved by using convex optimization techniques. A typical iterative procedure for Problem (1) is the projected gradient method [7, 9], and it is expressed as $x_1\in C$ and $x_{n+1}=P_C(I-r_{n}A)x_n$ for $n=1,2,\dots$ , where $P_C$ stands for the metric projection onto C, I is the identity mapping on H, and $\{r_n\}\subset (0,\mathrm{\infty })$. However, as the method requires repetitive use of $P_C$, it can only be applied when the explicit form of $P_C$ is known (e.g., C is a closed ball or a closed cone). The following method, called the hybrid steepest descent method (HSDM) [10], enables us to consider the case in which C has a more complicated form: $x_1\in H$ and

$$x_{n+1}=(I-r_{n}A)T{x}_n$$

for all $n=1,2,\dots$ , where $\{r_n\}\subset (0,1]$ and $T:H\to H$ is an easily implemented nonexpansive mapping satisfying $Fix(T):=\{x\in H:Tx=x\}=C$. HSDM converges strongly to a unique solution to the variational inequality problem over $Fix(T)$,

$$\text{find }z\in Fix(T)\text{ such that }〈y-z,Az〉\ge 0\text{ for all }y\in Fix(T),$$

(2)

when $A:H\to H$ is strongly monotone and Lipschitz continuous. Problem (2) contains many applications such as signal recovery problems [11], beam-forming problems [12], power-control problems [13, 14], bandwidth allocation problems [15–17], and optimal control problems [18]. References [11, 19], and [20] presented acceleration methods for solving Problem (2) when A is strongly monotone and Lipschitz continuous. Algorithms were presented to solve Problem (2) when A is (strictly) monotone and Lipschitz continuous [15, 17]. When $H={\mathbb{R}}^N$ and $A:{\mathbb{R}}^N\to {\mathbb{R}}^N$ is continuous (and is not necessarily monotone), a simple algorithm, $x_{n+1}:={\alpha }_n{x}_n+(1-{\alpha }_n)(1/2)(I+T)(x_n-r_{n}A{x}_n)$ (${\alpha }_n,r_n\in [0,1]$), was presented in [14] and the algorithm converges to a solution to Problem (2) under some conditions.

Reference [21] proposed an iterative algorithm for solving Problem (2) when $A:H\to H$ is monotone and hemicontinuous and showed that the algorithm weakly converges to a solution to the problem under certain assumptions. The results in [21] are summarized as follows: suppose that $F:H\to H$ is a firmly nonexpansive mapping with $Fix(F)\ne \mathrm{\varnothing }$ and that $A:H\to H$ is a monotone, hemicontinuous mapping with

$$VI(Fix(F),A):=\{z\in Fix(F):〈y-z,Az〉\ge 0\text{ for all }y\in Fix(F)\}\ne \mathrm{\varnothing }.$$

Define a sequence $\{x_n\}\subset H$ by $x_1\in H$ and

$$\{\begin{array}{c}{y}_n=F(I-r_{n}A)x_n,\hfill \\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)y_n\hfill \end{array}$$

(3)

for all $n=1,2,\dots$ , where $\{{\alpha }_n\}\subset [0,1)$ and $\{r_n\}\subset (0,1)$. Assume that $\{A{x}_n\}$ in algorithm (3) is bounded, and that there exists $n_0\in \mathbb{N}$ such that $VI(Fix(F),A)\subset \mathrm{\Omega }:={\bigcap }_{n=n_0}^{\mathrm{\infty }}\{x\in Fix(F):〈x_n-x,A{x}_n〉\ge 0\}$. If $\{{\alpha }_n\}$ and $\{r_n\}$ satisfy ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\alpha }_n<1$, ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n^2<\mathrm{\infty }$, and ${lim}_{n\to \mathrm{\infty }}\parallel x_n-y_n\parallel /r_n=0$, then $\{x_n\}$ weakly converges to a point in $VI(Fix(F),A)$. To relax the strong monotonicity condition of A considered in [10], a firmly nonexpansive mapping F is used in algorithm (3) in place of a nonexpansive mapping T. From the fact that a firmly nonexpansive mapping F can be represented by the form, $F=(1/2)(I+T)$, for some nonexpansive mapping T, algorithm (3) when ${\alpha }_n:=0$ and $F:=(1/2)(I+T)$ can be simplified as follows: $x_1\in H$ and

$$x_{n+1}=\frac{1}{2}(I+T)(x_n-r_{n}A{x}_n)=\frac{1}{2}(x_n-r_{n}A{x}_n)+\frac{1}{2}T(x_n-r_{n}A{x}_n).$$

(4)

In constrained optimization problems, one is required to satisfy constraint conditions early in the process of executing an iterative algorithm. From this viewpoint, we introduce the following algorithm with a weighted parameter α, which is more than $1/2$:

$$\begin{array}{rl}{x}_{n+1}& =(1-\alpha )(x_n-r_{n}A{x}_n)+\alpha T(x_n-r_{n}A{x}_n)\\ =[(1-\alpha )I+\alpha T](x_n-r_{n}A{x}_n)=:S(x_n-r_{n}A{x}_n).\end{array}$$

(5)

Algorithm (5) potentially converges in the fixed point set faster than algorithm (4). Here, we can see that the mapping, $S:=(1-\alpha )I+\alpha T$, satisfies the strong nonexpansivity condition [22], which is a weaker condition than firm nonexpansivity. This implies that the previous algorithms in [14, 21], which can be applied to Problem (2) when T is firmly nonexpansive, cannot solve Problem (2) when T is strongly nonexpansive.

In this paper, we present an iterative algorithm for solving the variational inequality problem with a monotone, hemicontinuous operator over the fixed point set of a strongly nonexpansive mapping and show that the algorithm weakly converges to a solution to the problem under certain assumptions.

The rest of the paper is organized as follows. Section 2 covers the mathematical preliminaries. Section 3 presents the algorithm for solving the variational inequality problem for a monotone, hemicontinuous operator over the fixed point set of a strongly nonexpansive mapping, and its convergence analyses. Section 4 provides numerical comparisons of the algorithm with the previous algorithm in [21] and shows that the algorithm converges to a solution to a concrete variational inequality problem faster than the previous algorithm. Section 5 concludes the paper.

2 Preliminaries

Throughout this paper, we will denote the set of all positive integers by ℕ and the set of all real numbers by ℝ. Let H be a real Hilbert space with inner product $〈\cdot ,\cdot 〉$ and its induced norm $\parallel \cdot \parallel$. We denote the strong convergence and weak convergence of $\{x_n\}$ to $x\in H$ by $x_n\to x$ and $x_n\rightharpoonup x$, respectively. It is well known that H satisfies the following condition, called Opial’s condition [23]: for any $\{x_n\}\subset H$ satisfying $x_n\rightharpoonup x_0$, ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}\parallel x_n-x_0\parallel <{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}\parallel x_n-y\parallel$ holds for all $y\in H$ with $y\ne x_0$; see also [5, 6, 24]. To prove our main theorems, we need the following lemma, which was proven in [25]; see also [5, 6, 26].

Lemma 2.1 ([25])

Assume that $\{s_n\}$ and $\{e_n\}$ are sequences of non-negative numbers such that $s_{n+1}\le s_n+e_n$ for all $n\in \mathbb{N}$. If ${\sum }_{n=1}^{\mathrm{\infty }}{e}_n<\mathrm{\infty }$, then ${lim}_{n\to \mathrm{\infty }}{s}_n$ exists.

2.1 Strong nonexpansivity and fixed point set

Let T be a mapping of H into itself. We denote the fixed point set of T by $Fix(T)$; i.e., $Fix(T)=\{z\in H:Tz=z\}$. A mapping $T:H\to H$ is said to be nonexpansive if $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$ for all $x,y\in H$. $Fix(T)$ is closed and convex when T is nonexpansive [5, 6, 24, 27]. $T:H\to H$ is said to be strongly nonexpansive [22] if T is nonexpansive and if, for bounded sequences $\{x_n\},\{y_n\}\subset H$, $\parallel x_n-y_n\parallel -\parallel T{x}_n-T{y}_n\parallel \to 0$ implies $\parallel x_n-y_n-(T{x}_n-T{y}_n)\parallel \to 0$. The following properties for strongly nonexpansive mappings were shown in [22]:

• $Fix(T)$ is closed and convex when $T:H\to H$ is strongly nonexpansive because T is also nonexpansive.

• A strongly nonexpansive mapping, $T:H\to H$, with $Fix(T)\ne \mathrm{\varnothing }$ is asymptotically regular[24, 28], i.e., for each $x\in H$, ${lim}_{n\to \mathrm{\infty }}\parallel T^{n}x-T^{n+1}x\parallel =0$.

• If $S,T:H\to H$ are strongly nonexpansive, then ST is also strongly nonexpansive, and $Fix(ST)=Fix(S)\cap Fix(T)$ when $Fix(S)\cap Fix(T)\ne \mathrm{\varnothing }$.

• If $S:H\to H$ is strongly nonexpansive and if $T:H\to H$ is nonexpansive, then $\alpha S+(1-\alpha )T$ is strongly nonexpansive for $\alpha \in (0,1)$. If $Fix(S)\cap Fix(T)\ne \mathrm{\varnothing }$, then $Fix(\alpha S+(1-\alpha )T)=Fix(S)\cap Fix(T)$[29]. In particular, since the identity mapping I is strongly nonexpansive, the mapping $U:=\alpha I+(1-\alpha )T$ is strongly nonexpansive. Such U is said to be averaged nonexpansive.

Example 2.1 Let $D\subset H$ be a closed convex set, which is simple in the sense that $P_D$ can be calculated explicitly. Furthermore, let $f:H\to \mathbb{R}$ be Fréchet differentiable and $\mathrm{\nabla }f:H\to H$ be Lipschitz continuous; i.e., there exists $L>0$ such that $\parallel \mathrm{\nabla }f(x)-\mathrm{\nabla }f(y)\parallel \le L\parallel x-y\parallel$ for all $x,y\in H$. Then, for $r\in (0,2/L]$, $S_r:=P_D(I-r\mathrm{\nabla }f)$ is nonexpansive [30], [[31], Lemma 2.1]. Define $T:H\to H$ by

$$T:=\alpha I+(1-\alpha )S_r(\alpha \in (0,1)).$$

(6)

Then T is strongly nonexpansive and $Fix(T)=\{x\in D:f(x)={min}_{y\in D}f(y)\}$.

Example 2.2 Let $D_i\subset H$ ($i=0,1,\dots ,m$) be a closed convex set, which is simple in the sense that $P_{D_i}$ can be calculated explicitly. Define $\mathrm{\Phi }(x):=(1/2){\sum }_{i=1}^m{\omega }_{i}d(x,D_i)$ for all $x\in H$, where ${\omega }_i\in (0,1)$ with ${\sum }_{i=1}^m{\omega }_i=1$ and $d(x,D_i):=min\{\parallel x-y\parallel :y\in D_i\}$ ($i=1,2,\dots ,m$). Also, we define $S:H\to H$ and $T:H\to H$ as

$$S:=P_{D_0}\left[\sum _{i=1}^m{\omega }_i{P}_{D_i}\right],T:=\alpha I+(1-\alpha )S(\alpha \in (0,1)).$$

(7)

Then S is nonexpansive [[10], Proposition 4.2] and $Fix(S)=C_{\mathrm{\Phi }}:=\{x\in D_0:\mathrm{\Phi }(x)={min}_{y\in D_0}\mathrm{\Phi }(y)\}$. Hence, T is strongly nonexpansive and $Fix(T)=C_{\mathrm{\Phi }}$. $C_{\mathrm{\Phi }}$ is referred to as a generalized convex feasible set [10, 32] and is defined as the subset of $D_0$ that is closest to $D_1,D_2,\dots ,D_m$ in the mean square sense. Even if ${\bigcap }_{i=0}^m{D}_i=\mathrm{\varnothing }$, $C_{\mathrm{\Phi }}$ is well defined. $C_{\mathrm{\Phi }}={\bigcap }_{i=0}^m{D}_i$ holds when ${\bigcap }_{i=0}^m{D}_i\ne \mathrm{\varnothing }$. Accordingly, $C_{\mathrm{\Phi }}$ is a generalization of ${\bigcap }_{i=0}^m{D}_i$.

A mapping $F:H\to H$ is said to be firmly nonexpansive [33] if ${\parallel Fx-Fy\parallel }^2\le 〈x-y,Fx-Fy〉$ for all $x,y\in H$ (see also [24, 27, 34]). Every firmly nonexpansive mapping F can be expressed as $F=(1/2)(I+T)$ given some nonexpansive mapping T [24, 27, 34]. Hence, the class of averaged nonexpansive mappings includes the class of firmly nonexpansive mappings.

2.2 Variational inequality

An operator $A:H\to H$ is said to be monotone if $〈x-y,Ax-Ay〉\ge 0$ for all $x,y\in H$. $A:H\to H$ is said to be hemicontinuous [[5], p.204] if, for any $x,y\in H$, the mapping $g:[0,1]\to H$ defined by $g(t)=A(tx+(1-t)y)$ is continuous, where H has a weak topology. Let C be a nonempty, closed convex subset of H. The variational inequality problem [2, 4] for a monotone operator $A:H\to H$ is as follows (see also [1, 3, 5–8]):

$$\text{find }z\in C\text{ such that }〈y-z,Az〉\ge 0\text{ for all }y\in C.$$

We denote the solution set of the variational inequality problem by $VI(C,A)$. The monotonicity and hemicontinuity of A imply that $VI(C,A)=\{z\in C:〈y-z,Ay〉\ge 0\text{ for all }y\in C\}$ [[5], Subsection 7.1]. This means that $VI(C,A)$ is closed and convex. $VI(C,A)$ is nonempty when $A:H\to H$ is monotone and hemicontinuous, and $C\subset H$ is nonempty, compact, and convex [[5], Theorem 7.1.8].

Example 2.3 Let $g:H\to \mathbb{R}$ be convex and continuously Fréchet differentiable and $A:=\mathrm{\nabla }g$. Then A is monotone and hemicontinuous.

(i) Suppose that $f:H\to \mathbb{R}$ is as in Example 2.1 and $T:H\to H$ is defined as in (6) and set $G:=\{z\in D:f(z)={min}_{w\in D}f(w)\}$. Then

$$VI(Fix(T),A)=\{x\in G:g(x)=\underset{y\in G}{min}g(y)\}.$$

A solution of this problem is a minimizer of g over the set of all minimizers of f over D. Therefore, the problem has a triplex structure [16, 31, 35].

(ii) Suppose that $T:H\to H$ is defined as in (7). Then

$$VI(Fix(T),A)=\{x\in C_{\mathrm{\Phi }}:g(x)=\underset{y\in C_{\mathrm{\Phi }}}{min}g(y)\}.$$

This problem is to find a minimizer of g over the generalized convex feasible set [10, 13, 14, 16, 18].

3 Optimization of variational inequality over fixed point set

In this section, we present an iterative algorithm for solving the variational inequality problem for a monotone, hemicontinuous operator over the fixed point set of a strongly nonexpansive mapping and its convergence analyses. We assume that $T:H\to H$ is a strongly nonexpansive mapping with $Fix(T)\ne \mathrm{\varnothing }$ and that $A:H\to H$ is a monotone, hemicontinuous operator.

Algorithm 3.1

Step 0. Choose $x_1\in H$, $r_1\in (0,1)$, and ${\alpha }_1\in [0,1)$ arbitrarily, and let $n:=1$.

Step 1. Given $x_n\in H$, choose $r_n\in (0,1)$ and ${\alpha }_n\in [0,1)$ and compute $x_{n+1}\in H$ as

$$y_n:=T(x_n-r_{n}A{x}_n),x_{n+1}:={\alpha }_n{x}_n+(1-{\alpha }_n)y_n.$$

Step 2. Update $n:=n+1$, and go to Step 1.

To prove our main theorems, we need the following lemma.

Lemma 3.1 Suppose that $\{x_n\}$ is a sequence generated by Algorithm 3.1 and that $\{A{x}_n\}$ is bounded. Moreover, assume that

• (A) ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n<\mathrm{\infty }$, or

• (B) ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n^2<\mathrm{\infty }$, $VI(Fix(T),A)\ne \mathrm{\varnothing }$, and the existence of an $n_0\in \mathbb{N}$ satisfying $VI(Fix(T),A)\subset \mathrm{\Omega }:={\bigcap }_{n=n_0}^{\mathrm{\infty }}\{x\in Fix(T):〈x_n-x,A{x}_n〉\ge 0\}$.

Then $\{x_n\}$ is bounded.

Proof Put $z_n:=x_n-r_{n}A{x}_n$ for all $n\in \mathbb{N}$. We first assume that condition (A) is satisfied and choose $u\in Fix(T)$ arbitrarily. Accordingly, we see that, for any $n\in \mathbb{N}$,

$$\begin{array}{rl}\parallel x_{n+1}-u\parallel & =\parallel {\alpha }_n{x}_n+(1-{\alpha }_n)y_n-u\parallel \\ \le {\alpha }_n\parallel x_n-u\parallel +(1-{\alpha }_n)\parallel z_n-u\parallel \\ ={\alpha }_n\parallel x_n-u\parallel +(1-{\alpha }_n)\parallel (x_n-u)-r_{n}A{x}_n\parallel \\ \le \parallel x_n-u\parallel +r_n\parallel A{x}_n\parallel .\end{array}$$

(8)

From ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n<\mathrm{\infty }$, the boundedness of $\{A{x}_n\}$, and Lemma 2.1, the limit of $\{\parallel x_n-u\parallel \}$ exists for all $u\in Fix(T)$, which implies that $\{x_n\}$ is bounded.

Next, suppose that condition (B) is satisfied, and let $u\in Fix(T)$. Then, from the monotonicity of A, we find that, for any $n\in \mathbb{N}$,

$$\begin{array}{rl}{\parallel x_{n+1}-u\parallel }^2=& {\parallel {\alpha }_n{x}_n+(1-{\alpha }_n)y_n-u\parallel }^2\\ \le & {\alpha }_n{\parallel x_n-u\parallel }^2+(1-{\alpha }_n){\parallel y_n-u\parallel }^2\\ \le & {\alpha }_n{\parallel x_n-u\parallel }^2+(1-{\alpha }_n){\parallel z_n-u\parallel }^2\\ =& {\alpha }_n{\parallel x_n-u\parallel }^2+(1-{\alpha }_n){\parallel (x_n-u)-r_{n}A{x}_n\parallel }^2\\ =& {\alpha }_n{\parallel x_n-u\parallel }^2+(1-{\alpha }_n)({\parallel x_n-u\parallel }^2+2r_n〈u-x_n,A{x}_n〉+r_n^2{\parallel A{x}_n\parallel }^2)\\ \le & {\parallel x_n-u\parallel }^2+(1-{\alpha }_n)(2r_n〈u-x_n,A{x}_n〉+K{r}_n^2)\\ =& {\parallel x_n-u\parallel }^2+(1-{\alpha }_n)(2r_n〈u-x_n,A{x}_n-Au〉\\ +2r_n〈u-x_n,Au〉+K{r}_n^2)\\ \le & {\parallel x_n-u\parallel }^2+2r_n(1-{\alpha }_n)〈u-x_n,Au〉+K{r}_n^2,\end{array}$$

(9)

where $K:=sup\{{\parallel A{x}_n\parallel }^2:n\in \mathbb{N}\}<\mathrm{\infty }$. Especially in the case of $u\in VI(Fix(T),A)\subset \mathrm{\Omega }$, it follows from condition (B) that, for any $n\ge n_0$,

$$\begin{array}{rl}{\parallel x_{n+1}-u\parallel }^2& \le {\parallel x_n-u\parallel }^2+2r_n(1-{\alpha }_n)〈u-x_n,A{x}_n〉+K{r}_n^2\\ \le {\parallel x_n-u\parallel }^2+K{r}_n^2.\end{array}$$

Hence, the condition, ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n^2<\mathrm{\infty }$, and Lemma 2.1 guarantee that the limit of $\{\parallel x_n-u\parallel \}$ exists for all $u\in VI(Fix(T),A)$. We thus conclude that $\{x_n\}$ is bounded. □

Now, we are in the position to perform the convergence analysis on Algorithm 3.1 under condition (A) in Lemma 3.1.

Theorem 3.1 Let $\{x_n\}$ be a sequence generated by Algorithm 3.1 and assume that $\{A{x}_n\}$ is bounded and that the sequences $\{{\alpha }_n\}\subset [0,1)$ and $\{r_n\}\subset (0,1)$ satisfy

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{\alpha }_n<1,\sum _{n=1}^{\mathrm{\infty }}{r}_n<\mathrm{\infty },\mathit{\text{and}}\underset{n\to \mathrm{\infty }}{lim}\frac{\parallel x_n-y_n\parallel }{r_n}=0.$$

Then Algorithm 3.1 converges weakly to a point in $VI(Fix(T),A)$.

Proof Put $z_n:=x_n-r_{n}A{x}_n$ for all $n\in \mathbb{N}$. The proof consists of the following steps:

• (a) Prove that $\{x_n\}$ and $\{z_n\}$ are bounded.

• (b) Prove that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-y_n\parallel =0$ and ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$ hold.

• (c) Prove that $\{x_n\}$ converges weakly to a point in $\mathrm{VI}(Fix(T),A)$.

• (a) Choose $u\in Fix(T)$ arbitrarily. From the inequality, $\parallel z_n-u\parallel =\parallel (x_n-r_{n}A{x}_n)-u\parallel \le \parallel x_n-u\parallel +r_n\parallel A{x}_n\parallel$, and Lemma 3.1, we deduce that $\{z_n\}$ is bounded.

• (b) Put $c:={lim}_{n\to \mathrm{\infty }}\parallel x_n-u\parallel$ for any $u\in Fix(T)$. Then, from ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n<\mathrm{\infty }$, for any $\epsilon >0$, we can choose $m\in \mathbb{N}$ such that $|\parallel x_n-u\parallel -c|\le \epsilon$, and $r_n\le \epsilon$ for all $n\ge m$. Also, there exists $a>0$ such that ${\alpha }_n<a<1$ for all $n\ge m$ because of ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\alpha }_n<1$. Since $y_n=(1/(1-{\alpha }_n))x_{n+1}-({\alpha }_n/(1-{\alpha }_n))x_n$, we have

  $$\parallel y_n-u\parallel \ge \frac{1}{1-{\alpha }_n}\parallel x_{n+1}-u\parallel -\frac{{\alpha }_n}{1-{\alpha }_n}\parallel x_n-u\parallel$$

for all $n\in \mathbb{N}$. We find that, for any $n\ge m$,

$$\parallel y_n-u\parallel \ge \frac{1}{1-{\alpha }_n}(c-\epsilon )-\frac{{\alpha }_n}{1-{\alpha }_n}(c+\epsilon )=c-\frac{1+{\alpha }_n}{1-{\alpha }_n}\epsilon \ge c-\frac{1+a}{1-a}\epsilon .$$

Hence, for any $u\in Fix(T)$ and for any $n\ge m$, we have

$$\begin{array}{rl}0& \le \parallel z_n-u\parallel -\parallel T{z}_n-Tu\parallel \le \parallel x_n-u\parallel +r_n\parallel A{x}_n\parallel -\parallel y_n-u\parallel \\ \le c+\epsilon +\sqrt{K}\epsilon -(c-\frac{1+a}{1-a}\epsilon )=(\frac{2}{1-a}+\sqrt{K})\epsilon ,\end{array}$$

where $K=sup\{{\parallel A{x}_n\parallel }^2:n\in \mathbb{N}\}<\mathrm{\infty }$, which implies that ${lim}_{n\to \mathrm{\infty }}(\parallel z_n-u\parallel -\parallel T{z}_n-Tu\parallel )=0$. Since T is strongly nonexpansive, we get

$$\underset{n\to \mathrm{\infty }}{lim}\parallel (z_n-u)-(T{z}_n-u)\parallel =\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-T{z}_n\parallel =\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-y_n\parallel =0.$$

(10)

From (10) and $\parallel x_n-z_n\parallel =r_n\parallel A{x}_n\parallel \to 0$ as $n\to \mathrm{\infty }$, we also get

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-y_n\parallel =0.$$

(11)

From $\parallel x_n-T{x}_n\parallel \le \parallel x_n-y_n\parallel +\parallel y_n-T{x}_n\parallel \le \parallel x_n-y_n\parallel +\parallel z_n-x_n\parallel$, and (11), we deduce that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-T{x}_n\parallel =0.$$

(12)

• (c) From the boundedness of $\{x_n\}$, there exists a subsequence $\{x_{n_i}\}$ of $\{x_n\}$ such that $\{x_{n_i}\}$ converges weakly to a point $v\in H$. From the nonexpansivity of T and (12), it is guaranteed that T is demiclosed (i.e., $x_n\rightharpoonup u$ and $\parallel x_n-T{x}_n\parallel \to 0$ imply $u\in Fix(T)$). Hence, we have $v\in Fix(T)$. From (9), we get, for any $u\in Fix(T)$ and for any $n\in \mathbb{N}$,

  $$\begin{array}{rl}0\le & (\parallel x_n-u\parallel +\parallel x_{n+1}-u\parallel )(\parallel x_n-u\parallel -\parallel x_{n+1}-u\parallel )\\ +2r_n(1-{\alpha }_n)〈u-x_n,Au〉+K{r}_n^2,\end{array}$$

which means

$$\begin{array}{rl}0& \le \frac{L\parallel x_n-x_{n+1}\parallel }{r_n}+2(1-{\alpha }_n)〈u-x_n,Au〉+K{r}_n\\ =\frac{L(1-{\alpha }_n)\parallel x_n-y_n\parallel }{r_n}+2(1-{\alpha }_n)〈u-x_n,Au〉+K{r}_n\\ \le \frac{L\parallel x_n-y_n\parallel }{r_n}+2(1-{\alpha }_n)〈u-x_n,Au〉+K{r}_n,\end{array}$$

where $L:=sup\{\parallel x_n-u\parallel +\parallel x_{n+1}-u\parallel :n\in \mathbb{N}\}<\mathrm{\infty }$. From $\parallel x_n-y_n\parallel /r_n\to 0$, $x_n\rightharpoonup v$, ${lim\hspace{0.17em}sup}_n{\alpha }_n<1$, and $r_n\to 0$, we have

$$0\le 〈u-v,Au〉\text{for all }u\in Fix(T).$$

The monotonicity and hemicontinuity of A imply that $v\in \mathrm{VI}(Fix(T),A)$. Finally, we show that $\{x_n\}$ converges weakly to $v\in VI(Fix(T),A)$. Assume that another subsequence $\{x_{n_j}\}$ of $\{x_n\}$ converges weakly to w. Then, from the discussion above, we also get $w\in VI(Fix(T),A)$. If $v\ne w$, Opial’s theorem [23] guarantees that

$$\begin{array}{rl}\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-v\parallel & =\underset{i\to \mathrm{\infty }}{lim}\parallel x_{n_i}-v\parallel \\ <\underset{i\to \mathrm{\infty }}{lim}\parallel x_{n_i}-w\parallel \\ =\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-w\parallel \\ =\underset{j\to \mathrm{\infty }}{lim}\parallel x_{n_j}-w\parallel \\ <\underset{j\to \mathrm{\infty }}{lim}\parallel x_{n_j}-v\parallel \\ =\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-v\parallel .\end{array}$$

This is a contradiction. Thus, $v=w$. This implies that every subsequence of $\{x_n\}$ converges weakly to the same point in $VI(Fix(T),A)$. Therefore, $\{x_n\}$ converges weakly to $v\in VI(Fix(T),A)$. This completes the proof. □

Remark 3.1 The numerical examples in [14, 16, 21] show that Algorithm 3.1 satisfies ${lim}_{n\to \mathrm{\infty }}\parallel x_n-y_n\parallel /r_n=0$ when T is firmly nonexpansive and $r_n:=1/n^{\alpha }$ ($1\le \alpha <2$). However, when $\alpha \ge 2$, there are counterexamples that do not satisfy ${lim}_{n\to \mathrm{\infty }}\parallel x_n-y_n\parallel /r_n=0$ [14, 16, 21].

Remark 3.2 If the sequence $\{x_n\}$ satisfies the assumptions in Theorem 3.1, we need not assume that $VI(Fix(T),A)\ne \mathrm{\varnothing }$ or that $n_0\in \mathbb{N}$ exists such that $VI(Fix(T),A)\subset \mathrm{\Omega }$ in condition (B) (see also [[14], Remark 7(c)]).

Remark 3.3 Let us provide the sufficient condition of the boundedness of $\{A{x}_n\}$. Suppose that $Fix(T)$ is bounded and A is Lipschitz continuous. Then we can set a bounded set V with $Fix(T)\subset V$ onto which the projection can be computed within a finite number of arithmetic operations (e.g., V is a closed ball with a large enough radius). Accordingly, we can compute

$$x_{n+1}:=P_V({\alpha }_n{x}_n+(1-{\alpha }_n)y_n)(n=1,2,\dots )$$

(13)

instead of $x_{n+1}$ in Algorithm 3.1. Since $\{x_n\}\subset V$ and V is bounded, $\{x_n\}$ is bounded. The Lipschitz continuity of A means that $\parallel A{x}_n-Ax\parallel \le L\parallel x_n-x\parallel$ ($x\in H$), where L (>0) is a constant, and hence, $\{A{x}_n\}$ is bounded. We can prove that Algorithm 3.1 with Equation (13) and $\{{\alpha }_n\}$ and $\{r_n\}$ satisfying the conditions in Theorem 3.1 (or Theorem 3.2) weakly converges to a point in $VI(Fix(T),A)$ by referring to the proof of Theorem 3.1 (or Theorem 3.2).

We prove the following theorem under condition (B) in Lemma 3.1. The essential parts of a proof are similar those of Lemma 3.1 and Theorem 3.1, so we will only give an outline of the proof below.

Theorem 3.2 Let $\{x_n\}$ be a sequence generated by Algorithm 3.1. Assume that $\{A{x}_n\}$ is bounded and that $\{{\alpha }_n\}\subset [0,1)$ and $\{r_n\}\subset (0,1)$ satisfy

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{\alpha }_n<1,\sum _{n=1}^{\mathrm{\infty }}{r}_n^2<\mathrm{\infty },\mathit{\text{and}}\underset{n\to \mathrm{\infty }}{lim}\frac{\parallel x_n-y_n\parallel }{r_n}=0.$$

If $VI(Fix(T),A)\ne \mathrm{\varnothing }$ and if there exists $n_0\in \mathbb{N}$ such that $VI(Fix(T),A)\subset {\bigcap }_{n=n_0}^{\mathrm{\infty }}\{x\in Fix(T):〈x_n-x,A{x}_n〉\ge 0\}$, then the sequence $\{x_n\}$ converges weakly to a point in $VI(Fix(T),A)$.

Proof Put $z_n:=x_n-r_{n}A{x}_n$ for all $n\in \mathbb{N}$. As in the proof of Theorem 3.1, we proceed with the following steps:

• (a) Prove that $\{x_n\}$ and $\{z_n\}$ are bounded.

• (b) Prove that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$ holds.

• (c) Prove that $\{x_n\}$ converges weakly to a point in $\mathrm{VI}(Fix(T),A)$.

• (a) From Lemma 3.1, it follows that the limit of $\{\parallel x_n-u\parallel \}$ exists for all $u\in VI(Fix(T),A)$, and hence $\{x_n\}$ and $\{z_n\}$ are bounded.

• (b) Let $u\in VI(Fix(T),A)$ and put $c:={lim}_{n\to \mathrm{\infty }}\parallel x_n-u\parallel$. Since ${\sum }_{n=1}^{\mathrm{\infty }}{r}_n^2<\mathrm{\infty }$, the condition, $r_n\to 0$, holds. As in the proof of Theorem 3.1(b), for any $\epsilon >0$, there exists $m\in \mathbb{N}$ such that

  $$|\parallel x_n-u\parallel -c|\le \epsilon ,\text{and}\parallel y_n-u\parallel \ge c-\frac{1+a}{1-a}\epsilon$$

for all $n\ge m$. By ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\alpha }_n<1$, there exists $a>0$ such that ${\alpha }_n<a<1$. Since the inequality $\parallel z_n-u\parallel =\parallel (x_n-r_{n}A{x}_n)-u\parallel \le \parallel x_n-u\parallel +r_n\parallel A{x}_n\parallel$ holds, we have

$$\begin{array}{rl}0& \le \parallel z_n-u\parallel -\parallel T{z}_n-Tu\parallel \\ \le \parallel x_n-u\parallel +r_n\parallel A{x}_n\parallel -\parallel y_n-u\parallel \\ \le c+\epsilon +\sqrt{K}\epsilon -(c-\frac{1+a}{1-a}\epsilon )\\ =(\frac{2}{1-a}+\sqrt{K})\epsilon ,\end{array}$$

where $K=sup\{{\parallel A{x}_n\parallel }^2:n\in \mathbb{N}\}<\mathrm{\infty }$. This implies that ${lim}_{n\to \mathrm{\infty }}(\parallel z_n-u\parallel -\parallel T{z}_n-Tu\parallel )=0$. From the strong nonexpansivity of T, we get ${lim}_{n\to \mathrm{\infty }}\parallel z_n-T{z}_n\parallel =0$. The rest of the proof is the same as the proof of Theorem 3.1(b). Accordingly, we obtain ${lim}_{n\to \mathrm{\infty }}\parallel x_n-T{x}_n\parallel =0$.

• (c) Following the proof of Theorem 3.1(c), there exists a subsequence $\{x_{n_i}\}\subset \{x_n\}$ such that $\{x_{n_i}\}$ converges weakly to $v\in VI(Fix(T),A)$. Assume that another subsequence $\{x_{n_j}\}$ of $\{x_n\}$ converges weakly to w. Then we also have $w\in VI(Fix(T),A)$. Since the limit of $\{\parallel x_n-u\parallel \}$ exists for $u\in \mathrm{VI}(Fix(T),A)$, Opial’s theorem [23] guarantees that $v=w$. This implies that every subsequence of $\{x_n\}$ converges weakly to the same point in $VI(Fix(T),A)$, and hence, $\{x_n\}$ converges weakly to $v\in VI(Fix(T),A)$. This completes the proof. □

As we mentioned in Section 1, to solve constrained optimization problems whose feasible set is the fixed point set of a nonexpansive mapping T, Algorithm 3.1 must converge in $Fix(T)$ early in the execution. Therefore, it would be useful to use a large parameter α ($\in (0,1)$) when a strongly nonexpansive mapping is represented by $(1-\alpha )I+\alpha T$. Theorem 3.1 has the following consequences.

Corollary 3.1 Let $T:H\to H$ be a nonexpansive mapping with $Fix(T)\ne \mathrm{\varnothing }$ and let $A:H\to H$ be a monotone, hemicontinuous mapping. Let $\{x_n\}$ be a sequence generated by $x_1\in H$ and

$$\{\begin{array}{c}{y}_n=((1-\alpha )I+\alpha T)(x_n-r_{n}A{x}_n),\hfill \\ x_{n+1}={\alpha }_n{x}_n+(1-{\alpha }_n)y_n\hfill \end{array}$$

(14)

for all $n\in \mathbb{N}$, where $\{{\alpha }_n\}\subset [0,1)$, $\alpha \in (0,1)$ and $\{r_n\}\subset (0,1)$. Assume that $\{A{x}_n\}$ is a bounded sequence and that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{\alpha }_n<1,\sum _{n=1}^{\mathrm{\infty }}{r}_n<\mathrm{\infty },\mathit{\text{and}}\underset{n\to \mathrm{\infty }}{lim}\frac{\parallel x_n-y_n\parallel }{r_n}=0.$$

Then $\{x_n\}$ converges weakly to a point in $VI(Fix(T),A)$.

Proof Since every averaged nonexpansive mapping is strongly nonexpansive and $Fix((1-\alpha )I+\alpha T)=Fix(T)$ for $\alpha \in (0,1)$, Theorem 3.1 implies Corollary 3.1. □

By following the proof of Theorem 3.2 and Corollary 3.1, we get the following.

Corollary 3.2 Let $T:H\to H$ be a nonexpansive mapping with $Fix(T)\ne \mathrm{\varnothing }$ and let $A:H\to H$ be a monotone, hemicontinuous mapping. Let $\{x_n\}$ be a sequence in algorithm (14). Assume that $\{A{x}_n\}$ is a bounded sequence and that

$$\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{\alpha }_n<1,\sum _{n=1}^{\mathrm{\infty }}{r}_n^2<\mathrm{\infty },\mathit{\text{and}}\underset{n\to \mathrm{\infty }}{lim}\frac{\parallel x_n-y_n\parallel }{r_n}=0.$$

If $VI(Fix(T),A)\ne \mathrm{\varnothing }$ and if there exists $n_0\in \mathbb{N}$ such that $VI(Fix(T),A)\subset {\bigcap }_{n=n_0}^{\mathrm{\infty }}\{x\in Fix(T):〈x_n-x,A{x}_n〉\ge 0\}$, then $\{x_n\}$ converges weakly to a point in $VI(Fix(T),A)$.

4 Numerical examples

Let us apply Algorithm 3.1 and the algorithm in [21] to the following variational inequality problem.

Problem 4.1 Define $f:{\mathbb{R}}^{1,000}\to \mathbb{R}$ and $C_i$ ($\subset {\mathbb{R}}^{1,000}$) ($i=1,2$) by

$$\begin{array}{r}f(x):=\frac{1}{2}〈x,Qx〉(x\in {\mathbb{R}}^{1,000}),\\ C_i:=\{x\in {\mathbb{R}}^{1,000}:〈a_i,x〉\le b_i\}(i=1,2),\end{array}$$

where $Q\in {\mathbb{R}}^{1,000\times 1,000}$ is positive semidefinite, $a_i:=(a_i^{(1)},a_i^{(2)},\dots ,a_i^{(1,000)})\in {\mathbb{R}}^{1,000}$, and $b_i\in {\mathbb{R}}_{+}$ ($i=1,2$). Find $z\in VI(C_1\cap C_2,\mathrm{\nabla }f)$.

We set Q as a diagonal matrix with diagonal components $0,1,\dots ,999$ and choose $a_i^{(j)}\in (0,100)$ ($i=1,2$, $j=1,2,\dots ,1,000$) to be Mersenne Twister pseudo-random numbers given by the random-real function of srfi-27, Gauche.^a We also set $b_1:=5,000$ and $b_2:=4,000$. The compiler used in this experiment was gcc.^b The double-precision floating points were used for arithmetic processing of real numbers. The language was C.

In the experiment, we used the following algorithm:

$$\{\begin{array}{c}{y}_n:=((1-\alpha )I+\alpha P_{C_1}{P}_{C_2})(x_n-\frac{{10}^{-3}}{{(n+1)}^{1.001}}\mathrm{\nabla }f(x_n)),\hfill \\ x_{n+1}:=\frac{1}{2}{x}_n+\frac{1}{2}{y}_n(n\in \mathbb{N}),\hfill \end{array}$$

(15)

where $\alpha \in (0,1)$. Note that the projection $P_{C_i}$ ($i=1,2$) can be computed within a finite number of arithmetic operations [[36], p.406] because $C_i$ ($i=1,2$) is halfspace. More precisely,

$$P_{C_i}(x)=x+\frac{min\{0,b_i-〈a_i,x〉\}}{{\parallel a_i\parallel }^2}{a}_i(x\in {\mathbb{R}}^{1,000},i=1,2).$$

We can see that algorithm (15) with $\alpha :=1/2$ coincides with the previous algorithm in [21]. Hence, we compare^c algorithm (15) with $\alpha :=9/10$ with algorithm (15) with $\alpha :=1/2$ and verify that algorithm (15) with $\alpha :=9/10$ converges in $C_1\cap C_2=Fix(P_{C_1}{P}_{C_2})$ faster than algorithm (15) with $\alpha :=1/2$. We selected one hundred initial points $x=x(k)\in {\mathbb{R}}^{1,000}$ ($k=1,2,\dots ,100$) as pseudo-random numbers generated by the rand function of the C Standard Library. We executed algorithm (15) with $\alpha :=9/10$ and algorithm (15) with $\alpha :=1/2$ for these initial points. Let $\{x_n(k)\}$ be the sequence generated by $x(k)$ and algorithm (15). Here, we define

$$D_n:=\frac{1}{100}\sum _{k=1}^{100}\parallel x_n(k)-P_{C_1}{P}_{C_2}(x_n(k))\parallel (n\in \mathbb{N}).$$

The convergence of $\{D_n\}$ to 0 implies that algorithm (15) converges to a point in $C_1\cap C_2$.

Corollary 3.1 guarantees that algorithm (15) converges to a solution to Problem 4.1 if $\{\mathrm{\nabla }f(x_n)\}$ is bounded and if

$$\underset{n\to \mathrm{\infty }}{lim}{(n+1)}^{1.001}\parallel x_n-y_n\parallel =0.$$

(16)

To verify whether algorithm (15) satisfies condition (16), we employed

$$X_n:=\frac{1}{100}\sum _{k=1}^{100}{(n+1)}^{1.001}\parallel x_n(k)-y_n(k)\parallel (n\in \mathbb{N}),$$

where $y_n(k):=((1-\alpha )I+\alpha P_{C_1}{P}_{C_2})(x_n(k)-({10}^{-3}/{(n+1)}^{1.001})\mathrm{\nabla }f(x_n(k)))$ ($k=1,2,\dots ,100$, $n\in \mathbb{N}$). The convergence of $\{X_n\}$ to 0 implies that algorithm (15) satisfies condition (16). We also used

$$F_n:=\frac{1}{100}\sum _{k=1}^{100}f(x_n(k))(n\in \mathbb{N})$$

to check that algorithm (15) is stable.

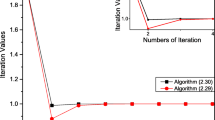
Figure 1 indicates the behaviors of $D_n$ for algorithm (15) with $\alpha :=9/10$ and algorithm (15) with $\alpha :=1/2$. This figure shows that $\{D_n\}$ in algorithm (15) with $\alpha :=9/10$ converges to 0 faster than $\{D_n\}$ in algorithm (15) with $\alpha :=1/2$; i.e., algorithm (15) with $\alpha :=9/10$ converges in $C_1\cap C_2$ faster than the previous algorithm in [21].

Figure 1

Behavior of ${\mathit{D}}_{\mathit{n}}$ for algorithm ( 15 ) with $\mathit{\alpha }\mathbf{:}\mathbf{=}\mathbf{9}\mathbf{/}\mathbf{10}$ and algorithm ( 15 ) with $\mathit{\alpha }\mathbf{:}\mathbf{=}\mathbf{1}\mathbf{/}\mathbf{2}$ .

Figure 2 compares the behaviors of $X_n$ for algorithm (15) with $\alpha :=9/10$ and algorithm (15) with $\alpha :=1/2$ and shows that the $\{X_n\}$ generated by each algorithm converges to 0; i.e., they each satisfy (16). Therefore, from Corollary 3.1, we can conclude that they can find a solution to Problem 4.1.

Figure 2

Behavior of ${\mathit{X}}_{\mathit{n}}$ for algorithm ( 15 ) with $\mathit{\alpha }\mathbf{:}\mathbf{=}\mathbf{9}\mathbf{/}\mathbf{10}$ and algorithm ( 15 ) with $\mathit{\alpha }\mathbf{:}\mathbf{=}\mathbf{1}\mathbf{/}\mathbf{2}$ .

We can see from Figure 3 that $\{F_n\}$ generated by the two algorithms converge to the same value. Figures 1, 2, and 3 indicate that algorithm (15) with $\alpha :=9/10$ converges to a solution to Problem 4.1 faster than the previous algorithm in [21]. This is because algorithm (15) uses a parameter ($\alpha :=9/10$) that is larger than $1/2$ and algorithm (15) with $\alpha >1/2$ potentially converges in the constraint set $C_1\cap C_2$ faster than the previous algorithm in [21] with $\alpha :=1/2$.

Figure 3

Behavior of ${\mathit{F}}_{\mathit{n}}$ for algorithm ( 15 ) with $\mathit{\alpha }\mathbf{:}\mathbf{=}\mathbf{9}\mathbf{/}\mathbf{10}$ and algorithm ( 15 ) with $\mathit{\alpha }\mathbf{:}\mathbf{=}\mathbf{1}\mathbf{/}\mathbf{2}$ .

5 Conclusion

We studied a variational inequality problem for a monotone, hemicontinuous operator over the fixed point set of a strongly nonexpansive mapping in a Hilbert space and devised an iterative algorithm for solving it. Our convergence analyses guarantee that the algorithm weakly converges to a solution under certain assumptions. We gave numerical results to support the convergence analyses on the algorithm. The results showed that the algorithm converges to a solution to a concrete variational inequality problem faster than the previous algorithm.

6 Endnotes

We used the Gauche scheme shell, 0.9.3.3 [utf-8,pthreads], x86_64-apple-darwin12.4.1.

We used gcc version 4.2.1 (Based on Apple Inc. build 5658) (LLVM build 2336.11.00).

For example, we set a large parameter, i.e., much more than $1/2$: $\alpha =9/10$.