Tripled common fixed point theorems under probabilistic φ-contractive conditions in generalized Menger probabilistic metric spaces

Abstract

In this paper, the new concepts of generalized Menger probabilistic metric spaces and tripled common fixed point for a pair of mappings $T:X\times X\times X\to X$ and $A:X\to X$ are introduced. Utilizing the properties of the pseudo-metric and the triangular norm, some tripled common fixed point problems of hybrid probabilistic contractions with a gauge function φ are studied. The obtained results generalize some coupled common fixed point theorems in the corresponding literature. Finally, an example is given to illustrate our main results.

MSC:47H10, 46S50.

1 Introduction

Coupled fixed points were considered by Bhaskar and Lakshmikantham [1]. Recently, some new results for the existence and uniqueness of coupled fixed points were presented for the cases of partially ordered metric spaces, cone metric spaces and fuzzy metric spaces (see [2–12]). The concept of probabilistic metric space was initiated and studied by Menger which is a generalization of the metric space notion [13]. Many results on the existence of fixed points or solutions of nonlinear equations under various types of conditions in Menger spaces have been extensively studied by many scholars (see [14–18]). In 2010, Jachymski established a fixed point theorem for probabilistic φ-contractions and give a characterization of function φ having the property that there exists a probabilistic φ-contraction, which is not a probabilistic k-contraction ($k\in [0,1)$) [19]. In 2011, Xiao et al. obtained some common coupled fixed point results for hybrid probabilistic contractions with a gauge function φ in Menger probabilistic metric spaces and in non-Archimedean Menger probabilistic metric spaces without assuming any continuity or monotonicity conditions for φ [20].

The purpose of this paper is to introduce the concept of generalized Menger probabilistic metric spaces and tripled common fixed point for a pair of mappings $T:X\times X\times X\to X$ and $A:X\to X$. Utilizing the properties of the pseudo-metric and the triangular norm, some tripled common fixed points problems for pairs of commutative mappings under hybrid probabilistic contractions with a gauge function φ are studied in generalized Menger PM-spaces and in generalized non-Archimedean Menger PM-space, respectively. The obtained results generalize some coupled common fixed point theorems in corresponding literatures. Finally, an example is given to illustrate our main results.

2 Preliminaries

Consistent with Menger [13] and Zhang [14], the following results will be needed in the sequel.

Denote by R the set of real numbers, $R^{+}$ the nonnegative real numbers, and $Z^{+}$ the set of all positive integers.

If $\phi :R^{+}\to R^{+}$ is a function such that $\phi (0)=0$, then φ is called a gauge function. If $t\in R^{+}$, then ${\phi }^n(t)$ denotes the n th iteration of $\phi (t)$ and ${\phi }^{-1}(\{0\})=\{t\in R^{+}:\phi (t)=0\}$.

A mapping $f:R\to R^{+}$ is called a distribution function if it is nondecreasing and left-continuous with ${inf}_{t\in R}f(t)=0$, ${sup}_{t\in R}f(t)=1$.

We shall denote by $\mathcal{D}$ the set of all distribution functions while H will always denote the specific distribution function defined by

$$H(t)=\{\begin{array}{ll}0,& t\le 0,\\ 1,& t>0.\end{array}$$

Definition 2.1 ([14])

A function $\mathrm{\Delta }:[0,1]\times [0,1]\times [0,1]\to [0,1]$ is called a triangular norm (for short, a t-norm) if the following conditions are satisfied for any $a,b,c,d,e,f\in [0,1]$:

(Δ-1) $\mathrm{\Delta }(a,1,1)=a$, $\mathrm{\Delta }(0,0,0)=0$;

(Δ-2) $\mathrm{\Delta }(a,b,c)=\mathrm{\Delta }(a,c,b)=\mathrm{\Delta }(c,b,a)$;

(Δ-3) $a\ge d,b\ge e,c\ge f\Rightarrow \mathrm{\Delta }(a,b,c)\ge \mathrm{\Delta }(d,e,f)$;

(Δ-4) $\mathrm{\Delta }(a,\mathrm{\Delta }(b,c,d),e)=\mathrm{\Delta }(\mathrm{\Delta }(a,b,c),d,e)=\mathrm{\Delta }(a,b,\mathrm{\Delta }(c,d,e))$.

Two typical examples of t-norms are ${\mathrm{\Delta }}_m(a,b,c)=min\{a,b,c\}$ and ${\mathrm{\Delta }}_p(a,b,c)=abc$ for all $a,b,c\in [0,1]$.

We now introduce the definition of generalized Menger probabilistic metric space.

Definition 2.2 A triplet $(X,\mathcal{F},\mathrm{\Delta })$ is called a generalized Menger probabilistic metric space (for short, a generalized Menger PM-space) if X is a non-empty set, Δ is a t-norm and ℱ is a mapping from $X\times X$ into $\mathcal{D}$ (we shall denote the distribution function $\mathcal{F}(x,y)$ by $F_{x,y}$ and $F_{x,y}(t)$ will represent the value of $F_{x,y}$ at $t\in R$) satisfying the following conditions:

(GPM-1) $F_{x,y}(0)=0$;

(GPM-2) $F_{x,y}(t)=H(t)$ for all $t\in R$ if and only if $x=y$;

(GPM-3) $F_{x,y}(t)=F_{y,x}(t)$ for all $x,y\in X$ and $t\in R$;

(GPM-4) $F_{x,w}(t_1+t_2+t_3)\ge \mathrm{\Delta }(F_{x,y}(t_1),F_{y,z}(t_2),F_{z,w}(t_3))$ for all $x,y,z,w\in X$ and $t_1,t_2,t_3\in R^{+}$.

$(X,\mathcal{F},\mathrm{\Delta })$ is called a generalized non-Archimedean Menger PM-space if it is a generalized Menger PM-space satisfying the following condition:

(GPM-5) $F_{x,y}(max\{t,s,r\})\ge \mathrm{\Delta }(F_{x,z}(t),F_{z,w}(s),F_{w,y}(r))$ for all $x,y,z,w\in X$ and $t,s,r\in R^{+}$.

Remark 2.1 In 1942, Menger [13] proposed a generalization of a metric space called a Menger probabilistic metric space (briefly a Menger PM-space). Our definition of a generalized Menger PM-space is different from the one of Menger, since the t-norm we used here is an associative function of three variables rather than a function of two variables. Note that Definition 2.1 is first used by Chang to define a probabilistic 2-metric space. Our definition is also different from the one of Chang since the distribution function of the latter is from $X\times X\times X$ to $\mathcal{D}$.

Example 2.1 Suppose that $X=[-1,1]\subset R$. Define $\mathcal{F}:X\times X\to \mathcal{D}$ by

$$\mathcal{F}(x,y)(t)=F_{x,y}(t)=\{\begin{array}{ll}{(\frac{t}{t+1})}^{|x-y|},& t>0,\\ 0,& t\le 0\end{array}$$

for $x,y\in X$. It is easy to verify that $(X,\mathcal{F},{\mathrm{\Delta }}_p)$ is a generalized Menger PM-space. Now, assume that $t,s,r>0$ and $x,y,z,w\in X$. Then we have

$$\begin{array}{rcl}{\mathrm{\Delta }}_p(F_{x,z}(t),F_{z,w}(s),F_{w,y}(r))& =& {\left(\frac{t}{t+1}\right)}^{|x-z|}{\left(\frac{s}{s+1}\right)}^{|z-w|}{\left(\frac{r}{r+1}\right)}^{|w-y|}\\ \le & {\left(\frac{max\{t,s,r\}}{max\{t,s,r\}+1}\right)}^{|x-z|+|z-w|+|w-y|}\\ \le & {\left(\frac{max\{t,s,r\}}{max\{t,s,r\}+1}\right)}^{|x-y|}\\ =& F_{x,y}(max\{t,s,r\}).\end{array}$$

Hence $(X,\mathcal{F},{\mathrm{\Delta }}_p)$ is a generalized non-Archimedean Menger PM-space.

Proposition 2.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a generalized Menger PM-space and Δ be a continuous t-norm. Then $(X,\mathcal{F},\mathrm{\Delta })$ is a Hausdorff topological space in the $(\epsilon ,\l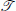ambda )$-topology , i.e., the family of sets

$$\{U_x(\epsilon ,\lambda ):\epsilon >0,\lambda \in (0,1],x\in X\}$$

is a base of neighborhoods of a point x for 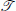, where

$$U_x(\epsilon ,\lambda )=\{y\in X:F_{x,y}(\epsilon )>1-\lambda \}.$$

Proof It suffices to prove that:

• (i) For any $x\in X$, there exists an $U=U_x(\epsilon ,\lambda )$ such that $x\in U$.

• (ii) For any given $U_x({\epsilon }_1,{\lambda }_1)$ and $U_x({\epsilon }_2,{\lambda }_2)$, there exist $\epsilon >0$ and $\lambda >0$, such that $U_x(\epsilon ,\lambda )\subset U_x({\epsilon }_1,{\lambda }_1)\cap U_x({\epsilon }_2,{\lambda }_2)$.

• (iii) For any $y\in U_x(\epsilon ,\lambda )$, there exist ${\epsilon }^{\prime }>0$ and ${\lambda }^{\prime }>0$, such that $U_y({\epsilon }^{\prime },{\lambda }^{\prime })\subset U_x(\epsilon ,\lambda )$.

• (iv) For any $x,y\in X$, $x\ne y$, there exist $U_x({\epsilon }_1,{\lambda }_1)$ and $U_y({\epsilon }_2,{\lambda }_2)$, such that $U_x({\epsilon }_1,{\lambda }_1)\cap U_y({\epsilon }_2,{\lambda }_2)=\mathrm{\varnothing }$.

It is easy to check that (i)-(iii) are true. Now we prove that (iv) is also true. In fact, suppose that $x,y\in X$ and $x\ne y$. Then there exist $t_0>0$ and $0\le a<1$, such that $F_{x,y}(t_0)=a$. Let

$$U_x=\{r:F_{x,r}\left(\frac{t_0}{3}\right)>b\},U_y=\{r:F_{y,r}\left(\frac{t_0}{3}\right)>b\},$$

where $0<b<1$ and $\mathrm{\Delta }(b,1,b)>a$ (since Δ is continuous and $\mathrm{\Delta }(1,1,1)=1$, such b exists). Now suppose that there exists a point $w\in U_x\cap U_y$, which implies that $F_{x,w}(\frac{t_0}{3})>b$ and $F_{y,w}(\frac{t_0}{3})>b$. Take $v=w$. Then we have

$$a=F_{x,y}(t_0)\ge \mathrm{\Delta }(F_{x,w}\left(\frac{t_0}{3}\right),F_{w,v}\left(\frac{t_0}{3}\right),F_{v,y}\left(\frac{t_0}{3}\right))\ge \mathrm{\Delta }(b,1,b)>a,$$

which is a contradiction. Thus the conclusion (iv) is proved. This completes the proof. □

Definition 2.3 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a generalized Menger PM-space, Δ be a continuous t-norm.

• (i) A sequence $\{x_n\}$ in X is said to be 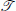-convergent to $x\in X$ if ${lim}_{n\to \mathrm{\infty }}{F}_{x_n,x}(t)=1$ for all $t>0$.

• (ii) A sequence $\{x_n\}$ in X is said to be a 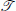-Cauchy sequence, if for any given $\epsilon >0$ and $\lambda \in (0,1]$, there exists a positive integer $N=N(\epsilon ,\lambda )$, such that $F_{x_n,x_m}(\epsilon )>1-\lambda$ whenever $n,m\ge N$.

• (iii) $(X,\mathcal{F},\mathrm{\Delta })$ is said to be 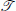-complete, if each 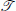-Cauchy sequence in X is 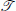-convergent to some point in X.

Definition 2.4 A t-norm Δ is said to be of H-type if the family of functions ${\{{\mathrm{\Delta }}^n(t)\}}_{n=1}^{\mathrm{\infty }}$ is equicontinuous at $t=1$, where

$${\mathrm{\Delta }}^1(t)=t,{\mathrm{\Delta }}^{n+1}(t)=\mathrm{\Delta }(t,t,{\mathrm{\Delta }}^n(t)),n=1,2,\dots ,t\in [0,1].$$

Definition 2.5 Let X be a non-empty set, $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings. A is said to be commutative with T, if $AT(x,y,z)=T(Ax,Ay,Az)$ for all $x,y,z\in X$. A point $u\in X$ is called a tripled common fixed point of T and A, if $u=Au=T(u,u,u)$.

Imitating the proof in [9], we can easily obtain the following lemma.

Lemma 2.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a generalized Menger PM-space. For each $\lambda \in (0,1]$, define a function $d_{\lambda }:X\times X\to R^{+}$ by

$$d_{\lambda }(x,y)=inf\{t>0:F_{x,y}(t)>1-\lambda \}.$$

(2.1)

Then the following statements hold:

• (1) $d_{\lambda }(x,y)<t$ if and only if $F_{x,y}(t)>1-\lambda$;

• (2) $d_{\lambda }(x,y)=d_{\lambda }(y,x)$ for all $x,y\in X$ and $\lambda \in (0,1]$;

• (3) $d_{\lambda }(x,y)=0$ if and only if $x=y$;

• (4) $d_{\lambda }(x,z)\le d_{\mu }(x,y)+d_{\mu }(y,z)$ for all $x,y,z\in X$ and $\mu \in (0,\lambda ]$.

The following lemmas play an important role in proving our main results in Sections 3 and 4.

Lemma 2.2 ([17])

Suppose that $F\in \mathcal{D}$. For any $n\in Z^{+}$, let $F_n:R\to [0,1]$ be nondecreasing, and $g_n:(0,+\mathrm{\infty })\to (0,+\mathrm{\infty })$ satisfy ${lim}_{n\to \mathrm{\infty }}{g}_n(t)=0$ for all $t>0$. If $F_n(g_n(t))\ge F(t)$ for all $t>0$, then ${lim}_{n\to \mathrm{\infty }}{F}_n(t)=1$ for all $t>0$.

Lemma 2.3 Let X be a nonempty set, $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings. If $T(X\times X\times X)\subset A(X)$, then there exist three sequences ${\{x_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{y_n\}}_{n=0}^{\mathrm{\infty }}$, and ${\{z_n\}}_{n=0}^{\mathrm{\infty }}$ in X, such that $A{x}_{n+1}=T(x_n,y_n,z_n)$, $A{y}_{n+1}=T(y_n,x_n,z_n)$, and $A{z}_{n+1}=T(z_n,x_n,y_n)$.

Proof Let $x_0$, $y_0$, $z_0$ be any given points in X. Since $T(X\times X\times X)\subset A(X)$, we can choose $x_1,y_1,z_1\in X$, such that $A{x}_1=T(x_0,y_0,z_0)$, $A{y}_1=T(y_0,x_0,z_0)$, and $A{z}_1=T(z_0,x_0,y_0)$. Continuing this process, we can construct three sequences ${\{x_n\}}_{n=1}^{\mathrm{\infty }}$, ${\{y_n\}}_{n=1}^{\mathrm{\infty }}$, and ${\{z_n\}}_{n=1}^{\mathrm{\infty }}$ in X, such that $A{x}_{n+1}=T(x_n,y_n,z_n)$, $A{y}_{n+1}=T(y_n,x_n,z_n)$, and $A{z}_{n+1}=T(z_n,x_n,y_n)$. □

3 Tripled common fixed point results in generalized PM-spaces

Lemma 3.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a generalized Menger PM-space, ${\{d_{\lambda }\}}_{\lambda \in (0,1]}$ be a family of pseudo-metrics on X defined by (2.1). If Δ is a t-norm of H-type, then for each $\lambda \in (0,1]$, there exists $\mu \in (0,\lambda ]$ such that for all $m\in Z^{+}$ and $x_0,x_1,\dots ,x_m\in X$,

$$d_{\lambda }(x_0,x_m)\le \sum _{i=0}^{m-1}{d}_{\mu }(x_i,x_{i+1}).$$

Proof Since Δ is a t-norm of H-type, ${\{{\mathrm{\Delta }}^n(t)\}}_{n=1}^{\mathrm{\infty }}$ is equicontinuous at $t=1$, and so for each $\lambda \in (0,1]$, there exists $\mu \in (0,\lambda ]$, such that

$${\mathrm{\Delta }}^n(1-\mu )>1-\lambda ,\mathrm{\forall }n\in Z^{+}.$$

(3.1)

For any given $m\in Z^{+}$ and $x_0,x_1,\dots ,x_m\in X$, we write $d_{\mu }(x_i,x_{i+1})=t_i$ ($i=0,1,\dots ,m-1$). For any $\epsilon >0$, it is evident that $d_{\mu }(x_i,x_{i+1})<t_i+\epsilon$. By Lemma 2.1, we have

$$F_{x_i,x_{i+1}}(t_i+\epsilon )>1-\mu ,i=0,1,\dots ,m-1.$$

(3.2)

It follows from (3.1)-(3.2), and (GPM-4) that

$$\begin{array}{c}{F}_{x_0,x_m}(\sum _{i=0}^{m-1}{t}_i+m\epsilon )\hfill \\ \ge \mathrm{\Delta }(F_{x_0,x_1}(t_0+\epsilon ),F_{x_1,x_2}(t_1+\epsilon ),\mathrm{\Delta }(F_{x_2,x_3}(t_2+\epsilon ),F_{x_3,x_4}(t_3+\epsilon ),\hfill \\ \mathrm{\Delta }(\dots ,\mathrm{\Delta }(F_{x_{m-3},x_{m-2}}(t_{m-3}+\epsilon ),F_{x_{m-2},x_{m-1}}(t_{m-2}+\epsilon ),F_{x_{m-1},x_m}(t_{m-1}+\epsilon ))\cdots )\left)\right)\hfill \\ \ge {\mathrm{\Delta }}^m(1-\mu )>1-\lambda .\hfill \end{array}$$

Using Lemma 2.1 again, we have $d_{\lambda }(x_0,x_m)<{\sum }_{i=0}^{m-1}{t}_i+m\epsilon$. By the arbitrariness of ε, we have

$$d_{\lambda }(x_0,x_m)\le \sum _{i=0}^{m-1}{t}_i=\sum _{i=0}^{m-1}{d}_{\mu }(x_i,x_{i+1}).$$

This completes the proof. □

Theorem 3.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$, $\phi (t)<t$, and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for any $t>0$. Let $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(\phi (t))\ge {[F_{Ax,Ap}(t)F_{Ay,Aq}(t)F_{Az,Ar}(t)]}^{\frac{1}{3}}$$

(3.3)

for all $x,y,z,p,q,r\in X$ and $t>0$, where $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

Proof By Lemma 2.3, we can construct three sequences ${\{x_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{y_n\}}_{n=0}^{\mathrm{\infty }}$, and ${\{z_n\}}_{n=0}^{\mathrm{\infty }}$ in X, such that $A{x}_{n+1}=T(x_n,y_n,z_n)$, $A{y}_{n+1}=T(y_n,x_n,z_n)$, and $A{z}_{n+1}=T(z_n,x_n,y_n)$.

From (3.3), for all $t>0$ we have

$$\begin{array}{c}{F}_{A{x}_n,A{x}_{n+1}}(\phi (t))=F_{T(x_{n-1},y_{n-1},z_{n-1}),T(x_n,y_n,z_n)}(\phi (t))\hfill \\ \phantom{F_{A{x}_n,A{x}_{n+1}}(\phi (t))}\ge {[F_{A{x}_{n-1},A{x}_n}(t)F_{A{y}_{n-1},A{y}_n}(t)F_{A{z}_{n-1},A{z}_n}(t)]}^{\frac{1}{3}},\hfill \end{array}$$

(3.4)

$$\begin{array}{c}{F}_{A{y}_n,A{y}_{n+1}}(\phi (t))=F_{T(y_{n-1},x_{n-1},z_{n-1}),T(y_n,x_n,z_n)}(\phi (t))\hfill \\ \phantom{F_{A{y}_n,A{y}_{n+1}}(\phi (t))}\ge {[F_{A{y}_{n-1},A{y}_n}(t)F_{A{x}_{n-1},A{x}_n}(t)F_{A{z}_{n-1},A{z}_n}(t)]}^{\frac{1}{3}}\hfill \end{array}$$

(3.5)

and

$$\begin{array}{rcl}{F}_{A{z}_n,A{z}_{n+1}}(\phi (t))& =& F_{T(z_{n-1},x_{n-1},y_{n-1}),T(z_n,x_n,y_n)}(\phi (t))\\ \ge & {[F_{A{z}_{n-1},A{z}_n}(t)F_{A{x}_{n-1},A{x}_n}(t)F_{A{y}_{n-1},A{y}_n}(t)]}^{\frac{1}{3}}.\end{array}$$

(3.6)

Denote $P_n(t)={[F_{A{x}_{n-1},A{x}_n}(t)F_{A{y}_{n-1},A{y}_n}(t)F_{A{z}_{n-1},A{z}_n}(t)]}^{\frac{1}{3}}$. From (3.4)-(3.6), we have

$$\begin{array}{rcl}{P}_{n+1}(\phi (t))& =& {\left[F_{A{x}_n,A{x}_{n+1}}(\phi (t))F_{A{y}_n,A{y}_{n+1}}(\phi (t))F_{A{z}_n,A{z}_{n+1}}(\phi (t))\right]}^{\frac{1}{3}}\\ \ge & {[P_n(t)P_n(t)P_n(t)]}^{\frac{1}{3}}=P_n(t),\end{array}$$

which implies that

$$F_{A{x}_n,A{x}_{n+1}}({\phi }^n(t))\ge P_n({\phi }^{n-1}(t))\ge \cdots \ge P_1(t),$$

(3.7)

$$F_{A{y}_n,A{y}_{n+1}}({\phi }^n(t))\ge P_n({\phi }^{n-1}(t))\ge \cdots \ge P_1(t)$$

(3.8)

and

$$F_{A{z}_n,A{z}_{n+1}}({\phi }^n(t))\ge P_n({\phi }^{n-1}(t))\ge \cdots \ge P_1(t).$$

(3.9)

Since $P_1(t)={[F_{A{x}_0,A{x}_1}(t)F_{A{y}_0,A{y}_1}(t)F_{A{z}_0,A{z}_1}(t)]}^{\frac{1}{3}}\in \mathcal{D}$ and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for each $t>0$, using Lemma 2.2, we have

$$\underset{n\to \mathrm{\infty }}{lim}{F}_{A{x}_n,A{x}_{n+1}}(t)=1,\underset{n\to \mathrm{\infty }}{lim}{F}_{A{y}_n,A{y}_{n+1}}(t)=1,\underset{n\to \mathrm{\infty }}{lim}{F}_{A{z}_n,A{z}_{n+1}}(t)=1.$$

(3.10)

Thus

$$\underset{n\to \mathrm{\infty }}{lim}{P}_n(t)=1,\mathrm{\forall }t>0.$$

(3.11)

We claim that for any $k\in Z^{+}$ and $t>0$,

$$F_{A{x}_n,A{x}_{n+k}}(t)\ge {\mathrm{\Delta }}^k\left(P_n\left(\frac{t-\phi (t)}{2}\right)\right),$$

(3.12)

$$F_{A{y}_n,A{y}_{n+k}}(t)\ge {\mathrm{\Delta }}^k\left(P_n\left(\frac{t-\phi (t)}{2}\right)\right)$$

(3.13)

and

$$F_{A{z}_n,A{z}_{n+k}}(t)\ge {\mathrm{\Delta }}^k\left(P_n\left(\frac{t-\phi (t)}{2}\right)\right).$$

(3.14)

In fact, by (3.7)-(3.9), it is easy to see that (3.12)-(3.14) hold for $k=1$. Assume that (3.12)-(3.14) hold for some k. Since $\phi (t)<t$, by (3.4) we have $F_{A{x}_n,A{x}_{n+1}}(t)\ge F_{A{x}_n,A{x}_{n+1}}(\phi (t))\ge P_n(t)$. By (3.3) and (3.12)-(3.14), we have

$$\begin{array}{rcl}{F}_{A{x}_{n+1},A{x}_{n+k+1}}(\phi (t))& \ge & {[F_{A{x}_n,A{x}_{n+k}}(t)F_{A{y}_n,A{y}_{n+k}}(t)F_{A{z}_n,A{z}_{n+k}}(t)]}^{\frac{1}{3}}\\ \ge & {\mathrm{\Delta }}^k\left(P_n\left(\frac{t-\phi (t)}{2}\right)\right).\end{array}$$

Hence, by the monotonicity of Δ, we have

$$\begin{array}{rcl}{F}_{A{x}_n,A{x}_{n+k+1}}(t)& =& F_{A{x}_n,A{x}_{n+k+1}}(t-\phi (t)+\phi (t))\\ \ge & \mathrm{\Delta }(F_{A{x}_n,A{x}_{n+1}}\left(\frac{t-\phi (t)}{2}\right),F_{A{x}_{n+1},A{x}_{n+1}}\left(\frac{t-\phi (t)}{2}\right),\\ F_{A{x}_{n+1},A{x}_{n+k+1}}(\phi (t)))\\ \ge & \mathrm{\Delta }(P_n\left(\frac{t-\phi (t)}{2}\right),P_n\left(\frac{t-\phi (t)}{2}\right),{\mathrm{\Delta }}^k\left(P_n\left(\frac{t-\phi (t)}{2}\right)\right))\\ =& {\mathrm{\Delta }}^{k+1}\left(P_n\left(\frac{t-\phi (t)}{2}\right)\right).\end{array}$$

Similarly, we have $F_{A{y}_n,A{y}_{n+k+1}}(t)\ge {\mathrm{\Delta }}^{k+1}(P_n(\frac{t-\phi (t)}{2}))$ and $F_{A{z}_n,A{z}_{n+k+1}}(t)\ge {\mathrm{\Delta }}^{k+1}(P_n(\frac{t-\phi (t)}{2}))$. Therefore, by induction, (3.12)-(3.14) hold for all $k\in Z^{+}$ and $t>0$.

Suppose that $\lambda \in (0,1]$ is given. Since Δ is a t-norm of H-type, there exists $\delta >0$ such that

$${\mathrm{\Delta }}^k(s)>1-\lambda ,s\in (1-\delta ,1],k\in Z^{+}.$$

(3.15)

By (3.11), there exists $N\in Z^{+}$, such that $P_n(\frac{t-\phi (t)}{2})>1-\delta$ for all $n\ge N$. Hence, from (3.12)-(3.15), we get $F_{A{x}_n,A{x}_{n+k}}(t)>1-\lambda$, $F_{A{y}_n,A{y}_{n+k}}(t)>1-\lambda$, $F_{A{z}_n,A{z}_{n+k}}(t)>1-\lambda$ for all $n\ge N$, $k\in Z^{+}$. Therefore $\{A{x}_n\}$, $\{A{y}_n\}$, and $\{A{z}_n\}$ are Cauchy sequences.

Since $(X,\mathcal{F},\mathrm{\Delta })$ is complete, there exist $u,v,w\in X$, such that ${lim}_{n\to \mathrm{\infty }}A{x}_n=u$, ${lim}_{n\to \mathrm{\infty }}A{y}_n=v$ and ${lim}_{n\to \mathrm{\infty }}A{z}_n=w$. By the continuity of A, we have

$$\underset{n\to \mathrm{\infty }}{lim}AA{x}_n=Au,\underset{n\to \mathrm{\infty }}{lim}AA{y}_n=Av,\underset{n\to \mathrm{\infty }}{lim}AA{z}_n=Aw.$$

The commutativity of A with T implies that $AA{x}_{n+1}=AT(x_n,y_n,z_n)=T(A{x}_n,A{y}_n,A{z}_n)$. From (3.3) and $\phi (t)<t$, we obtain

$$\begin{array}{rcl}{F}_{AA{x}_{n+1},T(u,v,w)}(t)& \ge & F_{AA{x}_{n+1},T(u,v,w)}(\phi (t))\\ =& F_{T(A{x}_n,A{y}_n,A{z}_n),T(u,v,w)}(\phi (t))\\ \ge & {[F_{AA{x}_n,Au}(t)F_{AA{y}_n,Av}(t)F_{AA{z}_n,Aw}(t)]}^{\frac{1}{3}}.\end{array}$$

(3.16)

Letting $n\to \mathrm{\infty }$ in (3.16), we have ${lim}_{n\to \mathrm{\infty }}AA{x}_n=T(u,v,w)$. Hence, $T(u,v,w)=Au$. Similarly, we can show that $T(v,u,w)=Av$ and $T(w,u,v)=Aw$.

Next we show that $Au=v$, $Av=u$, and $Aw=w$. In fact, from (3.3), for all $t>0$ we have

$$\begin{array}{c}{F}_{Au,A{y}_n}(\phi (t))=F_{T(u,v,w),T(y_{n-1},x_{n-1},z_{n-1})}(\phi (t))\hfill \\ \phantom{F_{Au,A{y}_n}(\phi (t))}\ge {[F_{Au,A{y}_{n-1}}(t)F_{Av,A{x}_{n-1}}(t)F_{Aw,A{z}_{n-1}}(t)]}^{\frac{1}{3}},\hfill \end{array}$$

(3.17)

$$F_{Av,A{x}_n}(\phi (t))\ge {[F_{Av,A{x}_{n-1}}(t)F_{Au,A{y}_{n-1}}(t)F_{Aw,A{z}_{n-1}}(t)]}^{\frac{1}{3}}$$

(3.18)

and

$$F_{Aw,A{z}_n}(\phi (t))\ge {[F_{Aw,A{z}_{n-1}}(t)F_{Au,A{x}_{n-1}}(t)F_{Av,A{y}_{n-1}}(t)]}^{\frac{1}{3}}.$$

(3.19)

Denote $Q_n(t)=F_{Au,A{y}_n}(t)F_{Av,A{x}_n}(t)F_{Aw,A{z}_n}(t)$. By (3.17)-(3.19), we have $Q_n(\phi (t))\ge Q_{n-1}(t)$, and hence for all $t>0$

$$Q_n({\phi }^n(t))\ge Q_{n-1}({\phi }^{n-1}(t))\ge \cdots \ge Q_0(t).$$

Thus, for all $t>0$ we have

$$\begin{array}{c}{F}_{Au,A{y}_n}({\phi }^n(t))\ge {[Q_0(t)]}^{\frac{1}{3}},F_{Av,A{x}_n}({\phi }^n(t))\ge {[Q_0(t)]}^{\frac{1}{3}},\hfill \\ F_{Aw,A{z}_n}({\phi }^n(t))\ge {[Q_0(t)]}^{\frac{1}{3}}.\hfill \end{array}$$

Since ${[Q_0(t)]}^{\frac{1}{3}}\in \mathcal{D}$ and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for all $t>0$, by Lemma 2.2, we conclude that

$$\underset{n\to \mathrm{\infty }}{lim}A{x}_n=Av,\underset{n\to \mathrm{\infty }}{lim}A{y}_n=Au,\underset{n\to \mathrm{\infty }}{lim}A{z}_n=Aw.$$

(3.20)

This shows that $Au=v$, $Av=u$, and $Aw=w$. Hence, $v=T(u,v,w)$, $u=T(v,u,w)$, and $w=T(w,u,v)$. Finally, we prove that $u=v$. By (3.3), for all $t>0$ we have

$$\begin{array}{rcl}{F}_{u,v}(\phi (t))& =& F_{T(v,u,w),T(u,v,w)}(\phi (t))\\ \ge & {[F_{Av,Au}(t)F_{Au,Av}(t)F_{Aw,Aw}(t)]}^{\frac{1}{3}}={[F_{u,v}(t)]}^{\frac{2}{3}},\end{array}$$

(3.21)

which implies that $F_{u,v}({\phi }^n(t))\ge {[F_{u,v}(t)]}^{{(\frac{2}{3})}^n}$. Using Lemma 2.2, we have $F_{u,v}(t)=1$ for all $t>0$, i.e., $u=v$. Similarly, we can show that $u=w$. Hence, there exists $u\in X$, such that $u=Au=T(u,u,u)$.

Finally, we show the uniqueness of the tripled common fixed point of T and A. Suppose that $u^{\prime }\in X$ is another tripled common fixed point of T and A, i.e., $u^{\prime }=A{u}^{\prime }=T(u^{\prime },u^{\prime },u^{\prime })$. By (3.3), for all $t>0$ we have

$$\begin{array}{rcl}{F}_{u,u^{\prime }}(\phi (t))& =& F_{T(u,u,u),T(u^{\prime },u^{\prime },u^{\prime })}(\phi (t))\\ \ge & {[F_{Au,A{u}^{\prime }}(t)F_{Au,A{u}^{\prime }}(t)F_{Au,A{u}^{\prime }}(t)]}^{\frac{1}{3}}\\ \ge & F_{Au,A{u}^{\prime }}(t)=F_{u,u^{\prime }}(t),\end{array}$$

(3.22)

which implies that $F_{u,u^{\prime }}({\phi }^n(t))\ge F_{u,u^{\prime }}(t)$ for all $t>0$. Using Lemma 2.2, we have $F_{u,u^{\prime }}(t)=1$ for all $t>0$, i.e., $u=u^{\prime }$. This completes the proof. □

Corollary 3.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type and $\mathrm{\Delta }\ge {\mathrm{\Delta }}_p$, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}{\phi }^n(t)<+\mathrm{\infty }$, for each $t>0$. Let $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(\phi (t))\ge {\left[\mathrm{\Delta }(F_{Ax,Ap}(t),F_{Ay,Aq}(t),F_{Az,Ar}(t))\right]}^{\frac{1}{3}}$$

(3.23)

for all $x,y,z,p,q,r\in X$ and $t>0$, where $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

Letting $A=I$ (I is the identity mapping) in Corollary 3.1, we can obtain the following corollary.

Corollary 3.2 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type and $\mathrm{\Delta }\ge {\mathrm{\Delta }}_p$, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$ and ${\sum }_{n=1}^{\mathrm{\infty }}{\phi }^n(t)<+\mathrm{\infty }$, for any $t>0$. Let $T:X\times X\times X\to X$ be a mapping satisfying

$$F_{T(x,y,z),T(p,q,r)}(\phi (t))\ge {\left[\mathrm{\Delta }(F_{x,p}(t),F_{y,q}(t),F_{z,r}(t))\right]}^{\frac{1}{3}}$$

for all $x,y,z,p,q,r\in X$ and $t>0$. Then T has a unique fixed point in X.

Letting $\phi (t)=\alpha t$ ($0<\alpha <1$) in Corollary 3.1, we can obtain the following corollary.

Corollary 3.3 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type and $\mathrm{\Delta }\ge {\mathrm{\Delta }}_p$, $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(\alpha t)\ge {\left[\mathrm{\Delta }(F_{Ax,Ap}(t),F_{Ay,Aq}(t),F_{Az,Ar}(t))\right]}^{\frac{1}{3}}$$

for all $x,y,z,p,q,r\in X$ and $t>0$, where $0<\alpha <1$, $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

Letting $A=I$ (I is the identity mapping) in Theorem 3.1, we can obtain the following corollary.

Corollary 3.4 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$, $\phi (t)<t$, and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for any $t>0$. Let $T:X\times X\times X\to X$ be a mapping satisfying

$$F_{T(x,y,z),T(p,q,r)}(\phi (t))\ge {[F_{x,p}(t)F_{y,q}(t)F_{z,r}(t)]}^{\frac{1}{3}}$$

for all $x,y,z,p,q,r\in X$ and $t>0$. Then T has a unique fixed point in X.

Letting $\phi (t)=\alpha t$ ($0<\alpha <1$) in Theorem 3.1, we can obtain the following corollary.

Corollary 3.5 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type, $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(\alpha t)\ge {[F_{Ax,Ap}(t)F_{Ay,Aq}(t)F_{Az,Ar}(t)]}^{\frac{1}{3}}$$

for all $x,y,z,p,q,r\in X$ and $t>0$, where $0<\alpha <1$, $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

From the proof of Theorem 3.1, we can similarly prove the following result.

Theorem 3.2 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$, $\phi (t)>t$, and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=+\mathrm{\infty }$ for any $t>0$. Let $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(t)\ge min\{F_{Ax,Ap}(\phi (t)),F_{Ay,Aq}(\phi (t)),F_{Az,Ar}(\phi (t))\}$$

(3.24)

for all $x,y,z,p,q,r\in X$ and $t>0$, where $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

Letting $A=I$ (I is the identity mapping) in Theorem 3.2, we can obtain the following corollary.

Corollary 3.6 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized Menger PM-space with Δ a t-norm of H-type, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$, $\phi (t)>t$, and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=+\mathrm{\infty }$ for any $t>0$. Let $T:X\times X\times X\to X$ be a mapping satisfying

$$F_{T(x,y,z),T(p,q,r)}(t)\ge min\{F_{x,p}(\phi (t)),F_{y,q}(\phi (t)),F_{z,r}(\phi (t))\}$$

for all $x,y,z,p,q,r\in X$ and $t>0$. Then T has a unique fixed point in X.

4 Tripled common fixed point results in generalized non-Archimedean PM-spaces

In this section, we will use the results in Section 3 to get some corresponding results in generalized non-Archimedean Menger spaces.

Lemma 4.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized non-Archimedean Menger PM-space, ${\{d_{\lambda }\}}_{\lambda \in (0,1]}$ be a family of pseudo-metrics on X defined by (2.1). If Δ is a t-norm of H-type, then for each $\lambda \in (0,1]$, there exists $\mu \in (0,\lambda ]$, such that for all $m\in Z^{+}$ and $x_0,x_1,\dots ,x_m\in X$,

$$d_{\lambda }(x_0,x_m)\le \underset{0\le i\le m-1}{max}{d}_{\mu }(x_i,x_{i+1}).$$

Proof Since Δ is a t-norm of H-type, ${\{{\mathrm{\Delta }}^n(t)\}}_{n=1}^{\mathrm{\infty }}$ is equicontinuous at $t=1$, and so for each $\lambda \in (0,1]$, there exists $\mu \in (0,\lambda ]$ such that

$${\mathrm{\Delta }}^n(1-\mu )>1-\lambda ,\mathrm{\forall }n\in Z^{+}.$$

(4.1)

For any given $m\in Z^{+}$, and $x_0,x_1,\dots ,x_m\in X$, write $d_{\mu }(x_i,x_{i+1})=t_i$ ($i=0,1,\dots ,m-1$). For any $\epsilon >0$, we have $F_{x_i,x_{i+1}}(t_i+\epsilon )>1-\mu$. It follows from (4.1) and (GPM-5) that

$$\begin{array}{c}{F}_{x_0,x_m}(\underset{0\le i\le m-1}{max}{t}_i+\epsilon )\hfill \\ \ge \mathrm{\Delta }(F_{x_0,x_1}(t_0+\epsilon ),F_{x_1,x_2}(t_1+\epsilon ),\mathrm{\Delta }(F_{x_2,x_3}(t_2+\epsilon ),F_{x_3,x_4}(t_3+\epsilon ),\hfill \\ \mathrm{\Delta }(\dots ,\mathrm{\Delta }(F_{x_{m-3},x_{m-2}}(t_{m-3}+\epsilon ),F_{x_{m-2},x_{m-1}}(t_{m-2}+\epsilon ),F_{x_{m-1},x_m}(t_{m-1}+\epsilon ))\cdots )\left)\right)\hfill \\ \ge {\mathrm{\Delta }}^m(1-\mu )>1-\lambda .\hfill \end{array}$$

By Lemma 2.1, we have $d_{\lambda }(x_0,x_m)<{max}_{0\le i\le m-1}{t}_i+\epsilon$. By the arbitrariness of ε, we have

$$d_{\lambda }(x_0,x_m)\le \underset{0\le i\le m-1}{max}{t}_i=\underset{0\le i\le m-1}{max}{d}_{\mu }(x_i,x_{i+1}).$$

This completes the proof. □

Theorem 4.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized non-Archimedean Menger PM-space such that ${sup}_{0<t<1}\mathrm{\Delta }(t,t,t)=1$ and $\mathrm{\Delta }\ge {\mathrm{\Delta }}_p$, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$ and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=+\mathrm{\infty }$ for any $t>0$. Let $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(t)\ge {\left[\mathrm{\Delta }(F_{Ax,Ap}(\phi (t)),F_{Ay,Aq}(\phi (t)),F_{Az,Ar}(\phi (t)))\right]}^{\frac{1}{3}}$$

(4.2)

for all $x,y,z,p,q,r\in X$ and $t>0$, where $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Suppose that there exist $b,c,d\in X$, such that for any $t>0$,

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\prod _{i=n}^{\mathrm{\infty }}{F}_{Ab,T(b,c,d)}({\phi }^i(t))=1,\underset{n\to \mathrm{\infty }}{lim}\prod _{i=n}^{\mathrm{\infty }}{F}_{Ac,T(c,d,b)}({\phi }^i(t))=1,\\ \underset{n\to \mathrm{\infty }}{lim}\prod _{i=n}^{\mathrm{\infty }}{F}_{Ad,T(d,b,c)}({\phi }^i(t))=1.\end{array}$$

(4.3)

Then T and A have a unique tripled common fixed point in X.

Proof Take $x_0=b$, $y_0=c$, and $z_0=d$. By Lemma 2.3, we can construct three sequences ${\{x_n\}}_{n=0}^{\mathrm{\infty }}$, ${\{y_n\}}_{n=0}^{\mathrm{\infty }}$, and ${\{z_n\}}_{n=0}^{\mathrm{\infty }}$ in X, such that $A{x}_{n+1}=T(x_n,y_n,z_n)$, $A{y}_{n+1}=T(y_n,x_n,z_n)$, and $A{z}_{n+1}=T(z_n,x_n,y_n)$.

From (4.2), for all $t>0$, we have

$$\begin{array}{c}{F}_{A{x}_n,A{x}_{n+1}}(t)=F_{T(x_{n-1},y_{n-1},z_{n-1}),T(x_n,y_n,z_n)}(t)\hfill \\ \phantom{F_{A{x}_n,A{x}_{n+1}}(t)}\ge {\left[\mathrm{\Delta }(F_{A{x}_{n-1},A{x}_n,}(\phi (t)),F_{A{y}_{n-1},A{y}_n}(\phi (t)),F_{A{z}_{n-1},A{z}_n}(\phi (t)))\right]}^{\frac{1}{3}},\hfill \end{array}$$

(4.4)

$$\begin{array}{c}{F}_{A{y}_n,A{y}_{n+1}}(t)=F_{T(y_{n-1},x_{n-1},z_{n-1}),T(y_n,x_n,z_n)}(t)\hfill \\ \phantom{F_{A{y}_n,A{y}_{n+1}}(t)}\ge {\left[\mathrm{\Delta }(F_{A{y}_{n-1},A{y}_n}(\phi (t)),F_{A{x}_{n-1},A{x}_n}(\phi (t)),F_{A{z}_{n-1},A{z}_n}(\phi (t)))\right]}^{\frac{1}{3}}\hfill \end{array}$$

(4.5)

and

$$\begin{array}{rcl}{F}_{A{z}_n,A{z}_{n+1}}(t)& =& F_{T(z_{n-1},x_{n-1},y_{n-1}),T(z_n,x_n,y_n)}(t)\\ \ge & {\left[\mathrm{\Delta }(F_{A{z}_{n-1},A{z}_n}(\phi (t)),F_{A{x}_{n-1},A{x}_n}(\phi (t)),F_{A{y}_{n-1},A{y}_n}(\phi (t)))\right]}^{\frac{1}{3}}.\end{array}$$

(4.6)

Denote $G_n(t)={[\mathrm{\Delta }(F_{A{x}_{n-1},A{x}_n}(t),F_{A{y}_{n-1},A{y}_n}(t),F_{A{z}_{n-1},A{z}_n}(t))]}^{\frac{1}{3}}$. From (4.4)-(4.6), and $\mathrm{\Delta }\ge {\mathrm{\Delta }}_p$, we obtain

$$\begin{array}{rcl}{G}_{n+1}(t)& \ge & {\left[\mathrm{\Delta }(G_n(\phi (t)),G_n(\phi (t)),G_n(\phi (t)))\right]}^{\frac{1}{3}}\\ \ge & {\left[G_n(\phi (t))G_n(\phi (t))G_n(\phi (t))\right]}^{\frac{1}{3}}=G_n(\phi (t)),\end{array}$$

which implies that

$$G_{n+1}(t)\ge G_n(\phi (t))\ge G_{n-1}({\phi }^2(t))\ge \cdots \ge G_1({\phi }^n(t)).$$

(4.7)

Thus, by (4.4)-(4.7), we have

$$\begin{array}{r}{F}_{A{x}_n,A{x}_{n+1}}(t)\ge G_1({\phi }^n(t)),F_{A{y}_n,A{y}_{n+1}}(t)\ge G_1({\phi }^n(t)),\\ F_{A{z}_n,A{z}_{n+1}}(t)\ge G_1({\phi }^n(t)).\end{array}$$

(4.8)

Suppose that $\epsilon >0$ and $\lambda \in (0,1]$. By (4.3), there exists $N\in Z^{+}$, such that

$$\prod _{i=n}^{n+k-1}{F}_{A{x}_0,A{x}_1}\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)>1-\lambda ,\prod _{i=n}^{n+k-1}{F}_{A{y}_0,A{y}_1}\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)>1-\lambda$$

and

$$\prod _{i=n}^{n+k-1}{F}_{A{z}_0,A{z}_1}\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)>1-\lambda$$

for all $n\ge N$ and $k\in Z^{+}$.

Hence, it follows from (4.8) and (GPM-4) that

$$\begin{array}{c}{F}_{A{x}_n,A{x}_{n+k}}(\epsilon )\hfill \\ \ge \mathrm{\Delta }(F_{A{x}_n,A{x}_{n+1}}\left(\frac{\epsilon }{k}\right),F_{A{x}_{n+1},A{x}_{n+2}}\left(\frac{\epsilon }{k}\right),\mathrm{\Delta }(F_{A{x}_{n+2},A{x}_{n+3}}\left(\frac{\epsilon }{k}\right),F_{A{x}_{n+3},A{x}_{n+4}}\left(\frac{\epsilon }{k}\right),\hfill \\ \mathrm{\Delta }(\dots ,\mathrm{\Delta }(F_{A{x}_{n+k-3},A{x}_{n+k-2}}\left(\frac{\epsilon }{k}\right),F_{A{x}_{n+k-2},A{x}_{n+k-1}}\left(\frac{\epsilon }{k}\right),F_{A{x}_{n+k-1},A{x}_{n+k}}\left(\frac{\epsilon }{k}\right))\cdots )\left)\right)\hfill \\ \ge \mathrm{\Delta }(G_1\left({\phi }^n\left(\frac{\epsilon }{k}\right)\right),G_1\left({\phi }^{n+1}\left(\frac{\epsilon }{k}\right)\right),\mathrm{\Delta }(G_1\left({\phi }^{n+2}\left(\frac{\epsilon }{k}\right)\right),G_1\left({\phi }^{n+3}\left(\frac{\epsilon }{k}\right)\right),\hfill \\ \mathrm{\Delta }(\dots ,\mathrm{\Delta }(G_1\left({\phi }^{n+k-3}\left(\frac{\epsilon }{k}\right)\right),G_1\left({\phi }^{n+k-2}\left(\frac{\epsilon }{k}\right)\right),G_1\left({\phi }^{n+k-1}\left(\frac{\epsilon }{k}\right)\right))\cdots )\left)\right)\hfill \\ \ge \prod _{i=n}^{n+k-1}{G}_1\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)\hfill \\ \ge \prod _{i=n}^{n+k-1}{\left[F_{A{x}_0,A{x}_1}\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)F_{A{y}_0,A{y}_1}\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)F_{A{z}_0,A{z}_1}\left({\phi }^i\left(\frac{\epsilon }{k}\right)\right)\right]}^{\frac{1}{3}}\hfill \\ >1-\lambda .\hfill \end{array}$$

(4.9)

This shows that $\{A{x}_n\}$ is a Cauchy sequence. Similarly, we can show that $\{A{y}_n\}$ and $\{A{z}_n\}$ are Cauchy sequences.

Since $(X,\mathcal{F},\mathrm{\Delta })$ is complete, there exist $u,v,w\in X$, such that ${lim}_{n\to \mathrm{\infty }}A{x}_n=u$, ${lim}_{n\to \mathrm{\infty }}A{y}_n=v$, and ${lim}_{n\to \mathrm{\infty }}A{z}_n=w$. By the continuity of A, we have

$$\underset{n\to \mathrm{\infty }}{lim}AA{x}_n=Au,\underset{n\to \mathrm{\infty }}{lim}AA{y}_n=Av,\underset{n\to \mathrm{\infty }}{lim}AA{z}_n=Aw.$$

(4.10)

From (4.2) and the commutativity of A with T, we have

$$\begin{array}{rcl}{F}_{AA{x}_{n+1},T(u,v,w)}(t)& =& F_{AT(x_n,y_n,z_n),T(u,v,w)}(t)=F_{T(A{x}_n,A{y}_n,A{z}_n),T(u,v,w)}(t)\\ \ge & {\left[\mathrm{\Delta }(F_{AA{x}_n,Au}(\phi (t)),F_{AA{y}_n,Av}(\phi (t)),F_{AA{z}_n,Aw}(\phi (t)))\right]}^{\frac{1}{3}}\\ \ge & {\left[F_{AA{x}_n,Au}(\phi (t))F_{AA{y}_n,Av}(\phi (t))F_{AA{z}_n,Aw}(\phi (t))\right]}^{\frac{1}{3}}.\end{array}$$

(4.11)

Letting $n\to \mathrm{\infty }$ in (4.11), we have ${lim}_{n\to \mathrm{\infty }}AA{x}_n=T(u,v,w)$. Hence, $T(u,v,w)=Au$. Similarly, we have $T(v,u,w)=Av$ and $T(w,u,v)=Aw$.

Next we claim that $Au=v$, $Av=u$, and $Aw=w$. In fact, by (4.2), we have

$$\begin{array}{c}{F}_{Au,A{y}_n}(t)=F_{T(u,v,w),T(y_{n-1},x_{n-1},z_{n-1})}(t)\hfill \\ \phantom{F_{Au,A{y}_n}(t)}\ge {\left[\mathrm{\Delta }(F_{Au,A{y}_{n-1}}(\phi (t)),F_{Av,A{x}_{n-1}}(\phi (t)),F_{Aw,A{z}_{n-1}}(\phi (t)))\right]}^{\frac{1}{3}}\hfill \\ \phantom{F_{Au,A{y}_n}(t)}\ge {\left[F_{Au,A{y}_{n-1}}(\phi (t))F_{Av,A{x}_{n-1}}(\phi (t))F_{Aw,A{z}_{n-1}}(\phi (t))\right]}^{\frac{1}{3}},\hfill \end{array}$$

(4.12)

$$F_{Av,A{x}_n}(t)\ge {\left[F_{Av,A{x}_{n-1}}(\phi (t))F_{Au,A{y}_{n-1}}(\phi (t))F_{Aw,A{z}_{n-1}}(\phi (t))\right]}^{\frac{1}{3}}$$

(4.13)

and

$$F_{Aw,A{z}_n}(t)\ge {\left[F_{Aw,A{z}_{n-1}}(\phi (t))F_{Au,A{x}_{n-1}}(\phi (t))F_{Av,A{y}_{n-1}}(\phi (t))\right]}^{\frac{1}{3}}.$$

(4.14)

Denote $Q_n(t)=F_{Au,A{y}_n}(t)F_{Av,A{x}_n}(t)F_{Aw,A{z}_n}(t)$. It follows from (4.12)-(4.14) that

$$Q_n(t)\ge Q_{n-1}(\phi (t))\ge \cdots \ge Q_0({\phi }^n(t)),$$

and thus

$$\begin{array}{r}{F}_{Au,A{y}_n}(t)\ge {\left[Q_0({\phi }^n(t))\right]}^{\frac{1}{3}},F_{Av,A{x}_n}(t)\ge {\left[Q_0({\phi }^n(t))\right]}^{\frac{1}{3}},\\ F_{Aw,A{z}_n}(t)\ge {\left[Q_0({\phi }^n(t))\right]}^{\frac{1}{3}}.\end{array}$$

(4.15)

Since ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=+\mathrm{\infty }$, we have

$${\left[Q_0({\phi }^n(t))\right]}^{\frac{1}{3}}={\left[F_{Au,A{y}_0}({\phi }^n(t))F_{Av,A{x}_0}({\phi }^n(t))F_{Aw,A{z}_0}({\phi }^n(t))\right]}^{\frac{1}{3}}\to 1,$$

as $n\to \mathrm{\infty }$. From (4.15), we have

$$\underset{n\to \mathrm{\infty }}{lim}A{x}_n=Av,\underset{n\to \mathrm{\infty }}{lim}A{y}_n=Au,\underset{n\to \mathrm{\infty }}{lim}A{z}_n=Aw.$$

(4.16)

Hence, $Au=v$, $Av=u$, and $Aw=w$, i.e., $v=T(u,v,w)$, $u=T(v,u,w)$, and $w=T(w,u,v)$. Now we prove that $u=v$. In fact, by (4.2), we have

$$\begin{array}{rcl}{F}_{u,v}(t)& =& F_{T(v,u,w),T(u,v,w)}(t)\\ \ge & {\left[\mathrm{\Delta }(F_{Av,Au}(\phi (t)),F_{Au,Av}(\phi (t)),F_{Aw,Aw}(\phi (t)))\right]}^{\frac{1}{3}}\\ \ge & {\left[F_{u,v}(\phi (t))\right]}^{\frac{2}{3}},\end{array}$$

(4.17)

which implies that $F_{u,v}(t)\ge {[F_{u,v}({\phi }^n(t))]}^{{(\frac{2}{3})}^n}$. Letting $n\to \mathrm{\infty }$, we have $F_{u,v}(t)=1$ for all $t>0$, i.e., $u=v$. Similarly, we can show that $v=w$. Hence, there exists $u\in X$, such that $u=Au=T(u,u,u)$.

Finally, we show the uniqueness of the tripled common fixed point of T and A. Suppose that $u^{\prime }\in X$ is another tripled common fixed point of T and A, i.e., $u^{\prime }=A{u}^{\prime }=T(u^{\prime },u^{\prime },u^{\prime })$. By (4.2), for all $t>0$, we have

$$\begin{array}{rcl}{F}_{u,u^{\prime }}(t)& =& F_{T(u,u,u),T(u^{\prime },u^{\prime },u^{\prime })}(t)\\ \ge & {\left[\mathrm{\Delta }(F_{Au,A{u}^{\prime }}(\phi (t)),F_{Au,A{u}^{\prime }}(\phi (t)),F_{Au,A{u}^{\prime }}(\phi (t)))\right]}^{\frac{1}{3}}\\ \ge & F_{Au,A{u}^{\prime }}(\phi (t))=F_{u,u^{\prime }}(\phi (t)),\end{array}$$

(4.18)

which implies that $F_{u,u^{\prime }}(t)\ge F_{u,u^{\prime }}({\phi }^n(t))$ for all $t>0$. Letting $n\to \mathrm{\infty }$, we have $F_{u,u^{\prime }}(t)=1$ for all $t>0$, i.e., $u=u^{\prime }$. This completes the proof. □

Letting $A=I$ (I is the identity mapping) in Theorem 4.1, we can obtain the following corollary.

Corollary 4.1 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized non-Archimedean Menger PM-space such that ${sup}_{0<t<1}\mathrm{\Delta }(t,t,t)=1$ and $\mathrm{\Delta }\ge {\mathrm{\Delta }}_p$, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$ and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=+\mathrm{\infty }$ for any $t>0$. Let $T:X\times X\times X\to X$ be a mapping satisfying

$$F_{T(x,y,z),T(p,q,r)}(t)\ge {\left[\mathrm{\Delta }(F_{x,p}(\phi (t)),F_{y,q}(\phi (t)),F_{z,r}(\phi (t)))\right]}^{\frac{1}{3}}$$

for all $x,y,z,p,q,r\in X$ and $t>0$. Suppose that there exist $b,c,d\in X$, such that for any $t>0$,

$$\begin{array}{r}\underset{n\to \mathrm{\infty }}{lim}\prod _{i=n}^{\mathrm{\infty }}{F}_{b,T(b,c,d)}({\phi }^i(t))=1,\underset{n\to \mathrm{\infty }}{lim}\prod _{i=n}^{\mathrm{\infty }}{F}_{c,T(c,d,b)}({\phi }^i(t))=1,\\ \underset{n\to \mathrm{\infty }}{lim}\prod _{i=n}^{\mathrm{\infty }}{F}_{d,T(d,b,c)}({\phi }^i(t))=1.\end{array}$$

(4.19)

Then T has a unique fixed point in X.

In a similar way, we can obtain the following result.

Theorem 4.2 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized non-Archimedean Menger PM-space such that Δ is a t-norm of H-type, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$ and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for any $t>0$. Let $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(\phi (t))\ge min\{F_{Ax,Ap}(t),F_{Ay,Aq}(t),F_{Az,Ar}(t)\}$$

(4.20)

for all $x,y,z,p,q,r\in X$ and $t>0$, where $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

Letting $A=I$ (I is the identity mapping) in Theorem 4.2, we can obtain the following corollary.

Corollary 4.2 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized non-Archimedean Menger PM-space such that Δ is a t-norm of H-type, $\phi :R^{+}\to R^{+}$ be a gauge function such that ${\phi }^{-1}(\{0\})=\{0\}$ and ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for any $t>0$. Let $T:X\times X\times X\to X$ be a mapping satisfying

$$F_{T(x,y,z),T(p,q,r)}(\phi (t))\ge min\{F_{x,p}(t),F_{y,q}(t),F_{z,r}(t)\}$$

(4.21)

for all $x,y,z,p,q,r\in X$ and $t>0$. Then T has a unique fixed point in X.

Letting $\phi (t)=\alpha t$ ($0<\alpha <1$) in Theorem 4.2, we can obtain the following corollary.

Corollary 4.3 Let $(X,\mathcal{F},\mathrm{\Delta })$ be a complete generalized non-Archimedean Menger PM-space such that Δ is a t-norm of H-type. Let $T:X\times X\times X\to X$ and $A:X\to X$ be two mappings satisfying

$$F_{T(x,y,z),T(p,q,r)}(\alpha t)\ge min\{F_{Ax,Ap}(t),F_{Ay,Aq}(t),F_{Az,Ar}(t)\}$$

for all $x,y,z,p,q,r\in X$ and $t>0$, where $0<\alpha <1$, $T(X\times X\times X)\subset A(X)$, A is continuous and commutative with T. Then T and A have a unique tripled common fixed point in X.

Remark 4.1 If $(X,\mathcal{F},\mathrm{\Delta })$ is a generalized non-Archimedean Menger PM-space, then the hypotheses concerning gauge functions can be weakened. Let us note that in Theorem 4.2 the gauge function only satisfies ${lim}_{n\to \mathrm{\infty }}{\phi }^n(t)=0$ for all $t>0$, and it does not necessarily satisfy $\phi (t)<t$ for all $t>0$.

5 An application

In this section, we shall provide an example to show the validity of the main results of this paper.

Example 5.1 Suppose that $X=[-1,1]\subset R$, $\mathrm{\Delta }={\mathrm{\Delta }}_m$. Then ${\mathrm{\Delta }}_m$ is a t-norm of H-type and ${\mathrm{\Delta }}_m\ge {\mathrm{\Delta }}_p$. Define $\mathcal{F}:X\times X\to \mathcal{D}$ by

$$\mathcal{F}(x,y)(t)=F_{x,y}(t)=\{\begin{array}{ll}{e}^{-\frac{|x-y|}{t}},& t>0,x,y\in X,\\ 0,& t\le 0,x,y\in X.\end{array}$$

We claim that $(X,\mathcal{F},{\mathrm{\Delta }}_m)$ is a generalized Menger PM-space. In fact, it is easy to verify (GPM-1), (GPM-2), and (GPM-3). Assume that for any $s,t,r>0$ and $x,y,z,w\in X$,

$${\mathrm{\Delta }}_m(F_{x,z}(t),F_{z,w}(s),F_{w,y}(r))=min\{e^{-\frac{|x-z|}{t}},e^{-\frac{|z-w|}{s}},e^{-\frac{|w-y|}{r}}\}=e^{-\frac{|x-z|}{t}}.$$

Then we have $t|z-w|\le s|x-z|$, $t|w-y|\le r|x-z|$, and so $\frac{t+s+r}{t}|x-z|=|x-z|+\frac{s}{t}|x-z|+\frac{r}{t}|x-z|\ge |x-z|+|z-w|+|w-y|\ge |x-y|$. It follows that

$$F_{x,y}(t+s+r)=e^{-\frac{|x-y|}{t+s+r}}\ge e^{-\frac{|x-z|}{t}}={\mathrm{\Delta }}_m(F_{x,z}(t),F_{z,w}(s),F_{w,y}(r)).$$

Hence (GPM-4) holds. It is obvious that $(X,\mathcal{F},{\mathrm{\Delta }}_m)$ is complete. Suppose that $\phi (t)=\frac{t}{3}$. For $x,y,z\in X$, define $T:X\times X\times X\to X$ as follows:

$$T(x,y,z)=\frac{1}{81}-\frac{x^2}{81}-\frac{y^2}{81}-\frac{|z|}{27}.$$

Then for each $t>0$ and $x,y,z,p,q,r\in X$, we have

$$\begin{array}{rcl}|p^2-x^2+q^2-y^2+3(|r|-|z|)|& \le & |p-x|(|p|+|x|)+|q-y|(|q|+|y|)+3|r-z|\\ \le & 9max\{|x-p|,|y-q|,|z-r|\},\end{array}$$

and so

$$\begin{array}{rcl}{F}_{T(x,y,z),T(p,q,r)}(\phi (t))& =& F_{T(x,y,z),T(p,q,r)}\left(\frac{t}{3}\right)\\ =& e^{-\frac{|p^2-x^2+q^2-y^2+3(|r|-|z|)|}{27t}}\\ \ge & min\{e^{-\frac{|x-p|}{3t}},e^{-\frac{|y-q|}{3t}},e^{-\frac{|z-r|}{3t}}\}\\ =& {(min\{e^{-\frac{|x-p|}{t}},e^{-\frac{|y-q|}{t}},e^{-\frac{|z-r|}{t}}\})}^{\frac{1}{3}}\\ =& {\left[{\mathrm{\Delta }}_m(F_{x,p}(t),F_{y,q}(t),F_{z,r}(t))\right]}^{\frac{1}{3}}.\end{array}$$

Thus, all the conditions of Corollary 3.2 are satisfied. Therefore, T has a unique fixed point in X.