Fixed point results for $(\alpha \psi ,\beta \phi )$-contractive mappings for a generalized altering distance

Abstract

In this manuscript, we extend the concept of altering distance, and we introduce a new notion of $(\alpha \psi ,\beta \phi )$-contractive mappings. We prove the existence and uniqueness of a fixed point for such mapping in the context of complete metric space. The presented theorems of this paper generalize, extend and improve some remarkable existing results in the literature. We also present several applications and consequences of our results.

1 Introduction and preliminaries

Fixed point theory is one of the core research areas in nonlinear functional analysis since it has a broad range of application potential in various fields such as engineering, economics, computer science, and many others. Banach contraction mapping principle [1] is considered to be the initial and fundamental result in this direction. Fixed point theory and hence the Banach contraction mapping principle have evidently attracted many prominent mathematicians due to their wide application potential. Consequently, the number of publications in this theory increases rapidly; we refer the reader to [2–19].

In this paper, by introducing a new notion of $(\alpha \psi ,\beta \phi )$-contractive mappings, we aim to establish a more general result to collect/combine a number of existing results in the literature.

We start by recalling the notion of altering distance function introduced by Khan et al. [12] as follows.

Definition 1.1 A function $\psi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ is called an altering distance function if the following properties are satisfied:

• $\psi (t)$ is continuous and nondecreasing.

• $\psi (t)=0$ if and only if $t=0$.

Now, we present a definition, which will be useful later.

Definition 1.2 Let X be a set, and let ℛ be a binary relation on X. We say that $T:X\to X$ is an ℛ-preserving mapping if

$$x,y\in X:x\mathcal{R}y⟹Tx\mathcal{R}Ty.$$

In the sequel, let ℕ denote the set of all non-negative integers, let ℝ denote the set of all real numbers.

Example 1.1 Let $X=\mathbb{R}$ and a function $T:X\to X$ defined as $Tx=e^x$.

Define $\alpha (x,y):X\times X\to [0,\mathrm{\infty })$ and $\beta (x,y):X\times X\to [0,\mathrm{\infty })$ by

$$\alpha (x,y)=\{\begin{array}{cc}1\hfill & \text{if }x\le y,\hfill \\ 2\hfill & \text{otherwise};\hfill \end{array}\beta (x,y)=\{\begin{array}{cc}1\hfill & \text{if }x\le y,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$

Define the first binary relation ${\mathcal{R}}_1$ by $x{\mathcal{R}}_{1}y$ if and only if $\alpha (x,y)\le 1$, and define the second binary relation by $x{\mathcal{R}}_{2}y$ if and only if $\beta (x,y)\ge 1$. Then, we easily obtain that T is simultaneously ${\mathcal{R}}_1$-preserving and ${\mathcal{R}}_2$-preserving.

Definition 1.3 Let $N\in \mathbb{N}$. We say that ℛ is N-transitive on X if

$$x_0,x_1,\dots ,x_{N+1}\in X:x_i\mathcal{R}{x}_{i+1}\text{for all }i\in \{0,1,\dots ,N\}⟹x_0\mathcal{R}{x}_{N+1}.$$

The following remark is a consequence of the previous definition.

Remark 1.1 Let $N\in \mathbb{N}$. We have:

• (i) If ℛ is transitive, then it is N-transitive for all $N\in \mathbb{N}$.

• (ii) If ℛ is N-transitive, then it is kN-transitive for all $k\in \mathbb{N}$.

Definition 1.4 Let $(X,d)$ be a metric space and ${\mathcal{R}}_1$, ${\mathcal{R}}_2$ two binary relations on X. We say that $(X,d)$ is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-regular if for every sequence $\{x_n\}$ in X such that $x_n\to x\in X$ as $n\to +\mathrm{\infty }$, and

$$x_n{\mathcal{R}}_1{x}_{n+1},x_n{\mathcal{R}}_2{x}_{n+1}\text{for all }n\in \mathbb{N},$$

there exists a subsequence $\{x_{n(k)}\}$ such that

$$x_{n(k)}{\mathcal{R}}_{1}x,x_{n(k)}{\mathcal{R}}_{2}x\text{for all }k\in \mathbb{N}.$$

Definition 1.5 We say that a subset D of X is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-directed if for all $x,y\in D$, there exists $z\in X$ such that

$$(x{\mathcal{R}}_{1}z)\wedge (y{\mathcal{R}}_{1}z)\text{and}(x{\mathcal{R}}_{2}z)\wedge (y{\mathcal{R}}_{2}z).$$

2 Main results

Before we start the introduction of the concept $(\alpha \psi ,\beta \phi )$-contractive mappings, we introduce the notion of a pair of generalized altering distance as follows:

Definition 2.1 We say that the pair of functions $(\psi ,\phi )$ is a pair of generalized altering distance where $\psi ,\phi :[0,+\mathrm{\infty })\to [0,+\mathrm{\infty })$ if the following hypotheses hold:

• (a1) ψ is continuous;

• (a2) ψ is nondecreasing;

• (a3) ${lim}_{n\to \mathrm{\infty }}\phi (t_n)=0⟹{lim}_{n\to \mathrm{\infty }}{t}_n=0$.

The condition (a3) was introduced by Popescu in [15] and Moradi and Farajzadeh in [14].

Definition 2.2 Let $(X,d)$ be a metric space, and let $T:X\to X$ be a given mapping. We say that T is $(\alpha \psi ,\beta \phi )$-contractive mappings if there exists a pair of generalized distance $(\psi ,\phi )$ such that

$$\psi (d(Tx,Ty))\le \alpha (x,y)\psi (d(x,y))-\beta (x,y)\phi (d(x,y))\text{for all }x,y\in X,$$

(1)

where $\alpha ,\beta :X\times X\to [0,+\mathrm{\infty })$.

In the sequel, the binary relations ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ are defined as following.

Definition 2.3 Let X be a set and $\alpha ,\beta :X\times X\to [0,+\mathrm{\infty })$ are two mappings. We define two binary relations ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ on X by

$$x,y\in X:x{\mathcal{R}}_{1}y⟺\alpha (x,y)\le 1$$

and

$$x,y\in X:x{\mathcal{R}}_{2}y⟺\beta (x,y)\ge 1.$$

Now we are ready to state our first main result.

Theorem 2.1 Let $(X,d)$ be a complete metric space, $N\in \mathbb{N}\mathrm{\setminus }\{0\}$, and let $T:X\to X$ be an $(\alpha \psi ,\beta \phi )$-contractive mapping satisfying the following conditions:

• (i) ${\mathcal{R}}_i$ is N-transitive for $i=1,2$;

• (ii) T is ${\mathcal{R}}_i$-preserving for $i=1,2$;

• (iii) there exists $x_0\in X$ such that $x_0{\mathcal{R}}_{i}T{x}_0$ for $i=1,2$;

• (iv) T is continuous.

Then, T has a fixed point, that is, there exists $x^{\ast }\in X$ such that $T{x}^{\ast }=x^{\ast }$.

Proof Let $x_0\in X$ such that $x_0{\mathcal{R}}_{i}T{x}_0$ for $i=1,2$. Define the sequence $\{x_n\}$ in X by

$$x_{n+1}=T{x}_n\text{for all }n\ge 0.$$

If $x_n=x_{n+1}$ for some $n\ge 0$, then $x^{\ast }=x_n$ is a fixed point T. Assume that $x_n\ne x_{n+1}$ for all $n\ge 0$. From (ii) and (iii), we have

$$x_0{\mathcal{R}}_{1}T{x}_0⟹\alpha (x_0,T{x}_0)=\alpha (x_0,x_1)\le 1⟹\alpha (T{x}_0,T{x}_1)=\alpha (x_1,x_2)\le 1.$$

Similarly, we have

$$x_0{\mathcal{R}}_{2}T{x}_0⟹\beta (x_0,T{x}_0)=\beta (x_0,x_1)\ge 1⟹\beta (T{x}_0,T{x}_1)=\beta (x_1,x_2)\ge 1.$$

By induction, from (ii) it follows that

$$\alpha (x_n,x_{n+1})\le 1\text{for all }n\ge 0,$$

(2)

and, similarly, we have

$$\beta (x_n,x_{n+1})\ge 1\text{for all }n\ge 0.$$

(3)

Substituting $x=x_n$ and $y=x_{n+1}$ in (1), we obtain

$$\psi (d(T{x}_n,T{x}_{n+1}))\le \alpha (x_n,x_{n+1})\psi (d(x_n,x_{n+1}))-\beta (x_n,x_{n+1})\phi (d(x_n,x_{n+1})).$$

So, by (2) and (3) it follows that

$$\psi (d(x_{n+1},x_{n+2}))\le \psi (d(x_n,x_{n+1}))-\phi (d(x_n,x_{n+1})).$$

(4)

Using the monotone property of the ψ-function, we get

$$d(x_{n+1},x_{n+2})\le d(x_n,x_{n+1}).$$

It follows that $\{d(x_n,x_{n+1})\}$ is monotone decreasing, and, consequently, there exists $r\ge 0$ such that

$$d(x_n,x_{n+1})\to r\text{as }n\to \mathrm{\infty }.$$

Letting $n\to +\mathrm{\infty }$ in (4), we obtain

$$\psi (r)\le \psi (r)-\underset{n\to \mathrm{\infty }}{lim}\phi (d(x_n,x_{n+1})),$$

which implies that ${lim}_{n\to \mathrm{\infty }}\phi (d(x_n,x_{n+1}))=0$, then by (a3) we get

$$d(x_n,x_{n+1})\to 0\text{as }n\to \mathrm{\infty }.$$

(5)

On the other hand, by (2) and (i), we obtain

$$\alpha (x_m,x_{m+kN+1})\le 1\text{for all }m,k\ge 0.$$

(6)

Similarly, by (3) and (i), we get

$$\beta (x_m,x_{m+kN+1})\ge 1\text{for all }m,k\ge 0.$$

(7)

Now, for some $m,k\ge 0$, substituting $x=x_m$ and $y=x_{m^{\prime }}$ in (1), where $m^{\prime }:=m+kN+1$, we get

$$\psi (d(T{x}_m,T{x}_{m^{\prime }}))\le \alpha (x_m,x_{m^{\prime }})\psi (d(x_m,x_{m^{\prime }}))-\beta (x_m,x_{m^{\prime }})\phi (d(x_m,x_{m^{\prime }})).$$

So, by (6) and (7), we have

$$\psi (d(x_{m+1},x_{m^{\prime }+1}))\le \psi (d(x_m,x_{m^{\prime }}))-\phi (d(x_m,x_{m^{\prime }})).$$

(8)

Using the monotone property of the ψ-function, we get

$$d(x_{m+1},x_{m^{\prime }+1})\le d(x_m,x_{m^{\prime }}).$$

It follows that $\{d(x_m,x_{m^{\prime }})\}$ is monotone decreasing and consequently, there exists $s\ge 0$ such that

$$d(x_m,x_{m^{\prime }})\to s\text{as }m\to \mathrm{\infty }.$$

Letting $m\to +\mathrm{\infty }$, we obtain

$$\psi (s)\le \psi (s)-\underset{m\to +\mathrm{\infty }}{lim}\phi (d(x_m,x_{m^{\prime }})),$$

which implies that ${lim}_{m\to +\mathrm{\infty }}\phi (d(x_m,x_{m^{\prime }}))=0$, then by (a3) we get

$$d(x_m,x_{m^{\prime }})\to 0\text{as }m\to \mathrm{\infty }.$$

(9)

Next, we claim that $\{x_n\}$ is a Cauchy sequence. Suppose if we obtain a contradiction, that T is not a Cauchy sequence. Then, there exists $\epsilon >0$, for which we can find subsequences $\{x_{m(k)}\}$ and $\{x_{n(k)}\}$ of $\{x_n\}$ with $n(k)>m(k)>k$ such that

$$d(x_{m(k)},x_{n(k)})\ge \epsilon .$$

(10)

Further, corresponding to $m(k)$, we can choose $n(k)$ in such a way that it is the smallest integer with $n(k)>m(k)$ and satisfying (10). Then

$$d(x_{m(k)},x_{n(k)-1})<\epsilon .$$

(11)

Then we have

$$\epsilon \le d(x_{m(k)},x_{n(k)})\le d(x_{m(k)},x_{n(k)-1})+d(x_{n(k)-1},x_{n(k)})<\epsilon +d(x_{n(k)-1},x_{n(k)}).$$

(12)

Letting $k\to \mathrm{\infty }$ and using (5),

$$\underset{k\to \mathrm{\infty }}{lim}d(x_{m(k)},x_{n(k)})=\epsilon .$$

(13)

Furthermore, for each $k\ge 0$, there exist ${\mu }_k,{\eta }_k>0$ such that $m^{\prime }(k):=m(k)+N{\mu }_k+1=n(k)+{\eta }_k$. Hence, by (11) we have

$$\epsilon \le d(x_{m(k)},x_{m^{\prime }(k)})\le d(x_{m(k)},x_{n(k)-1})+\sum _{i=n(k)-1}^{m^{\prime }(k)-1}d(x_i,x_{i+1})<\epsilon +\sum _{i=n(k)-1}^{m^{\prime }(k)-1}d(x_i,x_{i+1}).$$

(14)

Again, letting $k\to \mathrm{\infty }$ and using (5),

$$\underset{k\to \mathrm{\infty }}{lim}d(x_{m(k)},x_{m^{\prime }(k)})=\epsilon .$$

(15)

On the other hand, we have

$$\begin{array}{r}d(x_{m(k)},x_{m^{\prime }(k)})\le d(x_{m(k)},x_{m(k)-1})+d(x_{m(k)-1},x_{m^{\prime }(k)-1})+d(x_{m^{\prime }(k)-1},x_{m^{\prime }(k)}),\\ d(x_{m(k)-1},x_{m^{\prime }(k)-1})\le d(x_{m(k)-1},x_{m(k)})+d(x_{m(k)},x_{m^{\prime }(k)})+d(x_{m^{\prime }(k)},x_{m^{\prime }(k)-1}).\end{array}$$

Letting $k\to \mathrm{\infty }$ in the above inequalities, using (5), (9) and (15), we obtain

$$\underset{k\to \mathrm{\infty }}{lim}d(x_{m(k)-1},x_{m^{\prime }(k)-1})=\epsilon .$$

(16)

By setting $x=x_{m(k)-1}$ and $y=x_{m^{\prime }(k)-1}$, in (1), we get

$$\begin{array}{rcl}\psi (d(T{x}_{m(k)-1},T{x}_{m^{\prime }(k)-1}))& \le & \alpha (x_{m(k)-1},x_{m^{\prime }(k)-1})\psi (d(x_{m(k)-1},x_{m^{\prime }(k)-1}))\\ -\beta (x_{m(k)-1},x_{m^{\prime }(k)-1})\phi (d(x_{m(k)-1},x_{m^{\prime }(k)-1})),\end{array}$$

that is,

$$\begin{array}{rcl}\psi (d(x_{m(k)},x_{m^{\prime }(k)}))& \le & \alpha (x_{m(k)-1},x_{m^{\prime }(k)-1})\psi (d(x_{m(k)-1},x_{m^{\prime }(k)-1}))\\ -\beta (x_{m(k)-1},x_{m^{\prime }(k)-1})\phi (d(x_{m(k)-1},x_{m^{\prime }(k)-1})).\end{array}$$

Now, using (6) and (7), we get

$$\psi (d(x_{m(k)},x_{m^{\prime }(k)}))\le \psi (d(x_{m(k)-1},x_{m^{\prime }(k)-1}))-\phi (d(x_{m(k)-1},x_{m^{\prime }(k)-1})).$$

Letting $k\to \mathrm{\infty }$, using (15), (16) and the continuity of ψ and φ, we obtain

$$\psi (\epsilon )\le \psi (\epsilon )-\underset{k\to \mathrm{\infty }}{lim}\phi (d(x_{m(k)-1},x_{m^{\prime }(k)-1})),$$

(17)

which implies by (a3) that $\epsilon =0$, a contradiction with $\epsilon >0$. Hence, our claim holds, that is, $\{x_n\}$ is a Cauchy sequence. Since $(X,d)$ is a complete metric space, then there exists $x^{\ast }\in X$ such that

$$x_n\to x^{\ast }\text{as }n\to \mathrm{\infty }.$$

From the continuity of T, it follows that $x_{n+1}=T{x}_n\to T{x}^{\ast }$ as $n\to \mathrm{\infty }$. Due to the uniqueness of the limit, we derive that $T{x}^{\ast }=x^{\ast }$, that is, $x^{\ast }$ is a fixed point of T. □

Theorem 2.2 In Theorem  2.1, if we replace the continuity of T by the $({\mathcal{R}}_1,{\mathcal{R}}_2)$-regularity of $(X,d)$, then the conclusion of Theorem  2.1 holds.

Proof Following the lines of the proof of Theorem 2.1, we get that $\{x_n\}$ is a Cauchy sequence. Since $(X,d)$ is a complete metric space, then there exists $x^{\ast }\in X$ such that $x_n\to x^{\ast }$ as $n\to \mathrm{\infty }$. Furthermore, the sequence $\{x_n\}$ satisfies (2) and (3), that is,

$$x_n{\mathcal{R}}_1{x}_{n+1},x_n{\mathcal{R}}_2{x}_{n+1}\text{for all }n\in \mathbb{N}.$$

Now, since $(X,d)$ is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-regular, then there exists a subsequence $\{x_{n(k)}\}$ of $\{x_n\}$ such that $x_{n(k)}{\mathcal{R}}_1{x}^{\ast }$, that is, $\alpha (x_{n(k)},x^{\ast })\le 1$ and $x_{n(k)}{\mathcal{R}}_2{x}^{\ast }$, that is, $\beta (x_{n(k)},x^{\ast })\ge 1$ for all k. By setting $x=x_{n(k)}$ and $y=x^{\ast }$, in (1), we obtain

$$\psi \left(d(x_{n(k)+1},T{x}^{\ast })\right)\le \alpha (x_{n(k)},x^{\ast })\psi \left(d(x_{n(k)},x^{\ast })\right)-\beta (x_{n(k)},x^{\ast })\phi \left(d(x_{n(k)},x^{\ast })\right)\text{for all }k,$$

that is,

$$\psi \left(d(x_{n(k)+1},T{x}^{\ast })\right)\le \psi \left(d(x_{n(k)},x^{\ast })\right)-\phi \left(d(x_{n(k)},x^{\ast })\right)\text{for all }k.$$

Using the monotone property of the ψ-function, we get

$$d(x_{n(k)+1},T{x}^{\ast })\le d(x_{n(k)},x^{\ast })\text{for all }k.$$

Letting $k\to \mathrm{\infty }$ in the above inequality, we get $d(x^{\ast },T{x}^{\ast })=0$, that is, $x^{\ast }=T{x}^{\ast }$. □

Theorem 2.3 Adding to the hypotheses of Theorem  2.1 (respectively, Theorem  2.2) that X is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-directed, we obtain uniqueness of the fixed point of T.

Proof Suppose that $x^{\ast }$ and $y^{\ast }$ are two fixed points of T. Since X is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-directed, there exists $z\in X$ such that

$$\alpha (x^{\ast },z)\le 1,\alpha (y^{\ast },z)\le 1$$

(18)

and

$$\beta (x^{\ast },z)\ge 1,\beta (y^{\ast },z)\ge 1.$$

(19)

Since T is ${\mathcal{R}}_i$-preserving for $i=1,2$, from (18) and (19), we get

$$\alpha (x^{\ast },T^{n}z)\le 1,\alpha (y^{\ast },T^{n}z)\le 1,\mathrm{\forall }n\ge 0$$

(20)

and

$$\beta (x^{\ast },T^{n}z)\ge 1,\beta (y^{\ast },T^{n}z)\ge 1,\mathrm{\forall }n\ge 0.$$

(21)

Using (20), (21) and (1), we have

$$\begin{array}{rl}\psi \left(d(x^{\ast },T^{n+1}z)\right)& =\psi \left(d(T{x}^{\ast },T\left(T^{n}z\right))\right)\\ \le \alpha (x^{\ast },T^{n}z)\psi \left(d(x^{\ast },T^{n}z)\right)-\beta (x^{\ast },T^{n}z)\phi \left(d(x^{\ast },T^{n}z)\right)\\ \le \psi \left(d(x^{\ast },T^{n}z)\right)-\phi \left(d(x^{\ast },T^{n}z)\right).\end{array}$$

This implies that

$$\psi \left(d(x^{\ast },T^{n+1}z)\right)\le \psi \left(d(x^{\ast },T^{n}z)\right)-\phi \left(d(x^{\ast },T^{n}z)\right),\mathrm{\forall }n\ge 0.$$

(22)

Using the monotone property of the ψ-function, we get

$$d(x^{\ast },T^{n+1}z)\le d(x^{\ast },T^{n}z),\mathrm{\forall }n\ge 0.$$

It follows that $\{d(x^{\ast },T^{n}z)\}$ is monotone decreasing and consequently, there exists $r\ge 0$ such that

$$d(x^{\ast },T^{n}z)\to r\text{as }n\to \mathrm{\infty }.$$

Letting $n\to +\mathrm{\infty }$ in (22), we obtain

$$\psi (r)\le \psi (r)-\underset{n\to \mathrm{\infty }}{lim}\phi \left(d(x^{\ast },T^{n}z)\right),$$

which implies that ${lim}_{n\to \mathrm{\infty }}\phi (d(x^{\ast },T^{n}z))=0$, then by (a3) we get

$$d(x^{\ast },T^{n}z)\to 0\text{as }n\to \mathrm{\infty }.$$

(23)

Similarly, we get

$$d(y^{\ast },T^{n}z)\to 0\text{as }n\to \mathrm{\infty }.$$

(24)

Using (23) and (24), the uniqueness of the limit gives us $x^{\ast }=y^{\ast }$. □

3 Some corollaries

In this section, we derive new results from the previous theorems.

3.1 Coupled fixed point results in complete metric spaces

Let us recall the definition of a coupled fixed point introduced by Guo and Lakshmikantham in [5].

Definition 3.1 (Guo and Lakshmikantham [5])

Let $F:X\times X\to X$ be a given mapping. We say that $(x,y)\in X\times X$ is a coupled fixed point of F if

$$F(x,y)=x\text{and}F(y,x)=y.$$

Lemma 3.1 A pair $(x,y)$ is a coupled fixed point of F if and only if $(x,y)$ is a fixed point of T where $T:X\times X\to X\times X$ is given by

$$T(x,y)=(F(x,y),F(y,x))\mathit{\text{for all}}(x,y)\in X\times X.$$

(25)

Definition 3.2 Let $(X,d)$ be a metric space and $F:X\times X\to X$ be a given mapping. We say that F is an $(\alpha \psi ,\beta \phi )$-contractive mappings if there exists a pair of generalized distance $(\psi ,\phi )$ such that

$$\begin{array}{rcl}\psi \left(d(F(x,y),F(u,v))\right)& \le & \alpha ((x,y),(u,v))\psi (max\{d(x,u),d(y,v)\})\\ -\beta ((x,y),(u,v))\phi (max\{d(x,u),d(y,v)\}),\end{array}$$

where $\alpha ,\beta :X^2\times X^2\to [0,+\mathrm{\infty })$.

In this section, we define two binary relations ${\mathcal{S}}_1$ and ${\mathcal{S}}_2$ as follows.

Definition 3.3 Let X be a set, and let ${\mathcal{S}}_1$, ${\mathcal{S}}_2$ be two binary relations on $X\times X$ defined by

$$(x,y),(u,v)\in X\times X:(x,y){\mathcal{S}}_1(u,v)⟺\alpha ((x,y),(u,v))\le 1$$

and

$$(x,y),(u,v)\in X\times X:(x,y){\mathcal{S}}_2(u,v)⟺\beta ((x,y),(u,v))\ge 1.$$

Definition 3.4 Let $(X,d)$ be a metric space. We say that $(X\times X,d)$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-biregular if for all sequences $\{x_n,y_n\}$ in $X\times X$ such that $x_n\to x\in X$, $y_n\to y\in X$ as $n\to +\mathrm{\infty }$, and

$$(x_n,y_n){\mathcal{S}}_i(x_{n+1},y_{n+1}),(y_{n+1},x_{n+1}){\mathcal{S}}_i(y_n,x_n)\text{for }i=1,2\text{ and for all }n\in \mathbb{N},$$

there exists a subsequence $\{x_{n(k)},y_{n(k)}\}$ such that

$$(x_{n(k)},y_{n(k)}){\mathcal{S}}_i(x,y),(y,x){\mathcal{S}}_i(y_{n(k)},x_{n(k)})\text{for }i=1,2\text{ and for all }k\in \mathbb{N}.$$

Definition 3.5 We say that $X\times X$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-bidirected if for all $(x,y),(u,v)\in X\times X$, there exists $(z_1,z_2)\in X\times X$ such that

$$\begin{array}{c}((x,y){\mathcal{S}}_i(z_1,z_2))\wedge ((z_2,z_1){\mathcal{S}}_i(y,x))\text{and}\hfill \\ ((u,v){\mathcal{S}}_i(z_1,z_2))\wedge ((z_2,z_1){\mathcal{S}}_i(v,u))\text{for }i=1,2.\hfill \end{array}$$

We have the following result.

Corollary 3.1 Let $(X,d)$ be a complete metric space and $F:X\times X\to X$ be an $(\alpha \psi ,\beta \phi )$-contractive mapping satisfying the following conditions:

• (i) ${\mathcal{S}}_i$ is N-transitive for $i=1,2$ ($N>0$);

• (ii) For all $(x,y),(u,v)\in X\times X$, we have

  $$(x,y){\mathcal{S}}_i(u,v)⟹(F(x,y),F(y,x)){\mathcal{S}}_i(F(u,v),F(v,u))\mathit{\text{for}}i=1,2;$$

• (iii) There exists $(x_0,y_0)\in X\times X$ such that

  $$(x_0,y_0){\mathcal{S}}_i(F(x_0,y_0),F(y_0,x_0)),(F(y_0,x_0),F(x_0,y_0)){\mathcal{S}}_i(y_0,x_0)\mathit{\text{for}}i=1,2;$$

• (iv) F is continuous, or $(X\times X,d)$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-biregular.

Then, F has a coupled fixed point $(x^{\ast },y^{\ast })\in X\times X$. Moreover, if $X\times X$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-bidirected, then we have the uniqueness of the coupled fixed point.

Proof By Lemma 3.1, a pair $(x,y)$ is a coupled fixed point of F if and only if $(x,y)$ is a fixed point of T. Now, consider the complete metric space $(Y,\delta )$, where $Y=X\times X$ and

$$\delta ((x,y),(u,v))=max\{d(x,u),d(y,v)\}\text{for all }(x,y),(u,v)\in X\times X.$$

From (iv), we have

$$\begin{array}{rcl}\psi \left(d(F(x,y),F(u,v))\right)& \le & \alpha ((x,y),(u,v))\psi \left(\delta ((x,u),(y,v))\right)\\ -\beta ((x,y),(u,v))\phi \left(\delta ((x,u),(y,v))\right)\end{array}$$

(26)

and

$$\begin{array}{rcl}\psi \left(d(F(v,u),F(y,x))\right)& \le & \alpha ((v,u),(y,x))\psi \left(\delta ((x,u),(y,v))\right)\\ -\beta ((v,u),(y,x))\phi \left(\delta ((x,u),(y,v))\right).\end{array}$$

(27)

Since $\psi :[0,\mathrm{\infty })\to [0,+\mathrm{\infty })$ is nondecreasing, then $\psi (max(r,s))=max(\psi (r),\psi (s))$ for all $r,s\in [0,\mathrm{\infty })$. Hence, for all $({\xi }_1,{\xi }_2),({\eta }_1,{\eta }_2)\in X\times X$, we have

$$\psi (\delta (T\xi ,T\eta ))\le a(\xi ,\eta )\psi (\delta (\xi ,\eta ))-b(\xi ,\eta )\phi (\delta (\xi ,\eta )),$$

where $a,b:Y\times Y\to [0,+\mathrm{\infty })$ are the functions defined by

$$\begin{array}{r}a(({\xi }_1,{\xi }_2),({\eta }_1,{\eta }_2))=max\{\alpha (({\xi }_1,{\xi }_2),({\eta }_1,{\eta }_2)),\alpha (({\eta }_2,{\eta }_1),({\xi }_2,{\xi }_1))\},\\ b(({\xi }_1,{\xi }_2),({\eta }_1,{\eta }_2))=min\{\beta (({\xi }_1,{\xi }_2),({\eta }_1,{\eta }_2)),\beta (({\eta }_2,{\eta }_1),({\xi }_2,{\xi }_1))\},\end{array}$$

and $T:Y\to Y$ is given by (25). We shall prove that T is $(a\psi ,b\phi )$-contractive mapping.

Define two binary relations ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ by

$$\xi {\mathcal{R}}_1\eta ⟺a(\xi ,\eta )\le 1\text{and}\xi {\mathcal{R}}_2\eta ⟺b(\xi ,\eta )\ge 1\text{for all }\xi ,\eta \in X\times X.$$

First, we claim that ${\mathcal{R}}_j$ for $j=1,2$ are N-transitive. Let $(x_i,y_i)\in X\times X$ for all $i\in \{0,\dots ,N\}$ such that

$$(x_i,y_i){\mathcal{R}}_j(x_{i+1},y_{i+1})\text{for }j=1,2\text{ and for all }i\in \{0,\dots ,N\},$$

that is,

$$a((x_i,y_i),(x_{i+1},y_{i+1}))\le 1\text{and}b((x_i,y_i),(x_{i+1},y_{i+1}))\ge 1\text{for all }i\in \{0,\dots ,N\}.$$

By definitions of a and b, it follows that

$$\begin{array}{r}\alpha ((x_i,y_i),(x_{i+1},y_{i+1}))\le 1\text{and}\alpha ((y_{i+1},x_{i+1}),(y_i,x_i))\le 1\text{for all }i\in \{0,\dots ,N\},\\ \beta ((x_i,y_i),(x_{i+1},y_{i+1}))\ge 1\text{and}\beta ((y_{i+1},x_{i+1}),(y_i,x_i))\ge 1\text{for all }i\in \{0,\dots ,N\}\end{array}$$

or

$$(x_i,y_i){\mathcal{S}}_j(x_{i+1},y_{i+1})\text{and}(x_{i+1},y_{i+1}){\mathcal{S}}_j(x_i,y_i)\text{for }j=1,2\text{ and for all }i\in \{0,\dots ,N\}.$$

Hence, by (i), we have

$$(x_0,y_0){\mathcal{S}}_j(x_{N+1},y_{N+1})\text{and}(x_{N+1},y_{N+1}){\mathcal{S}}_j(x_0,y_0)\text{for }j=1,2,$$

that is,

$$\begin{array}{r}\alpha ((x_0,y_0),(x_{N+1},y_{N+1}))\le 1;\alpha ((y_{N+1},x_{N+1}),(y_0,x_0))\le 1;\\ \beta ((x_0,y_0),(x_{N+1},y_{N+1}))\ge 1;\beta ((y_{N+1},x_{N+1}),(y_0,x_0))\ge 1\end{array}$$

or

$$(x_0,y_0){\mathcal{R}}_j(x_{N+1},y_{N+1})\text{for }j=1,2.$$

Then our claim holds.

Let $\xi =({\xi }_1,{\xi }_2),\eta =({\eta }_1,{\eta }_2)\in Y$ such that $a(\xi ,\eta )\le 1$ and $b(\xi ,\eta )\ge 1$. Using condition (ii), we obtain immediately that $a(T\xi ,T\eta )\le 1$ and $b(T\xi ,T\eta )\ge 1$. Then T is ${\mathcal{R}}_j$-preserving for $j=1,2$. Moreover, from condition (iii), we know that there exists $(x_0,y_0)\in Y$ such that $(x_0,y_0){\mathcal{R}}_{j}T(x_0,y_0)$ for $j=1,2$. If F is continuous, then T also is continuous. Then all the hypotheses of Theorem 2.1 are satisfied. If $(X\times X,d)$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-biregular, then we easily have that $(X\times X,d)$ is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-regular. Hence, Theorem 2.2 yields the result. We deduce the existence of a fixed point of T that gives us from (25) the existence of a coupled fixed point of F. Now, since $X\times X$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-bidirected, one can easily derive that $X\times X$ is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-directed by regarding Lemma 3.1 and Definition 3.5. Finally, by using Theorem 2.3, we obtain the uniqueness of the fixed point of T, that is, the uniqueness of the coupled fixed point of F. □

3.2 Fixed point results on metric spaces endowed with N-transitive binary relation

In [18], Samet and Turinci established fixed point results for contractive mappings on metric spaces, endowed with an amorphous arbitrary binary relation. Very recently, this work has been extended by Berzig in [2] to study the coincidence and common fixed points.

In this section, we establish a fixed point theorem on metric space endowed with N-transitive binary relation .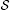

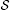Corollary 3.2 Let X be a non-empty set endowed with a binary relation . Suppose that there is a metric d on X such that $(X,d)$ is complete. Let $T:X\to X$ satisfy the -weakly $(\psi ,\phi )$-contractive conditions, that is,

$$\psi (d(Tx,Ty))\le \psi (d(x,y))-\phi (d(x,y))\mathit{\text{for all}}x\mathcal{S}y,$$

where ψ and φ are altering distance functions. Suppose also that the following conditions hold:

• (i) 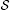is N-transitive ($N>0$);

• (ii) T is a 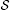-preserving mapping;

• (iii) there exists $x_0\in X$ such that $x_0\mathcal{S}T{x}_0$;

• (iv) T is continuous or $(X,d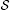)$ is -regular.

Then T has a fixed point. Moreover, if X is -directed, we have the uniqueness of the fixed point.

Proof In order to link this theorem to the main result, we define the mapping $\alpha :X\times X\to [0,+\mathrm{\infty })$ by

$$\alpha (x,y)=\{\begin{array}{cc}1\hfill & \text{if }x\mathcal{S}y\text{ or }x=y,\hfill \\ 1+\frac{\psi (d(Tx,Ty))}{\psi (d(x,y))}+\frac{\phi (d(x,y))}{\phi (d(x,y))+\psi (d(x,y))}\hfill & \text{otherwise},\hfill \end{array}$$

(28)

and we define the mapping $\beta :X\times X\to [0,+\mathrm{\infty })$ by

$$\beta (x,y)=\{\begin{array}{cc}1\hfill & \text{if }x\mathcal{S}y\text{ or }x=y,\hfill \\ \frac{\psi (d(x,y))}{\phi (d(x,y))+\psi (d(x,y))}\hfill & \text{otherwise}.\hfill \end{array}$$

(29)

Next, by using (28), (29) and Definition 2.3, the conclusion follows directly from Theorems 2.1, 2.2 and 2.3. □

3.3 Fixed point results for cyclic contractive mappings

In [13], Kirk et al. have generalized the Banach contraction principle. They obtained a new fixed point results for cyclic contractive mappings.

Theorem 3.1 (Kirk et al. [13])

For $i\in \{1,\dots ,N\}$, let $A_i$ be a nonempty closed subsets of a complete metric space $(X,d)$, and let $T:X\to X$ be a given mapping. Suppose that the following conditions hold:

• (i) $T(A_i)\subseteq A_{i+1}$ for all $i\in \{1,\dots ,N\}$ with $A_{N+1}:=A_1$;

• (ii) there exists $k\in (0,1)$ such that

  $$d(Tx,Ty)\le kd(x,y).$$

Then T has a unique fixed point in ${\bigcap }_{i=1}^N{A}_i$.

Let us define the binary relations ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$.

Definition 3.6 Let X be a nonempty set and let $A_i$, $i\in \{1,\dots ,N\}$ be nonempty closed subsets of X. We define two binary relations ${\mathcal{R}}_k$ for $k=1,2$ by

$$x,y\in X:x{\mathcal{R}}_{k}y⟺(x,y)\in \mathrm{\Gamma }:=\bigcup _{i=1}^N(A_i\times A_{i+1})\text{with }{A}_{N+1}:=A_1.$$

Now, based on Theorem 2.2, we will derive a more general result for cyclic mappings.

Corollary 3.3 For $i\in \{1,\dots ,N\}$, let $A_i$ be nonempty closed subsets of a complete metric space $(X,d)$, and let $T:X\to X$ be a given mapping. Suppose that the following conditions hold:

• (i) $T(A_i)\subseteq A_{i+1}$ for all $i\in \{1,\dots ,N\}$ with $A_{N+1}:=A_1$;

• (ii) there exist two altering distance functions ψ and φ such that

  $$\psi (d(Tx,Ty))\le \psi (d(x,y))-\phi (d(x,y))\mathit{\text{for all}}(x,y)\in A_i\times A_{i+1}\mathit{\text{for all}}i\in \{1,\dots ,N\}.$$

Then T has a unique fixed point in ${\bigcap }_{i=1}^N{A}_i$.

Proof Let $Y:={\bigcup }_{i=1}^N{A}_i$. For all $i\in \{1,\dots ,N\}$, we have by assumption that each $A_i$ is nonempty closed subset of the complete metric space X, which implies that $(Y,d)$ is complete.

Define the mapping $\alpha :Y\times Y\to [0,+\mathrm{\infty })$ by

$$\alpha (x,y)=\{\begin{array}{cc}1\hfill & \text{if }(x,y)\in \mathrm{\Gamma }\text{ or }x=y,\hfill \\ 1+\frac{\psi (d(Tx,Ty))}{\psi (d(x,y))}+\frac{\phi (d(x,y))}{\phi (d(x,y))+\psi (d(x,y))}\hfill & \text{otherwise},\hfill \end{array}$$

and define the mapping $\beta :Y\times Y\to [0,+\mathrm{\infty })$ by

$$\beta (x,y)=\{\begin{array}{cc}1\hfill & \text{if }(x,y)\in \mathrm{\Gamma }\text{ or }x=y,\hfill \\ \frac{\psi (d(x,y))}{\phi (d(x,y))+\psi (d(x,y))}\hfill & \text{otherwise}.\hfill \end{array}$$

Hence, Definition 2.3 is equivalent to Definition 3.6.

We start by checking that ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ are N-transitive. Indeed, let $x_0,\dots ,x_{N+1}\in Y$ such that $x_k{\mathcal{R}}_1{x}_{k+1}$ and $x_k{\mathcal{R}}_2{x}_{k+1}$ for all $k\in \{0,\dots ,N\}$, that is, $\alpha (x_k,x_{k+1})\le 1$ and $\beta (x_k,x_{k+1})\ge 1$ for all $k\in \{0,\dots ,N\}$ such that

$$x_0\in A_i,x_1\in A_{i+1},\dots ,x_k\in A_{i+k},\dots ,x_{N+1}\in A_{i+N+1}=A_{i+1},$$

which implies that $(x_0,x_{N+1})\in A_i\times A_{i+1}\subseteq Y$. Hence, we obtain $\alpha (x_0,x_{N+1})\le 1$ and $\beta (x_0,x_{N+1})\ge 1$, that is, $x_0{\mathcal{R}}_1{x}_{N+1}$ and $x_0{\mathcal{R}}_2{x}_{N+1}$, which implies that ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ are N-transitive.

Next, from (ii) and the definition of α and β, we can write

$$\psi (d(Tx,Ty))\le \alpha (x,y)\psi (d(x,y))-\beta (x,y)\phi (d(x,y))$$

for all $x,y\in Y$. Thus, T is $(\alpha \psi ,\beta \phi )$-contractive mapping.

We claim next that T is ${\mathcal{R}}_1$-preserving and ${\mathcal{R}}_2$-preserving. Indeed, let $x,y\in Y$ such that $x{\mathcal{R}}_{1}y$ and $x{\mathcal{R}}_{2}y$, that is, $\alpha (x,y)\le 1$ and $\beta (x,y)\ge 1$; hence, there exists $i\in \{1,\dots ,N\}$ such that $x\in A_i$, $y\in A_{i+1}$. Thus, $(Tx,Ty)\in A_{i+1}\times A_{i+2}\subseteq \mathrm{\Gamma }$, then $\alpha (Tx,Ty)\le 1$ and $\beta (Tx,Ty)\ge 1$, that is, $Tx{\mathcal{R}}_{1}Ty$ and $Tx{\mathcal{R}}_{2}Ty$. Hence, our claim holds.

Also, from (i), for any $x_0\in A_i$ for all $i\in \{1,\dots ,N\}$, we have $(x_0,T{x}_0)\in A_i\times A_{i+1}$, which implies that $\alpha (x_0,T{x}_0)\le 1$ and $\beta (x_0,T{x}_0)\ge 1$, that is, $x_0{\mathcal{R}}_{1}T{x}_0$ and $x_0{\mathcal{R}}_{2}T{x}_0$.

Now, we claim that Y is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-regular. Let $\{x_n\}$ be a sequence in Y such that $x_n\to x\in Y$ as $n\to \mathrm{\infty }$, and

$$x_n{\mathcal{R}}_1{x}_{n+1},x_n{\mathcal{R}}_2{x}_{n+1}\text{for all }n,$$

that is,

$$\alpha (x_n,x_{n+1})\le 1,\beta (x_n,x_{n+1})\ge 1\text{for all }n.$$

It follows that there exist $i,j\in \{1,\dots ,N\}$ such that

$$x_n\in A_{i+n}\text{for all }n\in \mathbb{N}\text{and}x\in A_j,$$

so

$$x_{(j-i-1+N)+kN}\in A_{j-1+(k+1)N}=A_{j-1}\text{for all }k\in \mathbb{N}.$$

By letting

$$n(k):=(j-i-1+N)+kN\text{for all }k\in \mathbb{N},$$

we conclude that the subsequence $\{x_{n(k)}\}$ satisfies

$$(x_{n(k)},x)\in A_{j-1}\times A_j\subseteq \mathrm{\Gamma }\text{for all }k\in \mathbb{N},$$

hence $\alpha (x_{n(k)},x)\le 1$ and $\beta (x_{n(k)},x)\ge 1$ for all k, that is, $x_{n(k)}{\mathcal{R}}_{1}x$ and $x_{n(k)}{\mathcal{R}}_{2}x$, which proves our claim.

Hence, all the hypotheses of Theorem 2.2 are satisfied on $(Y,d)$, and we deduce that T has a fixed point $x^{\ast }$ in Y. Since $x^{\ast }\in A_i$ for some $i\in \{1,\dots ,N\}$ and $x^{\ast }=T{x}^{\ast }\in A_{i+1}$ for all $i\in \{1,\dots ,N\}$, then $x^{\ast }\in {\bigcap }_{i=1}^N{A}_i$.

Moreover, it is easy to check that X is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-directed. Indeed, let $x,y\in Y$ with $x\in A_i$, $y\in A_j$, $i,j\in \{1,\dots ,N\}$. For $z=x^{\ast }\in Y$, we have $((\alpha (x,z)\le 1)\wedge (\alpha (y,z)\le 1))$ and $((\beta (x,z)\ge 1)\wedge (\beta (y,z)\ge 1))$. Thus, X is $({\mathcal{R}}_1,{\mathcal{R}}_2)$-directed.

Finally, the uniqueness follows by Theorem 2.3. □

4 Related fixed point theorems

In this section, we show that many existing results in the literature can be deduced from our results.

4.1 Classical fixed point results

Corollary 4.1 (Dutta and Choudhury [4])

Let $(X,d)$ be a complete metric space, and let $T:X\to X$ be a self-mapping satisfying the inequality

$$\psi (d(Tx,Ty))\le \psi (d(x,y))-\phi (d(x,y))\mathit{\text{for all}}x,y\in X,$$

where ψ and φ are altering distance functions. Then T has a unique fixed point.

Proof Let $\alpha ,\beta :X\times X\to [0,+\mathrm{\infty })$ be the mapping defined by $\alpha (x,y)=\beta (x,y)=1$ for all $x,y\in X$. Then T is $(\alpha \psi ,\beta \phi )$-contractive mappings. It is easy to show that all the hypotheses of Theorems 2.1 and 2.2 are satisfied. Consequently, T has a unique fixed point. □

Corollary 4.2 (Rhoades [17])

Let $(X,d)$ be a complete metric space, and let $T:X\to X$ be a self-mapping satisfying the inequality

$$d(Tx,Ty)\le d(x,y)-\phi (d(x,y))\mathit{\text{for all}}x,y\in X,$$

where φ is an altering distance functions. Then T has a unique fixed point.

Proof Following the lines of the proof of Corollary 4.1, by taking $\psi (t)=t$, we get the desired result. □

4.2 Fixed point results in partially ordered metric spaces

We start by defining the binary relations ${\mathcal{R}}_i$ for $i=1,2$ and the concept of ≤-directed.

Definition 4.1 Let $(X,\le )$ be a partially ordered set.

• 1. We define two binary relations ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ on X by

  $$x,y\in X:x{\mathcal{R}}_{i}y⟺x\le y\text{for }i=1,2.$$

• 2. We say that X is ≤-directed if for all $x,y\in X$ there exists a $z\in X$ such that $x\le z$ and $y\le z$.

Corollary 4.3 (Harjani and Sadarangani [8])

Let $(X,\le )$ be a partially ordered set and d be a metric on X such that $(X,d)$ is complete. Suppose that the mapping $T:X\to X$ is weakly contractive, that is,

$$\psi (d(Tx,Ty))\le \psi (d(x,y))-\phi (d(x,y))\mathit{\text{for all}}x\le y,$$

where ψ and φ are altering distance functions. Suppose also that the following conditions hold:

• (i) T is a nondecreasing mapping;

• (ii) there exists $x_0\in X$ with $x_0\le T{x}_0$;

If either:

• (iii) T is continuous or,

(iii′) for every sequence $\{x_n\}$ in X such that $x_n\to x\in X$, and $\{x_n\}$ is a nondecreasing sequence, there exists a subsequence $\{x_{n(k)}\}$ such that $x_{n(k)}\le x$ for all $k\ge 0$.

Then T has a fixed point. Moreover, if X is ≤-directed, we have the uniqueness of the fixed point.

Proof Using Definition 2.3, we can define the binary relations ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ by the mappings $\alpha ,\beta :X\times X\to [0,+\mathrm{\infty })$:

$$\alpha (x,y)=\{\begin{array}{cc}1\hfill & \text{if }x\le y,\hfill \\ 1+\frac{\psi (d(Tx,Ty))}{\psi (d(x,y))}+\frac{\phi (d(x,y))}{\phi (d(x,y))+\psi (d(x,y))}\hfill & \text{if }x\nleqq y,\hfill \end{array}$$

and

$$\beta (x,y)=\{\begin{array}{cc}1\hfill & \text{if }x\le y,\hfill \\ \frac{\psi (d(x,y))}{\phi (d(x,y))+\psi (d(x,y))}\hfill & \text{if }x\nleqq y.\hfill \end{array}$$

In case $x\nleqq y$, the functions α and β are well defined, because the altering functions $\phi (d(x,y))$ and $\psi (d(x,y))$ are null only, and only if $d(x,y)=0$, that is, $x=y$ which is not the case.

We can verify easily that ${\mathcal{R}}_1$ and ${\mathcal{R}}_2$ are 1-transitive.

Next, we claim that T is $(\alpha \psi ,\beta \phi )$-contractive mappings. Indeed, in case $x\le y$, we easily get

$$\psi (d(Tx,Ty))\le \alpha (x,y)\psi (d(x,y))-\beta (x,y)\phi (d(x,y)),$$

and in case $x\nleqq y$, we have

$$\alpha (x,y)\psi (d(x,y))-\beta (x,y)\phi (d(x,y))=\psi (d(x,y))+\psi (d(Tx,Ty))\ge \psi (d(Tx,Ty)),$$

hence, our claim holds.

Moreover, from the monotone property of T, we get

$$\begin{array}{c}x,y\in X,x{\mathcal{R}}_{1}y⟹\alpha (x,y)\le 1⟹x\le y⟹Tx\le Ty\hfill \\ ⟹\alpha (Tx,Ty)\le 1⟹Tx{\mathcal{R}}_{1}Ty,\hfill \end{array}$$

and similarly, we have

$$\begin{array}{c}x,y\in X,x{\mathcal{R}}_{2}y⟹\beta (x,y)\ge 1⟹x\le y⟹Tx\le Ty\hfill \\ ⟹\beta (Tx,Ty)\ge 1⟹Tx{\mathcal{R}}_{2}Ty.\hfill \end{array}$$

Thus T is ${\mathcal{R}}_i$-preserving for $i=1,2$. Now, if condition (iii) is satisfied, that is, T is continuous, the existence of a fixed point follows from Theorem 2.1. Suppose now, that the condition (iii′) is satisfied, and let $\{x_n\}$ be a nondecreasing sequence in X, that is, $\alpha (x_n,x_{n+1})\le 1$ and $\beta (x_n,x_{n+1})\ge 1$ for all n. Suppose also that $x_n\to x\in X$ as $n\to \mathrm{\infty }$. From (iii′), there exists a subsequence $\{x_{n(k)}\}$ such that $x_{n(k)}\le x$ for all k. This implies from the definition of α and β that $\alpha (x_{n(k)},x)\le 1$ and $\beta (x_{n(k)},x)\ge 1$ for all k, which implies $x_{n(k)}{\mathcal{R}}_{i}x$ for $i=1,2$ and for all k. In this case, the existence of a fixed point follows from Theorem 2.2.

To show the uniqueness, suppose that X is ≤-directed, that is, for all $x,y\in X$ there exists a $z\in X$ such that $x\le z$ and $y\le z$, which implies from the definition of α and β that $(\alpha (x,z)\le 1)\wedge (\alpha (y,z)\le 1)$ and $(\beta (x,z)\ge 1)\wedge (\beta (y,z)\ge 1)$. Hence, Theorem 2.3 gives us the uniqueness of this fixed point. □

4.3 Coupled fixed point theorems

Next, in order to prove a coupled fixed point results in partially ordered set, we need to define an order relation on the set $X\times X$.

Let $(X,\le )$ be a partially ordered set endowed with a metric d, and let $F:X\times X\to X$ be a given mapping. We endow the product set $X\times X$ with the partial order:

$$(x,y),(u,v)\in X\times X,(x,y)⪯(u,v)⟺x\le u,y\ge v.$$

Definition 4.2 Let X be a set and binary relations ${\mathcal{S}}_k$ for $k=1,2$ on $X\times X$ defined by

$$(x,y),(u,v)\in X\times X:(x,y){\mathcal{S}}_k(u,v)⟺(x,y)⪯(u,v).$$

Corollary 4.4 (Harjani et al. [6])

Let $(X,d)$ be a partially ordered set and suppose that there exists a metric d in X such that $(X,d)$ is a complete metric space. Suppose that the mapping $F:X\times X\to X$ is weakly $(\psi ,\phi )$-contractive, that is,

$$\begin{array}{c}\psi (F(x,y),F(u,v))\le \psi (max\{d(x,u),d(y,v)\})-\phi (max\{d(x,u),d(y,v)\})\hfill \\ \mathit{\text{for all}}(x,y)⪯(u,v),\hfill \end{array}$$

where ψ and φ are altering distance functions. Suppose also that the following conditions hold:

• (i) F is a mixed monotone mapping;

• (ii) there exists $x_0,y_0\in X$ with $(x_0,y_0)⪯(F{x}_0,F{y}_0)$;

• (iii) F is continuous or $(X\times X,d)$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-biregular.

Then F has a coupled fixed point $(x^{\ast },y^{\ast })\in X\times X$. Moreover, if $X\times X$ is $({\mathcal{S}}_1,{\mathcal{S}}_2)$-bidirected, we have the uniqueness of the fixed point.

Proof The conclusions then follows directly from Corollary 3.1. □

4.4 Fixed point results for cyclic contractive mappings

In this section, we will derive from our results the fixed point theorem of Karapınar and Sadarangani [11] for cyclic weak $(\phi -\psi )$-contractive mappings.

Definition 4.3 (Păcurar and Rus [16])

Let X be a nonempty set, m a positive integer and $T:X\to X$ an operator. By definition, $X={\bigcup }_{i=1}^m{X}_i$ is a cyclic representation of X with respect to T if

• 1. $X_i$, $i=1,\dots ,m$ are nonempty sets;

• 2. $T(X_1)\subset X_2,\dots ,T(X_{m-1})\subset X_m$, $T(X_m)\subset X_1$.

Definition 4.4 (Karapınar and Sadarangani [10])

Let $(X,d)$ be a metric space, let m be a positive integer, let $A_1,A_2,\dots ,A_m$ be closed non-empty subsets of X, and let $Y:={\bigcup }_{i=1}^m{A}_i$. An operator $T:Y\to Y$ is called a cyclic weak $(\phi -\psi )$-contraction if

• 1. ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to T, and

• 2. $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is an altering distance function such that

  $$\psi (d(Tx,Ty))\le \psi (d(x,y))-\phi (d(x,y))$$

  (30)

for any $x\in A_i$, $y\in A_{i+1}$, where $A_{m+1}:=A_1$.

Corollary 4.5 (Karapınar and Sadarangani [10])

Let $(X,d)$ be a complete metric space, let m be a positive integer, let $A_1,A_2,\dots ,A_m$ be closed non-empty subsets of X and let $Y={\bigcup }_{i=1}^m{A}_i$. Suppose that $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is an altering distance function, and T is a cyclic weak φ-contraction, where $Y={\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to T. Then, T has a unique fixed point $z\in {\bigcap }_{i=1}^m{A}_i$.

Proof The proof follows immediately from Corollary 3.3. □