Abstract
In this manuscript, we extend the concept of altering distance, and we introduce a new notion of -contractive mappings. We prove the existence and uniqueness of a fixed point for such mapping in the context of complete metric space. The presented theorems of this paper generalize, extend and improve some remarkable existing results in the literature. We also present several applications and consequences of our results.
Similar content being viewed by others
1 Introduction and preliminaries
Fixed point theory is one of the core research areas in nonlinear functional analysis since it has a broad range of application potential in various fields such as engineering, economics, computer science, and many others. Banach contraction mapping principle [1] is considered to be the initial and fundamental result in this direction. Fixed point theory and hence the Banach contraction mapping principle have evidently attracted many prominent mathematicians due to their wide application potential. Consequently, the number of publications in this theory increases rapidly; we refer the reader to [2–19].
In this paper, by introducing a new notion of -contractive mappings, we aim to establish a more general result to collect/combine a number of existing results in the literature.
We start by recalling the notion of altering distance function introduced by Khan et al. [12] as follows.
Definition 1.1 A function is called an altering distance function if the following properties are satisfied:
-
is continuous and nondecreasing.
-
if and only if .
Now, we present a definition, which will be useful later.
Definition 1.2 Let X be a set, and let ℛ be a binary relation on X. We say that is an ℛ-preserving mapping if
In the sequel, let ℕ denote the set of all non-negative integers, let ℝ denote the set of all real numbers.
Example 1.1 Let and a function defined as .
Define and by
Define the first binary relation by if and only if , and define the second binary relation by if and only if . Then, we easily obtain that T is simultaneously -preserving and -preserving.
Definition 1.3 Let . We say that ℛ is N-transitive on X if
The following remark is a consequence of the previous definition.
Remark 1.1 Let . We have:
-
(i)
If ℛ is transitive, then it is N-transitive for all .
-
(ii)
If ℛ is N-transitive, then it is kN-transitive for all .
Definition 1.4 Let be a metric space and , two binary relations on X. We say that is -regular if for every sequence in X such that as , and
there exists a subsequence such that
Definition 1.5 We say that a subset D of X is -directed if for all , there exists such that
2 Main results
Before we start the introduction of the concept -contractive mappings, we introduce the notion of a pair of generalized altering distance as follows:
Definition 2.1 We say that the pair of functions is a pair of generalized altering distance where if the following hypotheses hold:
-
(a1)
ψ is continuous;
-
(a2)
ψ is nondecreasing;
-
(a3)
.
The condition (a3) was introduced by Popescu in [15] and Moradi and Farajzadeh in [14].
Definition 2.2 Let be a metric space, and let be a given mapping. We say that T is -contractive mappings if there exists a pair of generalized distance such that
where .
In the sequel, the binary relations and are defined as following.
Definition 2.3 Let X be a set and are two mappings. We define two binary relations and on X by
and
Now we are ready to state our first main result.
Theorem 2.1 Let be a complete metric space, , and let be an -contractive mapping satisfying the following conditions:
-
(i)
is N-transitive for ;
-
(ii)
T is -preserving for ;
-
(iii)
there exists such that for ;
-
(iv)
T is continuous.
Then, T has a fixed point, that is, there exists such that .
Proof Let such that for . Define the sequence in X by
If for some , then is a fixed point T. Assume that for all . From (ii) and (iii), we have
Similarly, we have
By induction, from (ii) it follows that
and, similarly, we have
Substituting and in (1), we obtain
So, by (2) and (3) it follows that
Using the monotone property of the ψ-function, we get
It follows that is monotone decreasing, and, consequently, there exists such that
Letting in (4), we obtain
which implies that , then by (a3) we get
On the other hand, by (2) and (i), we obtain
Similarly, by (3) and (i), we get
Now, for some , substituting and in (1), where , we get
So, by (6) and (7), we have
Using the monotone property of the ψ-function, we get
It follows that is monotone decreasing and consequently, there exists such that
Letting , we obtain
which implies that , then by (a3) we get
Next, we claim that is a Cauchy sequence. Suppose if we obtain a contradiction, that T is not a Cauchy sequence. Then, there exists , for which we can find subsequences and of with such that
Further, corresponding to , we can choose in such a way that it is the smallest integer with and satisfying (10). Then
Then we have
Letting and using (5),
Furthermore, for each , there exist such that . Hence, by (11) we have
Again, letting and using (5),
On the other hand, we have
Letting in the above inequalities, using (5), (9) and (15), we obtain
By setting and , in (1), we get
that is,
Now, using (6) and (7), we get
Letting , using (15), (16) and the continuity of ψ and φ, we obtain
which implies by (a3) that , a contradiction with . Hence, our claim holds, that is, is a Cauchy sequence. Since is a complete metric space, then there exists such that
From the continuity of T, it follows that as . Due to the uniqueness of the limit, we derive that , that is, is a fixed point of T. □
Theorem 2.2 In Theorem 2.1, if we replace the continuity of T by the -regularity of , then the conclusion of Theorem 2.1 holds.
Proof Following the lines of the proof of Theorem 2.1, we get that is a Cauchy sequence. Since is a complete metric space, then there exists such that as . Furthermore, the sequence satisfies (2) and (3), that is,
Now, since is -regular, then there exists a subsequence of such that , that is, and , that is, for all k. By setting and , in (1), we obtain
that is,
Using the monotone property of the ψ-function, we get
Letting in the above inequality, we get , that is, . □
Theorem 2.3 Adding to the hypotheses of Theorem 2.1 (respectively, Theorem 2.2) that X is -directed, we obtain uniqueness of the fixed point of T.
Proof Suppose that and are two fixed points of T. Since X is -directed, there exists such that
and
Since T is -preserving for , from (18) and (19), we get
and
Using (20), (21) and (1), we have
This implies that
Using the monotone property of the ψ-function, we get
It follows that is monotone decreasing and consequently, there exists such that
Letting in (22), we obtain
which implies that , then by (a3) we get
Similarly, we get
Using (23) and (24), the uniqueness of the limit gives us . □
3 Some corollaries
In this section, we derive new results from the previous theorems.
3.1 Coupled fixed point results in complete metric spaces
Let us recall the definition of a coupled fixed point introduced by Guo and Lakshmikantham in [5].
Definition 3.1 (Guo and Lakshmikantham [5])
Let be a given mapping. We say that is a coupled fixed point of F if
Lemma 3.1 A pair is a coupled fixed point of F if and only if is a fixed point of T where is given by
Definition 3.2 Let be a metric space and be a given mapping. We say that F is an -contractive mappings if there exists a pair of generalized distance such that
where .
In this section, we define two binary relations and as follows.
Definition 3.3 Let X be a set, and let , be two binary relations on defined by
and
Definition 3.4 Let be a metric space. We say that is -biregular if for all sequences in such that , as , and
there exists a subsequence such that
Definition 3.5 We say that is -bidirected if for all , there exists such that
We have the following result.
Corollary 3.1 Let be a complete metric space and be an -contractive mapping satisfying the following conditions:
-
(i)
is N-transitive for ();
-
(ii)
For all , we have
-
(iii)
There exists such that
-
(iv)
F is continuous, or is -biregular.
Then, F has a coupled fixed point . Moreover, if is -bidirected, then we have the uniqueness of the coupled fixed point.
Proof By Lemma 3.1, a pair is a coupled fixed point of F if and only if is a fixed point of T. Now, consider the complete metric space , where and
From (iv), we have
and
Since is nondecreasing, then for all . Hence, for all , we have
where are the functions defined by
and is given by (25). We shall prove that T is -contractive mapping.
Define two binary relations and by
First, we claim that for are N-transitive. Let for all such that
that is,
By definitions of a and b, it follows that
or
Hence, by (i), we have
that is,
or
Then our claim holds.
Let such that and . Using condition (ii), we obtain immediately that and . Then T is -preserving for . Moreover, from condition (iii), we know that there exists such that for . If F is continuous, then T also is continuous. Then all the hypotheses of Theorem 2.1 are satisfied. If is -biregular, then we easily have that is -regular. Hence, Theorem 2.2 yields the result. We deduce the existence of a fixed point of T that gives us from (25) the existence of a coupled fixed point of F. Now, since is -bidirected, one can easily derive that is -directed by regarding Lemma 3.1 and Definition 3.5. Finally, by using Theorem 2.3, we obtain the uniqueness of the fixed point of T, that is, the uniqueness of the coupled fixed point of F. □
3.2 Fixed point results on metric spaces endowed with N-transitive binary relation
In [18], Samet and Turinci established fixed point results for contractive mappings on metric spaces, endowed with an amorphous arbitrary binary relation. Very recently, this work has been extended by Berzig in [2] to study the coincidence and common fixed points.
In this section, we establish a fixed point theorem on metric space endowed with N-transitive binary relation 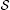 .
.
Corollary 3.2 Let X be a non-empty set endowed with a binary relation  . Suppose that there is a metric d on X such that is complete. Let satisfy the
. Suppose that there is a metric d on X such that is complete. Let satisfy the 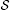 -weakly -contractive conditions, that is,
-weakly -contractive conditions, that is,
where ψ and φ are altering distance functions. Suppose also that the following conditions hold:
-
(i)
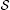 is N-transitive ();
is N-transitive (); -
(ii)
T is a
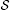 -preserving mapping;
-preserving mapping; -
(iii)
there exists such that ;
-
(iv)
T is continuous or is
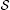 -regular.
-regular.
Then T has a fixed point. Moreover, if X is  -directed, we have the uniqueness of the fixed point.
-directed, we have the uniqueness of the fixed point.
Proof In order to link this theorem to the main result, we define the mapping by
and we define the mapping by
Next, by using (28), (29) and Definition 2.3, the conclusion follows directly from Theorems 2.1, 2.2 and 2.3. □
3.3 Fixed point results for cyclic contractive mappings
In [13], Kirk et al. have generalized the Banach contraction principle. They obtained a new fixed point results for cyclic contractive mappings.
Theorem 3.1 (Kirk et al. [13])
For , let be a nonempty closed subsets of a complete metric space , and let be a given mapping. Suppose that the following conditions hold:
-
(i)
for all with ;
-
(ii)
there exists such that
Then T has a unique fixed point in .
Let us define the binary relations and .
Definition 3.6 Let X be a nonempty set and let , be nonempty closed subsets of X. We define two binary relations for by
Now, based on Theorem 2.2, we will derive a more general result for cyclic mappings.
Corollary 3.3 For , let be nonempty closed subsets of a complete metric space , and let be a given mapping. Suppose that the following conditions hold:
-
(i)
for all with ;
-
(ii)
there exist two altering distance functions ψ and φ such that
Then T has a unique fixed point in .
Proof Let . For all , we have by assumption that each is nonempty closed subset of the complete metric space X, which implies that is complete.
Define the mapping by
and define the mapping by
Hence, Definition 2.3 is equivalent to Definition 3.6.
We start by checking that and are N-transitive. Indeed, let such that and for all , that is, and for all such that
which implies that . Hence, we obtain and , that is, and , which implies that and are N-transitive.
Next, from (ii) and the definition of α and β, we can write
for all . Thus, T is -contractive mapping.
We claim next that T is -preserving and -preserving. Indeed, let such that and , that is, and ; hence, there exists such that , . Thus, , then and , that is, and . Hence, our claim holds.
Also, from (i), for any for all , we have , which implies that and , that is, and .
Now, we claim that Y is -regular. Let be a sequence in Y such that as , and
that is,
It follows that there exist such that
so
By letting
we conclude that the subsequence satisfies
hence and for all k, that is, and , which proves our claim.
Hence, all the hypotheses of Theorem 2.2 are satisfied on , and we deduce that T has a fixed point in Y. Since for some and for all , then .
Moreover, it is easy to check that X is -directed. Indeed, let with , , . For , we have and . Thus, X is -directed.
Finally, the uniqueness follows by Theorem 2.3. □
4 Related fixed point theorems
In this section, we show that many existing results in the literature can be deduced from our results.
4.1 Classical fixed point results
Corollary 4.1 (Dutta and Choudhury [4])
Let be a complete metric space, and let be a self-mapping satisfying the inequality
where ψ and φ are altering distance functions. Then T has a unique fixed point.
Proof Let be the mapping defined by for all . Then T is -contractive mappings. It is easy to show that all the hypotheses of Theorems 2.1 and 2.2 are satisfied. Consequently, T has a unique fixed point. □
Corollary 4.2 (Rhoades [17])
Let be a complete metric space, and let be a self-mapping satisfying the inequality
where φ is an altering distance functions. Then T has a unique fixed point.
Proof Following the lines of the proof of Corollary 4.1, by taking , we get the desired result. □
4.2 Fixed point results in partially ordered metric spaces
We start by defining the binary relations for and the concept of ≤-directed.
Definition 4.1 Let be a partially ordered set.
-
1.
We define two binary relations and on X by
-
2.
We say that X is ≤-directed if for all there exists a such that and .
Corollary 4.3 (Harjani and Sadarangani [8])
Let be a partially ordered set and d be a metric on X such that is complete. Suppose that the mapping is weakly contractive, that is,
where ψ and φ are altering distance functions. Suppose also that the following conditions hold:
-
(i)
T is a nondecreasing mapping;
-
(ii)
there exists with ;
If either:
-
(iii)
T is continuous or,
(iii′) for every sequence in X such that , and is a nondecreasing sequence, there exists a subsequence such that for all .
Then T has a fixed point. Moreover, if X is ≤-directed, we have the uniqueness of the fixed point.
Proof Using Definition 2.3, we can define the binary relations and by the mappings :
and
In case , the functions α and β are well defined, because the altering functions and are null only, and only if , that is, which is not the case.
We can verify easily that and are 1-transitive.
Next, we claim that T is -contractive mappings. Indeed, in case , we easily get
and in case , we have
hence, our claim holds.
Moreover, from the monotone property of T, we get
and similarly, we have
Thus T is -preserving for . Now, if condition (iii) is satisfied, that is, T is continuous, the existence of a fixed point follows from Theorem 2.1. Suppose now, that the condition (iii′) is satisfied, and let be a nondecreasing sequence in X, that is, and for all n. Suppose also that as . From (iii′), there exists a subsequence such that for all k. This implies from the definition of α and β that and for all k, which implies for and for all k. In this case, the existence of a fixed point follows from Theorem 2.2.
To show the uniqueness, suppose that X is ≤-directed, that is, for all there exists a such that and , which implies from the definition of α and β that and . Hence, Theorem 2.3 gives us the uniqueness of this fixed point. □
4.3 Coupled fixed point theorems
Next, in order to prove a coupled fixed point results in partially ordered set, we need to define an order relation on the set .
Let be a partially ordered set endowed with a metric d, and let be a given mapping. We endow the product set with the partial order:
Definition 4.2 Let X be a set and binary relations for on defined by
Corollary 4.4 (Harjani et al. [6])
Let be a partially ordered set and suppose that there exists a metric d in X such that is a complete metric space. Suppose that the mapping is weakly -contractive, that is,
where ψ and φ are altering distance functions. Suppose also that the following conditions hold:
-
(i)
F is a mixed monotone mapping;
-
(ii)
there exists with ;
-
(iii)
F is continuous or is -biregular.
Then F has a coupled fixed point . Moreover, if is -bidirected, we have the uniqueness of the fixed point.
Proof The conclusions then follows directly from Corollary 3.1. □
4.4 Fixed point results for cyclic contractive mappings
In this section, we will derive from our results the fixed point theorem of Karapınar and Sadarangani [11] for cyclic weak -contractive mappings.
Definition 4.3 (Păcurar and Rus [16])
Let X be a nonempty set, m a positive integer and an operator. By definition, is a cyclic representation of X with respect to T if
-
1.
, are nonempty sets;
-
2.
, .
Definition 4.4 (Karapınar and Sadarangani [10])
Let be a metric space, let m be a positive integer, let be closed non-empty subsets of X, and let . An operator is called a cyclic weak -contraction if
-
1.
is a cyclic representation of Y with respect to T, and
-
2.
is an altering distance function such that
(30)
for any , , where .
Corollary 4.5 (Karapınar and Sadarangani [10])
Let be a complete metric space, let m be a positive integer, let be closed non-empty subsets of X and let . Suppose that is an altering distance function, and T is a cyclic weak φ-contraction, where is a cyclic representation of Y with respect to T. Then, T has a unique fixed point .
Proof The proof follows immediately from Corollary 3.3. □
References
Banach S: Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales. Fundam. Math. 1922, 3(1):133–181.
Berzig M: Coincidence and common fixed point results on metric spaces endowed with an arbitrary binary relation and applications. J. Fixed Point Theory Appl. 2013, 12(1–2):221–238.
Berzig M, Samet B: An extension of coupled fixed point’s concept in higher dimension and applications. Comput. Math. Appl. 2012, 63(8):1319–1334. 10.1016/j.camwa.2012.01.018
Dutta PN, Choudhury BS: A generalisation of contraction principle in metric spaces. Fixed Point Theory and Appl. 2008., 2008: Article ID 406368
Guo D, Lakshmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Anal. 1987, 11(5):623–632. 10.1016/0362-546X(87)90077-0
Harjani J, López B, Sadarangani K: Fixed point theorems for mixed monotone operators and applications to integral equations. Nonlinear Anal. 2011, 74(5):1749–1760. 10.1016/j.na.2010.10.047
Harjani J, Sadarangani K: Fixed point theorems for weakly contractive mappings in partially ordered sets. Nonlinear Anal. 2009, 71(7):3403–3410.
Harjani J, Sadarangani K: Generalized contractions in partially ordered metric spaces and applications to ordinary differential equations. Nonlinear Anal. 2010, 72(3):1188–1197.
Karapınar E: Fixed point theory for cyclic weak ϕ -contraction. Appl. Math. Lett. 2011, 24(6):822–825. 10.1016/j.aml.2010.12.016
Karapınar E, Sadarangani K:Fixed point theory for cyclic -contractions. Fixed Point Theory Appl. 2011., 2011: Article ID 69
Karapınar E, Samet B:Generalized contractive type mappings and related fixed point theorems with applications. Abstr. Appl. Anal. 2012., 2012: Article ID 793486
Khan MS, Swaleh M, Sessa S: Fixed point theorems by altering distances between the points. Bull. Aust. Math. Soc. 1984, 30(1):1–9. 10.1017/S0004972700001659
Kirk WA, Srinivasan PS, Veeramani P: Fixed points for mappings satisfying cyclical contractive conditions. Fixed Point Theory 2003, 4(1):79–89.
Moradi S, Farajzadeh A:On the fixed point of -weak and generalized -weak contraction mappings. Appl. Math. Lett. 2012, 25(10):1257–1262. 10.1016/j.aml.2011.11.007
Popescu O:Fixed points for -weak contractions. Appl. Math. Lett. 2011, 24(1):1–4. 10.1016/j.aml.2010.06.024
Păcurar M, Rus IA: Fixed point theory for cyclic φ -contractions. Nonlinear Anal. 2010, 72(3):1181–1187.
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Anal. 2001, 47(4):2683–2693. 10.1016/S0362-546X(01)00388-1
Samet B, Turinici M: Fixed point theorems on a metric space endowed with an arbitrary binary relation and applications. Commun. Math. Anal. 2012, 13(2):82–97.
Samet B, Vetro C, Vetro P: Fixed point theorems for α - ψ -contractive type mappings. Nonlinear Anal. 2012, 75(4):2154–2165. 10.1016/j.na.2011.10.014
Acknowledgements
The authors thank Professor Mircea-Dan Rus for his remarkable comments, suggestion and ideas that helped to improve this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Berzig, M., Karapınar, E. Fixed point results for -contractive mappings for a generalized altering distance. Fixed Point Theory Appl 2013, 205 (2013). https://doi.org/10.1186/1687-1812-2013-205
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-205


