Abstract
In this paper, we obtain some new fixed point theorems and existence theorems of solutions for the equation Ax = μx using properties of strictly convex (concave) function and theories of topological degree. Our results and methods are different from the corresponding ones announced by many others.
MSC: 47H09, 47H10
Similar content being viewed by others
1 Introduction
For convenience, we first recall the topological degree of 1-set-contractive fields due to Petryshyn [1].
Let E be a real Banach space, p ∈ E, Ω be a bounded open subset of E. Suppose that  is a 1-set-contractive operator such that
is a 1-set-contractive operator such that

In addition, if there exists a k-set-contractive operator  such that
such that

then (I - W)x ≠ p, ∀x ∈ ∂D, and so it is easy to see that deg(I - W, D, p) is well defined and independent of W. Therefore, we are led to define the topological degree as follows:

Without loss of generality, we set p = θ in the above definition.
Let  be a 1-set-contractive operator. A is said to be a semi-closed 1-set-contractive operator, if I -A is closed operator (see [2]).
be a 1-set-contractive operator. A is said to be a semi-closed 1-set-contractive operator, if I -A is closed operator (see [2]).
It should be noted that this class of operators, as special cases, includes completely continuous operators, strict set-contractive operators, condensing operators, semi-compact 1-set-contractive operators and others (see [2]).
Petryshyn [1] and Nussbaum [3] first introduced the topological degree of 1-set-contractive fields, studied its basic properties and obtained fixed point theorems of 1-set-contractive operators. Amann [4] and Nussbaum [5] have introduced the fixed point indices of k-set contractive operators (0 ≤ k < 1) and condensing operators to derive some fixed point theorems. As a complement, Li [2] has defined the fixed point index of 1-set-contractive operators and obtained some fixed point theorems of 1-set-contractive operators. Recently, Li [6] obtained some fixed point theorems for 1-set-contractive operators and existence theorems of solutions for the equation Ax = μx. Very recently, Xu [7] extended the results of Li [6] and obtained some fixed point theorems. In this paper, we continue to investigate boundary conditions, under which the topological degree of 1-set contractive fields, deg(I - A, Ω, p), is equal to unity or zero. Consequently, we obtain some new fixed point theorems and existence theorems of solutions for the equation Ax = μx using properties of strictly convex (concave) functions. Our results and methods are different from the corresponding ones announced by many others (e.g., Li [6], Xu [7]).
We need the following concepts and lemmas for the proof of our main results.
Suppose that  is a semi-closed 1-set-contractive operator and θ ∉ (I - A)∂Ω, then, by the standard method, we can easily see that the topological degree has the basic properties as follows:
is a semi-closed 1-set-contractive operator and θ ∉ (I - A)∂Ω, then, by the standard method, we can easily see that the topological degree has the basic properties as follows:
-
(a)
(Normalization) deg(I, Ω, p) = 1, when p ∈ Ω; deg(I, Ω, p) = 0, when p ∉ Ω;
-
(b)
(Solution property) If deg(I - A, Ω, θ) ≠ 0, then A has at least one fixed point in Ω.
-
(c)
(Additivity) For every pair of disjoint open subsets Ω1, Ω2 of Ω such that {x ∈ Ω |(I - A)x = 0} ⊂ Ω1 ∪ Ω2, we have
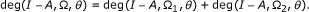
-
(d)
(Homotopy invariance) Let
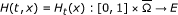 be a continuous operator such that
be a continuous operator such that 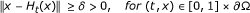
and the measure of non-compactness γ(H([0, 1] × Q)) ≤ γ(Q) for every
 . Then deg(I - H
t
, Ω, θ) = const, for any t ∈ [0, 1].
. Then deg(I - H
t
, Ω, θ) = const, for any t ∈ [0, 1]. -
(e)
Let B be an open ball with center θ,
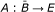 a semi-closed 1-set-contractive operator and (I - A)x ≠ 0 for all x ∈ ∂B. Suppose that A is odd on ∂B (i.e., A(-x) = Ax, for x ∈ ∂B), then deg(I - A, B, θ) ≠ 0.
a semi-closed 1-set-contractive operator and (I - A)x ≠ 0 for all x ∈ ∂B. Suppose that A is odd on ∂B (i.e., A(-x) = Ax, for x ∈ ∂B), then deg(I - A, B, θ) ≠ 0. -
(f)
(Change of base) Let p ≠ θ, then deg(I - A, Ω, p) = deg(I - A - p, Ω, θ).
Lemma 1.1. [7]. Let E be a real Banach space, Ω a bounded open subset of E and θ ∈ Ω.  is a semi-closed 1-set-contractive operator and satisfies the Leray-Schauder boundary condition
is a semi-closed 1-set-contractive operator and satisfies the Leray-Schauder boundary condition

then deg(I - A, Ω, θ) = 1 and so A has a fixed point in Ω.
Definition 1.2. Let D be a nonempty subset of R. If φ : D → R is a real function such that

then φ is called strictly convex function on D. If φ : D → R is a real function such that

then φ is called strictly concave function on D.
2 Main results
We are now in the position to apply the topological degree and properties of strictly convex (concave) function to derive some new fixed point theorems for semi-closed 1-set-contractive operators and existence theorems of solutions for the equation Ax = μx which generalize a great deal of well-known results and relevant recent ones.
Theorem 2.1. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist strictly convex function φ : R+ → R+with φ (0) = 0 and real function ϕ : R+ → R with ϕ (t) ≥ 1, for all t > 1, such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. If the operator A has a fixed point on ∂Ω, then A has at least one fixed point in  . Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
. Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
Suppose this is not true. Then there exists x0 ∈ ∂Ω, t0 ≥ 1 such that Ax0 = t0x0, i.e.,  . It is easy to see that ||Ax0|| ≠ 0 and t0 > 1.
. It is easy to see that ||Ax0|| ≠ 0 and t0 > 1.
From (1), we have

which implies

By strict convexity of φ and φ(0) = 0, we obtain

It is easy to see from (2) and (3) that

Noting that t0 > 1 and ϕ(t) ≥ 1, for all t > 1, we have

which contradicts (4), and so the condition (L-S) is satisfied. Therefore, it follows from Lemma 1.1 that the conclusions of Theorem 2.1 hold. □
Remark 2.2. If there exist convex function φ : R+ → R+, φ(0) = 0 and real function ϕ : R+ → R, ϕ (t) > 1, ∀t > 1 satisfied (1), the conclusions of Theorem 2.1 also hold.
Theorem 2.3. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist strictly concave function φ : R+ → R+with φ (0) = 0 and real function ϕ : R+ → R, ϕ (t) ≤ 1, ∀t > 1, such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. If the operator A has a fixed point on ∂Ω, then A has at least one fixed point in  . Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
. Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
Suppose this is not true. Then there exists x0 ∈ ∂Ω, t0 ≥ 1 such that Ax0 = t0x0, i.e.,  . It is easy to see that ||Ax0|| ≠ 0 and t0 > 1. From (5), we have
. It is easy to see that ||Ax0|| ≠ 0 and t0 > 1. From (5), we have

This implies that

By strict concavity of φ and φ (0) = 0, we obtain

It follows from (6) and (7) that

On the other hand, by t0 > 1 and ϕ(t) ≤ 1, ∀t > 1, we have

which contradicts (8), and so the condition (L-S) is satisfied. Therefore, it follows from Lemma 1.1 that the conclusions of Theorem 2.3 hold. □
Remark 2.4. If there exist concave function φ : R+ → R+, φ (0) = 0 and real function ϕ : R+ → R, ϕ (t) < 1, ∀t > 1 satisfied (5), the conclusions of Theorem 2.3 also hold.
Corollary 2.5. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist α ∈ (-∞, 0) ∪ (1, +∞) and β ≥ 0 such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. Putting φ(t) = tα , ϕ(t) = tβ , we have φ (t) is a strictly convex function with φ (0) = 0 and ϕ(t) ≥ 1, ∀t > 1. Therefore, from Theorem 2.1, the conclusions of Corollary 2.5 hold.. □
Remark 2.6. 1. Corollary 2.5 generalizes Theorem 2.2 of Xu [7] from α > 1 to α ∈ (-∞, 0) ∪ (1, +∞). Moreover, our methods are different from those in many recent works (e.g., Li [6], Xu [7]).
2. Putting α > 1, β = 0 in Corollary 2.5, we can obtain Theorem 5 of Li [6].
Corollary 2.7. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist α ∈ (0, 1) and β ≤ 0 such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. Putting φ(t) = tα , ϕ(t) = tβ , we have φ(t) is a strictly concave function with φ (0) = 0 and ϕ(t) ≤ 1, ∀t > 1. Therefore, from Theorem 2.3, the conclusions of Corollary 2.7 hold. □
Remark 2.8. Corollary 2.7 extends Theorem 8 of Li [6]. Putting β = 0 in Corollary 2.7, we can obtain Theorem 8 of Li [6].
Theorem 2.9. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist strictly convex function φ : R+ → R+with φ (0) = 0 and real function ϕ : R+ → R with ϕ(t) ≥ 1, for all t > 1, such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. If the operator A has a fixed point on ∂Ω, then A has at least one fixed point in  . Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
. Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
Suppose this is not true. Then there exists x0 ∈ ∂Ω, t0 ≥ 1 such that Ax0 = t0x0, i.e.,  . It is easy to see that ||Ax0|| ≠ 0 and t0 > 1. By virtue of (9), we have
. It is easy to see that ||Ax0|| ≠ 0 and t0 > 1. By virtue of (9), we have

which implies

By strict convexity of φ and φ (0) = 0, we obtain (3) holds. From (3) and (10), we have

Noting that t0 > 1 and ϕ(t) ≥ 1, for all t > 1, we have  , and so
, and so

which contradicts (11), and so the condition (L-S) is satisfied. Therefore, it follows from Lemma 1.1 that the conclusions of Theorem 2.9 hold. □
Remark 2.10. If there exist convex function φ : R+ → R+, φ (0) = 0 and real function ϕ : R+ → R, ϕ(t) > 1, ∀t > 1 satisfied (9), the conclusions of Theorem 2.9 also hold.
Theorem 2.11. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist strictly concave function φ : R+ → R+with φ (0) = 0 and real function ϕ : R+ → R, ϕ (t) ≤ 1, ∀t > 1, such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. If the operator A has a fixed point on ∂Ω, then A has at least one fixed point in  . Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
. Now suppose that A has no fixed points on ∂Ω. Next we shall prove that the condition (L-S) is satisfied.
Suppose this is not true. Then there exists x0 ∈ ∂Ω, t0 ≥ 1 such that Ax0 = t0x0, i.e.,  . It is easy to see that ||Ax0|| ≠ 0 and t0 > 1. By (12), we have
. It is easy to see that ||Ax0|| ≠ 0 and t0 > 1. By (12), we have

which implies

By strict concavity of φ and φ (0) = 0, we have (7) holds. From (7) and (13), we obtain

On the other hand, by t0 > 1, we have  . Therefore, it follows from ϕ(t) ≤ 1, ∀t > 1 that
. Therefore, it follows from ϕ(t) ≤ 1, ∀t > 1 that

which contradicts (14), and so the condition (L-S) is satisfied. Therefore, it follows from Lemma 1.1 that the conclusions of Theorem 2.11 hold. □
Remark 2.12. If there exist convex function φ : R+ → R+, φ (0) = 0 and real function ϕ : R+ → R, ϕ (t) > 1, ∀t > 1 satisfied (12), the conclusions of Theorem 2.11 also hold.
Corollary 2.13. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist α ∈ (-∞, 0)∪(1, +∞) and β ≥ 0 such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. From (15), we have

Taking φ(t) = tα , ϕ(t) = tβ , we have φ (t) is a strictly convex function with φ (0) = 0 and ϕ(t) ≥ 1, ∀t > 1. Therefore, from Theorem 2.9, the conclusions of Corollary 2.13 hold. □
Remark 2.14. 1. Corollary 2.13 generalizes Theorem 2.4 of Xu [7] from α > 1 to α ∈ (-∞, 0) ∪ (1, +∞). Moreover, our methods are different from those in many recent works (e.g., Li [6], Xu [7]).
2. Putting α > 1, β = 0 in Corollary 2.13, we can obtain Theorem 5 of Li [6].
Corollary 2.15. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist α ∈ (0, 1) and β ≤ 0 such that

then deg(I - A, Ω, θ) = 1 if A has no fixed point on ∂Ω, and so A has at least one fixed point in .
.
Proof. From (16), we have

Putting φ(t) = tα , ϕ(t) = tβ , we have φ (t) is a strictly concave function with φ (0) = 0 and ϕ(t) ≤ 1, ∀t > 1. Therefore, from Theorem 2.11, the conclusions of Corollary 2.15 hold. □
Remark 2.16. Corollary 2.15 extends Theorem 8 of Li [6]. Putting β = 0 in Corollary 2.15, we can obtain Theorem 8 of Li [6].
Theorem 2.17. Let E, Ω, A be the same as in Lemma 1.1. Moreover, if there exist α ∈ (-∞, 0)∪(1, +∞), β ≥ 0 and μ ≥ 1 such that

then the equation Ax = μx possesses a solution in .
.
Proof. Without loss of generality, suppose that  A has no fixed point on ∂Ω. From (17), we have
A has no fixed point on ∂Ω. From (17), we have

which implies

It is easy to see that  A is a semi-closed 1-set-contractive operator. It follows from Corollary 2.5 that
A is a semi-closed 1-set-contractive operator. It follows from Corollary 2.5 that  , and so the equation Ax = μx possesses a solution in
, and so the equation Ax = μx possesses a solution in  .
.
Remark 2.18. Similarly, from Corollary 2.7, Corollary 2.13 or Corollary 2.15, we can obtain the equation Ax = μx possesses a solution in  .
.
References
Petryshyn WV: Remark on condensing and k-set-contractive mappings. J. Math. Anal. Appl 1972, 39: 717–741. 10.1016/0022-247X(72)90194-1
Li GZ: The fixed point index and the fixed point theorems for 1- set-contraction mappings. Proc. Am. Math. Soc 1988, 104: 1163–1170.
Nussbaum RD: Degree theory for local condensing maps. J. Math. Anal. Appl 1972, 37: 741–766. 10.1016/0022-247X(72)90253-3
Amann H: Fixed point equations and nonlinear eigenvalue problems in ordered Banach space. SIAM Rev 1976, 18: 620–709. 10.1137/1018114
Nussbaum RD: The fixed index and asymptotic fixed point theorems for k-set-contractions. Bull. Am. Math. Soc 1969, 75: 490–495. 10.1090/S0002-9904-1969-12213-5
Li GZ, Xu SY, Duan HG: Fixed point theorems for 1-set-contractive operators in Banach spaces. Appl. Math. Lett 2006, 19: 403–412. 10.1016/j.aml.2005.02.035
Xu SY: New fixed point theorems for 1-set-contractive operators in Banach spaces. Nonlinear Anal 2007, 67: 938–944. 10.1016/j.na.2006.06.051
Acknowledgements
This study was supported by the Natural Science Foundation of Yancheng Teachers University under Grant(10YCKL022).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, S. The fixed point theorems of 1-set-contractive operators in Banach space. Fixed Point Theory Appl 2011, 15 (2011). https://doi.org/10.1186/1687-1812-2011-15
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-15




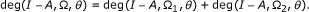
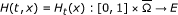 be a continuous operator such that
be a continuous operator such that 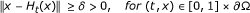
 . Then deg(I - H
t
, Ω, θ) = const, for any t ∈ [0, 1].
. Then deg(I - H
t
, Ω, θ) = const, for any t ∈ [0, 1].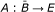 a semi-closed 1-set-contractive operator and (I - A)x ≠ 0 for all x ∈ ∂B. Suppose that A is odd on ∂B (i.e., A(-x) = Ax, for x ∈ ∂B), then deg(I - A, B, θ) ≠ 0.
a semi-closed 1-set-contractive operator and (I - A)x ≠ 0 for all x ∈ ∂B. Suppose that A is odd on ∂B (i.e., A(-x) = Ax, for x ∈ ∂B), then deg(I - A, B, θ) ≠ 0.