EVM and achievable data rate analysis of clipped OFDM signals in visible light communication

Abstract

Abstract

Orthogonal frequency division multiplexing (OFDM) has been considered for visible light communication (VLC); thanks to its ability to boost data rates as well as its robustness against frequency-selective fading channels. A major disadvantage of OFDM is the large dynamic range of its time-domain waveforms, making OFDM vulnerable to nonlinearity of light emitting diodes. DC-biased optical OFDM (DCO-OFDM) and asymmetrically clipped optical OFDM (ACO-OFDM) are two popular OFDM techniques developed for the VLC. In this article, we will analyze the performance of the DCO-OFDM and ACO-OFDM signals in terms of error vector magnitude (EVM), signal-to-distortion ratio (SDR), and achievable data rates under both average optical power and dynamic optical power constraints. EVM is a commonly used metric to characterize distortions. We will describe an approach to numerically calculate the EVM for DCO-OFDM and ACO-OFDM. We will derive the optimum biasing ratio in the sense of minimizing EVM for DCO-OFDM. In addition, we will formulate the EVM minimization problem as a convex linear optimization problem and obtain an EVM lower bound against which to compare the DCO-OFDM and ACO-OFDM techniques. We will prove that the ACO-OFDM can achieve the lower bound. Average optical power and dynamic optical power are two main constraints in VLC. We will derive the achievable data rates under these two constraints for both additive white Gaussian noise channel and frequency-selective channel. We will compare the performance of DCO-OFDM and ACO-OFDM under different power constraint scenarios.

Introduction

With rapidly growing wireless data demand and the saturation of radio frequency (RF) spectrum, visible light communication (VLC) [1–4] has become a promising candidate to complement conventional RF communication, especially for indoor and medium range data transmission. VLC uses white light emitting diodes (LEDs) which already provide illumination and are quickly becoming the dominant lighting source to transmit data. At the receiving end, a photo diode (PD) or an image sensor is used as light detector. VLC has many advantages including low-cost front-ends, energy-efficient transmission, huge (THz) bandwidth, no electromagnetic interference, no eye safety constraints like infrared, etc. [5]. In VLC, simple and low-cost intensity modulation and direct detection (IM/DD) techniques are employed, which means that only the signal intensity is modulated and there is no phase information. At the transmitter, the white LED converts the amplitude of the electrical signal to the intensity of the optical signal, while at the receiver, the PD or image sensor generates the electrical signal proportional to the intensity of the received optical signal. The IM/DD requires that the electric signal must be real-valued and unipolar (positive-valued).

Recently, orthogonal frequency division multiplexing (OFDM) has been considered for VLC; thanks to its ability to boost data rates and efficiently combat inter-symbol interference [5–10]. To ensure that the OFDM time-domina signal is real-valued, Hermitian symmetry condition must be satisfied in the frequency-domain. Three methods have been discussed in the literature for creating real-valued unipolar OFDM signal for VLC.

• (1) DC-biased optical OFDM (DCO-OFDM)—adding a DC bias to the original signal [6, 7, 11];

• (2) Asymmetrically clipped optical OFDM (ACO-OFDM)—only mapping the data to the odd subcarriers and clipping the negative parts without information loss [8];

• (3) Flip-OFDM—transmitting positive and negative parts in two consecutive unipolar symbols [10].

One disadvantage of OFDM is its high peak-to-average-power ratio (PAPR) due to the summation over a large number of terms [12]. The high PAPR or dynamic range of OFDM makes it very sensitive to nonlinear distortions. In VLC, the LED is the main source of nonlinearity. The nonlinear characteristics of LED can be compensated by digital pre-distortion (DPD) [13], but the dynamic range of any physical device is still limited. The input signal outside this range will be clipped. A number of papers [14–17] have studied the clipping effects on the RF OFDM signals. However, clipping in the VLC system has two important differences: (i) the RF baseband signal is complex-valued whereas time-domain signals in the VLC system are real-valued; (ii) the main power limitation for VLC is average optical power and dynamic optical power, rather than average electrical power and peak power as in RF communication. Therefore, most of the theory and analyses developed for RF OFDM are not directly applicable to optical OFDM. A number of papers [13, 18–20] have analyzed the LED nonlinearity on DCO-OFDM and ACO-OFDM and compared their bit error rate, power efficiency, bandwidth efficiency, etc.

In this article, we will investigate the performance of DCO-OFDM and ACO-OFDM signals in terms of error vector magnitude (EVM), signal-to-distortion ratio (SDR), and achievable data rates. EVM is a frequently used performance metric in modern communication standards. In [13, 19], the EVM is measured by simulations for varying power back-off and biasing levels. In this article, we will describe an approach to numerically calculate the EVM for DCO-OFDM and ACO-OFDM, and derive the optimum biasing ratio for DCO-OFDM. We will formulate the EVM minimization problem as a convex linear optimization problem and obtain an EVM lower bound. In contrast to [21] which investigated the achievable data rates for ACO-OFDM with only average optical power limitation, we will derive the achievable data rates subject to both the average optical power and dynamic optical power constraints. We will first derive the SDR for a given data-bearing subcarrier based on the Bussgang’s theory. Upon the SDR analysis, we will derive the achievable data rates for additive white Gaussian noise (AWGN) channel and frequency-selective channel. Finally, we will compare the performance of two optical OFDM techniques.

System model

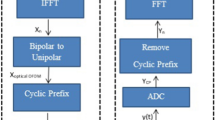
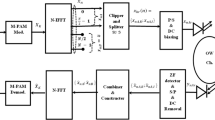
The system model discussed in this study is depicted in Figure 1. In an OFDM system, a discrete time-domain signal x =[x[0], x[1], …, x[N-1]] is generated by applying the inverse DFT (IDFT) operation to a frequency-domain signal X =[X₀, X₁, …, X_N-1] as

$$\begin{array}{l}x\left[n\right]=\text{IDFT}\left(X_k\right)=\frac{1}{\sqrt{N}}\sum _{k=0}^{N-1}{X}_{k}exp(j2\mathrm{\Pi kn}/N),\\ 0\le n\le N-1,\end{array}$$

(1)

Figure 1

OFDM system model in VLC.

where $j=\sqrt{-1}$ and N are the size of IDFT, assumed to be an even number in this article. In a VLC system using LED, the IM/DD schemes require that the electric signal be real-valued and unipolar (positive-valued). According to the property of IDFT, a real-valued time-domain signal x[n] corresponds to a frequency-domain signal X _k that is Hermitian symmetric, i.e.,

$$\begin{array}{l}{X}_k=X_{N-k}^{\ast },1\le k\le N-1,\\ X_k\in \mathbb{R},k=0,N/2,\end{array}$$

(2)

where ∗ denotes complex conjugate.

In Figure 1, y[n] is obtained from x[n] after both a clipping and a biasing operation are implemented. The resulting signal, y[n], is non-negative (i.e., y[n] ≥ 0) and has a limited dynamic range. In a VLC system, the light emitted is used for illumination and communication simultaneously. The intensity of light emitted by the LED is proportional to y[n], while the electrical power is proportional to y²[n]. In the optical communication literature, the average optical power of the LED input signal y[n] is defined as

$$O_y\triangleq \mathcal{E}\left\{y\right[n\left]\right\},$$

(3)

where $\mathcal{E}[·]$ denotes statistical expectation. Usually, the VLC system operates under some average optical power constraint P _A , i.e.,

$$O_y\le P_A.$$

(4)

This constraint is in place for two reasons: (i) the system power consumption needs to be kept under a certain limit, (ii) the system should still be able to communicate even under dim illumination conditions. The VLC system is further limited by the dynamic range of the LED. In this article, we assume that the DPD has perfectly linearized the LED between the interval [P _L ,P _H ], where P _L is the turn-on voltage (TOV) for the LED. If the TOV is provided by an analog module at the LED and we assume that LED is already turned on, the linear range for the input signal is [0, P _H -P _L ]. We define the dynamic optical power of y[n] as

$$G_y\triangleq max\left(y\left[n\right]\right)-min\left(y\left[n\right]\right).$$

(5)

G _y should be constrained by P _H -P _L as

$$G_y\le P_H-P_L.$$

(6)

Moreover, y[n] must be non-negative, i.e., y[n] ≥ 0.

According to the Central Limit Theorem, x[n] is approximately Gaussian distributed with zero mean and variance σ² with probability density function (pdf):

$$p\left(x\left[n\right]=z\right)=\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right),$$

(7)

where $\varphi \left(x\right)=\frac{1}{\sqrt{2\Pi }}{e}^{-\frac{1}{2}{x}^2}$ is the pdf of the standard Gaussian distribution. As a result, the time-domain OFDM signal x[n] tends to occupy a large dynamic range and is bipolar. In order to fit into the dynamic range of the LED, clipping is often necessary, i.e.,

$$\begin{array}{c}\bar{x}\left[n\right]=\left\{\begin{array}{cc}{c}_u,& \hfill x\left[n\right]>c_u\\ x\left[n\right],& \hfill c_l\le x\left[n\right]\le c_u\\ c_l,& \hfill x\left[n\right]<c_l\end{array}\right.\end{array}$$

(8)

where c _u denotes the upper clipping level, and c _l denotes the lower clipping level. In order for the LED input y[n] to be non-negative, we may need to add a DC bias B to the clipped signal $\bar{x}\left[n\right]$ to obtain

$$\begin{array}{c}y\left[n\right]=\bar{x}\left[n\right]+B,0\le n\le N-1.\end{array}$$

(9)

For y[n] ≥ 0, we need B = -c _l .

To facilitate the analysis, we define the clipping ratio γ and the biasing ratio ς as

$$\gamma \triangleq \frac{(c_u-c_l)/2}{\sigma }$$

(10)

$$\varsigma \triangleq \frac{B}{c_u-c_l}=\frac{-c_l}{c_u-c_l}$$

(11)

Thus, the upper and lower clipping levels can be written as

$$c_u=2\mathrm{\sigma \gamma }(1-\varsigma ),$$

(12)

$$c_l=-2\mathrm{\sigma \gamma \varsigma .}$$

(13)

The ratios γ and ς can be adjusted independently causing c _u and c _l to vary.

Clipping in the time-domain gives rise to distortions on all subcarriers in the frequency domain. On the other hand, DC-bias only affects the DC component in the frequency-domain. The clipped and DC-biased signal y[n] is then converted into analog signal and subsequently modulate the intensity of the LED. At the receiver, the photodiode, or the image sensor, converts the received optical signal to electrical signal and transforms it to digital form. The received sample can be expressed as

$$r\left[n\right]=\left(\bar{x}\right[n]+B)\otimes h\left[n\right]+w\left[n\right],$$

(14)

where h[n] is the impulse response of the wireless optical channel, w[n] is AWGN, and ⊗ denotes convolution. By taking the DFT of Equation (14), we can obtain the received data on the k th subcarrier as

$$R_k={\bar{X}}_k{H}_k+W_k,k\ne 0,$$

(15)

where H _k is the channel frequency response on the k th subcarrier.

Based on the subcarrier arrangement, DC-biasing, or transmission scheme, several optical OFDM techniques have been proposed in the literature. In this article, we will focus on the performance analysis of two widely studied optical OFDM techniques, namely, DCO-OFDM and ACO-OFDM. In the following, we shall use superscripts ^(D) and ^(A) to indicate DCO-OFDM and ACO-OFDM, respectively.

In DCO-OFDM, subcarriers of the frequency-domain signal X^(D) are arranged as

$$\begin{array}{ll}{\mathbf{X}}^{\left(D\right)}=[0& X_1^{\left(D\right)}{X}_2^{\left(D\right)}\dots X_{N/2-1}^{\left(D\right)}0X_{N/2-1}^{\ast \left(D\right)}\dots \\ \left.X_2^{\ast \left(D\right)}{X}_1^{\ast \left(D\right)}\right]\end{array}$$

(16)

where the 0th and N/2th subcarriers are null (do not carry data). Equation (16) reveals Hermitian symmetry with respect to k = N/2. Let ${\mathcal{K}}_d$ denote the set of data-carrying subcarriers with cardinality $\left|{\mathcal{K}}_d\right|$. The set of data-carrying subcarriers for DCO-OFDM is ${\mathcal{K}}_d^{\left(D\right)}=\{1,2,\dots ,N/2-1,N/2+1,\dots ,N-2,N-1\}$ and $\left|{\mathcal{K}}_d^{\left(D\right)}\right|=N-2$. The time-domain signal x^(D)[n] can be obtained as

$$\begin{array}{ccc}{x}^{\left(D\right)}\left[n\right]& =& \frac{2}{\sqrt{N}}\sum _{k=1}^{N/2-1}\left(\mathcal{R}\left(X_k^{\left(D\right)}\right)cos(2\mathrm{\Pi kn}/N)\right.\\ \left.-\Im \left(X_k^{\left(D\right)}\right)sin(2\mathrm{\Pi kn}/N)\right),\end{array}$$

(17)

which is real-valued. In DCO-OFDM, we first obtain a clipped signal ${\bar{x}}^{\left(D\right)}\left[n\right]$ similar to the procedure in (8), and then add DC-bias B = -c _l to obtain the LED input signal

$$\begin{array}{c}{y}^{\left(D\right)}\left[n\right]={\bar{x}}^{\left(D\right)}\left[n\right]+B=\left\{\begin{array}{cc}{c}_u-c_l,& x^{\left(D\right)}\left[n\right]>c_u\hfill \\ x^{\left(D\right)}\left[n\right]-c_l,& c_l\le x^{\left(D\right)}\left[n\right]\le c_u\hfill \\ 0,& x^{\left(D\right)}\left[n\right]<c_l\hfill \end{array}\right.\end{array}$$

(18)

In the frequency domain,

$$\begin{array}{c}{Y}_k^{\left(D\right)}=X_k^{\left(D\right)}+C_k,\forall k\ne 0,\end{array}$$

(19)

where C _k is clipping noise on the k th subcarrier.

In ACO-OFDM, only odd subcarriers of the frequency-domain signal X^(A) carry data

$$\begin{array}{ccc}{X}^{\left(A\right)}& =& \left[0X_1^{\left(A\right)}0X_3^{\left(A\right)}\dots 0X_{N/2-1}^{\left(A\right)}\right.\\ \left.0X_{N/2-1}^{\ast \left(A\right)}\dots 0X_3^{\ast \left(A\right)}0X_1^{\ast \left(A\right)}\right],\end{array}$$

(20)

and X^(A)meets the Hermitian symmetry condition (2). The set of data-carrying subcarriers for ACO-OFDM is ${\mathcal{K}}_d^{\left(A\right)}=\{1,3,\dots ,N-1\}$ and $\left|{\mathcal{K}}_d^{\left(A\right)}\right|=N/2$. Thus, the time-domain signal x^(A)[n] can be obtained as

$$\begin{array}{ll}{x}^{\left(A\right)}\left[n\right]=\frac{2}{\sqrt{N}}\sum _{q=0}^{N/4-1}& \left(\mathfrak{R}\left(X_{2q+1}^{\left(A\right)}\right)cos\left(2\Pi (2q+1)n/N\right)\right.\\ \left.-\mathfrak{J}\left(X_{2q+1}^{\left(A\right)}\right)sin\left(2\Pi (2q+1)n/N\right)\right),\end{array}$$

(21)

which is real-valued. It follows easily that x^(A)[n] satisfies the following negative half symmetry condition:

$$x^{\left(A\right)}[n+N/2]=-x^{\left(A\right)}\left[n\right],n=0,1,\dots ,N/2-1.$$

(22)

Denote by z[n] a generic discrete-time signal that satisfies z[n + N/2] = -z[n], n = 0, 1,…,N/2-1 and by $\bar{z}\left[n\right]$ its clipped version where the negative values are removed, i.e.,

$$\begin{array}{c}\bar{z}\left[n\right]=\left\{\begin{array}{cc}z\left[n\right],& z\left[n\right]\ge 0,\\ 0,& \text{otherwise}.\end{array}\right.\end{array}$$

(23)

It was proved in [22] that in the frequency-domain,

$${\bar{Z}}_k=\frac{1}{2}{Z}_k,\forall k\text{odd}.$$

(24)

In ACO-OFDM, we obtain the LED input signal y^(A)[n] via

$$\begin{array}{l}{y}^{\left(A\right)}\left[n\right]=\left\{\begin{array}{cc}{c}_u,& x^{\left(A\right)}\left[n\right]>c_u\hfill \\ x^{\left(A\right)}\left[n\right],\hfill & 0\le x^{\left(A\right)}\left[n\right]\le c_u\hfill \\ 0,& x^{\left(A\right)}\left[n\right]<0\hfill \end{array}\right.\end{array}$$

(25)

Equation (25) can be regarded as a 2-step clipping process, whereby we first remove those negative values in x^(A)[n], and then replace those x^(A)[n] values that exceed c _u by c _u . Since x^(A)[n] satisfies (22), we infer based on (24) that

$$\begin{array}{c}{Y}_k^{\left(A\right)}=\frac{1}{2}{X}_k^{\left(A\right)}+C_k,\forall k,\end{array}$$

(26)

where C _k is clipping noise on the k th subcarrier in the frequency-domain. For ACO-OFDM, no DC-biasing is necessary and thus the biasing ratio ς = 0.

As an example, suppose that we need to transmit a sequence of eight quadrature phase-shift keying (QPSK) symbols. Table 1 shows the subcarrier arrangement for DCO-OFDM, whereas Table 2 shows the subcarrier arrangement for ACO-OFDM. The time-main signals x^(D)[n] and x^(A)[n] and the corresponding LED input signals y^(D)[n] and y^(A)[n] are shown in Figure 2. We see that in x^(A)[n], the last 16 values are a repetition of the first 16 values but with the opposite sign. It takes ACO-OFDM more bandwidth than DCO-OFDM to transmit the same message, although ACO-OFDM is less demanding in terms of dynamic range requirement of the LED and power consumption.

Table 1 DCO-OFDM subcarrier arrangement for transmitting eight QPSK symbols—an example

Table 2 ACO-OFDM subcarrier arrangement for transmitting eight QPSK symbols—an example

Figure 2

An example of x^(D)[n] , y^(D)[n] , x^(A)[n] , and y^(A)[n] to convey a sequence eight QPSK symbols. For DCO-OFDM, γ = 1.41 = 3 dB, ς = 0.45, c _l  = -1.70, c _u  = 2.07, B = 1.70; for ACO-OFDM, γ = 0.79 = -2 dB, ς = 0, c _l  = 0, c _u  = 1.59, B = 0.

EVM analysis

EVM is a figure-of-merit for distortions. Let ${\mathbf{X}}^{†}=[X_0^{†},X_1^{†},\dots ,X_{N-1}^{†}]$ denote the N-length DFT of the modified time-domain signal x^†. EVM can be defined as

$$\xi ({\mathbf{X}}^{\left(r\right)},{\mathbf{X}}^{†})\triangleq \sqrt{\frac{\mathcal{E}\left[{\sum }_{k\in {\mathcal{K}}_d}|X_k^{\left(r\right)}-X_k^{†}{|}^2\right]}{\mathcal{E}\left[{\sum }_{k\in {\mathcal{K}}_d}|X_k^{\left(r\right)}{|}^2\right]}},$$

(27)

where ${\mathbf{X}}^{\left(r\right)}=[X_0^{\left(r\right)},X_1^{\left(r\right)},\dots ,X_{N-1}^{\left(r\right)}]$ denotes the reference constellation. For DCO-OFDM, $X_k^{\left(r\right)}=X_k^{\left(D\right)}$ for $k\in {\mathcal{K}}_d^{\left(D\right)}$. For ACO-OFDM, $X_k^{\left(r\right)}=\frac{1}{2}{X}_k^{\left(A\right)}$ for $k\in {\mathcal{K}}_d^{\left(A\right)}$.

EVM calculation

In DCO-OFDM, clipping in the time-domain generates distortions on all the subcarriers. We denote the clipping error power by ${\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}={\sum }_{k\in {\mathcal{K}}_d^{\left(D\right)}}\mathcal{E}\left[\right|X_k^{\left(D\right)}-{\bar{X}}_k^{\left(D\right)}{|}^2]$. Since the sum distortion power on the 0th and N/2th subcarriers is small relative to the total distortion power of N subcarriers, according to the Parseval’s theorem, we can approximate ${\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}$ as

$$\begin{array}{ll}{\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}& =\sum _{k\in {\mathcal{K}}_d^{\left(D\right)}}\mathcal{E}\left[\right|X_k^{\left(D\right)}-{\bar{X}}_k^{\left(D\right)}{|}^2]\\ \approx \sum _{n=0}^{N-1}\mathcal{E}\left[\right|x^{\left(D\right)}\left[n\right]-{\bar{x}}^{\left(D\right)}\left[n\right]{|}^2]\\ =N\left(\underset{c_u}{\overset{\infty }{\int }}{(z-c_u)}^2\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\right.\\ \left.+\underset{-\infty }{\overset{c_l}{\int }}{(z-c_l)}^2\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\right)\\ =N{\sigma }^2\left(1+4{\gamma }^2{(1-\varsigma )}^2-2\gamma (1-\varsigma )\varphi \left(2\gamma (1-\varsigma )\right)\right.\\ -2\mathrm{\gamma \varsigma \varphi }\left(2\mathrm{\gamma \varsigma }\right)-\Phi \left(2\gamma (1-\varsigma )\right)\\ -4{\gamma }^2{(1-\varsigma )}^2\Phi \left(2\gamma (1-\varsigma )\right)\\ \left.+\Phi \left(-2\mathrm{\gamma \varsigma }\right)+4{\gamma }^2{\varsigma }^2\Phi \left(-2\mathrm{\gamma \varsigma }\right)\right),\end{array}$$

(28)

where $\Phi \left(x\right)=\underset{-\infty }{\overset{x}{\int }}\varphi \left(t\right)\mathit{dt}$. Thus, we obtain the EVM for the DCO-OFDM scheme as

$$\begin{array}{ll}{\xi }_{\gamma ,\varsigma }^{\left(D\right)}& =\sqrt{\frac{{\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}}{N{\sigma }^2}}\\ =\left(1+4{\gamma }^2{(1-\varsigma )}^2-2\gamma (1-\varsigma )\varphi \left(2\gamma (1-\varsigma )\right)\right.\\ -2\mathrm{\gamma \varsigma \varphi }\left(2\mathrm{\gamma \varsigma }\right)-\Phi \left(2\gamma (1-\varsigma )\right)\\ -4{\gamma }^2{(1-\varsigma )}^2\Phi \left(2\gamma (1-\varsigma )\right)+\Phi \left(-2\mathrm{\gamma \varsigma }\right)\\ {\left.+4{\gamma }^2{\varsigma }^2\Phi \left(-2\mathrm{\gamma \varsigma }\right)\right)}^{1/2}.\end{array}$$

(29)

To find the optimum biasing ratio ς^⋆, we take the first-order partial derivative and the second-order partial derivative of ${\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}$ with respect to the biasing ratio ς

$$\begin{array}{ll}\frac{\partial {\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}}{\mathrm{\partial \varsigma }}& =N{\sigma }^2\left(4\mathrm{\gamma \varphi }\left(2\gamma (1-\varsigma )\right)-4\mathrm{\gamma \varphi }\left(2\mathrm{\gamma \varsigma }\right)\right.\\ \left.-8{\gamma }^2(1-\varsigma )\Phi \left(2\gamma (\varsigma -1)\right)+8{\gamma }^2\mathrm{\varsigma \Phi }\left(-2\mathrm{\gamma \varsigma }\right)\right),\end{array}$$

(30)

$$\begin{array}{l}\frac{{\partial }^2{\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}}{\partial {\varsigma }^2}=N{\sigma }^2\left(8{\gamma }^2\Phi \left(2\gamma (\varsigma -1)\right)+8{\gamma }^2\Phi \left(-2\mathrm{\gamma \varsigma }\right)\right).\end{array}$$

(31)

We can see that if ς=0.5, $\partial {\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}/\mathrm{\partial \varsigma }=0$. The second-order partial derivative ${\partial }^2{\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}/\partial {\varsigma }^2>0$ for all ς. Hence, if ς < 0.5, $\partial {\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}/\mathrm{\partial \varsigma }<0$. If ς > 0.5, $\partial {\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}/\mathrm{\partial \varsigma }>0$. Therefore, ς^⋆ = 0.5 is the optimum biasing ratio which minimizes ${\bar{P}}_{\gamma ,\varsigma }^{\left(D\right)}$. By substituting ς^⋆ into Equation (29) we obtain the EVM for the DCO-OFDM scheme at the optimum biasing ratio as

$$\begin{array}{ll}{\xi }_{\gamma ,{\varsigma }^{\ast }}^{\left(D\right)}& =\sqrt{\frac{{\bar{P}}_{\gamma ,{\varsigma }^{\ast }}^{\left(D\right)}}{N{\sigma }^2}}\\ =\sqrt{2(1+{\gamma }^2)\Phi (-\gamma )-2\mathrm{\gamma \varphi }\left(\gamma \right)}.\end{array}$$

(32)

Remark 1

• (i) ς ^⋆ = 0.5 is the optimum biasing ratio for DCO-OFDM, regardless of the clipping ratio. (ii) When ς = 0.5, we infer that c _u  = -c _l , i.e., when the x ^(D)[n] waveform is symmetrically clipped at the negative and positive tails, the clipping error power is always less than that when the two tails are asymmetrically clipped (i.e., when c _u  ≠ c _l or when ς ≠ 0.5).

Denote by e[n], n = 0, 1, …, N - 1 a generic discrete-time signal with DFT E _k , k = 0, 1, …, N - 1. When k is odd, E _k can be written as

$$\begin{array}{lcl}{E}_k& =& \frac{1}{\sqrt{N}}\sum _{n=0}^{N-1}e\left[n\right]exp\left(-j2\Pi \frac{\mathit{kn}}{N}\right)\\ =& \frac{1}{\sqrt{N}}\sum _{n=0}^{N/2-1}e\left[n\right]exp\left(-j2\Pi \frac{\mathit{kn}}{N}\right)\\ +\frac{1}{\sqrt{N}}\sum _{n=0}^{N/2-1}e[n+N/2]exp\left(-j2\Pi \frac{\mathit{kn}}{N}-\mathrm{jk\Pi }\right)\\ =& \frac{1}{\sqrt{N}}\sum _{n=0}^{N/2-1}\left(e\left[n\right]-e[n+N/2]\right)exp\left(-j2\Pi \frac{\mathit{kn}}{N}\right).\end{array}$$

(33)

Let k = 2q + 1, q = 0, 1, …, N / 2 - 1, Equation (33) can be further written as

$$\begin{array}{lcl}{E}_{2q+1}& =& \frac{1}{\sqrt{N}}\sum _{n=0}^{N/2-1}\left(e\left[n\right]-e[n+N/2]\right)\\ \times exp\left(-j2\Pi \frac{\mathit{qn}}{N/2}-j2\Pi \frac{n}{N}\right)\\ =& \frac{1}{\sqrt{N}}\sum _{n=0}^{N/2-1}exp\left(-j2\Pi \frac{n}{N}\right)\left(e\left[n\right]-e[n+N/2]\right)\\ \times exp\left(-j2\Pi \frac{\mathit{qn}}{N/2}\right)\end{array}$$

(34)

Therefore, ${\{E_k=E_{2q+1}\}}_{q=0}^{N/2-1}$ can be viewed as the DFT coefficients of a new discrete-time sequence $\underset{n=0}{\overset{N/2-1}{\{exp\left(-j2\Pi \frac{n}{N}\right)\left(e\left[n\right]-e[n+N/2]\right)\}}}$. Applying the Parseval’s theorem to $\underset{n=0}{\overset{N/2-1}{\{exp\left(-j2\Pi \frac{n}{N}\right)(e\left[n\right]-e[n+N/2]\left)\right\}}}$, we obtain,

$$\begin{array}{lcl}\sum _{k=\text{odd}}|E_k{|}^2& =& \sum _{q=0}^{N/2-1}|E_{2q+1}{|}^2\\ =& \frac{1}{2}\sum _{n=0}^{N/2-1}{\left(e\left[n\right]-e[n+N/2]\right)}^2.\end{array}$$

(35)

In ACO-OFDM, we denote the clipping error power by ${\bar{P}}_{\gamma }^{\left(A\right)}={\sum }_{k\in {\mathcal{K}}_d^{\left(A\right)}}\mathcal{E}\left[{\left|X_k^{\left(A\right)}/2-{\bar{X}}_k^{\left(A\right)}\right|}^2\right]$. According to (35), we can calculate ${\bar{P}}_{\gamma }^{\left(A\right)}$ as

$$\begin{array}{lcl}{\bar{P}}_{\gamma }^{\left(A\right)}& =& \sum _{k\in {\mathcal{K}}_d^{\left(A\right)}}\mathcal{E}\left[{\left|X_k^{\left(A\right)}/2-{\bar{X}}_k^{\left(A\right)}\right|}^2\right]\\ =& \frac{1}{2}\sum _{n=0}^{N/2-1}\mathcal{E}\left[\left(\frac{x^{\left(A\right)}\left[n\right]}{2}-{\bar{x}}^{\left(A\right)}\left[n\right]-\frac{x^{\left(A\right)}[n+N/2]}{2}\right.\right.\\ \left.{\left.+{\bar{x}}^{\left(A\right)}[n+N/2]\right)}^2\right]\\ =& \frac{N}{4}\mathcal{E}\left[{\left(x^{\left(A\right)}\left[n\right]-{\bar{x}}^{\left(A\right)}\left[n\right]+{\bar{x}}^{\left(A\right)}[n+N/2]\right)}^2\right]\\ =& \frac{N}{4}\underset{-\infty }{\overset{-c_u}{\int }}{(z+c_u)}^2\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\\ +\frac{N}{4}\underset{c_u}{\overset{\infty }{\int }}{(z-c_u)}^2\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\\ =& \frac{N}{2}{\sigma }^2\left(-2\mathrm{\gamma \varphi }\left(2\gamma \right)+\Phi \left(-2\gamma \right)+4{\gamma }^2\Phi \left(-2\gamma \right)\right).\end{array}$$

(36)

Then we obtain the EVM for the ACO-OFDM scheme as

$$\begin{array}{lcl}{\xi }_{\gamma }^{\left(A\right)}& =& \sqrt{\frac{{\bar{P}}_{\gamma }^{\left(A\right)}}{{\sum }_{k\in {\mathcal{K}}_d^{\left(A\right)}}\mathcal{E}\left[{\left|X_k^{\left(A\right)}/2\right|}^2\right]}}=\sqrt{\frac{4{\bar{P}}_{\gamma ,0}^{\left(A\right)}}{N{\sigma }^2}}\\ =& \sqrt{-4\mathrm{\gamma \varphi }\left(2\gamma \right)+2\Phi \left(-2\gamma \right)+8{\gamma }^2\Phi \left(-2\gamma \right)}.\end{array}$$

(37)

Lower bound on the EVM

Let us consider the setting

$$\widehat{x}\left[n\right]=x\left[n\right]+c\left[n\right],0\le n\le N-1,$$

(38)

where x[n] is the original signal, c[n] is a distortion signal, and the resulting $\widehat{x}\left[n\right]$ is expected to have a limited dynamic range

$$max\left(\widehat{x}\right[n\left]\right)-min\left(\widehat{x}\right[n\left]\right)\le 2\mathrm{\gamma \sigma .}$$

(39)

In (38), all quantities involved are real-valued.

Clipping can produce one such $\widehat{x}\left[n\right]$ signal, but there are other less straightforward algorithms that can generate other $\widehat{x}\left[n\right]$ waveforms that also satisfy (39).

In the frequency-domain,

$${\widehat{X}}_k=X_k+C_k.$$

(40)

Since x[n], c[n], and $\widehat{x}\left[n\right]$ are all real-valued, X _k , C _k , and ${\widehat{X}}_k$ all should satisfy the Hermitian symmetry condition (2). Therefore, c[n] has the form

$$\begin{array}{ll}c\left[n\right]=& \frac{2}{\sqrt{N}}\sum _{k=1}^{N/2-1}\left(\mathcal{R}\left(C_k\right)cos(2\mathrm{\Pi kn}/N)-\Im \left(C_k\right)sin(2\mathrm{\Pi kn}/N)\right)\\ +\frac{1}{\sqrt{N}}{C}_0+\frac{1}{\sqrt{N}}{C}_{N/2}cos\left(\mathrm{\Pi n}\right)\end{array}$$

(41)

We are interested in knowing the lowest possible EVM,

$$\xi =\sqrt{\frac{\mathcal{E}\left[{\sum }_{k\in {\mathcal{K}}_d}|C_k{|}^2\right]}{\mathcal{E}\left[{\sum }_{k\in {\mathcal{K}}_d}|X_k{|}^2\right]}}$$

(42)

among all such $\widehat{x}\left[n\right]$ waveforms. Afterwards, we can compare the EVM from the DCO-OFDM and ACO-OFDM methods to get a sense of how far these algorithms are from being optimum (in the EVM sense).

We formulate the following linear optimization problem:

$$\begin{array}{ll}\text{minimize}& \sum _{k\in {\mathcal{K}}_d}|C_k{|}^2\\ \text{subject to}& max\left(\widehat{x}\left[n\right]\right)-min\left(\widehat{x}\left[n\right]\right)\le 2\mathrm{\gamma \sigma }\\ \widehat{x}\left[n\right]=x\left[n\right]+\frac{2}{\sqrt{N}}\sum _{k=1}^{N/2-1}\left(\mathcal{R}\left(C_k\right)cos(2\mathrm{\Pi kn}/N)\right.\\ \left.-\Im \left(C_k\right)sin(2\mathrm{\Pi kn}/N)\right)\\ +\frac{1}{\sqrt{N}}{C}_0+\frac{1}{\sqrt{N}}{C}_{N/2}cos\left(\mathrm{\Pi n}\right),\\ 0\le n\le N-1\\ C_0,C_{N/2}\in \mathbb{R}\end{array}$$

(43)

When the distortion of each OFDM symbol is minimized by the above convex optimization approach, the corresponding EVM of $\widehat{x}\left[n\right]$ (which is proportional to $\sqrt{\mathcal{E}\left[{\sum }_{k\in {\mathcal{K}}_d}|C_k{|}^2\right]}$) serves as the lower bound for the given dynamic range 2γσ.

Optimality for ACO-OFDM

In this section, we will prove that the ACO-OFDM scheme achieves the minimum EVM and thus is optimal in the EVM sense.

For ACO-OFDM, let us write

$$\widehat{x}\left[n\right]=x^{\left(A\right)}\left[n\right]+c\left[n\right],$$

(44)

where c[n] is the clipping noise to ensure that $\widehat{x}\left[n\right]$ has a limited dynamic range as described in (39). In the frequency-domain, we have

$${\widehat{X}}_k=X_k^{\left(A\right)}+C_k$$

(45)

where the $X_k^{\left(A\right)}$ subcarriers are laid out as in (20). According to (35), when k is odd, the objective function in (43) can be written as

$$\begin{array}{ccc}\sum _{k=\text{odd}}|C_k{|}^2& =& \frac{1}{2}\sum _{n=0}^{N/2-1}{\left(c\right[n]-c[n+N/2\left]\right)}^2.\end{array}$$

(46)

The dynamic range constraints in problem (43) can be viewed as two constraints put together.

$$\begin{array}{l}max\left(x^{\left(A\right)}\left[n\right]+c\left[n\right]\right)-min\left(x^{\left(A\right)}\left[n\right]+c\left[n\right]\right)\le 2\mathrm{\gamma \sigma },\\ 0\le n\le N/2-1,\end{array}$$

(47)

$$\begin{array}{l}max\left(x^{\left(A\right)}\left[n\right]+c\left[n\right]\right)-min\left(x^{\left(A\right)}\left[n\right]+c\left[n\right]\right)\le 2\mathrm{\gamma \sigma },\\ N/2\le n\le N-1.\end{array}$$

(48)

Since x^(A)[n] = -x^(A)[n - N / 2] when N / 2 ≤ n ≤ N - 1, Equation (48) can be further written as

$$\begin{array}{l}max\left(x^{\left(A\right)}\left[n\right]-c[n+N/2]\right)\\ -min\left(x^{\left(A\right)}\left[n\right]-c[n+N/2]\right)\le 2\mathrm{\gamma \sigma },\\ 0\le n\le N/2-1.\end{array}$$

(49)

From Equations (46), (47), and (49), the problem (43) can be recast as

$$\begin{array}{ll}\text{minimize}& \sum _{n=0}^{N/2-1}{c}^2\left[n\right]\\ \text{subject to}& max\left(x^{\left(A\right)}\left[n\right]+c\left[n\right]\right)-min\left(x^{\left(A\right)}\left[n\right]+c\left[n\right]\right)\\ \le 2\mathrm{\gamma \sigma },0\le n\le N/2-1\end{array}$$

(50)

which is equivalent to

$$\begin{array}{ll}\text{minimize}& \sum _{n=0}^{N/2-1}{c}^2\left[n\right]\\ \text{subject to}& x^{\left(A\right)}\left[n\right]+c\left[n\right]\le 2\mathrm{\gamma \sigma },0\le n\le N/2-1\\ x^{\left(A\right)}\left[n\right]+c\left[n\right]\ge 0,0\le n\le N/2-1\end{array}$$

(51)

In Appendix, we prove that the solution c^⋆[n] to (51) yields

$$\begin{array}{l}{\bar{x}}^{\left(A\right)}\left[n\right]=x^{\left(A\right)}\left[n\right]+c^{\star }\left[n\right]=\left\{\begin{array}{cc}2\mathrm{\gamma \sigma },& x^{\left(A\right)}\left[n\right]>2\mathrm{\gamma \sigma }\hfill \\ x^{\left(A\right)}\left[n\right],& 0\le x^{\left(A\right)}\left[n\right]\le 2\mathrm{\gamma \sigma }\hfill \\ 0,& x^{\left(A\right)}\left[n\right]<0\hfill \end{array}\right.\end{array}$$

(52)

and thus the ACO-OFDM scheme is optimum in the EVM sense.

SDR analysis

Based on the Bussgang’s theorem [23], any nonlinear function of x[n] can be decomposed into a scaled version of x[n] plus a distortion term d[n] that is uncorrelated with x[n]. For example, we can write

$$\bar{x}\left[n\right]=\alpha ·x\left[n\right]+d\left[n\right],n=0,\dots ,N-1.$$

(53)

Let $R_{\mathit{\text{xx}}}\left[m\right]=\mathcal{E}\left\{x\right[n\left]x\right[n+m\left]\right\}$ denote the auto-correlation function of x[n], and let $R_{\mathit{\text{xy}}}\left[m\right]=\mathcal{E}\left\{x\right[n\left]y\right[n+m\left]\right\}$ denote the cross-correlation function between x[n] and y[n] at lag m. For any given m, the correlation functions satisfy

$$R_{\mathit{\text{xd}}}\left[m\right]=0,$$

(54)

$$R_{\bar{x}x}\left[m\right]=\alpha R_{\mathit{\text{xx}}}\left[m\right].$$

(55)

Thus, the scaling factor α can be calculated as

$$\begin{array}{lcl}\alpha & =& \frac{R_{\bar{x}x}\left[0\right]}{R_{\mathit{\text{xx}}}\left[0\right]}\\ =& \frac{\mathcal{E}\left\{\bar{x}\right[n\left]x\right[n\left]\right\}}{{\sigma }^2}\\ =& \frac{1}{{\sigma }^2}\underset{-\infty }{\overset{\infty }{\int }}\bar{x}x·p\left(x\right)\mathit{dx}\end{array}$$

(56)

Let f(·) denote the function linking the original signal to the clipped signal, it is shown in [24] that the output auto-correlation function $R_{\bar{x}\bar{x}}\left[m\right]$ is related to the input auto-correlation function R _xx m via

$$\begin{array}{c}{R}_{\bar{x}\bar{x}}\left[m\right]=\sum _{\ell =0}^{\infty }\frac{b_{\ell }^2}{\ell !}{\left[\frac{R_{\mathit{\text{xx}}}\left[m\right]}{{\sigma }^2}\right]}^{\ell },\end{array}$$

(57)

where the coefficients

$$\begin{array}{c}{b}_{\ell }=\frac{{(-1)}^{\ell }{\sigma }^{\ell -1}}{\sqrt{2\Pi }}{\int }_{-\infty }^{\infty }f\left(x\right)\frac{d^{\ell }[exp(-\frac{x^2}{2{\sigma }^2}\left)\right]}{d{x}^{\ell }}\mathrm{dx.}\end{array}$$

(58)

The input auto-correlation function R _xx [m] can be obtained from taking IDFT of the input power spectrum density (PSD)

$$\begin{array}{c}{R}_{\mathit{\text{xx}}}\left[m\right]=\mathtt{\text{IDFT}}{\left\{P_{X,k}\right\}}_m,m=0,\dots ,N-1,\end{array}$$

(59)

where $P_{X,k}=\mathcal{E}\left[\right|X_k{|}^2]$ is the expected value of the power on the k th subcarrier before clipping. Then it is straightforward to calculate the output PSD by taking the DFT of the auto-correlation of the output signal:

$$\begin{array}{c}{P}_{\bar{X},k}=\mathtt{\text{DFT}}{\left\{R_{\bar{x}\bar{x}}\right[m\left]\right\}}_k,k=0,\dots ,N-1.\end{array}$$

(60)

Taking the DFT of Equation (53), the data at the k th subcarrier are expressed as

$$\begin{array}{lcl}{\bar{X}}_k& =& \mathtt{\text{DFT}}{\{\alpha ·x[n\left]\right\}}_k+\mathtt{\text{DFT}}{\left\{d\right[n\left]\right\}}_k\\ =& \alpha ·X_k+D_k,k\in {\mathcal{K}}_d.\end{array}$$

(61)

Here, we assume that D _k is Gaussian distributed, which is the common assumption when N is large [15]. The SDR at the k th subcarrier is given by

$${\mathtt{\text{SDR}}}_k=\frac{\mathcal{E}\left[\right|\alpha ·X_k{|}^2]}{\mathcal{E}\left[\right|D_k{|}^2]}=\frac{{\alpha }^2{P}_{X,k}}{P_{D,k}}=\frac{{\alpha }^2{P}_{X,k}}{P_{\bar{X},k}-{\alpha }^2{P}_{X,k}},k\in {\mathcal{K}}_d,$$

(62)

where $P_{D,k}=\mathcal{E}\left[\right|D_k{|}^2]=P_{\bar{X},k}-{\alpha }^2{P}_{X,k}$ is the average power of the distortion on the k th subcarrier.

According to Equation (56), we can obtain the scaling factor α as a function of the clipping ratio γ and the biasing ratio ς:

$$\begin{array}{lcl}\alpha & =& \frac{1}{{\sigma }^2}\underset{-\infty }{\overset{\infty }{\int }}\bar{x}x·p\left(x\right)\mathit{dx}\\ =& \frac{1}{{\sigma }^2}\underset{c_l}{\overset{c_u}{\int }}{z}^2\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}+\frac{1}{{\sigma }^2}\underset{-\infty }{\overset{c_l}{\int }}{c}_{l}z\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\\ +\frac{1}{{\sigma }^2}\underset{c_u}{\overset{\infty }{\int }}{c}_{u}z\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\\ =& \Phi \left(2\gamma (1-\varsigma )\right)-\Phi \left(-2\mathrm{\gamma \varsigma }\right).\end{array}$$

(63)

Note that in (63) we have used Equations (13) and (12) for c _l and c _u . According to Equation (58), we can obtain the coefficient b _ℓ as a function of the clipping ratio γ and the biasing ratio ς:

$$\begin{array}{c}{b}_{\ell }=\left\{\begin{array}{cc}\mathrm{\sigma \varphi }\left(2\mathrm{\gamma \varsigma }\right)-\mathrm{\sigma \varphi }\left(2\gamma (1-\varsigma )\right)-2\mathrm{\sigma \gamma \varsigma \Phi }\left(-2\mathrm{\gamma \varsigma }\right)+2\mathrm{\sigma \gamma }(1-\varsigma )\Phi \left(-2\gamma (1-\varsigma )\right),& \ell =0\\ \mathrm{\sigma \Phi }\left(2\gamma (1-\varsigma )\right)-\mathrm{\sigma \Phi }(-2\mathrm{\gamma \varsigma }),& \ell =1\\ \frac{\sigma }{\sqrt{2\Pi }}exp\left(-2{\gamma }^2{\varsigma }^2\right)H{e}_{(\ell -2)}\left(-2\mathrm{\gamma \varsigma }\right)-\frac{\sigma }{\sqrt{2\Pi }}exp\left(-2{\gamma }^2{(1-\varsigma )}^2\right)H{e}_{(\ell -2)}\left(2\gamma (1-\varsigma )\right),& \ell >1\end{array}\right.\end{array}$$

(64)

where $H{e}_n\left(t\right)={(-1)}^{\ell }exp\left(\frac{t^2}{2}\right)\frac{d^{\ell }[exp(-\frac{t^2}{2}\left)\right]}{d{t}^{\ell }}$ is the probabilists’ Hermite polynomials [25].

Achievable data rate

In VLC, average optical power and dynamic optical power are two main constraints. Recall from Equation (3), we can obtain the average optical power of y[n] as

$$\begin{array}{lcl}{O}_y& =& \mathcal{E}\left\{y\right[n\left]\right\}\\ =& \mathcal{E}\left\{\bar{x}\right[n\left]\right\}+B\\ =& \underset{c_l}{\overset{c_u}{\int }}z\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}+c_u\underset{c_u}{\overset{\infty }{\int }}\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}\\ +c_l\underset{-\infty }{\overset{c_l}{\int }}\frac{1}{\sigma }\varphi \left(\frac{z}{\sigma }\right)\mathit{dz}-c_l\\ =& \sigma \left(\varphi \left(2\mathrm{\gamma \varsigma }\right)-\varphi \left(2\gamma (1-\varsigma )\right)-2\mathrm{\gamma \varsigma \Phi }\left(-2\mathrm{\gamma \varsigma }\right)\right.\\ \left.+2\gamma (1-\varsigma )\Phi \left(-2\gamma (1-\varsigma )\right)+2\mathrm{\gamma \varsigma }\right).\end{array}$$

(65)

Let ${\sigma }_w^2=\mathcal{E}\left\{w^2\right[n\left]\right\}$ denote the power of AWGN w[n], we define the optical signal-to-noise ratio (OSNR) as

$$\mathtt{\text{OSNR}}=\frac{O_y}{{\sigma }_w}.$$

(66)

Recall from Equation (5), we can obtain the dynamic optical power of y[n] as

$$G_y=max\left(y\left[n\right]\right)-min\left(y\left[n\right]\right)=c_u-c_l=2\mathrm{\sigma \gamma .}$$

(67)

We define the dynamic signal-to-noise ratio (DSNR) as

$$\mathtt{\text{DSNR}}=\frac{G_y}{{\sigma }_w}.$$

(68)

Let η_OSNR = P _A  / σ _w denote the OSNR constraint and η_DSNR = (P _H  - P _L ) / σ _w denote the DSNR constraint, we have

$$\frac{\sigma }{{\sigma }_w}\le \frac{{\eta }_{\text{OSNR}}}{O_y/\sigma },$$

(69)

$$\frac{\sigma }{{\sigma }_w}\le \frac{{\eta }_{\text{DSNR}}}{G_y/\sigma }.$$

(70)

The maximum σ / σ _w value can be obtained as

$$\frac{\sigma }{{\sigma }_w}=min\left(\frac{{\eta }_{\text{OSNR}}}{\varphi \left(2\mathrm{\gamma \varsigma }\right)-\varphi \left(2\gamma (1-\varsigma )\right)-2\mathrm{\gamma \varsigma \Phi }\left(-2\mathrm{\gamma \varsigma }\right)+2\gamma (1-\varsigma )\Phi \left(-2\gamma (1-\varsigma )\right)+2\mathrm{\gamma \varsigma }},\frac{{\eta }_{\text{DSNR}}}{2\gamma }\right),$$

(71)

by substituting (65) and (67) into the right-hand side of (69) and (70), respectively. The ratio η_DSNR / η_OSNR = (P _H  - P _L ) / P _A is determined by specific system requirements.

AWGN channel

For AWGN channel, recall from Equation (15), the received data on the k th subcarrier can be expressed as

$$R_k={\bar{X}}_k+W_k=\alpha X_k+D_k+W_k,k\in {\mathcal{K}}_d.$$

(72)

The signal-to-noise-and-distortion ratio (SNDR) for the k th subcarrier is given by

$$\begin{array}{lcl}{\mathtt{\text{SNDR}}}_k& =& \frac{{\alpha }^2\mathcal{E}\left\{\right|X_k{|}^2\}}{\mathcal{E}\left\{\right|D_k{|}^2\}+\mathcal{E}\{\left|W_k{|}^2\right\}}\\ =& \frac{{\alpha }^2{P}_{X,k}}{P_{D,K}+{\sigma }_w^2}\\ =& \frac{1}{{\mathtt{\text{SDR}}}_k^{-1}+{\sigma }_w^2·\frac{1}{{\alpha }^2{P}_{X,k}}}.\end{array}$$

(73)

In this article, we assume the power is equally distributed on all data-carrying subcarriers,

$$\begin{array}{c}{P}_{X,k}=\frac{N{\sigma }^2}{\left|{\mathcal{K}}_d\right|},\end{array}$$

(74)

then Equation (73) is reduced to

$$\begin{array}{c}{\mathtt{\text{SNDR}}}_k=\frac{1}{{\mathtt{\text{SDR}}}_k^{-1}+\frac{{\sigma }_w^2}{{\sigma }^2}·\frac{\left|{\mathcal{K}}_d\right|}{N{\alpha }^2}}.\end{array}$$

(75)

By substituting Equation (71) into (75), we obtain the reciprocal of SNDR at the k th subcarrier:

$$\begin{array}{l}{\left({\mathtt{\text{SNDR}}}_k\right)}^{-1}={\left({\mathtt{\text{SDR}}}_k\right)}^{-1}+\frac{\left|{\mathcal{K}}_d\right|}{N{\alpha }^2}\\ ·max\left(\frac{{\left(\varphi \left(2\mathrm{\gamma \varsigma }\right)-\varphi \left(2\gamma (1-\varsigma )\right)-2\mathrm{\gamma \varsigma \Phi }\left(-2\mathrm{\gamma \varsigma }\right)+2\gamma (1-\varsigma )\Phi \left(-2\gamma (1-\varsigma )\right)+2\mathrm{\gamma \varsigma }\right)}^2}{{\eta }_{\text{OSNR}}^2},\frac{4{\gamma }^2}{{\eta }_{\text{DSNR}}^2}\right).\end{array}$$

(76)

Therefore, the achievable data rate, as a function of clipping ratio γ, ς, η_OSNR, and η_DSNR, is given by

$$\begin{array}{l}\mathcal{R}\left(\gamma ,\varsigma ,{\eta }_{\text{OSNR}},{\eta }_{\text{DSNR}}\right)\\ =\frac{1}{2N}\sum _{k\in {\mathcal{K}}_d}\underset{2}{log}\left(1+{\mathtt{\text{SNDR}}}_k\right)\frac{\mathtt{\text{bits}}}{\mathtt{\text{subcarrier}}}.\end{array}$$

(77)

Frequency-selective channel

In the presence of frequency-selective channel, the received data on the k th subcarrier obey the following in the frequency-domain:

$$R_k=H_k{\bar{X}}_k+W_k=H_k(\alpha X_k+D_k)+W_k,k\in {\mathcal{K}}_d.$$

(78)

In this article, we consider the ceiling bounce channel model [26] given by

$$h\left(t\right)=H\left(0\right)\frac{6a^6}{{(t+a)}^7}u\left(t\right),$$

(79)

where H(0) is the gain constant, $a=12\sqrt{11/23}D$ and u(t) is the unit step function. D denotes the rms delay. From Equation (78), the SNDR is given by

$$\begin{array}{c}{\mathtt{\text{SNDR}}}_k\left(H_k\right)=\frac{\left|H_k{|}^2{\alpha }^2\mathcal{E}\right\{\left|X_k{|}^2\right\}}{\left|H_k{|}^2\mathcal{E}\right\{\left|D_k{|}^2\right\}+\mathcal{E}\left\{\right|W_k{|}^2\}}\end{array}$$

(80)

$$\begin{array}{c}=\frac{1}{{\mathtt{\text{SDR}}}_k^{-1}+{\sigma }_w^2·\frac{1}{|H_k{|}^2{\alpha }^2{P}_{X,k}}}.\end{array}$$

(81)

With the assumption of equal power distribution, we can obtain the 1 / SNDR as

$$\begin{array}{l}{\left({\mathtt{\text{SNDR}}}_k\right)}^{-1}={\left({\mathtt{\text{SDR}}}_k\right)}^{-1}+\frac{\left|{\mathcal{K}}_d\right|}{N|H_k{|}^2{\alpha }^2}\\ ·max\left(\frac{{\left(\varphi \left(2\mathrm{\gamma \varsigma }\right)-\varphi \left(2\gamma (1-\varsigma )\right)-2\mathrm{\gamma \varsigma \Phi }\left(-2\mathrm{\gamma \varsigma }\right)+2\gamma (1-\varsigma )\Phi \left(-2\gamma (1-\varsigma )\right)+2\mathrm{\gamma \varsigma }\right)}^2}{{\eta }_{\text{OSNR}}^2},\frac{4{\gamma }^2}{{\eta }_{\text{DSNR}}^2}\right).\end{array}$$

(82)

The achievable data rate, in the presence of frequency-selective channel, is given by

$$\begin{array}{l}\mathcal{R}\left(\gamma ,\varsigma ,{\eta }_{\text{OSNR}},{\eta }_{\text{DSNR}},\mathbf{H}\right)\\ =\frac{1}{2N}\sum _{k\in {\mathcal{K}}_d}\underset{2}{log}\left(1+{\mathtt{\text{SNDR}}}_k\left(H_k\right)\right)\frac{\mathtt{\text{bits}}}{\mathtt{\text{subcarrier}}}.\end{array}$$

(83)

Numerical results

In this section, we show EVM simulation results and achievable data rates of clipped optical OFDM signals under various average optical power and dynamic optical power constraints.

EVM simulation

The EVM analyses for DCO-OFDM and ACO-OFDM are validated through computer simulations. In the simulations, we chose the number of subcarriers N = 512, and QPSK modulation. One thousand OFDM symbols were generated based on which we calculated the EVM. In order to experimentally determine the optimum biasing ratio for DCO-OFDM, we used biasing ratios ranging from 0.3 to 0.7 in step size of 0.02, and clipping ratios ranging from 5 to 9 dB in step size of 1 dB. Their simulated and theoretical EVM curves are plotted in Figure 3. As expected, the minimum EVM was achieved when the biasing ratio was 0.5, regardless of the clipping ratio. This agrees with the analysis in “EVM calculation” section. Next, we compared the EVM for DCO-OFDM with biasing ratio 0.5, EVM for ACO-OFDM with biasing ratio 0, and their respective lower bounds. To obtain the lower bounds, we used CVX, a package for specifying and solving convex programs [27], to solve Equation (43). The resulting EVM curves for DCO-OFDM are plotted in Figure 4. The resulting EVM curves for ACO-OFDM are plotted in Figure 5. We see that the EVM for ACO-OFDM achieves its lower bound, thus corroborating the discussion in “Optimality for ACO-OFDM” section. For DCO-OFDM, the gap above the lower bound increases with the clipping ratio (i.e., with increasing dynamic range of the LED). This implies that there exists another (more complicated) way of mapping x^Dn into a limited dynamic range signal $\widehat{x}\left[n\right]$ that can yield a lower EVM.

Figure 3

EVM as a function of biasing ratio for DCO-OFDM with clipping ratio = 5, 6,…,9 dB.

Figure 4

EVM as a function of the clipping ratio γ for DCO-OFDM along with the EVM lower bound for a given dynamic range limit 2γσ.

Figure 5

EVM as a function of the clipping ratio γ for ACO-OFDM along with the EVM lower bound for a given dynamic range limit 2γσ.

Achievable data rates performance

We now show achievable data rates of clipped OFDM signals under various average optical power and dynamic optical power constraints. The number of subcarriers was N = 512. For the frequency-selective channel, we chose the rms delay spread D = 10 ns and sampling frequency 100 MHz. The normalized frequency response for each subcarrier is shown in Figure 6.

Figure 6

Normalized frequency response for each subcarrier (rms delay spread D = 10 ns, 100 MHz sampling rate).

As examples, we chose η_OSNR = 20 dB, η_DSNR = 32 dB, and AWGN channel. Figures 7 and 8 show the achievable data rate as a function of the clipping ratio and the biasing ratio for DCO-OFDM and ACO-OFDM, respectively. We see that for given η_OSNR and η_DSNR values, a pair of optimum clipping ratio γ^† and optimum biasing ratio ς^† exist that maximize the achievable data rate. It is worthwhile to point out that the optimum biasing ratio ς^† is different from ς^⋆ (recall that ς^⋆ minimizes the EVM). If the system is only subject to the dynamic power constraint, ς^† should be equal to ς^⋆. If the dominant constraint is the average power, ς^† should be less than or equal to ς^⋆ because reducing the biasing ratio can make the signal average power lower. We can obtain the optimum clipping ratio and biasing ratio for given η_OSNR, η_DSNR by

$$({\gamma }^{†},{\varsigma }^{†})=\underset{(\gamma ,\varsigma )}{\mathtt{\text{argmax}}}\mathcal{R}{|}_{{\eta }_{\text{OSNR}},{\eta }_{\text{DSNR}}}$$

(84)

Figure 7

Achievable data rate as a function of the clipping ratio and the biasing ratio for DCO-OFDM with η _OSNR  = 20 dB, η _DSNR  = 32 dB, and AWGN channel.

Figure 8

Achievable data rate as a function of the clipping ratio and the biasing ratio for ACO-OFDM with η _OSNR  = 20 dB, η _DSNR  = 32 dB, and AWGN channel.

Figure 9a shows the optimal clipping ratio as a function of η_OSNR for DCO-OFDM. Figure 9b shows the optimum biasing ratio as a function of η_OSNR for DCO-OFDM. Similar plots are shown as Figure 10a,b for ACO-OFDM. In all cases, η_OSNR varied from 0 to 25 dB in step size of 1 dB, η_DSNR / η_OSNR = 18 dB, and the channel was AWGN. The main observation is, with a lower average optical power constraint, the clipping ratio and the biasing ratio can be increased to achieve higher data rates. Intuitively, when η_OSNR is large, the channel noise has little effect and the nonlinear distortion dominates.

Figure 9

Optimal clipping ratio (a) and optimum biasing ratio (b) of DCO-OFDM for η _OSNR  = 0, 1, …, 25 dB (in step size of 1 dB), η _DSNR  / η _OSNR  = 18 dB, and AWGN channel.

Figure 10

Optimal clipping ratio (a) and optimum biasing ratio (b) of ACO-OFDM for η _OSNR  = 0, 1, …, 25 dB (in step size of 1 dB), η _DSNR  / η _OSNR  = 18 dB, and AWGN channel.

Next, we chose the ratio η_DSNR/η_OSNR from 6 dB, 12 dB, and no η_DSNR constraints. For each pair of η_OSNR, η_DSNR, AWGN channel, or frequency-selective channel, we can calculate the optimum clipping ratio γ^† and biasing ratio ς^† according to Equation (84) and the corresponding achievable data rates. Figures 11, 12, and 13 show the achievable data rates with optimal clipping ratio and biasing ratio for the case η_DSNR / η_OSNR = 6 dB, η_DSNR / η_OSNR = 12 dB, and no η_DSNR constraint, respectively. We observe that the performance of ACO-OFDM and DCO-OFDM depends on the specific optical power constraints scenario. In general, DCO-OFDM outperforms ACO-OFDM for all the cases. With the increase of the ratio η_DSNR / η_OSNR, the average optical power becomes the dominant constraint. The ACO-OFDM moves closer to the DCO-OFDM.

Figure 11

Achievable data rate with optimal clipping ratio and optimal biasing ratio for η _OSNR  = 0, 1, …, 25 dB (in step size of 1 dB), and η _DSNR  / η _OSNR  = 6 dB.

Figure 12

Achievable data rate with optimal clipping ratio and biasing ratio for η _OSNR  = 0, 1, …, 25 dB (in step size of 1 dB), and η _DSNR  / η _OSNR  = 12 dB.

Figure 13

Achievable data rate with optimal clipping ratio and biasing ratio for η _OSNR  = 0, 1, …, 25 dB (in step size of 1 dB), and no η _DSNR constraint.

As seen in Figure 13, when there is no DSNR constraint and the OSNR constraint is large, the DCO-OFDM curve closely matches the ACO-OFDM curve. This is in contrast to the performance curves in Figures 11 and 12. The reason for the curve coincidence in Figure 13 is twofold. First, we have already discussed that the performance difference between DCO-OFDM and ACO-OFDM is less when the OSNR constraint dominates, which is the case for Figure 13. Second, the suddenness of the convergence of the two curves can be explained by the fact that with only OSNR constraint, there will be more flexibility in the signal optimization to adjust the clipping ratio and biasing ratio to achieve the best performance. That means that the achievable data rates in the middle-OSNR region (5–22 dB) are improved significantly compared with Figures 11 and 12. However, for high-OSNR region (greater than 22 dB), since the nonlinear distortion is negligible, the improvement becomes less pronounced compared to Figures 11 and 12. Therefore, the transition from the middle-OSNR region to the high-OSNR region will become sharper with only an OSNR constraint.

Conclusions

In this article, we analyzed the performance of the DCO-OFDM and ACO-OFDM systems in terms of EVM, SDR, and achievable data rates under both the average optical power and dynamic optical power constraints. We numerically calculated the EVM and compared with the corresponding lower bound. Both the theory and the simulation results showed that ACO-OFDM can achieve the EVM lower bound. We derived the achievable data rates for AWGN channel as well as frequency-selective channel scenarios. We investigated the trade-off between the optical power constraint and distortion. We analyzed the optimum clipping ratio and biasing ratio and compared the performance of two optical OFDM techniques. Numerical results showed that DCO-OFDM outperforms the ACO-OFDM for all the optical power constraint scenarios.

Appendix

Proof that $c^{\star }\left[n\right]=x^{\left(A\right)}\left[n\right]-{\bar{x}}^{\left(A\right)}\left[n\right]$ is optimum for Equation (51)

Denote by u(c[n]) the objective function for the problem in (51):

$$u\left(c\right[n\left]\right)=\sum _{n=0}^{N/2-1}{\left(c\left[n\right]\right)}^2,$$

(85)

and denote by g _i (c[n]) the i th constraint function for the problem in (51):

$$\begin{array}{c}{g}_i\left(c\right[n\left]\right)=\left\{\begin{array}{cc}{x}^{\left(A\right)}\left[i\right]+c\left[i\right]-2\mathrm{\gamma \sigma },& 0\le i\le \frac{N}{2}-1\\ -x^{\left(A\right)}[i-N/2]-c[i-N/2],& \frac{N}{2}\le i\le N-1\end{array}\right..\end{array}$$

(86)

Let μ _i denote the i th Kuhn–Tucker (KT) multiplier. We inter that

$$\begin{array}{c}\nabla u\left(c\right[n\left]\right)=\left[2c\left[0\right],2c\left[1\right],\dots ,2c[N/2-1]\right],\end{array}$$

(87)

$$\begin{array}{lcl}\sum _{i=0}^{N-1}{\mu }_i\nabla g_i\left(c\right[n\left]\right)& =& \left[{\mu }_0-{\mu }_{N/2},{\mu }_i-{\mu }_{N/2+1},\dots ,\right.\\ \left.{\mu }_{N/2-1}-{\mu }_{N-1}\right].\end{array}$$

(88)

Next, we prove that $c^{\star }\left[n\right]=x^{\left(A\right)}\left[n\right]-{\bar{x}}^{\left(A\right)}\left[n\right]$ satisfies the KT conditions [28].

Stationarity

$$\nabla u\left(c\right[n\left]\right)+\sum _{i=0}^{N-1}{\mu }_i\nabla g_i\left(c\right[n\left]\right)=0.$$

(89)

Primary feasibility

$${\mu }_i\ge 0,\forall i=0,1,\dots ,N-1.$$

(90)

Dual feasibility

$$g_i\left(c\right[n\left]\right)\le 0,\forall i=0,1,\dots ,N-1.$$

(91)

Complementary slackness

$${\mu }_i{g}_i\left(c\right[n\left]\right)=0,\forall i=0,1,\dots ,N-1.$$

(92)

Substituting c^⋆[n] into Equation (89), we obtain,

$${\mu }_i-{\mu }_{i+N/2}=-2x^{\left(A\right)}\left[i\right]+2{\bar{x}}^{\left(A\right)}\left[i\right],i=0,1,\dots ,\frac{N}{2}-1.$$

(93)

In order to satisfy all the other conditions (90)–(92), we can choose μ _i as follows

• (1) if $x^{\left(A\right)}\left[i\right]={\bar{x}}^{\left(A\right)}\left[i\right]$,

  $${\mu }_i={\mu }_{i+N/2}=0;$$

  (94)

• (2) if x ^(A)[i]>2γσ and ${\bar{x}}^{\left(A\right)}\left[i\right]=2\mathrm{\gamma \sigma }$,

  $${\mu }_i=2{\bar{x}}^{\left(A\right)}\left[i\right],{\mu }_{i+N/2}=2x^{\left(A\right)}\left[i\right];$$

  (95)

• (3) if x ^(A)[i]<0 and ${\bar{x}}^{\left(A\right)}\left[i\right]=0$,

  $${\mu }_i=-2x^{\left(A\right)}\left[i\right],{\mu }_{i+N/2}=-2{\bar{x}}^{\left(A\right)}\left[i\right].$$

  (96)

Therefore, there exits constants μ _i (i = 0, 1, …, N - 1) that make $c^{\star }\left[n\right]=x^{\left(A\right)}\left[n\right]-{\bar{x}}^{\left(A\right)}\left[n\right]$ satisfy the KT conditions. It was shown in [29] that if the objective function and the constraint functions are continuously differentiable convex functions, KT conditions are sufficient for optimality. It is obvious that u and g are all continuously differentiable convex functions. Therefore, c^⋆n is optimal for the minimization problem (51).