Abstract
Background
Support vector machines, one of the non-parametric controlled classifiers, is a two-class classification method introduced in the context of statistical learning theory and structural risk minimization. Support vector machines are basically divided into two groups as linear support vector machines and nonlinear support vector machines. Nonlinear support vector machines are designed to make classifications by creating a plane in a space by mapping data to that higher dimensional input space. This method basically involves solving a quadratic programming problem. In this study, the support vector machines, which have an increasing rate of use in pattern recognition area, are used in the quality control of DNA sequencing data. Consequently, the classification of quality of all the DNA sequencing data will automatically be made as ‘high quality/low quality’.
Results
The proposed method is tested against a dataset created from public DNA sequences provided by InSNP. We first transformed all DNA chromatograms into feature vectors. An optimal hyperplane is first determined by applying SVM to the training dataset. The instances in the testing dataset are then labeled by using the hyperplane. Finally, the estimated class labels are compared against the true labels by computing a confusion matrix. As the confusion matrix reveals, our method successfully determines the labels of 23 out of 24 chromatograms.
Conclusions
We devised a new method to fulfill the quality screening of DNA chromatograms. It is a composition of feature extraction and support vector machines. It has been tested on a public dataset and it provided quite satisfactory results. We believe that it is a strong solution for DNA sequencing institutions to be used in automatic quality labeling of DNA chromatograms.
Similar content being viewed by others
Introduction
Life sciences is one of the most demanding disciplines requiring advanced pattern recognition algorithms like clustering and classification techniques that are frequently used in molecular genetics and bioinformatics studies [1, 2]. With the advent of new DNA sequencing techniques in the last two decades, the amount of data used in classification tasks has grown exponentially [3]. One of the main tasks in DNA sequencing centers is to classify the quality of DNA sequencing data [4–6]. Regarding this problem, a quality of DNA data, which is indeed a four-channel time series, needs to be classified as high or low quality. It is a critically important service especially for large DNA sequencing institutions since they need to know in advance before doing further analysis on data. It is also not a good practice to service low quality data to the customers. If the quality of data is known to be low, data might be reproduced by repeating necessary reactions. Manual labeling is prohibitive or, in most cases, impossible because of large data size. It also requires human intervention which is sometimes error prone. Therefore automatic screening tools need to be devised.
In order to estimate the quality of DNA data, the classification method of support vector machines (SVM), whose aim is to find an optimal hyperplane separating two different classes, can be used. It was first developed by Vapnik in 1995 [7]. It is applied to tremendous number of diverse application fields like finance, telecommunication, life sciences and others [8–13]. Deterministic approach, strong mathematical ground, widely available software implementations and ease of use are the key factors of its success [14].
Our aim in this article is to verify that SVM can be used as a powerful classification technique to classify the quality of DNA chromatograms. In order to show this, we prepared a dataset consisting of publicly available DNA chromatograms [15]. We then manually determined the quality of each chromatogram in the dataset with the help of a bioinformatics expert. We also divided the dataset into training and testing [16]. We then transformed the chromatograms into a suitable format for SVM by extracting a set of feature vectors [17]. The next thing was the learning phase in which SVM was trained to find an optimal hyperplane. Finally, we classified each data in testing dataset according to the trained SVM classifier. We measured the performance of the method by calculating a confusion matrix.
The next two sections are reserved for explaining SVM and its variant in brief. In the fourth section, we explained the details of our approach in four steps: dataset preparation, feature extraction, training and testing. The article finishes with a conclusion.
Linear support vector machines
Linear support vector machines (LSVM) try to find an optimum hyperplane which has the maximum margin among an infinite number of hyperplanes separating the instances in the input space.
Linearly separable case
Let X denote the training set consisting of n samples
where and are the sets of input vectors and corresponding labels, respectively [18]. The decision function is , where is the discriminant function associated with the hyperplane and defined as
Our aim here is to determine the vector w and the scalar b which together define the optimum hyperplane shown in Figure 1. The hyperplane should satisfy the following constraints:


These constraints can be written in a single form with little effort
A margin band is defined as the region between hyperplanes and [18]. The width of the margin band can easily be calculated as . For the separable case, a maximum margin band can be determined by minimizing the inverse of the distance as in the following quadratic optimization problem with linear constraints:


It is proved that an optimal hyperplane exists and is unique so that the negative instances lie on one side of the hyperplane and the positive instances lie on the other [19]. The optimization problem in Eq. 6 can be formulated as an unconstrained optimization problem by introducing Lagrange multipliers:
where are Lagrange multipliers. The Lagrangian function has to be minimized with respect to w and b and maximized with respect to . By using Karush-Kuhn-Tucker (KKT) conditions, the design variables w and b in Eq. 8 can be expressed in terms of , which then transforms the problem into a dual problem that requires only maximization with respect to the Lagrangian multipliers


The dual problem is constructed by substituting Eq. 9 and Eq. 10 into Eq. 8, from which the dual form of a quadratic programming (QP) problem can be obtained as follows:
Then we solve the dual problem with respect to and subject to the constraints
This QP problem is then solved by any standard quadratic optimization method to determine . Although there are n such variables, most of them vanish. The instances corresponding to positive values are called support vectors. Finally, the vector w is determined by using Eq. 9. The last unknown parameter b is determined by taking average of
for all support vectors [20].
Linearly nonseparable case
In the previous section, we assumed that the data can be perfectly separable in the sense that the data samples of different class labels resides on different regions. However, in practice, such a hyperplane may not be found because of the specific distribution of instances in the data. This makes linear separability difficult as the basic linear decision boundaries are often not sufficient to classify patterns with high accuracy.
If the data is not separable, then the constraint in Eq. 5 may not hold. This corresponds to the data sample that falls within the margin or on the wrong side of the decision boundary as shown in Figure 2. In order to handle the nonseparable data, the formulation is generalized by introducing a slack variable ξ for each instance
Optimal separating hyperplane in SVM for a linearly nonseparable case[20].
The new optimization problem is defined as the combination of two goals: margin maximization and error minimization. If , the instances are correctly classified (the point 1 in Figure 2). When , the instances are also correctly classified, but they are inside the margin (the point 2 in Figure 2). Finally, , the instances are wrongly classified (the point 3 in Figure 2). The number of misclassifications is the number of ξ greater than 1. On the other hand, the number of nonseparable points is the number of positive . Finally, the soft error is defined as follows:
It is added also to the primal of Eq. 8:
values are guaranteed to be positive by the new Lagrange parameters . The parameter C is used to set the weight between the number of support vectors and the number of nonseparable points. In other words, the instances inside the margin band are penalized together with the misclassified instances to reach a better generalization in testing.
The dual problem is
subject to
The methods in the separable case can be applied to the nonseparable case. The instances for which hold are not support vectors. The remaining part of the equation that defines the parameters w and b can be determined similarly [20].
Nonlinear support vector machines
When the data is nonlinearly separable, the linear SVM is not profitable. It is better to use a nonlinear SVM for this situation. In order to transform this input, the nonlinear SVM first uses a nonlinear kernel and then a linear SVM. The nonlinear kernel function, which most probably is a large matrix, makes the nonlinear SVM take a very long time when mapping the input to a higher dimensional space [21]. Here, the purpose is to find the separating hyperplane that has the highest margin in the new dimension, the one where the data are transformed.
To transform the nonlinearly separable data into linearly separable data, the data are mapped in the form using a nonlinear function ϕ into a higher dimensional feature space which is also a Hilbert space. Consequently, the maximum margin hyperplane fits in a feature space with the help of the nonlinear SVM. Then, in this feature space, a linear classification problem is formulated [22]. Depending on this, Eqs. 11 and 12, which point to the Lagrangian of the dual optimization problem, need to change as follows:
A kernel function is expressed as follows and it involves the input vectors:
The majority of the transformations are not known. However, it is possible to get the dot product of the corresponding space using an input vector function [23].
Kernel functions need to have a corresponding inner product in the feature space which is transformed. This is stated in Mercer’s theorem [24]. In this way, the solution of a dual problem gets simpler because there is no need to make calculations for the inner products in the transformed space. Commonly used kernels are shown in Table 1.
Application
The experimental study consists of (i) dataset preparation, (ii) feature extraction, (iii) SVM learning (iv) SVM testing as summarized in Figure 3. We used the software package libsvm which is a popular implementation of SVM [25].
Dataset
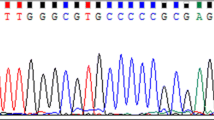
In order to evaluate the performance of the proposed method, a benchmark dataset should be available. To create the dataset, we selected 48 DNA chromatograms from InSNP database. The data in each chromatogram is a four-channel time series with different lengths. Each channel is a series of Gaussian shaped peaks along the time axis which contains information about the nucleotides A, C, G and T, respectively.
We then manually screened each data and labeled the quality of a data as high if its peaks were well resolved. We labeled the quality of a data as low if its peaks were overlapped and had low signal to noise ratio. The example for such a case is shown in Figure 4. We followed SVM labeling convention and chose the labels −1 and +1 for high and low quality.
Feature extraction
We cannot give DNA chromatograms directly as input data to SVM. First of all, they have different lengths and are too long. Using whole length data is not a good strategy. So, we should create a set of features representing the statistical characteristics of each data. The number of features should be low and fixed. Also, the features should be chosen to best represent the quality of the chromatograms [26]. To fulfill these requirements, the following set of features are chosen:
1. Average of all values in the data.
2. Standard deviation of all values in the data.
3. Median of all values in the data.
4. Average of all values created for each peak available in all of the four channels of the data.
5. Standard deviation of all values created for each peak available in all of the four channels of the data.
6. Median of all values created for each peak available in all of the four channels of the data.
7. The number of peaks.
8. Average of all values created for each peak available in the combination of channels.
Having determined the features, we processed each data and obtained a feature vector. Each feature vector is accompanied with a label determined in the previous step. In conclusion, we converted the dataset of DNA chromatograms into an input matrix and output vector. From now on, the data is ready for SVM.
Training
SVM needs to be trained before making classification. So, we reserved some of the data for training by randomly selecting 24 data. We need to give a training set into SVM so that it can create a hyperplane. However, we must first adjust the parameters. The most important parameter is C in Eq. 15. We can set if we are sure that the data is linearly separable. We know that it is generally not perfectly linearly separable. So, we give to make it flexible. SVM is then run for the training samples.
Testing
Now we have a hyperplane provided by SVM. We should use this hyperplane to classify other samples in the data using . We used 24 of them in training, so the testing set has 24 samples. We run SVM for testing. A confusion matrix for SVM testing is presented in Table 2. As indicated in the table, SVM correctly classifies almost all instances in the testing set. There is only one mistake which is false positive. This is a very promising result. It means we can use SVM for automatic quality screening of DNA chromatograms.
Conclusion
We developed a new quality evaluation technique in which the quality of a DNA chromatogram is classified as low or high. In this sense, it is a two-class classification problem for which SVM is chosen. To apply SVM, some sets of features of the chromatograms are extracted. SVM is trained on a training set to learn the hyperplane; SVM is then run on the testing set, from which a confusion matrix is created. As it clearly shows, the results are quite satisfactory as only one mistake was made. Therefore, our method is a good solution for automatic screening of DNA data, especially for large DNA sequencing facilities.
References
Furey T, Cristianini N, Duffy N, Bednarski D, Schummer M, Haussler D: Support vector machine classification and validation of cancer tissue samples using microarray expression data. Bioinformatics 2000, 16(10):906–914. 10.1093/bioinformatics/16.10.906
Mateos A, Dopazo J, Jansen R, Tu Y, Gerstein M, Stolovitzky G: Systematic learning of gene functional classes from DNA array expression data by using multilayer perceptrons. Genome Res. 2002, 12(11):1703–1715. 10.1101/gr.192502
Lander E, et al.: Initial sequencing and analysis of the human genome. Nature 2001, 409(6822):860–921. 10.1038/35057062
Ewing B, Hillier L, Wendl M, Green P: Base-calling of automated sequencer traces using Phred. I. Accuracy assessment. Genome Res. 1998, 8(3):175–185.
Chou HH, Holmes MH: DNA sequence quality trimming and vector removal. Bioinformatics 2001, 17(12):1093–1104. http://bioinformatics.oxfordjournals.org/content/17/12/1093.abstract 10.1093/bioinformatics/17.12.1093
Otto TD, Vasconcellos EA, Gomes LHF, Moreira AS, Degrave WM, Mendonca-Lima L, Alves-Ferreira M: ChromaPipe: a pipeline for analysis, quality control and management for a DNA sequencing facility. Genet. Mol. Res. 2008, 7(3):861–871. (3rd International Conference of the Brazilian-Association-for-Bioinformatics-and-Computational-Biology, Sao Paulo, BRAZIL, NOV 01–03, 2007) 10.4238/vol7-3X-Meeting04
Cortes C, Vapnik V: Support-vector networks. Mach. Learn. 1995, 20(3):273–297.
Guyon I, Weston J, Barnhill S, Vapnik V: Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46(1–3):389–422.
Bhardwaj N, Langlois R, Zhao G, Lu H: Kernel-based machine learning protocol for predicting DNA-binding proteins. Nucleic Acids Res. 2005, 33(20):6486–6493. 10.1093/nar/gki949
Brown M, Grundy W, Lin D, Cristianini N, Sugnet C, Furey T, Ares M, Haussler D: Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc. Natl. Acad. Sci. USA 2000, 97(1):262–267. 10.1073/pnas.97.1.262
Vercoutere W, Winters-Hilt S, Olsen H, Deamer D, Haussler D, Akeson M: Rapid discrimination among individual DNA hairpin molecules at single-nucleotide resolution using an ion channel. Nat. Biotechnol. 2001, 19(3):248–252. 10.1038/85696
Ravi V, Kurniawan H, Thai PNK, Kumar PR: Soft computing system for bank performance prediction. Appl. Soft Comput. 2008, 8(1):305–315. 10.1016/j.asoc.2007.02.001
Elish KO, Elish MO: Predicting defect-prone software modules using support vector machines. J. Syst. Softw. 2008, 81(5):649–660. (Joint Meeting of the International Workshop on Software Measurement (IWSM)/International Conference on Software Process and Product Measurement (MENSURA), Palma de Majorque, SPAIN, NOV 05–07, 2007) 10.1016/j.jss.2007.07.040
Hearst M: Support vector machines. IEEE Intell. Syst. Appl. 1998, 13(4):18–21. 10.1109/5254.708428
Manaster C, Zheng W, Teuber M, Wachter S, Doring F, Schreiber S, Hampe J: InSNP: a tool for automated detection and visualization of SNPs and InDels. Human Mutat. 2005, 26(1):11–19. 10.1002/humu.20188
Jain A, Duin R, Mao J: Statistical pattern recognition: a review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22(1):4–37. 10.1109/34.824819
Sun S, Zhang C: Adaptive feature extraction for EEG signal classification. Med. Biol. Eng. Comput. 2006, 44(10):931–935. 10.1007/s11517-006-0107-4
Campbell C, Ying Y: Learning with Support Vector Machines. Morgan & Claypool Publishers, San Rafael; 2011.
Vapnik VN: Statistical Learning Theory. Wiley, New York; 1998.
Alpaydin E: Introduction to Machine Learning. MIT Press, Cambridge; 2004.
Yue S, Li P, Hao P: SVM classification: its contents and challenges, applied mathematics. Appl. Math. J. Chin. Univ. Ser. B 2003, 18(3):332–342. 10.1007/s11766-003-0059-5
Cherkassky V, Mulier FM: Learning from Data: Concepts, Theory, and Methods. Wiley-Interscience, New York; 1998.
Martínez-Ramon M, Cristodoulou C: Support Vector Machines for Antenna Array Processing and Electromagnetics. Morgan & Claypool Publishers, San Rafael; 2006.
Scholkopf B, Smola A: Learning with Kernels. MIT Press, Cambridge; 2001.
Chang CC, Lin CJ: LIBSVM: a library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011., 2(3): Article ID 27. (Software available at http://www.csie.ntu.edu.tw/~cjlin/libsvm)
Andrade-Cetto L, Manolakos E: Feature extraction for DNA base-calling using NNLS. Statistical Signal Processing, 2005 IEEE/SP 13th Workshop on 2005, 1408–1413.
Acknowledgements
Dedicated to Professor Hari M Srivastava.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
HK conceived of the study and participated in its design and coordination. EO participated in the implementation and classification. EO drafted the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Öz, E., Kaya, H. Support vector machines for quality control of DNA sequencing. J Inequal Appl 2013, 85 (2013). https://doi.org/10.1186/1029-242X-2013-85
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-85