Abstract
Let G be a simple connected graph of order n, m edges, maximum degree and minimum degree δ. Li et al. (Appl. Math. Lett. 23:286-290, 2010) gave an upper bound on number of spanning trees of a graph in terms of n, m, and δ:
The equality holds if and only if , , or , where e is any edge of . Unfortunately, this upper bound is erroneous. In particular, we show that this upper bound is not true for complete graph .
In this paper we obtain some upper bounds on the number of spanning trees of graph G in terms of its structural parameters such as the number of vertices (n), the number of edges (m), maximum degree (), second maximum degree (), minimum degree (δ), independence number (α), clique number (ω). Moreover, we give the Nordhaus-Gaddum-type result for number of spanning trees.
MSC:05C50, 15A18.
Similar content being viewed by others
Dedication
Dedicated to Professor Hari M Srivastava
1 Introduction
Let be a simple connected graph with a vertex set and an edge set . Its order is , denoted by n, and its size is , denoted by m. For , the degree (= number of the first neighbors) of the vertex is denoted by . The maximum vertex degree is denoted by , the second maximum by , and the minimum vertex degree δ. The number of spanning trees of G, denoted by , is the total number of distinct spanning subgraphs of G that are trees.
The Laplacian matrix of a graph G is , where is the diagonal matrix of vertex degrees, and is the -adjacency matrix of graph G. Let denote the eigenvalues of . They are usually called the Laplacian eigenvalues of G. When more than one graph is under discussion, we may write instead of . For a connected graph of order n, it has been proven [1] that
The normalized Laplacian matrix of G is denoted by ℒ and defined to be
where is the Laplacian matrix and is the diagonal matrix of vertex degrees of graph G. The eigenvalues of ℒ are non-negative, we label them so that . For a connected graph of order n, it has been proven [2] that
We now give some known popular upper bounds on
-
1.
Grimmett [3].
(3) -
2.
Grone and Merris [4].
(4) -
3.
Nosal [5].
(5) -
4.
Kelmans [[6], p.222].
(6) -
5.
Das [7].
(7)
The third bound only applies to regular graphs of degree r. The first three bounds are sharp for complete graphs only. The fifth bound is sharp for star or complete graph. Moreover, the bound in (5) was also obtained by McKay [8]. Chung et al. [9] studied the number of spanning trees for regular graphs. As usual, , () and denote, respectively, the complete graph, the complete bipartite graph and the star on n vertices.
The paper is organized as follows. In Section 2, we give a list of some previously known results. In Section 3, we obtain some upper bounds on the number of spanning trees. In Section 4, we obtain Nordhaus-Gaddum-type result for the number of spanning trees of graph G.
2 Lemmas
In this section, we shall list some previously known results that will be needed in the next two sections. The next lemma is firstly obtained in Theorem 2.6 [7].
Lemma 1 ([7])
Let G be a connected graph of order n. Then if and only if .
We now give a lower bound on the sum of the largest two Laplacian eigenvalues of graph G.
Lemma 2 ([10])
Let G be a connected graph of order . Then .
Lemma 3 ([10])
Let G be a graph on n vertices, which has at least one edge. Then
Moreover, if G is connected, then the equality in (8) holds if and only if .
A well-known theorem in an algebraic graph theory is the interlacing of the Laplacian spectrum in Theorem 13.6.2 [1].
Lemma 4 ([1])
Let G be a graph of n vertices, and let H be a subgraph of G obtained by deleting an edge in G. Then
where is the ith largest Laplacian eigenvalue of G, and is the ith largest Laplacian eigenvalue of H.
Lemma 5 ([11])
Let G be a simple graph with the Laplacian spectrum
Then the Laplacian spectrum of is , where is the complement graph of G.
We also have the following result, which is obtained in [12].
Lemma 6 ([12])
Let G be a graph of order n without isolated vertices. Then if and only if .
The result is the following lemma, known as Kober’s inequality.
Lemma 7 ([13])
Let be non negative numbers, and also let
be their arithmetic and geometric means. Then
Moreover, the equality holds if and only if .
3 Bounds on the number of spanning trees
In [14], an upper bound for is obtained as follows.
Theorem 1 ([14])
Let G be a connected graph of order n () with m edges, maximum degree and minimum degree δ. Then
The equality holds if and only if , , or , where e is any edge of .
Here we show that Theorem 1 is not true for complete graph . For this, we need the following lemma.
Lemma 8 For positive integer ,
Proof We have
In fact, this satisfies
Now, we have to show that
that is,
which is always true, as a is a positive integer. This completes the proof. □
Upper bound of in Theorem 1 is not true for (). It is well known that . Here, we have to show that
Now, putting in (9), we get
which gives result (11).
Hence the correct statement is as follows.
Theorem 2 ([14])
Let G () be a connected graph of order n () with m edges, maximum degree and minimum degree δ. Then
with the equality holding in (12) if and only if , or , where e is any edge of .
Proof Since , we have , where δ is the minimum degree in G. The remaining part of the proof is same as in Theorem 3.1 [14]. □
We now give an upper bound on the number of spanning trees in terms of n, m, and δ.
Theorem 3 Let G be a connected graph on n vertices with m edges, maximum degree and minimum degree δ. Then
with the equality holding in (13) if and only if .
Proof By the arithmetic-geometric mean inequality, we have
and
Using the above results in (2), we get
Let us consider the function
Then we have
Thus, is an increasing function on and a decreasing function on . Hence the maximum value of is
Using (14), we get the required result in (13). Thus, the first part of the proof is done.
Now, we suppose that the equality holds in (13). Then all inequalities in the argument above must be equalities. Thus, we have . From the equality in (14), we get and . Therefore, . By Lemma 6, .
Conversely, one can easily see that the equality holds in (13) for complete graph . □
Here, we give an upper bound on the number of spanning trees in terms of n, m, and .
Theorem 4 Let G be a connected graph on n vertices, m edges with maximum degree and second maximum degree . Then
Proof By the arithmetic-geometric mean inequality, we have
and
Using the above results in (1), we get
Let us consider a function
We, thus, have
For , we have as . Thus, is a decreasing function and , by Lemma 2, and hence
By contradiction, we will show that the inequality in (17) is strict. Suppose that the equality holds in (17). Then all the inequalities in the argument above must be equalities. Thus, we have . From equality in (16), we get and . By Lemma 3, we have , a contradiction.
This completes the proof. □
For , let be a split graph on n vertices consisting of a (complement of the complete graph on α vertices) and a (complete graph on the remaining vertices), in which each vertex of the is adjacent to each vertex of the . Therefore,
We now give another upper bound on the number of spanning trees in terms of n and α.
Theorem 5 Let G be a simple connected graph of order n with an independence number α. Then
with the equality holding in (18) if and only if .
Proof By Lemma 4, we have
where e is an edge. So if we add one by one edges in G such that independence number α is fixed of the resultant graph, then finally, we obtain a split graph . One can easily see that
as Laplacian spectrum of is  , that is, Laplacian spectrum of is
, that is, Laplacian spectrum of is  , by Lemma 5.
, by Lemma 5.
Since G is connected, one can easily see that
This completes the proof of this theorem. □
We now give another upper bound on in terms of n, m and ω.
Theorem 6 Let G be a connected graph of order n, m edges and clique number ω. Then
with the equality holding if and only if .
Proof By the arithmetic-geometric mean inequality, we have
Since ω is the clique number of G, by using (1), we get
Let us consider a function
Then, we have
Since , we have
that is,
By using this inequality above, we conclude that is a decreasing function, as . Since ω is a clique number of G, we must have , , and hence . Thus, we have
Using the above result with (20), we get the required result (19). The first part of the proof is done.
Now, we suppose that the equality holds in (19). Then all the inequalities in the argument above must be equalities. Thus, we have and . Hence , . By Lemma 1, .
Conversely, one can easily see that the equality holds in (19) for complete graph . □
The first Zagreb index is defined as follows:
The first Zagreb index was introduced in [15] and elaborated in [16]. The main properties of were summarized in [17]. Some recent results on the first Zagreb index are reported in [18–21]. Now, we are ready to give some lower and upper bounds on the number of spanning trees.
Theorem 7 Let G be a connected graph of order n with m edges and first Zagreb index . Then
with the equality holding in (21) if and only if . Moreover,
with the equality holding in (22) if and only if .
Proof We have
Since G is connected, . Now, by setting , and by Lemma 7, we obtain
that is, by considering (1),
since . From this last inequality, we then get
which gives the required result (21). Similarly, by Lemma 7, we obtain
as required in (22). Hence the first part of the proof is completed.
Now, we suppose that the equality holds in (21) or (22). Then all the inequalities in the argument above must be equalities. By Lemma 7, we have . By Lemma 1, we get .
Conversely, one can easily see that the equalities in (21) and (22) hold for complete graphs . □
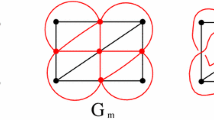
Example 1 For the three graphs , and in Figure 1, , and are 3, 8 and 9, respectively. The numerical results related to the bounds (that were mentioned above) are listed in the following. At this point, we should note that these results are presenting as rounded the one decimal place.
4 Nordhaus-Gaddum-type results for the number of spanning trees of a graph
For a graph G , the chromatic number is the minimum number of colors needed to color the vertices of G in such a way that no two adjacent vertices are assigned the same color. In 1956, Nordhaus and Gaddum [22] gave bounds involving the chromatic number of a graph G and its complement :
Motivated by the results above, we now obtain analogous conclusions for the number of spanning trees.
Theorem 8 Let G be a connected graph on vertices and m edges with a connected complement . Then
where is the maximum degree in G.
Proof By Lemma 5, from (1), we have
Let us consider a function
We have
Thus, is a decreasing function on . Using the result above in (25), we obtain the required result (24). □
The next result presents another upper bound for . In fact, the proof of it is clear by considering Theorem 7.
Theorem 9 Let G be a graph on n vertices and m edges. Then
where is the first Zagreb index of graph G. Moreover, the equality in (26) holds if and only if or .
References
Godsil C, Royle G Graduate Texts in Mathematics 207. In Algebraic Graph Theory. Springer, Berlin; 2001.
Chung FRK: Spectral Graph Theory. Am. Math. Soc., Providence; 1997.
Grimmett GR: An upper bound for the number of spanning trees of a graph. Discrete Math. 1976, 16: 323–324. 10.1016/S0012-365X(76)80005-2
Grone R, Merris R: A bound for the complexity of a simple graph. Discrete Math. 1988, 69: 97–99. 10.1016/0012-365X(88)90182-3
Nosal, E: Eigenvalues of Graphs. Master thesis, University of Calgary (1970)
Cvetković DM, Doob M, Sachs H Pure and Applied Mathematics 87. In Spectra of Graphs. Academic press, San Diego; 1980.
Das KC: A sharp upper bound for the number of spanning trees of a graph. Graphs Comb. 2007, 23: 625–632. 10.1007/s00373-007-0758-4
McKay BD: Spanning trees in regular graphs. Eur. J. Comb. 1983, 4: 149–160. 10.1016/S0195-6698(83)80045-6
Chung F, Yau S-T: Coverings, heat kernels and spanning trees. Electron. J. Comb. 1999., 6: Article ID R12
Grone R, Merris R: The Laplacian spectrum of a graph II. SIAM J. Discrete Math. 1994, 7(2):221–229. 10.1137/S0895480191222653
Merris R: Laplacian matrices of graphs: a survey. Linear Algebra Appl. 1994, 197(198):143–176.
Das KC, Maden AD, Cevik AS: Sharp upper bounds on the spectral radius of the Signless Laplacian matrix of a graph. Appl. Math. Comput. 2013, 219(10):5025–5032. 10.1016/j.amc.2012.11.039
Kober H: On the arithmetic and geometric means and on Holder’s inequality. Proc. Am. Math. Soc. 1958, 59: 452–459.
Li J, Shiu WC, Chang A: The number of spanning trees of a graph. Appl. Math. Lett. 2010, 23: 286–290. 10.1016/j.aml.2009.10.006
Gutman I, Trinajstić N: Graph theory and molecular orbitals. Total π -electron energy of alternant hydrocarbons. Chem. Phys. Lett. 1972, 17: 535–538. 10.1016/0009-2614(72)85099-1
Gutman I, Ruščić B, Trinajstić N, Wilcox CF: Graph theory and molecular orbitals. XII. Acyclic polyenes. J. Chem. Phys. 1975, 62: 3399–3405. 10.1063/1.430994
Nikolić S, Kovačević G, Milićević A, Trinajstić N: The Zagreb indices 30 years after. Croat. Chem. Acta 2003, 76: 113–124.
Das KC: Maximizing the sum of the squares of the degrees of a graph. Discrete Math. 2004, 285: 57–66. 10.1016/j.disc.2004.04.007
Das KC, Gutman I: Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem. 2004, 52: 103–112.
Das KC: On comparing Zagreb indices of graphs. MATCH Commun. Math. Comput. Chem. 2010, 63(2):433–440.
Das KC, Gutman I, Zhou B: New upper bounds on Zagreb indices. J. Math. Chem. 2009, 46(2):514–521. 10.1007/s10910-008-9475-3
Nordhaus EA, Gaddum JW: On complementary graphs. Am. Math. Mon. 1956, 63: 175–177. 10.2307/2306658
Acknowledgements
The authors are grateful to the referees for their valuable comments, which lead to an improvement of the original manuscript. This paper was prepared during the first author’s visit in Selcuk and Uludag Universities. Moreover, we are thankful to Mr. SA Mojallal for computing the values in Example 1. The first author is supported by the Faculty research Fund, Sungkyunkwan University, 2012 and the National Research Foundation funded by the Korean government with the grant no. 2013R1A1A2009341. The second and the third authors are both partially supported by the Research Project Offices of Selcuk and Uludag Universities, and TUBITAK (The Scientific and Technological Research Council of Turkey).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors completed the paper together. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Das, K.C., Cevik, A.S. & Cangul, I.N. The number of spanning trees of a graph. J Inequal Appl 2013, 395 (2013). https://doi.org/10.1186/1029-242X-2013-395
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-395