Abstract
The general coupled matrix equations
(including the generalized coupled Sylvester matrix equations as special cases) have numerous applications in control and system theory. In this paper, an iterative algorithm is constructed to solve the general coupled matrix equations and their optimal approximation problem over generalized reflexive matrix solution . When the general coupled matrix equations are consistent over generalized reflexive matrices, the generalized reflexive solution can be determined automatically by the iterative algorithm within finite iterative steps in the absence of round-off errors. The least Frobenius norm generalized reflexive solution of the general coupled matrix equations can be derived when an appropriate initial matrix group is chosen. Furthermore, the unique optimal approximation generalized reflexive solution to a given matrix group in Frobenius norm can be derived by finding the least-norm generalized reflexive solution of the corresponding general coupled matrix equations , , where , . A numerical example is given to illustrate the effectiveness of the proposed iterative algorithm.
MSC:15A18, 15A57, 65F15, 65F20.
Similar content being viewed by others
1 Introduction
Let and be two real generalized reflection matrices, i.e., , , , , denotes the n order identity matrix. A matrix is called generalized reflexive matrix with respect to the matrix pair if . The set of all m-by-n real generalized reflexive matrices with respect to a matrix pair is denoted by . We denote by the superscript T the transpose of a matrix. In a matrix space , we define an inner product as for all , represents the Frobenius norm of A, represents the column space of A, represents the vector operator, i.e., for the matrix , , , stands for the Kronecker product of matrices A and B.
Least-squares-based iterative algorithms are very important in system identification, parameter estimation, and signal processing, including the recursive least squares (RLS) and iterative least squares (ILS) methods for solving the solutions of some matrix equations, for example, the Lyapunov matrix equation, Sylvester matrix equations, and coupled matrix equations as well. For example, novel gradient-based iterative (GI) method [1–5] and least-squares-based iterative methods [3, 4, 6] with highly computational efficiencies for solving (coupled) matrix equations are presented and have good stability performances based on the hierarchical identification principle, which regards the unknown matrix as the system parameter matrix to be identified. In this paper, we consider the following two problems.
Problem I Let and be generalized reflection matrices. For given matrices , , and , find a generalized reflexive matrix solution group with such that
Problem II When Problem I is consistent, let denote the set of the generalized reflexive solution group of Problem I, i.e.,
For a given generalized reflexive matrix group
find such that
General coupled matrix equation (1) (including the generalized coupled Sylvester matrix equations as special cases) may arise in many areas of control and system theory. Problem II occurs frequently in experiment design; see, for instance, [7].
Many theoretical and numerical results on Eq. (1) and some of its special cases have been obtained. Ding and Chen [1] presented the gradient-based iterative algorithms by applying the gradient search principle and the hierarchical identification principle for Eq. (1) with . Wu et al. [8, 9] gave the finite iterative solutions to coupled Sylvester-conjugate matrix equations. Wu et al. [10] gave the finite iterative solutions to a class of complex matrix equations with conjugate and transpose of the unknowns. Jonsson and Kågström [11, 12] proposed recursive block algorithms for solving the coupled Sylvester matrix equations and the generalized Sylvester and Lyapunov matrix equations. By extending the idea of conjugate gradient method, Dehghan and Hajarian [13] constructed an iterative algorithm to solve Eq. (1) with over generalized bisymmetric matrices. Very recently, Huang et al. [14] presented a finite iterative algorithm for the one-sided and generalized coupled Sylvester matrix equations over generalized reflexive solutions. Yin et al. [15] presented a finite iterative algorithm for the two-sided and generalized coupled Sylvester matrix equations over reflexive solutions. Zhou et al.[16] gave the gradient based iterative solutions for coupled matrix equation (1) and a more general case over general solution. Li et al. [17] presented a numerical solution to linear matrix equation by finite steps iteration. For more results, we refer to [7, 18–36]. However, to our knowledge, the generalized reflexive solution to the more general coupled matrix equation (1) and the optimal approximation reflexive solution have not been derived. In this paper, we consider the generalized reflexive solution of Eq. (1) and the optimal approximation generalized reflexive solution.
This paper is organized as follows. In Section 2, we solve Problem I by constructing an iterative algorithm. The convergence of the proposed algorithm is proved. For an arbitrary initial matrix group, we can obtain a generalized reflexive solution group of Problem I within finite iteration steps in the absence of round-off errors. Furthermore, for a special initial matrix group, we can obtain the least Frobenius norm solutions of Problem I. Then in Section 3, we give the optimal approximate solution group of Problem II by finding the least Frobenius norm generalized reflexive solution group of the corresponding general coupled matrix equations. In Section 4, a numerical example is given to illustrate the effectiveness of our method. Finally, some conclusions are drawn in Section 5.
2 An iterative algorithm for solving Problem I
In this section, we first introduce an iterative algorithm to solve Problem I, then we prove its convergence. In addition, we give the least-norm generalized reflexive solutions of Problem I when an appropriate initial iterative matrix group is chosen.
Algorithm 2.1 Step 1: Input matrices , , , and generalized reflection matrices and , , ;
Step 2: Choose an arbitrary matrix group
Compute
Step 3: If , then stop and is the solution group of Eq. (1); else if , but , , then stop and Eq. (1) is not consistent over a generalized reflexive matrix group; else ;
Step 4: Compute
Step 5: Go to Step 3.
Obviously, it can be seen that for all and .
Lemma 2.1 For the sequences , () generated by Algorithm 2.1, and , we have
The proof of Lemma 2.1 is similar to that of Lemma 2.2 in [21] and is omitted.
Lemma 2.2 Suppose is an arbitrary generalized reflexive solution group of Problem I, then for any initial generalized reflexive matrix group , we have
where the sequences , and are generated by Algorithm 2.1.
Proof We prove the conclusion by induction for the positive integer k.
For , we have that
Assume that (4) holds for . When , by Algorithm 2.1, we have that
Therefore, (4) holds for . Thus (4) holds by the principle of induction. This completes the proof. □
Remark 2.1 If there exists a positive number k such that , , but , then by Lemma 2.2, we have that Eq. (1) is not consistent over generalized reflexive matrices.
Theorem 2.1 Suppose that Problem I is consistent, then for an arbitrary initial matrix group with , a generalized reflexive solution group of Problem I can be obtained with finite iteration steps in the absence of round-off errors.
Proof If , , , by Lemma 2.2 and Remark 2.1, we have for all and , then we can compute and by Algorithm 2.1.
By Lemma 2.1, we have
and
It can be seen that the set of is an orthogonal basis of the matrix subspace
which implies that , i.e., with is a generalized reflexive solution group of Problem I. This completes the proof. □
To show the least Frobenius norm generalized reflexive solution of Problem I, we first introduce the following result.
Lemma 2.3 (see [[23], Lemma 2.4])
Suppose that the consistent system of linear equation has a solution , then is a unique least Frobenius norm solution of the system of linear equations.
By Lemma 2.3, the following result can be obtained.
Theorem 2.2 Suppose that Problem I is consistent. If we choose the initial iterative matrices , , where , are arbitrary matrices, especially, , then the solution group generated by Algorithm 2.1 is the unique least Frobenius norm generalized reflexive solution group of Problem I.
Proof We know the solvability of Eq. (1) over generalized reflexive matrices is equivalent to the following matrix equations:
Then the system of matrix equations (5) is equivalent to
Let , , where are arbitrary matrices, then
Furthermore, we can see that all generalized reflexive matrix solution groups generated by Algorithm 2.1 satisfy
By Lemma 2.3 we know that is the least Frobenius norm generalized reflexive solution group of the system of linear equations (6). Since a vector operator is isomorphic, is the unique least Frobenius norm generalized reflexive solution group of the system of matrix equations (5). Thus is the unique least Frobenius norm generalized reflexive solution group of Problem I. □
3 The solution of Problem II
In this section, we show that the optimal approximate generalized reflexive solution group of Problem II to a given generalized reflexive matrix group can be derived by finding the least Frobenius norm generalized reflexive solution group of the corresponding general coupled matrix equations.
When Problem I is consistent, the set of generalized reflexive solution group of Problem I denoted by is not empty. For a given matrix pair with , , we have
Set , , then solving Problem II is equivalent to finding the least Frobenius norm generalized reflexive solution group of the corresponding general coupled matrix equations
Let initial iteration matrices be
where , are arbitrary matrices, especially, , . By using Algorithm 2.1, we can get the least Frobenius norm generalized reflexive solution group of (8). Thus the generalized reflexive solution group of Problem II can be represented as
4 A numerical example
In this section, we show a numerical example to illustrate the proposed iterative method. All the tests are performed by MATLAB 7.8.
Example 4.1 Consider the generalized reflexive solution of the general coupled matrix equations
where
Let
be generalized reflection matrices.
We will find the generalized reflexive solution of Eq. (9) by using Algorithm 2.1. It can be verified that Eq. (9) is consistent over generalized reflexive matrices and the solutions are
Because of the influence of the error of calculation, the residual is usually unequal to zero in the process of iteration, where . For any chosen positive number ε, however small it is, e.g., , whenever , stop the iteration, and are regarded to be generalized reflexive solutions of Eq. (9). Let the initially iterative matrices be as follows:
By Algorithm 2.1, we have
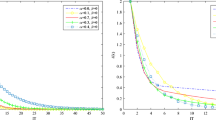
Thus we obtain the reflexive solution of Eq. (9). The relative error and the residual of the solution are shown in Figure 1, where the relative error and the residual .
Let denote the set of all generalized reflexive solution group of Eq. (9). For two given generalized reflexive matrices
we will find the optimal approximate generalized reflexive solution group to the given matrix group in in Frobenius norm, i.e., find such that
Let , , , . By the method mentioned in Section 3, we can obtain the least-norm generalized reflexive solution group of the matrix equations , by choosing the initially iterative matrices and . Then by Algorithm 2.1, we have that
and the optimal approximate generalized reflexive solution to the matrix group in Frobenius norm is
The relative error and the residual of the solution are shown in Figure 2, where the relative error and the residual .
From Figures 1 and 2, we can see that the iterative solutions generated by Algorithm 2.1 can quickly converge to the exact generalized reflexive solution of Eq. (9). This illustrates that our iterative algorithm is quite effective.
5 Conclusions
In this paper, an iterative algorithm is presented to solve the general coupled matrix equations () and their optimal approximation problem over generalized reflexive matrices. When the general coupled matrix equations are consistent over generalized reflexive matrices, for any initially generalized reflexive matrix group, the generalized reflexive solution group can be obtained by the iterative algorithm within finite iterative steps in the absence of round-off errors. When a special kind of initial iteration matrix group is chosen, the unique least-norm generalized reflexive solution of the general coupled matrix equations can be derived. Furthermore, the optimal approximate generalized reflexive solution of the general coupled matrix equations to a given generalized reflexive matrix group can be derived by finding the least-norm generalized reflexive solution of new corresponding general coupled matrix equations. Finally, a numerical example is given to show that our iterative algorithm is quite effective.
References
Ding F, Chen T: On iterative solutions of general coupled matrix equations. SIAM J. Control Optim. 2006, 44(6):2269–2284. 10.1137/S0363012904441350
Ding F, Chen T: Gradient based iterative algorithms for solving a class of matrix equations. IEEE Trans. Autom. Control 2005, 50(8):1216–1221.
Ding F, Liu PX, Ding J: Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle. Appl. Math. Comput. 2008, 197(1):41–50. 10.1016/j.amc.2007.07.040
Ding J, Liu Y, Ding F:Iterative solutions to matrix equations of the form . Comput. Math. Appl. 2010, 59(11):3500–3507.
Xie L, Ding J, Ding F: Gradient based iterative solutions for general linear matrix equations. Comput. Math. Appl. 2009, 58(7):1441–1448.
Ding F, Chen T: Iterative least-squares solutions of coupled Sylvester matrix equations. Syst. Control Lett. 2005, 54(2):95–107. 10.1016/j.sysconle.2004.06.008
Wang QW: Bisymmetric and centrosymmetric solutions to systems of real quaternion matrix equations. Comput. Math. Appl. 2005, 49(5–6):641–650.
Wu AG, Feng G, Duan GR, Wu WJ: Iterative solutions to coupled Sylvester-conjugate matrix equations. Comput. Math. Appl. 2010, 60(1):54–66.
Wu AG, Li B, Zhang Y, Duan GR: Finite iterative solutions to coupled Sylvester-conjugate matrix equations. Appl. Math. Model. 2011, 35(3):1065–1080. 10.1016/j.apm.2010.07.053
Wu AG, Feng G, Duan GR, Wu WJ: Finite iterative solutions to a class of complex matrix equations with conjugate and transpose of the unknowns. Math. Comput. Model. 2010, 52(9–10):1463–1478. 10.1016/j.mcm.2010.06.010
Jonsson I, Kågström B: Recursive blocked algorithms for solving triangular systems - part I: one-sided and coupled Sylvester-type matrix equations. ACM Trans. Math. Softw. 2002, 28(4):392–415. 10.1145/592843.592845
Jonsson I, Kågström B: Recursive blocked algorithms for solving triangular systems - part II: two-sided and generalized Sylvester and Lyapunov matrix equations. ACM Trans. Math. Softw. 2002, 28(4):416–435. 10.1145/592843.592846
Dehghan M, Hajarian M: The general coupled matrix equations over generalized bisymmetric matrices. Linear Algebra Appl. 2010, 432(6):1531–1552. 10.1016/j.laa.2009.11.014
Huang GX, Wu N, Yin F, Zhou ZL, Guo K: Finite iterative algorithms for solving generalized coupled Sylvester systems - part I: one-sided and generalized coupled Sylvester matrix equations over generalized reflexive solutions. Appl. Math. Model. 2012, 36(4):1589–1603. 10.1016/j.apm.2011.09.027
Yin F, Huang GX, Chen DQ: Finite iterative algorithms for solving generalized coupled Sylvester systems - part II: two-sided and generalized coupled Sylvester matrix equations over reflexive solutions. Appl. Math. Model. 2012, 36(4):1604–1614. 10.1016/j.apm.2011.09.025
Zhou B, Duan GR, Li ZY: Gradient based iterative algorithm for solving coupled matrix equations. Syst. Control Lett. 2009, 58(5):327–333. 10.1016/j.sysconle.2008.12.004
Li ZY, Zhou B, Wang Y, Duan GR: Numerical solution to linear matrix equation by finite steps iteration. IET Control Theory Appl. 2010, 4(7):1245–1253. 10.1049/iet-cta.2009.0015
Cai J, Chen GX:An iterative algorithm for the least squares bisymmetric solutions of the matrix equations , . Math. Comput. Model. 2009, 50(7–8):1237–1244. 10.1016/j.mcm.2009.07.004
Chen D, Yin F, Huang G:An iterative algorithm for the generalized reflexive solution of the matrix equations , . J. Appl. Math. 2012. doi:10.1155/2012/492951
Ding F, Chen T: Hierarchical gradient-based identification of multivariable discrete-time systems. Automatica 2005, 41(2):315–325. 10.1016/j.automatica.2004.10.010
Ding F, Chen T: Hierarchical least squares identification methods for multivariable systems. IEEE Trans. Autom. Control 2005, 50(3):397–402.
Ding F, Chen T: Hierarchical identification of lifted state-space models for general dual-rate systems. IEEE Trans. Circuits Syst. I, Regul. Pap. 2005, 52(6):1179–1187.
Huang GX, Yin F, Guo K:An iterative method for the skew-symmetric solution and the optimal approximate solution of the matrix equation . J. Comput. Appl. Math. 2008, 212(2):231–244. 10.1016/j.cam.2006.12.005
Liao AP, Lei Y:Least-squares solution with the minimum-norm for the matrix equation . Comput. Math. Appl. 2005, 50(3–4):539–549.
Peng ZH, Hu XY, Zhang L:An efficient algorithm for the least-squares reflexive solution of the matrix equation , . Appl. Math. Comput. 2006, 181(2):988–999. 10.1016/j.amc.2006.01.071
Wang QW: The general solution to a system of real quaternion matrix equations. Comput. Math. Appl. 2005, 49(5–6):665–675.
Wang QW, Li CK: Ranks and the least-norm of the general solution to a system of quaternion matrix equations. Linear Algebra Appl. 2009, 430(5–6):1626–1640. 10.1016/j.laa.2008.05.031
Yin F, Huang GX:An iterative algorithm for the least squares generalized reflexive solutions of the matrix equations , . Abstr. Appl. Anal. 2012, 2012: 1–18.
Yin F, Huang G: An iterative algorithm for the generalized reflexive solutions of the generalized coupled Sylvester matrix equations. J. Appl. Math. 2012, 2012: 1–28.
Zhou B, Li ZY, Duan GR, Wang Y: Weighted least squares solutions to general coupled Sylvester matrix equations. J. Comput. Appl. Math. 2009, 224(2):759–776. 10.1016/j.cam.2008.06.014
Cheng G, Tan Q, Wang Z: Some inequalities for the minimum eigenvalue of the Hadamard product of an M -matrix and its inverse. J. Inequal. Appl. 2013., 2013: Article ID 65. doi:10.1186/1029–242X-2013–65
Liu Y, Sheng J, Ding R: Convergence of stochastic gradient estimation algorithm for multivariable ARX-like systems. Comput. Math. Appl. 2010, 59(8):2615–2627.
Liu Y, Xiao Y, Zhao X: Multi-innovation stochastic gradient algorithm for multiple-input single-output systems using the auxiliary model. Appl. Math. Comput. 2009, 215(4):1477–1483. 10.1016/j.amc.2009.07.012
Ding F, Liu Y, Bao G: Gradient based and least squares based iterative estimation algorithms for multi-input multi-output systems. Proc. Inst. Mech. Eng., Part I, J. Syst. Control Eng. 2012, 226(1):43–55. 10.1177/0959651811409491
Ding F, Liu G, Liu XP: Parameter estimation with scarce measurements. Automatica 2011, 47(8):1646–1655. 10.1016/j.automatica.2011.05.007
Xie L, Liu Y, Yang H:Gradient based and least squares based iterative algorithms for matrix equations . Appl. Math. Comput. 2010, 217(5):2191–2199. 10.1016/j.amc.2010.07.019
Acknowledgements
The authors are grateful to the anonymous referee for the constructive and helpful comments and Professor R Agarwal for all the communications. This work was partially supported by National Natural Science Fund (41272363), Open Fund of Geomathematics Key Laboratory of Sichuan Province (scsxdz2012001, scsxdz2012002), Key Natural Science Foundation of Sichuan Education Department (12ZA008, 12ZB289) and the young scientific research backbone teachers of CDUT.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors have the same contributions on this paper. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yin, F., Guo, K. & Huang, GX. An iterative algorithm for the generalized reflexive solutions of the general coupled matrix equations. J Inequal Appl 2013, 280 (2013). https://doi.org/10.1186/1029-242X-2013-280
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-280