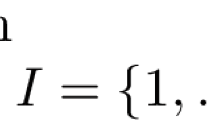Optimality conditions of E-convex programming for an E-differentiable function

Abstract

In this paper we introduce a new definition of an E-differentiable convex function, which transforms a non-differentiable function to a differentiable function under an operator $E:R^n\to R^n$. By this definition, we can apply Kuhn-Tucker and Fritz-John conditions for obtaining the optimal solution of mathematical programming with a non-differentiable function.

1 Introduction

The concepts of E-convex sets and an E-convex function have been introduced by Youness in [1, 2], and they have some important applications in various branches of mathematical sciences. Youness in [1] introduced a class of sets and functions which is called E-convex sets and E-convex functions by relaxing the definition of convex sets and convex functions. This kind of generalized convexity is based on the effect of an operator $E:R^n\to R^n$ on the sets and the domain of the definition of functions. Also, in [2] Youness discussed the optimality criteria of E-convex programming. Xiusu Chen [3] introduced a new concept of semi E-convex functions and discussed its properties. Yu-Ru Syan and Stanelty [4] introduced some properties of an E-convex function, while Emam and Youness in [5] introduced a new class of E-convex sets and E-convex functions, which are called strongly E-convex sets and strongly E-convex functions, by taking the images of two points x and y under an operator $E:R^n\to R^n$ besides the two points themselves. In [6] Megahed et al. introduced a combined interactive approach for solving E-convex multiobjective nonlinear programming. Also, in [7, 8] Iqbal and et al. introduced geodesic E-convex sets, geodesic E-convex and some properties of geodesic semi-E-convex functions.

In this paper we present the concept of an E-differentiable convex function which transforms a non-differentiable convex function to a differentiable function under an operator $E:R^n\to R^n$, for which we can apply the Fritz-John and Kuhn-Tucker conditions [9, 10] to find a solution of mathematical programming with a non-differentiable function.

In the following, we present the definitions of E-convex sets, E-convex functions, and semi E-convex functions.

Definition 1[1]

A set M is said to be an E-convex set with respect to an operator $E:R^n\to R^n$ if and only if $\lambda E(x)+(1-\lambda )E(y)\in M$ for each $x,y\in M$ and $\lambda \in [0,1]$.

Definition 2[1]

A function $f:R^n\to R$ is said to be an E-convex function with respect to an operator $E:R^n\to R^n$ on an E-convex set $M\subseteq R^n$ if and only if

$$f(\lambda E(x)+(1-\lambda )E(y))\le \lambda (f\circ E)(x)+(1-\lambda )(f\circ E)(y)$$

for each $x,y\in M$ and $\lambda \in [0,1]$.

Definition 3[3]

A real-valued function $f:M\subseteq R^n\to R$ is said to be semi E-convex function with respect to an operator $E:R^n\to R^n$ on M if M is an E-convex set and

$$f(\lambda E(x)+(1-\lambda )E(y))\le \lambda f(x)+(1-\lambda )f(y)$$

for each $x,y\in M$ and $\lambda \in [0,1]$.

Proposition 4[1]

1- Let a set$M\subseteq R^n$be an E-convex set with respect to an operator E, $E:R^n\to R^n$, then$E(M)\subseteq M$.

2- If$E(M)$is a convex set and$E(M)\subseteq M$, then M is an E-convex set.

3- If$M_1$and$M_2$are E-convex sets with respect to E, then$M_1\cap M_2$is an E-convex set with respect to E.

Lemma 5[1]

Let$M\subseteq R^n$be an$E_1$- and$E_2$-convex set, then M is an$(E_1\circ E_2)$- and$(E_2\circ E_1)$-convex set.

Lemma 6[1]

Let$E:R^n\to R^n$be a linear map and let$M_1,M_2\subset R^n$be E-convex sets, then$M_1+M_2$is an E-convex set.

Definition 7[1]

Let $S\subset R^n\times R$ and $E:R^n\to R^n$, we say that the set S is E-convex if for each $(x,\alpha ),(y,\beta )\in S$ and each $\lambda \in [0,1]$, we have

$$(\lambda Ex+(1-\lambda )Ey,\lambda \alpha +(1-\lambda )\beta )\in S.$$

2 Generalized E-convex function

Definition 8[1]

Let $M\subseteq R^n$ be an E-convex set with respect to an operator $E:R^n\to R^n$. A function $f:M\to R$ is said to be a pseudo E-convex function if for each $x_1,x_2\in M$ with $\mathrm{\nabla }(f\circ E)(x_1)(x_2-x_1)\ge 0$ implies $f(E{x}_2)\ge f(E{x}_1)$ or for all $x_1,x_2\in M$ and $f(E{x}_2)<f(E{x}_1)$ implies $\mathrm{\nabla }(f\circ E)(x_1)(x_2-x_1)<0$.

Definition 9[1]

Let $M\subseteq R^n$ be an E-convex set with respect to an operator $E:R^n\to R^n$. A function $f:M\to R$ is said to be a quasi-E-convex function if and only if

$$f(\lambda Ex+(1-\lambda )Ey)\le max\{(f\circ E)x,(f\circ E)y\}$$

for each $x,y\in M$ and $\lambda \in [0,1]$.

3 E-differentiable function

Definition 10 Let $f:M\subseteq R^n\to R$ be a non-differentiable function at $\overline{x}$ and let $E:R^n\to R^n$ be an operator. A function f is said to be E-differentiable at $\overline{x}$ if and only if $(f\circ E)$ is a differentiable function at $\overline{x}$ and

$$\begin{array}{c}(f\circ E)(x)=(f\circ E)(\overline{x})+\mathrm{\nabla }(f\circ E)(\overline{x})(x-\overline{x})+\parallel x-\overline{x}\parallel \alpha (\overline{x},x-\overline{x}),\hfill \\ \alpha (\overline{x},x-\overline{x})\to 0\text{as }x\to \overline{x.}\hfill \end{array}$$

Example 11 Let $f(x)=|x|$ be a non-differentiable function at the point $x=0$ and let $E:R\to R$ be an operator such that $E(x)=x^2$, then the function $(f\circ E)(x)=f(Ex)=x^2$ is a differentiable function at the point $x=0$, and hence f is an E-differentiable function.

3.1 Problem formulation

Now, we formulate problems P and $P_E$, which have a non-differentiable function and an E-differentiable function, respectively.

Let $E:R^n\to R^n$ be an operator, M be an E-convex set and f be an E-differentiable function. The problem P is defined as

$$P\{\begin{array}{c}Minf(x),\hfill \\ \text{subject to }M=\{x:g_i(x)\le 0,i=1,2,\dots ,m\},\hfill \end{array}$$

where f is a non-differentiable function, and the problem $P_E$ is defined as

$$P_E\{\begin{array}{c}Min(f\circ E)(x),\hfill \\ \text{subject to }{M}^{\mathrm{\prime }}=\{x:(g_i\circ E)(x)\le 0,i=1,2,\dots ,m\},\hfill \end{array}$$

where f is an E-differentiable function.

Now, we will discuss the relationship between the solutions of problems P and $P_E$.

Lemma 12[11]

Let$E:R^n\to R^n$be a one-to-one and onto operator and let$M^{\mathrm{\prime }}=\{x:(g_i\circ E)(x)\le 0,i=1,2,\dots ,m\}$. Then$E(M^{\mathrm{\prime }})=M$, where M and$M^{\mathrm{\prime }}$are feasible regions of problems P and$P_E$, respectively.

Theorem 13 Let$E:R^n\to R^n$be a one-to-one and onto operator and let f be an E-differentiable function. If f is non-differentiable at$\overline{x}$, and$\overline{x}$is an optimal solution of the problem P, then there exists$\overline{y}\in M^{\mathrm{\prime }}$such that$\overline{x}=E(\overline{y})$and$\overline{y}$is an optimal solution of the problem$P_E$.

Proof Let $\overline{x}$ be an optimal solution of the problem P. From Lemma 12 there exists $\overline{y}\in M^{\mathrm{\prime }}$ such that $\overline{x}=E(\overline{y})$. Let $\overline{y}$ be a not optimal solution of the problem $P_E$, then there is $\hat{y}\in M^{\mathrm{\prime }}$ such that $(f\circ E)(\hat{y})\le (f\circ E)(\overline{y})$. Also, there exists $\hat{x}\in M$ such that $\hat{x}=E(\hat{y})$ . Then $f(\hat{x})<f(\overline{x})$ contradicts the optimality of $\overline{x}$ for the problem P. Hence the proof is complete. □

Theorem 14 Let$E:R^n\to R^n$be a one-to-one and onto operator, and let f be an E-differentiable function and strictly quasi-E-convex. If$\overline{x}$is an optimal solution of the problem P, then there exists$\overline{y}\in M^{\mathrm{\prime }}$such that$\overline{x}=E(\overline{y})$and$\overline{y}$is an optimal solution of the problem $P_E$.

Proof Let $\overline{x}$ be an optimal solution of the problem P. Then from Lemma 12 there is $\overline{y}\in M^{\mathrm{\prime }}$ such that $\overline{x}=E(\overline{y})$. Let $\overline{y}$ be a not optimal solution of the problem $P_E$, then there is $\hat{y}\in M^{\mathrm{\prime }}$ and also $\hat{x}\in M$, $\hat{x}=E(\hat{y})$ such that $(f\circ E)(\hat{y})\le (f\circ E)(\overline{y})$. Since f is strictly quasi-E-convex function, then

$$\begin{array}{rcl}f(\lambda E(\overline{y})+(1-\lambda )E(\hat{y}))& <& max\{(f\circ E)(\overline{y}),(f\circ E)(\hat{y})\}\\ <& max\{f(\overline{x}),f(\hat{x})\}\\ <& f(\overline{x}).\end{array}$$

Since M is an E-convex set and $E(M)\subset M$, then $\lambda E(\overline{y})+(1-\lambda )E(\hat{y})\in M$ contradicts the assumption that $\overline{x}$ is a solution of the problem P, then there exists $\overline{y}\in M^{\mathrm{\prime }}$, a solution of the problem $P_E$, such that $\overline{x}=E(\overline{y})$. □

Theorem 15 Let M be an E-convex set, $E:R^n\to R^n$be a one-to-one and onto operator and$f:M\subseteq R^n\to R$be an E-differentiable function at$\overline{x}$. If there is a vector$d\subset R^n$such that$\mathrm{\nabla }(f\circ E)(\overline{x})d<0$, then there exists$\delta >0$such that

$$(f\circ E)(\overline{x}+\lambda d)<(f\circ E)(\overline{x})\mathit{\text{for each}}\lambda \in (0,\delta ).$$

Proof Since f is an E-differentiable function at $\overline{x}$, then

$$\begin{array}{c}(f\circ E)(\overline{x}+\lambda d)=(f\circ E)(\overline{x})+\lambda \mathrm{\nabla }(f\circ E)(\overline{x})+\lambda \parallel d\parallel \alpha (\overline{x},\lambda d),\hfill \\ \alpha (\overline{x},\lambda d)\to 0\text{as }\lambda \to 0.\hfill \end{array}$$

Since $\mathrm{\nabla }(f\circ E)(\overline{x})d<0$ and $\alpha (\overline{x},\lambda d)\to 0$ as $\lambda \to 0$, then there exists $\delta >0$ such that

$$\mathrm{\nabla }(f\circ E)(\overline{x})+\parallel d\parallel \alpha (\overline{x},\lambda d)<0\text{for each }\lambda \in (0,\delta )$$

and thus $(f\circ E)(\overline{x}+\lambda d)<(f\circ E)(\overline{x})$. □

Corollary 16 Let M be an E-convex set, let$E:R^n\to R^n$be a one-to-one and onto operator, and let$f:M\subseteq R^n\to R$be an E-differentiable and strictly E-convex function at$\overline{x}$. If$\overline{x}$is a local minimum of the function$(f\circ E)$, then$\mathrm{\nabla }(f\circ E)(\overline{x})=0$.

Proof Suppose that $\mathrm{\nabla }(f\circ E)(\overline{x})\ne 0$ and let $d=-\mathrm{\nabla }(f\circ E)(\overline{x})$, then $\mathrm{\nabla }(f\circ E)(\overline{x})d=-{\parallel \mathrm{\nabla }(f\circ E)(\overline{x})\parallel }^2<0$. By Theorem 15 there exists $\delta >0$ such that

$$(f\circ E)(\overline{x}+\lambda d)<(f\circ E)(\overline{x})\text{for each }\lambda \in (0,\delta )$$

contradicting the assumption that $\overline{x}$ is a local minimum of $(f\circ E)(x)$, and thus $\mathrm{\nabla }(f\circ E)(\overline{x})=0$. □

Theorem 17 Let M be an E-convex set, $E:R^n\to R^n$be a one-to-one and onto operator, and$f:M\subseteq R^n\to R$be twice E-differentiable and strictly E-convex function at$\overline{x}$. If$\overline{x}$is a local minimum of$(f\circ E)$, then$\mathrm{\nabla }(f\circ E)(\overline{x})=0$and the Hessian matrix$H(\overline{x})={\mathrm{\nabla }}^2(f\circ E)(\overline{x})$is positive semidefinite.

Proof Suppose that d is an arbitrary direction. Since f is a twice E-differentiable function at $\overline{x}$, then

$$\begin{array}{rcl}(f\circ E)(\overline{x}+\lambda d)& =& (f\circ E)(\overline{x})+\lambda \mathrm{\nabla }(f\circ E)(\overline{x})d+\frac{1}{2}{\lambda }^2{d}^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})d\\ +{\lambda }^2{\parallel d\parallel }^2\alpha (\overline{x},\lambda d),\end{array}$$

where $\alpha (\overline{x},\lambda d)\to 0$ as $\lambda \to 0$.

From Corollary 16 we have $\mathrm{\nabla }(f\circ E)(\overline{x})=0$, and

$$\frac{(f\circ E)(\overline{x}+\lambda d)-(f\circ E)(\overline{x})}{{\lambda }^2}=\frac{1}{2}{d}^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})d.$$

Since $\overline{x}$ is a local minimum of $(f\circ E)$, then $(f\circ E)(\overline{x})<(f\circ E)(\overline{x}+\lambda d)$, and

$$d^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})d\ge 0,\mathit{\text{i.e.}}\text{,}H(\overline{x})={\mathrm{\nabla }}^2(f\circ E)(\overline{x})\text{is positive semidefinite}.$$

 □

Example 18 Let $f(x,y)=x+2y^2-2x^{\frac{1}{3}}$ be a non-differentiable function at $(0,y)$, and let $E(x,y)=(x^3,y)$, then $(f\circ E)(x,y)=x^3+2y^2-2x$, and

$$\begin{array}{c}\frac{\partial (f\circ E)}{\partial x}=3x^2-2=0\text{implies}x=\pm \sqrt{\frac{2}{3}},\hfill \\ \frac{\partial (f\circ E)}{\partial y}=4y=0\text{implies}y=0,\hfill \\ \frac{{\partial }^2(f\circ E)}{\partial x^2}=6x,\frac{{\partial }^2(f\circ E)}{\partial y\partial x}=0,\frac{{\partial }^2(f\circ E)}{\partial y^2}=4,\frac{{\partial }^2(f\circ E)}{\partial x\partial y}=0.\hfill \end{array}$$

Then $(x_1,y_1)=(\sqrt{\frac{2}{3}},0)$ and $(x_2,y_2)=(-\sqrt{\frac{2}{3}},0)$ are extremum points of $(f\circ E)(x,y)$, and the Hessian matrix $H(\sqrt{\frac{2}{3}},0)=\left[\begin{array}{cc}6\sqrt{\frac{2}{3}}& 0\\ 0& 4\end{array}\right]$ is positive definite. And thus the point $(\sqrt{\frac{2}{3}},0)$ is a local minimum of the function $(f\circ E)(x,y)$, but the Hessian matrix $H(-\sqrt{\frac{2}{3}},0)=\left[\begin{array}{cc}-6\sqrt{\frac{2}{3}}& 0\\ 0& 4\end{array}\right]$ is indefinite.

Theorem 19 Let M be an E-convex set, let$E:R^n\to R^n$be a one-to-one and onto operator, and let$f:M\subseteq R^n\to R$be a twice E-differentiable and strictly E-convex function at$\overline{x}$. If$\mathrm{\nabla }(f\circ E)(\overline{x})=0$and the Hessian matrix$H(\overline{x})={\mathrm{\nabla }}^2(f\circ E)(\overline{x})$is positive definite, then$\overline{x}$is a local minimum of$(f\circ E)$.

Proof Suppose that $\overline{x}$ is not a local minimum of $(f\circ E)(x)$, and there exists a sequence $\{x_k\}$ is converging to $\overline{x}$ such that $(f\circ E)(x_k)<(f\circ E)(\overline{x})$ for each k. Since $\mathrm{\nabla }(f\circ E)(\overline{x})=0$, and f is twice E-differentiable at $\overline{x}$, then

$$\begin{array}{rcl}(f\circ E)(x_k)& =& (f\circ E)(\overline{x})+\lambda \mathrm{\nabla }(f\circ E)(\overline{x})(x_k-\overline{x})\\ +\frac{1}{2}{(x_k-\overline{x})}^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})(x_k-\overline{x})+{\parallel (x_k-\overline{x})\parallel }^2\alpha (\overline{x},(x_k-\overline{x})),\end{array}$$

where $\alpha (\overline{x},(x_k-\overline{x}))\to 0$ as $k\to \mathrm{\infty }$, and

$$\frac{1}{2}{(x_k-\overline{x})}^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})(x_k-\overline{x})+{\parallel (x_k-\overline{x})\parallel }^2\alpha (\overline{x},(x_k-\overline{x}))<0\text{for each }k.$$

By dividing on ${\parallel (x_k-\overline{x})\parallel }^2$, and letting $d_k=\frac{(x_k-\overline{x})}{\parallel (x_k-\overline{x})\parallel }$, we get

$$\frac{1}{2}{d}_k^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})d_k+\alpha (\overline{x},(x_k-\overline{x}))<0\text{for each }k.$$

But $\parallel d_k\parallel =1$ for each k, and hence there exists an index set K such that ${\{d_k\}}_K\to d$, where $\parallel d\parallel =1$. Considering this subsequence and the fact that $\alpha (\overline{x},(x_k-\overline{x}))\to 0$ as $k\to \mathrm{\infty }$, then $d^t{\mathrm{\nabla }}^2(f\circ E)(\overline{x})d<0$. This contradicts the assumption that $H(\overline{x})$ is positive definite. Therefore $\overline{x}$ is indeed a local minimum. □

Example 20 Let $f(x,y)=x^{\frac{2}{3}}+y^2-1$ be a non-differentiable at the point $(0,y)$, and let $E(x,y)=(x^3,y)$, then $(f\circ E)(x,y)=x^2+y^2-1$

$$\begin{array}{c}\frac{\partial (f\circ E)}{\partial x}=2x,\frac{{\partial }^2(f\circ E)}{\partial y\partial x}=0,\frac{{\partial }^2(f\circ E)}{\partial x^2}=2,\hfill \\ \frac{\partial (f\circ E)}{\partial y}=2y,\frac{{\partial }^2(f\circ E)}{\partial x\partial y}=0,\frac{{\partial }^2(f\circ E)}{\partial y^2}=2.\hfill \end{array}$$

The necessary condition for $\overline{x}$ is a local minimum of $(f\circ E)$ is $\mathrm{\nabla }(f\circ E)(\overline{x})=0$, then $\overline{x}=(0,0)$, and the Hessian matrix $H(\overline{x})$

$$H=\left[\begin{array}{cc}\frac{{\partial }^2(f\circ E)}{\partial x^2}& \frac{{\partial }^2(f\circ E)}{\partial y\partial x}\\ \frac{{\partial }^2(f\circ E)}{\partial x\partial y}& \frac{{\partial }^2(f\circ E)}{\partial y^2}\end{array}\right]=\left[\begin{array}{cc}2& 0\\ 0& 2\end{array}\right]$$

is positive definite.

Example 21 Let $f(x,y)=x^{\frac{1}{3}}+y-1$ be non-differentiable at the point $(0,y)$, and let $E(x,y)=(x^3,y)$, then $(f\circ E)(x,y)=x+y-1$.

Now, let $M=\{{\lambda }_1(0,0)+{\lambda }_2(0,3)+{\lambda }_3(1,2)+{\lambda }_4(1,0)\}\cup \{{\lambda }_1(0,0)+{\lambda }_2(0,-3)+{\lambda }_3(1,-2)+{\lambda }_4(1,0)\}$, ${\sum }_{i=1}^4{\lambda }_i=1$, ${\lambda }_i\ge 0$ be an E-convex set with respect to operator E (the feasible region is shown in Figure 1) and

$$\begin{array}{c}f(0,0)=-1,(f\circ E)(0,0)=-1,f(0,-3)=-4,(f\circ E)(0,3)=-4,\hfill \\ f(1,2)=2,(f\circ E)(1,2)=2,f(1,0)=0,(f\circ E)(1,0)=0,\hfill \\ f(0,3)=2,(f\circ E)(0,3)=2,f(1,-2)=-2,(f\circ E)(1,2)=-2.\hfill \end{array}$$

Figure 1

The feasible region M.

Then $\overline{x}=(0,-3)$ is a solution of the problem $P_E$ and $E(\overline{x})=E(0,-3)=(0,-3)$ is a solution of the problem P.

Definition 22 Let M be a nonempty E-convex set in $R^n$ and let $E(\overline{x})\in clM$. The cone of feasible direction of $E(M)$ at $E(\overline{x})$ denoted by D is given by

$$D=\{d:d\ne 0,E(\overline{x})+\lambda d\in M\text{ for each }\lambda \in [0,\delta ],\delta >0\}.$$

Lemma 23 Let M be an E-convex set with respect to an operator$E:R^n\to R^n$, and let$f:M\subseteq R^n\to R$be E-differentiable at$\overline{x}$. If$\overline{x}$is a local minimum of the problem$P_E$, then$F_0\cap D=\varphi$, where$F_0=\{d:\mathrm{\nabla }(f\circ E)(\overline{x})d<0\}$, and D is the cone of feasible direction of M at $\overline{x}$.

Proof Suppose that there exists a vector $d\in F_0\cap D$. Then by Theorem 15, there exists ${\delta }_1$ such that

$$(f\circ E)(\overline{x}+\lambda d)<(f\circ E)(\overline{x})\text{for each }\lambda \in (0,{\delta }_1).$$

(3.1)

By the definition of the cone of feasible direction, there exists ${\delta }_2$ such that

$$E(\overline{x})+\lambda d\in M\text{for each }\lambda \in (0,{\delta }_2).$$

(3.2)

From 3.1 and 3.2 we have $(f\circ E)(\overline{x}+\lambda d)<(f\circ E)(\overline{x})$ for each $\lambda \in (0,\delta )$, where $\delta =min\{{\delta }_1,{\delta }_2\}$, which contradicts the assumption that $\overline{x}$ is a local optimal solution, then $F_0\cap D=\varphi$. □

Lemma 24 Let M be an open E-convex set with respect to an operator$E:R^n\to R^n$, let$f:M\subseteq R^n\to R$be E-differentiable at$\overline{x}$and let$g_i:R^n\to R$for$i=1,2,\dots ,m$. Let$\overline{x}$be a feasible solution of the problem$P_E$and let$I=\{i:(g_i\circ E)(\overline{x})=0\}$. Furthermore, suppose that$g_i$for$i\in I$is E-differentiable at$\overline{x}$and that$g_i$for$i\notin I$is continuous at$\overline{x}$. If$\overline{x}$is a local optimal solution, then$F_0\cap G_0=\varphi$, where

$$\begin{array}{c}{F}_0=\{d:\mathrm{\nabla }(f\circ E)(\overline{x})d<0\},\hfill \\ G_0=\{d:\mathrm{\nabla }(g_i\circ E)(\overline{x})d<0,\mathit{\text{for each}}i\in I\}\hfill \end{array}$$

and E is one-to-one and onto.

Proof Let $d\in G_0$. Since $E(\overline{x})\in M$ and M is an open E-convex set, there exists a ${\delta }_1>0$ such that

$$E(\overline{x})+\lambda d\in M\text{for }\lambda \in (0,{\delta }_1).$$

(3.3)

Also, since $(g_i\circ E)(\overline{x})<0$ and since $g_i$ is continuous at $\overline{x}$ for $i\notin I$, there exists a ${\delta }_2>0$ such that

$$(g_i\circ E)(\overline{x}+\lambda d)<0\text{for }\lambda \in (0,{\delta }_2)\text{ and for }i\notin I.$$

(3.4)

Finally, since $d\in G_0$, $\mathrm{\nabla }(g_i\circ E)(\overline{x})d<0$ for each $i\in I$ and by Theorem 15, there exists ${\delta }_3>0$ such that

$$(g_i\circ E)(\overline{x}+\lambda d)<(g_i\circ E)(\overline{x})\text{for }\lambda \in (0,{\delta }_3)\text{ and }i\in I.$$

(3.5)

From 3.3, 3.4 and 3.5, it is clear that points of the form $E(\overline{x})+\lambda d$ are feasible to the problem $P_E$ for each $\lambda \in (0,\delta )$, where $\delta =min({\delta }_1,{\delta }_2,{\delta }_3)$. Thus $d\in D$, where D is the cone of feasible direction of the feasible region at $\overline{x}$. We have shown that for $d\in G_0$ implies that $d\in D$, and hence $G_0\subset D$. By Lemma 23, since $\overline{x}$ is a local solution of the problem $P_E,F_0\cap D=\varphi$. It follows that $F_0\cap G_0=\varphi$. □

Theorem 25 (Fritz-John optimality conditions)

Let M be an open E-convex set with respect to the one-to-one and onto operator$E:R^n\to R^n$, let$f:M\subseteq R^n\to R$be E-differentiable at$\overline{x}$and let$g_i:R^n\to R$for$i=1,2,\dots ,m$. Let$\overline{x}$be feasible solution of the problem$P_E$and let$I=\{i:(g_i\circ E)(\overline{x})=0\}$. Furthermore, suppose that$g_i$for$i\in I$is differentiable at$\overline{x}$and that$g_i$for$i\notin I$is continuous at$\overline{x}$. If$\overline{x}$is a local optimal solution, then there exist scalars$u_0$and$u_i$for$i\in I$such that

and$E(\overline{x})$is a local solution of the problem P.

Proof Let $\overline{x}$ be a local solution of the problem $P_E$, then there is no vector d such that $\mathrm{\nabla }(f\circ E)(\overline{x})d<0$ and $\mathrm{\nabla }(g_i\circ E)(\overline{x})d<0$. Let A be a matrix with rows $\mathrm{\nabla }(f\circ E)(\overline{x})$ and $\mathrm{\nabla }(g_i\circ E)(\overline{x})$. From Gordon’s theorem [10], we have the system $Ad<0$ is inconsistent, then there exists a vector $b\ge 0$ such that $Ab=0$, where $b=(u_0\cdot u_i)$ for each $i\in I$. And thus

$$u_{\circ }\mathrm{\nabla }(f\circ E)(\overline{x})+\sum _{i\in I}{u}_i\mathrm{\nabla }(g_i\circ E)(\overline{x})=0$$

holds and $E(\overline{x})$ is a local solution of the problem P. □

Theorem 26 Let$E:R^n\to R^n$be a one-to-one and onto operator and let$f:M\subseteq R^n\to R$be an E-differentiable function. If$\overline{x}$is an optimal solution of the problem P, then there exists$\overline{y}\in M^{\mathrm{\prime }}$such that$\overline{x}=E(\overline{y})$is an optimal solution of the problem$P_E$and the Fritz-John optimality condition of the problem$P_E$is satisfied.

Proof Let $\overline{x}$ be an optimal solution of the problem P. Since E is one-to-one and onto, according to Theorem 13, there exists $\overline{y}\in M^{\mathrm{\prime }}$, $\overline{x}=E(\overline{y})$ is an optimal solution of the problem $P_E$. Hence there exist scalars $u_0.u_i$ satisfying the Fritz-John optimality conditions of the problem $P_E$

$$\begin{array}{c}{u}_{\circ }\mathrm{\nabla }(f\circ E)(\overline{x})+\sum _{i\in I}{u}_i\mathrm{\nabla }(g_i\circ E)(\overline{x})=0,\hfill \\ (u_0,u_i)=0,\hfill \\ u_0,u_i\ge 0.\hfill \end{array}$$

 □

Theorem 27 (Kuhn-Tucker necessary condition)

Let M be an open E-convex set with respect to the one-to-one and onto operator$E:R^n\to R^n$, let$f:M\subseteq R^n\to R$be E-differentiable and strictly E-convex at$\overline{x}$and let$g_i:R^n\to R$for$i=1,2,\dots ,m$. Let$\overline{y}$be a feasible solution of the problem$P_E$and let$I=\{i:(g_i\circ E)(\overline{y})=0\}$. Furthermore, suppose that$(g_i\circ E)$is continuous at$\overline{y}$for$i\notin I$and$\mathrm{\nabla }(g_i\circ E)(\overline{y})$for$i\in I$are linearly independent. If$\overline{x}$is a solution of the problem P, $\overline{x}=E(\overline{y})$and$\overline{y}$is a local solution of the problem$P_E$, then there exist scalars$u_i$for$i\in I$such that

$$\mathrm{\nabla }(f\circ E)(\overline{y})+\sum _{i\in I}{u}_i\mathrm{\nabla }(g_i\circ E)(\overline{y})=0,u_i\ge 0\mathit{\text{for each}}i\in I.$$

Proof From the Fritz-John optimality condition theorem, there exist scalars $u_0$ and $u_i$ for each $i\in I$ such that

$$u_0\mathrm{\nabla }(f\circ E)(\overline{y})+\sum _{i\in I}{\hat{u}}_i\mathrm{\nabla }(g_i\circ E)(\overline{y})=0,u_0,{\hat{u}}_i\ge 0\text{ for each }i\in I.$$

If $u_0=0$, the assumption of linear independence of $\mathrm{\nabla }(g_i\circ E)(\overline{y})$ does not hold, then $u_0>0$. By taking $u_i=\frac{{\hat{u}}_i}{u_0}$, then $\mathrm{\nabla }(f\circ E)(\overline{y})+{\sum }_{i\in I}{u}_i\mathrm{\nabla }(g_i\circ E)(\overline{y})=0$, $u_i\ge 0$ holds for each $i\in I$. From Theorem 26, $\overline{y}$ is a local solution of the problem $P_E$. □

Theorem 28 Let M be an open E-convex set with respect to the one-to-one and onto operator$E:R^n\to R^n$, $g_i:R^n\to R$for$i=1,2,\dots ,m$, and let$f:M\subseteq R^n\to R$be E-differentiable at$\overline{x}$and strictly E-convex at$\overline{x}$. Let$\overline{x}=E(\overline{y})$be a feasible solution of the problem$P_E$and$I=\{i:(g_i\circ E)(\overline{y})=0\}$. Suppose that f is pseudo-E-convex at$\overline{y}$and that$g_i$is quasi-E-convex and differentiable at$\overline{y}$for each$i\in I$. Furthermore, suppose that the Kuhn-Tucker conditions hold at$\overline{y}$. Then$\overline{y}$is a global optimal solution of the problem$P_E$and hence$\overline{x}=E(\overline{y})$is a solution of the problem P.

Proof Let $\hat{y}$ be a feasible solution of the problem $P_E$, then $(g_i\circ E)(\hat{y})\le (g_i\circ E)(\overline{y})$ for each $i\in I$. Since $(g_i\circ E)(\hat{y})\le 0$, $(g_i\circ E)(\overline{y})=0$ and $g_i$ is quasi-E-convex at $\overline{y}$, then

$$\begin{array}{rcl}(g_i\circ E)(\overline{y}+\lambda (\hat{y}-\overline{y}))& =& (g_i\circ E)(\lambda \hat{y}+(1-\lambda )\overline{y})\\ \le & max\{(g_i\circ E)(\hat{y}),(g_i\circ E)(\overline{y})\}\\ =& (g_i\circ E)(\overline{y}).\end{array}$$

This means that $(g_i\circ E)$ does not increase by moving from $\overline{y}$ along the direction $\hat{y}-\overline{y}$. Then we must have from Theorem 15 that $\mathrm{\nabla }(g_i\circ E)(y-\overline{y})\le 0$. Multiplying by $u_i$ and summing over I, we get

$$[\sum _{i\in I}{u}_i\mathrm{\nabla }(g_i\circ E)(\overline{y})](y-\overline{y})\le 0.$$

But since

$$\mathrm{\nabla }(f\circ E)(\overline{y})+\sum _{i\in I}{u}_i\mathrm{\nabla }(g_i\circ E)(\overline{y})=0,$$

it follows that $\mathrm{\nabla }(f\circ E)(\overline{y})(y-\overline{y})⩾0$. Since f is pseudo E-convex at $\overline{y}$, we get

$$(f\circ E)(y)\ge (f\circ E)(\overline{y}).$$

Then $\overline{y}$ is a global solution of the problem $P_E$ and from Theorem 13 $\overline{x}=E(\overline{y})$ is a global solution of the problem P. □

Example 29 Consider the following problem (problem P):

$$\begin{array}{c}Minf(x,y)=x^{\frac{2}{3}}+y^2,\hfill \\ \text{subject to }{x}^2+y^2\le 5,\hfill \\ x+2y\le 4,\hfill \\ x,y\ge 0.\hfill \end{array}$$

The feasible region of this problem is shown in Figure 2.

Figure 2

The feasible region M.

Let $E(x,y)=(\frac{1}{8}{x}^3,\frac{1}{3}y)$, then the problem $P_E$ is as follows:

$$\begin{array}{c}min(f\circ E)(x,y)=\frac{1}{4}{x}^2+\frac{1}{9}{y}^2,\hfill \\ \text{subject to }\frac{x^6}{64}+\frac{y^2}{9}\le 5,\hfill \\ \frac{1}{8}{x}^3+\frac{2}{3}y\le 4,\hfill \\ x,y\ge 0.\hfill \end{array}$$

We note that $E(M)\subset M$, where

$$\begin{array}{c}(\sqrt{5},0)\in M\text{implies}E(\sqrt{5},0)=(5\frac{\sqrt{5}}{8},0)\in M,\hfill \\ (0,2)\in M\text{implies}E(0,2)=(0,\frac{2}{3})\in M,\hfill \\ (0,0)\in M\text{implies}E(0,0)=(0,0)\in M,\hfill \\ (2,1)\in M\text{implies}E(2,1)=(1,\frac{1}{3})\in M.\hfill \end{array}$$

The Kuhn-Tucker conditions are as follows:

$$\begin{array}{c}\mathrm{\nabla }(f\circ E)(x,y)+u_1\mathrm{\nabla }(g_1\circ E)(x,y)+u_2\mathrm{\nabla }(g_2\circ E)(x,y)=0,\hfill \\ \left[\begin{array}{c}\frac{1}{2}x\\ \frac{2}{9}y\end{array}\right]+u_1\left[\begin{array}{c}\frac{6}{64}{x}^5\\ \frac{2}{9}y\end{array}\right]+u_2\left[\begin{array}{c}\frac{3}{8}{x}^2\\ \frac{2}{3}\end{array}\right]=0,\hfill \\ u_1[\frac{x^6}{64}+\frac{y^2}{9}-5]=0,\hfill \\ u_2[\frac{1}{8}{x}^3+\frac{2}{3}y-4]=0.\hfill \end{array}$$

The solution is $\{[x=0.0,u_1=0.0,u_2=0.0,y=0.0]\}$, $\overline{z}=(0,0)$, and $\overline{x}=E(\overline{z})=(0,0)$ is a solution of the problem P.

4 Conclusion

In this paper we introduced a new definition of an E-differentiable convex function, which transforms a non-differentiable function to a differentiable function under an operator $E:R^n\to R^n$, and we studied Kuhn-Tucker and Fritz-John conditions for obtaining an optimal solution of mathematical programming with a non-differentiable function. At the end, some examples have been presented to clarify the results.