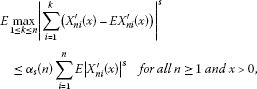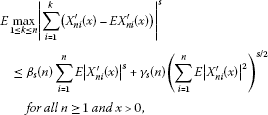Complete q th moment convergence for arrays of random variables

Abstract

Let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of random variables with $E{X}_{ni}=0$ and $E{|X_{ni}|}^q<\mathrm{\infty }$ for some $q\ge 1$. For any sequences $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ of positive real numbers, sets of sufficient conditions are given for complete q th moment convergence of the form ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}E{({max}_{1\le k\le n}|{\sum }_{i=1}^k{X}_{ni}|-ϵa_n)}_{+}^q<\mathrm{\infty }$, $\mathrm{\forall }ϵ>0$, where $x_{+}=max\{x,0\}$. From these results, we can easily obtain some known results on complete q th moment convergence.

1 Introduction

The concept of complete convergence was introduced by Hsu and Robbins [1]. A sequence $\{X_n,n\ge 1\}$ of random variables is said to converge completely to the constant θ if

$$\sum _{n=1}^{\mathrm{\infty }}P(|X_n-\theta |>ϵ)<\mathrm{\infty }\text{for all }ϵ>0\text{.}$$

Hsu and Robbins [1] proved that the sequence of arithmetic means of i.i.d. random variables converges completely to the expected value if the variance of the summands is finite. Erdös [2] proved the converse.

The result of Hsu, Robbins, and Erdös has been generalized and extended in several directions. Baum and Katz [3] proved that if $\{X_n,n\ge 1\}$ is a sequence of i.i.d. random variables with $E{X}_1=0$, $E{|X_1|}^{pt}<\mathrm{\infty }$ ($1\le p<2$, $t\ge 1$) is equivalent to

$$\sum _{n=1}^{\mathrm{\infty }}{n}^{t-2}P\left(\right|\sum _{i=1}^n{X}_i|>ϵn^{1/p})<\mathrm{\infty }\text{for all }ϵ>0\text{.}$$

(1.1)

Chow [4] generalized the result of Baum and Katz [3] by showing the following complete moment convergence. If $\{X_n,n\ge 1\}$ is a sequence of i.i.d. random variables with $E{X}_1=0$ and $E({|X_1|}^{pt}+|X_1|log(1+|X_1|))<\mathrm{\infty }$ for some $0<p<2$, $t\ge 1$, and $pt\ge 1$, then

$$\sum _{n=1}^{\mathrm{\infty }}{n}^{t-2-1/p}E{\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_i|-ϵn^{1/p})}_{+}<\mathrm{\infty }\text{for all }ϵ>0\text{,}$$

(1.2)

where $x_{+}=max\{x,0\}$. Note that (1.2) implies (1.1). Li and Spătaru [5] gave a refinement of the result of Baum and Katz [3] as follows. Let $\{X_n,n\ge 1\}$ be a sequence of i.i.d. random variables with $E{X}_1=0$, and let $0<p<2$, $t\ge 1$, $q>0$, and $pt\ge 1$. Then

$$\{\begin{array}{cc}E{|X_1|}^q<\mathrm{\infty }\hfill & \text{if }q>pt\text{,}\hfill \\ E{|X_1|}^{pt}log(1+|X_1|)<\mathrm{\infty }\hfill & \text{if }q=pt\text{,}\hfill \\ E{|X_1|}^{pt}<\mathrm{\infty }\hfill & \text{if }q<pt\text{,}\hfill \end{array}$$

(1.3)

if and only if

$${\int }_{ϵ}^{\mathrm{\infty }}\sum _{n=1}^{\mathrm{\infty }}{n}^{t-2}P\left(\right|\sum _{i=1}^n{X}_i|>x^{1/q}{n}^{1/p})dx<\mathrm{\infty }\text{for all }ϵ>0\text{.}$$

Recently, Chen and Wang [6] proved that for any $q>0$, any sequences $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ of positive real numbers and any sequence $\{Z_n,n\ge 1\}$ of random variables,

$${\int }_{ϵ}^{\mathrm{\infty }}\sum _{n=1}^{\mathrm{\infty }}{b}_{n}P(|Z_n|>x^{1/q}{a}_n)dx<\mathrm{\infty }\text{for all }ϵ>0$$

and

$$\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}E{(|Z_n|-ϵa_n)}_{+}^q<\mathrm{\infty }\text{for all }ϵ>0,$$

are equivalent. Therefore, if $\{X_n,n\ge 1\}$ is a sequence of i.i.d. random variables with $E{X}_1=0$ and $0<p<2$, $t\ge 1$, $q>0$, and $pt\ge 1$, then the moment condition (1.3) is equivalent to

$$\sum _{n=1}^{\mathrm{\infty }}{n}^{t-2-q/p}E{\left(\right|\sum _{i=1}^n{X}_i|-ϵn^{1/p})}_{+}^q<\mathrm{\infty }\text{for all }ϵ>0\text{.}$$

(1.4)

When $q=1$, the complete q th moment convergence (1.4) is reduced to complete moment convergence.

The complete q th moment convergence for dependent random variables was established by many authors. Chen and Wang [7] showed that (1.3) and (1.4) are equivalent for φ-mixing random variables. Zhou and Lin [8] established complete q th moment convergence theorems for moving average processes of φ-mixing random variables. Wu et al. [9] obtained complete q th moment convergence results for arrays of rowwise ${\rho }^{\ast }$-mixing random variables.

The purpose of this paper is to provide sets of sufficient conditions for complete q th moment convergence of the form

$$\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}E{\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|-ϵa_n)}_{+}^q<\mathrm{\infty }\text{for all }ϵ>0\text{,}$$

(1.5)

where $q\ge 1$, $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ are sequences of positive real numbers, and $\{X_{ni},1\le i\le n,n\ge 1\}$ is an array of random variables satisfying Marcinkiewicz-Zygmund and Rosenthal type inequalities. When $q=1$, similar results were established by Sung [10]. From our results, we can easily obtain the results of Chen and Wang [7] and Wu et al. [9].

2 Main results

In this section, we give sets of sufficient conditions for complete q th moment convergence (1.5). The following theorem gives sufficient conditions under the assumption that the array $\{X_{ni},1\le i\le n,n\ge 1\}$ satisfies a Marcinkiewicz-Zygmund type inequality.

Theorem 2.1 Let $1\le q<2$ and let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of random variables with $E{X}_{ni}=0$ and $E{|X_{ni}|}^q<\mathrm{\infty }$ for $1\le i\le n$ and $n\ge 1$. Let $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ be sequences of positive real numbers. Suppose that the following conditions hold:

• (i) for some s ($1\le q<s\le 2$), there exists a positive function ${\alpha }_s(x)$ such that

  

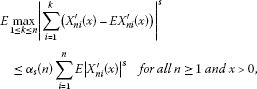  (2.1)

where $X_{ni}^{\prime }(x)=X_{ni}I(|X_{ni}|\le x^{1/q})+x^{1/q}I(X_{ni}>x^{1/q})-x^{1/q}I(X_{ni}<-x^{1/q})$,

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-s}{\alpha }_s(n){\sum }_{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)<\mathrm{\infty }$,

• (iii) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}(1+{\alpha }_s(n)){\sum }_{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n)<\mathrm{\infty }$,

• (iv) ${\sum }_{i=1}^{n}E|X_{ni}|I(|X_{ni}|>a_n)/a_n\to 0$.

Then (1.5) holds.

Proof It is obvious that

$$\begin{array}{c}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}E{\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|-ϵa_n)}_{+}^q\hfill \\ =\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\int }_0^{\mathrm{\infty }}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>ϵa_n+x^{1/q})dx\hfill \\ \le \sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}\{{\int }_0^{a_n^q}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>ϵa_n)dx+{\int }_{a_n^q}^{\mathrm{\infty }}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>x^{1/q})dx\}\hfill \\ :=I_1+I_2.\hfill \end{array}$$

We first show that $I_1<\mathrm{\infty }$. For $1\le i\le n$ and $n\ge 1$, define

$$X_{ni}^{\prime }=X_{ni}I(|X_{ni}|\le a_n)+a_{n}I(X_{ni}>a_n)-a_{n}I(X_{ni}<-a_n),X_{ni}^{″}=X_{ni}-X_{ni}^{\prime }.$$

Then we have by $E{X}_{ni}=0$, Markov’s inequality, and (i) that

$$\begin{array}{c}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>ϵa_n)\hfill \\ =P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k(X_{ni}^{\prime }-E{X}_{ni}^{\prime }+X_{ni}^{″}-E{X}_{ni}^{″})|>ϵa_n)\hfill \\ \le P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k(X_{ni}^{\prime }-E{X}_{ni}^{\prime })|>ϵa_n/2)+P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k(X_{ni}^{″}-E{X}_{ni}^{″})|>ϵa_n/2)\hfill \\ \le 2^s{ϵ}^{-s}{a}_n^{-s}E\underset{1\le k\le n}{max}|\sum _{i=1}^k(X_{ni}^{\prime }-E{X}_{ni}^{\prime }){|}^s+2{ϵ}^{-1}{a}_n^{-1}E\underset{1\le k\le n}{max}|\sum _{i=1}^k(X_{ni}^{″}-E{X}_{ni}^{″})|\hfill \\ \le 2^s{ϵ}^{-s}{a}_n^{-s}{\alpha }_s(n)\sum _{i=1}^{n}E{\left|X_{ni}^{\prime }\right|}^s+4{ϵ}^{-1}{a}_n^{-1}\sum _{i=1}^{n}E\left|X_{ni}^{″}\right|\hfill \\ \le 2^s{ϵ}^{-s}{a}_n^{-s}{\alpha }_s(n)\sum _{i=1}^n(E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)+a_n^{s}P(|X_{ni}|>a_n))\hfill \\ +4{ϵ}^{-1}{a}_n^{-1}\sum _{i=1}^{n}E|X_{ni}|I(|X_{ni}|>a_n)\hfill \\ \le 2^s{ϵ}^{-s}{a}_n^{-s}{\alpha }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)+2^s{ϵ}^{-s}{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n)\hfill \\ +4{ϵ}^{-1}{a}_n^{-q}\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n).\hfill \end{array}$$

It follows that

$$\begin{array}{rcl}{I}_1& =& \sum _{n=1}^{\mathrm{\infty }}{b}_{n}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>ϵa_n)\\ \le & 2^s{ϵ}^{-s}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-s}{\alpha }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)\\ +\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}(2^s{ϵ}^{-s}{\alpha }_s(n)+4{ϵ}^{-1})\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n).\end{array}$$

Hence $I_1<\mathrm{\infty }$ by (ii) and (iii).

We next show that $I_2<\mathrm{\infty }$. By the definition of $X_{ni}^{\prime }(x)$, we have that

$$\begin{array}{c}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>x^{1/q})\hfill \\ \le \sum _{i=1}^{n}P(|X_{ni}|>x^{1/q})+P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}^{\prime }(x)|>x^{1/q}).\hfill \end{array}$$

We also have by $E{X}_{ni}=0$ and (iv) that

$$\begin{array}{c}\underset{x\ge a_n^q}{sup}\underset{1\le k\le n}{max}{x}^{-1/q}|\sum _{i=1}^{k}E{X}_{ni}^{\prime }(x)|\hfill \\ =\underset{x\ge a_n^q}{sup}\underset{1\le k\le n}{max}{x}^{-1/q}\left|\sum _{i=1}^{k}E(X_{ni}-X_{ni}^{\prime }(x))\right|\hfill \\ \le \underset{x\ge a_n^q}{sup}{x}^{-1/q}\sum _{i=1}^{n}E|X_{ni}|I(|X_{ni}|>x^{1/q})\hfill \\ \le a_n^{-1}\sum _{i=1}^{n}E|X_{ni}|I(|X_{ni}|>a_n)\to 0.\hfill \end{array}$$

Hence to prove that $I_2<\mathrm{\infty }$, it suffices to show that

$$\begin{array}{c}{I}_3:=\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}\sum _{i=1}^n{\int }_{a_n^q}^{\mathrm{\infty }}P(|X_{ni}|>x^{1/q})dx<\mathrm{\infty },\hfill \\ I_4:=\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\int }_{a_n^q}^{\mathrm{\infty }}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k(X_{ni}^{\prime }(x)-E{X}_{ni}^{\prime }(x))|>x^{1/q}/2)dx<\mathrm{\infty }.\hfill \end{array}$$

If $x>a_n^q$, then $P(|X_{ni}|>x^{1/q})=P(|X_{ni}|I(|X_{ni}|>a_n)>x^{1/q})$ and so

$$\begin{array}{rcl}{\int }_{a_n^q}^{\mathrm{\infty }}P(|X_{ni}|>x^{1/q})dx& =& {\int }_{a_n^q}^{\mathrm{\infty }}P(|X_{ni}|I(|X_{ni}|>a_n)>x^{1/q})dx\\ \le & {\int }_0^{\mathrm{\infty }}P(|X_{ni}|I(|X_{ni}|>a_n)>x^{1/q})dx=E{|X_{ni}|}^{q}I(|X_{ni}|>a_n),\end{array}$$

which implies that

$$I_3\le \sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n).$$

Hence $I_3<\mathrm{\infty }$ by (iii).

Finally, we show that $I_4<\mathrm{\infty }$. We get by Markov’s inequality and (i) that

$$\begin{array}{rcl}{I}_4& \le & 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}E\underset{1\le k\le n}{max}|\sum _{i=1}^k(X_{ni}^{\prime }(x)-E{X}_{ni}^{\prime }(x)){|}^{s}dx\\ \le & 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^n{\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}E{|X_{ni}^{\prime }(x)|}^{s}dx\\ =& 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^n{\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}(E{|X_{ni}|}^{s}I(|X_{ni}|\le x^{1/q})+x^{s/q}P(|X_{ni}|>x^{1/q}))dx\\ =& 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n){\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}dx\\ +2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^n{\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}E{|X_{ni}|}^{s}I(a_n<|X_{ni}|\le x^{1/q})dx\\ +2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^n{\int }_{a_n^q}^{\mathrm{\infty }}P(|X_{ni}|>x^{1/q})dx:=I_5+I_6+I_7.\end{array}$$

Using a simple integral and Fubini’s theorem, we obtain that

Similarly to $I_3$,

$$I_7\le 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\alpha }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n).$$

Hence $I_4<\mathrm{\infty }$ by (ii) and (iii). □

The next theorem gives sufficient conditions for complete q th moment convergence (1.5) under the assumption that the array $\{X_{ni},1\le i\le n,n\ge 1\}$ satisfies a Rosenthal type inequality.

Theorem 2.2 Let $q\ge 1$ and let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of random variables with $E{X}_{ni}=0$ and $E{|X_{ni}|}^q<\mathrm{\infty }$ for $1\le i\le n$ and $n\ge 1$. Let $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ be sequences of positive real numbers. Suppose that the following conditions hold:

• (i) for some $s>max\{2,2q/r\}$ (r is the same as in (v)), there exist positive functions ${\beta }_s(x)$ and ${\gamma }_s(x)$ such that

  

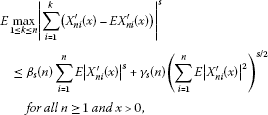  (2.2)

where $X_{ni}^{\prime }(x)=X_{ni}I(|X_{ni}|\le x^{1/q})+x^{1/q}I(X_{ni}>x^{1/q})-x^{1/q}I(X_{ni}<-x^{1/q})$,

• (ii) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-s}{\beta }_s(n){\sum }_{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)<\mathrm{\infty }$,

• (iii) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}(1+{\beta }_s(n)){\sum }_{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n)<\mathrm{\infty }$,

• (iv) ${\sum }_{i=1}^{n}E|X_{ni}|I(|X_{ni}|>a_n)/a_n\to 0$,

• (v) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{\gamma }_s(n){({\sum }_{i=1}^n{a}_n^{-r}E{|X_{ni}|}^r)}^{s/2}<\mathrm{\infty }$ for some $0<r\le 2$.

Then (1.5) holds.

Proof The proof is similar to that of Theorem 2.1. As in the proof of Theorem 2.1,

$$\begin{array}{c}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}E{\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|-ϵa_n)}_{+}^q\hfill \\ \le \sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}\{{\int }_0^{a_n^q}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>ϵa_n)dx+{\int }_{a_n^q}^{\mathrm{\infty }}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>x^{1/q})dx\}\hfill \\ :=J_1+J_2.\hfill \end{array}$$

Similarly to $I_1$ in the proof of Theorem 2.1, we have by the $c_r$-inequality that

$$\begin{array}{c}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_{ni}|>ϵa_n)\hfill \\ \le 2^s{ϵ}^{-s}{a}_n^{-s}{\beta }_s(n)\sum _{i=1}^n(E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)+a_n^{s}P(|X_{ni}|>a_n))\hfill \\ +2^s{ϵ}^{-s}{a}_n^{-s}{\gamma }_s(n){(\sum _{i=1}^{n}E{|X_{ni}|}^{2}I(|X_{ni}|\le a_n)+a_n^{2}P(|X_{ni}|>a_n))}^{s/2}\hfill \\ +4{ϵ}^{-1}{a}_n^{-1}\sum _{i=1}^{n}E|X_{ni}|I(|X_{ni}|>a_n)\hfill \\ \le 2^s{ϵ}^{-s}{a}_n^{-s}{\beta }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)\hfill \\ +(2^s{ϵ}^{-s}{\beta }_s(n)+4{ϵ}^{-1})a_n^{-q}\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n)\hfill \\ +2^{3s/2-1}{ϵ}^{-s}{\gamma }_s(n){\left(\sum _{i=1}^n{a}_n^{-r}E{|X_{ni}|}^{r}I(|X_{ni}|\le a_n)\right)}^{s/2}\hfill \\ +2^{3s/2-1}{ϵ}^{-s}{\gamma }_s(n){\left(\sum _{i=1}^n{a}_n^{-r}E{|X_{ni}|}^{r}I(|X_{ni}|>a_n)\right)}^{s/2}.\hfill \end{array}$$

Hence $J_1<\mathrm{\infty }$ by (ii), (iii), and (v).

As in the proof of Theorem 2.1, to prove that $J_2<\mathrm{\infty }$, it suffices to show that

$$\begin{array}{c}{J}_3:=\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}\sum _{i=1}^n{\int }_{a_n^q}^{\mathrm{\infty }}P(|X_{ni}|>x^{1/q})dx<\mathrm{\infty },\hfill \\ J_4:=\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\int }_{a_n^q}^{\mathrm{\infty }}P\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k(X_{ni}^{\prime }(x)-E{X}_{ni}^{\prime }(x))|>x^{1/q}/2)dx<\mathrm{\infty }.\hfill \end{array}$$

The proof of $J_3<\mathrm{\infty }$ is same as that of $I_3$ in the proof of Theorem 2.1.

For $J_4$, we have by Markov’s inequality and (i) that

$$\begin{array}{rcl}{J}_4& \le & 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}E\underset{1\le k\le n}{max}|\sum _{i=1}^k(X_{ni}^{\prime }(x)-E{X}_{ni}^{\prime }(x)){|}^{s}dx\\ \le & 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}\{{\beta }_s(n)\sum _{i=1}^{n}E{|X_{ni}^{\prime }(x)|}^s+{\gamma }_s(n){\left(\sum _{i=1}^{n}E{|X_{ni}^{\prime }(x)|}^2\right)}^{s/2}\}dx\\ :=& J_5+J_6.\end{array}$$

Similarly to $I_4$ in the proof of Theorem 2.1, we get that

$$\begin{array}{rcl}{J}_5& \le & 2^s\frac{q}{s-q}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-s}{\beta }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)\\ +2^s(\frac{q}{s-q}+1)\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\beta }_s(n)\sum _{i=1}^{n}E{|X_{ni}|}^{q}I(|X_{ni}|>a_n).\end{array}$$

Hence $J_5<\mathrm{\infty }$ by (ii) and (iii).

Finally, we show that $J_6<\mathrm{\infty }$. By the $c_r$-inequality,

$$\begin{array}{rcl}{J}_6& =& 2^s\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\gamma }_s(n){\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}{(\sum _{i=1}^{n}E{|X_{ni}|}^{2}I(|X_{ni}|\le x^{1/q})+x^{2/q}P(|X_{ni}|>x^{1/q}))}^{s/2}dx\\ \le & 2^{3s/2-1}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\gamma }_s(n){\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}{\left(\sum _{i=1}^{n}E{|X_{ni}|}^{2}I(|X_{ni}|\le x^{1/q})\right)}^{s/2}dx\\ +2^{3s/2-1}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\gamma }_s(n){\int }_{a_n^q}^{\mathrm{\infty }}{\left(\sum _{i=1}^{n}P(|X_{ni}|>x^{1/q})\right)}^{s/2}dx\\ \le & 2^{3s/2-1}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\gamma }_s(n){\int }_{a_n^q}^{\mathrm{\infty }}{x}^{-s/q}{\left(\sum _{i=1}^{n}E{|X_{ni}|}^r{x}^{(2-r)/q}\right)}^{s/2}dx\\ +2^{3s/2-1}\sum _{n=1}^{\mathrm{\infty }}{b}_n{a}_n^{-q}{\gamma }_s(n){\int }_{a_n^q}^{\mathrm{\infty }}{\left(\sum _{i=1}^n{x}^{-r/q}E{|X_{ni}|}^r\right)}^{s/2}dx\\ =& 2^{3s/2}\frac{2q}{rs-2q}\sum _{n=1}^{\mathrm{\infty }}{b}_n{\gamma }_s(n){\left(\sum _{i=1}^n{a}_n^{-r}E{|X_{ni}|}^r\right)}^{s/2}.\end{array}$$

Hence $J_6<\mathrm{\infty }$ by (v). □

Remark 2.1 Marcinkiewicz-Zygmund and Rosenthal type inequalities hold for dependent random variables as well as independent random variables.

• (1) Let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of rowwise negatively associated random variables. Then, for $1<s\le 2$, (2.1) holds for ${\alpha }_s(n)=2^s{2}^{3-s}=8$. For $s>2$, (2.2) holds for ${\beta }_s(n)=2^{s}2{(15s/logs)}^s$ and ${\gamma }_s(n)=2{(15s/logs)}^s$ (see Shao [11]). Note that ${\alpha }_s(n)$ and ${\beta }_s(n)$ are multiplied by the factor $2^s$ since $E{|X_{ni}^{\prime }(x)-E{X}_{ni}^{\prime }(x)|}^s\le 2^{s}E{|X_{ni}^{\prime }(x)|}^s$.

• (2) Let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of rowwise negatively orthant dependent random variables. By Corollary 2.2 of Asadian et al. [12] and Theorem 3 of Móricz [13], (2.1) holds for ${\alpha }_s(n)=C_1{(logn)}^s$, and (2.2) holds for ${\beta }_s(n)=C_2{(logn)}^s$ and ${\gamma }_s(n)=C_2{(logn)}^s$, where $C_1$ and $C_2$ are constants depending only on s.

• (3) Let $\{X_n,n\ge 1\}$ be a sequence of identically distributed φ-mixing random variables. Set $X_{ni}=X_i$ for $1\le i\le n$ and $n\ge 1$. By Shao’s [14] result, (2.2) holds for a constant function ${\beta }_s(x)$ and a slowly varying function ${\gamma }_s(x)$. In particular, if ${\sum }_{n=1}^{\mathrm{\infty }}{\phi }^{1/2}(2^n)<\mathrm{\infty }$, then (2.2) holds for some constant functions ${\beta }_s(x)$ and ${\gamma }_s(x)$.

• (4) Let $\{X_n,n\ge 1\}$ be a sequence of identically distributed ρ-mixing random variables. Set $X_{ni}=X_i$ for $1\le i\le n$ and $n\ge 1$. By Shao’s [15] result, (2.2) holds for some slowly varying functions ${\beta }_s(x)$ and ${\gamma }_s(x)$. In particular, if ${\sum }_{n=1}^{\mathrm{\infty }}{\rho }^{2/s}(2^n)<\mathrm{\infty }$, then (2.2) holds for some constant functions ${\beta }_s(x)$ and ${\gamma }_s(x)$.

• (5) Let $\{X_n,n\ge 1\}$ be a sequence of ${\rho }^{\ast }$-mixing random variables. Set $X_{ni}=X_i$ for $1\le i\le n$ and $n\ge 1$. By the result of Utev and Peligrad [16], (2.2) holds for some constant functions ${\beta }_s(x)$ and ${\gamma }_s(x)$.

3 Corollaries

In this section, we establish some complete q th moment convergence results by using the results obtained in the previous section.

Corollary 3.1 (Chen and Wang [7])

Let $\{X_n,n\ge 1\}$ be a sequence of identically distributed φ-mixing random variables with $E{X}_1=0$, and let $t\ge 1$, $0<p<2$, $q\ge 1$, and $pt\ge 1$. Assume that (1.3) holds. Furthermore, suppose that

$$\sum _{n=1}^{\mathrm{\infty }}{\phi }^{1/2}\left(2^n\right)<\mathrm{\infty }$$

if $t=1$ and $max\{q,pt\}<2$. Then

$$\sum _{n=1}^{\mathrm{\infty }}{n}^{t-2-q/p}E{\left(\underset{1\le k\le n}{max}\right|\sum _{i=1}^k{X}_i|-ϵn^{1/p})}_{+}^q<\mathrm{\infty }\mathit{\text{for all }}ϵ>0.$$

Proof Let $a_n=n^{1/p}$ and $b_n=n^{t-2}$ for $n\ge 1$, and let $X_{ni}=X_i$ for $1\le i\le n$ and $n\ge 1$. Then, for $s\ge 2$, (2.2) holds for a constant function ${\beta }_s(x)$ and a slowly varying function ${\gamma }_s(x)$ (see Remark 2.1(3)). Under the additional condition that ${\sum }_{n=1}^{\mathrm{\infty }}{\phi }^{1/2}(2^n)<\mathrm{\infty }$, (2.2) holds for some constant functions ${\beta }_s(x)$ and ${\gamma }_s(x)$. In particular, for $s=2$, (2.1) holds for a constant function ${\alpha }_s(x)$ under this additional condition.

By a standard method, we have that

$$\begin{array}{c}\sum _{n=1}^{\mathrm{\infty }}{n}^{t-1-s/p}E{|X_1|}^{s}I(|X_1|\le n^{1/p})\le CE{|X_1|}^{pt}\text{if }pt<s\text{,}\hfill \\ \sum _{n=1}^{\mathrm{\infty }}{n}^{t-1-q/p}E{|X_1|}^{q}I(|X_1|>n^{1/p})\le \{\begin{array}{cc}CE{|X_1|}^q\hfill & \text{if }q>pt\text{,}\hfill \\ CE{|X_1|}^{pt}log(1+|X_1|)\hfill & \text{if }q=pt\text{,}\hfill \\ CE{|X_1|}^{pt}\hfill & \text{if }q<pt\text{,}\hfill \end{array}\hfill \\ n^{1-1/p}E|X_1|I(|X_1|>n^{1/p})\le n^{1-t}E{|X_1|}^{pt}I(|X_1|>n^{1/p})\text{if }pt\ge 1\text{,}\hfill \end{array}$$

where C is a positive constant which is not necessarily the same one in each appearance. Hence, the conditions (i)-(iv) of Theorem 2.2 hold if we take $s>max\{pt,2,2q/r\}$. Under the additional conditions that $max\{q,pt\}<2$ and ${\sum }_{n=1}^{\mathrm{\infty }}{\phi }^{1/2}(2^n)<\mathrm{\infty }$, all conditions of Theorem 2.1 hold if we take $s=2$. Therefore, the result follows from Theorems 2.1 and 2.2 if we only show that the condition (v) of Theorem 2.2 holds when $t>1$ or $max\{q,pt\}\ge 2$. To do this, we take $r=2$ if $max\{q,pt\}\ge 2$ and $r=max\{q,pt\}$ if $max\{q,pt\}<2$. If $t>1$ or $max\{q,pt\}\ge 2$, then $r>p$ and so we can choose $s>2$ large enough such that $t-1+(1-r/p)s/2<0$. Then

$$\sum _{n=1}^{\mathrm{\infty }}{b}_n{\gamma }_s(n){\left(\sum _{i=1}^n{a}_n^{-r}E{|X_{ni}|}^r\right)}^{s/2}={\left(E{|X_1|}^r\right)}^{s/2}\sum _{n=1}^{\mathrm{\infty }}{\gamma }_s(n)n^{t-2+(1-r/p)s/2}<\mathrm{\infty }.$$

Hence the condition (v) of Theorem 2.2 holds. □

Let $\{{\mathrm{\Psi }}_n(x),n\ge 1\}$ be a sequence of positive even functions satisfying

$$\frac{{\mathrm{\Psi }}_n(|x|)}{{|x|}^q}\uparrow \text{and}\frac{{\mathrm{\Psi }}_n(|x|)}{{|x|}^s}\downarrow \text{as }|x|\uparrow$$

(3.1)

for some $1\le q<s$.

Corollary 3.2 Let $\{{\mathrm{\Psi }}_n(x),n\ge 1\}$ be a sequence of positive even functions satisfying (3.1) for some $1\le q<s\le 2$. Let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of random variables satisfying $E{X}_{ni}=0$ for $1\le i\le n$ and $n\ge 1$, and (2.1) for some constant function ${\alpha }_s(x)$. Let $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ be sequences of positive real numbers. Suppose that the following conditions hold:

• (i) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{\sum }_{i=1}^{n}E{\mathrm{\Psi }}_i(|X_{ni}|)/{\mathrm{\Psi }}_i(a_n)<\mathrm{\infty }$,

• (ii) ${\sum }_{i=1}^{n}E{\mathrm{\Psi }}_i(|X_{ni}|)/{\mathrm{\Psi }}_i(a_n)\to 0$.

Then (1.5) holds.

Proof First note by ${\mathrm{\Psi }}_i(|x|)/{|x|}^q\uparrow$ that ${\mathrm{\Psi }}_i(|x|)$ is an increasing function. Since ${\mathrm{\Psi }}_i(|x|)/{|x|}^s\downarrow$,

$$\frac{{|X_{ni}|}^{s}I(|X_{ni}|\le a_n)}{a_n^s}\le \frac{{\mathrm{\Psi }}_i(|X_{ni}|I(|X_{ni}|\le a_n))}{{\mathrm{\Psi }}_i(a_n)}\le \frac{{\mathrm{\Psi }}_i(|X_{ni}|)}{{\mathrm{\Psi }}_i(a_n)}.$$

Since $q\ge 1$ and ${\mathrm{\Psi }}_i(|x|)/{|x|}^q\uparrow$,

$$\frac{|X_{ni}|I(|X_{ni}|>a_n)}{a_n}\le \frac{{|X_{ni}|}^{q}I(|X_{ni}|>a_n)}{a_n^q}\le \frac{{\mathrm{\Psi }}_i(|X_{ni}|I(|X_{ni}|>a_n))}{{\mathrm{\Psi }}_i(a_n)}\le \frac{{\mathrm{\Psi }}_i(|X_{ni}|)}{{\mathrm{\Psi }}_i(a_n)}.$$

It follows that all conditions of Theorem 2.1 are satisfied and so the result follows from Theorem 2.1. □

Corollary 3.3 Let $\{{\mathrm{\Psi }}_n(x),n\ge 1\}$ be a sequence of positive even functions satisfying (3.1) for some $q\ge 1$ and $s>max\{2,q\}$. Let $\{X_{ni},1\le i\le n,n\ge 1\}$ be an array of random variables satisfying $E{X}_{ni}=0$ for $1\le i\le n$ and $n\ge 1$, and (2.2) for some constant functions ${\beta }_s(x)$ and ${\gamma }_s(x)$. Let $\{a_n,n\ge 1\}$ and $\{b_n,n\ge 1\}$ be sequences of positive real numbers. Suppose that the following conditions hold:

• (i) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{\sum }_{i=1}^{n}E{\mathrm{\Psi }}_i(|X_{ni}|)/{\mathrm{\Psi }}_i(a_n)<\mathrm{\infty }$,

• (ii) ${\sum }_{i=1}^{n}E{\mathrm{\Psi }}_i(|X_{ni}|)/{\mathrm{\Psi }}_i(a_n)\to 0$,

• (iii) ${\sum }_{n=1}^{\mathrm{\infty }}{b}_n{({\sum }_{i=1}^n{a}_n^{-2}E{|X_{ni}|}^2)}^{s/2}<\mathrm{\infty }$.

Then (1.5) holds.

Proof The proof is similar to that of Corollary 3.2. By the proof of Corollary 3.2 and the condition (iii), all conditions of Theorem 2.2 are satisfied and so the result follows from Theorem 2.2. □

Remark 3.1 When $b_n=1$ for $n\ge 1$, the condition (i) of Corollaries 3.2 and 3.3 is reduced to the condition ${\sum }_{n=1}^{\mathrm{\infty }}{\sum }_{i=1}^{n}E{\mathrm{\Psi }}_i(|X_{ni}|)/{\mathrm{\Psi }}_i(a_n)<\mathrm{\infty }$, and so the condition (ii) of Corollaries 3.2 and 3.3 follows from this reduced condition. For a sequence of ${\rho }^{\ast }$-mixing random variables, (2.1) holds for some constant function ${\alpha }_s(x)$ if $s=2$, and (2.2) holds for some constant functions ${\beta }_s(x)$ and ${\gamma }_s(x)$ if $s>2$ (see Remark 2.1(5)). Wu et al. [9] proved Corollaries 3.2 and 3.3 when $b_n=1$ for $n\ge 1$, and $\{X_{ni}\}$ is an array of rowwise ${\rho }^{\ast }$-mixing random variables.