A viscosity hybrid steepest-descent method for a system of equilibrium and fixed point problems for an infinite family of strictly pseudo-contractive mappings

Abstract

Based on a viscosity hybrid steepest-descent method, in this paper, we introduce an iterative scheme for finding a common element of a system of equilibrium and fixed point problems of an infinite family of strictly pseudo-contractive mappings which solves the variational inequality $〈(\gamma f-\mu F)q,p-q〉\le 0$ for $p\in {\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. Furthermore, we also prove the strong convergence theorems for the proposed iterative scheme and give a numerical example to support and illustrate our main theorem.

MSC:46C05, 47D03, 47H05,47H09, 47H10, 47H20.

1 Introduction

Throughout this paper, we assume that H is a real Hilbert space with inner product $〈\cdot ,\cdot 〉$ and norm $\parallel \cdot \parallel$. Let C be a nonempty closed convex subset of H. A self-mapping $f:C\to C$ is said to be a contraction on C if there exists a constant $\alpha \in (0,1)$ such that $\parallel f(x)-f(y)\parallel \le \alpha \parallel x-y\parallel$, $\mathrm{\forall }x,y\in C$. We denote by ${\mathrm{\Pi }}_C$ the collection of mappings f verifying the above inequality and note that each $f\in {\mathrm{\Pi }}_C$ has a unique fixed point in C.

A mapping $T:C\to C$ is said to be λ-strictly pseudo-contractive if there exists a constant $\lambda \in [0,1)$ such that

$${\parallel Tx-Ty\parallel }^2\le {\parallel x-y\parallel }^2+\lambda {\parallel (I-T)x-(I-T)y\parallel }^2,\mathrm{\forall }x,y\in C,$$

(1.1)

and we denote by $F(T)$ the set of fixed points of the mapping T; that is, $F(T)=\{x\in C:Tx=x\}$.

Note that T is the class of λ-strictly pseudo-contractive mappings including the class of nonexpansive mappings T on C (that is, $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$, $x,y\in C$) as a subclass. That is, T is nonexpansive if and only if T is 0-strictly pseudo-contractive.

A mapping $F:C\to C$ is called k-Lipschitzian if there exists a positive constant k such that

$$\parallel Fx-Fy\parallel \le k\parallel x-y\parallel ,\mathrm{\forall }x,y\in C.$$

(1.2)

F is said to be η-strongly monotone if there exists a positive constant η such that

$$〈Fx-Fy,x-y〉\ge \eta {\parallel x-y\parallel }^2,\mathrm{\forall }x,y\in C.$$

(1.3)

Definition 1.1 A bounded linear operator A is said to be , if there exists a constant $\overline{\gamma }>0$ such that

$$〈Ax,x〉\ge \overline{\gamma }{\parallel x\parallel }^2,\mathrm{\forall }x\in H.$$

In 2006, Marino and Xu [1] introduced the following iterative scheme: for $x_1=x\in C$,

$$x_{n+1}={\alpha }_n\gamma f(x_n)+(I-{\alpha }_{n}A)T{x}_n,n\ge 1.$$

(1.4)

They proved that under appropriate conditions of the sequence $\{{\alpha }_n\}$, the sequence $\{x_n\}$ generated by (1.4) converges strongly to the unique solution of the variational inequality $〈(\gamma f-A)q,p-q〉\le 0$, $p\in F(T)$, which is the optimality condition for the minimization problem

$$\underset{x\in C}{min}\frac{1}{2}〈Ax,x〉-h(x),$$

where h is a potential function for γf (i.e., $h^{\prime }(x)=\gamma f(x)$ for $x\in H$).

In 2010, Jung [2] extended the result of Marino and Xu [1] to the class of k-strictly pseudo-contractive mappings $T:C\to H$ with $F(T)\ne \mathrm{\varnothing }$ and introduced the following iterative scheme: for $x_1=x\in C$,

$$\{\begin{array}{c}{y}_n={\beta }_n{x}_n+(1-{\beta }_n)P_{C}S{x}_n,\hfill \\ x_{n+1}={\alpha }_n\gamma f(x_n)+(I-{\alpha }_{n}A)y_n,n\ge 1,\hfill \end{array}$$

(1.5)

where $S:C\to H$ is a mapping defined by $Sx=kx+(1-k)Tx$. He proved that the sequence $\{x_n\}$ generated by (1.5) converges strongly to a fixed point q of T, which is the unique solution of the variational inequality

$$〈\gamma f(q)-Aq,p-q〉\le 0,p\in F(T).$$

Later, Tian [3] considered the following iterative method for a nonexpansive mapping $T:H\to H$ with $F(T)\ne \mathrm{\varnothing }$,

$$x_{n+1}={\alpha }_n\gamma f(x_n)+(I-\mu {\alpha }_{n}F)T{x}_n,n\ge 1,$$

(1.6)

where F is a k-Lipschitzian and η-strongly monotone operator. He proved that the sequence $\{x_n\}$ generated by (1.6) converges to a fixed point q in $F(T)$, which is the unique solution of the variational inequality

$$〈(\gamma f-\mu F)q,p-q〉\le 0,p\in F(T).$$

In 2010, Saeidi [4] introduced the following modified hybrid steepest-descent iterative algorithm for finding a common element of the set of solutions of a system of equilibrium problems for a family $\mathcal{F}=\{F_j:C\times C\to \mathbb{R},j=1,2,\dots ,M\}$ and the set of common fixed points for a family of infinitely nonexpansive mappings $\mathcal{S}=\{S_i:C\to C\}$ with respect to W-mappings (see [5]):

$$\{\begin{array}{c}{y}_n=W_n{J}_{r_M,n}^{F_M}\cdots J_{r_2,n}^{F_2}{J}_{r_1,n}^{F_1}{x}_n,\hfill \\ x_{n+1}=\beta x_n+(1-\beta )(I-{\lambda }_{n}B)y_n,\mathrm{\forall }n\in \mathbb{N},\hfill \end{array}$$

(1.7)

where B is a relaxed $(\gamma ,r)$-cocoercive, k-Lipschitzian mapping such that $r>\gamma k^2$. Then, under weaker hypotheses on coefficients, he proved the strongly convergence of the proposed iterative algorithm to the unique solution of the variational inequality.

Recently, Wang [6] extended and improved all the above results. He introduced a new iterative scheme: for $x_1=x\in C$,

$$\{\begin{array}{c}{y}_n={\beta }_n{x}_n+(1-{\beta }_n)W_n{x}_n,\hfill \\ x_{n+1}={\alpha }_n\gamma f(x_n)+(I-\mu {\alpha }_{n}F)y_n,n\ge 1,\hfill \end{array}$$

(1.8)

where $W_n$ is a mapping defined by (2.3), and F is a k-Lipschitzian and η-strongly monotone operator with $0<\mu <2\eta /k^2$. He proved that the sequence $\{x_n\}$ generated by (1.7) converges strongly to a common fixed point of an infinite family of ${\lambda }_i$-strictly pseudo-contractive mappings, which is a unique solution of the variational inequality

$$〈(\gamma f-\mu F)q,p-q〉\le 0,p\in \bigcap _{i=1}^{\mathrm{\infty }}F(T_i).$$

Very recently, He, Liu and Cho [7] introduced an explicit scheme which was defined by the following suitable sequence:

$$z_{n+1}={ϵ}_n\gamma f(z_n)+(I-{ϵ}_{n}A)W_n{S}_{r_{1,n}}^1{S}_{r_{2,n}}^2\cdots S_{r_{K,n}}^K{z}_n,\mathrm{\forall }n\in N.$$

They generated $W_n$-mapping by $\{T_i\}$ and $\{{\lambda }_n\}$ where $\{T_i\}$ is a family of nonexpansive mappings from H into itself. They found that if ${\{r_{k,n}\}}_{k=1}^K$, $\{{ϵ}_n\}$ and $\{{\lambda }_n\}$ satisfy appropriate conditions and $F:=({\bigcap }_{k=1}^{K}SEP(G_K))\cap ({\bigcap }_{n\in N}F(T_n))\ne \mathrm{\varnothing }$, then $\{z_n\}$ converges strongly to $x^{\ast }\in F$, which satisfies the variational inequality $〈(A-\gamma f)x^{\ast },x-x^{\ast }〉\ge 0$ for all $x\in F$.

In this paper, we introduce a new iterative scheme in a Hilbert space H which is a mixed iterative scheme of (1.7) and (1.8). We prove that the sequence converges strongly to a common element of the set of solutions of the system of equilibrium problems and the set of common fixed points of an infinite family of strictly pseudo-contractive mappings by using a viscosity hybrid steepest-descent method. The results obtained in this paper improved and extended the above mentioned results and many others. Finally, we give a simple numerical example to support and illustrate our main theorem in the last part.

2 Preliminaries

Let H be a real Hilbert space and C be a nonempty closed convex subset of H. We have

$${\parallel x-y\parallel }^2={\parallel x\parallel }^2+{\parallel y\parallel }^2-2〈x,y〉,\mathrm{\forall }x,y\in H.$$

(2.1)

Recall that the nearest projection $P_C$ from H to C assigns to each $x\in H$ the unique point $P_{C}x\in C$ satisfying the property

$$\parallel x-P_{C}x\parallel =\underset{y\in C}{min}\parallel x-y\parallel .$$

We recall some lemmas which will be needed in the rest of this paper.

Lemma 2.1 In a Hilbert space H, the following inequality holds:

$${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2〈y,x+y〉,x,y\in H.$$

Lemma 2.2 Let B be a k-Lipschitzian and η-strongly monotone operator on a Hilbert space H with $k>0$, $\eta >0$, $0<\mu <2\eta /k^2$ and $0<t<1$. Then $S=(I-t\mu B):H\to H$ is a contraction with a contractive coefficient $1-t\tau$ and $\tau =\frac{1}{2}\mu (2\eta -\mu k^2)$.

Proof From (1.2), (1.3) and (2.1), we have

$$\begin{array}{rcl}{\parallel Sx-Sy\parallel }^2& =& {\parallel (x-y)-t\mu (Bx-By)\parallel }^2\\ =& {\parallel x-y\parallel }^2+t^2{\mu }^2{\parallel Bx-By\parallel }^2-2\mu t〈Bx-By,x-y〉\\ \le & {\parallel x-y\parallel }^2+t^2{\mu }^2{k}^2{\parallel x-y\parallel }^2-2\mu t\eta {\parallel x-y\parallel }^2\\ =& [1-t\mu (2\eta -\mu k^2)]{\parallel x-y\parallel }^2\\ \le & {(1-t\tau )}^2{\parallel x-y\parallel }^2,\end{array}$$

where $\tau =\frac{1}{2}\mu (2\eta -\mu k^2)$, and so, $\parallel Sx-Sy\parallel \le (1-t\tau )\parallel x-y\parallel$.

Hence, S is a contraction with a contractive coefficient $1-t\tau$. □

Lemma 2.3 Let H be a Hilbert space. For a given $z\in H$ and $u\in C$,

$$u=P_{C}z\iff 〈u-z,v-u〉\ge 0,\mathrm{\forall }v\in C.$$

Lemma 2.4 Let H be a real Hilbert space. For q which solves the variational inequality $〈(\gamma f-\mu B)q,p-q〉\le 0$, $f\in {\mathrm{\Pi }}_H$, $p\in F(T)$, the following statement is true:

$$〈(\gamma f-\mu B)q,p-q〉\le 0\iff P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q=q,$$

(2.2)

where $\mathrm{\Theta }:=({\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i))\cap ({\bigcap }_{j=1}^{M}SEP(F_j))$.

Proof From Lemma (2.3), it follows that

$$\begin{array}{rcl}q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q& \iff & 〈q-(I-\mu B+\gamma f)q,p-q〉\ge 0,p\in \mathrm{\Theta },\\ \iff & 〈(\mu B-\gamma f)q,p-q〉\ge 0\\ \iff & 〈(\gamma f-\mu B)q,p-q〉\le 0.\end{array}$$

 □

Lemma 2.5 [8]

Let C be a closed convex subset of a Hilbert space H and $T:C\to C$ be a nonexpansive mapping with $F(T)\ne \mathrm{\varnothing }$; if the sequence $\{x_n\}$ weakly converges to x and $(I-T)x_n$ converges strongly to y, then $(I-T)x=y$.

Lemma 2.6 [9]

Let $\{x_n\}$ and $\{z_n\}$ be bounded sequences in a Banach space E and $\{{\gamma }_n\}$ be a sequence in $[0,1]$ which satisfies the following condition:

$$0<\underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}inf}{\gamma }_n\le \underset{n\to \mathrm{\infty }}{lim\hspace{0.17em}sup}{\gamma }_n<1.$$

Suppose that $x_{n+1}={\gamma }_n{x}_n+(1-{\gamma }_n)z_n$, $n\ge 0$ and ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}(\parallel z_{n+1}-z_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0$. Then ${lim}_{n\to \mathrm{\infty }}\parallel z_n-x_n\parallel =0$.

Lemma 2.7 [10, 11]

Let $\{s_n\}$ be a sequence of non-negative real numbers satisfying

$$s_{n+1}\le (1-{\lambda }_n)s_n+{\lambda }_n{\delta }_n+{\gamma }_n,n\ge 0,$$

where $\{{\lambda }_n\}$, $\{{\delta }_n\}$ and $\{{\gamma }_n\}$ satisfy the following conditions:

• (i) $\{{\lambda }_n\}\subset [0,1]$ and ${\sum }_{n=0}^{\mathrm{\infty }}=\mathrm{\infty }$;

• (ii) ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\delta }_n\le 0$ or ${\sum }_{n=0}^{\mathrm{\infty }}{\lambda }_n{\delta }_n<\mathrm{\infty }$;

• (iii) ${\gamma }_n\ge 0$ ($n\ge 0$), ${\sum }_{n=0}^{\mathrm{\infty }}{\gamma }_n<\mathrm{\infty }$.

Then ${lim}_{n\to \mathrm{\infty }}{s}_n=0$.

Lemma 2.8 [12]

Let C be a nonempty closed convex subset of a real Hilbert space H and $T:C\to C$ be a λ-strictly pseudo-contractive mapping. Define a mapping $S:C\to C$ by $Sx=\alpha x+(1-\alpha )Tx$ for all $x\in C$ and $\alpha \in [\lambda ,1)$. Then S is a nonexpansive mapping such that $F(S)=F(T)$.

In this work, we defined the mapping $W_n$ by

$$\begin{array}{r}{U}_{n,n+1}=I,\\ U_{n,n}={\gamma }_n{T}_n^{\prime }{U}_{n,n+1}+(1-{\gamma }_n)I,\\ U_{n,n-1}={\gamma }_{n-1}{T}_{n-1}^{\prime }{U}_{n,n}+(1-{\gamma }_{n-1})I,\\ ⋮\\ U_{n,k}={\gamma }_k{T}_k^{\prime }{U}_{n,k+1}+(1-{\gamma }_k)I,\\ U_{n,k-1}={\gamma }_{k-1}{T}_{k-1}^{\prime }{U}_{n,k}+(1-{\gamma }_{k-1})I,\\ ⋮\\ U_{n,2}={\gamma }_2{T}_2^{\prime }{U}_{n,3}+(1-{\gamma }_2)I,\\ W_n=U_{n,1}={\gamma }_1{T}_1^{\prime }{U}_{n,2}+(1-{\gamma }_1)I,\end{array}$$

(2.3)

where ${\gamma }_1,{\gamma }_2,\dots$ are real numbers such that $0\le {\gamma }_n\le 1$, $T_i^{\prime }={\theta }_{i}I+(1-{\theta }_i)T_i$ where $T_i$ is a ${\lambda }_i$-strictly pseudo-contractive mapping of C into itself and ${\theta }_i\in [{\lambda }_i,1)$. By Lemma 2.8, we know that $T_i^{\prime }$ is a nonexpansive mapping and $F(T_i)=F(T_i^{\prime })$. As a result, it can be easily seen that $W_n$ is also a nonexpansive mapping.

Lemma 2.9 [5]

Let C be a nonempty closed convex subset of a strictly convex Banach space E. Let $T_1^{\prime },T_2^{\prime },\dots$ be nonexpansive mappings of C into itself such that ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i^{\prime })\ne \mathrm{\varnothing }$ and ${\gamma }_1,{\gamma }_2,\dots$ be real numbers such that $0<{\gamma }_i\le b<1$ for each $i=1,2,\dots$. Then for any $x\in C$ and $k\in N$, the limit ${lim}_{n\to \mathrm{\infty }}{U}_{n,k}x$ exists.

By using Lemma 2.8, one can define the mapping W of C into itself as follows:

$$Wx:=\underset{n\to \mathrm{\infty }}{lim}{W}_{n}x=\underset{n\to \mathrm{\infty }}{lim}{U}_{n,1}x,x\in C.$$

(2.4)

Such a mapping W is called the modified W-mapping generated by $T_1,T_2,\dots$ , ${\gamma }_1,{\gamma }_2,\dots$ and ${\theta }_1,{\theta }_2,\dots$ .

Lemma 2.10 [5]

Let C be a nonempty closed convex subset of a strictly convex Banach space E. Let $T_1^{\prime },T_2^{\prime },\dots$ be nonexpansive mappings of C into itself such that ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i^{\prime })\ne \mathrm{\varnothing }$ and ${\gamma }_1,{\gamma }_2,\dots$ be real numbers such that $0<{\gamma }_i\le b<1$ for each $i=1,2,\dots$. Then $F(W)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i^{\prime })$.

Combining Lemmas 2.7-2.9, one can get that $F(W)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i^{\prime })={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$.

Lemma 2.11 [13]Let C be a nonempty closed convex subset of a Hilbert space H, $\{T_i^{\prime }:C\to C\}$ be a family of infinite nonexpansive mappings with ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i^{\prime })\ne \mathrm{\varnothing }$, $\{{\gamma }_i\}$ be a real sequence such that $0<{\gamma }_i\le b<1$, for each $i\ge 1$. If K is any bounded subset of C, then

$$\underset{n\to \mathrm{\infty }}{lim}\underset{x\in K}{sup}\parallel Wx-W_{n}x\parallel =0.$$

(2.5)

For solving the equilibrium problem, let us give the following assumptions on a bifunction $F:C\times C\to \mathbb{R}$, which were imposed in [14]:

(A1) $F(x,x)=0$ for all $x\in C$;

(A2) F is monotone, i.e., $F(x,y)+F(y,x)\le 0$ for all $x,y\in C$;

(A3) for each $x,y,z\in C$, ${lim}_{t\downarrow 0}F(tz+(1-t)x,y)\le F(x,y)$;

(A4) for each $x\in C$, $y\mapsto F(x,y)$ is convex and lower semicontinuous.

Lemma 2.12 [14]

Let C be a nonempty closed convex subset of H, and let F be a bifunction of $C\times C$ into ℝ satisfying (A1)-(A4). Then for $r>0$ and $x\in H$, there exists $z\in C$ such that

$$F(z,y)+\frac{1}{r}〈y-z,z-x〉\ge 0.$$

(2.6)

Lemma 2.13 [15]

Let C be a nonempty closed convex subset of H, and let F be a bifunction of $C\times C$ into ℝ satisfying (A1)-(A4). For $r>0$, define a mapping $J_r^F:H\to C$ as follows:

$$J_r^F(x)=\{z\in C:F(z,y)+\frac{1}{r}〈y-z,z-x〉\ge 0,\mathrm{\forall }y\in C\}$$

(2.7)

for all $x\in H$. Then the following conclusions hold:

• (1) $J_r^F$ is single-valued;

• (2) $J_r^F$ is firmly nonexpansive, i.e., for any $x,y\in H$,

  $${\parallel J_r^F(x)-J_r^F(y)\parallel }^2\le 〈J_r^F(x)-J_r^F(y),x-y〉;$$

• (3) $F(J_r^F)=EP(F)$;

• (4) $EP(F)$ is closed and convex.

Lemma 2.14 [5]

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $\mathcal{T}={\{T_i\}}_{i=1}^N$ be an infinite family of nonexpanxive mappings with $F(\mathcal{T})={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$ and $\{{\gamma }_i\}$ be a real sequence such that $0<{\gamma }_i\le b<1$ for each $i\ge 1$. Then:

• (1) $W_n$ is nonexpansive and $F(W_n)={\bigcap }_{i=1}^{n}F(T_i)$ for each $n\ge 1$;

• (2) for each $x\in C$ and for each positive integer k, the limit ${lim}_{n\to \mathrm{\infty }}{U}_{n,k}x$ exists;

• (3) the mapping $W:C\to C$ defined by $Wx={lim}_{n\to \mathrm{\infty }}{W}_{n}x={lim}_{n\to \mathrm{\infty }}{U}_{n,1}x$ is a nonexpansive mapping satisfying $F(W)=F(\mathcal{T})$ and it is called the W-mapping generated by $T_1,T_2,\dots$ and ${\gamma }_1,{\gamma }_2,\dots$;

• (4) if K is any bounded subset of C, then ${lim}_{n\to \mathrm{\infty }}{sup}_{x\in K}\parallel Wx-W_{n}x\parallel =0$.

3 Main results

In this section, we will introduce an iterative scheme by using a viscosity hybrid steepest-descent method for finding a common element of the set of variational inequalities, fixed points for an infinite family of strictly pseudo-contractive mappings and the set of solutions of a system of equilibrium problems in a real Hilbert space.

Theorem 3.1 Let C be a nonempty closed convex subset of a real Hilbert space H, let $T_i:H\to H$ be a ${\lambda }_i$-strictly pseudo-contractive mapping with ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$, $\mathcal{F}=\{F_j:j=1,2,3,\dots ,M\}$ be a finite family of bifunctions $C\times C$ into ℝ satisfying (A1)-(A4) and ${\gamma }_i$ be a real sequence such that $0\le {\gamma }_i\le b\le 1$ for each $i\ge 1$. Let B be a k-Lipschitzian and η-strongly monotone operator on C with $0<\mu <\eta /k^2$ and $f\in {\mathrm{\Pi }}_H$ with $0<\gamma <\mu (\eta -\frac{\mu k^2}{2})/\alpha =\tau /\alpha$ and $\tau <1$. Assume that $\mathrm{\Theta }:=({\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i))\cap ({\bigcap }_{j=1}^{M}SEP(F_j))\ne \mathrm{\varnothing }$. Let the mapping $W_n$ be defined by (2.3). Let $\{x_n\}$ be the sequence generated by $x_1\in H$ and

$$\{\begin{array}{c}{u}_n=J_{r_{M,n}}^{F_M}{J}_{r_{M-1,n}}^{F_{M-1}}\cdots J_{r_{2,n}}^{F_2}{J}_{r_{1,N}}^{F_1}{x}_n,\hfill \\ y_n={\beta }_n{x}_n+(1-{\beta }_n)W_n{u}_n,\hfill \\ x_{n+1}={\alpha }_n\gamma f(x_n)+(I-{\alpha }_n\mu B)y_n,\mathrm{\forall }n\in \mathbb{N}\mathit{\text{and}}n\ge 1,\hfill \end{array}$$

(3.1)

where $\{{\alpha }_n\}$ and $\{{\beta }_n\}$ are sequences in $(0,1)$ which satisfy the following conditions:

(C1) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\mathrm{\Sigma }}_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

(C2) $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\beta }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\beta }_n\le a<1$ for some constant $a\in (0,1)$;

(C3) ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{r}_{j,n}>0$, for each $j=1,2,\dots ,M$.

Then the sequence $\{x_n\}$ converges strongly to $q\in \mathrm{\Theta }$, where $q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q$, which is the unique solution of the variational inequality

$$〈(\gamma f-\mu B)q,p-q〉\le 0,\mathrm{\forall }p\in \mathrm{\Theta },$$

(3.2)

or equivalently, q is the unique solution of the minimization problem

$$\underset{x\in \mathrm{\Theta }}{min}\frac{1}{2}〈Ax,x〉+h(x),$$

where h is a potential function for γf.

Proof We will divide the proof of Theorem 3.1 into several steps.

Step 1. We show that $\{x_n\}$ is bounded. Let $p\in \mathrm{\Theta }$. Since for each $k=1,2,3,\dots ,M$, $J_{r_{k,n}}^{F_k}$ is nonexpansive. Given ${\mathrm{\Im }}_n^k=J_{r_{k,n}}^{F_k}{J}_{r_{k-1,n}}^{F_{k-1}}{J}_{r_{k-2,n}}^{F_{k-2}}\cdots J_{r_{2,n}}^{F_2}{J}_{r_{1,n}}^{F_1}$ for $k\in \{1,2,3,\dots ,M\}$ and ${\mathrm{\Im }}_n^0=I$, for each $n\in \mathbb{N}$, we have

$$\parallel {\mathrm{\Im }}_n^k{x}_n-p\parallel =\parallel {\mathrm{\Im }}_n^k{x}_n-{\mathrm{\Im }}_n^{k}p\parallel \le \parallel x_n-p\parallel .$$

Consider,

$$\begin{array}{rcl}\parallel y_n-p\parallel & =& \parallel {\beta }_n{x}_n+(1-{\beta }_n)W_n{u}_n-p\parallel \\ =& \parallel {\beta }_n(x_n-p)+(1-{\beta }_n)(W_n{u}_n-p)\parallel \\ \le & {\beta }_n\parallel x_n-p\parallel +(1-{\beta }_n)\parallel (W_n{u}_n-p)\parallel \\ =& {\beta }_n\parallel x_n-p\parallel +(1-{\beta }_n)\parallel W_n{\mathrm{\Im }}_n^M{x}_n-p\parallel \\ \le & {\beta }_n\parallel x_n-p\parallel +(1-{\beta }_n)\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel \\ \le & {\beta }_n\parallel x_n-p\parallel +(1-{\beta }_n)\parallel x_n-p\parallel \\ =& \parallel x_n-p\parallel .\end{array}$$

(3.3)

From Lemma 2.2, (3.1) and (3.3), it follows that

$$\begin{array}{rcl}\parallel x_{n+1}-p\parallel & =& \parallel {\alpha }_n\gamma f(x_n)+(I-{\alpha }_n\mu B)y_n-p\parallel \\ =& \parallel {\alpha }_n(\gamma f(x_n)-\mu Bp)+(I-{\alpha }_n\mu B)y_n-(I-{\alpha }_n\mu B)p\parallel \\ =& \parallel (I-{\alpha }_n\mu B)(y_n-p)+{\alpha }_n(\gamma f(x_n)-\mu Bp+\gamma f(p)-\gamma f(p))\parallel \\ \le & \parallel (I-{\alpha }_n\mu B)(y_n-p)\parallel +{\alpha }_n\gamma \parallel f(x_n)-f(p)\parallel +{\alpha }_n\parallel \gamma f(p)-\mu Bp\parallel \\ \le & (1-{\alpha }_n\tau )\parallel y_n-p\parallel +{\alpha }_n\gamma \alpha \parallel x_n-p\parallel +{\alpha }_n\parallel \gamma f(p)-\mu Bp\parallel \\ \le & (1-{\alpha }_n\tau )\parallel x_n-p\parallel +{\alpha }_n\gamma \alpha \parallel x_n-p\parallel +{\alpha }_n\parallel \gamma f(p)-\mu Bp\parallel \\ =& [1-{\alpha }_n(\tau -\gamma \alpha )]\parallel x_n-p\parallel +{\alpha }_n\frac{\tau -\gamma \alpha }{\tau -\gamma \alpha }\parallel \gamma f(p)-\mu Bp\parallel \\ \le & max\{\parallel x_n-p\parallel ,\frac{\parallel \gamma f(p)-\mu Bp\parallel }{\tau -\gamma \alpha }\};n\ge 1.\end{array}$$

(3.4)

By mathematical induction, we have

$$\parallel x_n-p\parallel \le max\{\parallel x_1-p\parallel ,\frac{\parallel \gamma f(p)-\mu Bp\parallel }{\tau -\gamma \alpha }\},\mathrm{\forall }n\ge 1,$$

(3.5)

and we obtain $\{x_n\}$ is bounded. So are $\{y_n\}$, $\{W_n{\mathrm{\Im }}_n^k(x_n)\}$ and $\{f(x_n)\}$.

Step 2. We claim that if $\{x_n\}$ is a bounded sequence in C, then

$$\underset{n\to \mathrm{\infty }}{lim}\parallel {\mathrm{\Im }}_n^k{x}_n-{\mathrm{\Im }}_{n+1}^k{x}_n\parallel =0$$

(3.6)

for every $k\in \{1,2,3,\dots ,M\}$. From Step 2 of the proof in [[16], Theorem 3.1], we have for $k\in \{1,2,3,\dots ,M\}$,

$$\underset{n\to \mathrm{\infty }}{lim}\parallel J_{r_{k,n+1}}^{F_k}{x}_n-J_{r_{k,n}}^{F_k}{x}_n\parallel =0.$$

(3.7)

Note that for every $k\in \{1,2,3,\dots ,M\}$, we have

$${\mathrm{\Im }}_n^k=J_{r_{k,n}}^{F_k}{J}_{r_{k-1,n}}^{F_{k-1}}{J}_{r_{k-2,n}}^{F_{k-2}}\cdots J_{r_{2,n}}^{F_2}{J}_{r_{1,n}}^{F_1}=J_{r_{k,n}}^{F_k}{\mathrm{\Im }}_n^{k-1}.$$

So, we note that

$$\begin{array}{rcl}\parallel {\mathrm{\Im }}_n^k{x}_n-{\mathrm{\Im }}_{n+1}^k{x}_n\parallel & =& \parallel J_{r_{k,n}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n-J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_{n+1}^{k-1}{x}_n\parallel \\ \le & \parallel J_{r_{k,n}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n-J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n\parallel +\parallel J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n-J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_{n+1}^{k-1}{x}_n\parallel \\ \le & \parallel J_{r_{k,n}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n-J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n\parallel +\parallel {\mathrm{\Im }}_n^{k-1}{x}_n-{\mathrm{\Im }}_{n+1}^{k-1}{x}_n\parallel \\ \le & \parallel J_{r_{k,n}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n-J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n\parallel +\parallel J_{r_{k-1,n}}^{F_{k-1}}{\mathrm{\Im }}_n^{k-2}{x}_n-J_{r_{k-1,n+1}}^{F_{k-1}}{\mathrm{\Im }}_n^{k-2}{x}_n\parallel \\ +\parallel {\mathrm{\Im }}_n^{k-2}{x}_n-{\mathrm{\Im }}_{n+1}^{k-2}{x}_n\parallel \\ \le & \parallel J_{r_{k,n}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n-J_{r_{k,n+1}}^{F_k}{\mathrm{\Im }}_n^{k-1}{x}_n\parallel +\parallel J_{r_{k-1,n}}^{F_{k-1}}{\mathrm{\Im }}_n^{k-2}{x}_n-J_{r_{k-1,n+1}}^{F_{k-1}}{\mathrm{\Im }}_n^{k-2}{x}_n\parallel \\ +\cdots +\parallel J_{r_{2,n}}^{F_2}{\mathrm{\Im }}_n^1{x}_n-J_{r_{2,n+1}}^{F_2}{\mathrm{\Im }}_n^1{x}_n\parallel +\parallel J_{r_{1,n}}^{F_1}{x}_n-J_{r_{1,n+1}}^{F_1}{x}_n\parallel .\end{array}$$

(3.8)

Now, applying (3.7) to (3.8), we conclude (3.6).

Step 3. We show that ${lim}_{n\to \mathrm{\infty }}\parallel x_{n+1}-x_n\parallel =0$.

We define a sequence $\{z_n\}$ by $z_n=(x_{n+1}-{\beta }_n{x}_n)/(1-{\beta }_n)$, so that $x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)z_n$. We now observe that

$$\begin{array}{rcl}{z}_{n+1}-z_n& =& \frac{x_{n+2}-{\beta }_{n+1}{x}_{n+1}}{1-{\beta }_{n+1}}-\frac{x_{n+1}-{\beta }_n{x}_n}{1-{\beta }_n}\\ =& \frac{{\alpha }_{n+1}\gamma f(x_{n+1})+(I-\mu {\alpha }_{n+1}B)y_{n+1}-{\beta }_{n+1}{x}_{n+1}}{1-{\beta }_{n+1}}\\ -\frac{{\alpha }_n\gamma f(x_n)+(I-\mu {\alpha }_{n}B)y_n-{\beta }_n{x}_n}{1-{\beta }_n}\\ =& \frac{{\alpha }_{n+1}(\gamma f(x_{n+1})-\mu B{y}_{n+1})}{1-{\beta }_{n+1}}-\frac{{\alpha }_n(\gamma f(x_n)-\mu B{y}_n)}{1-{\beta }_n}+W_{n+1}{u}_{n+1}-W_n{u}_n.\end{array}$$

(3.9)

It follows from (3.9) that

$$\begin{array}{rcl}\parallel z_{n+1}-z_n\parallel & \le & \frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}(\parallel \gamma f(x_{n+1})\parallel +\parallel \mu B{y}_{n+1}\parallel )+\frac{{\alpha }_n}{1-{\beta }_n}(\parallel \gamma f(x_n)\parallel +\parallel \mu B{y}_n\parallel )\\ +\parallel W_{n+1}{u}_{n+1}-W_n{u}_n\parallel .\end{array}$$

(3.10)

We observe that

(3.11)

and compute

$$\begin{array}{rcl}\parallel W_{n+1}{\mathrm{\Im }}_n^k{x}_{n+1}-W_n{\mathrm{\Im }}_n^k{x}_n\parallel & \le & \parallel W_{n+1}{\mathrm{\Im }}_n^k{x}_{n+1}-W_{n+1}{\mathrm{\Im }}_n^k{x}_n\parallel +\parallel W_{n+1}{\mathrm{\Im }}_n^k{x}_n-W_n{\mathrm{\Im }}_n^k{x}_n\parallel \\ \le & \parallel x_{n+1}-x_n\parallel +\parallel W_{n+1}{\mathrm{\Im }}_n^k{x}_n-W_n{\mathrm{\Im }}_n^k{x}_n\parallel .\end{array}$$

(3.12)

Consider,

$$\begin{array}{rcl}\parallel W_{n+1}{\mathrm{\Im }}_n^k{x}_n-W_n{\mathrm{\Im }}_n^k{x}_n\parallel & =& \parallel {\gamma }_1{T}_1^{\prime }{U}_{n+1,2}{\mathrm{\Im }}_n^k{x}_n-{\gamma }_1{T}_1^{\prime }{U}_{n,2}{\mathrm{\Im }}_n^k{x}_n\parallel \\ \le & {\gamma }_1\parallel U_{n+1,2}{\mathrm{\Im }}_n^k{x}_n-U_{n,2}{\mathrm{\Im }}_n^k{x}_n\parallel \\ =& {\gamma }_1\parallel {\gamma }_2{T}_2^{\prime }{U}_{n+1,3}{\mathrm{\Im }}_n^k{x}_n-{\gamma }_2{T}_2^{\prime }{U}_{n,3}{\mathrm{\Im }}_n^k{x}_n\parallel \\ \le & \cdots \\ \le & {\gamma }_1{\gamma }_2\cdots {\gamma }_n\parallel U_{n+1,n+1}{\mathrm{\Im }}_n^k{x}_n-U_{n,n+1}{\mathrm{\Im }}_n^k{x}_n\parallel \\ \le & M_1\prod _{i=1}^n{\gamma }_i,\end{array}$$

(3.13)

where $M_1\ge 0$ is a constant such that $\parallel U_{n+1,n+1}{u}_n-U_{n,n+1}{u}_n\parallel \le M_1$ for all $n\ge 1$.

Substituting (3.11) and (3.13) into (3.10), we can obtain

$$\begin{array}{rcl}\parallel z_{n+1}-z_n\parallel & \le & \frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}(\parallel \gamma f(x_{n+1})\parallel +\parallel \mu B{y}_{n+1}\parallel )+\frac{{\alpha }_n}{1-{\beta }_n}(\parallel \gamma f(x_n)\parallel +\parallel \mu B{y}_n\parallel )\\ +\parallel W_{n+1}{\mathrm{\Im }}_{n+1}^k{x}_{n+1}-W_{n+1}{\mathrm{\Im }}_n^k{x}_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel +M_1\prod _{i=1}^n{\gamma }_i\\ \le & M_2(\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}+\frac{{\alpha }_n}{1-{\beta }_n})+\parallel W_{n+1}{\mathrm{\Im }}_{n+1}^k{x}_{n+1}-W_{n+1}{\mathrm{\Im }}_n^k{x}_{n+1}\parallel \\ +\parallel x_{n+1}-x_n\parallel +M_1\prod _{i=1}^n{\gamma }_i\end{array}$$

(3.14)

where $M_2=sup\{\parallel \gamma f(x_n)\parallel +\parallel \mu B{y}_n\parallel ,n\ge 1\}$.

It follows from (3.14) that

$$\begin{array}{rcl}\parallel z_{n+1}-z_n\parallel & \le & M_2(\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}+\frac{{\alpha }_n}{1-{\beta }_n})+\parallel {\mathrm{\Im }}_{n+1}^k{x}_{n+1}-{\mathrm{\Im }}_n^k{x}_{n+1}\parallel \\ +\parallel x_{n+1}-x_n\parallel +M_1\prod _{i=1}^n{\gamma }_i.\end{array}$$

Hence, we have

$$\parallel z_{n+1}-z_n\parallel -\parallel x_{n+1}-x_n\parallel \le M_2(\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}+\frac{{\alpha }_n}{1-{\beta }_n})+\parallel {\mathrm{\Im }}_{n+1}^k{x}_{n+1}-{\mathrm{\Im }}_n^k{x}_{n+1}\parallel +M_1\prod _{i=1}^n{\gamma }_i.$$

From ${lim}_{n\to \mathrm{\infty }}\parallel {\mathrm{\Im }}_n^k{x}_n-{\mathrm{\Im }}_{n+1}^k{x}_n\parallel =0$ and the condition ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and $0<{lim}_{n\to \mathrm{\infty }}inf{\beta }_n<{lim}_{n\to \mathrm{\infty }}sup{\beta }_n\le a<1$ for some $a\in (0,1)$, it follows that

$$\underset{n\to \mathrm{\infty }}{lim}sup(\parallel z_{n+1}-z_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0.$$

(3.15)

By Lemma 2.5, we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel z_n-x_n\parallel =0.$$

(3.16)

From $x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)z_n$ and by (3.16), we get

$$\parallel x_{n+1}-x_n\parallel =(1-{\beta }_n)\parallel z_n-x_n\parallel .$$

(3.17)

Hence,

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_{n+1}-x_n\parallel =\underset{n\to \mathrm{\infty }}{lim}(1-{\beta }_n)\parallel z_n-x_n\parallel =0.$$

Step 4. We claim that ${lim}_{n\to \mathrm{\infty }}\parallel x_n-W_n{u}_n\parallel =0$.

$$\begin{array}{rcl}\parallel x_n-W_n{u}_n\parallel & \le & \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-W_n{u}_n\parallel \\ =& \parallel x_n-x_{n+1}\parallel +\parallel {\alpha }_n\gamma f(x_n)+(I-{\alpha }_n\mu B)y_n-W_n{u}_n\parallel \\ =& \parallel x_n-x_{n+1}\parallel +\parallel {\alpha }_n\gamma f(x_n)+y_n-{\alpha }_n\mu B{y}_n-W_n{u}_n\parallel \\ \le & \parallel x_{n+1}-x_n\parallel +{\alpha }_n\parallel \gamma f(x_n)-\mu B{y}_n\parallel +\parallel y_n-W_n{u}_n\parallel \\ \le & \parallel x_{n+1}-x_n\parallel +{\alpha }_n\parallel \gamma f(x_n)-\mu B{y}_n\parallel +\parallel {\beta }_n{x}_n+(1-{\beta }_n)W_n{u}_n-W_n{u}_n\parallel \\ \le & \parallel x_{n+1}-x_n\parallel +{\alpha }_n\parallel \gamma f(x_n)-\mu B{y}_n\parallel +{\beta }_n\parallel x_n-W_n{u}_n\parallel .\end{array}$$

It follows that

$$\parallel x_n-W_n{u}_n\parallel \le \frac{1}{1-{\beta }_n}\parallel x_n-x_{n+1}\parallel +\frac{{\alpha }_n}{1-{\beta }_n}\parallel \gamma f(x_n)-\mu B{y}_n\parallel .$$

By the conditions (C1) and (C2), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel x_n-W_n{u}_n\parallel =0.$$

(3.18)

Step 5. We show that

$$\underset{n\to \mathrm{\infty }}{lim}\parallel {\mathrm{\Im }}_n^k{x}_n-{\mathrm{\Im }}_n^{k+1}{x}_n\parallel =0,\mathrm{\forall }k=1,2,\dots ,M-1$$

(3.19)

for any $p\in \mathrm{\Theta }$ and $\mathrm{\forall }k=1,2,\dots ,M-1$. We note that $J_{r_{k+1,n}}^{F_{k+1}}$ is firmly nonexpansive by Lemma 2.12, then we observe that

$$\begin{array}{rcl}\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-p\parallel & =& \parallel J_{r_{k+1,n}}^{F_{k+1}}{\mathrm{\Im }}_n^k{x}_n-J_{r_{k+1,n}}^{F_{k+1}}p\parallel \\ \le & 〈J_{r_{k+1,n}}^{F_{k+1}}{\mathrm{\Im }}_n^k{x}_n-J_{r_{k+1,n}}^{F_{k+1}}p,{\mathrm{\Im }}_n^k{x}_n-p〉\\ =& 〈{\mathrm{\Im }}_n^{k+1}{x}_n-p,{\mathrm{\Im }}_n^k{x}_n-p〉\\ =& \frac{1}{2}({\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-p\parallel }^2+{\parallel {\mathrm{\Im }}_n^k{x}_n-p\parallel }^2-{\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n\parallel }^2),\end{array}$$

and hence

$$\begin{array}{rcl}{\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-p\parallel }^2& \le & {\parallel {\mathrm{\Im }}_n^k{x}_n-p\parallel }^2-{\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n\parallel }^2\\ \le & {\parallel x_n-p\parallel }^2-{\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n\parallel }^2.\end{array}$$

(3.20)

It follows that

$$\begin{array}{rcl}{\parallel x_{n+1}-p\parallel }^2& =& {\parallel {\alpha }_n(\gamma f(x_n)-\mu Bp)+(I-{\alpha }_n\mu B)(y_n-p)\parallel }^2\\ =& {\alpha }_n^2{\parallel (\gamma f(x_n)-\mu Bp)\parallel }^2+{(1-{\alpha }_n\tau )}^2{\parallel y_n-p\parallel }^2\\ +2{\alpha }_n〈(\gamma f(x_n)-\mu Bp),(I-{\alpha }_n\mu B)(y_n-p)〉\\ \le & {\alpha }_n^2{\parallel (\gamma f(x_n)-\mu Bp)\parallel }^2+{(1-{\alpha }_n\tau )}^2[{\beta }_n{\parallel x_n-p\parallel }^2+(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2]\\ +2{\alpha }_n〈(\gamma f(x_n)-\mu Bp),(I-{\alpha }_n\mu B)(y_n-p)〉\\ \le & {(1-{\alpha }_n\tau )}^2{\beta }_n{\parallel x_n-p\parallel }^2+{(1-{\alpha }_n\tau )}^2(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2+c_n\\ =& {(1-{\alpha }_n\tau )}^2{\beta }_n{\parallel x_n-p\parallel }^2+(1-2{\alpha }_n(\tau -\gamma ))(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2\\ +{\alpha }_n^2{\tau }^2(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2\\ -2{\alpha }_n\gamma (1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2+c_n\\ \le & {(1-{\alpha }_n\tau )}^2{\beta }_n{\parallel x_n-p\parallel }^2+(1-2{\alpha }_n(\tau -\gamma ))(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2\\ +{\alpha }_n^2{\tau }^2(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2+c_n\\ =& (1-2{\alpha }_n(\tau -\gamma )){\beta }_n{\parallel x_n-p\parallel }^2+{\alpha }_n^2{\tau }^2{\beta }_n{\parallel x_n-p\parallel }^2-2{\alpha }_n\gamma {\beta }_n{\parallel x_n-p\parallel }^2\\ +(1-2{\alpha }_n(\tau -\gamma ))(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-p\parallel }^2\\ +{\alpha }_n^2{\tau }^2(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2+c_n\\ =& (1-2{\alpha }_n(\tau -\gamma )){\beta }_n{\parallel x_n-p\parallel }^2+{\alpha }_n^2{\tau }^2{\beta }_n{\parallel x_n-p\parallel }^2-2{\alpha }_n\gamma {\beta }_n{\parallel x_n-p\parallel }^2\\ +(1-2{\alpha }_n(\tau -\gamma ))(1-{\beta }_n)[{\parallel x_n-p\parallel }^2-{\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n\parallel }^2]\\ +{\alpha }_n^2{\tau }^2(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^M{x}_n-p\parallel }^2+c_n\\ \le & (1-2{\alpha }_n(\tau -\gamma )){\parallel x_n-p\parallel }^2+{\alpha }_n^2{\tau }^2{\parallel x_n-p\parallel }^2\\ -(1-2{\alpha }_n(\tau -\gamma ))(1-{\beta }_n){\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n\parallel }^2+c_n,\end{array}$$

where

$$c_n=2{\alpha }_n〈(\gamma f(x_n)-\mu Bp),(I-{\alpha }_n\mu B)(y_n-p)〉.$$

(3.21)

It follows from the condition (C1) that

$$\underset{n\to \mathrm{\infty }}{lim}{c}_n=0.$$

(3.22)

So, we obtain

Using the condition (C1), (3.17) and (3.22), we obtain

$$\underset{n\to \mathrm{\infty }}{lim}\parallel {\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n\parallel =0,\mathrm{\forall }k=1,2,\dots ,M-1.$$

(3.23)

Step 6. We show that ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}〈(\gamma f-\mu B)q,x_n-q〉\le 0$, where $q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q$.

The Banach contraction principle guarantees that $P_{\mathrm{\Theta }}(I-\mu B+\gamma f)$ has a unique fixed point q which is the unique solution of (3.1). Let $\{x_{n_k}\}$ be a subsequence of $\{x_n\}$ such that

$$\underset{k\to \mathrm{\infty }}{lim}〈(\gamma f-\mu B)q,x_{n_m}-q〉=lim\underset{n\to \mathrm{\infty }}{sup}〈(\gamma f-\mu B)q,x_n-q〉.$$

Since $\{x_{n_k}\}$ is bounded, then there exists a subsequence $\{x_{n_{k_i}}\}$ which converges weakly to $z\in H$. Without loss of generality, we can assume that $x_{n_k}\rightharpoonup z$. We claim that $z\in \mathrm{\Theta }$.

Next, we need to show that $z\in {\bigcap }_{j=1}^{M}SEP(F_j)$. First, by (A2) and given $y\in C$ and $k\in \{1,2,\dots ,M-1\}$, we have

$$\frac{1}{r_{k+1,n}}〈y-{\mathrm{\Im }}_n^{k+1}{x}_n,{\mathrm{\Im }}_n^{k+1}{x}_n-{\mathrm{\Im }}_n^k{x}_n〉\ge F_{k+1}(y,{\mathrm{\Im }}_n^{k+1}{x}_n).$$

Thus,

$$〈y-{\mathrm{\Im }}_{n_m}^{k+1}{x}_{n_m},\frac{{\mathrm{\Im }}_{n_m}^{k+1}{x}_{n_m}-{\mathrm{\Im }}_{n_m}^k{x}_{n_m}}{r_{k+1,n_m}}〉\ge F_{k+1}(y,{\mathrm{\Im }}_{n_m}^{k+1}{x}_{n_m}).$$

(3.24)

From (A4), $F(y,\cdot )$ is a lower semicontinuous and convex, and thus weakly semicontinuous. The condition (C3) and (3.23) imply that

$$\frac{{\mathrm{\Im }}_{n_m}^{k+1}{x}_{n_m}-{\mathrm{\Im }}_{n_m}^k{x}_{n_m}}{r_{k+1,n_m}}\to 0,$$

(3.25)

in norm. Therefore, letting $m\to \mathrm{\infty }$ in (3.24) yields

$$F_{k+1}(y,z)\le \underset{m\to \mathrm{\infty }}{lim}{F}_{k+1}(y,{\mathrm{\Im }}_{n_m}^{k+1}{x}_{n_m})\le 0,$$

for all $y\in H$ and $k\in \{1,2,\dots ,M-1\}$. Replacing y with $y_t=ty+(1-t)z$ with $t\in (0,1)$ and using (A1) and (A4), we obtain

$$0=F_{k+1}(y_t,y_t)\le t{F}_{k+1}(y_t,y)+(1-t)F_{k+1}(y_t,z)\le t{F}_{k+1}(y_t,y).$$

Hence, $F_{k+1}(ty+(1-t)z,y)\ge 0$, for all $t\in (0,1)$ and $y\in H$. Letting $t\to 0^{+}$ and using (A3), we conclude that $F_{k+1}(z,y)\ge 0$ for all $y\in H$ and $k\in \{1,2,\dots ,M\}$. Therefore,

$$z\in EP(F_j),\mathrm{\forall }j=1,2,\dots ,M,$$

(3.26)

that is,

$$z\in \bigcap _{j=1}^{M}SEP(F_j).$$

(3.27)

Next, we show that $z\in {\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. By Lemma 2.6, we have

$$W_{n_m}z\to Wz,\mathrm{\forall }z\in C,$$

(3.28)

and $F(W)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. Assume that $z\notin F(W)$, then $z\ne Wz$. Therefore, from the Opial property of a Hilbert space, (3.27), (3.28) and Step 4, we have

$$\begin{array}{rcl}\underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_m}-z\parallel & <& \underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_m}-Wz\parallel \\ \le & \underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\{\parallel x_{n_m}-W_{n_m}{\mathrm{\Im }}_{n_m}^M{x}_{n_m}\parallel \\ +\parallel W_{n_m}{\mathrm{\Im }}_{n_m}^M{x}_{n_m}-W_{n_m}{\mathrm{\Im }}_{n_m}^{M}z\parallel +\parallel W_{n_m}{\mathrm{\Im }}_{n_m}^{M}z-Wz\parallel \}\\ \le & \underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\{\parallel x_{n_m}-z\parallel +\parallel W_{n_m}z-Wz\parallel \}\\ \le & \underset{m\to \mathrm{\infty }}{lim\hspace{0.17em}inf}\parallel x_{n_m}-z\parallel .\end{array}$$

It is a contradiction. Thus z belongs to $F(W)={\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)$. Hence, $z\in \mathrm{\Theta }$.

Hence, by Lemma 2.4, we obtain

$$\begin{array}{rcl}lim\underset{n\to \mathrm{\infty }}{sup}〈(\gamma f-\mu B)q,x_n-q〉& =& lim\underset{m\to \mathrm{\infty }}{sup}〈(\gamma f-\mu B)q,x_{n_m}-q〉\\ =& 〈(\gamma f-\mu B)q,z-q〉\le 0.\end{array}$$

Step 7. We claim that $x_n$ converges strongly to $q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q$. We observe that

$$\begin{array}{rcl}{\parallel x_{n+1}-q\parallel }^2& =& {\parallel {\alpha }_n\gamma f(x_n)+(I-\mu {\alpha }_{n}B)y_n-q\parallel }^2\\ =& {\parallel {\alpha }_n\gamma f(x_n)+(I-\mu {\alpha }_{n}B)y_n-q+\mu {\alpha }_{n}Bq-\mu {\alpha }_{n}Fq\parallel }^2\\ \le & {\parallel (I-\mu {\alpha }_{n}B)y_n-(I-\mu {\alpha }_{n}B)q\parallel }^2+2{\alpha }_n〈\gamma f(x_n)-\mu Bq,x_{n+1}-q〉\\ \le & {(1-{\alpha }_n\tau )}^2{\parallel y_n-q\parallel }^2\\ +2{\alpha }_n〈\gamma f(x_n)-\gamma f(q),x_{n+1}-q〉+2{\alpha }_n〈\gamma f(q)-\mu Bq,x_{n+1}-q〉\\ \le & {(1-{\alpha }_n\tau )}^2{\parallel x_n-q\parallel }^2+{\alpha }_n\gamma \alpha ({\parallel x_n-q\parallel }^2+{\parallel x_{n+1}-q\parallel }^2)\\ +2{\alpha }_n〈\gamma f(q)-\mu Bq,x_{n+1}-q〉\\ \le & \frac{{(1-{\alpha }_n\tau )}^2}{1-{\alpha }_n\gamma \alpha }{\parallel x_n-q\parallel }^2+\frac{{\alpha }_n\gamma \alpha }{1-{\alpha }_n\gamma \alpha }{\parallel x_n-q\parallel }^2\\ +\frac{2{\alpha }_n}{1-{\alpha }_n\gamma \alpha }〈\gamma f(q)-\mu Bq,x_{n+1}-q〉\\ =& (1-\frac{2{\alpha }_n(\tau -\gamma \alpha )+{\alpha }_n^2{\tau }^2}{1-{\alpha }_n\gamma \alpha }){\parallel x_n-q\parallel }^2+\frac{2{\alpha }_n}{1-{\alpha }_n\gamma \alpha }〈\gamma f(q)-\mu Bq,x_{n+1}-q〉\\ =& (1-\frac{2{\alpha }_n(\tau -\gamma \alpha )}{1-{\alpha }_n\gamma \alpha }){\parallel x_n-q\parallel }^2\\ +\frac{2{\alpha }_n(\tau -\gamma \alpha )}{1-{\alpha }_n\gamma \alpha }(\frac{1}{(\tau -\gamma \alpha )}〈\gamma f(q)-\mu Bq,x_{n+1}-q〉\\ +\frac{{\alpha }_n{\tau }^2}{2(\tau -\gamma \alpha )}{\parallel x_n-q\parallel }^2)\\ =& (1-\frac{2{\alpha }_n(\tau -\gamma \alpha )}{1-{\alpha }_n\gamma \alpha }){\parallel x_n-q\parallel }^2\\ +\frac{2{\alpha }_n(\tau -\gamma \alpha )}{1-{\alpha }_n\gamma \alpha }(\frac{1}{(\tau -\gamma \alpha )}〈\gamma f(q)-\mu Bq,x_{n+1}-q〉+\frac{{\alpha }_n{\tau }^2}{2(\tau -\gamma \alpha )}{M}_3),\end{array}$$

where $M_3={sup}_{n\ge 1}{\parallel x_n-q\parallel }^2$. Put ${\lambda }_n=\frac{2{\alpha }_n(\tau -\gamma \alpha )}{1-{\alpha }_n\gamma \alpha }$ and ${\delta }_n=\frac{1}{\tau -\gamma \alpha }〈\gamma f(q)-\mu Bq,x_{n+1}-q〉$. It follows that

$${\parallel x_{n+1}-q\parallel }^2\le (1-{\lambda }_n){\parallel x_n-q\parallel }^2+{\lambda }_n{\delta }_n+{\gamma }_n.$$

From (C1), (C2) and Step 5, it follows that ${\sum }_{n=0}^{\mathrm{\infty }}{\lambda }_n=\mathrm{\infty }$ and ${lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\delta }_n\le 0$. Hence, by Lemma 2.7, the sequence $\{x_n\}$ converges strongly to q. □

Using Theorem 3.1, we obtain the following corollaries.

Corollary 3.2 Let C be a nonempty closed convex subset of a real Hilbert space H. Let $\{T_i\}$ be an infinite family of nonexpansive mappings with ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$, $\mathcal{F}=\{F_j:j=1,2,3,\dots ,M\}$ be a finite family of bifunctions $C\times C$ into ℝ satisfying (A1)-(A4) and ${\gamma }_i$ be a real sequence such that $0\le {\gamma }_i\le b\le 1$ for each $i\ge 1$. Let B be a k-Lipschitzian and η-strongly monotone operator on C with $0<\mu <\eta /k^2$ and $f\in {\mathrm{\Pi }}_H$ with $0<\gamma <\mu (\eta -\frac{\mu k^2}{2})/\alpha =\tau /\alpha$ and $\tau <1$. Assume that $\mathrm{\Theta }:=({\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i))\cap ({\bigcap }_{j=1}^{M}SEP(F_j))\ne \mathrm{\varnothing }$. Let the mapping $W_n$ be defined by (2.3). Let $\{x_n\}$ be the sequence generated by $x_1\in H$ and

$$\{\begin{array}{c}{y}_n={\beta }_n{x}_n+(1-{\beta }_n)W_n{J}_{r_{M,n}}^{F_M}{J}_{r_{M-1,n}}^{F_{M-1}}\cdots J_{r_{2,n}}^{F_2}{J}_{r_{1,N}}^{F_1}{x}_n,\hfill \\ x_{n+1}={\alpha }_n\gamma f(x_n)+(I-{\alpha }_n\mu B)y_n,\mathrm{\forall }n\in \mathbb{N}\mathit{\text{and}}n\ge 1,\hfill \end{array}$$

where $\{{\alpha }_n\}$ and $\{{\beta }_n\}$ are the sequences in $(0,1)$ which satisfy the following conditions:

(C1) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\mathrm{\Sigma }}_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

(C2) $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\beta }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\beta }_n\le a<1$ for some constant $a\in (0,1)$;

(C3) ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{r}_{j,n}>0$, for each $j=1,2,\dots ,M$.

Then the sequence $\{x_n\}$ converges strongly to $q\in \mathrm{\Theta }$ where $q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q$, which is the unique solution of the variational inequality

$$〈(\gamma f-\mu B)q,p-q〉\le 0,\mathrm{\forall }p\in \mathrm{\Theta }.$$

Remark 3.3 Corollary 3.2 extends and improves Theorem 3.1 from f an infinite family of nonexpansive mappings to a family of strictly pseudo contractive mappings.

If $M=1$ in Theorem 3.1, we obtain the following corollary.

Corollary 3.4 Let C be a nonempty closed convex subset of a real Hilbert space H. Let $\{T_i\}$ be an infinite family of nonexpansive mappings with ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$, $\mathcal{F}=\{F_j:j=1,2,3,\dots ,M\}$ be a finite family of bifunctions $C\times C$ into ℝ satisfying (A1)-(A4) and ${\gamma }_i$ be a real sequence such that $0\le {\gamma }_i\le b\le 1$ for each $i\ge 1$. Let B be a k-Lipschitzian and η-strongly monotone operator on C with $0<\mu <\eta /k^2$ and $f\in {\mathrm{\Pi }}_H$ with $0<\gamma <\mu (\eta -\frac{\mu k^2}{2})/\alpha =\tau /\alpha$ and $\tau <1$. Assume that $\mathrm{\Theta }:=({\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i))\cap ({\bigcap }_{j=1}^{M}SEP(F_j))\ne \mathrm{\varnothing }$. Let the mapping $W_n$ be defined by (2.3). Let $\{x_n\}$ be the sequence generated by $x_1\in H$ and

$$\{\begin{array}{c}F(u_n,y)+\frac{1}{r}〈y-u_n,u_n-x_n〉\ge 0,\mathrm{\forall }y\in C,\hfill \\ y_n={\beta }_n{x}_n+(1-{\beta }_n)W_n{u}_n,\hfill \\ x_{n+1}={\alpha }_n\gamma f(x_n)+(I-{\alpha }_n\mu B)y_n,\mathrm{\forall }n\in \mathbb{N}\mathit{\text{and}}n\ge 1,\hfill \end{array}$$

where $\{{\alpha }_n\}$ and $\{{\beta }_n\}$ are the sequences in $(0,1)$ which satisfy the following conditions:

(C1) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\mathrm{\Sigma }}_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

(C2) $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\beta }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\beta }_n\le a<1$ for some constant $a\in (0,1)$;

(C3) ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{r}_{j,n}>0$, for each $j=1,2,\dots ,M$.

Then the sequence $\{x_n\}$ converges strongly to $q\in \mathrm{\Theta }$, where $q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q$, which is the unique solution of the variational inequality

$$〈(\gamma f-\mu B)q,p-q〉\le 0,\mathrm{\forall }p\in \mathrm{\Theta }.$$

If $M=1$, $W_n=W$, $\gamma =1$, $A=I$ and $\mu =1$ in Theorem 3.1, we obtain the following corollary:

Corollary 3.5 Let C be a nonempty closed convex subset of a real Hilbert space H. Let $\{T_i\}$ be an infinite family of nonexpansive mappings with ${\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i)\ne \mathrm{\varnothing }$, $\mathcal{F}=\{F_j:j=1,2,3,\dots ,M\}$ be a finite family of bifunctions $C\times C$ into ℝ satisfying (A1)-(A4) and ${\gamma }_i$ be a real sequence such that $0\le {\gamma }_i\le b\le 1$ for each $i\ge 1$. Let B be a k-Lipschitzian and η-strongly monotone operator on C with $0<\mu <\eta /k^2$ and $f\in {\mathrm{\Pi }}_H$ with $0<\gamma <\mu (\eta -\frac{\mu k^2}{2})/\alpha =\tau /\alpha$ and $\tau <1$. Assume that $\mathrm{\Theta }:=({\bigcap }_{i=1}^{\mathrm{\infty }}F(T_i))\cap ({\bigcap }_{j=1}^{M}SEP(F_j))\ne \mathrm{\varnothing }$. Let the mapping $W_n$ be defined by (2.3). Let $\{x_n\}$ be the sequence generated by $x_1\in H$ and

$$\{\begin{array}{c}{y}_n={\beta }_n{x}_n+(1-{\beta }_n)W{J}_{r_{M,n}}^{F_M}{J}_{r_{M-1,n}}^{F_{M-1}}\cdots J_{r_{2,n}}^{F_2}{J}_{r_{1,N}}^{F_1}{x}_n,\hfill \\ x_{n+1}={\alpha }_{n}f(x_n)+(I-{\alpha }_n\mu B)y_n,\mathrm{\forall }n\in \mathbb{N}\mathit{\text{and}}n\ge 1,\hfill \end{array}$$

where $\{{\alpha }_n\}$ and $\{{\beta }_n\}$ are the sequences in $(0,1)$ which satisfy the following conditions:

(C1) ${lim}_{n\to \mathrm{\infty }}{\alpha }_n=0$ and ${\mathrm{\Sigma }}_{n=1}^{\mathrm{\infty }}{\alpha }_n=\mathrm{\infty }$;

(C2) $0<{lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{\beta }_n<{lim\hspace{0.17em}sup}_{n\to \mathrm{\infty }}{\beta }_n\le a<1$ for some constant $a\in (0,1)$;

(C3) ${lim\hspace{0.17em}inf}_{n\to \mathrm{\infty }}{r}_{j,n}>0$, for each $j=1,2,\dots ,M$.

Then the sequence $\{x_n\}$ converges strongly to $q\in \mathrm{\Theta }$ where $q=P_{\mathrm{\Theta }}(I-\mu B+\gamma f)q$, which is the unique solution of the variational inequality

$$〈(\gamma f-\mu B)q,p-q〉\le 0,\mathrm{\forall }p\in \mathrm{\Theta }.$$

4 Numerical example

In this section, we give a real numerical example of Theorem 3.1 as follows.

Example 4.1 Let $H=\mathbb{R}$, $C=[0,\frac{1}{4}]$, $T_n=I$. $F_k(x,y)=0$, $\mathrm{\forall }x,y\in H$, $r_{k,n}=1$, $k\in \{1,2,3,\dots ,K\}$, $B=I$, $f(x)=x^2$, ${\beta }_n=\frac{1}{2}$, ${\alpha }_n=\frac{1}{n}$ for every $n\in \mathbb{N}$ and $\mu =1$. Then $\{x_n\}$ is the sequence generated by

$$x_{n+1}=\frac{x_n^2}{n}+(1-\frac{1}{n})x_n,$$

(4.1)

and $z\to 0$ as $n\to \mathrm{\infty }$, where 0 is the unique solution of the minimization problem

$$\underset{x\in C}{min}\frac{x^3}{3}+\frac{x^2}{2}+C_1,$$

(4.2)

where $C_1$ is a constant.

Proof We divide the proof into four steps.

Step 1. Using the idea in [7], we can show that

$$J_{r_{k,n}}^{k}x=P_{C}x,\mathrm{\forall }x\in H,k\in \{1,2,\dots ,K\},$$

(4.3)

where

$$P_{C}x=\{\begin{array}{cc}\frac{x}{|x|},\hfill & x\in H-C,\hfill \\ x,\hfill & x\in C.\hfill \end{array}$$

(4.4)

Since $F_k(x,y)=0$, $\mathrm{\forall }x,y\in C$, $k\in \{1,2,\dots ,K\}$, with the definition of $J_r(x)$, $\mathrm{\forall }x\in H$ in Lemma 2.13, we have

$$J_r^F(x)=\{z\in C:F(z,y)+\frac{1}{r}〈y-z,z-x〉\ge 0,\mathrm{\forall }y\in C\}.$$

(4.5)

By the equivalent property of the nearest projection $P_C$ from H to C, we can conclude that if we take $x\in C$, $J_{r_{k,n}}^{k}x=P_{C}x=Ix$. By (3) in Lemma 2.13, we have

$$\bigcap _{k=1}^{K}SEP(F_k)=C.$$

(4.6)

Step 2. We show that

$$W_n=I.$$

(4.7)

Since $T_i^{\prime }={\theta }_{i}I+(1-{\theta }_i)T_i$, where $T_i$ is a ${\lambda }_i$-strictly pseudo-contractive mapping and ${\theta }_i\in [{\lambda }_i,1)$, it can be easily seen that $T_i^{\prime }$ is a nonexpansive mapping. By (2.3), we have

and we compute (2.3) in the same way as above, so we obtain

$$\begin{array}{rcl}{W}_n& =& U_{n,1}={\gamma }_1{\gamma }_2\cdots {\gamma }_n{T}_1^{\prime }{T}_2^{\prime }\cdots T_n^{\prime }+{\gamma }_1{\gamma }_2\cdots {\gamma }_{n-1}(1-{\gamma }_n)T_1^{\prime }{T}_2^{\prime }\cdots T_{n-1}^{\prime }\\ +{\gamma }_1{\gamma }_2\cdots {\gamma }_{n-2}(1-{\gamma }_{n-1})T_1^{\prime }{T}_2^{\prime }\cdots T_{n-2}^{\prime }+\cdots +{\gamma }_1(1-{\gamma }_2)T_1^{\prime }+(1-{\gamma }_1)I.\end{array}$$

Since $T_n^{\prime }=I$, ${\gamma }_n=\beta$, $n\in \mathbb{N}$, hence,

$$W_n=[{\beta }^n+{\beta }^{n-1}(1-\beta )+\cdots +\beta (1-\beta )+(1-\beta )]I=I.$$

Step 3. We prove

$$x_{n+1}=\frac{x_n^2}{n}+(1-\frac{1}{n})x_n\text{and}{x}_n\to 0\text{as }n\to \mathrm{\infty },$$

where 0 is the unique solution of the minimization problem

$$\underset{x\in C}{min}\frac{x^3}{3}+\frac{x^2}{2}+C_1.$$

Since we let $B=I$, γ is a real number, so we choose $\gamma =1$. From (4.3), (4.4) and (4.7), we can obtain a special sequence $\{x_n\}$ of Theorem 3.1 as follows:

$$x_{n+1}=\frac{x_n^2}{n}+(1-\frac{1}{n})x_n.$$

Since $T_n=I$, $n\in \mathbb{N}$, we have

$$\bigcap _{n\in \mathbb{N}}F(T_n)=H.$$

Combining it with (4.6), we obtain

$$\mathrm{\Theta }:=(\bigcap _{k=1}^{K}SEP(F_k))\cap \left(\bigcap _{n\in \mathbb{N}F(T_n)}\right)=C=[0,\frac{1}{4}].$$

It is obvious that $x_n\to 0$, 0 is the unique solution of the minimization problem ${min}_{x\in C}\frac{x^3}{3}+\frac{x^2}{2}+C_1$, where $C_1$ is a constant number.

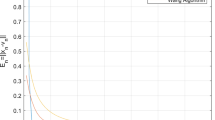
Step 4. In this step, we give the numerical results that support our main theorem as shown by plotting graphs using Matlab 7.11.0. We choose two different initial values as $x_1=0.1$ and $x_1=0.15$ in Table 1, Figure 1, and Figure 2, respectively. From the example, we can see that $\{x_n\}$ converges to 0.  □

Figure 1

The initial value $\mathit{x}\mathbf{(}\mathbf{1}\mathbf{)}\mathbf{=}\mathbf{0.1}$ and iteration steps $\mathit{n}\mathbf{=}\mathbf{250}$ .

Figure 2

The initial value $\mathit{x}\mathbf{(}\mathbf{1}\mathbf{)}\mathbf{=}\mathbf{0.15}$ and iteration steps $\mathit{n}\mathbf{=}\mathbf{250}$ .

Table 1 The sequence values on each different iteration step