1 Introduction

In order to mitigate and balance the impacts of climate change and to achieve sustainable management of forests it is essential to protect existing carbon pools and increase existing carbon sink. In this context, Reducing Emissions from Deforestation and Forest Degradation (REDD +), an initiative of United Nations Framework Convention on Climate Change (UNFCCC) has been designed as an economic incentive focusing on maintaining carbon (C) storage in the tropical forests of developing nations (Gibbs et al. 2007; Ganaméa et al. 2021). As recommended by IPCC (intergovernmental panel on climate change) the faithful execution of REDD + requires precise quantification of carbon storage potential through the monitoring, reporting and verification (MRV) strategies (Gibbs et al. 2007; Vashum and Jayakumar 2012; Ganaméa et al. 2021).

It is widely recognized that the tropical forests play a vital role in mitigating global climate change issues through acting as carbon sinks due to its 50% global carbon stock and one third global primary productivity (Pan et al. 2011; Baccini et al. 2017; Daba and Soromessa 2019). For the sustainable management of these tropical forest, estimation of carbon stock and biomass (above and belowground) is a crucial biophysical constraint, which provides information about growth, health and productivity of forest ecosystem (Ediriweera et al. 2014; Luo et al. 2017). However, the information related to carbon stock and biomass for many tropical forests is uncertain due to various methodologies as well as site specific (phytogeographic/ physiographic) allometric equations (Henry et al. 2011; Chave et al. 2014).

That the regional estimations are also sporadic with research gaps has been well noticed (Hertel et al. 2009; Djomo et al. 2011). At spatial scale, several researchers found uncertainties in carbon sinks/stocks of tropical forest ecosystems, which may be due to type of forest, level of anthropogenic disturbance, topographic variation and microclimate (Gandhi and Sundarapandian 2017; Naveenkumar et al. 2017). Field-based biomass estimates are vigorous for carbon stock/sink related studies as they provide significant inputs for data-deficient regional and global carbon and climate models (Behera et al. 2017; Yu et al. 2022). To estimate the large-scale forest biomass and carbon stock of tropical forests, there is also a need to used improved allometric models through field data accompanied with remote sensing techniques (Chave et al. 2014; Castillo et al. 2017; Raha et al. 2020). Therefore, applying vigorous method for carbon stock and biomass estimation is a key factor for effective execution of forest management, conservation and climate change mitigation strategies (Mani and Parthasarathy 2007; Saatchi et al. 2011). The application of best suited allometric equation is useful not only for local and national forest assessment but also for global carbon balance (Basuki et al. 2009).

The destructive sampling method for forest biomass and carbon stock estimation in India is not always permissible due to the large-scale falling of forest trees (Datta and Chatterjee 2012). Therefore, the estimation of biomass and C stock is mainly based on allometric models, growing stock volume (GSV) data of forest inventories and suitable conversion factor associated to biomass and C (Ravindranath et al. 1997; Lal and Singh 2000; Manhas et al. 2006; Chaturvedi et al. 2011; Dar and Sundarapandian 2015; Salunkhe et al. 2018).

The aboveground biomass (AGB) plays a significant role as an indicator of ecosystem structure and functioning. Therefore, forest carbon stock estimation is mainly based on biomass estimation (Brown S et al., 1997; Chave et al. 2005; Gibbs et al. 2007; Vashum and Jayakumar 2012). However, various earlier studies conveyed significant variations in AGB estimation in tropical dry deciduous forests ecosystems of central India (Pande 2005; Salunkhe et al. 2018; Raha et al. 2020; Jain et al. 2020; Karmakar et al. 2020). These variations are due to the lack of accurate local/regional allometric models and methodology (Mani and Parthasarathy 2007; Vashum and Jayakumar 2012; Chave et al. 2014; Salunkhe et al. 2018). Therefore, applying robust methods for carbon stock estimates is crucial for reliable national ground-based MRV of carbon storage (Balima et al. 2020; Bayen et al. 2016) and the implementation of climate change mitigation strategies such as REDD + (Ganaméa et al. 2021).

In India, maximum carbon stock has been stored in tropical dry deciduous forests (2,177 million tons) followed by tropical moist deciduous forests (1,303 million tons) and tropical semi-evergreen forests (686 million tons) (FSI (Forest Survey of India), 2021). The systematic data on biomass/carbon stocks of various regions and forest types of tropical forest ecosystems of India are sporadic and patchy (Salunkhe et al. 2018). However, most of these studies are limited to mainly tropical rain and temperate ecosystems of India and a very little information is available from dry deciduous forests of western central India (Salunkhe et al. 2016; Raha et al. 2020).

According to Forest Survey of India reports (FSI, 2021), Madhya Pradesh is the state of India having largest forest cover (25.15%) in the country of its total geographical area. Also, it is recorded that 30.72% of its total geographical area is covered by forests, mainly tropical dry deciduous forests. Despite having considerable amount of forest, the data related forest biomass and C stocks of this state is very limited and fragmented. Few studies have been done on central India specially in Madhya Pradesh (Pande 2005; Salunkhe et al. 2014, 2016; Jain et al. 2020; Raha et al. 2020; Karmakar et al. 2020).

The tropical dry deciduous forest of west central India has good diversity and it sturdily contributes to livelihoods of forest dwellers for their daily needs (Manhas et al. 2006). In recent decades the timber and non-timber forest resources have been rapidly depleted from this forest due to the conversion of forest land toagricultural land, development land and other land use change activities (Pande 2005; Manhas et al. 2006; Salunkhe 2016; Raha et al. 2020; Jain et al. 2020). Thus, in this forest the loss of biodiversity and low productivity of various species are increasing rapidly, which ultimately leads towards forest degradation and poor regeneration of important tree species in this forest areas in near future (Manhas et al. 2006; Pande 2005; Bahuguna 2000). These inconsistencies may also result into the spatial distribution of AGB. In the present study we aimed to estimate the amount of carbon stored in the AGB of natural forests of Western central Indian region using two allometric models (Brown et al. 1989; and Chave et al. 2005). Using two different allometric equation approaches we compared and explored stored carbon in Western central India; this is baseline information that will be useful for the application of future forest management and climate change mitigation programs.

2 Methodology

2.1 Description of the study area

Geographically western central Indian region contains most of the part of Nimar region of the state of Madhya Pradesh, India, lying between 21° 50′ 0.6864'' N 75° 36′ 53.9604'' E. The northern part of the region is covered with Vindhyan scabs and Satpura hill in south.

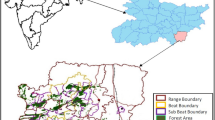
According to Köppen (1936) climate classification system, the climate of the region is type Am (tropical monsoon type) arid and dry, and the maximum-minimum temperature ranges 22° to 48° C while the average annual rainfall varies from about 800 to 1800 mm. The area has dry and hot summer from mid of March to mid of June and monsoon season from July to September, followed by cool and relatively dry winter. 90% of total rainfall receives from rainy months. According to Champion and Seth (1968), the main forest type of this region is tropical dry deciduous forest. The entire area is covered by black cotton soil (Expansive soil). Present carbon stock inventories were carried out in the year of 2021 at seven sites with total 28 selected plots (each site had 4 plots) of tropical dry deciduous forest of Nimar region of Madhya Pradesh, India. The predominant tree species of study area are Tectona grandis, Butea monosperma, Diospyros melanoxylon, Hardwickia binate, Lagerstromia parviflora and Terminalia tomentosa.

2.2 Sampling design

For plot level inventories of AGB/ BGB (belowground biomass)/ C, we laid down one super plot of 250 × 250 m in size at each site (i.e. 7 sites). Within this super plot four sub-sample plots, each 31.6 m × 31.6 m (≅ 0.1 ha) in size in all the four directions i.e. North East (NE), North West (NW), South West (SW) and South East (SE), were laid down. Thus, the total sample size consisted of 7 super plots and 28 sample plots within super plots. During the field visits, toposheets of survey of India and GPS device (Garmin 72) were used to approach the sites. A detail of sampling design at plot level study is presented in Fig. 1.

Fig. 1
figure 1

A detailed sampling design for plot level biomass and carbon estimation

Full size image

2.3 Data collection and observations

To estimate AGB and BGB, a suitable allometric model that expresses aboveground tree biomass as a function of its diameter at breast height (DBH) (Brown et al. 1989; Brown et al. 1997; Woldegerima et al. 2017) was selected and utilized. The ABG and C stock estimation of the present investigation was restricted up to tree level because trees significantly impact the magnitude and pattern of energy that is stored in trunk, branches, leaves and roots (Supriya Devi et al., 2009; Schwerz et al. 2020). At each sample plot those trees having DBH of 10 cm and above (DBH 1.37 m aboveground) were considered for AGB inventory in each sample plot (0.1 ha quadrate) as suggested by Hall et al. (2003). Forked trees were measured as distinct trees underneath the breast-height level (Walker et al. 2016). All species of trees have been classified with their botanical names and distributed to their respective families.

Height and DBH of all trees in four sample plots within each super plot were measured using Blume Leiss Hypsometer (which is based on the trigonometric method) and digital tree caliper (Haglof, Sweden), respectively. All the trees were marked with unique numbers. The identification of tree species was done with the help of herbarium section at Department of Botany, Dr H.S. Gour University, Sagar, India and Flora of Madhya Pradesh (BSI 1993).

The biomass of each tree species for every sample plot was estimated with the help of biomass equations developed by Brown et al. (1989) and Chave et al. (2005) for tropical dry forests. These biomass equations were providing aboveground plant biomass. The equation developed by Chave et al. (2005) needs species-specific gravity, and therefore, data of species-specific gravity of each tree species have been obtained from earlier published literature (Devagiri et al. 2013; Salunkhe et al. 2014; FAO n.d.). Using biomass equation and specific gravity of tree with the help of allometric model, the biomass and carbon content of each tree were calculated. The obtained stem biomass of each tree was then summed up within each plot to obtain the plot-level biomass, which was finally extrapolated into mega-grams per hectare (Mg ha−1). The biomass (above and below ground) of each tree was converted into a hectare with the help of equivalent plot sizes and carbon content was calculated as 47.5% (García et al. 2010).

2.4 Data computation and analysis

The basal area of tree is a main driver for AGB/C estimation, and it was calculated using following formula.

$$\mathrm{Basal area }\left(\mathrm{BA}\right): \mathrm{BA}= \left({\mathrm{\pi D}}^{2}\right) /4$$
(1)

where, BA = Basal area (m2), D = DBH (cm) and π = pi (3.142). The total BA for each plot was obtained by adding the BA of all trees in the plot.

Aboveground biomass (AGB) was estimated using the equation (Eq. 2) developed by Chave et al. (2005) for tropical dry forests, which was also used by various researchers (Sundarapandian et al. 2013; Vivek and Parthasarathy 2015; Djomo et al. 2016; Huy et al. 2016; Sahu et al. 2016).

$${\left(\mathrm{AGB}\right)}_{\mathrm{est}}=\mathrm{p }\times \mathrm{exp}\left({-0.667+1.784\mathrm{In }\left(\mathrm{D}\right) +0.207\left(\mathrm{In }\left(\mathrm{D}\right)\right)}^{2} {- 0.281 \left(\mathrm{In}\left(\mathrm{D}\right)\right)}^{3}\right)$$
(2)

where, AGB = aboveground biomass, p = wood specific gravity, D = Diameter.

Another equation for AGB estimation was (Eq. 3) developed by Brown et al. (1989) for biomass estimation in tropical dry forests which has been used by various researchers in the determination of carbon storage for some developing countries (McHale et al. 2009; Adekunle et al. 2014a; Woldegerima et al. 2017; Srinivas K and Sundarpandian, 2019).

$$\mathrm{AGB }= 34.4703 - 8.0671 \left(\mathrm{D}\right) + 0.6589 \left({\mathrm{D}}^{2}\right)$$
(3)

where, AGB = aboveground biomass per tree (kg), D = DBH (cm).

According to Woldegerima et al. (2017), it is possible to determine BGB by multiplying AGB by a factor of 0.26 based on the root-to-shoot ratio relationship (Ravindranath and Ostwald 2008), as used in the present research (Eq. 4).

$$\mathrm{BGB }=\mathrm{ AGB }\times 0.26$$
(4)

Biomass assessment was used to enumerate the amount of carbon stock and it was calculated with the help of Tang et al. (2016) i.e. Total carbon stock = AGB + BGB. Plant total biomass has direct relationship with the amount of carbon content in wood, and it was noticed that carbon varied between 45 to 50% for various ecosystems and it was assumed that all biomass pool contained 47.5% carbon (García et al. 2010) (Eq. 5).

$$\mathrm{Carbon }\left(\mathrm{C}\right) =\mathrm{ AGB}+\mathrm{BGB }\times 0.475$$
(5)

This carbon was converted to carbon dioxide (CO2) to estimate the amount of carbon sequestrated by the forest (Adekunle et al. 2014a). This correlation is given as: 1 t C = 3.67 t CO2 (NIACS 2008; Ranasinghe DM and Abasari, 2008; Adekunle et al. 2014a; Adekunle et al. 2014b). CO2 sequestered by each forest was quantified by multiplying the carbon stock value by 3.67 i.e. atomic weight difference of C and CO2 (Justine et al. 2015; Timothy et al. 2007).

Statistical analysis: All the data of present investigation were analyzed statistically with the help of SYSTAT version 12 by one-way analysis of variance (ANOVA). Least significant difference (LSD) was used to compare the total biomass and carbon stock from both allometric models.

3 Results

In the present study the number of trees i.e. tree density (ha−1) varied from 176 to 480 trees ha−1 at various studied sites of Nimar region (Table 1). Its maximum number was recorded at Site 2, which was statistically (P < 0.05) at par with all the sites, barring few exceptions, and least at Site 1, which was comparable with Site 5. Values of basal area (m2 ha−1) were consistent with the values on tree density. Site 2 recorded maximum basal area, followed by Site 3, Site 4 and Site 7, and these were comparable with each other. The minimum basal area was recorded at Site 5, closely followed by Site 6.

Table 1 Tree density, basal area, biomass and carbon content of trees at different sites of Nimar region
Full size table

The results of biomass and carbon stock were calculated by Eq. 2 by Chave et al. (2005) and Eq. 3 by Brown et al. (1989). The values on AGB (97.93–52.72 Mg ha−1), BGB (25.46—13.59 Mg ha−1) and total biomass (123.39–65.86 Mg ha−1) using Eq. 2 were comparatively higher than Eq. 3 AGB (86.38–44.37 Mg ha−1), BGB (22.46–11.53 Mg ha−1) and total biomass (108.84–55.91 Mg ha−1). The maximum AGB, BGB and total biomass were recorded at Site 2 which were comparable with Site 3, Site 4, and Site 7, and the minimum at Site 1, followed by Site 5 and Site 6 when the data were calculated by Eq. 2. Similar results were also recorded when data was calculated by Eq. 3. The result obtained from both the equations i.e. Equations 2 and 3 revealed that the maximum carbon content was recorded at Site 2, which was comparable with Site 3, Site 4, and Site 7, and the minimum was recorded at Site 5, which was comparable with Site 6 and Site 7 (Table 1).

When the results of total biomass estimation recorded using Eq. 2 were compared with the Eq. 3 the significant increase in difference was obtained amongst all study sites. At site 1 the highest 17.79% increase was observed followed by site 5 (16.10%), site 3 (15.32%) and site 7 (14.56%) while the lowest increase of 9.64% was observed at site 4 followed by site 6 (12.94%) and site 2 (13.36%) (Table 2). The results clearly showed that the Eq. 2 gives higher estimates of total biomass as compared with Eq. 3 at topical dry deciduous forests of central India (Table 2).

Table 2 Difference in percentage (%) increase in estimation of total biomass by Eq. 2 compared with that by Eq. 3 at different sites of Nimar region
Full size table

The results of site wise carbon dioxide (CO2) stock estimation obtained from Eq. 2 allometric model showed that the total and average CO2 was 1162.33 and 166.04 Mg CO2 ha−1, respectively, while the CO2 stock amongst all study sites varies between 114.79 to 215.09 Mg CO2 ha−1. On the other hand, estimation recorded with the help of Eq. 3 showed that the total and average CO2 was 1019.74 and 145.67 Mg CO2 ha−1, respectively, while CO2 stock varied from 97.43 to 189.73 Mg CO2 ha−1 at different study sites (Table 3).

Table 3 Amount of CO2 (Mg ha−1) content at various study sites estimated with the help of Eq. 2 and 3
Full size table

4 Discussion

Comparisons of local and regional level plant biomass estimations pose a considerable problem due to structural, environmental and compositional gradients (Hans ST et. al., 2000; Malhi et.al., 2002) and it might be misperceived with discrepancy resulting from the use of different equations. The allometric models for biomass estimation are very useful and are accepted worldwide due to their accuracy, applicability and nondestructive processes (Picard et al. 2015). Selection of variables and critical analysis of parameters are very important for accuracy of allometric models (Sileshi 2014; Birigazzi et al. 2015). In the present study we selected only diameter at breast height (DBH) as an independent variable and AGB as the dependent variable.

The aim of present study was to examine, explore and compare the total biomass and C stock content in tropical dry deciduous forests of western central India using two different allometric models established by Chave et al. 2005 (Eq. 2) and Brown et al. 1989 (Eq. 3).

A significant variation was observed in biomass and carbon using both allometric models. Both of the allometric models relied on DHB only, but in Eq. 2 wood density was also added as a variable. Therefore, the resulted values of biomass and carbon stock were higher as compared to Eq. 3. On the basis of various earlier studies (Chave et al. 2005 and Feldpausch et al. 2012), the equation by Chave et al. (2005) equation (DBH and wood specific gravity) in estimating the plant biomass and carbon stock would be better and have higher precision (Devine et al. 2013; Salvaña et al. 2019) than using the equation by Brown et al. 1989, in which the DBH is the only variable included. Because wood specific gravity (WSG) is an important parameter in allometric equations for accurate estimation of carbon stock and C-sequestration and other functional properties of a tree. Therefore, it was widely used in tropical forest biomass estimation (Sheikh et al. 2011; Bastin et al. 2015; Nam et al. 2018; Salvaña et al. 2019; Joshi and Dhyani 2019).

The total and average carbon stock of the study area was 316.72 and 45.24 Mg ha−1 recorded using Eq. 2 allometric model while it was 277.87 and 39.69 Mg ha−1 recorded using Eq. 3 equation. The AGB estimation in the present study ranged from 52.72–97.93 Mg ha−1 by Eq. 2 was higher than Eq. 3 (44.37–86.38 Mg ha−1). The results obtained from both the models were within the ranges (39–334 Mg ha−1) given by Becknell et al. (2012), who obtained the values while reviewing 40 published papers on seasonally dry tropical forests. The carbon stock of present study recorded by Chave et al. 2005 (31.28–58.61 Mg C ha−1) and Brown et al. 1989 (26.55–51.70 Mg C ha−1) was found well within the range of other tropical dry deciduous forests of the world (Murphy and Lugo 1996; Brown and Lugo 1982 and Navar-Chaidez 2011).

Here we also found the close positive relationship between tree density, basal area (BA) and AGB, because the values of AGB will increase with the increase of both. The BA of tree is a most authenticated substitute measure of total biomass estimation in tropical dry forests (Phillips et al. 1998; Murali et al. 2005; Mani and Parthasarathy 2007) and our estimated results also support to these findings.

By this study, it was found out that the tropical dry deciduous forests of central India is an important reservoir of biomass and carbon stock, and can play a significant role in mitigating the global climate change. The site level variations in terms of tree density, basal area, total biomass and carbon stock are primarily affected due to different types of internal as well as external factors like successional stage of forest, species composition, water stress tolerance, rain fall pattern, variability and distribution of species, geographical location and other development as well as anthropogenic activities (Whitmore 1984; Brunig 1983; Terakunpisut et al. 2007).

Thus, knowing to the carbon stock of this forest is important as it contributes to the sustainable management of these forest ecosystems to support the Reducing Emission from Deforestation and Degradation (REDD +) process and is a useful tool in formulating further conservation strategies. The finding also concluded that the Eq. 2 is most suitable of western central Indian tropical dry deciduous forest biomass and carbon stock estimations. A detailed comparison of present investigation with other similar work is difficult due to variation in the method adopted for AGB, BGB and Carbon estimation in different earlier studies.

5 Conclusion

The increased concentration of greenhouse gases into the atmosphere leads to global climate change issues. To mitigate this problem there is an urgent need to focus on studies related to forest biomass and carbon stock estimation of tropical forests of the world. Because it contributes 50% global carbon stocks and one third global primary productivity. The present research investigated the total forest biomass and carbon stock of tropical dry deciduous forests of west central India. Here, we used two types of allometric models which was previously used worldwide (Chave et al. 2005 and Brown et al. 1989) and compared the both models for their best suitable sustainable use for selected forest area of west central India.

Both the models are primarily based on DBH variable but in the model by Chave et al. 2005, the wood specific gravity was also added as a variable. The present and earlier various studies concluded that DBH and wood specific gravity would better estimate the plant biomass and carbon stocks and have higher precision. Therefore, the model having DBH and wood specific gravity will be useful for sustainable estimation of plant biomass and carbon stock in tropical dry deciduous forests of west central India.

The result also indicates the tropical dry deciduous forest of west central India has a good reservoir of plant diversity and carbon stock. We also found the positive relationship between tree diversity and basal area as both increase the biomass and carbon would increase substantially. The present study provided valuable data on forest biomass and carbon stock of woody plant species, thereby accentuating the role of woody plants of tropical dry deciduous forests in carbon sequestration potential. These are baseline data that might attract and help conservation managers, researchers and scientists in understanding the role of tropical dry deciduous forest ecosystems in carbon stocking and sequestration potential.