1 Introduction

In recent years, researchers have shifted their focus to the study of the behavior of nanostructured semiconductors that are currently developed in the semiconductor industry. It has been revealed that some models can simulate solid behaviors when moisture and heat are taken into account. Putting heat, moisture, and elasticity together in a calculation will provide a more realistic analysis of hygro-thermoelasticity. It is possible in engineering and science that moisture content can influence heat conduction in some cases and vice versa. When analyzing problems where the analyzed domain or medium is subject to the effects of temperature and moisture, it is important to consider the analogy and cross-coupling between heat conduction and moisture diffusion. Indeed, the combination of property and structure plays a crucial role in influencing the physical, electronic, and optical properties of nanostructures. Utilizing experimental techniques and computer simulations, researchers have formulated models to investigate the influence of nano-dimension and structural characteristics on the behavior of nanostructures. This enhanced understanding of the properties and behavior of nanostructures has paved the way for novel opportunities in technological applications. Nanostructured materials have found utility in a multitude of fields, encompassing electronics, optoelectronics, catalysis, energy storage, sensors, and biomedical devices. Their exceptional properties render them highly appealing for the development of advanced materials boasting enhanced performance and functionality.

The Green and Naghdi [1,2,3] hypothesis presents a reliable explanation for heat conduction in a variety of solids and liquids. It is important to further our understanding of the effects of diffusion in addition to thermal effects. Diffusion refers to the movement of particles from areas of high concentration to areas of low concentration. Thermo-diffusion occurs in elastic solids when temperatures, mass diffusions, and strains are coupled. Heat and mass transfer processes at high and low temperatures are crucial for many satellite problems, returning spacecraft, and landing on land or water. Integrated circuits are manufactured by introducing controlled amounts of dopants into the semiconductor substrate through diffusion. Bipolar transistor bases and emitters, embedded resistors, source & drain of metal–oxide–semiconductor transistors, and polysilicon gates are also formed through diffusion. Fick's law is often used to calculate concentration in these applications, but it does not take into consideration the introduction of a substance into a medium or its effect on that medium.

Tang and Song [4] conducted a comprehensive examination of the reflection of waves in nonlocal semiconductor rotating media. Their study employed a plasma diffusion equation to analyze this phenomenon. Alshaikh [5],on the other hand, focused on investigating the process of photothermal wave transmission through semiconducting media, taking into account the effects of diffusion and rotation. To establish a stable equilibrium state when encountering sudden temperature variations, Cattaneo [6] and Vernotte [7, 8] proposed the incorporation of a relaxation time into the heat flux vector:

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right){\varvec{q}}=-K\nabla \mathrm{T}.$$
(1)

Green and Naghdi [1,2,3] have made significant contributions to the field of thermo-elasticity, particularly in the areas of energy dissipation and the absence thereof. Their work has also led to advancements in the understanding of Fourier's law

$$q=-K\nabla \mathrm{T}-{K}^{*}\nabla \vartheta ,\dot{\vartheta }=T.$$
(2)

Numerous academic inquiries have been undertaken in recent times to explore the Moore-Gibson-Thompson equation (MGT). Quintanilla [9, 10] employed the MGT equation with 2 T to formulate a novel heat conduction model. Lasiecka and Wang [11] elucidate fluid dynamics through the utilization of a third-order differential equation. The Modified Fourier law, also known as the MGT equation, can be expressed as follows:

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right){\varvec{q}}=-K\nabla \mathbf{T}-{K}^{*}\nabla \boldsymbol{\vartheta },$$
(3)

\(\mathrm{where }\dot{\vartheta }=T.\) In the case of semiconductor materials exhibiting plasma effect, it is possible to formulate a generalized Fourier law as follows:

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right){\varvec{q}}=-K\nabla \mathrm{T}-{K}^{*}\nabla \vartheta -\int \frac{{E}_{g}{\varvec{N}}}{\tau }d{\varvec{x}},$$
(4)

\(\mathrm{ where }\dot{\vartheta }=T.\) In Eq. (4), the final term signifies the photo-excitation effect. Upon differentiating Eq. (4) with respect to \(x\), the outcome is

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\nabla .{\varvec{q}}=-\nabla .\left(K\nabla \mathrm{T}+{K}^{*}\nabla \vartheta \right)-\frac{{E}_{g}{\varvec{N}}}{\tau }, \mathrm{where} \dot{\vartheta }=T.$$
(5)

Hence

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\nabla .\dot{{\varvec{q}}}=-\nabla .\left(K\nabla \dot{\mathrm{T}}+{K}^{*}\nabla T\right)-\frac{{E}_{g}\dot{{\varvec{N}}}}{\tau },$$
(6)

where

$${q}_{i,i}=\left[\rho \mathrm{Q}-{\rho C}_{E}\dot{\mathrm{T}}-{\beta }_{ij}{T}_{0}{\dot{\mathrm{e}}}_{ij}\right].$$
(7)

Hence above equation becomes,

$$\nabla .\left(K\nabla \dot{\mathrm{T}}+{K}^{*}\nabla T\right)+\frac{{E}_{g}\dot{{\varvec{N}}}}{\tau }=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[{\rho C}_{E}\ddot{\mathrm{T}}+{\beta }_{ij}{T}_{0}\mathrm{\ddot{e} }ij-\rho \dot{Q}\right].$$
(8)

By employing Fourier's law, it is possible to express the heat flux in conduction in the following manner:

$${q}^{F}=-{D}_{T}{T}_{,i}.$$
(9)

The moisture flux potential can be defined by employing Fick's law as:

$${f}^{F}=-{D}_{m}{m}_{,i}.$$
(10)

Numerous experiments have revealed a significant correlation between moisture transport and the temperature field, and vice versa. The presence of moisture concentration gradients gives rise to heat fluxes, commonly referred to as Dufour fluxes. These fluxes can be precisely defined as follows [12,13,14]:

$${q}^{D}=-{D}_{T}^{m}{m}_{,i}.$$
(11)

The potential of moisture flux, commonly referred to as the Soret flux, may be influenced by variations in temperature gradients:

$${f}^{S}=-{\mathrm{D}}_{\mathrm{m}}^{\mathrm{T}}{T}_{,i}.$$
(12)

Heat and moisture flux potentials can be derived based on the coupled diffusion of heat and moisture as

$$q={q}^{F}+{q}^{D}=-{D}_{T}{T}_{,i}-{D}_{T}^{m}{m}_{,i}$$
(13)
$$f={f}^{F}+{f}^{S}=-{D}_{m}{m}_{,i}-{\mathrm{D}}_{\mathrm{m}}^{\mathrm{T}}{T}_{,i}.$$
(14)

The aforementioned cross-coupling enables the potential influence of material elastic properties on the temperature and moisture concentration field. By integrating the generalized equations of motion with the coupled generalized equations of heat conduction and moisture diffusion, the phenomenon of coupled hygro-thermoelasticity [12,13,14] can be accurately described using these governing equations as

$${\sigma }_{ij,j}+ {F}_{i}= \rho \left({\ddot{u}}_{i}\right)$$
(15)
$${D}_{T}{T}_{,ii}+{D}_{T}^{m}{m}_{,ii}-\dot{T}-\frac{{\beta }_{ij}^{T}{T}_{0}}{\rho {C}_{E}}{\dot{u}}_{j,j}=0$$
(16)
$${D}_{m}{m}_{,ii}+{\mathrm{D}}_{\mathrm{m}}^{\mathrm{T}}{T}_{,ii}-\dot{m}-\frac{{\beta }_{ij}^{m}{m}_{0}{D}_{m}}{{K}_{m}}{\dot{u}}_{j,j}=0,$$
(17)

where

$${\beta }_{ij}^{T}={\beta }_{T}{\delta }_{ij},{\beta }_{T}=\left(3\lambda +2\mu \right){\alpha }_{T}$$
(18)
$${\beta }_{ij}^{m}={\beta }_{m}{\delta }_{ij},{\beta }_{m}=\left(3\lambda +2\mu \right){\alpha }_{m}.$$
(19)

The stress–strain constitutive equation can be found as

$${\sigma }_{ij}={C}_{ijkl}{e}_{kl}-{\beta }_{ij}^{m}m-{\beta }_{ij}^{T}T.$$
(20)

The terms \({\beta }_{ij}^{m}={\beta }^{m}{\delta }_{ij}\) and \({\beta }_{ij}^{T}={\beta }^{T}{\delta }_{ij}\) are material coefficients responsible for coupling between the stresses and the moisture concentration or temperature fields, respectively.

El-Sapa et al. [15] have analyzed the one-dimensional photothermal MGT using moisture diffusivity to study moisture and heat equations. Hosseini and Ghadiri [16] have developed a model to investigate the propagation of moisture and thermoelastic waves under shock loading. Aouadi et al. [17] have presented a nonlinear theory of thermoelasticity involving diffusion by applying the Green-Naghdi types II and III theories of thermomechanics of continua. Lotfy et al. [18] have investigated a general solution to the problem of wave propagation under H2T theory in a generalized piezo-photo-thermoelastic medium. Alhashash et al. [19] have proposed a mathematical-physical model based on a two-temperature thermoelasticity theory to describe the influence of moisture diffusivity on semiconductor materials. Lotfy et al. [20] have developed a novel stochastic photo-thermoelasticity model by utilizing diffusion interaction processes within an excited semiconductor medium. Lotfy and Tantawi [21] have undertaken a comprehensive investigation of the intricate relationship between thermoelasticity theory and photothermal theory in a semiconductor, widely recognized as photo-thermoelasticity theory. The photothermal diffusion process is employed by Lotfy [22] to investigate the variable thermal conductivity of semiconductor samples by leveraging the temperature gradient. A thorough investigation has been carried out by Allam [23] regarding a matter concerning the theory of generalized thermoelastic diffusion, with a specific emphasis on the impact of an additive Gaussian white noise.

In addition to the aforementioned studies, it is worth noting that other researchers have also conducted investigations on semiconductor media, similar to the works of Kaur et al.[24,25,26,27,28], Lotfy et al. [29], Craciun et al.[30, 31], Lata et al. [32], Jafari et al. [33], Kaur and Singh[34,35,36], Lotfy and Hassan[37], Craciun et al.[38], Malik et al. [39]. However, it is important to highlight that no research has been conducted on the transient investigation of moisture and thermal diffusivity in a semiconducting solid cylinder within the context of the MGTPT thermoelasticity theory. Therefore, our study aims to explore the photo-thermoelasticity of an infinite semiconducting solid cylinder that is rotating, with the boundary surface being subjected to a laser pulse with a variable heat flux. To solve the proposed mathematical model, we employ the Laplace transform in a transformed domain.

Section 1 presents an overview of the development of the MGTPT heat transfer theory, specifically focusing on the GN III model with considerations for moisture and thermal diffusivity. Section 2 highlights the formulation of the equation of motion and the Modified MGT heat conduction equation for semiconducting mediums, incorporating moisture diffusion. In Sect. 3, the mathematical formulation of the research on semiconductor cylinders is outlined, utilizing the MGTPT heat transfer equation. This formulation allows for the derivation of dimensionless expressions for displacement, stress components, and moisture in the transformed domain through the application of Laplace Transforms. Section 4 examines the boundary conditions for the outer surface of the cylinder, which are influenced by time-dependent variable heat. Sections 5 and 6 provide the solution to the problem and explain the method for performing the inverse Laplace Transform. In Sect. 7, the numerical results and the impact of different thermoelasticity theories and Hall current on physical quantities are visually presented using MATLAB software. Finally, Sect. 8 concludes the paper.

2 Basic equations

The governing equations [40,41,42] for a MGTPT with thermal-plasma-elastic interaction is given by:

1. Constitutive relations

$${\sigma }_{ij}= \left(\lambda {u}_{k,k}-{\beta }^{T}T-{\beta }^{m}\mathrm{m}-{\delta }_{n}N\right){\delta }_{ij}+\mu \left({u}_{i,j}+{u}_{j,i}\right),$$
(21)
$${\beta }^{T}=\left(3\lambda +2\mu \right){\alpha }_{T},$$
(22)
$${\beta }^{m}=\left(3\lambda +2\mu \right){\alpha }_{m},$$
(23)
$${\delta }_{n}=\left(3\lambda +2\mu \right).$$
(24)

2. Equation of motion

$${\sigma }_{ij,j}+ {F}_{i}= \rho \left({\ddot{u}}_{i}\right).$$
(25)

3. Plasma diffusion equation

$$\frac{\partial N}{\partial t}=\left({D}_{E}{\nabla }^{2}{\varvec{N}}-\frac{{\varvec{N}}}{\tau }\right)+\kappa T,$$
(26)
$$\kappa =\frac{T}{\tau }\frac{\partial {N}_{0}}{\partial T}.$$
(27)

4. The equation of moisture diffusion for coupled hygro-photo-thermoelasticity is given by

$$\left[{D}_{m}{\left({\dot{m}}_{,j}\right)}_{,i}+{D}_{m}^{*}{\left({m}_{,j}\right)}_{,i}\right]+{D}_{m}^{T}{T}_{,ij}+\frac{{E}_{g}\dot{{\varvec{N}}}}{\tau {K}_{m}}=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}m}{\partial {t}^{2}}+\frac{{\beta }_{ij}^{m}{m}_{0}{D}_{m}\mathrm{\ddot{e} }ij}{{K}_{m}}\right].$$
(28)

5. Modified MGT heat conduction equation for coupled hygro-photo-thermoelasticity [12,13,14]

$$\left[{D}_{T}{\left({\dot{T}}_{,j}\right)}_{,i}+{D}_{T}^{*}{\left({T}_{,j}\right)}_{,i}\right]+{D}_{T}^{m}{m}_{,ij}+\frac{{E}_{g}\dot{{\varvec{N}}}}{\tau {\rho C}_{E}}=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[\ddot{\mathrm{T}}+\frac{{\beta }_{ij}^{T}{T}_{0}}{{\rho C}_{E}}\mathrm{\ddot{e} }ij\right],$$
(29)
$${D}_{T}{\rho C}_{E}=K,{\rho C}_{E}{D}_{T}^{*}= {\mathrm{K}}^{*},$$
(30)

\(i\) is not summed.

Also, the subscript followed by ‘,’ a comma denotes the partial derivative w.r.t. space coordinates and a superposed ‘.’ signifies differentiation w.r.t. time variable \(t\).

3 Mathematical model

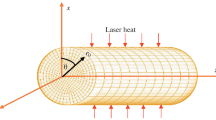
The semiconductor solid cylinder under consideration possesses the desirable qualities of symmetry, thermal homogeneity, and a radius of \({r}_{0}\). To heat the exterior of the cylinder, an external laser pulse heating device has been employed. Our analysis has been conducted with the \(z\)-axis aligned parallel to the cylinder axis, and a cylindrical coordinate system \(\left(r,\theta ,z\right)\) has been utilized, see Fig. 1. The initial temperatures of the cylinder, denoted as \({T}_{0}\), have been maintained at a constant and uniform.

Fig. 1
figure 1

Structure of problem

Full size image

In addition, it is important to note that, in accordance with the regularity criterion, all fields within a medium are presumed to possess finite characteristics. Moreover, when considering the functions under examination, it is crucial to acknowledge their dependence on both the radial distance \(r\) and time \(t\), particularly in the context of a one-dimensional problem where symmetry is a prevailing factor. Consequently, the expressions representing the relationships between displacement–strain and displacement components can be formulated as follows:

$${\varvec{u}}=\left(u,\mathrm{0,0}\right)\left(r,t\right),$$
(31)
$${e}_{rr}=\frac{u}{r},{e}_{\theta \theta }=\frac{\partial u}{\partial r},{e}_{r\theta }={e}_{rz}={e}_{\theta z}={e}_{zz}=0.$$
(32)

The Eq. (21) using (31) will be the form

$${\sigma }_{rr}=2\mu \frac{\partial u}{\partial r}+\lambda e-\left({\beta }^{T}T+{\beta }^{m}\mathrm{m}+{\delta }_{n}N\right),$$
(33)
$${\sigma }_{\theta \theta }=2\mu \frac{u}{r}+\lambda e-\left({\beta }^{T}T+{\beta }^{m}\mathrm{m}+{\delta }_{n}N\right),$$
(34)
$${\sigma }_{zz}=\lambda e-\left({\beta }^{T}T+{\beta }^{m}\mathrm{m}+{\delta }_{n}N\right),$$
(35)
$${\nabla }^{2}=\frac{{\partial }^{2}}{\partial {r}^{2}}+\frac{1}{r}\frac{\partial }{\partial r}\,and\,{e }_{kk}=e= \frac{1}{r}\frac{\partial \left(ru\right)}{\partial r}.$$
(36)

Hence, the dynamic motion equation becomes

$$\frac{\partial {\sigma }_{rr}}{\partial r}+\frac{1}{r}\left({\sigma }_{rr}-{\sigma }_{\theta \theta }\right)=\rho \left(\frac{{\partial }^{2}u}{\partial {t}^{2}}\right).$$
(37)

Using Eqs. (33–36), in Eqs. (37) yields:

$$\left(\lambda +2\mu \right)\frac{\partial }{\partial r}\left(\frac{1}{r}\frac{\partial \left(ru\right)}{\partial r}\right)-{\beta }^{T}\frac{\partial T}{\partial r}-{\beta }^{m}\frac{\partial m}{\partial r}-{\delta }_{n}\frac{\partial N}{\partial r}=\rho \left(\frac{{\partial }^{2}u}{\partial {t}^{2}}\right).$$
(38)

Also, Eqs. (26), (28), and (29) can be written as,

$$\frac{\partial N}{\partial t}=\left({D}_{E}\left({\nabla }^{2}N\right)-\frac{N}{\tau }\right)+\kappa T,$$
(39)
$${K}_{m}\left[{D}_{m}\frac{\partial }{\partial t}{\nabla }^{2}m+{D}_{m}^{*}{\nabla }^{2}m\right]+{K}_{m}{D}_{m}^{T}{\nabla }^{2}\mathrm{T}=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[{K}_{m}\frac{{\partial }^{2}m}{\partial {t}^{2}}+{\beta }^{m}{m}_{0}{D}_{m}\frac{{\partial }^{2}e}{\partial {t}^{2}}\right],$$
(40)
$$K\frac{\partial }{\partial t}{\nabla }^{2}T+{K}^{*}{\nabla }^{2}T+{\rho C}_{E}{D}_{T}^{m}{\nabla }^{2}\mathrm{m}+\frac{{E}_{g}\dot{N}}{\tau }=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[{\rho C}_{E}\frac{{\partial }^{2}T}{\partial {t}^{2}}+{\beta }^{T}{T}_{0}\frac{{\partial }^{2}e}{\partial {t}^{2}}\right].$$
(41)

Pre-operating both sides of Eq. (38) by \(\left(\frac{1}{r}+\frac{\partial }{\partial r}\right),\) we obtain

$$\left(\lambda +2\mu \right){\nabla }^{2}e-{\beta }^{T}{\nabla }^{2}T-{\beta }^{m}{\nabla }^{2}\mathrm{m}-{\delta }_{n}{\nabla }^{2}N=\left(\frac{{\partial }^{2}e}{\partial {t}^{2}}\right).$$
(42)

The subsequent dimensionless quantities are used to convert the aforementioned equations into dimensionless form:

$${(r}^{\mathrm{^{\prime}}},{u}^{\mathrm{^{\prime}}})={v}_{0}\eta \left(r,u\right), \left({T}^{\mathrm{^{\prime}}},{N}^{\mathrm{^{\prime}}},{\sigma }_{ij}^{\mathrm{^{\prime}}},m{\prime}\right)=\frac{1}{\rho {v}_{0}^{2}} \left({\beta }^{T}T,{\delta }_{n}N,{\sigma }_{ij},{\beta }^{m}\mathrm{m}\right),{(\tau }_{0}^{\mathrm{^{\prime}}},{\tau }^{\mathrm{^{\prime}}},{t}^{\mathrm{^{\prime}}})={v}_{0}^{2}\eta {(\tau }_{0},\tau ,t),{\mathrm{a}}^{\mathrm{^{\prime}}}=\frac{a}{{\eta }^{2}},\eta =\frac{\rho {C}_{E}}{K},\rho {v}_{0}^{2}=\lambda +2\mu ,\gamma =\sqrt{\frac{\mu }{\lambda +2\mu }}.$$
(43)

Applying (43) to Eqs. (39–42) and suppressing the primes, yields

$${\nabla }^{2}\mathrm{e}-{\nabla }^{2}T-{\nabla }^{2}m-\left({\nabla }^{2}N\right)=\left(\frac{{\partial }^{2}e}{\partial {t}^{2}}\right),$$
(44)
$$\frac{\partial N}{\partial t}=\left({\delta }_{1}\left({\nabla }^{2}N\right)-{\delta }_{2}N\right)+{\delta }_{3}T,$$
(45)
$$\left[\frac{\partial }{\partial t}{\nabla }^{2}m+{\delta }_{7}{\nabla }^{2}m\right]+{\delta }_{8}{\nabla }^{2}T+{\delta }_{9}\frac{\partial N}{\partial t}=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[{\delta }_{10}\frac{{\partial }^{2}m}{\partial {t}^{2}}+{\delta }_{11}\frac{{\partial }^{2}e}{\partial {t}^{2}}\right],$$
(46)
$$\frac{\partial }{\partial t}{\nabla }^{2}T+{\delta }_{4}{\nabla }^{2}T+{\delta }_{12}{\nabla }^{2}\mathrm{m}+{\delta }_{5}\frac{\partial N}{\partial t}=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[{\delta }_{13}\frac{{\partial }^{2}T}{\partial {t}^{2}}+{\delta }_{6}\frac{{\partial }^{2}e}{\partial {t}^{2}}\right],$$
(47)

where,

$${\delta }_{1}={D}_{E}\eta ,{\delta }_{2}=\frac{1}{\tau },{\delta }_{3}=\frac{\kappa {\delta }_{n}}{{\beta }^{T}},{\delta }_{4}=\frac{{K}^{*}}{\left(\lambda +2\mu \right){C}_{E}},{\delta }_{5}=\frac{{\beta }^{T}{E}_{g}}{{\delta }_{n}{C}_{E}\left(\lambda +2\mu \right)\eta \tau }, { \delta }_{6}=\frac{{\left({\beta }^{T}\right)}^{2}{T}_{0}}{\rho {C}_{E}\left(\lambda +2\mu \right)},{\delta }_{7}=\frac{{D}_{m}^{*}}{{\upsilon }_{0}^{2}\eta {K}_{m}{D}_{m}},{\delta }_{8}=\frac{{\beta }^{m}{D}_{m}^{T}}{{\upsilon }_{0}^{2}\eta {D}_{m}}, {\delta }_{9}=\frac{{E}_{g}{\beta }^{m}}{\tau {\upsilon }_{0}^{2}{\eta }^{2}{\delta }_{n}{K}_{m}{D}_{m}},{\delta }_{10}=\frac{1}{\eta {D}_{m}},{\delta }_{11}=\frac{{\left({\beta }^{m}\right)}^{2}{m}_{0}}{\rho {\nu }_{0}^{2}\eta {K}_{m}},{\delta }_{12}=\frac{{\beta }^{T}{D}_{T}^{m}}{{\upsilon }_{0}^{4}{\eta }^{2}}, {\delta }_{13}=\frac{{\beta }^{T}}{\left(\lambda +2\mu \right)}.$$

Using Eq. (43) in Eqs. (33–35) and after suppressing the primes, yields

$${\sigma }_{rr}=2{\gamma }^{2}\frac{\partial u}{\partial r}+\left(1-2{\gamma }^{2}\right)e-\left(T+N+m\right),$$
(48)
$${\sigma }_{\theta \theta }=2{\gamma }^{2}\frac{u}{r}+\left(1-2{\gamma }^{2}\right)e-\left(T+N+m\right),$$
(49)
$${\sigma }_{zz}=\left(1-2{\gamma }^{2}\right)e-\left(T+N+m\right).$$
(50)

Initial conditions are assumed as

$$u\left(r,0\right)=0=\frac{\partial u}{\partial r}\left(r,0\right)$$
(51)
$$T\left(r,0\right)=0=\frac{\partial T}{\partial r}\left(r,0\right)$$
(52)
$$N\left(r,0\right)=0=\frac{\partial N}{\partial r}\left(r,0\right), m\left(r,0\right)=0=\frac{\partial m}{\partial r}\left(r,0\right).$$
(53)

The Laplace transform of a function \(f\) w.r.t. time variable t, is defined as

$$\mathcal{L}\left(f\left(t\right)\right)=\overline{f }\left(s\right)= \underset{0}{\overset{\infty }{\int }}f\left(t\right){e}^{-st}dt.$$
(54)

Using Laplace transforms from Eq. (54) to Eqs. (44–47) yields

$$\left({\nabla }^{2}-{s}^{2}\right)\overline{e }-{\nabla }^{2}\overline{T }-{\nabla }^{2}\overline{m }-{\nabla }^{2}\overline{N }=0,$$
(55)
$$\left({\delta }_{1}{\nabla }^{2}-{\delta }_{14}\right)\overline{N }+{\delta }_{3}\overline{T }=0,$$
(56)
$${\delta }_{18}\overline{e }+\left({\delta }_{19}{\nabla }^{2}+{\delta }_{20}\right)\overline{m }+{\delta }_{8}{\nabla }^{2}\overline{T }+{\delta }_{9}s\overline{N }=0,$$
(57)
$${\delta }_{15}\overline{e }+\left({\delta }_{17}{\nabla }^{2}+{\delta }_{16}\right)\overline{T }+\mathrm{s}{\delta }_{5}\overline{N }+{\delta }_{12}{\nabla }^{2}\overline{m }=0,$$
(58)

where

$${\delta }_{14}={\delta }_{2}+s,{\delta }_{15}=-\left(1+{\tau }_{0}s\right){\delta }_{6}{s}^{2},$$
$${\delta }_{16}=-\left(1+{\tau }_{0}s\right){\delta }_{13}{s}^{2},{\delta }_{17}=\left(s+{\delta }_{4}\right).$$
$${\delta }_{18}=-\left(1+{\tau }_{0}s\right){\delta }_{11}{s}^{2},{\delta }_{19}=s+{\delta }_{7},{\delta }_{20}=-\left(1+{\tau }_{0}s\right){\delta }_{10}{s}^{2}.$$

Using Laplace transforms defined by Eqs. (54) to Eqs. (55–58), we obtain

$$\overline{{\sigma }_{rr}}=2{\gamma }^{2}\frac{\partial \overline{u}}{\partial r }+\left(1-2{\gamma }^{2}\right)\overline{e }-\left(\overline{T }+\overline{N }+\overline{m }\right),$$
(59)
$$\overline{{\sigma }_{\theta \theta }}=2{\gamma }^{2}\frac{\overline{u}}{r }+\left(1-2{\gamma }^{2}\right)\overline{e }-\left(\overline{T }+\overline{N }+\overline{m }\right),$$
(60)
$$\overline{{\sigma }_{zz}}=\left(1-2{\gamma }^{2}\right)\overline{e }-\left(\overline{T }+\overline{N }+\overline{m }\right).$$
(61)

When Eqs. (55–58) are decoupled, we get

$$\left({\nabla }^{8}+B{\nabla }^{6}+C{\nabla }^{4}+D{\nabla }^{2}+E\right)\left(\overline{e },\overline{\varphi },\overline{m },\overline{N }\right)=0,$$
(62)
$$A={\delta }_{1}{\delta }_{18}{\delta }_{12}{s}^{4}-{\delta }_{1}{\delta }_{19}{\delta }_{15}{s}^{4},$$
$$B=\left(-{\delta }_{1}{\delta }_{20}{\delta }_{17}{s}^{4}-{\delta }_{1}{\delta }_{19}{\delta }_{16}{s}^{4}-{\delta }_{1}{\delta }_{8}{\delta }_{12}{s}^{4}-{\delta }_{1}{\delta }_{19}{\delta }_{17}{s}^{6}-{\delta }_{1}{\delta }_{18}{\delta }_{12}{s}^{4}-{\delta }_{1}{\delta }_{19}{\delta }_{15}{s}^{4}-{\delta }_{1}{\delta }_{17}{\delta }_{18}{s}^{2}-{\delta }_{14}{\delta }_{8}{\delta }_{12}{s}^{4}+{\delta }_{14}{\delta }_{19}{\delta }_{17}{s}^{4}\right)/A,$$
$$C = \begin{array}{*{20}l} {(\delta _{5} \delta _{{19}} \delta _{3} s^{5} - \delta _{3} \delta _{{12}} \delta _{9} s^{5} - \delta _{{18}} \delta _{{12}} \delta _{3} s^{4} + \delta _{{15}} \delta _{{19}} \delta _{3} s^{4} - \delta _{1} \delta _{{20}} \delta _{{16}} s^{4} - \delta _{1} \delta _{{20}} \delta _{{17}} s^{4} } \\ { - \delta _{1} \delta _{{19}} \delta _{{16}} s^{4} - \delta _{1} \delta _{{20}} \delta _{{15}} s^{4} - \delta _{1} \delta _{{18}} \delta _{{16}} s^{2} - \delta _{1} \delta _{8} \delta _{{15}} s^{2} + \delta _{{14}} \delta _{{20}} \delta _{{17}} s^{4} + \delta _{{14}} \delta _{{19}} \delta _{{16}} s^{4} + } \\ {\delta _{{14}} \delta _{8} \delta _{{12}} s^{6} - \delta _{{14}} \delta _{{19}} \delta _{{17}} s^{6} - \delta _{{14}} \delta _{{18}} \delta _{{12}} s^{4} + \delta _{{14}} \delta _{{15}} \delta _{{19}} s^{4} + \delta _{{14}} \delta _{{18}} \delta _{{17}} s^{2} )/A} \\ \end{array}$$
$$D = \begin{array}{*{20}l} \begin{gathered} ( - \delta _{5} \delta _{{19}} \delta _{3} s^{5} + \delta _{{20}} \delta _{5} \delta _{3} s^{5} + \delta _{{12}} \delta _{9} \delta _{3} s^{5} + \delta _{{18}} \delta _{5} \delta _{3} s^{3} \hfill \\ - \delta _{{15}} \delta _{9} \delta _{3} s^{3} + \delta _{{15}} \delta _{{20}} \delta _{3} s^{4} - \delta _{1} \delta _{{20}} \delta _{{16}} s^{4} + \delta _{{14}} \delta _{{16}} \delta _{{20}} s^{4} \hfill \\ \end{gathered} \\ { - \delta _{{14}} \delta _{{19}} \delta _{{16}} s^{4} + \delta _{{14}} \delta _{{15}} \delta _{{20}} s^{4} + \delta _{{14}} \delta _{{18}} \delta _{{16}} s^{2} + \delta _{{14}} \delta _{8} \delta _{{15}} s^{2} - \delta _{{14}} \delta _{{20}} \delta _{{17}} s^{4} )/A} \\ \end{array}$$
$$E=\frac{\left(-{\delta }_{5}{\delta }_{20}{\delta }_{3}{s}^{7}-{\delta }_{14}{\delta }_{20}{\delta }_{16}{s}^{6}\right)}{A}.$$

Let \({\lambda }_{i}\), \(i=\mathrm{1,2},\mathrm{3,4}\) be roots of Eq. (62), so we can write

$$\left({\nabla }^{2}-{\lambda }_{1}^{2}\right)\left({\nabla }^{2}-{\lambda }_{2}^{2}\right)\left({\nabla }^{2}-{\lambda }_{3}^{2}\right)\left({\nabla }^{2}-{\lambda }_{4}^{2}\right)\left(\overline{e },\overline{T },\overline{m },\overline{N }\right)=0,$$
(63)

where \({\lambda }_{i}^{2},i=\mathrm{1,2},\mathrm{3,4}\) are the roots of the characteristic equation of Eq. (62)

$$\left({\lambda }^{8}+B{\uplambda }^{6}+C{\uplambda }^{4}+D{\lambda }^{2}+E\right)=0.$$
(64)

The general solution of Eq. (63) can be written in the form

$$\left(\overline{e },\overline{T },\overline{m },\overline{N }\right)=\sum_{i=1}^{4}\left(1,{\zeta }_{i},{\eta }_{i},{\omega }_{i}\right){g}_{i}{I}_{0}\left({\lambda }_{i}r\right),$$
(65)

where \({I}_{0}\)() specifies the 2.nd form of modified ns of order zero. We get the subsequent expressions by introducing Eq. (65) into Eqs. (55–58)

$${\zeta }_{i}=\frac{\left({\lambda }_{i}^{2}-1\right){s}^{2}\left[\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right){\delta }_{5}s-{\delta }_{9}{\delta }_{12}s{\lambda }_{i}^{2}\right]+{\lambda }_{i}^{2}\left({\delta }_{5}{\delta }_{18}s-{\delta }_{15}{\delta }_{9}s\right)-{\lambda }_{i}^{2}{s}^{2}\left[{\delta }_{18}{\delta }_{12}{\lambda }_{i}^{2}-{\delta }_{15}\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right)\right]}{\left({\delta }_{3}\right)\left[\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right){\delta }_{5}s-{\delta }_{9}{\delta }_{12}s{\lambda }_{i}^{2}\right]+\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{14}\right){s}^{2}\left({\delta }_{8}{\delta }_{12}{\lambda }_{i}^{4}-\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right)\left({\delta }_{17}{\lambda }_{i}^{2}+{\delta }_{16}\right)\right)},$$
(66)
$${\eta }_{i}=\frac{\left({\lambda }_{i}^{2}-1\right){s}^{2}\left[\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right){\delta }_{5}s-\left({\delta }_{17}{\lambda }_{i}^{2}+{\delta }_{16}\right)\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{14}\right){s}^{2}\right]+{\delta }_{15}\left[\left(-{\lambda }_{i}^{2}{s}^{2}\right)\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{14}\right){s}^{2}+{\lambda }_{i}^{2}{s}^{2}\left({\delta }_{3}{s}^{2}\right)\right]}{\left({\delta }_{3}\right)\left[\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right){\delta }_{5}s-{\delta }_{9}{\delta }_{12}s{\lambda }_{i}^{2}\right]+\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{14}\right){s}^{2}\left({\delta }_{8}{\delta }_{12}{\lambda }_{i}^{4}-\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right)\left({\delta }_{17}{\lambda }_{i}^{2}+{\delta }_{16}\right)\right)},$$
(67)
$${\omega }_{i}=\frac{\left({\delta }_{3}{s}^{2}\right)\left[\left({\lambda }_{i}^{2}-1\right){s}^{2}\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right)+{\delta }_{18}{\lambda }_{i}^{2}\right]}{\left({\delta }_{3}\right)\left[\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right){\delta }_{5}s-{\delta }_{9}{\delta }_{12}s{\lambda }_{i}^{2}\right]+\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{14}\right){s}^{2}\left({\delta }_{8}{\delta }_{12}{\lambda }_{i}^{4}-\left({\delta }_{19}{\lambda }_{i}^{2}+{\delta }_{20}\right)\left({\delta }_{17}{\lambda }_{i}^{2}+{\delta }_{16}\right)\right)}.$$
(68)

In the domain of the Laplace transform, the displacement u may be expressed as follows:

$$\overline{u }=\sum_{i=1}^{4}\frac{1}{{\lambda }_{i}}{g}_{i}{I}_{1}\left({\lambda }_{i}r\right),$$
(69)

where \({I}_{1}\)() specifies the 2nd form of modified Bessel functions of order one. We obtained Eq. (69) using Bessel function relation

$$\int x{I}_{0}\left(x\right)dx=x{I}_{1}\left(x\right).$$
(70)

Differentiating Eq. (69) in terms of r gives

$$\frac{\partial \overline{u}}{\partial r }=\sum_{i=1}^{4}{g}_{i}\left[{I}_{0}\left({\lambda }_{i}r\right)-\frac{1}{{\lambda }_{i}r}{I}_{1}\left({\lambda }_{i}r\right)\right].$$
(71)

As a result, the expression for thermal stress in closed form is obtained as follows:

$$\overline{{\sigma }_{rr}}=\sum_{i=1}^{4}{g}_{i}\left\{{p}_{i}{I}_{0}\left({\lambda }_{i}r\right)-\frac{2{\gamma }^{2}}{{\lambda }_{i}r}{I}_{1}\left({\lambda }_{i}r\right)\right\},$$
(72)
$$\overline{{\sigma }_{\theta \theta }}=\sum_{i=1}^{4}{g}_{i}\left\{\frac{2{\gamma }^{2}}{{\lambda }_{i}r}{I}_{1}\left({\lambda }_{i}r\right)+{l}_{i}{I}_{0}\left({\lambda }_{i}r\right)\right\},$$
(73)
$$\overline{{\sigma }_{zz}}=\sum_{i=1}^{4}{g}_{i}{l}_{i}{I}_{0}\left({\lambda }_{i}r\right),$$
(74)
$${p}_{i}=1-\left({\zeta }_{i}\left(1-a\frac{{\lambda }_{i}^{2}}{{s}^{2}}\right)+{\eta }_{i}\right),{l}_{i}=1-2{\gamma }^{2}-\left({\zeta }_{i}\left(1-a\frac{{\lambda }_{i}^{2}}{{s}^{2}}\right)+{\eta }_{i}\right).$$

4 Boundary conditions

We assume that the exterior surface of the cylinder is under a force. Because of this, the mechanical boundary condition can be written as

$$u\left(r,t\right)=0,\mathrm{ at }r={r}_{0}.$$
(75)

Additionally, a variable heat flux, specifically laser-pulsed heat, is applied at the boundary surface. Consequently, the boundary conditions are

$${q}_{p}={q}_{0}\frac{{t}^{2}}{16{t}_{p}^{2}}{e}^{-\frac{t}{{t}_{p}}},\mathrm{ at }r={r}_{0}.$$
(76)

Using dimensionless quantities (43) in Eq. (3) yields

$${\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\dot{q}}_{p}=-\left(\frac{\partial }{\partial t}+{\delta }_{4}\right)\frac{\partial T}{\partial r}.$$
(77)

Equations (76) and (77) give the following boundary condition

$$\frac{{q}_{0}}{16{t}_{p}^{2}}\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\frac{\partial }{\partial t}\left({{t}^{2}e}^{-\frac{t}{{t}_{p}}}\right)=-\left(\frac{\partial }{\partial t}+{\delta }_{4}\right)\frac{\partial T}{\partial r},\mathrm{ at }r={r}_{0}.$$
(78)

“The carriers can reach the sample surface during the diffusion phase, with a finite probability of recombination”. The carrier density’s boundary conditions are:

$${D}_{E}\frac{\partial N}{\partial r}={s}_{v}N,\mathrm{at }r={r}_{0}.$$
(79)

The moisture diffusion boundary condition at the boundary surface at \(\mathrm{ }r={r}_{0}\)

$$m=0 \mathrm{at }r={r}_{0}.$$
(80)

By applying the Laplace transform on the boundary conditions in (75), and after differentiating (68) w.r.t. \(t\) twice and using the value of temperature \(T\), in (78) applying the Laplace transform and also applying Laplace transform in (69) directly yield:

$$\overline{u }\left({r}_{0},s\right)=0,$$
(81)
$${\left.\frac{\partial \overline{T}}{\partial r }\right|}_{r={r}_{0}}=-\frac{{q}_{0}\left(1+{\tau }_{0}s\right){t}_{p}{s}^{3}}{8{\left(1+s{t}_{p}\right)}^{3}\left(s+{\delta }_{4}\right)}=-\overline{G }\left(s\right),$$
(82)
$${D}_{E}{\left.\frac{\partial \overline{N}}{\partial r }\right|}_{ r={r}_{0}}={s}_{v}\overline{N }\left({r}_{0},s\right),$$
(83)
$$\overline{m }=0 \mathrm{at }r={r}_{0}.$$
(84)

Equations (66) and (69) are substituted into Eq. (81–84), giving

$$\sum_{i=1}^{4}{g}_{i}\frac{1}{{\lambda }_{i}}{I}_{1}\left({\lambda }_{i}{r}_{0}\right)=0,$$
(85)
$$\sum_{i=1}^{4}{g}_{i}{I}_{1}\left({\lambda }_{i}{r}_{0}\right){\zeta }_{i}{\lambda }_{i}=-\overline{G }\left(s\right).$$
(86)
$$\sum_{i=1}^{4}{\omega }_{i}{g}_{i}\left\{{D}_{E}{\lambda }_{i}{I}_{1}\left({\lambda }_{i}{r}_{0}\right)-{s}_{v}{I}_{0}\left({\lambda }_{i}{r}_{0}\right)\right\}=0,$$
(87)
$$\sum_{i=1}^{4}{\eta }_{i}{g}_{i}{I}_{0}\left({\lambda }_{i}{r}_{0}\right)=0.$$
(88)

Solving Eqs. (85–88) using Cramer’s rule, we can get the values of \({g}_{i},i=\mathrm{1,2},3\)

$${g}_{i}\left(s\right)=\frac{{\Delta }_{i}}{\Delta },$$
(89)
$$\Delta =\left[\begin{array}{ccc}{G}_{11}& {G}_{12}& \begin{array}{cc}{G}_{13}& {G}_{14}\end{array}\\ {G}_{21}& {G}_{22}& \begin{array}{cc}{G}_{23}& {G}_{24}\end{array}\\ \begin{array}{c}{G}_{31}\\ {G}_{41}\end{array}& \begin{array}{c}{G}_{32}\\ {G}_{42}\end{array}& \begin{array}{cc}{G}_{33}& {G}_{34}\\ {G}_{43}& {G}_{44}\end{array}\end{array}\right].$$
(90)

\({\Delta }_{i}\) is obtained from \(\Delta\) by replacing its ith column by

$$\left[\begin{array}{ccc}0& -\overline{G }\left(s\right)& \begin{array}{cc}0& 0\end{array}\end{array}\right]{\prime}$$
(91)
$${\mathrm{G}}_{1\mathrm{i}}=\frac{1}{{\lambda }_{i}}{\phi }_{i},$$
$${\mathrm{G}}_{2\mathrm{i}}={\phi }_{i}{\zeta }_{i}{\lambda }_{i}\left(1-a{\lambda }_{i}^{2}\right),$$
$${\mathrm{G}}_{3\mathrm{i}}={\omega }_{i}\left\{{D}_{E}{\lambda }_{i}{\phi }_{i}-{s}_{v}{\psi }_{i}\right\},$$
$${\mathrm{G}}_{4\mathrm{i}}={\eta }_{i}{\phi }_{i}$$
$${I}_{1}\left({\lambda }_{i}{r}_{0}\right)={\phi }_{i}, {I}_{0}\left({\lambda }_{i}{r}_{0}\right)={\psi }_{i}, i=\mathrm{1,2},\mathrm{3,4}.$$

And by using the values of \({g}_{i}\left(s\right)\) from (89) in (65), (69), and (72, 73, 74) the expression for displacement, carrier density, stresses, and temperature distribution can be obtained.

5 Inversion of the transforms

The solution in the physical domain is obtained by inverting the transforms in Eqs. (65) and (69) so obtained, by using

$$f\left(x,t\right)= \frac{1}{2\pi i}\underset{{e}^{-i\infty }}{\overset{{e}^{+i\infty }}{\int }}\widetilde{f}\left(x,s\right){e}^{-st}ds.$$
(92)

Finally, apply Romberg's integration [43] with an adaptive step size to evaluate the integral in Eq. (92).

6 Particular cases

  • If \({K}^{*}\ne 0, {D}_{m}^{*}\ne 0, {D}_{m}\ne 0,K\ne 0\,and\,{\tau }_{0}\ne 0,\) in Eqs. (65), (69), and (72–74) so obtained, the results for the MGTPT for a coupled hygro-photo-thermoelastic system can be obtained.

  • If \({K}^{*}\ne 0,{D}_{m}^{*}\ne 0, {D}_{m}\ne 0, K\ne 0\,and\,{\tau }_{0}=0,\) in Eqs. (65), (69), and (72–74) so obtained, the results for a coupled hygro-photo-thermoelastic system with the GN III model can be acquired.

  • If \(K\ne 0, {D}_{m}\ne 0, and\,{\tau }_{0}=0,\) in Eqs. (65), (69), and (72–74) so obtained, the outcomes of for coupled hygro-photo-thermoelastic system with GN II model can be acquired.

  • If \({\tau }_{0}=0,{K}^{*}=0,and\,{D}_{m}^{*}= 0,\) in Eqs. (65), (69), and (72–74) so obtained, the outcomes of classic coupled photo-hygro-thermoelasticity theory (CPTE) are achieved.

  • If \({K}^{*}=0,{D}_{m}^{*}= 0,\) in equation ((65), (69) and (72)-(74) so obtained, the outcomes of generalized Lord and Shulman photo-hygro-thermoelasticity model (PLS) are achieved.

7 Numerical results and discussion

The following physical data of silicon (Si) material is used to illustrate the theoretical findings and to graphically depict the effects of reference moisture parameter and the MGTPT using MATLAB software:

\(\lambda =3.64\times {10}^{10} N{m}^{-2},\)

\({\mathrm{T}}_{0} = 300\mathrm{ K},\)

\(\mu =5.46\times {10}^{10} N{m}^{-2},\)

\({\mathrm{H}}_{0} = 1\mathrm{ J}{\mathrm{m}}^{-1}{\mathrm{nb}}^{-1},\)

\(\beta =7.04\times {10}^{6}N{m}^{-2}{deg}^{-1},\)

\(\uptau =5\times {10}^{-5}\mathrm{ s},\)

\({\delta }_{n}=-9\times {10}^{-31} {m}^{-3},\)

\({N}_{0}={10}^{20}{m}^{-3},\)

\(\rho =2.33\times {10}^{3}K{gm}^{-3},\)

\({\upvarepsilon }_{0}= 8.838 \times {10}^{-12}{\mathrm{Fm}}^{-1},\)

\({C}_{E}=695 JK{g}^{-1}{K}^{-1},\)

\({E}_{g}=1.11eV,\)

\(K=150 W{m}^{-1}{K}^{-1}\)

\({\alpha }_{T}=3\times {10}^{-6}{K}^{-1},\)

\({K}^{*}=1.54\times {10}^{2}Ws,\)

\({s}_{v}=2m{s}^{-1}.\)

\({D}_{E}=2.5\times {10}^{-3}{m}^{2}{s}^{-1},\)

\({H}_{0}={10}^{8}Col.{cm}^{-1}{s}^{-1},\)

\({\mu }_{0}=4\pi \times {10}^{-7}H{m}^{-1}\)

\({\sigma }_{0}=9.36\times {10}^{5}{Col}^{2}{C}^{-1}{m}^{-1}{s}^{-1}.\)

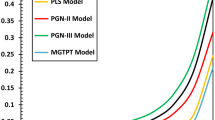
The figures analyze four cases of the reference moisture parameter, represented by solid black lines (\(m=20\%\)), solid red lines (\(m=40\%\)), solid blue lines (\(m=80\%\)), and solid purple lines (\(m=100\%\)). The variation in the radial displacement \(u\) for the MGTPT with reference moisture is depicted in Fig. 2, starting from a positive zero value and rapidly increasing until reaching a peak maximum value near half of the radius due to photo-excitation and moisture diffusivity. It has been noted that the radial displacement decreases as the reference moisture increases. For the parameter value \(m=20\%\) of the reference moisture, the radial displacement exhibits the greatest deviation at the center of the cylinder. At \(r=0\) and \(r={r}_{0}\), the radial displacement is zero, satisfying the boundary conditions stated in Eqs. (56) and (82).

Fig. 2
figure 2

The radial displacement variation with reference moisture

Full size image

The temperature distribution variance is illustrated in Fig. 3 as the reference moisture change, starting for each of the four reference moisture parameter from a positive maximum value and rapidly decrease until reaching the zero value near half of the radius due to photo-excitation and moisture diffusivity. It has been observed that the inner core of the cylinder displays a higher temperature distribution compared to the outer core. Furthermore, an increase in reference moisture leads to an increase in temperature distribution.

Fig. 3
figure 3

The variation in temperature distribution with reference moisture

Full size image

The moisture diffusion of the MGTPT at various values of reference moisture is illustrated in Fig. 4. It has been observed that a lower value of reference moisture results in greater variability in moisture diffusion compared to a higher value of reference moisture. The moisture diffusion for each of the for each of the four reference moisture parameter situations starts at zero, reaches maximum values near the surface, and then decreases exponentially to zero as it propagates. At \(r=0\) and \(r={r}_{0}\), the moisture diffusion is zero, satisfying the boundary condition stated in Eq. (87). The variation in the dilatation distributions for the MGTPT at different values of reference moisture is shown in Fig. 5. It has been noticed that lower values of reference moisture exhibit more variability in dilatation distributions compared to higher values of reference moisture. As the radial distance r increases, it has been observed that the variability in dilatation distributions significantly decreases. The figure presented in Fig. 6 illustrates the fluctuation in carrier density for the MGTPT at various reference moisture. It has been observed that an increase in reference moisture values corresponds to an increase in carrier density. Furthermore, it has been noted that as the radial distance r expands, the variance in carrier density significantly diminishes.

Fig. 4
figure 4

The moisture diffusion variation with reference moisture

Full size image
Fig. 5
figure 5

The variation in dilatation distributions with reference moisture

Full size image
Fig. 6
figure 6

The deviation in carrier density with reference moisture

Full size image

Figures 7, 8and9 depict the variation in stress components for the MGTPT with reference moisture. It is noticeable that there is a decrease in the stress components as the values of the reference moisture increase. Furthermore, as the radial distance r grows, there is a significant reduction in the variation of the stress components.

Fig. 7
figure 7

The deviation in radial stress with reference moisture

Full size image
Fig. 8
figure 8

The deviation in hoop stress with reference moisture

Full size image
Fig. 9
figure 9

Variation in the vertical stress with reference moisture

Full size image

8 Conclusions

In this study, we employ a distinctive methodology to investigate the impact of photo-thermoelasticity theory on moisture diffusivity in an elastic semiconductor cylinder. Specifically, we focus on the generalized Moore-Gibson-Thompson photothermal (MGTPT) model, while also incorporating the GN-III model in our investigation. Our study aims to examine the effects of applying an exponential laser pulse on the surface of an infinite semiconducting solid cylinder. The governing equations are obtained with the use of the MGTPT with thermal and moisture diffusivity.

  • The graphical illustrations provided in this study showcase the impact of reference moisture on various components such as displacement, thermal stresses, dilation distributions, moisture diffusivity, carrier density, and temperature field. These graphs clearly demonstrate that reference moisture factors play a significant role in the examined domains. The thermal effect occurs when semiconductor materials come into contact with concentrated laser beams or beams of sunlight. These materials have extensive applications in the renewable energy sector, particularly in the solar cell industry, where semiconductor materials are heavily relied upon.

  • It has been observed that temperature and moisture greatly influence mechanical deformation and diffusion. The relationship between deformation, temperature, and humidity is evident in a wide range of engineering problems. Therefore, it is crucial to closely monitor moisture and temperature levels in semiconductor fabrication to prevent any issues related to product quality and yield.

  • The model used in renewable energy research and engineering is highly beneficial for improving the performance of semiconductors, including diodes, triodes, modern electronic devices, solar cells, electrical circuits, and computer processors.