1 Introduction

With the advancement of the technology, the size of the components of Microelectronic devices is continuously reducing. More and more components are fabricated on the small semiconducting crystal chip. By using a sphere-shaped semiconductor integrated circuit, it is possible to utilize the semiconductor material (SM) more efficiently. A semiconductor with a spherical shape provides more surface area for a circuit to be fabricated. Semiconductor spheres could reduce the cost of manufacturing integrated circuits by 90% by replacing clean rooms with hermetically sealed tubes and by reducing the processing cycle time from months to days. Microprocessor manufacturers have invested on large scale in the production of large silicon crystals. When a semiconductor crystal is irradiated with an excitation laser, standard approaches can be used to determine the amount of light it emits. SM contribution to technological advancement was recently demonstrated when they were used to generate electrical energy from sunlight, even when irradiated to laser light. SM are used to fabricate the solar cell to generate the alternative energy sources. Moreover, in the field of electronics and electrical engineering, SM have been used for nanomaterials. In the current industry, they can be used for a variety of things, such as VLSI, solar cells, etc. The resemblance between thermoelasticity and photothermal equations has been described using numerous mathematical models.

A growing interest in semiconductor nanostructures has been observed among researchers working in nanotechnology. Further, it is impossible to fully investigate semiconducting micro/nano-devices without studying the thermoelasticity, as according to thermoelasticity, the SM can be classified as elastic materials. A number of theoretical models have been examined to determine how photothermal equations relate to thermoelasticity. The classical uncoupled thermoelasticity theory was introduced by Duhamel [1]. Two limitations are associated with this theory. Firstly, the state of elastic materials is independent of temperature. Furthermore, as a consequence of the parabolic heat equation, it expects that temperature travels at an infinite speed, again in conflict with physical experimentation. Biot [2] gave coupled thermoelasticity as a solution to these problems. This theory relates equations of heat conduction to elasticity equations. Despite this, this theory only predicts heat waves propagating at an unlimited speed. When a temperature gradient is abruptly imposed on a homogeneous and isotropic medium, Cattaneo [3] and Vernotte [4, 5] propose a broader form of Fourier law that incorporates a relaxation time to define a steady state, as follows:

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\varvec{q}=-{K}_{ij}\nabla \mathbf{T},$$
(1)

Lord and Shulman [6] then presented a generalized theory of thermoelasticity with one relaxation time for an isotropic body. The heat equation is hyperbolic in this theory, therefore, temperature propagates at a finite speed. Subsequent, Green and Lindsay [7] gave a more accurate interpretation of thermoelasticity that demonstrated the linear heat conduction tensor symmetry. Dhaliwal and Sherief [8] gave the comprehensive thermoelasticity equations for an anisotropic medium, Conversely, Green and Naghdi [9,10,11] introduced “the linear and the nonlinear thermoelastic theories with and without energy dissipation” and expanded the Fourier law as

$$q=-{K}_{ij}\nabla T-{K}_{ij}^{*}\nabla \vartheta ,\dot{\vartheta }=T.$$
(2)

Based on entropy equality, they proposed three new thermoelastic theories. Their theories are known as the thermoelasticity theory of type I, the thermoelasticity theory of type II (i.e., thermoelasticity without energy dissipation), and the thermoelasticity theory of type III (i.e., thermoelasticity with energy dissipation). On linearization, type I becomes the classical heat equation whereas on linearization type-II, as well as type-III theories, give the finite speed of thermal wave propagation.

In recent years, numerous academic works has been carried out to analyze and explain the MGT equation. A 3rd-order differential equation that is vital to several fluid dynamics is the basis of Lasiecka and Wang [12] theory. Quintanilla [13, 14] created a unique heat conduction model using the MGT equation with 2 T. The MGT theory states that the modified Fourier law as

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)q=-{K}_{ij}\nabla \mathrm{T}-{K}_{ij}^{*}\nabla \vartheta ,\quad {\text{where}} \,\,\dot{\vartheta }=T.$$
(3)

Linear thermoelastic deformations of dielectrics were explored by Fernandez and Quintanilla [15]. Assume that a SM is irradiated to an external laser beam, which causes excited free electrons with semiconductor gap energy \({E}_{\text{g}}\) to form a carrier-free charge density. Electronic distortion and elastic vibration change as a result of optical energy absorption. In this occurrence, thermal-elastic-plasma waves will have an impact on heat conductivity equations. The expanded definition of the modified Fourier law for SM with plasma impact is as follows:

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)q=-{K}_{ij}\nabla T-{K}_{ij}^{*}\nabla \vartheta -\int \frac{{E}_{\mathrm{g}}N}{\tau }{\text{d}}x, \quad {\text{where}}\,\, \dot{\vartheta }=T.$$
(4)

By differentiating the Eq. (4) w.r.t.\(\overrightarrow{x}\), yields

$$\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\nabla .q=-\nabla .\left({K}_{ij}\nabla T+{K}_{ij}^{*}\nabla \vartheta \right)-\frac{{E}_{\text{g}}N}{\tau },\quad {\text{where}} \,\,\dot{\vartheta }=T.$$
(5)

Kaur et al. [16] examined the semi-conducting solid cylinder exposed to exponential laser pulse with MGTPT and Hall current effect. In addition to these, Gupta et al. [17,18,19], Craciun et al. [20, 21], Kaur and Singh [22, 23], Kaur et al. [24], Tiwari and Mukhopadhyay [25], Kaur et al. [26], Tiwari et al. [27, 28], Marin et al. [29], Gupta et al. [30, 31], Kumar et al. [32] also done studies on the Hall current effect and other theories of thermoelasticity. The literature survey revealed, however, that no research had been done on the transient examination of a semiconductor sphere exposed to ultrashort pulsed laser heating and photogenerated plasma under the Hall Effect.

In this research, we have undertaken transient examination of a semiconductor sphere exposed to ultrashort pulsed laser heating and photogenerated plasma under the Hall Effect. The basic equations of semiconducting solid sphere are expressed with MGTPT heat transfer theory using GN III model. The Sect. 1 illustrated the evolution of the Fourier’s Law and the heat conduction equation. The Sect. 2 focuses on the basic equation for semiconducting medium viz equation of motion, equation of the plasma diffusion and MGTPT. Section 3 describe the mathematical formulation of the study of semiconductor solid sphere with MGTPT heat transfer equation to obtain the dimensionless expressions for Various components of displacement, thermodynamic temperature, conductive temperature, carrier density and axial stress as well as couple stress are found in the transformed domain using Laplace Transforms. Boundary conditions for sphere's exterior surface constrained by time dependent variable heat has been discussed in the Sect. 4. The Sects. 5 and 6 provide the solution to problem and method for the Laplace Transform inversion. The Sect. 7 presents the numerical results and shows the effect of various thermoelasticity theories and Hall current on the physical quantities graphically with MATLAB software. The Sect. 8 deals with the conclusions of the paper.

2 Basic equations

Following Mahdy et al. [33], Abouelregal and Atta [34], the governing equations for a photo-magneto-thermoelastic with new modified green Nagdhi model is given by.

Constitutive relations

$${\sigma }_{ij}= \left(\lambda {u}_{k,k}-\beta T-{\delta }_{n}N\right){\delta }_{ij}+\mu \left({u}_{i,j}+{u}_{j,i}\right),$$
(6)
$$\beta =\left(3\lambda +2\mu \right){\alpha }_{t}, {\delta }_{n}=\left(3\lambda +2\mu \right){d}_{n}.$$

Equation of motion

$${\sigma }_{ij,j}+ {F}_{i}= \rho {\ddot{u}}_{i},$$
(7)

Plasma diffusion equation

$$\frac{\partial {\varvec{N}}}{\partial t}={D}_\text{E}{\nabla }^{2}N-\frac{N}{\tau }+\kappa T,$$
(8)

where \(\kappa =\frac{T}{\tau }\frac{\partial {N}_{0}}{\partial T}\).

Modified Moore Gibson Thompson photo thermal equation

$$ \left( {K_{{ij}} \dot{T}_{{,j}} } \right)_{{,i}} + \left( {K_{{ij}}^{*} T_{{,j}} } \right)_{{,i}} + \frac{{E_{{\text{g}}} \dot{N}}}{\tau } = \left( {1 + \tau _{0} \frac{\partial }{{\partial t}}} \right)\left[ {\rho C_{E} \ddot{T} + \beta _{{ij}} T_{0} {\ddot{\text{e}}}_{{ij}} - \rho \dot{Q}} \right],$$
(9)

where \({K}_{ij}={K}_{i}{\delta }_{ij}, {K}_{ij}^{*}={K}_{i}^{*}{\delta }_{ij}, i\) is not summed.

Improved Ohm’s law with Hall effect

$${J}_{i}={\sigma }_{0}\left({E}_{i}+{\mu }_{0}{\epsilon }_{ijr}\left({u}_{j,t}-\frac{{\mu }_{0}}{e{n}_\text{e}}{J}_{j}\right){H}_{r}\right).$$
(10)

where \({\sigma }_{0}=\frac{{n}_\text{e}{e}^{2}{t}_\text{e}}{{m}_\text{e}},m={\omega }_\text{e}{t}_\text{e}=\frac{{\sigma }_{0}{\mu }_{0}{H}_{0}}{e{n}_\text{e}} ,{\omega }_\text{e}=\frac{e{\mu }_{0}{H}_{0}}{{m}_\text{e}}.\)

Vector form of Eq. (8) is

$$J={\sigma }_{0}\left\{E+{\mu }_{0}\left(\dot{u}\times H\right)-\frac{{\mu }_{0}}{e{n}_\text{e}}\left(J\times H\right)\right\}.$$

Lorentz force

$${F}_{i}={\mu }_{0}{\varepsilon }_{ijk}{J}_{j}{H}_{k},$$
(11)

Here, the subscript followed by ‘,’ comma denotes partial derivative w.r.t. respective space variable and a superposed dot represents derivative w.r.t. time variable \(t\).

$${\mathrm{where}\, \epsilon }_{ijk}{=\epsilon }_{jki}={\epsilon }_{kij}{=-\epsilon }_{jik}=-{\epsilon }_{kji}=-{\epsilon }_{ikj},$$
$$ \epsilon _{{ijk}} = \left\{ {\begin{array}{*{20}l} { + 1,} \hfill & {\quad {\text{if}}\,\,\left( {i,j,k} \right){\text{is\,even\,permutation\,of}}\,\left( {1,2,3} \right),} \hfill \\ { - 1,} \hfill & {\quad {\text{if}}\,\,\left( {i,j,k} \right){\text{is\,odd\,permutation\,of}}\,\left( {1,2,3} \right),} \hfill \\ {0,} \hfill & {\quad {\text{if\,\,two\,or\,more\,indices\,are\,equal}}.} \hfill \\ \end{array} } \right. $$
$$\left(i.e. {\epsilon }_{123}=+1,{\epsilon }_{132}=-1,{\epsilon }_{122}=0\right).$$

3 Mathematical model of the problem

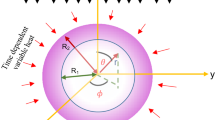
Consider a thermally homogenous, infinitesimal semiconductor solid sphere of radius \(R\) (Fig. 1) where the outer surface is traction-free and a time-dependent variable heat flux is applied to it. No heat sources exist inside the sphere. The spherical coordinate system \(\left(r,\theta ,\phi \right)\) are considered to model the problem with \(\left(0\le r\le R\right), \left(0\le \theta \le 2\pi \right),\left(0\le \phi \le 2\pi \right).\) Initially, the sphere is kept at constant and uniform temperature (\({T}_{0}\)).

Fig. 1
figure 1

Schematic diagram of semiconducting solid sphere

Full size image

For 1D problem, displacement components and the displacement–strain relations which depends on radial distance \(r\) and the time \(t\) due to symmetry are given by

$$u=\left({u}_{\rho },{u}_{\theta },{u}_{\phi }\right)=\left(u,\mathrm{0,0}\right)\left(r,t\right),$$
(12)
$${e}_{rr}=\frac{\partial u}{\partial r},{e}_{\theta \theta }={e}_{\phi \phi }=\frac{u}{r},{e}_{r\theta }={e}_{r\phi }={e}_{\theta \phi }=0.$$
(13)

The dilatation term e is given by

$$e=\frac{1}{{r}^{2}}\frac{\partial \left({r}^{2}u\right)}{\partial r}.$$
(14)

The Eq. (6) using (12) and (13) yields

$${\sigma }_{rr}=\left(\lambda +2\mu \right)+2\lambda \frac{u}{r}-\left(\beta T+{\delta }_{n}N\right),$$
(15)
$${\sigma }_{\theta \theta }={\sigma }_{\phi \phi }=\lambda \frac{\partial u}{\partial r}+2\left(\lambda +\mu \right)\frac{u}{r}-\left(\beta T+{\delta }_{n}N\right),$$
(16)

The dynamic equation of motion using the Lorentz force, turn into

$$\frac{\partial {\sigma }_{rr}}{\partial r}+\frac{1}{r}\left(2{\sigma }_{rr}-{\sigma }_{\theta \theta }-{\sigma }_{\phi \phi }\right)+{F}_{r}=\rho \frac{{\partial }^{2}u}{\partial {t}^{2}}.$$
(17)

Assume that the sphere is under a constant and extremely strong magnetic field \({{\varvec{H}}}_{0}=(0, 0,{H}_{0})\), in addition, assume that \({\varvec{E}}=0\). Under these conventions from the generalized Ohm’s law (8) we have.

$${J}_{\phi }=0.$$
(18)

Accordingly the components of current density \({J}_{r}\) and \({J}_{\theta }\) are given as

$${J}_{r}=\frac{{\sigma }_{0}{\mu }_{0}{H}_{0}}{1+{m}^{2}}\left(m\frac{\partial u}{\partial t}\right),$$
(19)
$${J}_{\theta }= \frac{{\sigma }_{0}{\mu }_{0}{H}_{0}}{1+ {m}^{2 }}\left(-\frac{\partial u}{\partial t}\right).$$
(20)

\({F}_{r}\) induced by \({{\varvec{H}}}_{0}\) is given by

$${F}_{r}={\mu }_{0}{\left({\varvec{J}}\times {\varvec{H}}\right)}_{r}.$$
(21)

Using Eqs. (15, 16 and 18–21) in Eqs. (17) and also from (8, 9) in spherical coordinates, the governing equations for the semiconducting solid sphere are:

$$\left(\lambda +2\mu \right)\frac{\partial e}{\partial r}-\beta \frac{\partial T}{\partial r}-{\delta }_{n}\frac{\partial N}{\partial r}-\frac{{\sigma }_{0}{\mu }_{0}^{2}{H}_{0}^{2}}{1+ {m}^{2 }}\left(\frac{\partial u}{\partial t}\right)=\rho \frac{{\partial }^{2}u}{\partial {t}^{2}},$$
(22)
$$\frac{\partial N}{\partial t}={D}_\text{E}\left({\nabla }^{2}N\right)-\frac{N}{\tau }+\kappa T,$$
(23)
$$K\frac{\partial }{\partial t}{\nabla }^{2}T+{K}^{*}{\nabla }^{2}T+\frac{{E}_\text{g}\dot{N}}{\tau }=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[{\rho C}_\text{E}\frac{{\partial }^{2}T}{\partial {t}^{2}}+\beta {T}_{0}\frac{{\partial }^{2}e}{\partial {t}^{2}}\right].$$
(24)

In the spherical coordinate system, the Laplacian operator \({\nabla }^{2}\), is given by.

$${\nabla }^{2}=\frac{{\partial }^{2}}{\partial {r}^{2}}+\frac{2}{r}\frac{\partial }{\partial r}=\frac{1}{{r}^{2}}\frac{\partial }{\partial r}\left({r}^{2}\frac{\partial }{\partial r}\right).$$
(25)

Pre-operating both sides of Eq. (22) by \(\left(\frac{2}{r}+\frac{\partial }{\partial r}\right),\) yields

$$\left(\lambda +2\mu \right){\nabla }^{2}e-\beta {\nabla }^{2}T-{\delta }_{n}{\nabla }^{2}N-\frac{{\sigma }_{0}{\mu }_{0}^{2}{H}_{0}^{2}}{1+ {m}^{2 }}\left(\frac{\partial e}{\partial t}\right)=\left(\frac{{\partial }^{2}e}{\partial {t}^{2}}\right).$$
(26)

The following dimensionless quantities are used to find the dimensionless form of above equations:

$${(r}^{^{\prime}},{u}^{^{\prime}})={v}_{0}\eta \left(r,u\right), \left({T}^{^{\prime}},{N}^{^{\prime}},{\sigma }_{ij}^{^{\prime}}\right)=\frac{1}{\rho {v}_{0}^{2}} \left(\beta T,{\delta }_{n}N,{\sigma }_{ij}\right),{(\tau }_{0}^{^{\prime}},{\tau }^{^{\prime}},{t}^{^{\prime}})={v}_{0}^{2}\eta {(\tau }_{0},\tau ,t),\eta =\frac{\rho {C}_\text{E}}{K},\rho {v}_{0}^{2}=\lambda +2\mu ,M=\frac{{\sigma }_{0}{\mu }_{0}^{2}{H}_{0}^{2}}{\eta \rho {v}_{0}^{2}},\gamma =\sqrt{\frac{2\mu }{\lambda +2\mu }}.$$
(27)

\(M\) is the Hartmann number or magnetic parameter in semiconductor elastic medium and it measures the magnetic field strength. Using the dimensionless quantities (27) in Eqs. (24, 25 and 26), and after suppressing the primes, yields

$${\nabla }^{2}e-{\nabla }^{2}T-{\nabla }^{2}N-\frac{M}{1+ {m}^{2 }}\left(\frac{\partial e}{\partial t}\right)=\left(\frac{{\partial }^{2}e}{\partial {t}^{2}}\right),$$
(28)
$$\frac{\partial N}{\partial t}={\delta }_{1}\left({\nabla }^{2}N\right)-{\delta }_{2}N+{\delta }_{3}T,$$
(29)
$$\frac{\partial }{\partial t}{\nabla }^{2}T+{\delta }_{4}{\nabla }^{2}T+{\delta }_{5}N=\left(1+{\tau }_{0}\frac{\partial }{\partial t}\right)\left[\frac{{\partial }^{2}T}{\partial {t}^{2}}+{\delta }_{6}\frac{{\partial }^{2}e}{\partial {t}^{2}}\right],$$
(30)

where

$${\delta }_{1}={D}_\text{E}\eta ,{\delta }_{2}=\frac{1}{\tau },{\delta }_{3}=\frac{\kappa {\delta }_{n}}{\beta },{\delta }_{4}=\frac{{K}^{*}}{\left(\lambda +2\mu \right){C}_\text{E}},{\delta }_{5}=\frac{{E}_\text{g}}{{\delta }_{n}{C}_\text{E}\left(\lambda +2\mu \right)\eta \tau },{\delta }_{6}=\frac{{\beta }^{2}{T}_{0}}{\rho {C}_\text{E}\left(\lambda +2\mu \right)}.$$

By using (27) in Eqs. (15, 16) and after suppressing the primes, yields

$${\sigma }_{rr}={\gamma }^{2}\frac{\partial u}{\partial r}+\left(1-{\gamma }^{2}\right)e-\left(T+N\right),$$
(31)
$${\sigma }_{\theta \theta }={\sigma }_{\phi \phi }={\gamma }^{2}\frac{u}{r}+\left(1-{\gamma }^{2}\right)e-\left(T+N\right),$$
(32)

The preliminary conditions of this model are

$$u\left(r,0\right)=0=\frac{\partial u}{\partial r}\left(r,0\right),$$
(33)
$$T\left(r,0\right)=0=\frac{\partial T}{\partial r}\left(r,0\right),$$
(34)
$$N\left(r,0\right)=0=\frac{\partial N}{\partial r}\left(r,0\right).$$
(35)

The Laplace transform of a function \(f\) w.r.t. time variable t, is defined as

$$\mathcal{L}\left(f\left(t\right)\right)=\overline{f }\left(s\right)= \underset{0}{\overset{\infty }{\int }}f\left(t\right){e}^{-st}{\text{d}}t,$$
(36)

where s as a Laplace Transform variable. Applying transform defined by (36) to Eqs. (28–32) yields

$$\left({\nabla }^{2}+\left(-{s}^{2}\right)-\frac{Ms}{1+ {m}^{2 }}\right)\overline{e }-{\nabla }^{2}\overline{T }-{\nabla }^{2}\overline{N }=0,$$
(37)
$$\left({\delta }_{1}{\nabla }^{2}-\left({\delta }_{2}+s\right)\right)\overline{N }+{\delta }_{3}\overline{T }=0,$$
(38)
$$\left(1+{\tau }_{0}s\right){\delta }_{6}{s}^{2}\overline{e }+\left(-\left(s+{\delta }_{4}\right){\nabla }^{2}+\left(1+{\tau }_{0}s\right){s}^{2}\right)\overline{T }-{\delta }_{5}{s}\overline{N }=0,$$
(39)
$$\overline{{\sigma }_{rr}}={\gamma }^{2}\frac{\partial \overline{u}}{\partial r }+\left(1-{\gamma }^{2}\right)\overline{e }-\left(\overline{T }+\overline{N }\right),$$
(40)
$$\overline{{\sigma }_{\theta \theta }}={\gamma }^{2}\frac{\overline{u}}{r }+\left(1-{\gamma }^{2}\right)\overline{e }-\left(\overline{T }+\overline{N }\right),$$
(41)

When Eqs. (37) to (39) are decoupled, we obtain

$$\left({\nabla }^{6}-B{\nabla }^{4}+C{\nabla }^{2}-D\right)\left(\overline{e },\overline{T },\overline{N }\right)=0,$$
(42)

where \(A=-{\delta }_{1}{\delta }_{11}, B=-\left(A{\delta }_{7}-{\delta }_{1}{\delta }_{10}-{\delta }_{1}{\delta }_{9}+{\delta }_{8}{\delta }_{11}\right)/A,\)

$$C=\left(-{\delta }_{3}{\delta }_{5}{s}+{\delta }_{3}{\delta }_{9}-{\delta }_{1}{\delta }_{7}{\delta }_{10}+{\delta }_{8}{\delta }_{7}{\delta }_{11}+{\delta }_{8}{\delta }_{10}+{\delta }_{8}{\delta }_{9}\right)/A,D=\left({\delta }_{3}{\delta }_{7}{\delta }_{5}{s}-{\delta }_{8}{\delta }_{7}{\delta }_{10}\right)/A,$$
$${\delta }_{7}=\left(-{s}^{2}\right)-\frac{Ms}{1+ {m}^{2 }},{\delta }_{8}={\delta }_{2}+s,{\delta }_{9}=\left(1+{\tau }_{0}s\right){\delta }_{6}{s}^{2},$$
$${\delta }_{10}=\left(1+{\tau }_{0}s\right){s}^{2},{\delta }_{11}=-\left(s+{\delta }_{4}\right).$$

Presenting \({\lambda }_{i}\), i = 1,2,3, in Eqs. (42), we obtain

$$\left({\nabla }^{2}-{\lambda }_{1}^{2}\right)\left({\nabla }^{2}-{\lambda }_{2}^{2}\right)\left({\nabla }^{2}-{\lambda }_{3}^{2}\right)\left(\overline{e },\overline{T },\overline{N }\right)=0,$$
(43)

where \({\lambda }_{i}^{2},i=\mathrm{1,2},3,\) are the roots of the equation

$$\left({\lambda }^{6}-B{\uplambda }^{4}+C{\uplambda }^{2}-D\right)=0,$$
(44)

Which are given by

$${\lambda }_{1}^{2}=\frac{1}{3}\left(2d\mathrm{sin}\chi +B\right),$$
$${\lambda }_{2}^{2}=\frac{1}{3}\left\{-d\left(\mathrm{sin}\chi +\sqrt{3}\mathrm{cos}\chi \right)+\frac{B}{3}\right\},$$
$${\lambda }_{3}^{2}=\frac{1}{3}\left\{d\left(\mathrm{sin}\chi -\sqrt{3}\mathrm{cos}\chi \right)+\frac{B}{3}\right\},$$

With

$$d=\sqrt{{B}^{2}-3C},\chi =\frac{1}{3}{\mathrm{sin}}^{-1}\left(-\frac{2{B}^{3}-9BC+27D}{2{d}^{3}}\right).$$

The common solution of (43) can be expressed as follows:

$$\left(\overline{e },\overline{T },\overline{N }\right)=\frac{1}{\sqrt{r}}\sum_{i=1}^{3}\left(1,{\zeta }_{i},{\eta }_{i}\right){g}_{i}{I}_{1/2}\left({\lambda }_{i}r\right),$$
(45)

where \({I}_{n}\)() indicates the second types of modified Bessel functions of order n. We get the following relations by inserting Eq. (45) into Eqs. (37–39)

$${\zeta }_{i}=\frac{-\left({\lambda }_{i}^{2}+{\delta }_{7}\right)\left({\delta }_{9}{\lambda }_{i}^{2}-{\delta }_{5}\right)}{{\delta }_{3}{\delta }_{5}+\left({\delta }_{11}{\lambda }_{i}^{2}+{\delta }_{10}\right)\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{8}\right)},$$
(46)
$${\eta }_{i}=\frac{-\left({\lambda }_{i}^{2}+{\delta }_{7}\right)\left({\delta }_{3}\right)}{{\delta }_{3}{\delta }_{5}+\left({\delta }_{11}{\lambda }_{i}^{2}+{\delta }_{10}\right)\left({\delta }_{1}{\lambda }_{i}^{2}-{\delta }_{8}\right)}.$$
(47)

We have the Bessel function relation

$$\int {x}^{3/2}{I}_{1/2}\left(x\right){\text{d}}x={x}^{3/2}{I}_{3/2}\left(x\right).$$
(48)

In the domain of the Laplace transform, displacement u can be expressed as:

$$\overline{u }=\frac{1}{\sqrt{r}}\sum_{i=1}^{3}{g}_{i}\frac{{I}_{3/2}\left({\lambda }_{i}r\right)}{{\lambda }_{i}},$$
(49)

The modified Bessel \({I}_{n}\) follows the following relationships for any positive number x.

$${I}_{1/2}\left(x\right)=\sqrt{\frac{2}{\pi x}}\mathrm{sinh}x,$$
(50)
$${I}_{3/2}\left(x\right)=\sqrt{\frac{2}{\pi x}}\left(\mathrm{cosh}x-\frac{sinhx}{x}\right).$$
(51)

Introducing Eq. (50) into Eqs. (45), we obtain

$$\left(\overline{e },\overline{T },\overline{N }\right)=\sqrt{\frac{2}{\pi }}\sum_{i=1}^{3}\left(1,{\zeta }_{i},{\eta }_{i}\right)\frac{{g}_{i}}{\sqrt{r{\lambda }_{i}}}\mathrm{sinh}\left({\lambda }_{i}r\right),$$
(52)

Using (51) in Eq. (49) the displacement \(\overline{u }\) may be represented as follows in the Laplace transform domain:

$$\overline{u }=\sqrt{\frac{2}{\pi }}\sum_{i=1}^{3}\frac{{g}_{i}}{r{\lambda }_{i}^{3/2}}\left(\mathrm{cosh}\left({\lambda }_{i}r\right)-\frac{sinh\left({\lambda }_{i}r\right)}{\left({\lambda }_{i}r\right)}\right),$$
(53)

Differentiating Eq. (53) in terms of r yields

$$\frac{\partial \overline{u}}{\partial r }=\sqrt{\frac{2}{\pi }}\sum_{i=1}^{3}{g}_{i}\left\{{l}_{i}\mathrm{sinh}\left({\lambda }_{i}r\right)-{n}_{i}\mathrm{cosh}\left({\lambda }_{i}r\right)\right\}.$$
(54)
$${l}_{i}=\left(\frac{2+{\lambda }_{i}^{2}{r}^{2}}{{r}^{3}{\lambda }_{i}^{5/2}}\right),{n}_{i}=\frac{2}{{r}^{2}{\lambda }_{i}^{3/2}}.$$

Thus, using (52)–(54) in Eqs. (40) and (41), the expressions for thermal stresses are derived as

$$\overline{{\sigma }_{rr}}=\sqrt{\frac{2}{\pi }}\sum_{i=1}^{3}{g}_{i}\left\{{l1}_{i}\mathrm{sinh}\left({\lambda }_{i}r\right)-{n1}_{i}\mathrm{cosh}\left({\lambda }_{i}r\right)\right\},$$
(55)
$$\overline{{\sigma }_{\theta \theta }}=\sqrt{\frac{2}{\pi }}\sum_{i=1}^{3}{g}_{i}\left\{{p}_{i}\mathrm{cosh}\left({\lambda }_{i}r\right)+{m}_{i}\mathrm{sinh}\left({\lambda }_{i}r\right)\right\},$$
(56)
$${p}_{i}=\frac{{\gamma }^{2}}{{r}^{2}{\lambda }_{i}^{3/2}},{m}_{i}=\left(\frac{-{\gamma }^{2}}{{r}^{5/2}{\lambda }_{i}^{2}}\right)+\frac{1-{\gamma }^{2}-\left({\zeta }_{i}+{\eta }_{i}\right)}{{r}^{1/2}{\lambda }_{i}^{1/2}}$$
(57)
$${l1}_{i}=\left({\gamma }^{2}{l}_{i}+\frac{1-{\gamma }^{2}-\left({\zeta }_{i}+{\eta }_{i}\right)}{{r}^{1/2}{\lambda }_{i}^{1/2}}\right),{n1}_{i}={\gamma }^{2}{n}_{i}.$$

4 Boundary conditions

Assume that the sphere's exterior surface is traction free and is constrained by time dependent variable heat. Hence, the mechanical boundary condition can be expressed as

$$T\left(R,t\right)={T}_{1}H\left(t\right),t>0$$
(58)
$${\sigma }_{rr}\left(R,t\right)=0,$$
(59)

During the diffusion phase, carriers can reach the sample surface, with a finite probability of recombination. Thus, the carrier density boundary condition is:

$${D}_\text{e}\frac{\partial N}{\partial r}={s}_{v}N, {\text{at}}\, r=R.$$
(60)

By applying the Laplace transform on (58–60) yields

$$\overline{T }\left(R,s\right)=\frac{{T}_{0}}{s},$$
(61)
$${\tilde{\sigma }}_{rr}\left(R,s\right)=0,$$
(62)
$${D}_\text{e}{\left.\frac{\partial \overline{N}}{\partial r }\right|}_{ r={r}_{0}}={s}_{v}\overline{N }\left({r}_{0},s\right).$$
(63)

Equations (52) and (55) are substituted into Eq. (61–63), giving

$$\sqrt{\frac{2}{\pi }}\sum_{i=1}^{3}{g}_{i}\left\{\frac{{\zeta }_{i}}{\sqrt{{\lambda }_{i}R}}\mathrm{sinh}\left({\lambda }_{i}R\right)\right\}=\frac{{T}_{0}}{s},$$
(64)
$$\sum_{i=1}^{3}{g}_{i}\left\{{l1}_{i}\mathrm{sinh}\left({\lambda }_{i}R\right)-{n1}_{i}\mathrm{cosh}\left({\lambda }_{i}R\right)\right\}=0,$$
(65)
$$\sum_{i=1}^{3}{g}_{i}{\eta }_{i}\left\{{a}_{i}\mathrm{cosh}\left({\lambda }_{i}R\right)+{b}_{i}\mathrm{sinh}\left({\lambda }_{i}R\right)\right\}=0,$$
(66)
$${a}_{i}=\frac{{D}_\text{E}{\lambda }_{i}^{1/2}}{{R}^{1/2}},{b}_{i}=\frac{-{D}_\text{E}}{2{R}^{3/2}{\lambda }_{i}^{3/2}}-\frac{{s}_{v}}{\sqrt{{\lambda }_{i}R}},$$
$${n}_{1i}=\left({\gamma }^{2}{l}_{1i}+\frac{1-{\gamma }^{2}-\left({\zeta }_{i}+{\eta }_{i}\right)}{R{\lambda }_{i}^{1/2}}\right),{l}_{1i}=\left(\frac{2+{\lambda }_{i}^{2}{R}^{2}}{{R}^{3}{\lambda }_{i}^{5/2}}\right).$$

The values of \({g}_{i},i=\mathrm{1,2},3\) can be obtained by solving Eqs. (64–66) by Cramer’s rule

$${g}_{i}\left(s\right)=\frac{{\Delta }_{i}}{\Delta },$$
(67)
$$\Delta ={\mathrm{G}}_{1}\left[{\mathrm{G}}_{5}{\mathrm{G}}_{9}-{\mathrm{G}}_{8}{\mathrm{G}}_{6}\right]-{\mathrm{G}}_{2}\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{6}{\mathrm{G}}_{7}\right]+{\mathrm{G}}_{3}\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right],$$
$${\Delta }_{1}=\frac{{T}_{0}}{s}\left[{\mathrm{G}}_{5}{\mathrm{G}}_{6}-{\mathrm{G}}_{8}{\mathrm{G}}_{9}\right],$$
$${\Delta }_{2}=-\frac{{T}_{0}}{s}\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{7}{\mathrm{G}}_{6}\right],$$
$${\Delta }_{3}=\frac{{T}_{0}}{s}\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right],$$
$${\mathrm{G}}_{\mathrm{i}}=\sqrt{\frac{2}{\pi }}\left\{\frac{{\zeta }_{i}}{\sqrt{{\lambda }_{i}R}}\mathrm{sinh}\left({\lambda }_{i}R\right)\right\},$$
$${\mathrm{G}}_{\mathrm{i}+3}=\left\{{l1}_{i}\mathrm{sinh}\left({\lambda }_{i}R\right)-{n1}_{i}\mathrm{cosh}\left({\lambda }_{i}R\right)\right\},$$
$${\mathrm{G}}_{\mathrm{i}+6}={\eta }_{i}\left\{{a}_{i}\mathrm{cosh}\left({\lambda }_{i}R\right)+{b}_{i}\mathrm{sinh}\left({\lambda }_{i}R\right)\right\}, i=\mathrm{1,2},3$$

And using the values of \({g}_{i}\left(s\right)\) from Eq. (67) in eqs. (52, 53, 55–56) the different constituents of displacement, temperature distribution, carrier density and stresses are

$$\overline{u }=\frac{1}{\Delta } \frac{{T}_{0}}{s}\left\{\left[{\mathrm{G}}_{5}{\mathrm{G}}_{6}-{\mathrm{G}}_{8}{\mathrm{G}}_{9}\right]{\alpha }_{1}-\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{7}{\mathrm{G}}_{6}\right]{\alpha }_{2}+\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right]{\alpha }_{3}\right\},$$
(68)
$$\overline{T }= \frac{1}{\Delta } \frac{{T}_{0}}{s}\left\{\left[{\mathrm{G}}_{5}{\mathrm{G}}_{6}-{\mathrm{G}}_{8}{\mathrm{G}}_{9}\right]{\zeta }_{1}{\beta }_{1}-\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{7}{\mathrm{G}}_{6}\right]{\zeta }_{2}{\beta }_{2}+\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right]{\zeta }_{3}{\beta }_{3}\right\},$$
(69)
$$\overline{N }=\frac{1}{\Delta } \frac{{T}_{0}}{s}\left\{\left[{\mathrm{G}}_{5}{\mathrm{G}}_{6}-{\mathrm{G}}_{8}{\mathrm{G}}_{9}\right]{\eta }_{1}{\beta }_{1}-\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{7}{\mathrm{G}}_{6}\right]{\eta }_{2}{\beta }_{2}+\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right]{\eta }_{3}{\beta }_{3}\right\},$$
(70)
$$\overline{{\sigma }_{rr}}=\frac{1}{\Delta } \frac{{T}_{0}}{s}\left\{\left[{\mathrm{G}}_{5}{\mathrm{G}}_{6}-{\mathrm{G}}_{8}{\mathrm{G}}_{9}\right]{\gamma }_{1}-\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{7}{\mathrm{G}}_{6}\right]{\gamma }_{2}+\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right]{\gamma }_{3}\right\},$$
(71)
$$\overline{{\sigma }_{\theta \theta }}=\frac{1}{\Delta } \frac{{T}_{0}}{s}\left\{\left[{\mathrm{G}}_{5}{\mathrm{G}}_{6}-{\mathrm{G}}_{8}{\mathrm{G}}_{9}\right]{\vartheta }_{1}-\left[{\mathrm{G}}_{4}{\mathrm{G}}_{9}-{\mathrm{G}}_{7}{\mathrm{G}}_{6}\right]{\vartheta }_{2}+\left[{\mathrm{G}}_{4}{\mathrm{G}}_{8}-{\mathrm{G}}_{5}{\mathrm{G}}_{7}\right]{\vartheta }_{3}\right\},$$
(72)

where

$${\alpha }_{i}=\sqrt{\frac{2}{\pi }}\frac{1}{r{\lambda }_{i}^{3/2}}\left(\mathrm{cosh}\left({\lambda }_{i}r\right)-\frac{sinh\left({\lambda }_{i}r\right)}{\left({\lambda }_{i}r\right)}\right),{\beta }_{i}=\sqrt{\frac{2}{\pi }}\frac{1}{\sqrt{r{\lambda }_{i}}}\mathrm{sinh}\left({\lambda }_{i}r\right)$$
$${\gamma }_{i}=\sqrt{\frac{2}{\pi }}\left\{{l1}_{i}\mathrm{sinh}\left({\lambda }_{i}r\right)-{n1}_{i}\mathrm{cosh}\left({\lambda }_{i}r\right)\right\},{\vartheta }_{i}=\sqrt{\frac{2}{\pi }}\left\{{p}_{i}\mathrm{cosh}\left({\lambda }_{i}r\right)+{m}_{i}\mathrm{sinh}\left({\lambda }_{i}r\right)\right\} i=\mathrm{1,2},3.$$

5 Inversion of the transforms

The results in the physical domain problem are obtained by inverting the transforms in Eqs. (68–72) using:

$$f\left(x,t\right)= \frac{1}{2\pi i}\underset{{e}^{-i\infty }}{\overset{{e}^{+i\infty }}{\int }}\widetilde{f}\left(x,s\right){e}^{-st}ds.$$
(73)

Finally evaluate the integral in Eq. (73) using Romberg’s integration (Press et al. [35]) with adaptive step size.

6 Particular cases

  1. i.

    If \({K}^{*}\ne 0, K\ne 0\, and\, {\tau }_{0}\ne 0\) in Eqs. (68–72) the results for the MGTPT can be obtained with Hall Effect.

  2. ii.

    If \({K}^{*}\ne 0, K\ne 0\, and\, {\tau }_{0}=0\) in Eqs. (68–72) the results for the photothermal Green-Naghdi (PGN) III model can be obtained with Hall Effect

  3. iii.

    If \(K\ne 0 \,and\, {\tau }_{0}=0\) in Eqs. (68–72) the results for the PGN-II can be obtained with Hall Effect.

  4. iv.

    If \({\tau }_{0}=0,{K}^{*}=0,\) in Eqs. (68–72), we get the results corresponding to the coupled photo-thermoelasticity theory (CPTE) with Hall Effect.

  5. v.

    If \({K}^{*}=0\), in Eqs. (68–72) we get the results corresponding to the generalized Lord and Shulman photo-thermoelasticity model (PLS) with Hall Effect.

7 Numerical results and discussion

With the MATLAB software the theoretical results are obtained by utilising the following physical data of the silicon (Si) material and the effect of Hall current, and the MGTPT heat equation are illustrated graphically.

\(\lambda =3.64\times {10}^{10}\, {\text{Nm}}^{-2}\)

\({\mathrm{T}}_{0} = 300\,\text{K}\)

\(\mu =5.46\times {10}^{10} {\text{Nm}}^{-2}\)

\({\mathrm{H}}_{0} = 1\,\text{Jm}^{-1}{\mathrm{nb}}^{-1}\)

\(\beta =7.04\times {10}^{6} \,{\text{Nm}}^{-2}{\text{deg}}^{-1}\)

\(\uptau =5\times {10}^{-5}\,\text{ s}\)

\({\delta }_{n}=-9\times {10}^{-31} \,{\text{m}}^{-3}\)

\({N}_{0}={10}^{20}\,{\text{m}}^{-3},\)

\(\rho =2.33\times {10}^{3}\,\text{K\,gm}^{-3}\)

\({\upvarepsilon }_{0}= 8.838 \times {10}^{-12}\,{\text{Fm}}^{-1}\)

\({C}_\text{e}=695\, {\text{J\,Kg}}^{-1} {\text{K}}^{-1}\)

\({E}_\text{g}=1.11\,\text{eV}\)

\(K=150\,\text{Wm}^{-1}{\text{K}}^{-1}\)

\({\alpha }_{T}=3\times {10}^{-6}\,{\text{K}}^{-1}\)

\({K}^{*}=1.54\times {10}^{2}\,\text{Ws}\)

\( {s}_{v}=2\,\text{ms}^{-1}\)

\({D}_\text{e}=2.5\times {10}^{-3}\,{\text{m}}^{2}{\text{s}}^{-1}\)

\({H}_{0}={10}^{8}\, \text{Col.cm}^{-1}{\text{s}}^{-1}\)

\({\mu }_{0}=4\pi \times {10}^{-7}\,{\text{Hm}}^{-1}\)

\({\sigma }_{0}=9.36\times {10}^{5}\,{\text{Col}}^{2}{\text{C}}^{-1}{\text{m}}^{-1}{\text{s}}^{-1}\)

A comparison of the dimensionless form of the field variables for a transversely isotropic plate with two temperature and frequency is demonstrated graphically as:

The dimensionless form of the field variables viz. components of displacement, thermodynamic temperature, conductive temperature, carrier density and axial stress as well as couple stress is visually represented as.

  1. i.

    The black line relates to MGTPT with, \(m=0\),

  2. ii.

    The red line relates to MGTPT with, \(m=5\),

  3. iii.

    The purple line relates to MGTPT with, \(m=7\),

  4. iv.

    The green line relates to MGTPT with, \(m=10\),

Figure 2 illustrates the deviation in the displacement component \(u\) of the semiconducting sphere for MGTPT theory with Hall Effect. It has been noticed that in absence of Hall Effect under MGTPT theory, there is maximum variation in \(u\). Though, in presence of Hall Effect, variation in the displacement is sharply decreases. Moreover, in the centre of the sphere, there is no variation in the displace component, but as radial distance increases, deviation in the \(u\) increases sharply. Figure 3 demonstrates the deviation in the temperature distribution \(T\) in the semiconducting sphere with Hall Effect. It has been noticed that \(T\) is lesser in the inside core of the sphere as compared to the external core of the sphere. Additionally, presence of Hall Effect cause the higher variation in \(T\).

Fig. 2
figure 2

The displacement deviation with Hall Effect under MGTPT

Full size image
Fig. 3
figure 3

The temperature deviation with Hall Effect under MGTPT

Full size image

Figure 4 shows the change in the carrier density in the semiconducting sphere for MGTPT theory with Hall Effect. It has been noticed that in absence of Hall Effect, the variation in carrier density is minimum. As soon as, Hall current increase, the carrier density sharply increases. In comparison to the sphere's outer core, the inner core's carrier density has been found to vary less. Figures 5, 6 shows the variation in the components of stress in the semiconducting sphere for MGTPT with Hall Effect. The radial stress in Fig. 5 illustrates that without Hall Effect with MGTPT theory, the variation are minimum. There is sharp change in the hoop stress as the Hall current increases. Furthermore, as compared to the outer core of the sphere, it has been observed that the inner core of the sphere experiences less variation in stress components.

Fig. 4
figure 4

The change in carrier density with Hall Effect under MGTPT

Full size image
Fig. 5
figure 5

The variation in radial stress with Hall Effect under MGTPT

Full size image
Fig. 6
figure 6

The change in hoop stress with Hall Effect under MGTPT

Full size image

Figure 7 illustrates the deviation in the displacement component \(u\) of the semiconducting sphere for various models. It has been observed that in absence of Hall Effect under PLS theory, there is maximum variation in \(u\). Though, with MGTPT theory in presence of Hall Effect, variation in the displacement is sharply increases. Moreover, in the centre of the sphere, there is no variation in the displace component, but as radial distance increases, deviation in the \(u\) increases sharply. Figure 8 demonstrates the deviation in the temperature distribution \(T\) in the semiconducting sphere with various models. It has been noticed that \(T\) is lesser in the inside core of the sphere as compared to the external core of the sphere. Additionally, presence of Hall Effect cause the higher variation in \(T\).

Fig. 7
figure 7

The change of displacement for various models with Hall effect

Full size image
Fig. 8
figure 8

The temperature change for different models

Full size image

Figure 9 shows the change in the carrier density in the semiconducting sphere for various models with Hall Effect. It has been noticed that with MGTPT, the variation in carrier density is maximum and PLS shows the minimum variations in the carrier density. In comparison to the sphere's outer core, the inner core's carrier density has been found to vary less. Figures 10, 11 shows the variation in the components of stress in the semiconducting sphere for various models with Hall Effect. The radial stress in Fig. 10 illustrates that MGTPT theory, the variation in radial stress is maximum whereas, hoop stress is minimum. There is sharp change in the hoop stress as the Hall current increases. However, PGN-III shows the minimum variation in radial stress and MGTPT illustrate maximum variation. Additionally, MGTPT shows the minimum variation in hoop stress and PLS illustrate maximum variation. Furthermore, as compared to the outer core of the sphere, it has been observed that the inner core of the sphere experiences less variation in stress components.

Fig. 9
figure 9

The change in carrier density for different models

Full size image
Fig. 10
figure 10

The change in radial stress for different models

Full size image
Fig. 11
figure 11

The change in hoop stress with different models

Full size image

8 Conclusions

  • The rotating infinite semiconducting solid sphere has been investigated in this study under the influence of high magnetic field along its axis with the exponentially laser pulse applied on its boundary surface.

  • The study is motivated not only by basic scientific interests, but also by the increasing need for faster interaction and information processing as well as the use of semiconductor optoelectronic and electronic devices. It is important to understand how semiconductors operate dynamically under Hall current effect so that microelectronic semiconductor devices may be improved. Hall Effect have an incredibly strong effect on the behavior of different distributions. In evaluating semiconducting materials, this should be taken into consideration, as the duration of the Hall current increases the carrier density and decreases the deviation in the displacement.

  • It has been noticed that with MGTPT theory, the variation in radial stress is maximum whereas, hoop stress is minimum. However, PLS theory shows the higher variation in different components.

  • The energy harvesting and generating the alternative energy sources is the need of the day. There is a significance contribution of the semiconductor materials to generate electrical energy from sunlight, even when subjected to laser light. The study may be helpful in designing of semiconductor nano-devices, Hall Effect sensors, magnetic switch, and applications in transistors, screens and solar cells as well as semiconductor nanostructure devices such as MEMS/NEMS.