Numerical Analysis of MHD Nanofluid Flow Characteristics with Heat and Mass Transfer over a Vertical Cone Subjected to Thermal Radiations and Chemical Reaction

Abstract

Nanoparticles have the ability to increase the impact of convective heat transfer in the boundary layer region. An investigation is made to analysis of magnetohdrodynamic nanofluid flow with heat and mass transfer over a vertical cone in porous media under the impact of thermal radiations and chemical reaction. In addition, thermal radiations, Hall current, and viscous and Joule dissipations and chemical reaction effects are considered. Considered three different nanoparticles types namely copper, silver, and titanium dioxide with water as base fluid. The governing equations are transformed by similarity transformations into a set of non-linear ordinary differential equations involving variable coefficients. Two numerically approaches are used to solve the transformed boundary layer system Finite Difference Method (FDM) and Chebyshev-Galerkin Method (CGM). As stated in the present analysis, it is appropriate to address a number of physical mechanisms, including velocity, temperature and concentration, as well as closed-form skin friction/mass transfer/heat transfer coefficients. Different comparisons are done with previously published data in order to validate the current study under specific special circumstances, and it is determined that there is a very high degree of agreement. The main results indicated that as the Prandtl number increases, the temperature profile decreases, but it grows for higher values of the thermophoresis parameter, Brownian motion, and Eckert number. Moreover, higher Brownian motion values lead to a less prominent concentration profile. Consequently, this speeds up the cooling process and enhances the surface’s durability and strength.

1 Introduction

Investigation of nanofluid flow over curved bodies has gained importance in recent years Due to its numerous applications in technology, science, biomechanics, and chemical industries such as solar energy collection, heat exchanger, thermal energy storage devices, and electronic cooling,...etc [1, 2]. The geometries of cones, cylinders, ellipses, and wavy channels are some examples of curved bodies. The term of nanofluid was first proposed by Choi [3] he found that when addition of small quantity nanoparticles in a base fluid likes oil, water, and ethylene enhance thermal conductivities. Several researchers have carried out experimental and theoretical investigations on nanofluid flow over cone bodies involves mass and heat transport underneath various physical circumstances. Chamkha and Rashad [4] examined the fluid flow through a permeable vertical cone embedded in a porous medium that was saturated with a nanofluid under a constant lateral mass flux. Noghrehabadi et al. [5] investigated the flow of non-Darcy nanofluid and natural convection through a vertical cone imbedded in a porous medium using the Forchheimer-extended Darcy law. Chamkha [6] analyzed the consistent lateral mass flux impacts a non-Newtonian nanofluid’s along a vertical cone buried in a porous media. The transient two-dimensional Newtonian nanofluid flow past through a cone and plate was numerically investigated by Buddakkagari, and Kumar [7]. The finite element analysis for unstable natural convection of a nanofluid flow passing through a vertical cone under the effect of an applied magnetic field and thermal radiation was performed by Balla, and Naikoti [8]. Reddy, and Chamkha [9] analysed numerically the heat and mass transmission of nanofluid past along a vertical cone with thermal radiation, electrically conducting natural convection and chemical reaction. The flow of a microporous nanofluid past a vertically permeable cone with fluctuating wall temperatures was discussed by Ahmed [10]. Maxwell nanofluid flow through a vertical cone packed with carbon nanotubes and heat and mass transport with velocity and thermal slip effects was examined by Prabhavathi et al. [11]. The effect of surface roughness on mixed convective nonlinear nanofluid flow over vertical cone was caried out by Patil et al. [12]. Sravanthi. [13] analyzed the effects of second order slip, nonuniform heat source/sink and nonlinear thermal radiation on nanofluid flow over a vertical cone. Hussain et al. [14] developed The heat transfer of multi-based nanofluids flow over a rotating vertical cone. The free convection heat transfer of a Darcy nanofluid-saturated porous medium over isothermal vertical cone was mathematically modeled by Rao et al. [15]. Ellahi et al. [16] examined the heat transfer of CNTs-water nanofluid flow passing on a vertical cone. Dharmaiah et al. [17] carried out the 2D non-Newtonian incompressible nanofluid flow over a cone with radiation absorption and Arrhenius activation energy impacts. The effects of mixed convection, variable viscosity, and viscous dissipation on the unsteady nanofluid flow across a cone was explored by Mustafa et al.[18]. Patil and Goudar [19] studied the entropy optimisation of non-Newtonian nanofluid flow over rotating sphere with the use of magnetised field, activation energy, and liquid hydrogen diffusion. On the basis of microscopic mechanics, a mechanoelectrical flexible hub-beam model of ionic-type solvent-free nanofluids was highlighted by Hu et al. [20]. Some further problems related to the flow of solvent, solvent-free nanofluids phenomena due to its many important applications can be found in the literature [21, 22].

The magnetohydrodynamics (MHD) fluid flow with heat and mass transfer through a permeable truncated cone with varying surface temperature while taking into account the effects of thermal radiation and chemical reactions was reported by Chamkha et al. [23]. Raju et al. [24] studied the MHD natural convective heat transfer of non-Newtonian nanofluid flow over vertical cone. The impact of viscous dissipation, temperature dependent, and viscosity on MHD unsteady nanofluid flow over a cone was studied by Raju et al. [25]. Reddy et al. [26] studied the effects of magnetic field, thermal radiation and chemical reaction on the nanofluid flow with heat and mass transfer over a vertical cone. the effects of MHD natural flow through a cone in the presence of cadmium telluride (CdTe) nanoparticles was analyzed by Hanif et al. [27]. Reddy et al. [28] exmined heat and mass transfer characteristics of MHD nanofluid flow over a vertical cone with chemical reaction and thermal radiation. The gyrotactic microorganism behaviour affect the MHD flow of Jeffrey nanofluid studied by Saleem et al. [29]. The heat transfer of unsteady MHD nanofluid flow passing through an inverted cone surrounded by a porous medium was examined by Hanif et al. [30]. Mogharrebi et al. [31] discussed a convective heat transfer of three-dimensional MHD nanofluid flow past on a rotating cone. Ashwinkumar et al. [32] investigated the impact of nonlinear heat radiation on 2-D hybrid nanoliquid magnetohydrodynamic flow over an embrittled cone. Ashraf et al. [33] studied numerically the impacts of varying surface temperature on periodic mixed convective flow past electrically and thermally conducting cones implanted in porous media. Maxwell nanofluid’s MHD mixed convection flow, which is debatable in the setting of a vertical cone containing porous material, was examined by Kodi et al [34]

Based on the research above, it has been found that the flow of nanofluid via curved bodies could play a vital part in a number of applications in the chemical, biomechanical, technology, and scientific fields. Therefore, the current work’s goal is to examine the impact of various physical parameters affect on flow and heat transfer of a nano-fluid from a vertical cone when thermal radiation is present. We considered three different types of nanoparticles: copper, silver, and titanium dioxide, with water serving as the fundamental nanofluid. The problem is formulated and solved by two methods semi-analytical using Chebyshev-Galerkin method and numerically by Finite Difference method. Graphs are used to illustrate, analyse, and discuss the relevant outcomes of physical parameters. To validate the current results, various comparisons with previously published data are undertaken in a few specific circumstances.

2 Mathematical Model and Formulation

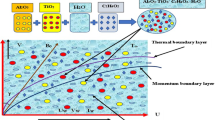
Consider MHD steady two dimensional laminar incompressible nanofluid flows with heat and mass transfer through the porous medium over a vertical cone in the presence of thermal radiation, viscous and Joule dissipations effects. Coordinate systems (x-y) have been employed, where $x\text {-axis}$ is chosen along the cone surface and the $y\text {-axis}$ is perpendicular to it, as shown in Fig. 1. Furthermore, in our research, we have considered that certain crucial nonlocal effects of nanoparticles in fluids encompass the Brownian motion of nanoparticles [35,36,37]. The cone’s vertex, designated O, serves as the coordinate system’s origin. Three different types of nano-particles are present in the water used as a base for the nanofluid, including, Cu, Ag, and $\text {TiO}_2$, the thermophyical properties are listed in Table 1. Uniform magnetic field applied by strength $B_o$ in normal to the flow direction ($y\text {-axis}$). Assumed to be the cone surface is maintained at a uniform temperature $T_w$, and the ambient temperature, $T_\infty$. The induced magnetic field could be disregarded because it is presumed that the magnetic Reynolds number is low. The governing equations for this issue can be expressed as follows using the standard boundary layer approximation [38, 39]:

Table 1 Thermophysical properties of water and nano-particles [1, 40]

Fig. 1

Physical model

The continuity equation:

$$\begin{aligned} \displaystyle \frac{ \partial u r}{\partial x} +\frac{ \partial v r}{\partial y}=0 \end{aligned}$$

(1)

The momentum formula:

$$\begin{aligned} \displaystyle \rho _{\text{nf}}\left[ u\frac{\partial u}{\partial x} +v \frac{\partial u}{\partial y}\right] =\mu _{\text{nf}} \frac{\partial ^{2} u}{\partial y^{2}}+g(\rho \beta )_{\text{nf}} \cos {(\gamma )} (T-T_\infty )-\frac{\sigma B_{o}^{2}}{1+m^{2}}u -\frac{\mu _{\text{nf}}}{\tilde{k}} u, \end{aligned}$$

(2)

The energy formula:

$$\begin{aligned} \displaystyle (\rho c_p)_{\text{nf}} \left[ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}\right]&=k_{\text{nf}}\frac{\partial ^{2} T}{\partial y^{2}} +\frac{\sigma B_{o}^{2}}{1+m^{2}}u^{2} -\frac{\partial q_r}{\partial y}+\rho _s {c_p}_s\nonumber \\&\quad \left[ D_{\text{B}} \frac{\partial C}{\partial y} \frac{\partial T}{\partial y}+\frac{D_{\text{T}}}{T_\infty } \left( \frac{\partial T}{\partial y}\right) ^2 \right] \end{aligned}$$

(3)

The concentration formula:

$$\begin{aligned} \displaystyle u\frac{\partial C}{\partial x} +v\frac{\partial C}{\partial y}=D_{\text{B}} \frac{\partial ^{2} C}{\partial y^{2}} +\frac{D_{\text{T}}}{T_\infty } \frac{\partial ^{2} T}{\partial y^{2}} -\lambda _{c}(C-C_{\infty }) \end{aligned}$$

(4)

depending on the boundary circumstances:

$$\begin{aligned}&y=0: \quad u=0, \quad v=0, \quad T=T_{w}, \quad C=C_{w} \nonumber \\&y\rightarrow \infty : \quad u=0, \quad T=T_{\infty }, \quad C=C_{\infty }. \end{aligned}$$

(5)

Radiative heat flux is formulated by Rosseland approximation as:

$$\begin{aligned} q_r=- \frac{4\sigma ^{*}}{3\alpha ^{*}} \frac{\partial T^4}{\partial y} \end{aligned}$$

(6)

Hence, expanding $\displaystyle T^4$ in a Taylor series about $\displaystyle T_\infty$ and neglecting higher-order terms, we get:

$$\begin{aligned} T^4\cong 4T_{\infty }^3 T-3T_{\infty }^4 \end{aligned}$$

(7)

From Eqs. (6-7), the Eq. (3) can be written as

$$\begin{aligned} \displaystyle (\rho c_p)_{\text{nf}}\left[ u\frac{\partial T}{\partial x} +v\frac{\partial T}{\partial y}\right]&=k_{\text{nf}} \frac{\partial ^{2} T}{\partial y^{2}} +\frac{\sigma B_{o}^{2}}{1+m^{2}}u^{2} +\frac{16\sigma ^{*} T_{\infty }^3}{3\alpha ^{*}} \frac{\partial ^2 T}{\partial y^2}+\rho _s {c_p}_s\nonumber \\&\quad \left[ D_{\text{B}} \frac{\partial C}{\partial y} \frac{\partial T}{\partial y}+\frac{D_{\text{T}}}{T_\infty } \left( \frac{\partial T}{\partial y}\right) ^2 \right] \end{aligned}$$

(8)

The thermophysical properties of the nano-fluid were determined as [41]:

$$\begin{aligned}&J_1=\frac{\mu _{\text{nf}}}{\mu _{\rm{f}}}=(1-\phi )^{-2.5} , \quad J_2=\frac{\rho _{\text{nf}}}{\rho _{\rm{f}}}=1-\phi +\phi \frac{\rho _s}{\rho _f},\nonumber \\&J_3=\frac{(\rho \beta )_{\text{nf}}}{(\rho \beta )_{\rm{f}}}=1 -\phi +\phi \frac{(\rho \beta )_s}{(\rho \beta )_f}, \nonumber \\&J_4=\frac{k_{\text{nf}}}{k_{\rm{f}}}=\frac{k_s+2k_f -2\phi (k_f-k_s)}{k_s+2k_f+\phi (k_f-k_s)}, \quad {J_5=\frac{(\rho c_p)_{\text{nf}}}{(\rho c_p)_{\rm{f}}} =1-\phi +\phi \frac{(\rho c_p)_s}{(\rho c_p)_f}}. \end{aligned}$$

(9)

By using the following dimensionless transformation [1],

$$\begin{aligned}&\eta =\frac{y}{x} (Gr_x)^{1/4},\,\, \psi =\nu _f r (Gr_x)^{1/4} f(\eta ),\,\, Gr_x=\frac{g \beta _f x^3 \cos \gamma (T_w-T_\infty )}{\nu ^2_f},\nonumber \\&\theta (\eta ) =\frac{T-T_\infty }{T_w-T_\infty },\,\, \Phi (\eta ) =\frac{C-C_\infty }{C_w-C_\infty } \end{aligned}$$

(10)

Where, $f(\eta )$, $\Phi (\eta )$ and $\theta (\eta )$ are the nanofluid stream, temperature, and concentration function, respectively. $r=x\sin \gamma$ and $\psi$ is the stream function which is defined as:

$$\begin{aligned} ru=\frac{\partial \psi }{\partial y}, \,\,\,\,\,\,\,\,\, and\,\,\,\,\,\,\,\, rv=-\frac{\partial \psi }{\partial x} \end{aligned}$$

The dimensionless transformation (10) satisfy Eq. (1) and reducing Eqs. (2–5) into following non-dimensional system of ODE by using Eq. (10):

$$\begin{aligned}&\frac{J_1}{J_2}f'''(\eta )+\frac{7}{4}f(\eta )\,f''(\eta ) -\frac{1}{2}f'^{2}(\eta )+\frac{J_3}{J_2}\Theta (\eta ) -\frac{M^2}{(1+m^2)J_2} \,f'-\frac{J_1}{J_2} K_{\text{p}} f'(\eta )=0, \end{aligned}$$

(11)

$$\begin{aligned}&\left[ \frac{N_R+J_4}{Pr\, J_5}\right] \Theta ''(\eta ) +\frac{7}{4}\, f(\eta )\, \Theta '(\eta )+\frac{M^2 Ec}{J_5(1+m^2)} f'^{2}(\eta )\nonumber \\&\quad +\frac{N_b}{J_5}\Theta '(\eta ) \Phi '(\eta ) +\frac{N_t}{J_5}\Theta '^2(\eta )=0, \end{aligned}$$

(12)

$$\begin{aligned}&\Phi ''(\eta )+\frac{7}{4}Sc \, f(\eta )\,\Phi '(\eta ) +\frac{N_t}{N_b} \Theta ''(\eta )-Sc\, \gamma _{c}\, \Phi (\eta )=0. \end{aligned}$$

(13)

where, $M={\sigma B_{o}^{2}}/{\rho b}$ is the Magnetic parameter, $Pr={\rho \nu c_{p}}/{k_{f}}$ is the Prandtl number, $Gr=(g\, \beta _f \,x^3 \cos {\gamma }\,(T_w-T_\infty ))/\nu _f^2$ is the Grashof number, $Ec={u_{w}^{2}}/{(c_{p}(T_{w}-T_{\infty }))}$ is the Eckert number, $Sc={\nu }/{D_{B}}$ is the Schmidt number. $N_b={\tau D_B \Delta C }/{\nu }$ Brownian parameter, $N_t={\tau D_T \Delta T }/{\nu }$ is the Thermophoresis parameter, $\ \gamma _{c}={k_{c} x^2}/{\nu Gr^{1/2}}$ is the chemical parameter, and $\ K_{\text{p}}={x^2/(\tilde{k} Gr^{1/2})}$ is Permeability parameter. In this context, it is evident that Grashof number, chemical parameter, and Permeability parameter are parameters that vary with the length scale x. It should be noted that Grashof number, chemical parameter, and Permeability parameter are dependent on x, and their values change locally as the flow progresses. Consequently, the equation presented is applicable solely for a locally similar solution [42].

The corresponding non-dimensional boundary conditions are:

$$\begin{aligned}&f(\eta )=0, \quad f'(\eta )=0, \quad \Theta (\eta )=1, \quad \Phi (\eta )=1,\text { at }\eta =0 \nonumber \\&f'(\eta )=0, \quad \Theta (\eta )=0, \quad \Phi (\eta )=0,\text { at }\eta \rightarrow \infty \end{aligned}$$

(14)

3 Solution Approach

3.1 Chebyshev-Galerkin Method

3.1.1 Preliminaries and Notions

Chebyshev polynomials $\displaystyle T_{n}(t)$ are frequently employed in numerical computations. In the numerical resolution of numerous boundary value issues, Chebyshev polynomials have been successfully demonstrated.

The product of Chebyshev polynomials is given:

$$\begin{aligned} \displaystyle T_n(t)T_m(t)= \displaystyle \frac{1}{2} \left[ T_{m+n}(t)+T_ {|m-n|}(t),\quad \forall m,n\ge 0 \right] . \end{aligned}$$

(15)

The analytical form of Chebyshev polynomial is given as:

$$\begin{aligned} T_n(t)=\frac{n}{2}\sum \limits _{k=0}^{\lfloor \frac{n}{2}\rfloor }(-1)^k \frac{(n-k-1)!}{k!\,(n-2k)!}\,(2t)^{n-2k},\quad n>0, \end{aligned}$$

(16)

with inverse,

$$\begin{aligned} t^k=2^{1-k} \mathop {{\mathop {\sum }\nolimits '}}\limits _{\begin{array}{c} j=0 \\ k-j \ \text {even} \end{array}}^{k} \left( {\begin{array}{c}k\\ \frac{k-j}{2}\end{array}}\right) T_j(t), \end{aligned}$$

(17)

where $\lfloor \frac{n}{2}\rfloor$ denotes the integer part of $\frac{n}{2}$.

The orthogonality of Chebyshev polynomials on $\displaystyle [-1, 1]$ is given as:

$$\begin{aligned} \displaystyle \int _{-1}^{1}T_{m}(t) T_{n}(t)\frac{dt}{\sqrt{1-t^2}} ={\left\{ \begin{array}{ll} \pi , &{}\text {if}\ m= n=0,\\ \frac{\pi }{2}, &{}\text {if}\ m=n\ne 0,\\ 0, &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

(18)

and Chebyshev roots $t_i$ is determined as

$$\begin{aligned} t_i=\cos \left( \frac{2i-1}{n}\frac{\pi }{2}\right) ,\quad i=1,2,3,\ldots , n. \end{aligned}$$

The Chebyshev-Gauss quadrature rule is given as:

$$\begin{aligned} \displaystyle \int _{-1}^{1} \bar{\omega }F(t)\,dt \cong \frac{\pi }{n} \displaystyle \sum _{i=1}^{n}F(t_{i}), \end{aligned}$$

(19)

and $\displaystyle \bar{\omega }=\displaystyle \frac{1}{\sqrt{1-t^2}}$ is the weight function.

Chebyshev polynomials that have special values at the end points $\displaystyle \{\pm 1\},$ are given as:

$$\begin{aligned}&T_{n}(-1)=(-1)^{n} ,\qquad T_{n}(1)=1, \qquad T'_n(-1)=(-1)^n n^2,\qquad T'_n(1)=n^2. \end{aligned}$$

(20)

$$\begin{aligned}&\frac{d^p T_n(t)}{d t^p}=2^p \cdot n \mathop {{\mathop {\sum }\nolimits '}}\limits _{\begin{array}{c} k=0\\ n-k\ \text {even} \end{array}}^{n} \left( {\begin{array}{c}\frac{n+p-k}{2}-1\\ \frac{n-p-k}{2}\end{array}}\right) \frac{\left( \frac{n+p+k}{2}-1\right) !}{\left( \frac{n+p+k}{2}\right) !} \,T_k(t),\,p\ge 1, \end{aligned}$$

(21)

Theorem 3.1

Let $r, n, \text { and } m\in {\mathbb {Z}}.$

$$\begin{aligned} \int _{-1}^{1}\frac{t^{r}T_{n}(t)T_{m}(t)}{\sqrt{1-t^{2}}} \,dt=2^{-r} \mathop {{\mathop {\sum }\nolimits '}}\limits _{\begin{array}{c} j=0\\ r-j\ \text {even} \end{array}}^{r} \left( {\begin{array}{c}r\\ \frac{r-j}{2}\end{array}}\right) \left( \delta _{m,n+j}+\delta _{m,|n-j|}\right) . \end{aligned}$$

(22)

where,

$$\begin{aligned} \delta _{m,n+j}={\left\{ \begin{array}{ll} \pi , &{}\text {if}\ m= n+j=0,\\ \frac{\pi }{2}, &{}\text {if}\ m=n+j\ne 0,\\ 0, &{}\text {otherwise}, \end{array}\right. }, \quad \delta _{m,|n-j|}={\left\{ \begin{array}{ll} \pi , &{}\text {if}\ m= |n-j|=0,\\ \frac{\pi }{2}, &{}\text {if}\ m=|n-j|\ne 0,\\ 0, &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

Proof

Expanding $t^{r}$ as series of Chebyshev $T_{j}(t)$ by recalling Eq. (17), then recalling product rule Eq. (15),then apply orthogonality rule (18). $\square$

Theorem 3.2

Let $r, n, m, \text { and } s \in {\mathbb {Z}}.$

$$\begin{aligned} \int _{-1}^{1}\frac{t^{r}T_{n}^{(s)}(t)T_{m}(t)}{\sqrt{1-t^{2}}} \,dt&= 2^{s-r} \cdot n \mathop {{\mathop {\sum }\nolimits '}}\limits _{\begin{array}{c} j=0\\ r-j\ \text {even} \end{array}}^{r} \mathop {{\mathop {\sum }\nolimits '}}\limits _{\begin{array}{c} k=0\\ n-k\ \text {even} \end{array}}^{n}\left( {\begin{array}{c}r\\ \frac{r-j}{2}\end{array}}\right) \left( {\begin{array}{c}\frac{n+s-k}{2}-1\\ \frac{n-s-k}{2}\end{array}}\right) \nonumber \\&\quad \frac{\left( \frac{n+s+k}{2}-1\right) !}{\left( \frac{n+s+k}{2}\right) !} \left( \delta _{m,k+j}+\delta _{m,|k-j|}\right) \end{aligned}$$

(23)

where,

$$\begin{aligned} \delta _{m,k+j}={\left\{ \begin{array}{ll} \pi , &{}\text {if}\ m= k+j=0,\\ \frac{\pi }{2}, &{}\text {if}\ m=k+j\ne 0,\\ 0, &{}\text {otherwise}, \end{array}\right. }, \quad \delta _{m,|k-j|}={\left\{ \begin{array}{ll} \pi , &{}\text {if}\ m= |k-j|=0,\\ \frac{\pi }{2}, &{}\text {if}\ m=|k-j|\ne 0,\\ 0, &{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

$\square$

Proof

Expanding $t^{r}$ as series of Chebyshev $T_{j}(t)$ by recalling Eqs. (17) and (21), then recalling product rule (15),then apply orthogonality rule (18). $\square$

3.1.2 Numerical Procedure

By making domain treatment and convert domain problem $\displaystyle 0\le \eta \le L,$ where $\displaystyle L$ is boundary edge into Chebyshev domain $\displaystyle -1\le t\le 1$ by using relation $\displaystyle \eta =\frac{L}{2}(t+1).$ For sake of simplicity, we may rewrite Eqs. (11–13) and (14)

$$\begin{aligned}&\frac{J_1}{J_2}f'''(t)+\frac{7}{4}\left( \frac{L}{2}\right) f(t)\,f''(t) -\frac{1}{2}\left( \frac{L}{2}\right) f'^{2}(t)+\left( \frac{L}{2}\right) ^{3} \frac{J_3}{J_2}\, \Theta (t)-\left( \frac{L}{2}\right) ^{2}\nonumber \\&\quad \left[ \frac{M^2}{(1+m^2)J_2}+\frac{J_1}{J_2}K_p\right] \,f'(t)=0, \end{aligned}$$

(24)

$$\begin{aligned}&\left[ \frac{N_R+J_4}{Pr J_5}\right] \Theta ''(t)+\frac{7}{4}\left( \frac{L}{2} \right) f(t)\Theta '(t)+\frac{M^2\,Ec}{(1+m^2)J_5}f'^2(t)\nonumber \\&\quad +\frac{N_b}{J_5}\Theta '(t) \Phi '(t) +\frac{N_t}{J_5}\Theta '^2(t)=0, \end{aligned}$$

(25)

$$\begin{aligned}&\Phi ''(t)+ \frac{7}{4} \left( \frac{L}{2}\right) Sc\, f(t)\,\Phi '(t) +\frac{N_t}{N_b}\Theta ''(t)-\left( \frac{L}{2}\right) ^2\,Sc\,\gamma _c \, \Phi (t)=0. \end{aligned}$$

(26)

with boundary conditions

$$\begin{aligned}&f=0, \quad f'=0, \quad \Theta =1 \quad \Phi =1 \quad \text { at }t=-1, \nonumber \\&f'=0, \quad \Theta =0 \quad \Phi =0 \quad \text {at } t=1. \end{aligned}$$

(27)

The solution of Eqs. (24−26) with boundary conditions (27), the approximated solution can be written as:

$$\begin{aligned} f_{n}(t)=\sum _{j=0}^{n}c_{j} T_{j}(t), \quad \Theta _{n}(t)=\sum _{j=0}^{n}b_{j} T_{j}(t), \quad \Phi _{n}(t)=\sum _{j=0}^{n}d_{j} T_{j}(t). \end{aligned}$$

(28)

After substituting at Eqs. (24−27), and apply Galerkin technique  can be written as:

$$\begin{aligned}&\frac{J_1}{J_2}\sum _{i=0}^{n}c_{i} \langle T_{i}'''(t),T_{k}\rangle + \frac{7L}{8}\sum _{i=0}^{n}\sum _{j=0}^{n}c_{i}c_{j} \langle T_{i}(t)T_{j}''(t),T_{k}\rangle \nonumber \\&\quad -\frac{L}{4} \sum _{i=0}^{n}\sum _{j=0}^{n}c_{i}c_{j} \langle T_{i}'(t)T_{j}'(t),T_{k}(t)\rangle \nonumber \\&\quad +\frac{J_3}{J_2}\frac{L^3}{8}\sum _{i=0}^{n}b_{i} \langle T_{i}(t),T_{k}\rangle -\frac{L^2}{4} \left[ \frac{M^2}{(1+m^2)J_2}+\frac{J_1 K_p}{J_2}\right] \nonumber \\&\quad \sum _{i=0}^{n}c_{i} \langle T_{i}'(t),T_{k}(t)\rangle =0, \; k=0,1,2,\ldots n-3, \end{aligned}$$

(29)

$$\begin{aligned}&\left[ \frac{N_R+J_4}{Pr\,J_5}\right] \sum _{i=0}^{n}b_{i} \langle T_{i}''(t),T_{k}\rangle +\frac{7L}{8}\sum _{i=0}^{n} \sum _{j=0}^{n}c_{i}b_{j} \langle T_{i}(t)T_{j}'(t),T_{k}\rangle \nonumber \\&\quad +\frac{M^2\,Ec}{(1+m^2)J_5}\sum _{i=0}^{n}\sum _{j=0}^{n}c_{i}c_{j} \langle T_{i}'(t)T_{j}'(t),T_{k}(t)\rangle \nonumber \\&\quad +\frac{N_b}{J_5}\,\sum _{i=0}^{n}\sum _{j=0}^{n}b_{i}d_{j} \langle T_{i}'(t)T_{j}'(t),T_{k}(t)\rangle \nonumber \\&\quad +\frac{N_t}{J_5} \,\sum _{i=0}^{n}\sum _{j=0}^{n}b_{i}b_{j} \langle T_{i}'(t) T_{j}'(t),T_{k}(t)\rangle =0, \; k=0,1,2,\ldots n-2, \end{aligned}$$

(30)

$$\begin{aligned}&\sum _{i=0}^{n}d_{i} \langle T_{i}''(t),T_{k}\rangle +\frac{7L Sc}{8} \,\sum _{i=0}^{n}\sum _{j=0}^{n}c_{j}d_{i} \langle T_{i}'(t)T_{j}(t),T_{k}\rangle \nonumber \\&\quad +\frac{N_t}{N_b} \sum _{i=0}^{n}b_{i} \langle T_{i}''(t),T_{k}\rangle -\frac{L^2 Sc \,\gamma _c}{4}\sum _{j=0}^{n}d_{j} \langle T_{j}(t),T_{k}\rangle =0,\nonumber \\&\quad k=0,1,2,\ldots n-2. \end{aligned}$$

(31)

subject to boundary conditions

$$\begin{aligned}&\sum _{j=0}^{n}(-1)^jc_{j}=0, \quad \sum _{j=0}^{n} (-1)^j j^2 c_j=0, \quad \sum _{j=0}^{n}(-1)^j b_{j}=1 \quad \sum _{j=0}^{n}(-1)^j d_{j}=1,\nonumber \\&\sum _{j=0}^{n} j^2 c_{j}=0 , \quad \sum _{j=0}^{n} b_{j}=0 , \quad \sum _{j=0}^{n} d_{j}=0. \end{aligned}$$

(32)

where inner product $\langle ,\rangle$ is described as:

$$\begin{aligned} \langle \Omega ,\varphi \rangle =\int _{-1}^{1} \frac{\Omega \, \varphi }{\sqrt{1-t^2}}\,dt, \end{aligned}$$

By applying the orthogonality rule (18) and theorems 3.1, 3.2 to evaluate the integrating terms of the Eqs. (29−31) lead to a nonlinear system containing $3n + 3$ unknowns $\displaystyle f(c_{i})$, $\displaystyle \Theta (b_{i}),\text { and } \Phi (d_{i})$. The reduced equations and boundary conditions (32) are represented a nonlinear algebraic system can be solved using Newton’s method. Finally, the relation $t=\dfrac{2}{L}\eta -1$ can be used to transform the solution domain $[-1,1]$ to the original domain [0, L].

3.2 Finite Difference Method

In this section, we can utilize the finite difference method to compute the numerical solution. We discretize the domain [0, L] with N subintervals with step size $\Delta \eta =\frac{L}{N}$,and for simplicity reduce third order term into second order by letting $u=f'$. The system ODE can be written as:

$$\begin{aligned}&f_i-f_{i-1}-\Delta \eta u_i=0,\;i=1,2,\ldots , N-1, \end{aligned}$$

(33)

$$\begin{aligned}&\frac{J_1}{J_2}(u_{i-1}-2u_i+u_{i+1})+\frac{7\Delta \eta }{8} f_i\,(u_{i+1}-u_{i-1})-\frac{(\Delta \eta )^2}{2}u_i^{2} +\frac{J_3(\Delta \eta )^2}{J_2}\Theta _i\nonumber \\&\qquad -\left[ \frac{M^2 (\Delta \eta )^2}{(1+m^2)J_2} +\frac{J_1(\Delta \eta )^2K_{\text{p}}}{J_2} \right] \,u_i \nonumber \\&\quad =0,\;i=1,2,\ldots , N-1, \end{aligned}$$

(34)

$$\begin{aligned}&\left[ \frac{N_R+J_4}{Pr\, J_5}\right] (\Theta _{i-1}-2\Theta _i +\Theta _{i+1})+\frac{7\Delta \eta }{8}\, f_i (\Theta _{i+1} -\Theta _{i-1})\nonumber \\&\qquad +\frac{M^2 Ec (\Delta \eta )^2}{J_5(1+m^2)} u_i^{2} +\frac{N_b}{4J_5}(\Theta _{i+1}-\Theta _{i-1}) (\Phi _{i+1}-\Phi _{i-1})\nonumber \\&\qquad +\frac{N_t}{4J_5}(\Theta _{i+1}-\Theta _{i-1})^2=0, \;i=1,2,\ldots , N-1, \end{aligned}$$

(35)

$$\begin{aligned}&\Phi _{i-1}-2\Phi _i+\Phi _{i+1}+\frac{7\Delta \eta }{8}Sc \, f_i\,(\Phi _{i+1}-\Phi _{i-1})\nonumber \\&\qquad +\frac{N_t}{N_b} (\Theta _{i-1}-2\Theta _i+\Theta _{i+1})-Sc \gamma _c (\Delta \eta )^2 \Phi _i=0, i=1,2,\ldots , N-1 \end{aligned}$$

(36)

These non-dimensional boundary conditions are equivalent:

$$\begin{aligned}&f_0=0, \quad u_0=0, \quad \Theta _0=1, \quad \Phi _0=1, \nonumber \\&u_N=0, \quad \Theta _N=0, \quad \Phi _N=0, \end{aligned}$$

(37)

Equations (33–37) represent a nonlinear system of unknowns $\displaystyle \{f_j\}_{j=1}^N,\; \displaystyle \{u_j\}_{j=1}^{N-1}, \; \displaystyle \{\Theta _j\}_{j=1}^{N-1}\text { and } \displaystyle \{\Phi _j\}_{j=1}^{N-1}$ which is solved by Newton method.

4 Methods validation

The physical quantities of interest to indicate physical surface shear stress and rate of heat transfer, which have a direct impact on the mechanical properties of the surface after heat treatment due to the surface’s increased capacity for heat transmission [43]. these quantities are skin friction coefficient, Nusselt number and Sherwood numbers which are formed by [1, 44]:

• surface shear stress

  $$\begin{aligned} \displaystyle \tau _{w}=\mu _{\text{nf}} \left( \frac{\partial u}{\partial y}\right) _{y=0} =\mu _{\rm{nf}} \left[ \sqrt{\frac{\nu _f (Gr)^{3/4}}{x^2}}f''(0) \right] \end{aligned}$$

• skin friction coefficient

  $$\begin{aligned} \displaystyle C_{f}=\frac{2\tau _{w}}{\rho _{f} u_{w}^{2}} \end{aligned}$$

  where $\displaystyle u_{w}=\frac{\nu _{f} (Gr)^{1/2}}{x}$ is the reference velocity.

• surface heat flux

  $$\begin{aligned} \displaystyle q_{w}=-k_{\text{nf}} \left( \frac{\partial T}{\partial y}\right) _{y=0}=-k_{\rm{nf}} \left[ \frac{(T_{w}-T_{\infty })(Gr)^{1/4}}{x} \Theta '(0)\right] \end{aligned}$$

  and the local surface flux transfer coefficient is given by

  $$\begin{aligned} \displaystyle h_{w}=\frac{q_{w}(x)}{(T_{w}-T_{\infty })} \end{aligned}$$

• Nusselt number

  $$\begin{aligned} \displaystyle {Nu}_{x}=\frac{x q_{w}}{k_{f}(T_{w}-T_{\infty })} \end{aligned}$$

• Mass heat flux

  $$\begin{aligned} \displaystyle q_{m}=-D_B\left( \frac{\partial C}{\partial y}\right) _{y=0} =-D_B \left[ \frac{(C_{w}-C_{\infty })(Gr)^{1/4}}{x} \Phi '(0)\right] \end{aligned}$$

• Sherwood number

  $$\begin{aligned} \displaystyle {Sh}_{x}=\frac{x q_{m}}{D_{B}(C_{w}-C_{\infty })} \end{aligned}$$

To introduce a confirmation for the validation and accuracy of our numerical methods and results, we comparing our results with the previously published work which was reported by Hering [45], Roy [46], and Abass and Sayed [1]. We recorded the compared values that signify $f''(0)$ and $-\Theta '(0)$ for various values of Prandtl number after ignoring M, m, Ec, $N_R$, $N_t$, $N_b$ and $\phi$ parameters, as shown in Table 2. Clearly, from this comparison that both results are in a very good agreement.

Table 2 Comparison of values $f''(0), \text { and } -\Theta '(0)$ for different values of Pr at $M=0,m=0,Ec=0, N_R=0,N_t=0, N_b\rightarrow 0$ and $\phi =0$

5 Results and discussion

In this section, we will discuss the results of the presence of some parameters impact on dimensionless velocity $\displaystyle f'(\eta )$, temperature $\displaystyle \Theta (\eta )$ and concentration $\displaystyle \Phi (\eta )$ corresponding to the movement of a nanofluid and the transport of heat along a vertical cone in a porous media while thermal radiation and viscous dissipation are present. The study used water as the base fluid and three distinct kinds of nanoparticles, including copper, silver, and titanium dioxide. The graphical results are illustrated in Figs. 2, 3, 4, 5, 6, 7, 8, 9.

Figure 2, illustrate the fluid velocity, temperature, and concentration as a function of nanoparticles type (Cu, Ag, and $TiO_{2}$) nanofluid. It is observed that, the fluid motion becomes faster by replacing the nanoparticles $TiO_{2}$ with Cu, then to Ag before decaying the velocity to zero. On the other hand, by rearranging the nanoparticles from $TiO_2$ to Cu and subsequently to Ag near the surface, the temperature rises as a result of higher thermal conductivity. Also, the concentration rises by reordering the nanoparticles from $TiO_{2}$ to Ag then to Cu. In order to see the impacts of nanoparticles volume fraction $\phi$, on the $\displaystyle f'(\eta )$, $\displaystyle \Theta (\eta )$, and $\displaystyle \Phi (\eta )$ for Cu-Water nanofluid are illustrated in Fig. 3. This graph shows that the volume fraction of nanoparticles is directly related to temperature and concentration distribution and inversely proportional to velocity distribution. In actuality, the fluid becomes more viscous as the concentration of nanoparticles rises. As a result, natural convection is decreased, which slows fluid flow and increases the thickness of the thermal boundary layer.

Fig. 2

a Velocity distribution of different nonopartilces, b temperature distribution of different nonopartilces c concentration distribution of different nonopartilces

Fig. 3

Effect of nanofraction particles $\phi$ on a velocity distribution, b temperature distribution and c concentration distribution

Furthermore, Figs. 4 and 5, illustrate the effects of thermophoretic and Brownian parameters on the temperature distributions of Cu-water nanofluid. It is seen that the temperature distribution increases with increasing thermophoretic and Brownian parameters. In fact, the thermophoretic and Brownian parameters assist to improve the thermal boundary layer thickness. The effect of the magnetic parameter on velocity, temperature, and concentration distribution of of Cu-water nanofluid is illustrated in Fig. 6. It was found that the temperature and concentration decrease with increasing the values of the magnetic parameter. Additionally, Velocity distribution is decreasing with rising the magnetic parameter. On other hand, Fig. 7 represents the impact of the Hall current parameter on velocity, temperature, and concentration distribution. It is clear that, the velocity distribution of nanofluid increasing with an increase in Hall current parameter and decreases the temperature and concentration.

Fig. 4

Effect of thermophesis parameter $N_t$ on temperature distribution

Fig. 5

Effect of Brownian moment $N_b$ on temperature distribution

Fig. 6

Effect of magentic field M on a velocity distribution, b temperature distribution and c concentration distribution

Fig. 7

Effect of Hall parameter m on a velocity distribution, b temperature distribution and c concentration distribution

The effects of the thermal radiation parameter on the temperature profiles are shown in Fig. 8. Figure 8 makes it evident that, the temperature profiles of the nanofluid rise as thermal radiation increases. It is commonly recognised that raising the radiation parameter improves the fluid’s ability to transport energy, which in turn raises the rate at which heat is transferred. In a physical sense, the temperature profiles of the nanofluid increase as thermal radiation intensifies because of the amplified energy transfer resulting from radiation and the improved heat absorption abilities of nanoparticles. This phenomenon holds significance in diverse engineering applications, like solar energy systems, where nanofluids are utilized to enhance heat transfer efficiency. In addition, the impact of a chemical parameter on the concentration profile is shown in Fig. 9. It is observed that the chemical parameter diminishes as the concentration profile increases. Physically, when the chemical parameter increases, it accelerates the chemical processes, leading to a faster depletion or transformation of the substance. The decrease in concentration directly results from the heightened chemical activity within the system. On the other hand, Table 3 demonstrates that as the chemical parameter increases, the Sherwood number rises. This suggests that the mass transfer rate at the surface plate may tend to rise due to the chemical reaction.

Fig. 8

Effect of radiation parameter $N_R$ on temperature distribution

Fig. 9

Effect of chemical reaction $\gamma _c$ on concentration distribution

Table 3 presents, the values of velocity, temperature, and concentration gradient at the surface for different values of embedded nanoparticles type, magnetic, Hall, Eckert, and thermal radiation parameters. It is observed that, when Cu nanoparticles are used in place of $TiO_2$ nanoparticles, it is seen that the velocity gradient rises while the temperature and concentration gradient fall. For Cu nanoparticles are replaced with Ag, the velocity gradient increases while the temperature and concentration gradient decreases. On other hand, the table, gives, the values of velocity, temperature, and concentration gradient at the surface and the corresponding values of Surface shear stress, Nusselt number, and skin friction. It is noticed that, Skin friction is seen to be greater when $Ag-nanofluid$ is employed than $\text {Tio}_2$ or $\text {Cu-nanofluid}$. Additionally, the fact that using $\text {Cu-nanofluid}$ results in a higher Nusselt number and heat transfer rate than using $\text {Tio}_2$ or $\text {Ag-nanofluids}$ suggests using $\text {Cu-nanofluid}$. The table also demonstrates that as thermal radiation parameters are raised, skin friction coefficient rises and the Nusselt number falls, whereas as Hall current values are raised, both skin friction and the Nusselt number rise. Finally, increasing skin friction and decreasing Nusselt number led to an increase in the Eckert number.

Table 3 Numerical values of $f''(0), \, \Theta '(0)$, and $\Phi (0)$ and $K_p=N_t=N_b=0.2$, and $Sc=1.2$

6 Conclusion

The numerical analysis of MHD nanofluid flow with heat and mass transfer over a vertical cone exposed to thermal radiations, chemical reaction, hall current, viscous, and joule dissipation effects has been the focus of this paper. Utilising three of kinds of nanoparticles (Cu, Ag, and $\text {Tio}_2$) with a water base fluid. The partial differential equations that describe the current problem are converted into ordinary differential equations. Then, these equations are numerically solved using the Chebyshev-Galerkin and finite difference techniques. The suggested methods were validated and found to be good agreement with previous investigations. Consequently, analyses of the velocity, temperature, and concentration profiles can be conducted as well as graphical depictions of them. The following is a condensed version of the conclusions that can be drawn from the numerical results:

• Depending on the kind and quantity of nanoparticles utilised, using nanofluid as a cooling medium can be advantageous to increase the mechanical qualities (hardness and strength).

• The velocity profile is inversely proportional to some characteristics, like the magnetic parameter and nanoparticle concentration, and directly proportional to others, including radiation, heat generation, and Hall parameters.

• With the exception of the Hall parameter, all of the relevant parameters that have been discussed cause the temperature to rise.

• As the nanoparticles $\text{TiO}_2$ are replaced by Cu, then Ag, the fluid motion near the cone surface accelerates, whereas the opposite happens farther away.

• Ag has a higher thermal conductivity than other nanoparticles, which raises the fluid’s temperature. Addition, the nanoparticles are subsequently rearranged from $\text{TiO}_2$ to Ag and then to Cu, increasing concentration.

• It is discovered that Cu-nanofluid is the most appropriate for enhancing the mechanical properties of the surface, while $\text{TiO}_2$-nanofluid is the best type for reducing the surface shear stress.

• Increasing the chemical reaction parameter results in a reduced concentration profile.

• The surface mechanical characteristics are negatively impacted by the magnetic field, thermal radiation, and Ohmic heating. However, the existence of Hall current has a favorable impact on the surface’s mechanical characteristics.

• Future research will advance upon this study by investigating the impact of variable fluid properties and slip phenomena on the flow of nanofluid, taking into account the presence of nonlinear thermal radiation.