1 Introduction

The explicit solutions of integrable models can provide an important guarantee for the analysis of their various properties, so finding a method to solve integrable models extensively is always an important research topic for a long period of time. The nonlinear Schrödinger equation (NLS) is one of the basic equations of quantum mechanics [1]. By now, several versions of DNLS equations were introduced to investigate the effect of high-order perturbations. Among them, there are three celebrate DNLS equations as follows:

DNLS-I equation or Kaup–Newell equation [2]

$$r_{t} + r_{xx} \pm i(\left| r \right|^{2} r)_{x} = 0.$$
(1.1)

DNLS-II equation or Chen–Lee–Liu equation [3]

$$ir_{t} + r_{xx} - i\left| r \right|^{2} r_{x} = 0.$$
(1.2)

DNLS-III equation or Gerdjikov–Ivanov equation [4]

$$ir_{t} + r_{xx} - i\left| r \right|^{2} \overline{r}_{x} + \frac{1}{2}\left| r \right|^{4} r = 0.$$
(1.3)

The DNLS equations have great applications in nonlinear optics and plasma physics. It can be used to describe large amplitude magnetohydrodynamic waves in plasma and also picosecond pulse in single-modle nonlinear fiber.

Chen–Lee–Liu derivative nonlinear Schrödinger equation (CLL-NLS equation) was firstly put forward by Kundu [5]

$$ir_{t} + r_{xx} { + }\left| r \right|^{2} r - \left| r \right|^{2} r_{x} = 0,$$
(1.4)

which is a completely integrable model, and it can be derived from the modified NLS equation which ignores the mean flow term in hydrodynamics [6]. In recent years, many excellent methods have been put forward by the deep study in integrable system, such as Darboux transformation [7, 8], Hirota bilinear method [9,10,11], similarity reduction [12], Riemann-Hilbert approach [13,14,15,16,17] and inverse scattering method [18, 19]. Among these but not limited to these methods, Zhang et al. obtained higher-order solutions of Eq. (1.4), Hu et al. gave spectral analysis of Lax pair and presented the RH problem of Eq. (1.4) [20].

However, as we know, there is still no research work on CLL–NLS equation by using \(\overline{\partial }\)-dressing method. The \(\overline{\partial }\)-dressing method was first proposed by Zakharov and Shabat [21], in subsequent works, this concept have been applied to different types of equations: (1 + 1)-dimensional and (2 + 1)-dimensional integrable differential equations such as KE equation [22], coupled GI equation [23], Sawada-Kotera equation [24] et al.

In this paper, different from considering the normalization boundary condition \(\psi (k) \to I\) at infinite, we mainly consider \(\overline{\partial }\)-equation with non-normalization \(\psi (k) \to D\) at infinite, where \(D\) is a non-degenerate matrix function of \(x\) and \(t\). The spectral problem and hierachies can be obtained by giving boundary condition matrix function \(D\) more general. In Sect. 2, starting from a \(\overline{\partial }\)-equation, we presented the general Lax pair for CLL-NLS equation using the \(\overline{\partial }\)-dressing method. In Sect. 3, we derived CLL-NLS hierarchy with source based on the relation between \(\overline{\partial }\)-dressing transformation matrix and its potential matrix. In Sect. 4, a formula for N-soliton solutions of CLL–NLS equation is constructed and we gave explicit two-soliton solutions for CLL–NLS equation for example.

2 Spectral analysis and Lax pair

2.1 The spatial spectral problem

Consider a matrix \(\overline{\partial }\) problem with a non-normalization boundary condition

$$\overline{\partial } \psi (x,t,k) = \psi (x,t,k)R(x,t,k),\quad \psi (x,t,k) \to D,k \to \infty ,$$
(2.1)

where \(D = D(x,t)\) is a non-degenerate matrix function of arbitrary independent variable \(x\) and \(t\), \(\psi (x,t,k)\) and \(R(x,t,k)\) are \(2 \times 2\) matrix, \(R(x,t,k)\) is spectral transform matrix.

Then the Eq. (2.1) admits a solution

$$\psi (x,t,k) = D + \frac{1}{2\pi i}\iint {\frac{\psi (\zeta )R(\zeta )}{{\zeta - k}}}d\zeta \wedge d\overline{\zeta } \equiv D + \psi RC_{k} ,$$
(2.2)

where \(C_{k}\) denotes the Cauchy-Green integral operator acting on the left. We can obtain a formal solution of the \(\overline{\partial }\)-problem Eq. (2.1)

$$\psi (x,t,k) = D \cdot (I - RC_{k} )^{ - 1} .$$
(2.3)

There are some necessary notations we need to fix first to making our presentation easy to understand and self-contained. For details refer [25], we define two pairings as follow

$$\left\langle {f,g} \right\rangle = \frac{1}{2\pi i}\iint {f(k)g^{T} }(k)dk \wedge d\overline{k} ,\quad \left\langle f \right\rangle = \left\langle {f,I} \right\rangle = \frac{1}{2\pi i}f(k)dk \wedge d\overline{k} ,$$
(2.4)

Which can be shown to admit properties

$$\left\langle {f,g} \right\rangle^{T} = \left\langle {g,f} \right\rangle ,\quad \left\langle {fR,g} \right\rangle^{T} = \left\langle {f,gR^{T} } \right\rangle ,\quad \left\langle {fC_{k} ,g} \right\rangle = - \left\langle {f,gC_{k} } \right\rangle .$$
(2.5)

For matrix functions \(f(k)\) and \(g(k)\), simple calculation shows that non-normalization \(\overline{\partial }\) problem

$$g(k)[f(k)C_{k} ]C_{k} + [g(k)C_{k} ]f(k)C_{k} = [g(k)C_{k} ][f(k)C_{k} ].$$
(2.6)

In the research of integrable systems, the Lax pairs of nonlinear equations are very important. There are many effective methods emerged base on their Lax pairs such as Darboux transformation, inverse scattering transformation, Riemann–Hilbert method that have been extensively studied. Here we show that spatial-time spectral problems for the general non-normalization boundary equation which can be established. We especially obtain the spatial-time spectral problems of CLL-NLS equation starting from Eq. (2.1).

Proposition 1

Let the transform matrix \(R\) satisfy

$$R_{x} = ik^{2} [R,\sigma_{3} ],$$
(2.7)

where \(\sigma_{3}\) is the Pauli matrix, then the solution \(\psi\) of\(\overline{\partial }\) Eq. (2.1) satisfies the following spatial problem for CLL-NLS Eq. (1.4).

$$\psi_{x} = D_{x} D^{ - 1} \psi + i[\left\langle {\psi R} \right\rangle ,\sigma_{3} ]D^{ - 1} \psi - ik[\sigma_{3} ,\psi ],$$
(2.8)

where

$$Q = - i[\sigma_{3} ,\left\langle {\psi R} \right\rangle ]D^{ - 1} = \left( {\begin{array}{*{20}c} 0 & u \\ { - \overline{u} } & 0 \\ \end{array} } \right),$$
(2.9)

and compared with the case where the boundary condition is an identity matrix, Eq. (2.9) satisfied some symmetry conditions as follows

$$u = - 2i\left\langle {\psi R} \right\rangle_{12} D_{22}^{ - 1} ,\quad \overline{u} = - 2i\left\langle {\psi R} \right\rangle_{21} D_{11}^{ - 1} ,$$

where \(M_{mn}\) represents the \(m\) row and \(n\) column elements of matrix \(M\) , \(D^{ - 1}\) is the inverse matrix of \(D\) .

Remark 1.

Let \(Q\) and \(D\) satisfies

$$D_{x} + \left( {\frac{1}{2}i\sigma_{3} - \frac{3}{4}iQ^{2} \sigma_{3} } \right)D = 0,$$
$$D_{t} - \left( {\frac{9}{8}iQ^{4} \sigma_{3} + 2ik^{2} \sigma_{3} - \frac{i}{2}\sigma_{3} - 2kQ^{3} - iQ^{2} \sigma_{3} + ( - 4k^{3} + 2k)Q - \frac{1}{4}[Q,Q_{x} ]} \right)D = 0,$$
(2.10)

the \(\overline{\partial }\)–Eq. (2.1) leads to a spatial spectral problem for CLL-NLS Eq. (1.4)

$$\psi_{x} + ik^{2} [\sigma_{3} ,\psi ] = \left( {kQ - \frac{i}{2}\sigma_{3} + \frac{i}{4}Q^{2} \sigma_{3} } \right)\psi ,$$
(2.11)

where the complex number \(k\) is a associated spectral parameter.

Proof .

Making use of Eqs. (2.3) and (2.7), we obtain

$$\psi_{x} = D_{x} (I - RC_{k} )^{ - 1} + ik\psi R\sigma_{3} C_{k} (I - RC_{k} )^{ - 1} - ik\psi \sigma_{3} RC_{k} (I - RC_{k} )^{ - 1} .$$
(2.12)

Direct computation gives

$$\begin{gathered} k\psi RC_{k} = \left\langle {\psi R} \right\rangle + k(\psi - D), \hfill \\ k^{2} \psi RC_{k} = \left\langle {\zeta \psi R} \right\rangle + k\left\langle {\psi R} \right\rangle + k^{2} \psi - k^{2} D, \hfill \\ k^{3} \psi RC_{k} = \left\langle {\zeta^{2} \psi R} \right\rangle + k\left\langle {\zeta \psi R} \right\rangle + k^{2} \left\langle {\psi R} \right\rangle + k^{3} \psi - k^{3} D, \hfill \\ k^{4} \psi RC_{k} = \left\langle {\zeta^{3} \psi R} \right\rangle + k\left\langle {\zeta^{2} \psi R} \right\rangle + k^{2} \left\langle {\zeta \psi R} \right\rangle + k^{3} \left\langle {\psi R} \right\rangle + k^{4} \psi - k^{4} D. \hfill \\ \end{gathered}$$
(2.13)

Since \(RC_{k} = I - I \cdot (I - RC_{k} ),\) we find

$$RC_{k} (I - RC_{k} )^{ - 1} = (I - RC_{k} )^{ - 1} - I.$$
(2.14)

Substituting the Eqs. (2.13–2.14), we find Eq. (2.8). By virtue of Eq. (2.9) and first equation of Eq. (2.10), we have Eq. (2.11).

2.2 The time spectral problem

Proposition 2

Suppose that transform matrix \(R\) satisfies the linear equation

$$R_{t} = [R,\Omega ],$$
(2.15)

where

$$\Omega = \Omega_{p} + \Omega_{s} = 2ik^{4} \sigma_{3} + \frac{1}{2\pi i}\iint {\frac{{\xi^{2} \omega (\xi^{2} )\sigma_{3} }}{{\xi^{2} - k^{2} }}d\xi \wedge d\overline{\xi } },$$
(2.16)

which comprises both a polynomial part \(\Omega_{p} (k)\) and a singular part \(\Omega_{s} (k)\) and \(\omega (\xi^{2} )\) is a scalar function. Based on the \(\overline{\partial }\) -Eq. ( 2.1 ), the time spectral problem of CLL-NLS equation can be given as follow

$$\begin{gathered} \psi_{t} + 2ik^{4} [\sigma_{3} ,\psi ] = [ - \frac{i}{8}Q^{4} \sigma_{3} - \frac{1}{2}kQ^{3} - ik^{2} Q^{2} \sigma_{3} + ( - 2k^{3} + k)Q + \frac{1}{4}(QQ_{x} - Q_{x} Q) - ikQ_{x} \sigma_{3} \\ + 2ik^{2} \sigma_{3} - \frac{i}{2}\sigma_{3} ]\psi - \frac{1}{2}k\omega (k^{2} )\psi \sigma_{3} C_{ - k} - \frac{1}{2}\psi \sigma_{3} \psi^{ - 1} k\omega (k^{2} )C_{k} \psi + \psi \Omega_{s.} \\ \end{gathered}$$
(2.17)

Remark 2.

As \(\omega (\xi^{2} ) = 0,\) Eq. (2.17) reduces to

$$\begin{gathered} \psi_{t} + 2ik^{4} [\sigma_{3} ,\psi ] = [ - \frac{i}{8}Q^{4} \sigma_{3} - \frac{1}{2}kQ^{3} - ik^{2} Q^{2} \sigma_{3} + ( - 2k^{3} + k)Q \\ + \frac{1}{4}(QQ_{x} - Q_{x} Q) - ikQ_{x} \sigma_{3} + 2ik^{2} \sigma_{3} - \frac{i}{2}\sigma_{3} ]\psi , \\ \end{gathered}$$
(2.18)

which together with the spatial spectral Eq. (2.11) gives the Lax pair of the CLL-NLS equation (1.4).

Proof.

In the time spectral problem, we first use the polynomial dispersion relation only \(\Omega = \Omega_{p} = 2ik^{4} \sigma_{3} .\) From Eqs. (2.2), (2.3) and (2.16), we find that

$$\psi_{t} = D_{t} D^{ - 1} \psi + 2ik^{4} \psi RC_{k} \sigma_{3} (I - RC_{k} )^{ - 1} - 2ik^{4} \psi \sigma_{3} (I - RC_{k} )^{ - 1} + 2ik^{4} \psi \sigma_{3} .$$
(2.19)

Furthermore, making use of Eq. (2.13), then Eq. (2.19) is changed to

$$\begin{gathered} \psi_{t} = D_{t} D^{ - 1} \psi - 2ik^{4} [\sigma_{3} ,\psi ] + 2i\left[ {\left\langle {\zeta^{3} \psi R} \right\rangle ,\sigma_{3} } \right]D^{ - 1} \psi \\ + 2i\left[ {\left\langle {\zeta^{2} \psi R} \right\rangle ,\sigma_{3} } \right]D^{ - 1} \left( {\left\langle {\psi R} \right\rangle D^{ - 1} + k} \right)\psi + 2i\left[ {\left\langle {\zeta \psi R} \right\rangle ,\sigma_{3} } \right]D^{ - 1} \left( {\left\langle {\zeta \psi R} \right\rangle D^{ - 1} } \right. \\ \left. { + \left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} + k\left\langle {\psi R} \right\rangle D^{ - 1} + k^{2} } \right)\psi + 2i\left( {\left[ {\left\langle {\psi R} \right\rangle ,\sigma_{3} } \right]} \right.D^{ - 1} \left( {\left\langle {\zeta^{2} \psi R} \right\rangle } \right.D^{ - 1} \\ \left. {\left. { + \left\langle {\zeta \psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} + \left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\zeta \psi R} \right\rangle D^{ - 1} } \right)} \right)\psi \\ + 2i\left( {\left[ {\left\langle {\psi R} \right\rangle ,\sigma_{3} } \right]} \right.D^{ - 1} \left( {\left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} + k\left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} } \right. \\ \left. {\left. { + k\left\langle {\zeta \psi R} \right\rangle D^{ - 1} + k^{2} \left\langle {\psi R} \right\rangle D^{ - 1} + k^{3} } \right)} \right)\psi . \\ \end{gathered}$$
(2.20)

By using Eqs. (2.7), (2.8) and (2.9), we obtain

$$\left\langle {\psi R} \right\rangle_{x}^{off} = i\left[ {\left\langle {\zeta^{2} \psi R} \right\rangle ,\sigma_{3} } \right] + Q\left\langle {\zeta \psi R} \right\rangle^{diag} + \frac{i}{4}Q^{2} \sigma_{3} \left\langle {\psi R} \right\rangle^{off} - \frac{i}{2}\sigma_{3} \left\langle {\psi R} \right\rangle^{off} .$$
(2.21)

Hence, we note that \(\psi\) obeys the parity properties

$$\psi^{diag} ( - k) = \psi^{diag} (k), \ \psi^{off} ( - k) = - \psi^{off} (k),$$

By which, we can show that

$$\left[ {\sigma_{3} ,\left\langle {\zeta^{2n - 1} \psi R} \right\rangle } \right] = 0, \ n = 1,2,...,N.$$

Substituting them into Eq. (2.20), we find

$$\begin{gathered} \psi_{t} = D_{t} D^{ - 1} \psi - 2ik^{4} [\sigma_{3} ,\psi ] + 2i\left[ {\left\langle {\zeta^{2} \psi R} \right\rangle ,\sigma_{3} } \right]D^{ - 1} \left( {\left\langle {\psi R} \right\rangle D^{ - 1} + k} \right)\psi \\ + 2i\left( {\left[ {\left\langle {\psi R} \right\rangle ,\sigma_{3} } \right]} \right.D^{ - 1} \left( {\left\langle {\zeta^{2} \psi R} \right\rangle } \right.D^{ - 1} + \left\langle {\zeta \psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} \\ \left. {\left. { + \left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\zeta \psi R} \right\rangle D^{ - 1} } \right)} \right)\psi + 2i\left( {\left[ {\left\langle {\psi R} \right\rangle ,\sigma_{3} } \right]} \right.D^{ - 1} \left( {\left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} } \right. \\ \left. {\left. { + k\left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\psi R} \right\rangle D^{ - 1} + k\left\langle {\zeta \psi R} \right\rangle D^{ - 1} + k^{2} \left\langle {\psi R} \right\rangle D^{ - 1} + k^{3} } \right)} \right)\psi . \\ \end{gathered}$$
(2.22)

By virtue of Eqs. (2.21) and (2.9), we have some calculation results as follow

$$\left\langle {\psi R} \right\rangle^{off} = \frac{i}{2}\sigma_{3} QD,\quad \left\langle {\psi R} \right\rangle_{x}^{off} = \frac{i}{2}\sigma_{3} Q_{x} D - \frac{1}{4}QD + \frac{3}{8}Q^{3} D,$$
$$\left\langle {\zeta^{2} \psi R} \right\rangle_{{}}^{off} = - \frac{1}{4}Q_{x} D - \frac{i}{8}\sigma_{3} QD + \frac{3}{16}i\sigma_{3} Q^{3} D,$$
(2.23)
$$\left\langle {\zeta^{2} \psi R} \right\rangle + \left\langle {\psi R} \right\rangle D^{ - 1} \left\langle {\zeta \psi R} \right\rangle = \left( { - \frac{i}{2}Q^{4} \sigma_{3} + \frac{i}{2}Q^{2} \sigma_{3} - \frac{1}{2}QQ_{x} } \right)\psi .$$

Substituting Eq. (2.23) into Eq. (2.22) leads to the time-dependent linear equation

$$\begin{gathered} \psi_{t} + 2ik^{4} [\sigma_{3} ,\psi ] = [ - \frac{i}{8}Q^{4} \sigma_{3} - \frac{1}{2}kQ^{3} - ik^{2} Q^{2} \sigma_{3} + ( - 2k^{3} + k)Q \\ + \frac{1}{4}(QQ_{x} - Q_{x} Q) - ikQ_{x} \sigma_{3} + 2ik^{2} \sigma_{3} - \frac{i}{2}\sigma_{3} ]\psi . \\ \end{gathered}$$
(2.24)

On the other hand, we consider the singular dispersion relation \(\Omega_{s}\), similarly, we have

$$\psi_{t} = \left( {\psi R\Omega_{s} C_{k} - \psi \Omega_{s} } \right)(I - RC_{k} )^{ - 1} + \psi \Omega_{s} .$$
(2.25)

By Eq. (2.2), we can express \(\Omega_{s}\) in another form

$$\Omega_{s} = \frac{1}{4\pi i}\iint {\frac{{\xi \omega \left( {\xi^{2} } \right)\sigma_{3} }}{\xi - k}d\xi \wedge d\overline{\xi } + \frac{1}{4\pi i}\iint {\frac{{\xi \omega \left( {\xi^{2} } \right)\sigma_{3} }}{\xi + k}d\xi \wedge d\overline{\xi } }}.$$

Resorting Eqs. (2.2) and (2.5), \(\psi R\Omega_{s} C_{k}\) in Eq. (2.25) satisfies

$$\begin{gathered} \psi R\Omega_{s} C_{k} = \psi \Omega_{s} - \frac{1}{4\pi i}\iint {\frac{{\xi \omega \left( {\xi^{2} } \right)\psi \left( \xi \right)\sigma_{3} }}{\xi - k}d\xi \wedge d\overline{\xi } } \\ - \frac{1}{4\pi i}\iint {\frac{{\xi \omega \left( {\xi^{2} } \right)\left( {I + \psi \left( \xi \right)R\left( \xi \right)C_{ - \xi } } \right)\sigma_{3} }}{\xi + k}d\xi \wedge d\overline{\xi } }. \\ \end{gathered}$$
(2.26)

Hence, we have

$$\begin{gathered} \psi_{t} = - \frac{1}{4\pi i}\left[ {\iint {\frac{{\xi \omega \left( {\xi^{2} } \right)\left( {I + \psi \left( \xi \right)R\left( \xi \right)C_{ - \xi } } \right)\sigma_{3} }}{\xi + k}d\xi \wedge d\overline{\xi } }} \right](I - RC_{k} )^{ - 1} \\ - \frac{1}{4\pi i}\left[ {\iint {\frac{{\xi \omega \left( {\xi^{2} } \right)\psi \left( \xi \right)\sigma_{3} }}{\xi - k}d\xi \wedge d\overline{\xi } }} \right](I - RC_{k} )^{ - 1} + \psi \Omega_{s} . \\ \end{gathered}$$
(2.27)

By using the relations

$$\frac{1}{\rho - k}\frac{1}{\xi - \rho } = \frac{1}{\xi - k}\left( {\frac{1}{\rho - k} - \frac{1}{\rho - \xi }} \right),\quad \frac{1}{\rho - k}\frac{1}{\xi + \rho } = \frac{1}{\xi + k}\left( {\frac{1}{\rho - k} - \frac{1}{\rho + \xi }} \right),$$

we find that

$$\begin{gathered} \frac{1}{k - \xi }(I - RC_{k} )^{ - 1} = \frac{1}{k - \xi }\psi^{ - 1} (\xi )\psi (k), \hfill \\ \frac{1}{k + \xi }\left( {I + \psi RC_{ - \xi } } \right)(I - RC_{k} )^{ - 1} = \frac{1}{k + \xi }\psi , \hfill \\ \end{gathered}$$
(2.28)

by which, then Eq. (2.25) gives a time-dependent linear equation with the singular dispersion relation

$$\psi_{t} = - \frac{1}{2}k\omega (k^{2} )\psi \sigma_{3} C_{ - k} - \frac{1}{2}\psi \sigma_{3} \psi^{ - 1} k\omega (k^{2} )C_{k} \psi + \psi \Omega ,$$
(2.29)

which together with Eq. (2.24) gives time spectral Eq. (2.17).

3 Recursive operators and CLL-NLS hierarchy

In this section, we derive the CLL-NLS hierarchy with source. In order to prove this we define matrix M as following form

$$M = \psi \sigma_{3} \psi ,$$
(3.1)

which \(M\) is depends on \(x\) and \(t\), then we can prove the following proposition.

Proposition 3

\(Q\) defined by Eq. (2.9) satisfies a coupled hierarchy with a source \(M\).

$$Q_{t} + 2\alpha_{n} \sigma_{3} \Lambda^{2n} Q = M^{0} + i\left[ {\sigma_{3} ,\left\langle {k^{2} \omega \left( {k^{2} } \right)M\left( k \right)} \right\rangle } \right],\quad n = 1,2,...,N,$$
(3.2)
$$M_{x} = (ik^{2} + \frac{1}{2}i - \frac{1}{4}iQ^{2} )\left[ {M,\sigma_{3} } \right] + k\left[ {Q,M} \right],$$
(3.3)

where

$$M^{0} = - \frac{9}{8}iQ^{5} \sigma_{3} - 4ik^{2} Q\sigma_{3} + iQ\sigma_{3} + 2kQ^{3} + 2iQ^{3} \sigma_{3} - (2k - 4k^{3} )Q^{2} - \frac{1}{4}[[Q,Q_{x} ],Q].$$
(3.4)

Proof.

Differentiating \(Q\) with respect to \(t\) gives

$$Q_{t} = - i[\sigma_{3} ,\left\langle {\psi R} \right\rangle_{t} ]D^{ - 1} - i[\sigma_{3} ,\left\langle {\psi R} \right\rangle ]D_{t}^{ - 1} .$$
(3.5)

Because of \(C_{k}\) is the inverse operator of \(\overline{\partial }\) then we have

$$\begin{gathered} \left( {\psi R} \right)_{t} = \overline{\partial } \psi_{t} (k) = \overline{\partial } \left( {D_{t} \cdot (I - RC_{k} )^{ - 1} + D \cdot (I - RC_{k} )_{t}^{ - 1} } \right) \\ = D_{t} D^{ - 1} \psi R + \psi R_{t} (I - RC_{k} )^{ - 1} , \\ \end{gathered}$$
(3.6)

and clearly

$$D_{t}^{ - 1} = - D^{ - 1} D_{t} D^{ - 1} .$$

Using Eqs. (2.4) and (3.6), the Eq. (3.5) can be rewritten as follow

$$\begin{gathered} Q_{t} = - i\left[ {\sigma_{3} ,\left\langle {\psi R_{t} ,I \cdot (I + R^{T} C_{k} )^{ - 1} } \right\rangle } \right]D^{ - 1} - \frac{9}{8}iQ^{5} \sigma_{3} - 4ik^{2} Q\sigma_{3} \\ + iQ\sigma_{3} + 2kQ^{3} + 2iQ^{3} \sigma_{3} - (2k - 4k^{3} )Q^{2} - \frac{1}{4}[[Q,Q_{x} ],Q]. \\ \end{gathered}$$
(3.7)

From the \(\overline{\partial }\)-Eq. (2.1), we have

$$\overline{\partial } \psi^{ - 1} = - R\psi^{ - 1} ,$$
(3.8)

which leads to

$$(\psi^{ - 1} )^{T} = D^{ - 1} \cdot (I + R^{T} C_{k} )^{ - 1} .$$
(3.9)

We further simplify the first term in Eq. (3.7),

$$\begin{gathered} - i\left[ {\sigma_{3} ,\left\langle {\psi R_{t} ,I \cdot \left( {I + R^{T} C_{k} } \right)^{ - 1} } \right\rangle } \right]D^{ - 1} \\ = - i\left[ {\sigma_{3} ,\left\langle {\psi R_{t} ,DD^{ - 1} \cdot \left( {I + R^{T} C_{k} } \right)^{ - 1} } \right\rangle } \right]D^{ - 1} \\ = - i\left[ {\sigma_{3} ,\left\langle {\psi R_{t} ,D\left( {\psi^{ - 1} } \right)^{T} } \right\rangle } \right]D^{ - 1} = - i\left[ {\sigma_{3} ,\left\langle {\psi R_{t} \psi^{ - 1} } \right\rangle } \right]. \\ \end{gathered}$$
(3.10)

Using the condition Eq. (2.15), the first term of Eq. (3.10) can be written as

$$\begin{gathered} - i\left[ {\sigma_{3} ,\left\langle {\psi R_{t} \psi^{ - 1} } \right\rangle } \right] = - i\left[ {\sigma_{3} ,\left\langle {\psi \left( {R\Omega - \Omega R} \right)\psi^{ - 1} ,I} \right\rangle } \right] \\ = - i\left[ {\sigma_{3} ,\left\langle {\psi R\Omega \psi^{ - 1} ,I} \right\rangle } \right] + i\left[ {\sigma_{3} ,\left\langle {\psi \Omega R\psi^{ - 1} ,I} \right\rangle } \right]. \\ \end{gathered}$$
(3.11)

Hence, using Eqs. (2.4) and (2.15), Eq. (3.7) reduces to the following form

$$Q_{t} = M^{0} - i\left[ {\sigma_{3} ,\left\langle {\psi \Omega \overline{\partial } \psi^{ - 1} } \right\rangle } \right] - i\left[ {\sigma_{3} ,\left\langle {\left( {\overline{\partial } \psi } \right)\Omega \psi^{ - 1} } \right\rangle } \right],$$
(3.12)

where

$$M^{0} = - \frac{9}{8}iQ^{5} \sigma_{3} - 4ik^{2} Q\sigma_{3} + iQ\sigma_{3} + 2kQ^{3} + 2iQ^{3} \sigma_{3} - (2k - 4k^{3} )Q^{2} - \frac{1}{4}[[Q,Q_{x} ],Q].$$
(3.13)

Here we shall consider \(\Omega_{p} = \alpha_{n} k^{2n} \sigma_{3} ,\) \(\alpha_{n} =\) constant, then the term

\(- i\left[ {\sigma_{3} ,\left\langle {\psi \Omega \overline{\partial } \psi^{ - 1} } \right\rangle } \right] - i\left[ {\sigma_{3} ,\left\langle {\left( {\overline{\partial } \psi } \right)\Omega \psi^{ - 1} } \right\rangle } \right]\) can be further simplified like

$$\begin{gathered} - i\left[ {\sigma_{3} ,\left\langle {\psi \Omega \overline{\partial } \psi^{ - 1} } \right\rangle + \left\langle {\left( {\overline{\partial } \psi } \right)\Omega \psi^{ - 1} } \right\rangle } \right] = - i\left[ {\sigma_{3} ,\left\langle {\overline{\partial } \left( {\psi \Omega \psi^{ - 1} } \right)} \right\rangle - \left\langle {\psi \left( {\overline{\partial } \Omega } \right)\psi^{ - 1} } \right\rangle } \right] \hfill \\ = - i\left[ {\sigma_{3} ,\left\langle {\overline{\partial } \left( {\psi \Omega_{p} \psi^{ - 1} } \right)} \right\rangle + \left\langle {\overline{\partial } \left( {\psi \Omega_{s} \psi^{ - 1} } \right)} \right\rangle - \left\langle {\psi \left( {\overline{\partial } \Omega_{s} } \right)\psi^{ - 1} } \right\rangle - \left\langle {\psi \left( {\overline{\partial } \Omega_{p} } \right)\psi^{ - 1} } \right\rangle } \right]. \hfill \\ \end{gathered}$$
(3.14)

Noticing that \(\Omega_{p} = \alpha_{n} k^{2n} \sigma_{3}\) is an analytic function on the k-plane, and the fact that \(\Omega_{s} \to 0\) as \(k \to 0,\) so we have

$$\psi \left( {\overline{\partial } \Omega_{p} } \right)\psi^{ - 1} = 0,\quad \left\langle {\overline{\partial } \left( {\psi \Omega_{s} \psi^{ - 1} } \right)} \right\rangle = 0.$$
(3.15)

Then we get

$$\begin{gathered} - i\left[ {\sigma_{3} ,\left\langle {\psi \Omega \overline{\partial } \psi^{ - 1} } \right\rangle + \left\langle {\left( {\overline{\partial } \psi } \right)\Omega \psi^{ - 1} } \right\rangle } \right] = - i\left[ {\sigma_{3} ,\left\langle {\overline{\partial } \left( {\psi \Omega_{p} \psi^{ - 1} } \right)} \right\rangle - \left\langle {\psi \left( {\overline{\partial } \Omega_{s} } \right)\psi^{ - 1} } \right\rangle } \right] \hfill \\ = - i\alpha_{n} \left[ {\sigma_{3} ,\left\langle {\overline{\partial } \left( {k^{2n} \psi \sigma_{3} \psi^{ - 1} } \right)} \right\rangle } \right] + i\left[ {\sigma_{3} ,\left\langle {\omega \left( k \right)\psi \sigma_{3} \psi^{ - 1} } \right\rangle } \right] \hfill \\ = - i\alpha_{n} \left[ {\sigma_{3} ,\left\langle {\overline{\partial } \left( {k^{2n} M\left( k \right)} \right)} \right\rangle } \right] + i\left[ {\sigma_{3} ,\left\langle {\omega \left( k \right)M\left( k \right)} \right\rangle } \right]. \hfill \\ \end{gathered}$$
(3.16)

The \(Q_{t}\) can be express as follows

$$Q_{t} = M^{0} - i\alpha_{n} \left[ {\sigma_{3} ,\left\langle {\overline{\partial } \left( {k^{2n} M\left( k \right)} \right)} \right\rangle } \right] + i\left[ {\sigma_{3} ,\left\langle {\omega \left( k \right)M\left( k \right)} \right\rangle } \right],$$
(3.17)

where \(M^{0}\) is given as Eq. (3.13). By using Eq. (2.11), it can be checked that \(M\left( k \right)\) satisfies the equation

$$M_{x} = (ik^{2} + \frac{1}{2}i - \frac{1}{4}iQ^{2} )\left[ {M,\sigma_{3} } \right] + k\left[ {Q,M} \right].$$
(3.18)

From Eq. (3.18), they satisfy the following equations

$$M_{x}^{diag} = k\left[ {Q,M^{off} } \right],$$
(3.19)
$$M_{x}^{off} = - i\left( {k^{2} + \frac{1}{2} - \frac{1}{4}Q^{2} } \right)\left[ {\sigma_{3} ,M} \right] + k\left[ {Q,M^{diag} } \right],$$
(3.20)

which lead to

$$M_{{}}^{diag} = \sigma_{3} + \partial^{ - 1} k\left[ {Q,M^{off} } \right],$$
(3.21)
$$M_{{}}^{off} = - i\left( {\Lambda - k} \right)^{ - 1} Q,$$
(3.22)

where

$$\Lambda \cdot = \frac{i}{2}\sigma_{3} \left( {\frac{1}{k}\partial_{x} - \left[ {Q,\partial^{ - 1} k\left[ {Q, \cdot } \right]} \right] - \frac{1}{k}i\sigma_{3} \left( {\frac{1}{2}Q^{2} - 1} \right)} \right).$$
(3.23)

The operator \(\Lambda \cdot\) usually be called as recursion operator. We expand \(\left( {\Lambda - k} \right)^{ - 1}\) in the series

$$\left( {\Lambda - k} \right)^{ - 1} = - \sum\limits_{j = 1}^{\infty } {\frac{{\Lambda^{j - 1} }}{{k^{j} }}} .$$
(3.24)

By using \(\overline{\partial } k^{n - j} = \pi \delta \left( k \right)\delta_{j,n + 1} ,j = 1,2,...,\) we can derive that

$$\sum\limits_{j = 1}^{\infty } {\left\langle {\overline{\partial } k^{n - j} } \right\rangle } \Lambda^{j - 1} Q = - \Lambda^{n} Q.$$
(3.25)

Substituting it into Eq. (3.17) leads to the Eq. (3.2)

4 N-soliton solutions of CLL-NLS equation

In this section, we will construct the N-soliton solutions of CLL-NLS equation.

Proposition 4

choose that spectral transform matrix \(R\) as

$$R = \sum\limits_{j = 1}^{N} {2\pi ie^{{ - i\theta \left( k \right)\sigma_{3} }} \left( {\begin{array}{*{20}c} 0 & {c_{j} \left[ {\delta \left( {k - k_{j} } \right) + \delta \left( {k + k_{j} } \right)} \right]} \\ { - \overline{{c_{j} }} \left[ {\delta \left( {k - \overline{{k_{j} }} } \right) + \delta \left( {k + \overline{{k_{j} }} } \right)} \right]} & 0 \\ \end{array} } \right)} e^{{i\theta \left( k \right)\sigma_{3} }} ,$$
(4.1)

where \(k_{j}\) and \(\overline{{k_{j} }}\) are \(2N\) discrete spectrals in complex plane \({\mathbb{C}}\) and \(\theta \left( k \right) = k^{2} x + 2k^{4} t.\)

Let \(\widehat{Q} = QD,\) then we have

$$\widehat{Q} = - i\left[ {\sigma_{3} ,\left\langle {\psi R} \right\rangle } \right] = \left( {\begin{array}{*{20}c} 0 & E \\ { - \overline{E} } & 0 \\ \end{array} } \right),$$
(4.2)

5 then the CLL-NLS equation have solution

$$u = 8q_{N} \exp \left( {i\int_{ - \infty }^{x} {(\frac{1}{2} - 48\left| {q_{N} } \right|^{2} )dy} } \right),$$
(4.3)
$$q_{N} \left( {x,t} \right) = \frac{{\det M^{aug} }}{\det M},$$
(4.4)

where \(M\) is \(N \times N\) matrices, and \(M^{aug}\) is \(\left( {N + 1} \right) \times \left( {N + 1} \right)\) matrices defined by

$$M^{aug} = \left( {\begin{array}{*{20}c} 0 & Y \\ D & M \\ \end{array} } \right), \ Y = \left( {Y_{1} ,Y_{2} ,...,Y_{N} } \right),$$
$$Y_{j} = c_{j} e^{{ - 2i\theta \left( {k_{j} } \right)}} , \ D = \left( {d_{1} ,d_{1} , \ldots ,d_{1} } \right)^{T} .$$

Proof.

Substituting Eq. (4.1) into Eq. (4.2) leads to.

$$E\left( {x,t} \right) = - 8\sum\limits_{j = 1}^{N} {c_{j} \psi_{11} \left( {k_{j} } \right)e^{{ - 2i\theta \left( {k_{j} } \right)}} } .$$
(4.5)

Substituting Eq. (4.1) into \(\overline{\partial }\)-Eq. (2.2) and resorting the properties of \(\delta\) function, we can obtain

$$\psi_{11} \left( k \right) = d_{1} - 4i\sum\limits_{j = 1}^{N} {\overline{{c_{j} }} e^{{2i\theta \left( {\overline{{k_{j} }} } \right)}} \psi_{12} \left( {\overline{{k_{j} }} } \right)\frac{{\overline{{k_{j} }} }}{{k^{2} - \overline{{k_{j} }}^{2} }}} ,$$
(4.6)
$$\psi_{12} \left( k \right) = 4i\sum\limits_{m = 1}^{N} {c_{m} e^{{ - 2i\theta \left( {k_{m} } \right)}} \psi_{11} \left( {k_{m} } \right)\frac{k}{{k^{2} - k_{{_{m} }}^{2} }}} .$$
(4.7)

Replacing \(k\) in Eq. (4.6) with \(k_{n}\), and \(k\) in Eq. (4.7) with \(\overline{{k_{j} }}\), we can obtain linear equations for \(\psi_{11} \left( {k_{n} } \right)\) as follow

$$\psi_{11} ( k_n ) + \sum\limits_{m = 1}^{N} {A_{n,m}} \psi_{11} ( k_m ) = d_{1} ,\,n = 1,2,...,N,$$
(4.8)

where

$$A_{n,m} = 16\sum\limits_{j = 1}^{N} {\overline{{k_{j} }}^{2} D_{j} \left( {k_{n} } \right)C_{m} \left( {\overline{{k_{j} }} } \right)} ,$$
$$C_{j} \left( k \right) = \frac{{c_{j} }}{{k^{2} - k_{j}^{2} }}e^{{ - 2i\theta \left( {k_{j} } \right)}} ,\quad D_{j} \left( k \right) = \frac{{ - \overline{{c_{j} }} }}{{k^{2} - \overline{{k_{j} }}^{2} }}e^{{2i\theta \left( {\overline{{k_{j} }} } \right)}} ,\quad n = 1,2,...,N.$$
(4.9)

We further introduce notations

$$M = I + \left( {A_{n,m} } \right),$$
$$\widehat{\psi }_{11} = \left( {\psi_{11} \left( {k_{1} } \right),...,\psi_{11} \left( {k_{N} } \right)} \right)^{T} ,$$
(4.10)

then Eq. (4.10) reduce to linear system in matrix form

$$M\widehat{\psi }_{11} = D = \left( {d_{1} ,...,d_{1} } \right)^{T} .$$
(4.11)

From which we can substituting \(\psi_{11}\) into Eq. (4.5), we can obtain

$$E\left( {x,t} \right) = 8d_{1} q_{N} ,$$
(4.12)

where \(q_{N}\) is given by Eq. (4.4). Clearly Eqs. (2.10) are compatible and admit a solution

$$d_{1} = \exp (i\int_{ - \infty }^{x} {(\frac{1}{2} - \frac{3}{4}\left| u \right|^{2} )} dy).$$
(4.13)

By virtue of Eqs. (4.2) and (4.13), we can obtain

$$u = 8q_{N} \exp (2i\int_{ - \infty }^{x} {(\frac{1}{2} - \frac{3}{4}\left| u \right|^{2} )} dy).$$
(4.14)

Taking the modulus on both sides of above equation, we have \(u = 8\left| {q_{N} } \right|,\) substituting it to Eq. (4.14), we can obtain the N-soliton solution of CLL-NLS equation

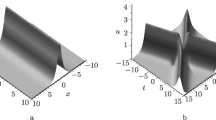
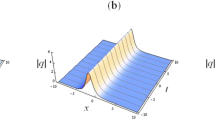
$$u = 8q_{N} \exp \left( {2i\int_{ - \infty }^{x} {\left( {\frac{1}{2} - 48\left| {q_{N} } \right|^{2} } \right)} dy} \right).$$
(4.15)

Example.

For \(N = 2,\) the formula Eq. (4.15) gives the two-soliton solutions of the CLL-NLS equation that are given by

$$u = 8q_{2} \exp (2i\int_{ - \infty }^{x} {(\frac{1}{2} - 48\left| {q_{2} } \right|^{2} )} dy), \, q_{2} \left( {x,t} \right) = \frac{{\det M^{aug} }}{\det M},$$
(4.16)

where

$$M = \left( {\begin{array}{*{20}c} {1 + A_{11} } & {A_{12} } \\ {A_{21} } & {1 + A_{22} } \\ \end{array} } \right),\quad M^{aug} = \left( {\begin{array}{*{20}c} 0 & {c_{1} e^{{ - 2ixk_{1}^{2} - 4itk_{1}^{4} }} } & {c_{2} e^{{ - 2ixk_{2}^{2} - 4itk_{2}^{4} }} } \\ 1 & {1 + A_{11} } & {A_{12} } \\ 1 & {A_{21} } & {1 + A_{22} } \\ \end{array} } \right),$$
(4.17)

and

$$A_{ij} = - \frac{{J_{j,1} }}{{\left( {k_{i}^{2} - \overline{{k_{1} }}^{2} } \right)\left( {k_{j}^{2} - \overline{{k_{1} }}^{2} } \right)}} - \frac{{J_{j,2} }}{{\left( {k_{i}^{2} - \overline{{k_{2} }}^{2} } \right)\left( {k_{j}^{2} - \overline{{k_{2} }}^{2} } \right)}},$$
$$- 16c_{j} \overline{{c_{i} }} = e^{{w_{2j} + w_{1i} }} ,\quad J_{i,j} = e^{{ - \left[ {2i\left( {k_{j}^{2} - \overline{{k_{i} }}^{2} } \right)x + 4i\left( {k_{j}^{4} - \overline{{k_{i} }}^{4} } \right)t - w_{2j} - w_{1i} } \right]}} ,\quad i,j = 1,2.$$
(4.18)

where \(w_{1} ,w_{2}\) being two arbitrary constants.

6 Conclusion

In this paper, we introduced the \(\overline{\partial }\)-dressing method. Through the \(\overline{\partial }\)-dressing method starting from a \(\overline{\partial }\)-equation, we presented the spatial-time spectral problems for CLL–NLS equation. Then we derived CLL–NLS hierarchy with source based on the relation between \(\overline{\partial }\)-dressing transformation matrix and its potential matrix, and the spectral problem and hierachies can be obtained by giving boundary condition matrix function \(D\) more general. In the end, we constructed a formula for N-soliton solutions of CLL–NLS equation.

In summary, the \(\overline{\partial }\)-dressing method is powerful for analyzing spectral problem of integrable systems. In our future work, we will continue to using \(\overline{\partial }\)-dressing method and Riemann-Hilbert approach to analyze the asymptotic behaviour for Eq. (1.4) and other integrable system.