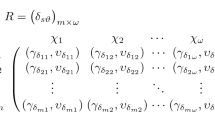Generalized Cubic Pythagorean Fuzzy Aggregation Operators and their Application to Multi-attribute Decision-Making Problems

Abstract

Cubic Pythagorean fuzzy (CPF) set (CPFS) is a hybrid set that can hold much more information and can be used to describe both an interval-valued Pythagorean fuzzy set (IVPFS) and Pythagorean fuzzy set (PFS) at the same time to handle data uncertainties. Based on it, the present study is classified into three phases. The first phase is to modify the existing operational laws and aggregation operators (AOs) in the article presented by Abbas et al. (Journal of Intelligent & Fuzzy Systems, vol. 37, no. 1, pp. 1529–1544, (2019)). The main objective of improved operational laws is to eliminate the flows and ambiguities in existing AOs. Secondly, based on these laws, various AOs to aggregate the information are acquired along with their requisite properties and relations. Lastly, an approach for interpreting the multi-attribute decision-making (MCDM) problem based on the stated operators is given and illustrated with an example. Some of the existing models are used to perform a comprehensive comparative analysis to demonstrate their impacts.

1 Introduction

MCDM is a tool that involves a set of criteria and a set of alternatives. Generally, the decision information is mathematically represented by a decision matrix. Several scholars have proposed a variety of approaches to achieve optimum decisions. In the past, decisions were made based on precise numerical data sets. However, as time goes on and the system gets more complex, it gets harder for decision-makers to deal with data uncertainties. therefore, judgments made using outdated methods are unable to identify the best alternative. To address this, Zadeh [1] began work on fuzzy sets (FSs) which is an extension of the classic set. Additionally, they presented the idea of a linguistic variable and its approximate reasoning [2]. To increase the results' accuracy and interpretability in word processing, Labella [3] presented a fuzzy linguistic representation model for comparative linguistic expressions that capitalizes on the strengths of the 2-tuple linguistic representation model. In FSs, each element is allocated a membership degree ($\mathrm{MD}$) which lies between zero and one. The researchers suggested various extensions of FSs including intuitionistic fuzzy (IF) set (IFS) [4] and interval-valued IFS (IVIFS) [5]. Yager [6, 7] proposed the idea of PFS, which is an extension of the IFS. Zhang [8] proposed the notion of IVPFS. These theories describe information in terms of their $\mathrm{MD}$ and non-membership degrees ($\widetilde{\mathrm{MD}}$) in the form of crisp or interval numbers. Various scholars have presented their theories and approaches for analyzing DM problems such as information measures and AOs, which are summarized in see [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35].

Even while all of these theories facilitate hesitations to a great extent, they still cannot tolerate the circumstances, where the decision-maker has to consider the falsity corresponding to the truth value ranging over an interval. However, Jun et al. [36] introduced the idea of the cubic set (CS), which is an effective tool for dealing with possible disagreement of the agreed interval values and vice versa. Furthermore, it allows the simultaneous consideration of two different time zones in a single CS. For example, suppose that experimenter has to perform experiment $E$ and is hesitant whether the outcome measure will range between $[0.3, 0.4]$ before performing it at time ${t}_{1}$, and after completing the experiment at ${t}_{2}$, he/her obtain a crisp value that may agree (p-order) or disagree (R-order) with the assumed interval. Consequently, this environment improves accuracy by broadening the scope of the membership interval by taking into account a fuzzy set membership value corresponding to it. CS is a great extension of the interval-valued fuzzy set to deal with the uncertainties by adding a fuzzy set to the analysis. CS and its applications in DM problems are discussed in [37,38,39,40,41,42]. The idea of cubic intuitionistic fuzzy (CIF) set (CIFS) was presented by Kaur and Garg [43, 44], which is characterized by two sections at the same time, one of which reflects the membership degrees by an IVIFS and the other by an IFS. each element in the CIFS is expressed by $\left(\langle \left[{\xi }^{-},{\xi }^{+}\right],\left[{\varphi }^{-},{\varphi }^{+}\right]\rangle ,\left\langle \xi , \varphi \right\rangle \right)$ satisfying the conditions ${\xi }^{+}+{\varphi }^{+}\preccurlyeq 1$ and $\xi +\varphi \preccurlyeq 1$. However, in some practical problems, the sum of ${\xi }^{+}$ and ${\varphi }^{+}$ may be bigger than one, but their square sum is less than or equal to one. For example, let ${\xi }^{+}=0.6$ and ${\varphi }^{+}=0.7$. Owing to the sum of two values being greater than one, they are not available for CIFS. To deal with such types of problems, Abbas et al. [45] introduced the idea of CPFS, which is an extension of CIFS. CPFS is the hybrid form that contains more information to express both IVPFS and PFS simultaneously to deal with uncertainties in data. Obviously, CPFS is a more capable model to deal with uncertainty and ambiguity in data and plays a very important role in DM problems. However, the operational laws of addition and multiplication under CPFS proposed by [38] have flaws and ambiguities which need to be modified.

In current communication, motivated by the concept of the Bonferroni mean and by taking the advantages of the CIFS to express the uncertainty, we modify the existing operational laws and their AOs presented by [38]. Further, some new operational laws such as P-union (rep. R-union) and P-intersection (rep. R-intersection) are defined to improve the score and accuracy function in a CPF-environment. Based on these operational laws, we propose a series of new AOs called cubic Pythagorean fuzzy order weighted averaging (CPFOWA), cubic Pythagorean fuzzy order weighted geometric (CPFOWG), and cubic Pythagorean fuzzy hybrid averaging (CPFHA) to aggregate the preferences of decision-makers. Various desired features of these operators such as Idempotency, monotonicity, Boundedness, Shift Invariance, and homogeneity properties are discussed in detail. The proposed operators have two major advantages:

• 1. These operators have considered the interrelationships of aggregated values.

• 2. Since CPFS is a significant indication that incorporates more information to express both IVPFS and PFS at the same time, which leads to a flexible and robust aggregation process so that they are more powerful than IVPFS and PFS.

Finally, an MCDM method for rating the different alternatives based on these AOs has been presented.

The remainder of this research work is organized as follows. Section 2 reviews some basic concepts concerning CPFS. In Sect. 3, the operational laws and AOs suggested by Abbas et al. [] are reviewed. Some new and modified operational laws and their properties are proposed in Sect. 4. Based on the operational laws, modified CPFWA, modified CPFWG, CPFOWA, CPFOWG, and CPFHA AOs are proposed in Sect. 5. In Sect. 6, an MCDM approach based on the proposed AOs and an illustrative example is provided to verify the approach is developed. Finally, Sect. 7 concludes the paper.

2 Preliminaries

In this section, we provide some introductory concepts about the cubic set, cubic intuitionistic fuzzy set, cubic Pythagorean fuzzy set, and their operational laws.

2.1 Cubic Set

Definition 1

[36] Let $X$ be a non-empty set. A CS $\dot{C}$ in $X$ is defined as

$$\dot{C}=\left\{x, C\left(x\right), \vartheta (x)\left|x\in X\right.\right\},$$

(1)

where $C\left(x\right)=[{C}^{-}\left(x\right), {C}^{+}(x)]$ is interval-valued fuzzy (IVF) set in $X$≤ and $\vartheta$ is a FS. A CS $\dot{C}(x)$ is said to be an internal cubic set if ${C}^{-}(x)\preccurlyeq \vartheta (x)\preccurlyeq {C}^{+}(x)$ and a CS $\dot{C}(x)$ an external cubic set if $\vartheta (x)\notin ({C}^{-}\left(x\right), {C}^{+}(x))$. A CS $\dot{C}=\left\{x, C\left(x\right), \vartheta (x)\left|x\in X\right.\right\}$ is simply denoted by $\dot{C}=\left\langle C, \vartheta \right\rangle$.

Definition 2

[36] Let ${\dot{C}}_{1}=\langle {C}_{1}, {\vartheta }_{1}\rangle$ and ${\dot{C}}_{2}=\langle {C}_{2}, {\vartheta }_{2}\rangle$ be CSs in $X$. Then

• (a) (Equality): If ${C}_{1}={C}_{2}$ and ${\vartheta }_{1}={\vartheta }_{2}$ then ${\dot{C}}_{1}={\dot{C}}_{2}$.

• (b) (P-order): If ${C}_{1}\subseteq {C}_{2}$ and ${\vartheta }_{1}\preccurlyeq {\vartheta }_{2}$ then ${\dot{C}}_{1}{\subseteq }_{P}{\dot{C}}_{2}$.

• (c) (R-order): If ${C}_{1}\subseteq {C}_{2}$ and ${\vartheta }_{1}\succcurlyeq {\vartheta }_{2}$ then ${\dot{C}}_{1}{\subseteq }_{R}{\dot{C}}_{2}$.

Definition 3

[36] Let $\dot{{C}_{i}}=\left\{x, {C}_{i}\left(x\right), {\vartheta }_{i} (x)\left|x\in X\right.\right\}$ be a collection CSs, where $i\in \Delta$, then

• (a) (P-union): ${\bigcup }_{i\in \Delta }^{P}{\dot{C}}_{i}(x)=\left\{\langle x, \bigcup_{i\in \Delta }{C}_{i}(x), \underset{i\in \Delta }{\bigvee }{\vartheta }_{i}(x)\rangle \left|x\in X\right.\right\}$

• (b) (P-intersection): ${\bigcap }_{i\in \Delta }^{P}{\dot{C}}_{i}\left(x\right)=\left\{\langle x, \bigcap_{i\in \Delta }{C}_{i}\left(x\right), \underset{i\in \Delta }{\bigwedge }{\vartheta }_{i}(x)\rangle \left|x\in X\right.\right\}$

• (c) (R-union): ${\bigcup }_{i\in \Delta }^{R}{\dot{C}}_{i}(x)=\left\{\langle x, \bigcup_{i\in \Delta }{C}_{i}(x), \underset{i\in \Delta }{\bigwedge }\vartheta (x)\rangle \left|x\in X\right.\right\}$

• (d) (R-intersection):${\bigcap }_{i\in \Delta }^{R}{\dot{C}}_{i}\left(x\right)=\left\{\langle x, \bigcap_{i\in \Delta }{C}_{i}\left(x\right), \underset{i\in \Delta }{\bigvee }{\vartheta }_{i}(x)\rangle \left|x\in X\right.\right\}$

2.2 Cubic Intuitionistic Fuzzy Set

Definition 4

[43, 44] Let $X$ be a non-empty set. A CIFS $\ddot{C}$ over $x\in X$ is defined as follows:

$$\ddot{C}=\left\{\langle x, B\left(x\right),\xi (x)\rangle \left|x\in X\right.\right\}$$

(2)

where $B\left(x\right)=\left\{x,\langle \left[{\mu }_{B}^{-}(x), {\mu }_{B}^{+}(x)\right], \left[{\upsilon }_{B}^{-}(x), {\upsilon }_{B}^{+}(x)\right]\rangle \left|x\in X\right.\right\}$ is IVIFS while $\xi \left(x\right)=\left\{x,\langle {\mu }_{\xi }(x), {\nu }_{\xi }(x)\rangle \left|x\in X\right.\right\}$ represents IFS such that $0\preccurlyeq {\mu }_{B}^{-}(x)\preccurlyeq {\mu }_{B}^{+}(x)\preccurlyeq 1$, $0\preccurlyeq \nu (x)\preccurlyeq {\nu }_{B}^{+}(x)\preccurlyeq 1$ and $0\preccurlyeq {\mu }_{B}^{+}(x)+{\nu }_{B}^{+}(x)\preccurlyeq 1$. Also, $0\preccurlyeq {\mu }_{\rho }\left(x\right), {\nu }_{\rho }(x)\preccurlyeq 1$ and $0\preccurlyeq {\mu }_{\xi }\left(x\right)+{\upsilon }_{\xi }(x)\preccurlyeq 1$. To keep it simple, the pair $\ddot{C}=\left\langle B, \xi \right\rangle$, where $\langle \left[{\mu }_{B}^{-}, {\mu }_{B}^{+}\right], \left[{\nu }_{B}^{-}, {\nu }_{B}^{+}\right]\rangle$ and $\langle {\mu }_{\xi }, {\nu }_{\xi }\rangle$ and called as CIF number (CIFN).

Definition 5

[44] Let $\ddot{C}=\left\{\langle x, B\left(x\right),\xi (x)\rangle \left|x\in X\right.\right\}$, where $B\left(x\right)=\left\{x,\langle \left[{\mu }_{B}^{-}(x), {\mu }_{B}^{+}(x)\right], \left[\nu (x), {\nu }_{B}^{+}(x)\right]\rangle \right\}$ and $\xi \left(x\right)=\left\{x,\langle {\mu }_{\xi }(x), {\nu }_{\xi }(x)\rangle \right\}$ for all $x\in X$. Then, $\ddot{C}$ is said to be internal CIFS if ${\mu }_{\xi }\left(x\right)\in \left[{\mu }_{B}^{-}, {\mu }_{B}^{+}\right]$ and ${\xi }_{\rho }(x)\in \left[{\nu }_{B}^{-}, {\nu }_{B}^{+}\right]$ for all $x\in X$, Otherwise called as external CIFS.

Definition 6

[43] For a family of CIFS $\left\{{\ddot{C}}_{i}, i\in \Delta \right\}$, then

• (a) (P-union): ${\bigcup }_{i\in \Delta }^{P}{\ddot{C}}_{i}=\left(\begin{array}{c}\left\langle \left[{max}_{i\in \Delta }\left({\mu }_{i}^{-}\right), {max}_{i\in \Delta }\left({\mu }_{i}^{+}\right)\right], \left[{min}_{i\in \Delta }\left({\nu }_{i}^{-}\right), {min}_{i\in \Delta }\left({\nu }_{i}^{+}\right)\right]\right\rangle ,\\ \left\langle {max}_{i\in \Delta }{\mu }_{i},{min}_{i\in \Delta }{\nu }_{i}\right\rangle \end{array}\right)$.

• (b) (P-intersection): ${\bigcap }_{i\in \Delta }^{R}{\ddot{C}}_{i}=\left(\begin{array}{c}\left\langle \left[{min}_{i\in \Delta }\left({\mu }_{i}^{-}\right), {min}_{i\in \Delta }\left({\mu }_{i}^{+}\right)\right], \left[{max}_{i\in \Delta }\left({\nu }_{i}^{-}\right), {max}_{i\in \Delta }\left({\nu }_{i}^{+}\right)\right]\right\rangle ,\\ \left\langle {min}_{i\in \Delta }{\mu }_{i},{max}_{i\in \Delta }{\nu }_{i}\right\rangle \end{array}\right)$.

• (c) (R-union): ${\bigcup }_{i\in \Delta }^{R}{\ddot{C}}_{i}=\left(\begin{array}{c}\left\langle \left[{max}_{i\in \Delta }\left({\mu }_{i}^{-}\right), {max}_{i\in \Delta }\left({\mu }_{i}^{+}\right)\right], \left[{min}_{i\in \Delta }\left({\nu }_{i}^{-}\right), {min}_{i\in \Delta }\left({\nu }_{i}^{+}\right)\right]\right\rangle ,\\ \left\langle {min}_{i\in \Delta }{\mu }_{i},{max}_{i\in \Delta }{\nu }_{i}\right\rangle \end{array}\right)$.

• (d) (R-intersection): ${\bigcup }_{i\in \Delta }^{P}{\ddot{C}}_{i}=\left(\begin{array}{c}\left\langle \left[{max}_{i\in \Delta }\left({\mu }_{i}^{-}\right), {max}_{i\in \Delta }\left({\mu }_{i}^{+}\right)\right], \left[{min}_{i\in \Delta }\left({\nu }_{i}^{-}\right), {min}_{i\in \Delta }\left({\nu }_{i}^{+}\right)\right]\right\rangle ,\\ \left\langle {min}_{i\in \Delta }{\mu }_{i},{max}_{i\in \Delta }{\nu }_{i}\right\rangle \end{array}\right)$.

Definition 7

[44] Let ${\alpha }_{1}=\left(\left\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\right\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ and ${\alpha }_{2}=\left(\langle \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right], \left[{\nu }_{2}^{-},{\nu }_{2}^{+}\right]\rangle , \left\langle {\mu }_{2}, {\nu }_{2}\right\rangle \right)$ be two CIFSs in $X$. Then

• (a) (Equality): ${\alpha }_{1}={\alpha }_{2}$, if and only if $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]=\left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]=\left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}={\mu }_{2}$ and ${\nu }_{1}={\nu }_{2}$.

• (b) (P-order): ${\alpha }_{1}{\subseteq }_{P}{\alpha }_{2}$ if $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}\preccurlyeq {\mu }_{2}$ and ${\nu }_{1}\succcurlyeq {\nu }_{2}$.

• (c) (R-order): ${\alpha }_{1}{\subseteq }_{R}{\alpha }_{2}$ if $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}\succcurlyeq {\mu }_{2}$ and ${\nu }_{1}\preccurlyeq {\nu }_{2}$.

Definition 8

[44] Let ${\alpha }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ be a CIFN, then score function is defined under R-order as

$$sc\left({\alpha }_{1}\right)=\frac{{\mu }_{1}^{-}+{\mu }_{1}^{+}-{\nu }_{1}^{-}-{\nu }_{1}^{+}}{2}+{(\nu }_{1}-{\mu }_{1})$$

(3)

while for P-order as

$$sc\left({\alpha }_{1}\right)=\frac{{\mu }_{1}^{-}+{\mu }_{1}^{+}-{\nu }_{1}^{-}-{\nu }_{1}^{+}}{2}+{(\mu }_{1}-{\nu }_{1})$$

(4)

where $-2\preccurlyeq sc{(\alpha }_{1})\preccurlyeq 2$.

Definition 9

[44] Let ${\alpha }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\upsilon }_{1}^{-},{\upsilon }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\upsilon }_{1}\right\rangle \right)$ be a CIFN, then accuracy function is defined under R-order as

$$ac\left({\alpha }_{1}\right)=\frac{{\mu }_{1}^{-}+{\mu }_{1}^{+}+{\nu }_{1}^{-}+{\nu }_{1}^{+}}{2}+{(\nu }_{1}+{\mu }_{1})$$

(5)

where $0\preccurlyeq ac{(\alpha }_{1})\preccurlyeq 2$.

Definition 10

[44] Let $\alpha =\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right], \left[{\nu }^{-}, {\nu }^{+}\right]\rangle , \left\langle \mu ,\nu \right\rangle \right)$, ${\alpha }_{1}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)$ $(i=\mathrm{1,2}$) be the collections of CIFNs, and $\psi \succ 0$ be a real number then

• $(a) {\alpha }_{1}\oplus {\alpha }_{2}=\left(\begin{array}{c}\left\langle \left[1-{\prod }_{i=1}^{2}\left(1-{\mu }_{i}^{-}\right), 1-{\prod }_{i=1}^{2}\left(1-{\mu }_{i}^{+}\right)\right], \left[{\prod }_{i=1}^{2}{\nu }_{i}^{-}, {\prod }_{i}^{2}{\nu }_{i}^{+}\right] \right\rangle ,\\ \left\langle {\prod }_{i=1}^{2}{\mu }_{i},1-{\prod }_{i=1}^{2}(1-{\upsilon }_{i}),\right\rangle \end{array}\right)$

• $(b) {\alpha }_{1}\otimes {\alpha }_{2}=\left(\begin{array}{c}\left\langle \left[{\prod }_{i=1}^{2}{\mu }_{i}^{-}, {\prod }_{i}^{2}{\mu }_{i}^{+}\right], \left[1-{\prod }_{i=1}^{2}\left(1-{\nu }_{i}^{-}\right),1-{\prod }_{i=1}^{2}\left(1-{\nu }_{i}^{+}\right)\right] \right\rangle ,\\ \left\langle 1-{\prod }_{i=1}^{2}\left(1-{\mu }_{i}\right),{\prod }_{i=1}^{2}{\upsilon }_{i}\right\rangle \end{array}\right)$

• $(c) \psi \alpha =\left(\begin{array}{c}\left\langle \left[1-{\left(1-{\mu }^{-}\right)}^{\psi }, 1-{\left(1-{\mu }^{+}\right)}^{\psi }\right], \left[{\left({\nu }^{-}\right)}^{\psi }, {\left({\nu }^{+}\right)}^{\psi }\right]\right\rangle ,\\ \left\langle {\mu }^{\psi }, 1-{(1-\nu )}^{\psi }\right\rangle \end{array}\right)$

• $(d) {\alpha }^{\psi }=\left(\begin{array}{c}\left\langle \left[{\left({\mu }^{-}\right)}^{\psi }, {\left({\mu }^{+}\right)}^{\psi }\right], \left[1-{\left(1-{\nu }^{-}\right)}^{\psi }, 1-{\left(1-{\nu }^{+}\right)}^{\psi }\right]\right\rangle ,\\ \left\langle { 1-{\left(1-\mu \right)}^{\psi }, \nu }^{\psi }\right\rangle \end{array}\right)$

Definition 14

[45] A CPFWA operator is a mapping $\mathrm{CPFWA}:{\Omega }^{n}\to\Omega$ defined as

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)={\mathcalligra{w}}_{1}{\beta }_{1}\oplus {\mathcalligra{w}}_{2}{\beta }_{2}\oplus\dots \oplus{\mathcalligra{w}}_{n}{\beta }_{n}$$

(9)

where $\Omega$ is the collections of CPFNs ${\beta }_{i}(i=\mathrm{1,2},\dots ,n)$, $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ is the weight vector of ${\beta }_{i}$ such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$.

Theorem 1

[45] For ${\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}$, the value obtained by CPFWA is a CPFN, which is determined by

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},{\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\right\rangle \end{array}\right)$$

(10)

Definition 15

[45] A CPFWG operator is a mapping $\mathrm{CPFWG}:{\Omega }^{n}\to\Omega$ defined as follows:

$$\mathrm{CPFWG}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)={\mathcalligra{w}}_{1}{\beta }_{1}\otimes {\mathcalligra{w}}_{2}{\beta }_{2}\otimes \dots \oplus{\mathcalligra{w}}_{n}{\beta }_{n}$$

(11)

where $\Omega$ is the collections of CPFNs ${\beta }_{i}(i=\mathrm{1,2},\dots ,n)$, $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ is the weight vector of ${\beta }_{i}$ such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$.

Theorem 2

[45] For ${\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}$, the value obtained by CPFWG is a CPFN, which is determined by

$$\mathrm{CPFWG}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\mu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\mu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right],\left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}, \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

(12)

3 Updated Operational Laws of CPFS

In this section, based On existing research [43, 44], this article suggests new operational laws for the addition and multiplication of CPFN.

Definition 16

For a family of CPFS $\left\{{\ddot{C}}_{i}, i\in \Delta \right\}$, then

• (a)
• (b)
• (c)
• (d)

Definition 17

Let ${\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ and ${\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right], \left[{\nu }_{2}^{-},{\nu }_{2}^{+}\right]\rangle , \left\langle {\mu }_{2}, {\nu }_{2}\right\rangle \right)$ be two CPFSs in $X$. Then

• (a) (Equality): ${\beta }_{1}={\beta }_{2}$, if and only if $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]=\left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]=\left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}={\mu }_{2}$ and ${\nu }_{1}={\nu }_{2}$.

• (b) (P-order): ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ if $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}\preccurlyeq {\mu }_{2}$ and ${\nu }_{1}\succcurlyeq {\nu }_{2}$.

• (c) (R-order): ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}$ if $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}\succcurlyeq {\mu }_{2}$ and ${\nu }_{1}\preccurlyeq {\nu }_{2}$.

Definition 18

Let ${\alpha }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ be a CIFN, then score function is defined under R-order as

$$sc\left({\beta }_{1}\right)=\frac{{\left({\mu }_{1}^{-}\right)}^{2}+{\left({\mu }_{1}^{+}\right)}^{2}-{\left({\nu }_{1}^{-}\right)}^{2}-{\left({\nu }_{1}^{+}\right)}^{2}}{2}+({\mu }_{1}^{2}-{\nu }_{1}^{2})$$

(13)

while for P-order as

$$sc\left({\beta }_{1}\right)=\frac{{\left({\mu }_{1}^{-}\right)}^{2}+{\left({\mu }_{1}^{+}\right)}^{2}-{\left({\nu }_{1}^{-}\right)}^{2}-{\left({\nu }_{1}^{+}\right)}^{2}}{2}+({\mu }_{1}^{2}-{\nu }_{1}^{2})$$

(14)

where $-2\preccurlyeq sc{(\beta }_{1})\preccurlyeq 2$.

Definition 19

Let ${\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ be a CPFN, then accuracy function is defined under R-order as

$$ac\left({\beta }_{1}\right)=\frac{{\left({\mu }_{1}^{-}\right)}^{2}+{\left({\mu }_{1}^{+}\right)}^{2}+{\left({\nu }_{1}^{-}\right)}^{2}+{\left({\nu }_{1}^{+}\right)}^{2}}{2}+({\mu }_{1}^{2}+{\nu }_{1}^{2})$$

(15)

where $0\preccurlyeq ac({\beta }_{1})\preccurlyeq 2$.

Theorem 3

For CPFNs ${\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)$ $(1, 2, 3, 4)$ we have

• (a) If ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ and ${\beta }_{2}{\subseteq }_{P}{\beta }_{3}$ then ${\beta }_{1}{\subseteq }_{P}{\beta }_{3}$.

• (b) If ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ then ${\beta }_{2}^{c}{\subseteq }_{P}{\beta }_{1}^{c}$.

• (c) If ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ and ${\beta }_{1}{\subseteq }_{P}{\beta }_{3}$ then ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}\cap {\beta }_{3}$.

• (d) If ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ and ${\beta }_{3}{\subseteq }_{P}{\beta }_{4}$ then ${\beta }_{1}\cup {\beta }_{3}{\subseteq }_{P}{\beta }_{2}\cup {\beta }_{4}$ and ${\beta }_{1}\cap {\beta }_{3}{\subseteq }_{P}{\beta }_{2}\cap {\beta }_{4}$.

• (e) If ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ and ${\beta }_{3}{\subseteq }_{P}{\beta }_{2}$ then ${\beta }_{1}\cup {\beta }_{3}{\subseteq }_{P}{\beta }_{2}$.

• (f) If ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}$ and ${\beta }_{2}{\subseteq }_{R}{\beta }_{3}$ then ${\beta }_{1}{\subseteq }_{R}{\beta }_{3}$.

• (g) If ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}$ then ${\beta }_{2}^{c}{\subseteq }_{R}{\beta }_{1}^{c}$.

• (h) If ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}$ and ${\beta }_{1}{\subseteq }_{R}{\beta }_{3}$ then ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}\cap {\beta }_{3}$.

• (i) If ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}$ and ${\beta }_{3}{\subseteq }_{R}{\beta }_{4}$ then ${\beta }_{1}\cup {\beta }_{3}{\subseteq }_{R}{\beta }_{2}\cup {\beta }_{4}$ and ${\beta }_{1}\cap {\beta }_{3}{\subseteq }_{R}{\beta }_{2}\cap {\beta }_{4}$.

• (j) If ${\beta }_{1}{\subseteq }_{R}{\beta }_{2}$ and ${\beta }_{3}{\subseteq }_{R}{\beta }_{2}$ then ${\beta }_{1}\cup {\beta }_{3}{\subseteq }_{R}{\beta }_{2}$.

Proof

(a) since ${\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$, ${\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right], \left[{\nu }_{2}^{-},{\nu }_{2}^{+}\right]\rangle , \left\langle {\mu }_{2}, {\nu }_{2}\right\rangle \right)$ and ${\beta }_{3}=\left(\langle \left[{\mu }_{3}^{-}, {\mu }_{3}^{+}\right], \left[{\nu }_{3}^{-},{\nu }_{3}^{+}\right]\rangle , \left\langle {\mu }_{3}, {\nu }_{3}\right\rangle \right)$. By Definition 17 if ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]$, ${\mu }_{1}\preccurlyeq {\mu }_{2}$ and ${\nu }_{1}\succcurlyeq {\nu }_{2}$. Similarly, if ${\beta }_{2}{\subseteq }_{P}{\beta }_{3}$ then $\left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]\subseteq \left[{\mu }_{3}^{-}, {\mu }_{3}^{+}\right]$, $\left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]\supseteq \left[{\nu }_{3}^{-}, {\nu }_{3}^{+}\right]$, ${\mu }_{2}\preccurlyeq {\mu }_{3}$ and ${\nu }_{2}\succcurlyeq {\nu }_{3}$ which implies that $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right]\subseteq \left[{\mu }_{3}^{-}, {\mu }_{3}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{2}^{-}, {\nu }_{2}^{+}\right]\supseteq \left[{\nu }_{3}^{-}, {\nu }_{3}^{+}\right]$, ${\mu }_{1}\preccurlyeq {\mu }_{2}\preccurlyeq {\mu }_{3}$ and ${\nu }_{1}\succcurlyeq {\nu }_{2}\succcurlyeq {\nu }_{3}$ and hence $\left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right]\subseteq \left[{\mu }_{3}^{-}, {\mu }_{3}^{+}\right]$, $\left[{\nu }_{1}^{-}, {\nu }_{1}^{+}\right]\supseteq \left[{\nu }_{3}^{-}, {\nu }_{3}^{+}\right]$, ${\mu }_{1}\preccurlyeq {\mu }_{3}$ and ${\nu }_{1}\succcurlyeq {\nu }_{3}$. Therefore, if ${\beta }_{1}{\subseteq }_{P}{\beta }_{2}$ and ${\beta }_{2}{\subseteq }_{P}{\beta }_{3}$ then ${\beta }_{1}{\subseteq }_{P}{\beta }_{3}$. Similarly, we can prove for remaining parts, so we omit here.

Definition 20

Let $\beta =\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right], \left[{\nu }^{-}, {\nu }^{+}\right]\rangle , \left\langle \mu +\nu \right\rangle \right)$, ${\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)$ $(i=\mathrm{1,2}$) be the collections of CPFNs, and $\psi \succ 0$ be a real number then

• $(a) {\beta }_{1}\oplus {\beta }_{2}=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{2}\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)},\\ \sqrt{1-{\prod }_{i=1}^{2}\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}\end{array}\right], \left[{\prod }_{i=1}^{2}{\nu }_{i}^{-}, {\prod }_{i}^{2}{\nu }_{i}^{+}\right] \right\rangle ,\\ \left\langle {\prod }_{i=1}^{2}{\mu }_{i},\sqrt{1-{\prod }_{i=1}^{2}(1-{\left({\nu }_{i}\right)}^{2})}\right\rangle \end{array}\right)$

• $(b) {\beta }_{1}\otimes {\beta }_{2}=\left(\begin{array}{c}\left\langle \left[{\prod }_{i=1}^{2}{\mu }_{i}^{-}, {\prod }_{i}^{2}{\mu }_{i}^{+}\right], \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{2}\left(1-{\left({\nu }_{i}^{-}\right)}^{2}\right)},\\ \sqrt{1-{\prod }_{i=1}^{2}\left(1-{\left({\nu }_{i}^{+}\right)}^{2}\right)}\end{array}\right] \right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{i=1}^{2}\left(1-{\left({\mu }_{i}\right)}^{2}\right)},{\prod }_{i=1}^{2}{\nu }_{i}\right\rangle \end{array}\right)$

• $(c) \psi \beta =\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\left(1-{\left({\mu }^{-}\right)}^{2}\right)}^{\psi }}, \\ \sqrt{1-{\left(1-{\left({\mu }^{+}\right)}^{2}\right)}^{\psi }}\end{array}\right], \left[{\left({\nu }^{-}\right)}^{\psi }, {\left({\nu }^{+}\right)}^{\psi }\right]\right\rangle ,\\ \left\langle {\mu }^{\psi },\sqrt{ 1-{(1-{\nu }^{2})}^{\psi }}\right\rangle \end{array}\right)$

• $(d) {\beta }^{\psi }=\left(\begin{array}{c}\left\langle \left[{\left({\mu }^{-}\right)}^{\psi }, {\left({\mu }^{+}\right)}^{\psi }\right], \left[\begin{array}{c}\sqrt{1-{\left(1-{\left({\nu }^{-}\right)}^{2}\right)}^{\psi }}, \\ \sqrt{1-{\left(1-{\left({\nu }^{+}\right)}^{2}\right)}^{\psi }}\end{array}\right]\right\rangle ,\\ \left\langle { \sqrt{1-{\left(1-{\mu }^{2}\right)}^{\psi }}, \nu }^{\psi }\right\rangle \end{array}\right)$.

Theorem 4

For two CPFNs ${\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ and ${\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right], \left[{\nu }_{2}^{-},{\nu }_{2}^{+}\right]\rangle , \left\langle {\mu }_{2}, {\nu }_{2}\right\rangle \right)$ and $\psi \succ 0$ be a real number then ${\beta }_{1}\oplus {\beta }_{2}$, ${\beta }_{1}\otimes {\beta }_{2}$, ${\beta }^{\psi }$ and $\psi {\beta }_{1}$ are also CPFNs.

Proof

Since ${\beta }_{1}=\left(\langle \left[{\mu }_{1}^{-}, {\mu }_{1}^{+}\right], \left[{\nu }_{1}^{-},{\nu }_{1}^{+}\right]\rangle , \left\langle {\mu }_{1}, {\nu }_{1}\right\rangle \right)$ and ${\beta }_{2}=\left(\langle \left[{\mu }_{2}^{-}, {\mu }_{2}^{+}\right], \left[{\nu }_{2}^{-},{\nu }_{2}^{+}\right]\rangle , \left\langle {\mu }_{2}, {\nu }_{2}\right\rangle \right)$ are two CPFNs such that $0\preccurlyeq {\mu }_{1}^{-}, {\mu }_{1}^{+},{\nu }_{1}^{+},{\nu }_{1}^{+}, {\mu }_{2}^{-},{\mu }_{2}^{+}, {\nu }_{2}^{-},{\nu }_{2}^{+}\preccurlyeq 1$ and ${\left({\mu }_{1}^{+}\right)}^{2}+{\left({\nu }_{1}^{+}\right)}^{2}\preccurlyeq 1$ which implies that $0\preccurlyeq \left(1-{\left({\mu }_{1}^{-}\right)}^{2}\right)\left(1-{\left({\mu }_{2}^{-}\right)}^{2}\right)\preccurlyeq 1$ and hence $0\preccurlyeq \sqrt{{\left({\mu }_{1}^{-}\right)}^{2}+{\left({\mu }_{2}^{-}\right)}^{2}-{\left({\mu }_{1}^{-}\right)}^{2}{\left({\mu }_{2}^{-}\right)}^{2}}\preccurlyeq 1$. Similarly, we can prove that $0\preccurlyeq \sqrt{{\left({\mu }_{1}^{+}\right)}^{2}+{\left({\mu }_{2}^{+}\right)}^{2}-{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{2}^{+}\right)}^{2}}\preccurlyeq 1$, $0\preccurlyeq {\nu }_{1}^{-}{\nu }_{2}^{-}\preccurlyeq 1$ and $0\preccurlyeq {\nu }_{1}^{+}{\nu }_{2}^{+}\preccurlyeq 1$. Also, $0\preccurlyeq {\mu }_{1}, {\nu }_{1}, {\mu }_{2},{\nu }_{2}\preccurlyeq 1$ and ${\mu }_{1}^{2}+{\nu }_{1}^{2}\preccurlyeq 1$, ${\mu }_{1}^{2}+{\nu }_{1}^{2}\preccurlyeq 1$, which implies that ${\mu }_{1}{\mu }_{2}\preccurlyeq 1$ and $\sqrt{{\mu }_{1}^{2}+{\mu }_{2}^{2}-{\mu }_{1}^{2}{\mu }_{2}^{2}}\preccurlyeq 1$. Finally, we have.

$$\sqrt{{\left({\mu }_{1}^{+}\right)}^{2}+{\left({\mu }_{2}^{+}\right)}^{2}-{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{2}^{+}\right)}^{2}+{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{2}^{+}\right)}^{2}}=\sqrt{1-\left(1-{\left({\mu }_{1}^{+}\right)}^{2}\right)\left(1-{\left({\mu }_{2}^{+}\right)}^{2}\right)+{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{2}^{+}\right)}^{2}}$$

$\preccurlyeq \sqrt{1-{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{2}^{+}\right)}^{2}+{\left({\mu }_{1}^{+}\right)}^{2}{\left({\mu }_{2}^{+}\right)}^{2}}\preccurlyeq 1$ and $\sqrt{{\mu }_{1}{\mu }_{2}+{\nu }_{1}^{2}+{\nu }_{1}^{2}-{\left({\nu }_{1}^{+}\right)}^{2}{\left({\nu }_{2}^{+}\right)}^{2}}$.

$=\sqrt{{\mu }_{1}{\mu }_{2}+1-\left(1-{\left({\mu }_{1}^{+}\right)}^{2}\right)\left(1-{\left({\mu }_{2}^{+}\right)}^{2}\right)}\preccurlyeq \sqrt{{\mu }_{1}{\mu }_{2}+1-{\mu }_{1}{\mu }_{2}}\preccurlyeq 1$ Therefore, ${\beta }_{1}{\oplus \beta }_{2}$ is CPFN.

Furthermore, for any positive real number $\psi$ and CPFN $\beta =\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right], \left[{\nu }^{-}, {\nu }^{+}\right]\rangle , \left\langle \mu +\nu \right\rangle \right)$, we have $0\preccurlyeq {\mu }^{\psi }\preccurlyeq 1$, $0\preccurlyeq \sqrt{1-{(1-{\nu }^{2})}^{\psi }}\preccurlyeq 1$, $0\preccurlyeq {\left({\nu }^{-}\right)}^{\psi }{\left({\nu }^{+}\right)}^{\psi }\preccurlyeq 1$ and $0\preccurlyeq \sqrt{1-{\left(1-{\left({\mu }^{-}\right)}^{2}\right)}^{\psi }{\left(1-{\left({\mu }^{+}\right)}^{2}\right)}^{\psi }}\preccurlyeq 1$. Hence $\psi \beta$ is also CPFN. Similarly, we can prove that ${\beta }_{1}\otimes {\beta }_{2}$ and ${\beta }^{\psi }$ are also CPFNs.

4 Proposed AOs for CPFNs

In this section, the existing AOs for CPFNs named CPFWA and CPFWG operators, have been modified based on established operational laws. Further, several novel AOs named CPFOWA, CPFOWG, and CPFHA operators are proposed. Furthermore, some properties, such as boundedness, idempotency, monotonicity, Shift Invariance, and homogeneity property of these AOs have been demonstrated.

4.1 Updated CPFWA Operator

Definition 21

A CPFWA operator is a mapping $\mathrm{CPFWA}:{\Omega }^{n}\to\Omega$ defined as

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)={\mathcalligra{w}}_{1}{\beta }_{1}\oplus {\mathcalligra{w}}_{2}{\beta }_{2}\oplus\dots \oplus{\mathcalligra{w}}_{n}{\beta }_{n}$$

(16)

where $\Omega$ is the collections of CPFNs ${\beta }_{i}(i=\mathrm{1,2},\dots ,n)$, $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ is the weight vector of ${\beta }_{i}$ such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$.

Theorem 5

For ${\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}$, the value obtained by CPFWA is a CPFN, which is determined by

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

(17)

Proof

For each ${\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}$, the steps below have to be followed while applying mathematical induction on $n$.

Step 1 For $n=2$, By Definition 21, we get

$$\mathrm{CPFWA}\left({\beta }_{1},{\beta }_{2}\right)={\mathcalligra{w}}_{1}{\beta }_{1}\oplus {\mathcalligra{w}}_{2}{\beta }_{2}$$

$$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\left(1-{\left({\mu }_{1}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{1}}{\left(1-{\left({\mu }_{2}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{2}}},\\ \sqrt{1-{\left(1-{\left({\mu }_{1}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{1}}{\left(1-{\left({\mu }_{2}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{2}}} \end{array}\right],\left[\begin{array}{c}{\left({\nu }_{1}^{-}\right)}^{{\mathcalligra{w}}_{1}}{\left({\nu }_{2}^{-}\right)}^{{\mathcalligra{w}}_{2}},\\ {\left({\nu }_{1}^{+}\right)}^{{\mathcalligra{w}}_{1}}{\left({\nu }_{2}^{+}\right)}^{{\mathcalligra{w}}_{2}}\end{array}\right]\right\rangle ,\\ \left\langle {\left({\mu }_{1}\right)}^{{\mathcalligra{w}}_{1}}{\left({\mu }_{2}\right)}^{{\mathcalligra{w}}_{2}},\sqrt{1-{\left(1-{\nu }_{1}^{2}\right)}^{{\mathcalligra{w}}_{1}}{\left(1-{\nu }_{2}^{2}\right)}^{{\mathcalligra{w}}_{2}}}\right\rangle \end{array}\right)$$

$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{2}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{2}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{2}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{2}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{2}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{2}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$.

As a result, it holds for $n=2$.

Step 2 Assume Eq. (17) hold for $n=k$

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{k}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{k}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{k}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{k}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{k}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{k}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{k}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

(18)

Step 3 For $n=k+1$, we have

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{k},{\beta }_{k+1}\right)={\beta }_{1}\oplus {\beta }_{2}\oplus \dots .\oplus{\beta }_{k}\oplus{\beta }_{k+1}$$

 $=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{k}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{k}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{k}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{k}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{k}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{k}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$

$$\oplus \left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\left(1-{\left({\mu }_{k+1}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{k+1}}},\\ \sqrt{1-{\left(1-{\left({\mu }_{k+1}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{k+1}}} \end{array}\right],\left[\begin{array}{c}{\left({\nu }_{k+1}^{-}\right)}^{{\mathcalligra{w}}_{k+1}},\\ {\left({\nu }_{k+1}^{+}\right)}^{{\mathcalligra{w}}_{k+1}}\end{array}\right]\right\rangle ,\\ \left\langle {\left({\mu }_{k+1}\right)}^{{\mathcalligra{w}}_{k+1}},\sqrt{1-{\left(1-{\nu }_{k+1}^{2}\right)}^{{\mathcalligra{w}}_{k+1}}}\right\rangle \end{array}\right)$$

$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{k+1}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{k+1}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{k+1}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{k+1}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{k+1}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{k+1}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$.

Thus, the result is valid for $n=k+1$. By principle mathematical induction, the holds for all positive integer $n$.

Example 1

Consider four CPFNs ${\beta }_{1}=\left(\langle \left[\mathrm{0.3,0.4}\right], \left[0.2, 0.4\right]\rangle , \left\langle 0.1, 0.2\right\rangle \right)$,

${\beta }_{2}=\left(\langle \left[\mathrm{0.2,0.3}\right], \left[0.5, 0.6\right]\rangle , \left\langle 0.3, 0.2\right\rangle \right)$, ${\beta }_{3}=\left(\langle \left[\mathrm{0.6,0.7}\right], \left[0.2, 0.3\right]\rangle , \left\langle 0.5, 0.1\right\rangle \right)$ and

${\beta }_{4}=\left(\langle \left[\mathrm{0.7,0.8}\right], \left[0.3, 0.6\right]\rangle , \left\langle 0.6, 0.3\right\rangle \right)$ with weight vector $\mathcalligra{w}=(0.2, 0.3, 0.1, 0.4)$, then using GGCPFWA operator as given Eq. (17), we get

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{\left(1-{\left(0.3\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.2\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.6\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.3\right)}^{2}\right)}^{0.2}}$$

$=0.5402$.

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{\left(1-{\left(0.4\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.3\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.7\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.8\right)}^{2}\right)}^{0.2}}$$

$=0.6454$.

${\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}={(0.2)}^{0.2}{(0.5)}^{0.3}{(0.2)}^{0.1}{(0.3)}^{0.4}=0.3096$.

${\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}={(0.4)}^{0.2}{(0.6)}^{0.3}{(0.3)}^{0.1}{(0.6)}^{0.4}=0.5162$.

${\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}={(0.1)}^{0.2}{(0.3)}^{0.3}{(0.5)}^{0.1}{(0.6)}^{0.4}=0.3344$.

$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{\left(1-{\left(0.2\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.2\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.1\right)}^{2}\right)}^{0.2}{\left(1-{\left(0.3\right)}^{2}\right)}^{0.2}}$

$=0.2396$.

$$CPFWA\left({\beta }_{1}, {\beta }_{2}, {\beta }_{3}, {\beta }_{4}\right)=\left(\langle \left[\begin{array}{c}0.5402,\\ 0.6454\end{array}\right],\left[\begin{array}{c}0.3096,\\ 0.5162\end{array}\right]\rangle ,\langle \begin{array}{c}0.3344,\\ 0.2396\end{array}\rangle \right)$$

.

Proposition 1

The CPFWA operator reduces to weighted averaging operator in IVPFS, if the PFS argument i.e., $\left({\mu }_{i}, {\nu }_{i}\right)=(0, 0)$ ${\forall }_{i}$ in CPFS.

Proof

Since $\left({\mu }_{i}, {\nu }_{i}\right)=(0, 0)$ and hence, Eq. (17) becomes

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left(0\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left(0\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

$$=\left(\left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right)$$

(19)

Equation (19) is the operator for weighted averaging in the IVPFS environment.

Proposition 2

If ${\mu }_{i}^{-}={\mu }_{i}^{+}$, ${\nu }_{i}^{-}={\nu }_{i}^{+},$ and $\left({\mu }_{i}, {\nu }_{i}\right)=(0, 0)$ for all $i$, then the CPFWA operator reduces to the Pythagorean fuzzy weighted averaging operator.

Proof

Let ${\mu }_{i}^{-}={\mu }_{i}^{+}=\mu$, ${\nu }_{i}^{-}={\nu }_{i}^{+}=\nu$. Also, $\left({\mu }_{i}, {\nu }_{i}\right)=(0, 0)$, then Eq. (3) becomes

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left(0\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left(0\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

$\left(\langle \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},{\prod }_{i=1}^{n}{\left({\nu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\rangle \right)$.

It has been observed that from Theorem 5, the properties of idempotency, boundedness, monotonicity, Shift Invariance, and homogeneity property hold for the CPFWA operator. These properties are demonstrated as follows:

4.2 Updated Properties

Property 1

If, ${\beta }_{i}=\beta$ for all $i$, where $\beta =\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right], \left[{\nu }^{-}, {\nu }^{+}\right]\rangle , \left\langle \mu , \nu \right\rangle \right)$, then $\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\beta$.

This property is called an Idempotency.

Proof

Since ${\mathcalligra{w}}_{i}\succ 0$, ${\sum }_{I=1}^{n}{\mathcalligra{w}}_{i}=1$ and ${\beta }_{i}=\beta$ for all $i$, then we have

$$\mathrm{CPFWA}\left(\beta , \beta ,\dots ,\beta \right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left(\mu \right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left(\nu \right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

$$=\left(\begin{array}{c}\left\langle \left[1-{\left(1-{\left({\mu }^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}, 1-{\left(1-{\left({\mu }^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}\right], \left[{\left({\nu }^{-}\right)}^{{\mathcalligra{w}}_{i}},{\left({\nu }^{+}\right)}^{{\mathcalligra{w}}_{i}} \right]\right\rangle ,\\ \left\langle {\left(\mu \right)}^{{\mathcalligra{w}}_{i}},1-{\left(1-{\left(\nu \right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}\right\rangle \end{array}\right)$$

$=\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right], \left[{\nu }^{-}, {\nu }^{+}\right]\rangle , \left\langle \mu , \nu \right\rangle \right)$ = $\beta$.

Property 2

Let ${\beta }_{i}=\left(\langle \left[{\mu }_{{\beta }_{i}}^{-}, {\mu }_{{\beta }_{i}}^{+}\right], \left[{\nu }_{{\beta }_{i}}^{-},{\nu }_{{\beta }_{i}}^{+}\right]\rangle , \left\langle {\mu }_{{\beta }_{i}}, {\nu }_{{\beta }_{i}}\right\rangle \right)$ and ${\widetilde{\beta }}_{i}=\left(\langle \left[{\mu }_{{\widetilde{\beta }}_{i}}^{-}, {\mu }_{{\widetilde{\beta }}_{i}}^{+}\right], \left[{\nu }_{{\widetilde{\beta }}_{i}}^{-},{\nu }_{{\widetilde{\beta }}_{i}}^{+}\right]\rangle , \left\langle {\mu }_{{\widetilde{\beta }}_{i}}, {\nu }_{{\widetilde{\beta }}_{i}}\right\rangle \right)$ be CPFNs, where $(i=\mathrm{1,2},\dots ,n)$, such that ${\beta }_{i}\preccurlyeq {\widetilde{\beta }}_{i}$, then

$$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)\preccurlyeq \mathrm{CPFWA}\left({\widetilde{\beta }}_{1}, {\widetilde{\beta }}_{2},\dots ,{\widetilde{\beta }}_{n}\right)$$

(20)

This property is called monotonicity.

Proof

For the sake of simplicity, let us denote

$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{{\beta }_{i}}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=a$, $\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{{\beta }_{i}}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=b$, ${\prod }_{i=1}^{n}{\left({\nu }_{{\beta }_{i}}^{-}\right)}^{{\mathcalligra{w}}_{i}}=c$, ${\prod }_{i=1}^{n}{\left({\nu }_{{\beta }_{i}}^{+}\right)}^{{\mathcalligra{w}}_{i}}=d$, ${\prod }_{i=1}^{n}{\left({\mu }_{{\beta }_{i}}\right)}^{{\mathcalligra{w}}_{i}}=e$, $\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{{\beta }_{i}}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=f,$ $\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{{\widetilde{\beta }}_{i}}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\widetilde{a}$, $\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{{\widetilde{\beta }}_{i}}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\widetilde{b}$, ${\prod }_{i=1}^{n}{\left({\nu }_{{\widetilde{\beta }}_{i}}^{-}\right)}^{{\mathcalligra{w}}_{i}}=\widetilde{c}$, ${\prod }_{i=1}^{n}{\left({\nu }_{{\widetilde{\beta }}_{i}}^{+}\right)}^{{\mathcalligra{w}}_{i}}=\widetilde{d}$, ${\prod }_{i=1}^{n}{\left({\mu }_{{\widetilde{\beta }}_{i}}\right)}^{{\mathcalligra{w}}_{i}}=\widetilde{e}$ and $\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{{\widetilde{\beta }}_{i}}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\widetilde{f}$

Also, ${\beta }_{i}\preccurlyeq {\widetilde{\beta }}_{i}$ for all $i$, then we have ${\mu }_{{\beta }_{i}}^{-}\preccurlyeq {\mu }_{{\widetilde{\beta }}_{i}}^{-}$, ${\mu }_{{\beta }_{i}}^{+}\preccurlyeq {\mu }_{{\widetilde{\beta }}_{i}}^{+}$, ${\nu }_{{\beta }_{i}}^{-}\succcurlyeq {\nu }_{{\widetilde{\beta }}_{i}}^{-}$, ${\nu }_{{\beta }_{i}}^{+}\succcurlyeq {\nu }_{{\widetilde{\beta }}_{i}}^{+}$, ${\mu }_{{\beta }_{i}}\succcurlyeq {\mu }_{{\widetilde{\beta }}_{i}}$ and ${\nu }_{{\beta }_{i}}\preccurlyeq {\nu }_{{\widetilde{\beta }}_{i}}$, then we have $a\preccurlyeq \widetilde{a}$, $b\preccurlyeq \widetilde{b}$, $c\succcurlyeq \widetilde{c}$, $d\succcurlyeq \widetilde{d}$, $e\succcurlyeq \widetilde{e},$ and $f\preccurlyeq \widetilde{f}$. As a result, using the score function as defined in Definition 18, we get

$$sc\left(\mathrm{CPFWA}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\right)=\frac{{a}^{2}+{b}^{2}-{c}^{2}-{d}^{2}}{2}+({f}^{2}-{e}^{2})$$

$$\preccurlyeq \frac{{\widetilde{a}}^{2}+{\widetilde{b}}^{2}-{\widetilde{c}}^{2}-{\widetilde{d}}^{2}}{2}+\left({\widetilde{f}}^{2}-{\widetilde{e}}^{2}\right)=sc\left(\mathrm{CPFWA}({\widetilde{\beta }}_{1}, {\widetilde{\beta }}_{2},\dots ,{\widetilde{\beta }}_{n})\right)$$

Hence, $\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)\preccurlyeq \mathrm{CPFWA}\left({\widetilde{\beta }}_{1}, {\widetilde{\beta }}_{2},\dots ,{\widetilde{\beta }}_{n}\right)$.

Property 3

For a collection of CPFNs ${\beta }_{i}$ $(i=1, 2,\dots , n)$. If

${\beta }^{-}=\left(\langle \left[\begin{array}{c}{min}_{i}\left({\mu }_{i}^{-}\right), \\ {min}_{i}({\mu }_{i}^{+})\end{array}\right], \left[\begin{array}{c}{max}_{i}\left({\nu }_{i}^{-}\right), \\ {max}_{i}({\nu }_{i}^{+})\end{array}\right]\rangle , \left\langle \begin{array}{c}{max}_{i}\left({\mu }_{i}\right),\\ {min}_{i}({\nu }_{i})\end{array}\right\rangle \right)$ and

${\beta }^{+}=\left(\langle \left[\begin{array}{c}{max}_{i}\left({\mu }_{i}^{-}\right),\\ {max}_{i}({\mu }_{i}^{+})\end{array}\right], \left[\begin{array}{c}{min}_{i}\left({\nu }_{i}^{-}\right), \\ {min}_{i}({\nu }_{i}^{+})\end{array}\right]\rangle , \left\langle \begin{array}{c}{min}_{i}\left({\mu }_{i}\right), \\ {max}_{i}({\nu }_{i})\end{array}\right\rangle \right)$, then ${\beta }^{-}\preccurlyeq \mathrm{CPFWA}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\preccurlyeq {\beta }^{+}$.

This property is called Boundedness.

Proof

Since ${min}_{i}\left({\mu }_{i}^{-}\right)\preccurlyeq {\mu }_{i}^{-}\preccurlyeq {max}_{i}\left({\mu }_{i}^{-}\right)$, ${min}_{i}\left({\mu }_{i}^{+}\right)\preccurlyeq {\mu }_{i}^{+}\preccurlyeq {max}_{i}\left({\mu }_{i}^{+}\right)$, ${min}_{i}\left({\nu }_{i}^{-}\right)\preccurlyeq {\nu }_{i}^{-}\preccurlyeq {max}_{i}\left({\nu }_{i}^{-}\right)$, ${min}_{i}\left({\nu }_{i}^{+}\right)\preccurlyeq {\nu }_{i}^{+}\preccurlyeq {max}_{i}\left({\nu }_{i}^{+}\right)$, ${min}_{i}\left({\mu }_{i}\right)\preccurlyeq {\mu }_{i}\preccurlyeq {max}_{i}\left({\mu }_{i}\right)$ and ${min}_{i}\left({\nu }_{i}\right)\preccurlyeq {\nu }_{i}\preccurlyeq {max}_{i}\left({\nu }_{i}\right)$, then

$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{{min}_{i}\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{max}_{i}{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}$;

$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{{min}_{i}\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{max}_{i}{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}$;

${\prod }_{i=1}^{n}{{max}_{i}\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {\prod }_{i=1}^{n}{{min}_{i}\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}$;

${\prod }_{i=1}^{n}{{max}_{i}\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {\prod }_{i=1}^{n}{min}_{i}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}$;

${\prod }_{i=1}^{n}{{max}_{i}\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {\prod }_{i=1}^{n}{{min}_{i}\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}$;

$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{{min}_{i}\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{max}_{i}{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}$,

which implies that

${{min}_{i}\left({\mu }_{i}^{-}\right)}^{2}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq {max}_{i}{\left({\mu }_{i}^{-}\right)}^{2}$;

${{min}_{i}\left({\mu }_{i}^{+}\right)}^{2}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq {max}_{i}{\left({\mu }_{i}^{+}\right)}^{2}$; ${max}_{i}\left({\nu }_{i}^{-}\right)\preccurlyeq {\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {min}_{i}\left({\nu }_{i}^{-}\right)$;

${max}_{i}\left({\nu }_{i}^{+}\right)\preccurlyeq {\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {min}_{i}\left({\nu }_{i}^{+}\right)$; ${max}_{i}\left({\mu }_{i}\right)\preccurlyeq {\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\preccurlyeq {min}_{i}\left({\mu }_{i}\right)$;

${{min}_{i}\left({\nu }_{i}\right)}^{2}\preccurlyeq \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\preccurlyeq {max}_{i}{\left({\nu }_{i}\right)}^{2}$.

Thus, ${\beta }^{-}\preccurlyeq \mathrm{CPFWA}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\preccurlyeq {\beta }^{+}$.

Property 4

For CPFNs ${\alpha }_{1}, {\alpha }_{2},\dots , {\alpha }_{n}$ and $\beta =\left(\langle \left[{\mu }_{\beta }^{-}, {\mu }_{\beta }^{+}\right], \left[{\nu }_{\beta }^{-},{\nu }_{\beta }^{+}\right]\rangle , \left\langle {\mu }_{\beta }, {\nu }_{\beta }\right\rangle \right)$, we have.

$\mathrm{CPFWA}({\alpha }_{1}\beta \oplus{\alpha }_{2}\beta \oplus\dots \oplus{\alpha }_{n}\beta )=\mathrm{CPFWA}({\alpha }_{1},{\alpha }_{2},\dots {,\alpha }_{n})\oplus \beta$.

This property called is called Shift Invariance.

Proof

We omit this proof since the proof is identical to that of Theorem 4.

Property 5

For any real number $\psi$, we have

$\mathrm{CPFWA}\left(\psi {\beta }_{1},\psi {\beta }_{2},\dots ,{\psi \beta }_{n}\right)= \psi \mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)$.

This property is called the homogeneity property.

Proof

easy to prove.

4.3 Updated CPFWG Operator

Definition 22

A CPFWG operator is a mapping $\mathrm{CPFWG}:{\Omega }^{n}\to\Omega$ defined as

$$\mathrm{CPFWG}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)={\mathcalligra{w}}_{1}{\beta }_{1}\otimes {\mathcalligra{w}}_{2}{\beta }_{2}\otimes \dots \oplus{\mathcalligra{w}}_{n}{\beta }_{n}$$

(21)

where $\Omega$ is the collections of CPFNs ${\beta }_{i}(i=\mathrm{1,2},\dots ,n)$, $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ is the weight vector of ${\beta }_{i}$ such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$.

Theorem 6

For ${\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}$, the value obtained by CPFWG is a CPFN, which is determined by

$$\mathrm{CPFWG}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\mu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\mu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right],\left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right]\right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}, {\prod }_{i=1}^{n}{\left({\nu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\right\rangle \end{array}\right)$$

(22)

Proof

Similar to Theorem 5, we omit here.

5 Novel Aos

In this section, a series of new aggregation operators are proposed.

5.1 CPFOWA Operator

Definition 23

A CPFOWA is a mapping defined as ${\mathrm{CPFOWA}:\Omega }^{n}\to\Omega$ on a collection of CPFNs ${\beta }_{i}$, $(i=\mathrm{1,2},\dots n)$ as follows:

$$\mathrm{CPFOWA}\left({\beta }_{1}, {\beta }_{2},\dots , {\beta }_{n}\right)={\mathcalligra{w}}_{1}{\beta }_{\sigma (1)}\oplus {\mathcalligra{w}}_{2}{\beta }_{\sigma (2)}\oplus\dots \oplus {\mathcalligra{w}}_{n}{\beta }_{\sigma (n)}$$

(23)

where $\sigma$ is a permutation of $(1, 2,\dots ,n)$, such that ${\beta }_{\sigma (i-1)}\succcurlyeq {\beta }_{i}$ for $i=\mathrm{1,2},\dots ,n$ and $\mathcalligra{w}={({\mathcalligra{w}}_{1},{\mathcalligra{w}}_{2}\dots ,{\mathcalligra{w}}_{n})}^{T}$ is its weight vector, such that $\mathcalligra{w}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$. Moreover, the ${i}^{th}$ largest CPFN among ${\beta }_{i}\mathrm{^{\prime}}\mathrm{s}$ is ${\beta }_{\sigma (i)}$.

Theorem 7

The value obtained using the CPFOWA operator for CPFNs ${\beta }_{i}$ $(i=\mathrm{1,2},\dots ,n)$ is again a CPFN and given by

$$\mathrm{CPFOWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{\sigma (i)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{\sigma (i)}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{\sigma (i)}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{\sigma (i)}^{-}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left({\mu }_{\sigma (i)}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{\sigma (i)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

(24)

Proof

Similar to Theorem 5, we omit here.

Example 2

Consider three CPFNs ${\beta }_{1}=\left(\langle \left[0.5, 0.6\right],\left[0.4, 0.5\right]\rangle ,\langle 0.3, 0.35\rangle \right)$,

${\beta }_{2}=\left(\langle \left[0.7, 0.8\right],\left[0.3, 0.4\right]\rangle ,\langle 0.75, 0.25\rangle \right)$ and ${\beta }_{3}=\left(\langle \left[0.3, 0.4\right],\left[0.7, 0.8\right]\rangle ,\langle 0.35, 0.4\rangle \right)$ with weight vector $\mathcalligra{w}={(0.4, 0.25, 0.35)}^{T}$. The score values of these CPFNs are calculated as $sc\left({\beta }_{1}\right)=0.0625$, $sc\left({\beta }_{2}\right)=0.9400$ and $sc\left({\beta }_{3}\right)=-0.4775$. Since $sc({\beta }_{2})\succcurlyeq sc({\beta }_{1})\succcurlyeq sc({\beta }_{3})$. Therefore, the permuted CPFNs are obtained as ${\beta }_{\sigma (1)}=\left(\langle \left[0.7, 0.8\right],\left[0.3, 0.4\right]\rangle ,\langle 0.75, 0.25\rangle \right)$, ${\beta }_{\sigma (2)}=\left(\langle \left[0.5, 0.6\right],\left[0.4, 0.5\right]\rangle ,\langle 0.3, 0.35\rangle \right)$ and ${\beta }_{\sigma (3)}=\left(\langle \left[0.3, 0.4\right],\left[0.7, 0.8\right]\rangle ,\langle 0.35, 0.4\rangle \right)$. therefore

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{\left(1-{\left(0.7\right)}^{2}\right)}^{0.4}{\left(1-{\left(0.5\right)}^{2}\right)}^{0.25}{\left(1-{\left(0.3\right)}^{2}\right)}^{0.35}}=0.5588,$$

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{\left(1-{\left(0.8\right)}^{2}\right)}^{0.4}{\left(1-{\left(0.6\right)}^{2}\right)}^{0.25}{\left(1-{\left(0.4\right)}^{2}\right)}^{0.35}}=0.6639,$$

${\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}}={(0.3)}^{0.4}{(0.4)}^{0.25}{(0.7)}^{0.35}=0.4337$,

${\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}={(0.4)}^{0.4}{(0.5)}^{0.25}{(0.8)}^{0.35}=0.5391$.

${\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}={\left(0.75\right)}^{0.4}{\left(0.3\right)}^{0.25}{\left(0.35\right)}^{0.35}=0.4568$,

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{\left(1-{\left(0.25\right)}^{2}\right)}^{0.4}{\left(1-{\left(0.35\right)}^{2}\right)}^{0.25}{\left(1-{\left(0.4\right)}^{2}\right)}^{0.35}}=0.1126$$

$\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2}, {\beta }_{3}, {\beta }_{4}\right)=\left(\langle \left[\begin{array}{c}0.5588,\\ 0.6639\end{array}\right],\left[\begin{array}{c}0.4337,\\ 0.5391\end{array}\right]\rangle ,\langle \begin{array}{c}0.4568,\\ 0.2396\end{array}\rangle \right)$.

Property 6

For a collection of CPFNs ${\beta }_{i}$ $(i=\mathrm{1,2},\dots ,n)$, we have the following:

• (a) If $\mathcalligra{w}={(\mathrm{1,0},\dots ,0)}^{T}$ then $\mathrm{CPFOWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\mathrm{max}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})$,

• (b) If $\mathcalligra{w}={(\mathrm{0,0},\dots ,1)}^{T}$ then $\mathrm{CPFOWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\mathrm{min}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})$,

5.2 CPFHA Operator

Definition 24

For CPFNs ${\beta }_{i}$ $(i=1, 2,\dots ,n)$; the operator $\mathrm{CPFHA}: {\Omega }^{n}\to\Omega$, is given as

$$\mathrm{CPFHA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)={\mathcalligra{w}}_{1}{\dot{\beta }}_{\sigma (1)}\oplus {\mathcalligra{w}}_{2}{\dot{\beta }}_{\sigma (2)}\oplus\dots \oplus{\mathcalligra{w}}_{n}{\dot{\beta }}_{\sigma (n)}$$

(25)

where $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ be the weight vector, such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$ and ${\dot{\beta }}_{i}{^{\prime}}\mathrm{s}$ $({\dot{\beta }}_{i}=n{\zeta }_{i}{\beta }_{i})$ is ${\dot{\beta }}_{\sigma (i)}$, where $n$ is the number of CPFNs and $\zeta ={({\zeta }_{1}, {\zeta }_{2},\dots ,{\zeta }_{n})}^{T}$ is the vector corresponding to ${\beta }_{i}$ with ${\zeta }_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\zeta }_{i}=1$.

Theorem 8

The value obtained using the CPFOWA operator for CPFNs ${\beta }_{i}$ $(i=\mathrm{1,2},\dots ,n)$ is again a CPFN and given by

$$\mathrm{CPFHA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\dot{\mu }}_{\sigma (i)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\dot{\mu }}_{\sigma (i)}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\dot{\nu }}_{\sigma (i)}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\dot{\nu }}_{\sigma (i)}^{-}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{i=1}^{n}{\left({\dot{\mu }}_{\sigma (i)}\right)}^{{\mathcalligra{w}}_{i}},\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\dot{\nu }}_{\sigma (i)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\right\rangle \end{array}\right)$$

(26)

Proof

The proof is omitted because it is straightforward.

Example 3

Consider three CPFNs ${\beta }_{i}$ $(i=1, 2, 3)$, such that ${\beta }_{1}=\left(\langle \left[0.3, 0.5\right], \left[0.6, 0.7\right]\rangle , \left\langle 0.5, 0.4\right\rangle \right)$, ${\beta }_{2}=\left(\langle \left[0.6, 0.7\right], \left[0.4, 0.5\right]\rangle , \left\langle 0.5, 0.6\right\rangle \right)$ and ${\beta }_{3}=\left(\langle \left[0.7, 0.8\right], \left[0.2, 0.4\right]\rangle , \left\langle 0.5, 0.4\right\rangle \right)$. Also, $\zeta ={(0.2, 0.3, 0.5)}^{T}$ be the weight vector of ${\beta }_{i}$ then ${\dot{\beta }}_{i}=3{\zeta }_{i}{\beta }_{i}=\left(\langle \left[{\dot{\mu }}_{i}^{-}, {\dot{\mu }}_{i}^{+}\right], \left[{\dot{\nu }}_{i}^{-}, {\dot{\nu }}_{i}^{+}\right]\rangle ,\langle {\dot{\mu }}_{i}, {\dot{\nu }}_{i}\rangle \right)$ $(i=1, 2, 3, 4)$ is computed for each CPFN as.

$${\dot{\beta }}_{1}=\left(\langle \left[\begin{array}{c}\sqrt{1-{\left(1-({0.3)}^{2}\right)}^{3\times 0.2}}, \\ \sqrt{1-{(1-({0.5)}^{2})}^{3\times 0.2}}\end{array}\right],\left[\begin{array}{c}{(0.6)}^{3\times 0.2},\\ {(0.7)}^{3\times 0.2}\end{array}\right] \rangle ,\langle \begin{array}{c}{(0.5)}^{3\times 0.2},\\ \sqrt{1-{(1-({0.4)}^{2})}^{3\times 0.2}}\end{array}\rangle \right)$$

$=\left(\langle \left[\begin{array}{c}0.2346,\\ 0.3982\end{array}\right],\left[\begin{array}{c}0.7360,\\ 0.8073\end{array}\right]\rangle ,\langle \begin{array}{c}0.6598,\\ 0.3982\end{array}\rangle \right)$,

$${\dot{\beta }}_{2}=\left(\langle \left[\begin{array}{c}\sqrt{1-{\left(1-({0.6)}^{2}\right)}^{3\times 0.3}}, \\ \sqrt{1-{(1-({0.7)}^{2})}^{3\times 0.3}}\end{array}\right],\left[\begin{array}{c}{(0.4)}^{3\times 0.3},\\ {(0.5)}^{3\times 0.3}\end{array}\right] \rangle ,\langle \begin{array}{c}{(0.5)}^{3\times 0.3},\\ \sqrt{1-{(1-({0.6)}^{2})}^{3\times 0.3}}\end{array}\rangle \right)$$

$=\left(\langle \left[\begin{array}{c}0.5751,\\ 0.6741\end{array}\right],\left[\begin{array}{c}0.4384,\\ 0.5359\end{array}\right]\rangle ,\langle \begin{array}{c}0.5359,\\ 0.6741\end{array}\rangle \right)$,

$${\dot{\beta }}_{3}=\left(\left\langle \left[\begin{array}{c}\sqrt{1-{\left(1-({0.7)}^{2}\right)}^{3\times 0.5}}, \\ \sqrt{1-{(1-({0.8)}^{2})}^{3\times 0.5}}\end{array}\right],\left[\begin{array}{c}{(0.2)}^{3\times 0.5},\\ {(0.4)}^{3\times 0.5}\end{array}\right] \rangle ,\langle \begin{array}{c}{(0.7)}^{3\times 0.5},\\ \sqrt{1-{(1-({0.4)}^{2})}^{3\times 0.5}}\end{array}\right\rangle \right)$$

$=\left(\left\langle \left[\begin{array}{c}0.7974,\\ 0.8854\end{array}\right],\left[\begin{array}{c}0.0894,\\ 0.2530\end{array}\right]\rangle ,\langle \begin{array}{c}0.3536,\\ 0.8854\end{array}\right\rangle \right)$.

Also, the score values of these numbers are calculated as

$sc\left({\dot{\beta }}_{1}\right)=\frac{{(0.2346)}^{2}+{(0.3982)}^{2}+{(0.7360)}^{2}{(0.8073)}^{2}}{2}-\left({\left(0.6598\right)}^{2}-{\left(0.3982\right)}^{2}\right)=-0.7667$,

$sc\left({\dot{\beta }}_{2}\right)=\frac{{(0.5751)}^{2}+{(0.6741)}^{2}+{(0.4384)}^{2}{(0.5359)}^{2}}{2}-\left({\left(0.5359\right)}^{2}-{\left(0.6741\right)}^{2}\right)=0.3201$,

$sc\left({\dot{\beta }}_{3}\right)=\frac{{(0.7974)}^{2}+{(0.8854)}^{2}+{(0.0894)}^{2}{(0.2530)}^{2}}{2}-\left({\left(0.3536\right)}^{2}-{\left(0.8854\right)}^{2}\right)=1.3328$.

Thus, $sc({\dot{\beta }}_{3})\succcurlyeq sc({\dot{\beta }}_{2})\succcurlyeq sc({\dot{\beta }}_{1})$, which gives.

${\dot{\beta }}_{\sigma (1)}=\left(\langle \left[\begin{array}{c}0.7974,\\ 0.8854\end{array}\right],\left[\begin{array}{c}0.0894,\\ 0.2530\end{array}\right]\rangle ,\langle \begin{array}{c}0.3536,\\ 0.8854\end{array}\rangle \right)$, ${\dot{\beta }}_{\sigma (2)}=\left(\langle \left[\begin{array}{c}0.5751,\\ 0.6741\end{array}\right],\left[\begin{array}{c}0.4384,\\ 0.5359\end{array}\right]\rangle ,\langle \begin{array}{c}0.5359,\\ 0.6741\end{array}\rangle \right)$ and ${\dot{\beta }}_{\sigma (3)}=\left(\langle \left[\begin{array}{c}0.2346,\\ 0.3982\end{array}\right],\left[\begin{array}{c}0.7360,\\ 0.8073\end{array}\right]\rangle ,\langle \begin{array}{c}0.6598,\\ 0.3982\end{array}\rangle \right).$

Let $\mathcalligra{w}=(0.35, 0.4, 0.25)$ be the position vector, then using Eq. (24), we have

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\dot{\mu }}_{\sigma (i)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{(1-{(0.7974)}^{2})}^{0.35}{(1-{(0.5751)}^{2})}^{0.4}{(1-{(0.2346)}^{2})}^{0.25}}$$

$=0.6406$,

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\dot{\mu }}_{\sigma (i)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{(1-{(0.8854)}^{2})}^{0.35}{(1-{(0.6741)}^{2})}^{0.4}{(1-{(0.3982)}^{2})}^{0.25}}$$

$=0.7486,$

$${\prod }_{i=1}^{n}{\left({\dot{\nu }}_{\sigma (i)}^{-}\right)}^{{\mathcalligra{w}}_{i}}={\left(0.0894\right)}^{0.35}{\left(0.4384\right)}^{0.4}{\left(0.7360\right)}^{0.25}=0.2860,$$

$${\prod }_{i=1}^{n}{\left({\dot{\nu }}_{\sigma (i)}^{+}\right)}^{{\mathcalligra{w}}_{i}}={\left(0.2530\right)}^{0.35}{\left(0.5359\right)}^{0.4}{\left(0.8073\right)}^{0.25}=0.4565,$$

${\prod }_{i=1}^{n}{\left({\dot{\mu }}_{\sigma (i)}\right)}^{{\mathcalligra{w}}_{i}}={\left(0.3536\right)}^{0.35}{\left(0.5359\right)}^{0.4}{\left(0.6598\right)}^{0.25}=0.4881$,

$$\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\dot{\nu }}_{\sigma (i)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}=\sqrt{1-{(1-{(0.8854)}^{2})}^{0.35}{(1-{(0.6741)}^{2})}^{0.4}{(1-{(0.3982)}^{2})}^{0.25}}$$

$=0.7486$.

Hence, we have

$\mathrm{CPFHA}\left({\beta }_{1},{\beta }_{2},{\beta }_{3}\right)=\left(\langle \left[\begin{array}{c}0.6406,\\ 0.7486\end{array}\right]\left[\begin{array}{c}0.2860,\\ 0.4565\end{array}\right]\rangle ,\langle \begin{array}{c}0.4881,\\ 0.7486\end{array}\rangle \right)$.

Theorem 9

For $\mathcalligra{w}={(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})}^{T}$, the operator CPFHA gets reduced to CPFWA.

Proof. As ${\dot{\beta }}_{\sigma (i)}=n{\zeta }_{i}{\beta }_{i}$ and $\mathcalligra{w}={(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})}^{T}$, thus ${{\mathcalligra{w}}_{i}\dot{\beta }}_{\sigma (i)}={\zeta }_{i}{\beta }_{i}$ and hence

$$\mathrm{CPFHA}\left({\beta }_{1}, {\beta }_{2},\dots , {\beta }_{n}\right)={\mathcalligra{w}}_{1}{\dot{\beta }}_{\sigma (1)}\oplus {\mathcalligra{w}}_{2}{\dot{\beta }}_{\sigma (2)}\oplus\dots \oplus {\mathcalligra{w}}_{n}{\dot{\beta }}_{\sigma (n)}$$

$={\zeta }_{1}{\beta }_{\sigma (1)}\oplus {\zeta }_{2}{\beta }_{\sigma (2)}\oplus\dots \oplus {\zeta }_{n}{\beta }_{\sigma (n)}=\mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots , {\beta }_{n}\right)$.

Proof

The proof is omitted because it is straightforward.

Theorem 10

For $\zeta ={(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n})}^{T}$, the operator CPFHA gets reduced to CPFOWA.

Proof

Similar to theorem 5, we omit here.

Definition 25

Let $\beta =\left(\langle \left[{\mu }^{-}, {\mu }^{+}\right], \left[{\nu }^{-}, {\nu }^{+}\right]\rangle , \left\langle \mu +\nu \right\rangle \right)$ be a CPFN, then the complement of $\beta$ is represented by ${\beta }^{c}$ and defined as follows:

$${\beta }^{c}=\left(\langle \left[{\nu }^{-}, {\nu }^{+}\right], \left[{\mu }^{-}, {\mu }^{+}\right]\rangle , \left\langle \nu ,\mu \right\rangle \right)$$

(27)

5.3 CPFOWG Operator

Definition 26

A CPFOWG is a mapping defined as ${\mathrm{CPFOWG}:\Omega }^{n}\to\Omega$ on a collection of CPFNs ${\beta }_{i}$, $(i=\mathrm{1,2},\dots n)$ as follows:

$$\mathrm{CPFOWG}\left({\beta }_{1}, {\beta }_{2},\dots , {\beta }_{n}\right)={\mathcalligra{w}}_{1}{\beta }_{\sigma (1)}\otimes {\mathcalligra{w}}_{2}{\beta }_{\sigma (2)}\oplus\dots \oplus{\mathcalligra{w}}_{n}{\beta }_{\sigma (n)}$$

(28)

where $\sigma$ is a permutation of $(1, 2,\dots ,n)$, such that ${\beta }_{\sigma (i-1)}\succcurlyeq {\beta }_{i}$ for $i=\mathrm{1,2},\dots ,n$ and $\mathcalligra{w}={({\mathcalligra{w}}_{1},{\mathcalligra{w}}_{2}\dots ,{\mathcalligra{w}}_{n})}^{T}$ is its weight vector, such that $\mathcalligra{w}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$. Moreover, the ${i}^{th}$ largest CPFN among ${\beta }_{i}\mathrm{^{\prime}}\mathrm{s}$ is ${\beta }_{\sigma (i)}$.

Theorem 11

The value obtained using the CPFOWG operator for CPFNs ${\beta }_{i}$ $(i=\mathrm{1,2},\dots ,n)$ is again a CPFN and given by

$$\mathrm{CPFOWG}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\mu }_{\sigma (i)}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\mu }_{\sigma (i)}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right], \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{\sigma (i)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{\sigma (i)}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right]\right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{\sigma (i)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},{\prod }_{i=1}^{n}{\left({\nu }_{\sigma (i)}\right)}^{{\mathcalligra{w}}_{i}}\right\rangle \end{array}\right)$$

(29)

Theorem 12

Let ${\beta }_{i}(i=\mathrm{1,2},\dots ,n)$, $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ is the weight vector of ${\beta }_{i}$ such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$, then we have

• 1. $\mathrm{CPFWA}\left({\beta }_{1}^{c}, {\beta }_{2}^{c},\dots ,{\beta }_{n}^{c}\right)={\left(\mathrm{CPFWG}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\right)}^{c}$,

• 2. $\mathrm{CPFWG}\left({\beta }_{1}^{c}, {\beta }_{2}^{c},\dots ,{\beta }_{n}^{c}\right)={\left(\mathrm{CPFWA}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\right)}^{c}$.

Proof

Since ${\beta }_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)$ and ${\beta }_{i}=\left(\langle \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right], \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right]\rangle , \left\langle {\nu }_{i}, {\mu }_{i}\right\rangle \right)$, then by Eq. (17), we have

$$\mathrm{CPFWA}\left({\beta }_{1}^{c}, {\beta }_{2}^{c},\dots ,{\beta }_{n}^{c}\right)=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}{\prod }_{i=1}^{n}{\left({\nu }_{i}^{-}\right)}^{{\mathcalligra{w}}_{i}},\\ {\prod }_{i=1}^{n}{\left({\nu }_{i}^{+}\right)}^{{\mathcalligra{w}}_{i}}\end{array}\right], \left[\begin{array}{c}\sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},\\ \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\mu }_{i}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}}\end{array}\right]\right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{i=1}^{n}{\left(1-{\left({\nu }_{i}\right)}^{2}\right)}^{{\mathcalligra{w}}_{i}}},{\prod }_{i=1}^{n}{\left({\mu }_{i}\right)}^{{\mathcalligra{w}}_{i}}\right\rangle \end{array}\right)$$

$={\left(\mathrm{CPFWG}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\right)}^{c}$.

Similarly, we can prove $\mathrm{CPFWG}\left({\beta }_{1}^{c}, {\beta }_{2}^{c},\dots ,{\beta }_{n}^{c}\right)={\left(\mathrm{CPFWA}({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n})\right)}^{c}$.

Theorem 13

Let ${\beta }_{i}(i=\mathrm{1,2},\dots ,n)$, $\mathcalligra{w}={\left({\mathcalligra{w}}_{1}, {\mathcalligra{w}}_{2},\dots ,{\mathcalligra{w}}_{n}\right)}^{T}$ is the weight vector of ${\beta }_{i}$ such that ${\mathcalligra{w}}_{i}\succ 0$ and ${\sum }_{i=1}^{n}{\mathcalligra{w}}_{i}=1$, then we have

$$\mathrm{CPFWG}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)\preccurlyeq \mathrm{CPFWA}\left({\beta }_{1}, {\beta }_{2},\dots ,{\beta }_{n}\right)$$

(30)

Proof

Easy to prove.

According to Theorem 13, the results calculated by the CPFWG operator are not greater than those obtained by the GGCPFWA operator. The proposed operator CPFOWA, CPFHA, and CPFWG also follow idempotent, bounded, monotonic, homogeneity, and shift-invariance properties.

6 DM Approach Based on the Proposed AOs

In this section, we proposed a new MCDM process to solve MCDM problems. impreciseness and ambiguity are a natural part of life that needs attentive attention in the management and DM process. CPFSs have been demonstrated to be an effective tool for solving high-precision DM problems involving ambiguous, vague, or uncertain information. We apply our proposed AOs in MCDM problems to exhibit real-world reasonability and rationality.

Let $\mathcal{A}=\left\{{\mathcal{A}}_{1}, {\mathcal{A}}_{2}, {\dots ,\mathcal{A}}_{m}\right\}$ be the set alternatives, and let the set of criteria for the alternatives ${\mathcal{A}}_{i} (i=\mathrm{1,2},\dots ,m)$ be represented by $\mathcal{C}=\left\{{\mathcal{C}}_{1},{\mathcal{C}}_{2},\dots ,{\mathcal{C}}_{n}\right\}$. The goal is to pick the best alternative out of the $m$ alternatives. The following are the steps for constructing a new MCDM method based on the proposed AOs.

Step 1 Arrange the rating values of each alternative ${\mathcal{A}}_{i} (i=\mathrm{1,2},\dots ,m)$ in the form of ${\beta }_{ij}=\left(\langle \left[{\mu }_{ij}^{-},{\mu }_{ij}^{+}\right], \left[{\nu }_{ij}^{-},{\nu }_{ij}^{+}\right]\rangle ,\langle {\mu }_{ij},{\nu }_{ij}\rangle \right)$; $(j=\mathrm{1,2},\dots ,n)$ as a decision matrix $\mathcal{D}$ given by

$$\mathcal{D}=\begin{array}{c}{\mathcal{A}}_{1}\\ \vdots \\ {\mathcal{A}}_{m}\end{array}\underset{\begin{array}{ccc}{\mathcal{C}}_{1}& \dots & {\mathcal{C}}_{n}\end{array}}{\underset{\oplus}{\left[\begin{array}{ccc}{\beta }_{11}& \dots & {\beta }_{1n}\\ \vdots & \ddots & \vdots \\ {\beta }_{m1}& \cdots & {\beta }_{mn}\end{array}\right]}}$$

(31)

Step 2 Use the following normalization procedure to transform the cost-type criteria into benefit-type criteria:

$${\fancyscript{r}}_{ij}=\left\{\begin{array}{c}\left(\langle \left[{\mu }_{ij}^{-},{\mu }_{ij}^{+}\right], \left[{\nu }_{ij}^{-},{\nu }_{ij}^{+}\right]\rangle ,\langle {\mu }_{ij},{\nu }_{ij}\rangle \right); If the benefit-type conditions are met\\ \left(\langle {{\nu }_{ij},\mu }_{ij}\rangle \right); If the cost-type conditions are met\end{array}\right.$$

(32)

Step 3. To determine the aggregated value ${\fancyscript{r}}_{i}$ $(i=\mathrm{1,2},\dots ,m)$ of the alternative ${\mathcal{A}}_{i}$, using CPFWA, CPFOWA, CPFHA, CPFWG, or CPFOWG operator:

• (a) By CPFWA operator

  $${\fancyscript{r}}_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)=\mathrm{CPFWA}\left({\beta }_{i1}, {\beta }_{i2},\dots ,{\beta }_{in}\right)$$
  $$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\mu }_{ij}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}},\\ \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\mu }_{ij}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{j=1}^{n}{\left({\nu }_{ij}^{-}\right)}^{{\mathcalligra{w}}_{j}},\\ {\prod }_{j=1}^{n}{\left({\nu }_{ij}^{+}\right)}^{{\mathcalligra{w}}_{j}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{j=1}^{n}{\left({\mu }_{ij}\right)}^{{\mathcalligra{w}}_{j}},\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\nu }_{ij}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\right\rangle \end{array}\right)$$

  (33)

• (b) By CPFWA operator

  $${\fancyscript{r}}_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)=\mathrm{CPFOWA}\left({\fancyscript{r}}_{\sigma (i1)}, {\fancyscript{r}}_{\sigma (i2)},\dots ,{\fancyscript{r}}_{\sigma (in)}\right)$$
  $$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\mu }_{\sigma (ij)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}},\\ \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\mu }_{\sigma (ij)}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{j=1}^{n}{\left({\nu }_{\sigma (ij)}^{-}\right)}^{{\mathcalligra{w}}_{j}},\\ {\prod }_{j=1}^{n}{\left({\nu }_{\sigma (ij)}^{+}\right)}^{{\mathcalligra{w}}_{j}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{j=1}^{n}{\left({\mu }_{\sigma (ij)}\right)}^{{\mathcalligra{w}}_{j}},\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\nu }_{\sigma (ij)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\right\rangle \end{array}\right)$$

  (34)

• (c) By CPFHA operator

  $${\fancyscript{r}}_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)=\mathrm{CPFOWA}\left({\dot{\fancyscript{r}}}_{\sigma (i1)}, {\dot{\fancyscript{r}}}_{\sigma (i2)},\dots ,{\dot{\fancyscript{r}}}_{\sigma (in)}\right)$$
  $$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\dot{\mu }}_{\sigma (ij)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}},\\ \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\dot{\mu }}_{\sigma (ij)}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\end{array}\right],\left[\begin{array}{c}{\prod }_{j=1}^{n}{\left({\dot{\nu }}_{\sigma (ij)}^{-}\right)}^{{\mathcalligra{w}}_{j}},\\ {\prod }_{j=1}^{n}{\left({\dot{\nu }}_{\sigma (ij)}^{+}\right)}^{{\mathcalligra{w}}_{j}}\end{array}\right]\right\rangle ,\\ \left\langle {\prod }_{j=1}^{n}{\left({\dot{\mu }}_{\sigma (ij)}\right)}^{{\mathcalligra{w}}_{j}},\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\dot{\nu }}_{\sigma (ij)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\right\rangle \end{array}\right)$$

  (35)

• (d) By CPFWG operator

  $${\fancyscript{r}}_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)=\mathrm{CPFWG}\left({\beta }_{i1}, {\beta }_{i2},\dots ,{\beta }_{in}\right)$$
  $$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}{\prod }_{j=1}^{n}{\left({\mu }_{ij}^{-}\right)}^{{\mathcalligra{w}}_{j}},\\ {\prod }_{j=1}^{n}{\left({\mu }_{ij}^{+}\right)}^{{\mathcalligra{w}}_{j}}\end{array}\right],\left[\begin{array}{c}\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\nu }_{ij}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}},\\ \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\nu }_{ij}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\end{array}\right]\right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\mu }_{ij}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}, {\prod }_{j=1}^{n}{\left({\nu }_{ij}\right)}^{{\mathcalligra{w}}_{j}}\right\rangle \end{array}\right)$$

  (36)

• (e) By CPFOWG operator

  $${\fancyscript{r}}_{i}=\left(\langle \left[{\mu }_{i}^{-}, {\mu }_{i}^{+}\right], \left[{\nu }_{i}^{-},{\nu }_{i}^{+}\right]\rangle , \left\langle {\mu }_{i}, {\nu }_{i}\right\rangle \right)=\mathrm{CPFOWG}\left({\beta }_{\sigma (i1)}, {\beta }_{\sigma (i2)},\dots ,{\beta }_{\sigma (in)}\right)$$
  $$=\left(\begin{array}{c}\left\langle \left[\begin{array}{c}{\prod }_{j=1}^{n}{\left({\mu }_{\sigma (ij)}^{-}\right)}^{{\mathcalligra{w}}_{j}},\\ {\prod }_{j=1}^{n}{\left({\mu }_{\sigma (ij)}^{+}\right)}^{{\mathcalligra{w}}_{j}}\end{array}\right],\left[\begin{array}{c}\sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\nu }_{\sigma (ij)}^{-}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}},\\ \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\nu }_{\sigma (ij)}^{+}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}\end{array}\right]\right\rangle ,\\ \left\langle \sqrt{1-{\prod }_{j=1}^{n}{\left(1-{\left({\mu }_{\sigma (ij)}\right)}^{2}\right)}^{{\mathcalligra{w}}_{j}}}, {\prod }_{j=1}^{n}{\left({\nu }_{\sigma (ij)}\right)}^{{\mathcalligra{w}}_{j}}\right\rangle \end{array}\right)$$

  (37)

Step 4 Calculate the aggregated score values of each alternative as follows:

$$sc\left({\fancyscript{r}}_{i}\right)=\frac{{\left({\mu }_{i}^{-}\right)}^{2}+{\left({\mu }_{i}^{+}\right)}^{2}-{\left({\nu }_{i}^{-}\right)}^{2}-{\left({\nu }_{i}^{+}\right)}^{2}}{2}+\left({\nu }_{i}^{2}-{\mu }_{i}^{2}\right)$$

(38)

if $sc\left({\fancyscript{r}}_{{i}_{1}}\right)=sc\left({\fancyscript{r}}_{{i}_{2}}\right)$ for any two indices ${i}_{1}$ and ${i}_{2}$, then calculate accuracy values as

$$ac\left({\fancyscript{r}}_{i}\right)=\frac{{\left({\mu }_{i}^{-}\right)}^{2}+{\left({\mu }_{i}^{+}\right)}^{2}-{\left({\nu }_{i}^{-}\right)}^{2}-{\left({\nu }_{i}^{+}\right)}^{2}}{2}+\left({\nu }_{i}^{2}+{\mu }_{i}^{2}\right)$$

(39)

Step 5 Select the most desired alternative by ranking all of the alternatives in descending order of the score values.

6.1 Illustrative Example

In this section, a numerical example related to disaster management is used to evaluate the efficiency of the proposed method.

6.1.1 Numerical Example

To demonstrate the validity of the new technique, we use a numerical example from [43] and a few comparison studies.

Consider the Indian subcontinent, where floods have devastated several states and resulted in massive loss of lives and properties. Concentrating on disaster risk management, particularly concerning four Indian states chosen as alternatives) ${\mathcal{A}}_{i}i=\mathrm{1,2},\mathrm{3,4}$, viz., (“Bihar”, “Assam”, “Gujrat” and “Arunachal Pradesh”) which were largely devastated during the first half of 2017, Assume the Indian government is trying to make the best decision on allocating funds to these four states. When the entire situation was assessed for important areas of fund allocation, it was discovered that funds should be distributed in such a way that three main elements represented by${\mathcal{C}}_{i}$, $j=1, 2, 3$ namely: “Food scarcity”, “Number of people rescued” and “Lack of infrastructure reconstruction facilities” needed to be coped up. Assume that different factors are prioritized state-by-state using the weight vector $\mathcalligra{w}={(0.3, 0.38, 0.32)}^{T}$ and$\zeta ={(0.48, 0.29, 0.23)}^{T}$. Hence, the problem's goal is to decide the order in which states should be granted the relief fund.

For this purpose, concerned specialist persons of the Indian Administration has constituted a commission that has taken the entire responsibility for finding the probable state(s). For it, they have recruited an expert to analyze these states and grade their information in terms of the CPFN using the three attributes specified above. Based on the information, the steps of the proposed scheme are carried out as follows:

Step 1 Table 1 shows the rating values for each alternative in the CPF-environment.

Table 1 Information related to the alternative in terms of CPF-environment

Step 2 Utilizing Eq. (32) to transform the values of the cost criteria ${\mathcal{C}}_{1}$ and ${\mathcal{C}}_{3}$ to the benefit type, the result is listed in Table 2.

Table 2 Normalized decision matrix for the alternatives

Step 3 Aggregate the different preferences into a single set of values.

• (a) Using CPFWA, as given in Eq. (33), we obtain

  $${\fancyscript{r}}_{1}=\left(\langle \left[\begin{array}{c}0.2249,\\ 0.2815\end{array}\right],\left[\begin{array}{c}0.2718,\\ 0.3537\end{array}\right]\rangle ,\langle \begin{array}{c}0.1892,\\ 0.3000\end{array}\rangle \right), {\fancyscript{r}}_{2}=\left(\langle \left[\begin{array}{c}0.2535,\\ 0.3025\end{array}\right],\left[\begin{array}{c}0.2471,\\ 0.3188\end{array}\right]\rangle ,\langle \begin{array}{c}0.3586,\\ 0.1773\end{array}\rangle \right),$$

  ${\fancyscript{r}}_{3}=\left(\langle \left[\begin{array}{c}0.782522,\\ 0.8380\end{array}\right],\left[\begin{array}{c}0.1000,\\ 0.1397\end{array}\right]\rangle ,\langle \begin{array}{c}0.1072,\\ 0.7972\end{array}\rangle \right) \mathrm{and}\, {\fancyscript{r}}_{4}=\left(\langle \left[\begin{array}{c}0.2428,\\ 0.3187\end{array}\right], \left[\begin{array}{c}0.2128,\\ 0.2821\end{array}\right]\rangle ,\langle \begin{array}{c}0.4178,\\ 0.1746\end{array}\rangle \right).$

• (b) Using CPFOWA operator, as given in Eq. (34), we get

  $${\fancyscript{r}}_{1}=\left(\langle \left[\begin{array}{c}0.2143,\\ 0.2719\end{array}\right],\left[\begin{array}{c}0.2620,\\ 0.3426\end{array}\right]\rangle ,\langle \begin{array}{c}0.2028,\\ 0.3000\end{array}\rangle \right), {\fancyscript{r}}_{2}=\left(\langle \left[\begin{array}{c}0.2479,\\ 0.2971\end{array}\right],\left[\begin{array}{c}0.2471,\\ 0.3182\end{array}\right]\rangle ,\langle \begin{array}{c}0.3586,\\ 0.1768\end{array}\rangle \right),$$

  ${\fancyscript{r}}_{3}=\left(\langle \left[\begin{array}{c}0.7821,\\ 0.8386\end{array}\right],\left[\begin{array}{c}0.1000,\\ 0.1378\end{array}\right]\rangle ,\langle \begin{array}{c}0.1056,\\ 0.7874\end{array}\rangle \right) \mathrm{and} {\fancyscript{r}}_{1}=\left(\langle \left[\begin{array}{c}0.2428,\\ 0.3187\end{array}\right],\left[\begin{array}{c}0.2128,\\ 0.2821\end{array}\right]\rangle ,\langle \begin{array}{c}0.4178,\\ 0.1746\end{array}\rangle \right)$.

• (c) Using CPFHA operator, as given in Eq. (35), we get

  $${\fancyscript{r}}_{1}=\left(\langle \left[\begin{array}{c}0.2087,\\ 0.2689\end{array}\right],\left[\begin{array}{c}0.2495,\\ 0.3241\end{array}\right]\rangle ,\langle \begin{array}{c}0.2204,\\ 0.2976\end{array}\rangle \right), {\fancyscript{r}}_{2}=\left(\langle \left[\begin{array}{c}0.2244,\\ 0.2755\end{array}\right],\left[\begin{array}{c}0.2585,\\ 0.3264\end{array}\right]\rangle ,\langle \begin{array}{c}0.3693,\\ 0.1772\end{array}\rangle \right)$$

  ${\fancyscript{r}}_{3}=\left(\langle \left[\begin{array}{c}0.7637,\\ 0.8188\end{array}\right],\left[\begin{array}{c}0.1039,\\ 0.1474\end{array}\right]\rangle ,\langle \begin{array}{c}0.1104,\\ 0.7983\end{array}\rangle \right) \mathrm{and} {\fancyscript{r}}_{4}=\left(\langle \left[\begin{array}{c}0.2803,\\ 0.3562\end{array}\right],\left[\begin{array}{c}0.2204,\\ 0.2919\end{array}\right]\rangle ,\langle \begin{array}{c}0.3922,\\ 0.1811\end{array}\rangle \right)$.

• (d) Using CPFWG operator, as given in Eq. (36), we get

  $${\fancyscript{r}}_{1}=\left(\langle \left[\begin{array}{c}0.1895,\\ 0.2657\end{array}\right],\left[\begin{array}{c}0.3132,\\ 0.4031\end{array}\right]\rangle ,\langle \begin{array}{c}0.2586,\\ 0.3000\end{array}\rangle \right), {\fancyscript{r}}_{2}=\left(\langle \left[\begin{array}{c}0.1760,\\ 0.2391\end{array}\right], \left[\begin{array}{c}0.2618,\\ 0.3317\end{array}\right]\rangle ,\langle \begin{array}{c}0.3661,\\ 0.1584\end{array}\rangle \right),$$

  ${\fancyscript{r}}_{3}=\left(\langle \left[\begin{array}{c}0.7747,\\ 0.8278\end{array}\right],\left[\begin{array}{c}0.1000,\\ 0.1411\end{array}\right]\rangle ,\langle \begin{array}{c}0.1080,\\ 0.7844\end{array}\rangle \right) \mathrm{and} {\fancyscript{r}}_{4}=\left(\langle \left[\begin{array}{c}0.1607,\\ 0.2601\end{array}\right],\left[\begin{array}{c}0.2321,\\ 0.2934\end{array}\right]\rangle ,\langle \begin{array}{c}0.4597,\\ 0.1602\end{array}\rangle \right)$.

• (e) Using CPFOWG operator, as given in Eq. (37), we get

  $${\fancyscript{r}}_{1}=\left(\langle \left[\begin{array}{c}0.1869,\\ 0.2645\end{array}\right],\left[\begin{array}{c}0.3112,\\ 0.4004\end{array}\right]\rangle ,\langle \begin{array}{c}0.2633,\\ 0.3000\end{array}\rangle \right), {\fancyscript{r}}_{2}=\left(\langle \left[\begin{array}{c}0.1726,\\ 0.2358\end{array}\right],\left[\begin{array}{c}0.2618,\\ 0.3307\end{array}\right]\rangle ,\langle \begin{array}{c}0.3661,\\ 0.1581\end{array}\rangle \right),$$

${\fancyscript{r}}_{3}=\left(\langle \left[\begin{array}{c}0.7661,\\ 0.8190\end{array}\right],\left[\begin{array}{c}0.1000,\\ 0.1417\end{array}\right]\rangle ,\langle \begin{array}{c}0.1068,\\ 0.7836\end{array}\rangle \right) \mathrm{and} {\fancyscript{r}}_{4}=\left(\langle \left[\begin{array}{c}0.1607,\\ 0.2601\end{array}\right],\left[\begin{array}{c}0.2321,\\ 0.2934\end{array}\right]\rangle ,\langle \begin{array}{c}0.4597,\\ 0.1602\end{array}\rangle \right)$.

Step 4 The aggregate CPFNs collected in step 3 are scored using Eq. (38), as follows:

• (a) $sc\left({\fancyscript{r}}_{1}\right)=0.0196$, $sc\left({\fancyscript{r}}_{2}\right)=-0.1006$, $sc\left({\fancyscript{r}}_{3}\right)=1.2666$, $sc\left({\fancyscript{r}}_{4}\right)=-0.1262$.

• (b) $sc\left({\fancyscript{r}}_{1}\right)=0.0158$, $sc\left({\fancyscript{r}}_{2}\right)=-0.1036$, $sc\left({\fancyscript{r}}_{3}\right)=1.2518$, $sc\left({\fancyscript{r}}_{4}\right)=-0.1262$.

• (c) $sc\left({\fancyscript{r}}_{1}\right)=0.0142$, $sc\left({\fancyscript{r}}_{2}\right)=-0.1285$, $sc\left({\fancyscript{r}}_{3}\right)=1.2357$, $sc\left({\fancyscript{r}}_{4}\right)=-0.0852$.

• (d) $sc\left({\fancyscript{r}}_{1}\right)=-0.0539$, $sc\left({\fancyscript{r}}_{2}\right)=-0.1541$, $sc\left({\fancyscript{r}}_{3}\right)=1.2341$, $sc\left({\fancyscript{r}}_{4}\right)=-0.2089$.

• (e) $sc\left({\fancyscript{r}}_{1}\right)=-0.0555$, $sc\left({\fancyscript{r}}_{2}\right)=-0.1553$, $sc\left({\fancyscript{r}}_{3}\right)=1.2164$, $sc\left({\fancyscript{r}}_{4}\right)=-0.2089.$

Step 5 Since $sc({\fancyscript{r}}_{3})\succ sc({\fancyscript{r}}_{1})\succ sc({\fancyscript{r}}_{2})\succ sc({\fancyscript{r}}_{4})$ by CPFWA, CPFOWA, CPFWG, and CPFOWG operator while $sc({\fancyscript{r}}_{3})\succ sc({\fancyscript{r}}_{1})\succ sc({\fancyscript{r}}_{4})\succ sc({\fancyscript{r}}_{2})$. Hence, the state of “Gujrat” requires maximum funding. The score values and ranking order of the alternatives are summarized in Table 3.

Table 3 Score values and rank of the alternatives

6.2 Comparative Analysis with Other Existing Methods

We compare the proposed AOs with some existing methods, including CIFWA, CIFOWA, and CIFHA operators [43]. Score values and order of alternatives are listed in Table 4.

Table 4 Score values and order of alternatives

We set the fuzzy results of the CPFNs as zero and hence the obtained information reduces to IVPFS or IVIFS. Then, using this converted data, we apply the various methods [10, 13,14,15, 18, 21, 46, 47] to find the most suitable alternative(s). the results and ranking of the alternatives are represented in Table 5.

Table 5 Comparative studies with existing approaches

Based on these results, it has been seen that ${\mathcal{A}}_{3}$ is still the best alternative. However, the worst scenario has been changed. This is owing to the fact that during these previous studies, only the preferences of the alternative were taken into account. The other words, the existing theories are unable to address scenarios in which the evaluator or decision-maker consider the degree of untruth corresponding previously assigned truth degree across an interval. Thus, if an experiment is done without taking into account the second judgments of the preferences, ${\mathcal{A}}_{1}$ is the poorest alternative and ${\mathcal{A}}_{4}$ is superior to ${\mathcal{A}}_{2}$. In comparison, if all of the decision maker’s features are described in terms of CPFNs, ${\mathcal{A}}_{3}$ remains the best alternative, while ${\mathcal{A}}_{4}$ is the worst and the remaining alternatives are ranked in order of ${\mathcal{A}}_{1}$ and ${\mathcal{A}}_{2}$.

From the above discussion, we conclude that under the under IVIFSs or IVPFSs environment, the best alternative coincides with the proposed one, but the other alternatives are different and hence it will lead to different results. Thus, CPFS and their AOs improve accuracy by boarding the scope of membership and non-membership interval by taking into account PFS membership values.

The score values and ranking of the alternatives using the existing AOs presented by Abbas et al. [45], are summarized in Table 6. From Table 6 we can get different results from the proposed method. Thus, the computational procedure and results are entirely different.

Table 6 Score values and ranking of alternatives based on existing AOs proposed by Abbas et al. [45]

6.3 Discussion

The results illustrate that the modified AOs can solve the complicated MCDM problems for choosing the best alternative. Under uncertainty, the proposed method is regarded as one applicable approach to implement within MCDM problems. The proposed AOs avoid the flaws and errors arising from the existing AOs. A comparative analysis is performed between proposed AOs and existing AOs presented in [10, 13,14,15, 18, 21, 46, 47]. It has been observed that the ranking of alternatives with respect three criteria are the same. However, the score values and ranking of alternatives obtained by existing AOs presented by [45] are the different. This is because of the flaws and errors in the existing AOs. Based on the comparative studies between the proposed and the existing studies, the following observations have been obtained:

• 1. As discussed above, CPFS handles the indeterminate and inconsistent information in a more consistent way than the existing studies. Therefore, the studies under the CPFS environment are more suitable to solve decision-making problems.

• 2. apart from these, there might be other situations, where the preferences related to an alternative can be assessed in an environment, where the weights of the attributes are in the form of IVPFSs and the bases are the real or CPF parameters. Therefore, the existing aggregation operators do not handle this information during the analysis. However, the suggested aggregation operators have the capacity to do so, making them the better candidates to address issues.

• 3. It has been observed that the nature of the relative score values follows the same trend (increasing or decreasing). Therefore, the proposed approach based on the proposed AOs is equivalently solved the decision-making problems under CPF environments.

7 Conclusion

CPFS is one of the most important and new environments in which preference corresponding to an element is expressed by means of the IVPFS and PFS, which shows the degree of disagreement (in the form of PFS values) corresponding to the agreed interval region (in form of IVPFS). By taking advantage of it, this paper presents the modified version of existing operational laws and aggregation operators presented by [40]. Further, some new operational laws and AOs are proposed. The various properties of the operators are studied also. From the work, it is deduced that the existing studies under IVPFS and PFS can be deduced from the proposed ones. Then, we utilized the proposed AOs to develop an MCDM method to solve the decision-making problem. An illustrative example is provided to demonstrate the work of the proposed method. A strong foundation of the obtained results is justified by carrying on a comparison study on the existing environments. From these studies, it has been analyzed that proposed operators can handle the problems in a more profitable way than the existing studies.