1 Introduction

Fiber-reinforced concrete (FRC) composites have been utilized to improve the performance of plain concrete materials [1]. Functionally graded material (FGM) is a new development for construction materials, proposed as new composites that aim to provide desired performance by changing the properties [2]. This concept was also used for FRC to improve structural performance while reducing its material cost. In recent decades, various functionally graded concrete (FGC) applications were developed quickly, ranging from repair to precast structural elements requiring high flexibility and a wide range in pavement infrastructure [3]. Many researchers were concerned with studying FGC beams according to flexural strength and the capability of plastic energy dissipation with various layers. They concluded that FGC is more efficient than full depth (FD) FRC with lower equivalent fiber volume fraction (Vf%), especially layered FGC with steel fibers (SF), see, for example, Ref. [4]. According to Naghibdehi et al. [5], this enhancement can be explained by two mechanisms, the fiber orientation and the architecture of RC layers of the beam. More layers lead to a lower thickness of the RC layer. These results in aligning fibers as planar in the RC layer, and the flexural performance will be improved. Many researchers explained these phenomena under a definition called the wall effect. The mold sides and the free surface caused fibers to orient parallel to the wall or surface [6]. Thus, Naghibdehi et al. [5] suggested that the minimum reinforced layers considered symmetric were three layers. However, in layers with high gradients on their properties, it was assumed that more than these layers should be considered to reduce shear stress distribution among these layers.

Linear elastic and nonlinear fracture mechanics theories were applied to understand the main controlling parameters of the fracture toughness (KIC) and/or the critical value of the fracture energy (Gf) of different types of concretes. Some researchers reported that the cracks are arrested by aggregate particles where additional energy is required for its propagation [7]. Bažant et al. [8] reported that much of the scatter in total fracture energy calculations come from inherent randomness in the tail end of the load-crack mouth opening displacement (CMOD) curve and uncertainty in extrapolating the tail end of the curve to zero loads beside sources of energy dissipation [9]. Due to the brittleness and heterogeneity of concrete, the fracture process zone (FPZ) is large and occupies nearly the entire nonlinear zone. Several fracture mechanics nonlinear models were proposed to characterize the failure of brittle materials such as concrete and rock. These nonlinear models can be categorized into two approaches: the cohesive-zone or softening zone mechanisms, such as the fictitious crack model [10] and the crack band model [11]. The equivalent elastic (or effective) crack approach is based on the Griffith–Irwin energy dissipation concept, such as the two-parameter fracture model (TPFM) by Jenq and Shah [12] and the size effect law (SEL) by Bažant [13]. The general idea of the Hillerborg model [10] is to measure the amount of energy absorbed when the specimen is broken into two halves [14]. SEL for notched beams (SEL, Type-ΙΙ) proposed by Bažant considered two material parameters, KIC and the critical effective crack extension Cf. On the other hand, four parameters were considered in the case of un-notched beams (SEL, Type-Ι). In the universal size effect law (USEL, Type-Ι&ΙΙ), 12 parameters [15] were undertaken. Ouyang et al. [16] suggested a relationship to calculate equivalent parameters of TPFM based on the equivalency of TPFM and SEL. Also, other researchers are concerned with determining KIC for FGM [17]. Since the physical specimen size is the major consideration in these models, the influence of crack length on concrete fracture is not explicitly expressed in these models. Experimental and theoretical studies showed that the FPZ in concrete has to have a certain width to allow various mechanisms such as multiple-cracking, aggregate-interlocking, and interface grain bridging in the width direction to create strain-softening [18].

Duan et al. [19] proposed a local fracture energy model to explain cementitious materials' non-constant local fracture energy distribution. The model assumed the proportionality of the local Gf to the FPZ length/height and characterized the FPZ height reduction when approaching a specimen back boundary. It was found that the reference ligament length, which determines the intersection of the two linear fracture energy functions from the proposed model, is influenced by the specimen geometry size (depth). They found an agreement between the estimated results and the experimental results for concrete specimens [20]. It was also found that the fracture energy of concrete specimens increases with increasing the specimen thickness, even when the thickness is four times the maximum grain size. Also, the specimens with thickness less than ten reference ligament transition lengths were used to investigate the thickness effect for given specimen geometry and size and loading conditions due to the boundary effect of specimens [21].

Hu and Wittmann [22] examined the fracture of a large plate with an edge crack. They pointed out that the failure transition from the strength-dominated to the linear elastic fracture mechanics (LEFM)-controlled fracture was due to the interactions between the crack, FPZ, and front boundary, leading to the common size effects. They proposed the boundary effect model (BEM) by an asymptotic approach to the strength-crack size relationship for the large plate. This asymptotic approach has been extended to concrete specimens with a finite size, which provides accurate predictions for the size-dependent fracture properties. However, Duan and Hu [23] reported that the predicted tensile strength is as high as two and a half times the splitting strength for Indiana limestone. This increase is attributed to the volume and configuration effects associated with statistical fracture behavior brittle materials. They considered this increase adequate because it is close to the experimental flexural strength.

Hu and Duan [24] compared their BEM with SEL. They concluded that the key mechanism of the size effect on quasi-brittle fracture transition is actually due to the interaction of FPZ with the nearest structure boundary rather than the variation of the physical size of specimens as in SEL. Thus, the size effect is true for geometrically similar specimens of different sizes. Still, it is limited applicable because of the special conditions, such as the same loading condition and same α ratio, and the variations in the asymptotic limits for any slight variation in the specimen conditions [25]. In addition, BEM can predict quasi-brittle fracture of concrete applicable to various specimen geometries and sizes with lower material constants, tensile strength, and KIC rather than SEL type Ι or ΙΙ or USEL with its twelve parameters [26].

On the other side, Bažant and his colleagues have published several papers on comparisons between SEL and BEM for quasi-brittle fracture of concrete and calibrated their results by the cohesive crack model, see, for example, Ref. [27]. They concluded that BEM was derived based on the assumption that linear stress distribution along the ligament differs from the real stress distribution without any physical argument. Thus, the equivalent crack length of asymptotic BEM cases was calculated based on this assumption. BEM cannot be applicable in many cases such as; arch, dams, mixed shear fracture modes, and complex geometries of engineering structures. In contrast, SEL can be applied as it is derived based on energy release rate at the crack tip related to specimens depth/size and without knowing the direction of crack propagation [28]. In addition, the BEM differs from SEL in a major way and gives incorrect results for very small sizes, vanishing ligaments, shallow notches, and un-notched specimens. Comparisons with experiments and cohesive crack calculations bear it out [29]. Statistical analysis is adopted to predict the tensile strength based on the suggested fictitious crack that depends on aggregate size distribution by discrete statistical number and the aggregate grain size [30].

All the previous works studied the fracture toughness of FRC using through-thickness notched beams, i.e., cutting the fibers between the notch surfaces. However, fibers must cross the notch surfaces to have actual field conditions and correct simulations in the actual field simulation of FRC beams. It was considered one of the difficult laboratory problems. Carpinteri [31] and Baluch et al. [32] focused on the problem of a single crack crossing a reinforcement layer with steel bars as a long fiber or deboned fiber-reinforced plate on the cracked surface of the beam. Using fracture mechanics, they calculated the effect of the produced closure force or moment due to steel bars in the notch. El-Sagheer et al. [33] suggested a new technique to create a matrix crack (MC) pattern with long glass fibers to calculate the translaminar fracture toughness of polymeric composite materials to avoid cutting fibers on pre-crack surfaces.

Recently, Elakhras et al. [34] suggested a novel method to create an MC, i.e., representing fibers bridging on the pre-cracked specimens. They used equivalent relationships of TPFM to measure the fracture toughness of FRC and FGC MC beams [35]. This technique was adopted in the present work to study the size and boundary effects on the real fracture toughness of full-depth (FD) FRC, FD FRC beams, and FGC beams. The reliability of the real fracture toughness predicted from SEL and BEM for MC-specimens was checked using the concept of the maximum size of the non-damaged defect (dmax) [36].

2 Experimental work

2.1 Experimental program

The experimental program consists of twenty-four MC-FD FRC beams and twenty-four MC-FGC beams with three different spans to depth ratios (L/d) equal 4, 5, and 6, and three different beam depths of the same beam span. The ratios of the beam depth to the nominal max aggregate size (d/NMAZ) are 12, 15, and 18. It is worth noting that the experimental results obtained by Bazant and Pfeiffer [37] were in agreement with three different ratios of (d/NMAZ) ranging from 6 to 24 and were sufficient to predict the size effect law [38]. On the other hand, Han et al. [39] investigated the fracture toughness for notched beams with six different L/d ratios ranging from 2 to 6. Although the present work focused on only three different L/d ratios, this work will be extended in the future to investigate other L/d ratios to get a better validation from the application of the size effect equations. All beams have been tested under three-point bending. The breadth of the beams kept constant equals 150 mm. The crack length is equal to one-third of the beam depth. Four beams were cast for each case study to take the average. Table 1 shows the experimental program and dimensions of the investigated beams.

Table 1 Dimensions in mm of the investigated beams
Full size table

2.2 Materials and mix proportions

Three mixes, including normal strength concrete (NSC), FRC, and high strength concrete (HSC), were designed for the experimental program. NSC was designed based on ACI 211.1-91 [40]. Steel fiber (SF) has many forms and lengths. In the present work, hooked end SF was used for better flexural performance and good bond with the cement matrix than crimped or straight SF [41]. The used hooked-end SFs were of length equal to 35 mm, a circular cross-section diameter of 0.80 mm, and tensile strength of 1150 MPa. FRC was designed by adding 1% hooked-end SF by volume fraction to NSC. For NSC and HSC, Type I ordinary Portland cement complies with ESS 4756-1:2013 [42], and EN 197-1:2011 [43] was used. Grade 42.5 N from this cement of minimum 28 days compressive strength equals 42.5 MPa was used for NSC, while Grade 52.5 N of minimum 28 days compressive strength equals 52.5 MPa was used for HSC manufacturing. The total cementitious materials for NSC and FRC were 400 kg/m3. The water/cementitious ratio (W/CM) was 0.53. The total cementitious materials used to produce HSC mix was 550 kg/m3, and the W/CM ratio was 0.27. HSC mix was produced by adding 10% silica fume, Master Life SF 100 complies with ASTM C1240-05 [44], as partial replacement of cement content and superplasticizer, Master Glenium RMC 315 complies with BS 5075-3 [45] and EN 934-2 [46], as a high range water reducer by 2.5% from the weight of the cementitious materials. Physical properties and chemical analysis of the used silica fume are, respectively, given in Tables 2 and 3.

Table 2 Physical properties of the used silica fume
Full size table
Table 3 Chemical analyses of the used silica fume
Full size table

Properties of the used superplasticizer are given in Table 4. In all mixes, ordinary siliceous sand was used as a fine aggregate, and dolomite with a nominal maximum size of 12.50 mm was used as coarse aggregate. A sieve analysis test was carried out on the used fine and coarse aggregates following ASTM C33/C33M-18 [47], and the results are given in Tables 5 and 6. Table 7 shows the quantity of each material in kg required to produce one cubic meter from each mix. As shown in Table 7, the coarse aggregate to cementitious ratios (ACR) for NSC and HSC are, respectively, 2.38 and 1.75. These ratios confirm with those reported by ACI 363R-10 [48], which stated ACR between 1.4 and 3 for the production of HSC. The fresh and hardened properties of the three investigated mixes are found in Table 8.

Table 4 Properties of superplasticizer (Master Glenium RMC 315)
Full size table
Table 5 Sieve analysis test results of the used aggregates
Full size table
Table 6 Physical properties of dolomite and sand
Full size table
Table 7 Mix ingredients for different mixes (kg/\({\mathrm{m}}^{3}\))
Full size table
Table 8 Properties of different concretes
Full size table

2.3 Specimen manufacture and testing

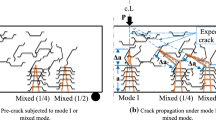
The real MC is a crack that must pass through the concrete and be bridged by short fibers in the case of FRC, as described in detail by Elakhras et al. [34], as shown in Fig. 1.

Fig. 1
figure 1

Methodology of MC formation

Full size image

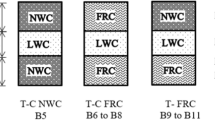
All specimens were cast in steel molds. For the compressive strength test, cubes 150 × 150 × 150 according to BS EN 12390-3:2009 [49] were cast. Cylindrical specimens (150 mm diameter × 300 mm height) according to BS EN 12390-6:2009 [50] were used for indirect tensile strength. A thin layer of oil-coated all molds for easy de-molded. The patch of dry materials required to produce the three concretes was weighted first. The dry materials for each type of concrete were mixed for 2 min, and after that, the required total amount of water was added, and the mixing was continued until reaching a homogenous mix. In the case of FRC, the fibers were sprayed continuously during the final mixing stage. In the case of HSC, two-thirds of the mixing water was added to the dray materials, and the MasterGlenium was stirred to the remaining third. All molds were prepared for casting. In the case of MC beams, the foam strip containing the fibers was in its position, as shown in Fig. 1. For FGC beams, marks were drawn along the height of the molds to define the depth of each layer. The same procedures used to cast the three layers by Othman et al. [51] were followed to cast FGC beams. Figure 2 shows the cross section of MC-FD FRC and MC-FGC beams.

Fig. 2
figure 2

Cross section of (a) MC-FD FRC beam and (b) MC-FGC beam

Full size image

A universal testing machine tested all beams under a three-point bending configuration. Load–CMOD results were recorded using a data acquisition system. A fixed camera with high pixels recorded crack propagation with time. The transparent measured tap was pasted vertically along with the beam depth besides the crack opening to monitor crack propagation development. Figure 3 shows a schematic diagram of test measurements and test setup.

Fig. 3
figure 3

The schematic diagram for setting CMOD and load measurements and test setup

Full size image

2.4 Methods of fracture parameter estimations

2.4.1 Size effect law (SEL) method

Bažant proposed SEL-Type II to predict the fracture parameters for quasi-brittle material. According to Bažant and RILEM recommendations [38], at least three different sizes notched specimens with similar; geometrical cross section, L/d ratio, and initial relative crack length to the specimen depth (αo) are recommended to obtain the material fracture parameters. Two fracture parameters were considered constant material parameters; the critical energy release rate (Gf) and the critical effective crack extension (Cf) can be calculated by the following sequences. The general formula of SEL-Type II can be obtained in a linear regression form as follows [15]:

$${\left(\frac{{f}_{\mathrm{t}}}{{f}_{\mathrm{fl}}}\right)}^{2}=\frac{ 1}{{B}^{2}{ d}_{0}}d+ \frac{1}{{B}^{2}},$$
(1)

where \({f}_{\mathrm{fl}}\) is the flexural strength for notched 3 PB specimens, \({f}_{\mathrm{t}}\) is tensile strength obtained from the indirect tensile test, B and do are empirical coefficients. The empirical coefficients (B, do) can be obtained from putting SEL in a linear regression form. Fitting the measured values of \({f}_{\mathrm{t}}\) corresponding to \({f}_{\mathrm{fl}}\) for notched specimens versus their different depths according to SEL Eq. (1) as follows:

$$Y=AX+C, \mathrm{ where} {Y=\left(\frac{{f}_{t}}{{f}_{fl}}\right)}^{2},X=d$$
(2)

The empirical coefficients can be obtained as

$$B=\frac{1}{\sqrt{C}},$$
(3)
$${d}_{0}=\frac{C}{A}.$$
(4)

The fracture parameters Gf, Cf, and KIC can be calculated as follows:

$${C}_{\mathrm{f}}={d}_{\mathrm{o}}\frac{g\left(\alpha \right)}{{g}^{^{\prime}}\left(\alpha \right)},$$
(5)
$${K}_{\mathrm{IC}}=\sqrt{{G}_{\mathrm{f}} E }=B{f}_{\mathrm{t}}\sqrt{{C}_{\mathrm{f}}{g}^{^{\prime}}\left(\alpha \right)},$$
(6)

where \(\alpha \) is the initial relative crack or notch depth (ao/d), ao is the initial crack depth. Cf is the effective crack length of FPZ, E is Young's modulus, g(\(\alpha \)) is the dimensionless energy release function of equivalent LEFM characterizing the specimen geometry. \({\mathrm{g}}^{\mathrm{^{\prime}}}\left(\mathrm{\alpha }\right)\) is the first-order relative to \(\mathrm{\alpha }\). The function g(\(\mathrm{\alpha }\)) can be obtained as follows:

$$g\left(\alpha \right)={[f(\alpha )]}^{2},$$
(7)

in which, f (\(\alpha \)) is the geometry function, given as

$$f\left(\alpha \right)=\frac{\sqrt{\alpha } [ 1.90- \alpha \left( -0.089+ 0.603(1- \alpha \right)- 0.441{\left(1- \alpha \right)}^{2}+ 1.223{\left(1 - \alpha \right)}^{3})]}{(1+ 2\alpha ){(1- \alpha )}^{3/2}}\mathrm{ for }L/d$$
(8)

2.4.2 Boundary effect model (BEM) method

According to the last version of BEM, KIC of concrete can be calculated for notched 3 PB specimens with various sizes, relative notch depth, and L/d ratios depending on the predicted tensile strength (\({f}_{\mathrm{t}}^{\mathrm{P}}\)). The predicted tensile strength is calculated to depend on the suggested fictitious crack that depends on the distribution of aggregate size by discrete statistical number (β) and the aggregate grain size (G). The essential equations of BEM for notched 3 PB tests are provided as follows [52]:

$${f}_{\mathrm{fl}}=\frac{A\left(\alpha \right){f}_{\mathrm{t}}^{\mathrm{P}}}{\sqrt{1 + \frac{{a}_{\mathrm{e}}}{{a}_{\mathrm{ch}}}}},$$
(9)

where \({f}_{\mathrm{fl}}\) is the flexural strength for notched 3 PB specimens, ae is the equivalent crack length, ach refers to the characteristic crack length, and \(A(\mathrm{\alpha })\) is a dimensionless factor depending on the loading distribution and the relative crack length (\(\mathrm{\alpha })\).

The fracture parameters of BEM (\({f}_{\mathrm{t}}^{\mathrm{P}}\), KIC) can be obtained by the following sequences:

$$A\left(\alpha \right)={\left(1-\alpha \right)}^{2}.$$
(10)

The geometry factor, \(Y\left(\alpha \right)\) of notched 3 PB specimens can be calculated for specimens of different L/d ratios using the linear interpolation method as follows:

$${Y}_{4}\left(\alpha \right)=\frac{1.99- \alpha \left(1 - \alpha \right)\left(2.15- 3.93 \alpha + 2.70 {\alpha }^{2}\right)}{\sqrt{\pi } (1 + 2\alpha ){ (1 - \alpha )}^{3/2}}\mathrm{ for }\,\frac{L}{d}=4,$$
(11)
$${Y}_{8}\left(\alpha \right)=1.107-2.12 \alpha +7.71{\alpha }^{2}-13.55{\alpha }^{3}+14.25{\alpha }^{4}\mathrm{ for }\,\frac{L}{d}=8,$$
(12)
$${Y}_{L/d}\left(\alpha \right)=\frac{8 -\frac{L}{d}}{4}{Y}_{4}\left(\alpha \right)- \frac{4 -\frac{L}{d}}{4}{Y}_{8}\left(\alpha \right)\mathrm{ For }\,\frac{L}{d}, \mathrm{ from }\,4 \,to\, 10$$
(13)

Then the values of \({a}_{\mathrm{e}}\) and \({a}_{\mathrm{ch}}\) can be obtained as follows:

$${{a}_{e}=\left[\frac{A(\alpha ) Y(\alpha )}{1.12}\right]}^{2}{a}_{0}.$$
(14)

The characteristic crack length (\({a}_{\mathrm{ch}}\)) is considered as a material constant. On the last development of BEM [52], ach was suggested to link with the aggregate size (G) by discrete statistical number (βch) for concrete, when depth/G < 30, as follows:

$${\Delta a}_{\mathrm{ch}}= {\beta }_{\mathrm{ch}}\times G,$$
(15)

\({f}_{\mathrm{t}}^{\mathrm{P}}\) can be obtained by transforming the general BEM formula Eq. (9) to a linear formula according to its last developments based on applied fracture load (\({P}_{\mathrm{f}}\)) and the suggested equivalent area (Ae) as follows:

$${P}_{\mathrm{f}}={f}_{\mathrm{t}}^{\mathrm{P}}{A}_{\mathrm{e}}\left(d,{a}_{0},G\right)={f}_{\mathrm{t}}^{\mathrm{P}}\frac{(d - {a}_{0})(d - {a}_{0}+ 2 \Delta {a}_{\mathrm{fic}} )}{1.5 \left(\frac{L}{b}\right)\sqrt{1 + \frac{{a}_{\mathrm{e}}}{{a}_{\mathrm{ch}}}}},$$
(16)

where Δafic is the fictitious crack and linked with the aggregate size (G) by discrete statistical number (βfic), as follows:

$${\Delta a}_{\mathrm{fic}}= {\beta }_{\mathrm{fic}}\times G.$$
(17)

Finally, the fracture toughness KIC can be obtained as follows:

$${K}_{\mathrm{IC}}=2 {f}_{\mathrm{t}}^{\mathrm{P}}\sqrt{{a}_{\mathrm{ch}}}.$$
(18)

To study the size effect of various specimens with the same geometry and constant L/d ratio, BEM can be obtained relative to specimen size represented by various depths (d), as follows:

$${f}_{\mathrm{fl}}=\frac{{A\left(\alpha \right) f}_{\mathrm{t}}^{\mathrm{P}}}{\sqrt{1+\frac{d}{{a}_{\mathrm{ch}}/B\left(\alpha \right) \alpha }}},$$
(19)
$$\mathrm{where }B\left(\alpha \right){=\left(\frac{A\left(\alpha \right) Y\left(\alpha \right)}{1.12}\right)}^{2}.$$
(20)

3 Results and discussion

3.1 Effect of geometrical parameters

Table 9 summarizes the flexural strength at first cracking and maximum load for MC-FD FRC and flexural strength at maximum load for MC-FGC specimens.

Table 9 Results of MC-FD FRC and MC-FGC beams
Full size table

Figure 4 shows load–CMOD curves for MC-FD FRC and MC-FGC beams having different sizes with constant L/d ratio and specimens with L/d ratios equal 4, 5, and 6. Also, the regression factor was calculated for the tested specimens according to the suggested multi-linear mean curve. The suggested mean curve was calculated based on average load and CMOD at each observed variation in the curve slope for the four specimens in each case. Figure 5 compares P-CMOD curves of FRC and FGC beams based on the mean curves. The crack initiation for MC-FD FRC specimens is compatible with ACI 544.4R-88 [41] and ASTM C1609 [53]. However, the sudden drop after the peak load of MC-FGC may be attributed to the material ahead of the crack tip in NSC, not FRC, as shown in Fig. 2. Therefore, the area under the descending portion (softening portion) for the MC-FD FRC specimens is larger than that of the MC-FGC specimens. Also, the presence of softening portion in the FGC specimens reflects the efficiency of the proposed new MC technique in simulating a real field crack in the laboratory.

Fig. 4
figure 4

Load–CMOD curves of MC-beams, (a) FRC, and (b) FGC

Full size image
Fig. 5
figure 5

Mean curves of P-CMOD for MC-FD FRC and MC-FGC beams

Full size image

Figure 6 shows a comparison between the flexural strength with various L/d ratios for MC-FD FRC and MC-FGC beams. The flexural strength differs inversely with the variation of L/d ratios. Most of the fracture models are based on the elastic fracture response of structures to the max load. Thus, flexural strength is directly proportional to stiffness and inversely proportional to the L/d ratio. To notice the significance of the size effect parameter on the mechanical properties of the beam, statically analysis was impeded to analysis results of the initial slope, P/CMOD ratio, at different beam sizes with its geometrical dimensions based on the mean values and the coefficient of variations (CV). Figure 7a–d shows a comparison between P/CMOD ratios and different beam geometrical parameters as (a) variable depth and constant length, (b) variable length and constant depth, (c) variable depth at constant L/d ratio, and (d) variable L/d ratios. Figure 7 shows that there are high significant variations on results of the initial slope, P/CMOD ratios, versus geometrical dimensions, depth or span, change (variable depth and constant length, Fig. 7-a, or variable length and constant depth, Fig. 7-b). The C.Vs are 0.19 and 0.24 for MC-FD FRC and 0.46 and 0.42 for MC-FGC, respectively, for the two cases. Also, the results in Fig. 7-d support the fact that the initial slope, P/CMOD ratio, is inversely proportional to (L/d), where the C.Vs for all tested beams at L/d = 4, 5, and 6 are equal to 0.17 and 0.29 for FD FRC and FGC beams, respectively. However, the statically C.V for P/CMOD ratio at constant L/d ratio equals 4 shows the minimum variations in C.Vs., 0.04 and 0.07 for MC-FD FRC and MC-FGC, respectively. This indicates that the geometrical factor L/d ratio for different tested specimens is recommended to be constant to capture independent size effect parameters.

Fig. 6
figure 6

Comparison between flexural strength with various span/depth ratios for MC-FD FRC and FGC

Full size image
Fig. 7
figure 7

Comparisons between P/CMOD ratios and different beam geometrical parameters

Full size image

3.2 Size effect law

According to Bažant, the first cracking occurs at the maximum load, Pmax [38]. In MC-FD FRC, the first cracking appeared before Pmax, but it can be due to the relaxation of microcracks at the strain hardening stage of FRC, as shown in the load–CMOD curves. The size effect law for notched specimens (type II) was applied on the three different sizes with a constant L/d ratio equal to 4 with \({\mathrm{\alpha }}_{o}\) = 1/3 at first cracking and maximum load for MC-FD FRC and MC-FGC. Figure 8a–c shows the fitted experimental results for different sizes of MC-FD FRC and MC-FGC to the linear regression form of SEL, see Eqs. (1)–(4). The empirical coefficients (B, do) can easily be obtained from Fig. 8. Table 10 shows the mechanical properties and the results from SEL, empirical coefficients, the fracture parameters (KIC, Cf), and the brittleness number (βb.) for MC-FD FRC and MC-FGC.

Fig. 8
figure 8

The fitted experimental results for different sizes of MC-FD FRC and MC-FGC to the linear form of SEL; (a) FRC at first crack, (b) FRC at max load, (c) FGC

Full size image
Table 10 The mechanical properties, equation constants, SEL parameters (KIC, Cf) for MC-FD FRC and MC-FGC, and brittleness number (βb.)
Full size table

Table 10 shows that SFs in front of the notch and crossing through the notch of MC-FD FRC directly affect the fracture parameters. The fracture toughness increases from 1.38 to 2.01 MPa m0.5 from first cracking to the maximum load by an increasing percentage of 46%. This significant increase includes the bridging and closing effect of fibers crossing the notch at the strain hardening stage of the specimen.

Bažant and Pfeiffer [37] calculated the fracture properties of NSC by SEL for four different beam sizes with constant L/d ratio equal 2.50 and E = 27,700 MPa, KIC = 1.01 MPa m0.5, and Cf = 13.47 mm. By comparing these NSC and MC-FD FRC results at first cracking, KIC shows a higher value by about 38% compared to NSC. In addition, by comparing KIC for MC-FD FRC at maximum load and NSC, there is a more significant effect due to fibers' bridging and closing effect across the notch, reaching twice the value of NSC by an increase of about 99%. Also, the value of Cf for MC-FD FRC at max load is slightly higher than NSC, as their values are 14.27 mm and 13.47 mm, respectively.

In addition, MC-FGC specimens KIC showed larger fracture toughness than MC-FD FRC at maximum load by 10%. This increase is expected better architect of FGC due to its high stiffness and the presence of HSC in the compression zone. Also, from laboratory observations, MC-FGC showed the occurrence of crack initiation at maximum load and jumping of crack inside the second NSC layer to the boundary of the third HSC layer. So, the value Cf can be approximately equal to 1/3 the depth of the tested specimens; 50, 62, 75 mm, and this is in good agreement with the SEL result equals 63.43 mm, as shown in Table 10.

Figure 9 shows a typical SEL curve compared to the present experimental results. It can be observed that the results of MC-FD FRC and MC-FGC at Pmax exhibited size effect transition zone between LEFM and plastic limit, and this was accomplished with the results of SEL brittleness number as it between 0.1 < βb. < 10 [54], see Table 10. Also, the results of MC-FD FRC at first cracking exhibit size effect compatible with LEFM (βb. ≫ 10) as its brittleness number ranged between 16 and 24. In addition, Fig. 9 shows the regression factor between SEL and experimental results of flexural strength for FD FRC and FGC specimens. SEL showed a good agreement with the experimental results for flexural strength with regression factors more than 0.97 for FD FRC and FGC at first cracking and maximum load.

Fig. 9
figure 9

Size effect curve compared to experimental results by regression factor; (a) MC-FD FRC at first cracking, (b) MC-FD FRC at max load, (c) MC-FGC at max load

Full size image

3.3 Boundary effect model

According to BEM, the KIC of concrete was calculated based on the predicted tensile strength. The predicted tensile strength was calculated based on the suggested characteristic crack length (ach) and the fictitious crack that depends on the aggregate size (G) and the aggregate distribution by discrete statistical number (β) to fit the experimental results.

According to Chen et al. [52], to evaluate \({f}_{\mathrm{t}}^{\mathrm{P}}\) for quasi-brittle materials for specimens with depth/G < 30, the discrete number (βch) for the relative characteristic crack (ach/G) was assumed in range of 1.5–4.0, and the discrete number (βfic) for the relative fictitious crack (Δafic/G) was assumed in range of 0.5–3.0 [52]. Also, Han et al. [52] suggested when studying the concrete fracture using the maximum aggregate size (Gmax), the discrete number βfic is suggested to be around 1.0. In contrast, using the average grain size (Gavg), the discrete numbers βfic = 1.5 and βch = 3 were more appropriate.

In the present study, to obtain the best fit of experimental results of MC-FRC and MC-FGC to BEM curve, by the previously suggested ratios (Gavg = 8.75 mm, βfic = 1.5 and βch = 3), the results showed it not adequate to MC-FD FRC and MC-FGC at max load by regression factors about 0.49. Also, using the maximum aggregate size (Gmax = 12.5 mm) with its βfic = 1 and βch = 3, the regression factors for specimens were about 0.49. However, the most suitable ratios were obtained for MC-FRC and FGC using the minimum limits; βfic = 0.5, βch = 1.5 for the maximum aggregate size (Gmax = 12.5 mm), by regression factors more than 0.98. This can be explained by SF's effect of closing and bridging cracks in concrete.

Applying BEM (Eqs. 9–17) for all specimens with L/d ratios equal 4, 5, and 6, the predicted tensile strength, \({f}_{\mathrm{t}}^{\mathrm{P}}\), can be obtained. Figure 10 shows the applied fracture load (P) and the equivalent area (Ae), predicted from tensile strength for each specimen according to Eq. (17). The slope of the mean line in Fig. 10 is the suggested mean tensile strength, \({f}_{\mathrm{t}}^{\mathrm{P}}\), that equals 7.46, 8.85 MPa for MC-FD FRC at first cracking and maximum load, and 7.34 MPa for MC-FGC, respectively. Also, most predicted results were in the range of upper and lower boundaries for normal distributions of the mean value and its standard deviations (\({f}_{\mathrm{t}}^{\mathrm{P}}\hspace{0.17em}\)± 2St.Dv.). The CVs for the mean curves are16 and 14% for MC-FD FRC and 15% for MC-FGC specimens with different ratios.

Fig. 10
figure 10

Prediction of cracking tensile strength, \({f}_{\mathrm{t}}^{\mathrm{P}`}\), of concrete with various span/depth ratios using linear BEM and normal distribution analysis

Full size image

Despite that, these predicted tensile strengths seem far from the result of indirect tensile strength for FRC, by error more than 150%, as shown in Table 8. However, these predicted tensile strength values were very close to the smooth specimens' flexural strength (\({f}_{\mathrm{fl}}\)) [34].

Table 11 shows the values of KIC for MC-FD FRC and MC-FGC at first crack and maximum load according to BEM for different three sizes with L/d ratio equal 4, and for different L/d ratios of 5 and 6 with constant relative initial crack length to depth ratio, \({\mathrm{\alpha }}_{o}\hspace{0.17em}\)= 1/3.

Table 11 The values of KIC in MPa m0.5 based on BEM for MC-FD FRC and MC-FGC
Full size table

MC-FD FRC and MC-FGC, KIC showed no significant trend, and slight variation for specimens with same geometrical different three sizes with L/d ratio equals 4. The mean KIC at max load was 2.63 and 2.10 MPa m0.5, with CV equal 0.06 and 0.12 for MC-FD FRC and MC-FGC, respectively. While at different L/d ratios equal 4, 5, and 6, the mean values of KIC decreased and showed inversely proportional to L/d ratios, as known, with CVs lower than 0.12.

Figure 11a–c shows the typical BEM curve compared to the experiment flexural strengths for all specimens with different L/d ratios. Also, statistical analysis was adopted and added to the BEM curve to consider substantial concrete heterogeneity and scatter on the results of specimens. The relation between flexural strength, \({f}_{\mathrm{fl}}\), and equivalent crack length, ae, was displayed with the nonlinear form with a domain of standard deviation (± 2St.Dv), as shown in Fig. 11. It can be observed that the results of the experiment flexural strengths for all specimens showed good agreement with the BEM curve and within its statistical domains (± 2St.Dv). Also, the BEM quasi-brittle fracture region is controlled by both \({f}_{\mathrm{t}}^{\mathrm{P}}\) and KIC in the range of 0.1 < ae/ach < 10. It was found that all the test scatters concentrate in the quasi-brittle fracture region for FD FRC and FGC specimens with different L/d ratios.

Fig. 11
figure 11

Non-LEFM prediction of fracture properties according to BEM

Full size image

To compare the results of BEM and SEL according to size effect for MC-FD FRC and MC-FGC, a series of three different specimens sizes with constant L/d ratio equal 4; B4-1, B4-2, B4-3 were considered. Thus, Fig. 12-a shows the BEM curve in dimensionless size effect plots of flexural strength versus size compared with the experimental flexural strength results for MC-FD FRC and MC-FGC by the regression factor, R2. The experimental results showed good agreement with the BEM curve by a regression factor of more than 0.98, as shown in Fig. 12-a. In addition, specimens with different L/d ratios 4, 5, and 6 showed an agreement with BEM with regression factors more than 0.95, see Fig. 12-b.

Fig. 12
figure 12

BEM and experimental results of flexural strength in dimensionless size effect plots versus different sizes for (a) L/d = 4, (b) L/d = 4, 5, 6

Full size image

3.4 The reliability of the predicted KIC from the different methods

To check the reliability of KIC predicted from the SEL and BEM, the concept of the dmax was used in this study [55]. It is worth noting that Pook [56] was the first to use this concept to predict the maximum imperfection size in metals under cyclic loading. On the other hand, dmax is similar to the characteristic length (\({l}_{\mathrm{ch}}=\frac{E{G}_{\mathrm{F}}}{{f}_{\mathrm{t}}^{2}}\)) [57]. Thus, dmax is equal to \(\frac{1}{\uppi }{\left(\frac{{K}_{\mathrm{IC}}}{1.12\times {f}_{\mathrm{fl }}}\right)}^{2}.\) The flexural strength of smooth specimen is \({f}_{\mathrm{fl}}\), see Ref. [34]. The consistency of KIC has been examined by comparing the value of dmax with nominal maximum aggregate size (NMAZ). Logically, dmax/NMAZ values should be around unity. Sallam et al. found that the ratio dmax/NMAZ was less than two for rigid pavement [36] and less than 0.75 for flexible pavement [58]. The values of KIC calculated by SEL and BEM of MC-FD FRC specimens; B4-1, B4-2, B4-3 with constant L/d ratio equal to four, were considered for investigating by dmax concept, at first cracking and max load.

Figure 13 shows the ratios of dmax/NMAZ for MC-FRC at first cracking for both SEL and BEM. The dmax/NMAZ ratios from SEL approach unity, while these ratios lie between two and three for BEM. On the other hand, the ratio of dmax/NMAZ was found lower than unity for through-thickness crack either in pure mode I [59] or pure mode II [60].

Fig. 13
figure 13

The fracture toughness reliability for MC-FD FRC for different specimen sizes and constant L/d ratio equals 4

Full size image

The previous analysis summarized that SEL and BEM are good candidates to predict the size effect since the minimum regression factor is greater than 0.97. On the other hand, the fracture toughness of MC-FD FRC specimens using SEL is lower than those estimated based on BEM. The ratios of dmax/NMAZ based on SEL are about unity, while BEM showed ratios between two and three. This means that the SEL is more reliable than BEM.

4 Conclusion

The results of the present work support the following conclusions:

  1. 1.

    MC-FD FRC and MC-FGC beams with the same geometry, different sizes, and of constant L/d ratio equals four showed the minimum variations in the flexural strength results due to its constant initial slope property, P/CMOD. Therefore, it is recommended to have specimens of constant L/d ratio to capture independent size effect parameters.

  2. 2.

    SEL shows a good agreement with the flexural strength experimental results for FD FRC and FGC with regression factors greater than 0.97 at first crack initiation and maximum load. MC-FD FRC and MC-FGC at maximum exhibited size effect intermediate between LEFM and plastic criteria. On the other hand, at first crack initiation, MC-FD FRC exhibited a size effect compatible with LEFM.

  3. 3.

    The most suitable statistical discrete numbers of BEM for MC-FD FRC and FGC having different L/d ratios were obtained using the minimum limits; βfic = 0.5, βch = 1.5 for maximum aggregate size equals 12.5 mm, by regression factors greater than 0.95. The efficiency of steel fibers can explain this in closing and bridging cracks in the front and through the MC specimens.

  4. 4.

    According to BEM, all MC-FD FRC and MC-FGC results exhibited transitional behavior between LEFM and plastic criteria as described by the quasi-brittle fracture region. The predicted tensile strengths from the BEM for MC-FD FRC and MC-FGC recorded higher values than predicted from indirect tensile strength for NSC and FD FRC by error greater than 150%.

  5. 5.

    The experimental results of flexural strengths for MC-FD FRC and MC-FGC showed good agreement with BEM curve versus size effect by a regression factor greater than 0.98 for specimen with constant L/d ratio equals 4. In addition, specimens with different L/d ratios 4, 5, and 6 showed an agreement with the BEM with regression factors greater than 0.95.

  6. 6.

    According to the maximum size of the non-damaged defect concept, SEL is more reasonable than BEM. Generally, the two methods are appropriate to measure the real fracture toughness of MC-FD FRC and MC-FGC.