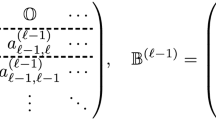Abstract
In this paper, we shall establish the superconvergence properties of the Runge-Kutta discontinuous Galerkin method for solving two-dimensional linear constant hyperbolic equation, where the upwind-biased numerical flux is used. By suitably defining the correction function and deeply understanding the mechanisms when the spatial derivatives and the correction manipulations are carried out along the same or different directions, we obtain the superconvergence results on the node averages, the numerical fluxes, the cell averages, the solution and the spatial derivatives. The superconvergence properties in space are preserved as the semi-discrete method, and time discretization solely produces an optimal order error in time. Some numerical experiments also are given.
Similar content being viewed by others
References
Cao, W., Huang, Q.: Superconvergence of local discontinuous Galerkin methods for partial differential equations with higher order derivatives. J. Sci. Comput. 72(2), 761–791 (2017)
Cao, W., Li, D., Yang, Y., Zhang, Z.: Superconvergence of discontinuous Galerkin methods based on upwind-biased fluxes for 1D linear hyperbolic equations. ESAIM Math. Model. Numer. Anal. 51(2), 467–486 (2017)
Cao, W., Li, D., Zhang, Z.: Optimal superconvergence of energy conserving local discontinuous Galerkin methods for wave equations. Commun. Comput. Phys. 21(1), 211–236 (2017)
Cao, W., Shu, C.-W., Yang, Y., Zhang, Z.: Superconvergence of discontinuous Galerkin methods for two-dimensional hyperbolic equations. SIAM J. Numer. Anal. 53(4), 1651–1671 (2015)
Cao, W., Shu, C.-W., Zhang, Z.: Superconvergence of discontinuous Galerkin methods for 1-D linear hyperbolic equations with degenerate variable coefficients. ESAIM Math. Model. Numer. Anal. 51(6), 2213–2235 (2017)
Cao, W., Zhang, Z.: Superconvergence of local discontinuous Galerkin methods for one-dimensional linear parabolic equations. Math. Comput. 85(297), 63–84 (2016)
Cao, W., Zhang, Z.: Some recent developments in superconvergence of discontinuous Galerkin methods for time-dependent partial differential equations. J. Sci. Comput. 77(3), 1402–1423 (2018)
Cao, W., Zhang, Z., Zou, Q.: Superconvergence of discontinuous Galerkin methods for linear hyperbolic equations. SIAM J. Numer. Anal. 52(5), 2555–2573 (2014)
Cheng, Y., Meng, X., Zhang, Q.: Application of generalized Gauss-Radau projections for the local discontinuous Galerkin method for linear convection-diffusion equations. Math. Comput. 86(305), 1233–1267 (2017)
Cheng, Y., Shu, C.-W.: Superconvergence and time evolution of discontinuous Galerkin finite element solutions. J. Comput. Phys. 227(22), 9612–9627 (2008)
Cheng, Y., Shu, C.-W.: Superconvergence of discontinuous Galerkin and local discontinuous Galerkin schemes for linear hyperbolic and convection-diffusion equations in one space dimension. SIAM J. Numer. Anal. 47(6), 4044–4072 (2010)
Ciarlet, P.G.: The Finite Element Method for Elliptic Problems. North-Holland Publishing Co., Amsterdam (1978)
Cockburn, B.: Discontinuous Galerkin methods for convection-dominated problems. In: Barth, T.J., Deconinck, H. (eds.) High-Order Methods for Computational Physics. Lecture Notes in Computer Science and Engineering, vol. 9, pp. 69–224. Springer, Berlin (1999)
Cockburn, B., Hou, S., Shu, C.-W.: The Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. IV. The multidimensional case. Math. Comput. 54(190), 545–581 (1990)
Cockburn, B., Lin, S.Y., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. III. One-dimensional systems. J. Comput. Phys. 84(1), 90–113 (1989)
Cockburn, B., Luskin, M., Shu, C.-W., Süli, E.: Enhanced accuracy by post-processing for finite element methods for hyperbolic equations. Math. Comput. 72(242), 577–606 (2003)
Cockburn, B., Shu, C.-W.: TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws. II. General framework. Math. Comput. 52(186), 411–435 (1989)
Cockburn, B., Shu, C.-W.: The Runge-Kutta local projection \(P^1\)-discontinuous-Galerkin finite element method for scalar conservation laws. RAIRO Modél. Math. Anal. Numér. 25(3), 337–361 (1991)
Cockburn, B., Shu, C.-W.: The Runge-Kutta discontinuous Galerkin method for conservation laws. V. Multidimensional systems. J. Comput. Phys. 141(2), 199–224 (1998)
Cockburn, B., Shu, C.-W.: Runge-Kutta discontinuous Galerkin methods for convection-dominated problems. J. Sci. Comput. 16(3), 173–261 (2001)
Guo, L., Yang, Y.: Superconvergence of discontinuous Galerkin methods for linear hyperbolic equations with singular initial data. Int. J. Numer. Anal. Model. 14(3), 342–354 (2017)
King, J., Mirzaee, H., Ryan, J.K., Kirby, R.M.: Smoothness-increasing accuracy-conserving (SIAC) filtering for discontinuous Galerkin solutions: improved errors versus higher-order accuracy. J. Sci. Comput. 53(1), 129–149 (2012)
Li, J., Zhang, D., Meng, X., Wu, B.: Analysis of discontinuous Galerkin methods with upwind-biased fluxes for one dimensional linear hyperbolic equations with degenerate variable coefficients. J. Sci. Comput. 78(3), 1305–1328 (2019)
Meng, X., Shu, C.-W., Wu, B.: Optimal error estimates for discontinuous Galerkin methods based on upwind-biased fluxes for linear hyperbolic equations. Math. Comput. 85(299), 1225–1261 (2016)
Reed, W.H., Hill, T.R.: Triangular mesh methods for the neutron transport equation. Los Alamos Scientific Laboratory report LA-UR-73-479 (1973)
Ryan, J., Shu, C.-W., Atkins, H.: Extension of a postprocessing technique for the discontinuous Galerkin method for hyperbolic equations with application to an aeroacoustic problem. SIAM J. Sci. Comput. 26(3), 821–843 (2005)
Shu, C.-W.: Discontinuous Galerkin methods: general approach and stability. In: Numerical Solutions of Partial Differential Equations, Advanced Mathematics Training Courses, pp. 149–201. CRM Barcelona, Birkhäuser, Basel (2009)
Shu, C.-W., Osher, S.: Efficient implementation of essentially nonoscillatory shock-capturing schemes. J. Comput. Phys. 77(2), 439–471 (1988)
Wang, H., Zhang, Q., Shu, C.-W.: Implicit-explicit local discontinuous Galerkin methods with generalized alternating numerical fluxes for convection-diffusion problems. J. Sci. Comput. 81(3), 2080–2114 (2019)
Xu, Y., Meng, X., Shu, C.-W., Zhang, Q.: Superconvergence analysis of the Runge-Kutta discontinuous Galerkin methods for a linear hyperbolic equation. J. Sci. Comput. 84, 23 (2020)
Xu, Y., Shu, C.-W., Zhang, Q.: Error estimate of the fourth-order Runge-Kutta discontinuous Galerkin methods for linear hyperbolic equations. SIAM J. Numer. Anal. 58(5), 2885–2914 (2020)
Xu, Y., Zhang, Q., Shu, C.-W., Wang, H.: The \(L^2\)-norm stability analysis of Runge-Kutta discontinuous Galerkin methods for linear hyperbolic equations. SIAM J. Numer. Anal. 57(4), 1574–1601 (2019)
Yang, Y., Shu, C.-W.: Analysis of optimal superconvergence of discontinuous Galerkin method for linear hyperbolic equations. SIAM J. Numer. Anal. 50(6), 3110–3133 (2012)
Zhang, Q., Shu, C.-W.: Error estimates to smooth solutions of Runge-Kutta discontinuous Galerkin methods for scalar conservation laws. SIAM J. Numer. Anal. 42(2), 641–666 (2004)
Zhang, Q., Shu, C.-W.: Stability analysis and a priori error estimates of the third order explicit Runge-Kutta discontinuous Galerkin method for scalar conservation laws. SIAM J. Numer. Anal. 48(3), 1038–1063 (2010)
Acknowledgements
Yuan Xu is supported by the NSFC Grant 11671199. Qiang Zhang is supported by the NSFC Grant 11671199.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of Interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Appendix A
Appendix A
In this section, we supplement some technical proofs.
1.1 Proofs of (37)
As an example, below we present the detailed proof with respect to \(\Vert [\![\mathbb {F}_{1,p}w]\!]\Vert _{L^2(\varGamma _{\!h}^2)}\). It depends on the one-dimensional correction technique.
Fix \(y\in [0,1]\) and assume \(v(x,y^{\pm })\in H^1(I_h)\). For \(0\leqslant p\leqslant k\), the correction function along the x-direction is defined in the form [30]
Consider the separation function \(v(x,y)=v_1(x)v_2(y)\), where either \(v_1(x)\) or \(v_2(y)\) is the piecewise polynomial of degree at most k. A direct application of (20) yields
As we have mentioned in Remark 2, we have
Note that \(\mathbb {F}_{1,p}^\mathrm{1d}(w^+_{x,j+1/2})=\mathbb {F}_{1,p}^\mathrm{1d}(w^-_{x,j+1/2})\), since \(w\in H^R(\varOmega )\subset H^2(\varOmega )\) is continuous. Then using (A2) and the triangle inequality, we get \(\Vert [\![\mathbb {F}_{1,p}w]\!]\Vert _{L^2(\varGamma _{\!h}^2)}\leqslant ({\text{I}})+({\text{II}})\), where
Each term in (I) is bounded in the form
where the inverse inequality (9b) and Lemma 3 with \(R=1\) are used. Each term in (II) is bounded in the form
where the result in [30, Lemma 4.3] is used for any horizontal edges. Finally using (21), we can get the boundedness of \(\Vert [\![\mathbb {F}_{1,p}w]\!]\Vert _{L^2(\varGamma _{\!h}^2)}\) as stated in (37).
Similarly, we can get the boundedness of the second term in (37), by showing
The detailed process is omitted here.
1.2 Proof of (59)
It is easy to prove the right inequality by taking \(v=\mathbb {H}_1 w\) in (39) and using Lemma 1. To prove the left inequality, we start from the formulation for any function \(w(x,y)\in V_h\), namely
For simplification of notations, the ranges in the summations are omitted. Due to the \(L^2\)-orthogonality of \(L^y_{j,\ell }(y)\), we can easily get that
where (55) has been used in the second conclusion. Then we can prove the left inequality using the inequality [29] for the single-variable function
1.3 Proof of (64)
Since \(w\in H^3(\varOmega )\) is continuous everywhere, we have
It has been proved in [30, Lemma 5.3] for every i that
which together with the standard trace inequity [12] yield (64a).
The proof of (64b) is almost the same, so omitted here. In what follows we devote to proving (64c).
The proof depends on the local projection related to (62), the parameter-dependent Radau polynomials. For any given function \(w\in L^2(\varOmega _h)\), the projection \(\mathbb {C}w\) is defined element by element, namely,
which belongs to \(\mathcal {P}^{k+1}(K_{ij})\cap \mathcal {Q}^k(K_{ij})\). Here
is the \(L^2\) projection of w onto \(\mathcal {P}^{k+1}(K_{ij})\). Note that the definition of this local projection is a little different to that in [2, 30], and we do not need to discuss whether \(\vartheta ^x_i\) and/or \(\vartheta ^y_j\) are equal to 0.
Let \(\mathbb {C}^\perp w=w-\mathbb {C}w\) be the projection error. By standard scaling argument, we have the approximation property
Furthermore, we can easily obtain the following lemmas.
Lemma A1
There exists a constant \(C>0\) independent of h and w, such that
Proof
As the applications of the Bramble-Hilbert lemma and the scaling argument, it is sufficient to prove for any \(w\in \mathcal {P}^{k+1}(K_{ij})\) that
which is implied by the definition of projection \(\mathbb {C}\), say (A6).
Lemma A2
There exists a constant \(C>0\) independent of h and w, such that
Proof
By the definitions of \(\mathbb {G}_{\theta _1,\theta _2}\) and \(\mathbb {C}\), we have
where \(\mathbb {R}w\) is the \(L^2\) projection of w onto \(\mathcal {P}^k(\varOmega _h)\), and \(\mathbb {R}^\perp w=w-\mathbb {R}w\) is the projection error. Here \(w_1\) and \(w_2\) are defined element-by-element by
Next we will estimate each term on the right-hand side of (A9).
Using the approximation properties of projections (16) and (A8), as well as the approximation property of projection \(\mathbb {R}\) (refer to (21)), we get
After some technical and direct manipulations, almost the same as that in [30], we also have
where definition (61), with respect to \(\{\vartheta ^x_{i}\}_{i=1}^{N_x}\) and \(\{\vartheta ^y_{j}\}_{j=1}^{N_y}\), plays an important role. For more details, please see [30].
Finally, summing up the above conclusions yields this lemma.
Using the inverse inequity \(\Vert v\Vert _{L^\infty (\varOmega _h)}\leqslant C h^{-1}\Vert v\Vert _{L^2(\varOmega _h)}\) for \(v\in V_h\), Lemma A2 implies
Hence it follows from Lemma A1 that
The others can be estimated similarly. Now we complete the proof of (54).
Rights and permissions
About this article
Cite this article
Xu, Y., Zhang, Q. Superconvergence Analysis of the Runge-Kutta Discontinuous Galerkin Method with Upwind-Biased Numerical Flux for Two-Dimensional Linear Hyperbolic Equation. Commun. Appl. Math. Comput. 4, 319–352 (2022). https://doi.org/10.1007/s42967-020-00116-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s42967-020-00116-z
Keywords
- Runge-Kutta discontinuous Galerkin method
- Upwind-biased flux
- Superconvergence analysis
- Hyperbolic equation
- Two dimensions