1 Introduction

Over the past few years, the use of renewable energy sources has steadily increased in many countries of the world. This is due to growing popular awarness to use clean energy and the electrical sectors have many initiatives in place to diversify energy resources and reduce reliance on traditional fuels. Wind energy is seen as one of the potential energy resources for commercial purposes. Wind speed is the main source of wind energy by converting it into electrical power at the rotor of the wind turbine. Because of wind speed has an intermittent and variability condition, the study of speed distribution is a vital task in determining the wind energy capacity of the site [1].

Due to the intermittent nature of wind speed, the energy produced by the wind is unstable but fluctuates. These variability and uncertainties make it difficult to make some judgments, such as operational and investment decisions. To overcome operational challenges, wind energy should be combined with other conventional technologies. In addition, more accurate utilization of wind speed distribution could contribute to the profitability of wind energy investments. [2]. In this context, many PDFs have been provided in the literature to represent the distribution of wind speed, and they have been compared to identify the most suited one.

The nature of wind speed introduces two major uncertainties, one of which is the uncertainty of wind speed, which can be addressed with an effective PDF, as demonstrated in several studies. The second uncertainty relates wind speed to power conversion, which may be resolved by employing several models to represent the nonlinear portion of the power curve [1, 3].Because wind speed is stochastic, statistical analysis is critical for dealing with uncertainties in two issues: wind speed forecasting and wind output power. The Weibull distribution is a statistical technique that is widely used and recommended for calculating the PDF of wind speed [4].

In addition to the Weibull distribution, a variety of probabilistic distributions, such as normal and log-normal distributions, were used to describe and transform wind speed data from discrete values to continuous functions [5]. Added to that, detailed comparisons of the Weibull and various distribution functions have been presented in [6]. The characterization of the wind regime may be determined from a probability distribution of wind speed, which is regarded the main stage in the construction of wind power projects as well as making investment decisions. Since uncertainty in generation or transmission or distribution planning is considered, the representation model is required to take care of the uncertainty in renewable generation. the two point estimation method has been employed to handle the renewable uncertainty for multi objective optimal power flow [7]. nother approach to managing uncertainty in renewable distributed generators is a combination of multiple uncertainties [8]. Also, The correlation of uncertainties is modeled by bounded intervals through a polyhedral uncertainty set in generation expansion planning [9].

The two main parameters of the Weibull distribution function are used to adapt the measured data of the wind farm. Numerous research papers were presented on analytical methods for estimating the process of parameters such as [4, 10,11,12]. In [4], the seven analytical methods have been employed for determining the best Weibull parameters for wind energy generation in the northeast region of Brazil, which are GraphicalMethod (GM), maximum likelihood method (MLM), moment method (MM), energy pattern factor method (EPFM), empirical method (EM), modified maximum likelihood method (MMLM), and equivalent energy method (EEM). The Weibull distribution of Zafarana project in Suez Gulf, Egypt has been determined based on monthly averaged data for one year as well as every 10 min for two days and compared with other analytical methods to achieve best Weibull parameters [10]. Also, the power density method (PD) has been presented to calculate Weibull distribution parameters and compared with other analytical methods [11]. Furthermore,a developed method called wind energy intensification method (WEIM) have been presentedto calculate Weibull parameters of sixty locations in Pakistan based on three years (2014–2017) hourly measured wind data at 50 m height [13] where as a comparative assessment of the analytical methods have been carried out and an energy variance method (EVM) has been performed [14].

The Rayleigh distribution, which is a special case of the Weibull distribution, have been compared to weibull distribution to fit the measured wind speed data at Iskenderun located in Turkey and wind energy potential has been evaluated based on a 1-year measured hourly time-series wind speed data [15]. Also, least square method (LSM) has been utilized to calculate the parameters of the Weibull distribution at Kayathar, Tamil Nadu, India [16, 17]. In [18], probability weighted moments based on the power density method has been executed as another analytical method and compared to other common methods. In this study, the MM, MLM, LSM, and maximum entropy principle method (MEPM) have been presented and compared as parametric models to estimate Weibull parameters. In this context, the modified method of moment (MMOM) has been given as a new methodology and compared to established methods, but not to any heuristic optimization algorithms [19]. There are different statistical tests which have been used to compare the performance of each method such as determination coefficient (R2), root mean square error (RMSE), mean absolute error (MAE), correlation coefficient (R), standard deviation, wind energy error (WEE), and Monte Carlo simulation [11, 20, 21]. Where iterative characteristics have been used, analytical approaches continue to have their limitations. Due to complexity calculation and iterative characteristics of the by analytical approaches, the wind speed distribution cannot always be represented efficiently. Accordingly, Weibull's optimum distribution parameters can be determined using heuristic optimization methods that use the goal function to obtain the best fit values. In this context, the mean squared, RMSE, MAE, and MSE can be used as objective functions to get optimal values of Weibull parameters.

In terms of optimization algorithms, one of the heuristic optimization algorithms called social spider optimization was introduced to estimate Weibull parameters for wind speed distribution and compared to MLM, MM, and LSM as analytical methods and particle swarm optimization (PSO), genetic algorithm (GA), and Cuckoo optimization algorithm (COA) as heuristic algorithms [2]. Also, the single and combined parameter PDFs, which are Weibull, Rayleigh, lognormal, and Gamma, were developed to overcome the shortcoming exit in asingle PDF. The comparison between some common analytical methods such as MMLM, EM, EPF, MM, and, GM and heuristic optimization algorithms such as Grey wolf algorithm (GWO), bat optimization algorithm (BOA), GA, and bee colony algorithm (BCA) have been presented to guarantee optimal fitting of Weibull parameters. Results from the Weibull fitness tests showed that heuristic optimisation algorithms were more accurate than numerical methods [22, 23]. Also, the results of a harmony search (HS), COA, PSO, and ant colony optimization (ACO) have been compared to evaluate the performance of each method with those obtained by MLM, MM, EM, and equivalent energy method (EEM) [24]. Furthermore, the CSA and AO results were compared with MM, MLM, EMP and PDF for the estimation of Weibull parameters. An investigated comparison between the analytical methods and heuristic estimation methods has been implied [23]and the results showed that the heuristic estimation outperforms the parametric methods in terms of the fitting accuracy and operational simplicity. Also, the parameters of the Weibull distribution estimated by using simulated annealing algorithm have been condicted in [25].

Another uncertainty source is the wind power curve [3] which is issued from the nonlinearity part of the power curve. In the literature, there are several studies that discussed many models for nonlinearity part of the wind power curve. The polynomial, exponential, and cubic models have been addressed to achieve an optimal model for wind energy site [15, 18, 26,27,28]. Accordingly, achieving the optimal wind PDF speed model is still considered as a challenging task. Therefore,in this paper, different optimization algorithms of CSA, AO and BES are developed, employed and compared with other analytical techniques for handling this task. CSA was presented which is based on crow's intelligence in storing and retrievingits food in hiding locations [29]. It has many applications for solving several engineering applications such as the optimal allocation of the capacitor devices in distribution networks in order to improve the performance of distribution networks, and combined economic and emission dispatch problem [30, 31]. Also, aquila optimizer (AO) is a meta-heuristic algorithm that presented in 2020 and implemented for solving several benchmarks [32]. Moreover, bald eagle search (BES) is a new optimizier for solving optimization problems which is based on behavier of bald eagle to reach the target prey. BES optimizer is fulfilling three steps to achieve this target [33].The simple structure, easy implementation, searching force, and faster convergence motivated it to be proposed in solving one of the important optimization problems. The contribution of this work can be summarized as follows:-

  • Discuss the distribution of real data obtained for Zafaranh and Shark El-Ouinate sites, Egypt.

  • Presenting the MLM, EM, MM, and EPFM as analytical methods for weibull parameters calculation and optimal fitting based on R2, RMSE, MAE, and wind production deviation (WPD).

  • Analysis the performance of a novel intelligence optimization methods called CSA, AO, PSO and, BES for calculating the accuracy of fitting by statistical tests.

  • Tunning the control parameters of the developed BES for fair comparison with CSA, AO, and BES based on statistical analysis of standard errors and standard deviations and their histogram graphs.

The paper is organized as 6 sections. Section 1 presents the introduction to the goal of the research and the existing researches that are related to the present. Section 2 handles the analytical and heuristic methods that are used for PDF of wind speed distribution. Section 3 presents the measurement of fitting for all methods. Section 4 provides wind speed data and wind turbine data for Zafaranh and Shark El-Ouinate sites and illustrates the comprehensive indexes intended to validate the Weibull parameter, statistical analysis and convergence characteristics of CSA, AO and BES. Section 5 develovs the different models for wind power curve to find the most efficient model for each site. Section 6 derives the conclusion to the research.

2 Weibull Probability Density Function

The crucial step before starting any wind energy project or making investment decisions is deciding the analysis of wind speed distribution at this site. The wind energy calculation in any site is affected by any error of wind speed distribution. Therefore, assessing the site wind energy potential is dependent on the wind speed distribution model accuracy. In literature, there are several density functions such as Weibull, Rayleigh, lognormal, and Gamma, which can be used to set up the wind speed distribution [2]. The Weibull distribution is the most commonly used which has two parameters while Rayleigh distribution is a subset of the Weibull distribution which has only one parameter. The Weibull probability distribution function \(f(v)\) for the speed (v) is expressed as follows [19, 24]:

$$f\left(v\right)=\left(\frac{k}{c}\right){\left(\frac{v}{c}\right)}^{k-1}exp\left[-{\left(\frac{v}{c}\right)}^{k}\right]$$
(1)

and the Weibull cumulative distribution function \(F(v)\) is given by:

$$F\left(v\right)=1-exp\left[- {\left(\frac{v}{c}\right)}^{k}\right]$$
(2)

2.1 Analytical Methods

The analytical methods of MLM, EPFM, MM, and EM have been used to estimate Weibull curves estimating parameters for wind speed analysis [4, 7, 12, 14, 24].

2.1.1 Maximum Likelihood Method (MLM)

The parameters of Weibull distribution function can be estimated by using MLM but it requires numerical iterations. Based on that method, the parameters are founded according to the following equations:

$$k={\left[\frac{\sum_{i=1}^{n}{v}_{i}^{k}\mathrm{ln}({v}_{i})}{\sum_{i=1}^{n}{v}_{i}^{k}}-\frac{\sum_{i=1}^{n}\mathrm{ln}({v}_{i})}{n}\right]}^{-1}$$
(3)
$$c={\left(\frac{1}{n}\sum_{i=1}^{n}{v}_{i}^{k}\right)}^\frac{1}{k}$$
(4)

2.1.2 Method of Moments (MM)

When the mean and standard deviation of the wind speed are known, the MM can be used to calculate the shape factor and scaling factors without the requirement for numerical iterations as in MLM. The following Eqs. (5) and (7) may be used to compute mean wind speed (\(\overline{v }\)):

$$\overline{v }=c\mathcal{T}\left(1+\frac{1}{k}\right) \to c=\frac{\overline{v}}{\mathcal{T }\left(1+\frac{1}{k}\right)}$$
(5)

where, \(\mathcal{T}\) is the gamma function defined by:

$$\mathcal{T}\left(x\right)={\int }_{0}^{\infty }{t}^{x-1}\mathrm{exp}(-t)dt$$
(6)
$$\sigma =c.\sqrt{\mathcal{T}\left(1+\frac{2}{k}\right)-{\mathcal{T}}^{2}\left(1+\frac{2}{k}\right)}$$
(7)

2.1.3 Empirical Method (EM)

Based on the EM, the value of scaling parameter can be calculated as [12, 14]:

$$k= {\left(\frac{\sigma }{\overline{v} }\right)}^{-1.086}$$
(8)

This method is also called mean wind speed and a standard deviation which considered as a special case of moments method [10]. Then, the value of shape factor can be obtained by the following equation:

$$c=\frac{\overline{v}}{\mathcal{T }(1+\frac{1}{k})}$$
(9)

2.1.4 Energy Pattern Factor Method (EPFM)

This analytical method is also called a power density method that is related to the mean value of wind speed. Energy pattern factor (Epf), is defined by the following equation:

$$E_{{pf}} = \frac{{\overline{{v^{3} }} }}{{\bar{v}^{3} }}$$
(10)
$$k=1+\frac{3.69}{{\left({E}_{pf}\right)}^{2}}$$
(11)
$$\overline{v }=c\mathcal{T}\left(1+\frac{1}{k}\right)$$
(12)

From Eqs. (11), and (12), EPFM has simple formulation since the values of the shape and scaling factors can be founded without solving linear least square problem or numerical iterations.

2.2 Heuristic Optimization Methods

Other approaches of handling the optimization problems are through using the artificial intelligence algorithms. The most of these algorithms have been utilized to obtain the best objective function in a problem's search space by utilizing intelligence. However, in order to calculate the optimal values of shape and scale factors, many heuristic techniques rely on probabilistic judgments rather than analytical methods based on a pure random search [22, 24]. The compared algorithms, include PSO, CSA, AO, and the proposed BES tuning parameters, are handled in this study. The main objective function represents as minimizing the sum of square error between the measured frequency distribution in the histogram of the data and forecasted values by the adjusted PDF. Hence, the objective function can be represented by the following equation:

$$\epsilon =\sum_{i=1}^{n}{({f}_{w}\left({v}_{i}\right)-{f}_{m}\left({v}_{i}\right))}^{2}$$
(13)

where, \({f}_{w}\left({v}_{i}\right)\) and \({f}_{m}\left({v}_{i}\right)\) are the wind speed probability from Weibull distribution and that observed in the histogram of measured values, respectively.

2.2.1 Aquila Optimizer Algorithm

The aquila optimizer (AO) is an intelligent swarm optimization algorithm inspired by the natural behavior of the Aquila during the prey capturing process. Aquila's speed and agility, along with robust feet and broad, pointed talons, allow it to capture a variety of prey, mostly rabbits, hares, deeps, marmots, squirrels, and other ground animals. As a result, there are many ways for hunting that are relying on the natural behavior of prey. The hunting tactics approach is also affected by the hunting environment and most Aquila's ability to switch back and forth between hunting strategies deftly and rapidly [32].The following steps express the model of hunting processes of AO algorithm:

  1. 1.

    Initialization process: optimization of any process starts with random solutions of candidate variable (Xij)in the range between the upper (upj)and lower limits (lbj)which is expressed as following:

    $${X}_{ij}=rand\times \left({up}_{ij}-{lp}_{ij}\right)+{lp}_{j}$$

    where, \(rand\) is a random number, \(i\)th is the number of population, and \(j\)th is the dimension size of the problem.

  2. 2.

    Then, Aquila investigates any prey in the search space. This exploration stage is accomplished at high soar which called expanded exploration in the search space. Once the Aquila finds out prey, it drops with a vertical stoop to grab the prey. This behavior is mathematically as follows:

    $$X_{1} \left( {t + 1} \right) = X_{b} \left( t \right)*\left( {1 - \left( {\frac{t}{T}} \right)} \right) + \left( {X_{M} \left( t \right) - X_{b} \left( t \right)*rand} \right)$$
    (15)

    where, \({X}_{1}\left(t+1\right)\) is the position of the Aquila in the next iteration of t, \({X}_{b}\left(t\right)\) is the best-obtained solution until tth iteration. \(\left(1-\left(\frac{t}{T}\right)\right)\) is used to control the exploration process in search space. \({X}_{M}\left(t\right)\) refers to the mean value of the solutions at the previous iteration which is calculated using Eq. (16).

    $${X}_{M}\left(t\right)=\frac{1}{N}\sum_{i=1}^{N}{X}_{i}\left(t\right) (16)$$
    (16)

    where, N is the number of population size.

  3. 3.

    The second step is that the hunting process is at contour flight with short glide attack which considered the most commonly used by Aquila. Therefore, the Aquila is close to the catched prey which lead to narrow exploration in the search space. This process is modeled as follows:

    $$X_{2} \left( {t + 1} \right) = X_{b} \left( t \right) \times Levy\left( D \right) + X_{R} \left( t \right) + \left( {y - x} \right) \times rand$$
    (17)

    where,\({ X}_{R}\left(t\right)\) is a random solution taken at the ith iteration. \(Levy\left(D\right)\) is the levy flight distribution function for dimension space (D), which is calculated as follows:

    $$Levy\left(D\right)=s\times \frac{u\times \omega }{{\left|\upsilon \right|}^{1/\beta }}$$
    (18)

    where, \(s\) is a constant value equal to 0.01, \(u\), and \(\upsilon\) are random values between 0 and 1. \(\omega\) is a dynamic adaptive coefficient that is calculated as follows:

    $$\omega =\left(\frac{\mathcal{T}\left(1+\beta \right)\times \mathrm{sin}\left(\frac{\pi \beta }{2}\right)}{\mathcal{T}\left(\frac{1+\beta }{2}\right)\times \beta \times {2}^{\left(\frac{\beta -1}{2}\right)}}\right)$$
    (19)

    where, \(\beta\) is a constant value equal to 1.5. The exploration process has a spiral shape, which is controlled by values of \(x\) and \(y\) that can be evaluated as follows:

    $$y=r\times \mathrm{cos}\left(\theta \right)$$
    (20)
    $$x=r\times \mathrm{sin}\left(\theta \right)$$
    (21)
    $$r={r}_{1}+U\times {D}_{1}$$
    (22)
    $$\theta =-W\times {D}_{1}+{\theta }_{1}$$
    (23)
    $${\theta }_{1}=3\times \frac{\pi }{2}$$
    (24)

    where, \({r}_{1}\) is a value between 1 and 20, \(U\) is equal to 0.00565, \({D}_{1}\) is integer numbers from 1 to the dimension of search space, and \(W\) is equal to 0.005.

  4. 4.

    The third step of the expanded exploitation (X3) concerns any flooring preys which have a slow escape. Aquila is flying with low level and once it selects its prey, it grabs progressively on the prey with a slow decent attack. This step is mathematically presented as in the following equation:

    $${X}_{3}\left(t+1\right)=\,\left({X}_{b}\left(t\right)-{X}_{M}\left(t\right)\right)\times \alpha -rand+\left( rand\times \left(up-lp\right)+lp\right)\times \delta$$
    (25)

    where, α and δ are the exploitation adjustment parameters which have range values from 0.1 to 0.9 and fixed at 0.1 according to tests for several benchmarks.

  5. 5.

    The fourth step (X4) is executed through Aquila walks on the land to capture and dealing with the large prey by pulling it which is described as narrowed exploitation step. This step is mathematically modeled as:

    $${X}_{4}\left(t+1\right)=QF\times {X}_{b}\left(t\right)-\left({G}_{1}\times X\left(t\right)\times rand\right)-{G}_{2}\times Levy\left(D\right)+rand\times {G}_{1} (26)$$
    (26)

    where, QF defined as a quality function used to equilibrium the search strategies, which is calculated using Eq. (27). \({G}_{1}\) pertains to miscellaneous motions of the AO which is generated as Eq. (28). \({G}_{2}\) is the flight slope of the AO which has value decreasing from 2 to 0 during the prey elope form first to last position and describe using Eq. (29).

    $$QF\left(t\right)={t}^{\frac{2\times rand()-1}{{(1-T)}^{2}}}$$
    (27)
    $${G}_{1}=2\times rand()-1$$
    (28)
    $${G}_{2}=2\times \left(1-\frac{t}{T}\right)$$

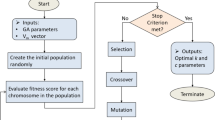
The considered optimization problem for weibull parameters estimation is solved by the AO optimizer as shown in the following flowchart of Fig. 1. The main drawback of AO implies that it has several parameters and constants which affect the final results, the convergence characteristics and make difficult to improve it.

Fig. 1
figure 1

Flowchart of the AO for optimal estimation of Weibull parameters

Full size image

2.2.2 Bald Eagle Search (BES) Algorithm

Bald eagle search (BES) algorithm is a novel meta-heuristic optimization algorithm developed in 2020 [33]that mimics the hunting process or intelligent behavior of the bald eagle as they search for fish. Hence, the hunting process of the proposed BES is represented in three stages, namely, selecting search space, searching within the selected search space, and swooping.

  1. 1.

    In the first stage, bald eagles select the best area which has mount of preys within the selected search space. This stage is used to select the best area in the search space and represented as follows:

    $${X}_{new1,i}={X}_{best}+{\alpha }_{q}\times rand\times \left({X}_{mean}-{X}_{i}\right) (30)$$
    (30)

where, \({X}_{new,i}\) is the new position of bald eagle, \({X}_{best}\) is the best position that is currently selected by bald eagle in the search space, and αq has a value between 1.5 and 2 that is the factor for controlling the changes in position. rand is a random number that takes a value between 0 and 1. \({X}_{mean}\) refers to the mean value of the previous solutions.

  1. 2.

    In the second stage, the eagle moves inside the best area which selected in the first stage to search for prey. The searching process is executed by moving in different directions within a spiral shape to accelerate their search. The new position for the hunting of prey is represented as follows:

    $${X}_{new2,i}={X}_{i}+y\left(i\right)\times \left({X}_{i}-{X}_{i+1}\right)+x\left(i\right)\times \left({X}_{i}-{X}_{mean}\right)$$
    (31)
    $$x\left(i\right)=\frac{xr(i)}{\mathrm{max}(\left|xr\right|)} , y\left(i\right)=\frac{yr(i)}{\mathrm{max}(\left|yr\right|)}$$
    (32)
    $$xr\left(i\right)=r\left(i\right)\times \mathrm{sin}\left(\theta \left(i\right)\right), yr\left(i\right)=r\left(i\right)\times \mathrm{cos}\left(\theta \left(i\right)\right)$$
    (33)
    $$\theta \left(i\right)=a\times \pi \times rand , r\left(i\right)=\theta \left(i\right)+R\times rand$$
    (34)

    where, \(a\) is a coefficient with value between 5 and 10 that takes for determining the corner between point search in the central point, and \(R\) is a coefficient that takes a value between 0.5 and 2. The movement of the bald eagle has a spiral shape which is mathematically represented by a polar plot probability (32, 33, and 34). Therefore, the BES algorithm can discover new spaces and increase diversification of positions. Moreover, the shape of spiral movement is changed by the parameters \(a\) and \(R\).

  1. 3.

    After the bald eagles determine their target prey, they will swing from the best position in the search space towards the best point. This stage is called swooping stage and represented mathematically as follows:

    $${X}_{new3,i}=\,rand\times {X}_{best}+{x1}_{i}\times \left({X}_{i}-c1\times {X}_{mean}\right) +{y1}_{i}\times \left({X}_{i}-c2\times {X}_{best}\right) (35)$$
    (35)
    $$x1\left(i\right)=\frac{xr(i)}{\mathrm{max}(\left|xr\right|)}, y1\left(i\right)=\frac{yr(i)}{\mathrm{max}(\left|yr\right|)} (36)$$
    (36)
    $$xr\left(i\right)=r\left(i\right)\times \mathrm{sin}h\left(\theta \left(i\right)\right)$$
    (37)
    $$yr\left(i\right)=r\left(i\right)\times \mathrm{cosh}\left(\theta \left(i\right)\right) (38)$$
    (38)
    $$\theta \left(i\right)=a\times \pi \times rand , and r\left(i\right)=\theta \left(i\right)$$
    (39)

    where, \(c1\) and \(c2\) have a value of [1, 2] which increase the movement intensity of bald eagles towards the best and center points. Each stage is dependent on two crucial characteristics in obtaining optimal solution and search around an optimal position which are intensification and diversification.

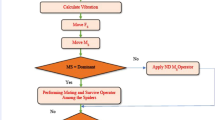
According to the above, the population of solutions has passed through three stages in which the best solution is updated three times at each iteration to reach the best solution. For a fair comparison of the BES and other optimization algorithms, the parameter of population size for BSE must be tuned by divide of three. This is proposed in this study to achieve the quality compareson between the four heuristic methods. Figure 2 shows the flowchart of the BES algorithm, summarizing all steps described previously.

Fig. 2
figure 2

Flowchart of the BES for estimation Weibull parameters

Full size image

3 Measurement the Goodness of Fit

Some statistical error analysis of estimation the Weibull parameters is needed to assess the performance of different estimation methods. Because of evaluation the PDF of wind speed depends on the estimation process accuracy, the most accurate estimation method is adopted based on its good statistical measures [2, 12, 19, 24]. The performance evaluation of the applied methods was compared by the following tests:

3.1 Root Mean Square Error (RMSE)

The accuracy of the wind speed model relative to the actual distribution can be measured by RMSE which is calculated as follows:

$$RMSE={\left[\frac{1}{n}\sum_{i=1}^{n}{({y}_{i}-{x}_{i})}^{2}\right]}^{0.5}$$
(40)

This value is an indication to the deviation of the predicted from actual probability values. Therefore, the method which has smaller value is more accurate.

3.2 Determination Coefficient (R2)

The determination coefficient (R2) is utilizied to measure the variance or the efficiency of the method which is modeled as the following:

$${R}^{2}=1-\frac{\sum_{i=1}^{n}{\left({y}_{i}-{x}_{i}\right)}^{2}}{\sum_{i=1}^{n}{\left({y}_{i}-\overline{y }\right)}^{2}}$$
(41)

3.3 Mean Absolute Error (MAE)

The accuracy of wind speed distribution model relative to the actual distribution can be determined by the mean absolute error which is calculated as follows:

$$\mathrm{MAE}=\frac{1}{n}\sum_{i=1}^{n}\left|{y}_{i}-{x}_{i}\right|$$
(42)

3.4 Wind Production Deviation (WPD)

The deviation between wind energy predicted probability distribution curve and the actual data is used for the wind energy production deviation calculation as following:

$$WPD=\left(\frac{{WPD}_{predicted}-{WPD}_{actual}}{{WPD}_{actual}}\right)\times 100$$
(43)
$${WPD}_{actual}=\frac{1}{2}\times \rho \times {v}^{3}$$
(44)
$${WPD}_{prdicted}=\frac{1}{2}\times \rho \times {c}^{3}\times \mathcal{T}\left(1+\frac{3}{k}\right)$$
(45)

4 Results and Discussion

4.1 Wind Speed Data Analysis

In this study, Zafarana, and Shark El-Ouinatwind farm sites are selected as candidate wind sites. The first site, Zafarana wind farm, is located in Suez Gulf which is approximately 200 KM south east Cairo. While the second site, Shark El-Ouinat, is located in depth southern Egyptian desert. The operational data of wind turbines which are considered in this study for the two sites is illustrated as in Table 1. Added to that, the time series data of the wind speed for the year 2019 in hourly time series based on the Zafarana, and Shark El-Ouinat wind farm sites are taken from web site [34]. The descriptive statistics for this data are given in Table 2.

Table 1 Wind turbine characteristics
Full size table
Table 2 Statistics analysis of wind speed data of sites
Full size table

4.2 Goodness of Fit

In this section, the various statistical tests and analysis are introduced to compare the accuracy of the analytical and heuristic methods that are presented in previous sections. MLM, EM, MM, EPFM as analytical methods and PSO, CSA, AO and BES algorithm as heuristic methods are applied for optimal fitting in estimating the weibull parameters. For the first site, Zafarana wind farm, Table 3 describes their statistical comparisons.

Table 3 Statistical analysis – Zafaranh, year 2019
Full size table

From Table 3, the novel meta-heuristic BES algorithm provides the highest value of R2 of 0.9913611. On the other side, the other heuristic optimizers such as CSA, AO and PSO finds R2 of 0.9913576, 0.9913570 and 0.9910771, respectively. Nevertheless, the analytical methods such as MLM, EMP, MM and EPF finds R2 of 0.990696, 0.98849, 0.972545 and 0.958787, respectively.

Added to that, the BES algorithm provides the least value of RMSE of 0.0065089. On the other side, the other heuristic optimizers such as CSA, AO and PSO finds RMSE of 0.0065105, 0.0065103 and 0.0066151, respectively. Nevertheless, the analytical methods such as MLM, EMP, MM and EPF finds RMSE of 0.006755, 0.007513, 0.011604 and 0.014217, respectively.

Moreover, the BES algorithm provides the least value of MAE of 0.0051592. On the other side, the other heuristic optimizers such as CSA, AO and PSO finds MAE of 0.0051568, 0.0051603 and 0.0051341, respectively. Nevertheless, the analytical methods such as MLM, EMP, MM and EPF finds MAE of 0.005216, 0.005485, 0.007059 and 0.01132, respectively. Also, the novel meta-heuristic BES algorithm shows acceptable value of the WPD test of -0.80716.For the second site, Shark El-Ouinate wind farm, Table 4 describes the statistical comparisons of the MLM, EM, MM, EPFM, PSO, CSA, AO and BES algorithms.

Table 4 Statistical analysis – Shark El-Ouinate, year 2019
Full size table

From Table 4, the novel meta-heuristic BES algorithm provides the highest value of R2 of 0.942593. On the other side, the other heuristic optimizers such as AO, CSA and PSO finds R2 of 0.942592, 0.942585 and 0.941294, respectively. Nevertheless, the analytical methods such as EPF, EMP, MLM and MM finds R2 of 0.896893, 0.892958, 0.888387 and 0.892456, respectively.

Otherwise, the BES algorithm provides the least value of RMSE of 0.010754. On the other side, the other heuristic optimizers such as AO, CSA and PSO finds RMSE of 0.010755, 0.010755 and 0.010875, respectively. Nevertheless, the analytical methods such as EPF, EMP, MLM and MM finds RMSE of 0.014413, 0.014685, 0.014996 and 0.014719, respectively.

Figures 3 and 4 the obtained Weibull PDF based on the MLM, EM, MM, EPFM, PSO, CSA, AO and BES algorithms in comparison to the provided probability function f(v), for hourly time series in the year 2019 for the two studied sites. As shown, the BES algorithm derives the greatest correctness with the most suiable adequacy to estimate the Weibull parameters. These findings concludes that the statistical tests for heuristic methods are better than those obtained by analytical methods. Moreover, it was further observed that the novel meta-heuristic BES algorithm has better perform to estimate the Weibull parameters with minimum square of errors since it provides the highest value.

Fig. 3
figure 3

Weibull distributions– Zafaranh-2019

Full size image
Fig. 4
figure 4

Weibull distributions– Shark El-Ouinate-2019

Full size image

4.3 Statistical Results for PSO, CSA, AO, and BES for Estimating Weibull Parameters

For heuristic optimization algorithms comparison, statistical results of a number of runs are recorded. In ordre to investigate the performance of the optimization algorithms of PSO, CSA [37, 38], AO [39], and BES, they are run for 50 separate runs and the statistical results of best, mean, worst, standard deviation (STD), and standard error (STE) are compared as recoreded in Tables 5 and 6 for Zafaranh and Shark El-Ouinate sites, respectively. The 5000 runs number is executed and fitness values are recorded for each considered algorithm. Also, for For PSO, CSA, and AO methods, the total number of iterations is 100 where as the population size is taken 50. For fair comparison guarantees between them, the total iteration number of BES is 100 whereas the population size is taken as 17.

Table 5 Statistical results of convergence characteristics – Zafaranh, year 2019
Full size table
Table 6 Statistical results of convergence characteristics – Shark El-Ouinate, year 2019
Full size table

From Table 5, the results of statistical tests based on the BES algorithm are always the least indicator compared to PSO, CSA and AO. The BES algorithm achieves the least Worst objective of 0.000635505 whereas PSO, CSA and AO achieves the Worst objectives of 0.022794503, 0.001033556 and 0.000717186, respectively. Added to that, the Mean objective, that is obtained by the BES algorithm, is less than the Best objectives that is attained by the others. Also, the BES algorithm achieves the least standard deviation, and standard error of 4.451E-19 and 6.295E-20, respectively.

Similar findings are obtained, from Table 6, the acquired statistical tests based on the BES algorithm are always the least indicator compared to PSO, CSA and AO. The BES algorithm achieves the least Best, Worst and Mean objective with same value of 0.001735. Besides, the BES algorithm achieves the least standard deviation, and standard error of 4.67E-19 and 6.6E-20, respectively.

Also, Figs. 5 and 6 describes the histogram of the obtained objectives by means of PSO, CSA, AO, and BES algorithms for Zafaranh and Shark El-Ouinate sites, respectively. Because of the fitness value has the small deviation through translation from run to another, the BES algorithm has greater stability and good performance over PSO, CSA, and AO as it is always capable to find the optimal value.

Fig. 5
figure 5

Bar chart of each run for zafaranh site, 2019

Full size image
Fig. 6
figure 6

Bar chart of each run for Shark El-Ouinate site

Full size image

Moreover, the convergence curves of PSO, CSA, AO, and BES algorithms for Zafaranh and Shark El-Ouinate sites, respectively are shown as Figs. 7 and 8. As shown, the error convergence sequence is compared to heuristic optimization algoritms at candidated sites. It can be observed that the BES optimization shows the fastest convergence compared to the others since it give its best solution through less than 40% of the total number of iterations.

Fig. 7
figure 7

Convergence curves of the compared algorithms for Zafaranh site, 2019

Full size image
Fig. 8
figure 8

Convergence curves of the compared algorithms for Shark El-Ouinate site, 2019

Full size image

5 Power Curve Modeling

The wind output power, which is another primary uncertainty source, is considered as a vital issue to make the investment decisions and other issues related to the planning and operation of the power system. Therefore, the wind power forecasted error should be reduced as possible by using efficient models. In addition to wind speed uncertainty, there is uncertainty in wind speed to power conversion. Although the most efficient power curve model may be created, the anticipated inaccuracy from speed to power conversion may persist. Because of the existence of power curve uncertainty, each wind speed does not have a single value of output power, but several values of output power can be produced at the same wind speed [1]. The parameters of forecasting model arenot fixed for the same site because of the nonlinearity and randomness of power curve [3, 35]. Thus, the traditional methods cannot be represented the power uncertainty in perfect manner. Figure 8 depicts the power curve that is produced in terms of the wind speed.

The power curve is divided into four major parts as shown in Fig. 9. The zero output power, which occurs at wind speeds less than the cut-in speed zone, is considered as the first part of the power curve. In the second part, the wind speed is is between cut-in (\({v}_{in}\)), and rated speed(\({v}_{r}\)) while the output power has nonlinear characteristics. The wind turbine output power has a constant value of rated output power for all models when the wind speed value is located between the rated and cut-out speed as shown in the third part. To protect the wind turbine from damage, the wind turbine must be stopped when the wind speed becomes greater than the cut-outspeed (\({v}_{out}\)) [27]. In literature, various models have been used to describe the non-linear relation such as the third degree polynomial curve in [18] as well as fitted polynomial function as [35, 36]. The general form can be represented as the following equation:

$$p\left(v\right)=\left\{\begin{array}{l} {v}_{r}\le v\le {v}_{co}\\ {p}_{r}*g\left(v\right){ v}_{ci}\le v\le {v }_{r } \\ 0 otherwise\end{array}\right.$$
(45)

where, g(v) represents the relation between the wind speed and the wind turbine output power that can be formed in several modeled as follows [26, 27]:

$${g}_{1}\left(v\right)=\left(\frac{v-{v}_{1}}{{v}_{r}-{v}_{1}}\right)$$
(46)
$${g}_{2}\left(v\right)= {\left(\frac{v-{v}_{1}}{{v}_{r}-{v}_{1}}\right)}^{2}$$
(47)
$${g}_{3}\left(v\right)= \frac{{v}^{2}-{v}_{1}^{2}}{{v}_{r}^{2}-{v}_{1}^{2}}$$
(48)
$${g}_{4}\left(v\right)= \frac{{v}^{3}-{v}_{1}^{3}}{{v}_{r}^{3}-{v}_{1}^{3}}$$
(49)
$${g}_{5}\left(v\right)= {\left(\frac{v}{{v}_{r}}\right)}^{3}$$
(50)
$${g}_{6}\left(v\right)={\left(\frac{v-{v}_{1}}{{v}_{r}-{v}_{1}}\right)}^{3}$$
(51)
$${g}_{7}\left(v\right)=\left({a}_{1}{v}^{2}+{a}_{2}v+{a}_{3}\right)$$
(52)
$${g}_{8}\left(v\right)=\left({{a}_{1}{v}^{3}+a}_{2}{v}^{2}+{a}_{3}v+{a}_{4}\right) (52)$$
(53)
$${g}_{9}\left(v\right)=\left({{{a}_{1}{v}^{4}+a}_{2}{v}^{3}+a}_{3}{v}^{2}+{a}_{4}v+{a}_{5}\right)$$
(54)

where,\({ a}_{1}\),\({a}_{2}\),\({a}_{3}\),\({a}_{4}\), and \({a}_{5}\) are polynominal coefficients calculated in MATLAB by polyfit function. The previous comparison between analytical and heuristic methods for estimation of the Weibull distribution parameters pertain to, the proposed BES method provides the best fit of wind speed distribution of the two sites. Therefore, the histogram of wind speed data is created and actual distribution is calculated at each speed ( \({f}_{actual}\left({v}_{i}\right)\)). Then, the shape and scale factors obtained by BES are utilized to calculate weibull distribution density (\({f}_{fitted}\left({v}_{i}\right)\)) and then the detailed models (g1-g9) is considered to find the best model for each site. In order to compare the performance of these nine models in estimating the energy from a wind turbine, the error (\(\upvarepsilon\))between the actual energy density (\({E}_{actual}\)) and estimated energy (\({E}_{fitted}\)) is calculated by the following expression [18]:

Fig. 9
figure 9

Typical wind turbine power curve

Full size image
$${E}_{actual}=\frac{1}{A}\sum_{i=1}^{N}{f}_{actual}\left({v}_{i}\right){p}_{m},i\left({v}_{i}\right) (54)$$
(55)
$${E}_{fitted}=\frac{1}{A}\sum_{i=1}^{N}{f}_{fitted}\left({v}_{i}\right){p}_{m,i}\left({v}_{i}\right)$$
(56)
$$\upvarepsilon = \frac{E_{fitted }- E_{actual} }{E_{actual} }*100$$
(57)

The distributions of energy density error for the nine models are calculated and shown in Figs. 10 and 11 for Zafaranh and Shark El-Ouinate site, respectively. From Fig. 10, Zafaranh site,, the second model (g2) provides the minimum error of energy density with 5.728%. After that, the fourth (g4) and seventh (g7) model is resulting with error of energy density of 6.005 and 6.167%, respectively. On the other side, all the models illustrates close error where no great divergence in the results as the worst model gives error of energy density of 6.593%. From Fig. 11, at Shark El-Ouinate site, the eighth model (g8), the cubic form, provides the minimum error of energy density with 13.2%. After that, the nineth (g4) and seventh (g7) model is coming with error of energy density of 13.6 and 16.6%, respectively.

Fig. 10
figure 10

Energy density error of the nine models for Zafaranh site

Full size image
Fig. 11
figure 11

Energy density error of the nine models for Shark El-Ouinate site

Full size image

A computational complexity analysis for metaheuristic algorithms can be carried out using the "Big O notation," an established mathematical shorthand in the computer fields. For comparative purposes, the methods' processing times and memory usage were discovered here. For each case study, the computational complexity and typical execution time are shown in Table 7. As can be seen, because there are two dimensional control variables for determining the form and scaling factors, the computational complexity of the issue of approximating the Weibull parameters reaches O(10,000). The BES also displays a marginally longer run time than the PSO, CSA, and AO algorithms.

Table 7 Run time and computational complexity of proposed BES for estimating Weibull Parameters
Full size table

6 Conclusion

The optimal parameter estimation of the Weibull distribution parameters is the crucial step of analyzing the wind speed profile for Zafaranh and Shark El-Ouinate sites, Egypt. In this study, four analytical methods of MLM, MM, EM, and EPFM, and other heuristic methods of PSO, CSA, AO, and BES algorithms are developed. Several fitness metrics are evaluated for comparative asssessment between the competitive methods. The novel meta-heuristic BES algorithm shows the best performance in acquiring the highest value of R2, the least value of RMSE and the least value of MAE. Also, the Mean objective obtained by the BES algorithm is better than the others. Further, the BES algorithm is the most robust technique as it achieves the least standard deviation, and standard error compared to the others. Otherwise, the BES algorithm demenstartes the greatest stability characteristics as its histogram of the obtained objectives is greatly better than PSO, CSA and AO algorithms. Moreover, the BES algorithms presents the fastest convergence compared to the others since it give its best solution through less than 40% of the total number of iterations. Furthermore, wind power curve models are analyzed to deduce the nonlinear relationship between the wind output power and the regarding speed where the error of wind energy density between actual and estimated is greatly minimized using more effective model for each wind site. A suggestion for future work is that the cost of a kWh generated from the wind farm having could be established based on different wind power models for each wind site.