On quantum ensembles of quantum classifiers

Abstract

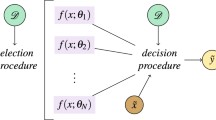
Quantum machine learning seeks to exploit the underlying nature of a quantum computer to enhance machine learning techniques. A particular framework uses the quantum property of superposition to store sets of parameters, thereby creating an ensemble of quantum classifiers that may be computed in parallel. The idea stems from classical ensemble methods where one attempts to build a stronger model by averaging the results from many different models. In this work, we demonstrate that a specific implementation of the quantum ensemble of quantum classifiers, called the accuracy-weighted quantum ensemble, can be fully dequantised. On the other hand, the general quantum ensemble framework is shown to contain the well-known Deutsch-Jozsa algorithm that notably provides a quantum speedup and creates the potential for a useful quantum ensemble to harness this computational advantage.

Appendices

Appendix 1: Analysis of the accuracy-weighted q-ensemble

Using the dequantised accuracy-weighted q-ensemble, we may study the behaviour of the algorithm. A problem occurs if it becomes difficult to select models with an accuracy greater than 0.5 for the ensemble. In particular, if models tend to an accuracy of 0.5 and the variance of these accuracies vanishes exponentially fast, both classical and quantum versions of the accuracy-weighted q-ensemble become intractable: exponentially more precision will be required to calculate the accuracies for the classical rejection criteria and the probabilities of the label in the quantum setting. Postselection is done on the |0〉-branch of the accuracy qubit in superposition $|{A_{\theta }}\rangle = \sqrt {a_{\theta }}|{0}\rangle +\sqrt {1-a_{\theta }}|{1}\rangle$. Looking at the probabilities, $p(\tilde {y}=-1) = {\sum }_{\theta \in \mathcal {E}^{+}} \frac {a_{\theta }}{E_{\mathcal {X}}}$ and $p(\tilde {y}=1) = {\sum }_{\theta \in \mathcal {E}^{-}} \frac {a_{\theta }}{E_{\mathcal {X}}}$, if a_𝜃 → 0.5 ∀ 𝜃 as $d \to \infty$ with increasing certainty, one requires increasingly more resources to obtain the necessary precision to compute the probabilities of the label. The resources needed are directly dependent on the rate of convergence of models’ accuracies to 0.5 and ultimately determine the feasibility of this strategy. In this analysis, we examine this rate of convergence with linear, perceptron and neural network models under specific data assumptions.

Data and model assumptions

We explicitly define the accuracy of a model with a parameter set 𝜃 as

$$ a_{\theta} = \frac{1}{M} \sum\limits_{m=1}^{M} \frac{1}{2}|f(x_{m};\theta) + f^{*}(x_{m};\theta^{*})|, $$

(7)

where f is a base model, f^∗ is a specified “ground truth” model with parameters 𝜃^∗ and a_𝜃 may be interpreted as the proportion of correct classifications of M data points in a dataset $\mathcal {D}$ containing d features. We can also define the average ensemble accuracy of n sampled models for a fixed dimension (i.e. a fixed number of features) d as $A_{\theta |d} = \frac {1}{n} {\sum }_{i=1}^{n} a_{\theta _{i}}$. To examine the behaviour of model accuracy, we consider base models with simple data to provide an indication as to whether the accuracy-weighted strategy is indeed viable. The entries of the input vectors x_m are drawn from a standard normal distribution and ℓ₂ normalised. Again, for simplicity, the labels are assigned based on the first entry of each input vector. If the first entry of the m th input vector denoted by $x_{m}^{(1)}$ is positive, f^∗(x_m; 𝜃^∗) = 1, else f^∗(x_m; 𝜃^∗) = − 1.

Model parameters 𝜃 contain entries drawn from a random uniform distribution over the interval [ − 1, 1] to create the respective ensembles. This follows directly from the accuracy-weighted q-ensemble routine in Schuld and Petruccione (2018) which assumes 𝜃 ∈ [a,b ] and initially encodes the parameter sets into a uniform superposition of computational basis states. Simulations are done with M = 10000 input vectors and labels, along with n = 100 parameter sets.

Accuracy in higher dimensions

Figure 1 plots A_𝜃|d for d ≤ 1000 using linear models and Fig. 3 contains the same plot for single-layer perceptron models and neural networks with three hidden layers. These models all satisfy the point symmetric property assumed in the original accuracy-weighted q-ensemble and are commonly deployed in machine learning. For simulations in low dimensions (d < 10), the distribution of A_𝜃|d has a relatively high dispersion around the mean value of 0.5 with all base models. This is desirable as it allows for models with accuracy a_𝜃 > 0.5 to be easily accepted into the ensemble. As the dimension increases, however, the dispersion rapidly decreases and all models tend to an accuracy of 0.5 with less deviation, making it increasingly difficult to build a strong ensemble. The sharp decline in standard deviation is plotted on a log scale for linear models in Figs. 2 and 4 for the perceptron and neural network models. This occurrence is due to the sampling method for the parameter vectors and the ℓ₂ normalisation of data which leads to “the curse of dimensionality” and “concentration of measure” phenomena discussed in Bellman (1966), Klartag (2010), and Beyer et al. (1999). Put briefly, most models become random guessers as the dimension increases.

Fig. 1

This plot contains the average accuracy of sampled parameter sets for linear models over increasing dimensions d. As d increases, it becomes more noticeable that models in the ensemble have accuracies close to 0.5 with declining dispersion represented by one standard deviation above and below the mean in yellow shading

Fig. 2

Declining standard deviation of average accuracies for linear models plotted on a log scale per dimension

Since A_𝜃|d is an average of the sum of random variables a_𝜃, by the central limit theorem, A_𝜃|d tends to a normal distribution as more random variables are added. The mean and standard deviation of this distribution depend on a_𝜃 which depends on the dimension of the data. We show in Appendix ?? that the mean of a_𝜃 is equal to 0.5 and the standard deviation tends to 0 as d increases to infinity for perceptron and linear models. Numerical simulations suggest the same behaviour for three-layer neural networks as seen in Fig. 3. The crucial issue is the rate of convergence of a_𝜃 (and hence A_𝜃|d) to 0.5 which depends on the statistical properties of the input data. For i.i.d data drawn from a standard normal distribution as done so here, by the Berry-Esseen theorem, the rate of convergence is $\mathcal {O}(d^{-\frac {1}{2}})$ (Friedrich et al. 1989; van Zwet 1984). For more realistic data, the convergence rate may differ. When data is represented as matrices, an expository survey of rates of convergence and asymptotic expansions in the context of the multi-dimensional central limit theorem may be found in Bhattacharya (1977). In short, the rates of convergence vary and are generally calculated (or estimated) on a case by case basis unless specific assumptions around the input data may be made. For the simple models deployed in this analysis, overall the results indicate convergence rates that are polynomial in d, and hence, the accuracy-weighted q-ensemble remains tractable (Fig. 4). This, however, does not say anything about whether the accuracy-weighted q-ensemble (even if computationally tractable) is a useful method. As such, we continue with the same data assumptions, making use of the known tractability, and build the accuracy-weighted ensemble for a high-dimensional dataset.

Fig. 3

The average accuracy of sampled parameter sets for ensembles over increasing dimensions d is depicted. Ensembles containing perceptron models are displayed in the top graph and neural networks with three hidden layers are contained in the bottom graph. The dispersion of model accuracies is represented by one standard deviation above and below the mean accuracies in the shaded orange and pink areas for perceptrons and neural networks respectively

Fig. 4

Declining standard deviation of average accuracies per dimension d is plotted on a log scale for perceptron models in the top graph (in orange) and neural networks with three hidden layers in the bottom graph (in pink)

Poor performance of the accuracy-weighted ensemble on simple high-dimensional data

Using the perceptron as a base model, numerical simulations of the standard deviation of accuracies indicate that the rate of convergence is faster than the Berry-Esseen asymptotic convergence for $d \leqslant 10000$ as plotted in Fig. 5. The standard deviation appears to level off for d ≥ 8000 and the rate of decay is notably not exponential. Thus, one may build an ensemble of weak classifiers in higher dimensions.

Fig. 5

This plot contains the standard deviation of average accuracies of perceptron models in orange plotted on a log scale per dimension. The black line is the Berry-Essen asymptotic convergence

We construct the ensemble for d = 8000 to determine its empirical success using M = 10,000 training data points. With n = 30,000 sampled models, 14,903 models achieved an accuracy greater than 0.5. These models were then selected for the ensemble and tested on 2000 test samples. The overall test accuracy was found to be 0.50167. Using n = 100,000 sampled models did not appear to improve the result as 49,580 models passed the selection criteria and provided a test accuracy of 0.50165. It is interesting that even with non-exponential convergence of the standard deviation to zero, the accuracy-weighted ensemble strategy reveals poor performance on a simple dataset that should be easy to classify. On the other hand, this does not imply that the accuracy-weighted method will perform poorly for all high-dimensional datasets. If, for example, data actually follows a mixture of distributions where classes are composed of natural clusters that each follow their own distribution, the curse of dimensionality may no longer be an issue (Beyer et al. 1999; Zimek et al. 2012; Shaft and Ramakrishnan 2006).

Appendix 2: Modelling the behaviour of the perceptron ensemble in higher dimensions

The perceptron model may be written as follows

$$ f(\mathbf{X,\theta}) = \sigma(\mathbf{X\theta}), $$

(8)

where σ is a thresholding function ensuring the prediction is 1 if the output is positive and − 1 otherwise. X is a M × d matrix where each row represents one data point and 𝜃 is a d × 1 column vector. The ground truth model in this example may be formulated with 𝜃^∗ = [1, 0,..., 0 ]^T for simplicity, although this may be any uniformly sampled 𝜃. One may now rewrite the accuracy of a model from Eq. (7) in terms of expectation values

$$ \mathrm{E}~ [a_{\theta}] = \frac{1}{M} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{d} \frac{1}{2} |\sigma(X_{ij}\theta_{j}) + \sigma(X_{ij}\theta_{j}^{*})|. $$

Since $X_{ij} \sim N(0,1)$ and $\theta _{j} \sim U\ [-1,1\ ]$, σ(X_ij𝜃_j) = ± 1 with equal probability, and similarly for σ(X_ij𝜃^∗). Looking at all possible outcomes presented in Table 1, the distribution of accuracy is 1 and 0 with approximately equal occurrence. As $d \to \infty$, by the law of large numbers, the distribution of accuracy contains an equal number of 0’s and 1’s with more certainty. Taking the expectation of this gives exactly 0.5 as confirmed by the simulated results

$$ \begin{array}{@{}rcl@{}} \lim_{d\to\infty} \mathrm{E}\ [a_{\theta} \ ] &= &\frac{1}{M} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{d} \frac{1}{2} |\sigma(X_{ij}\theta_{j}) + \sigma(X_{ij}\theta_{j}^{*})| \end{array} $$

(9)

$$ \begin{array}{@{}rcl@{}} &=& \frac{1}{M} \sum\limits_{i=1}^{M} \frac{1}{2} = \frac{1}{2}. \end{array} $$

(10)

Table 1 Truth table for the expected outcomes of the perceptron model

Using a similar logic, the variance of the accuracy of the perceptron model may be formulated as follows

$$ \begin{array}{@{}rcl@{}} \text{Var}\ [a_{\theta}\ ] &= \mathrm{E}\ [a_{\theta}^{2} \ ] - \mathrm{E}\ [a_{\theta} \ ]^{2}. \end{array} $$

(11)

The thresholding function applies to all f(X,𝜃) and so we leave it out of the notation for brevity but its effect is still present. The expectation of the squared accuracy is

$$ \begin{array}{lll} \mathrm{E}~ [a_{\theta}^{2}] = \frac{1}{M} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{d} \left (\frac{1}{2} |X_{ij}\theta_{j} + X_{ij}\theta_{j}^{*}|\right )^{2}, \\ = \frac{1}{M} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{d} (\frac{1}{4}X_{ij}\theta_{j}X_{ij}\theta_{j} + \frac{1}{4}X_{ij}\theta_{j}^{*}X_{ij}\theta_{j}^{*} \\ + \frac{2}{4}X_{ij}\theta_{j}X_{ij}\theta_{j}^{*}). \end{array} $$

Taking the expectation of each of the terms, it is clear that the first and last terms equal 0 as d increases to infinity since X_ij and 𝜃_j are independent with mean values of 0. The middle term may be further simplified using the fact that 𝜃^∗ = [1, 0,..., 0 ]^T

$$ \begin{array}{@{}rcl@{}} \lim\limits_{d \to \infty} \mathrm{E}\ [a_{\theta}^{2} \ ] &= \frac{1}{M} \sum\limits_{i=1}^{M} \sum\limits_{j=1}^{d} \frac{1}{4}X_{ij}\theta_{j}^{*}X_{ij}\theta_{j}^{*}, \\ &= \frac{1}{M} \sum\limits_{i=1}^{M} \frac{1}{4}X_{i1}^{2}, \\ &= \frac{1}{M} \sum\limits_{i=1}^{M} \frac{1}{4}(1), \\ &= \frac{1}{4}. \end{array} $$

Using this along with the result from Eq. (10), the variance from Eq. (11) becomes

$$ \begin{array}{@{}rcl@{}} \lim_{d \to \infty}\text{Var}\ [a_{\theta}\ ] &= \mathrm{E}\ [a_{\theta}^{2} \ ] - \mathrm{E}\ [a_{\theta} \ ]^{2}, \\ &= \frac{1}{4} - \left( \frac{1}{2}\right)^{2}, \\ &= 0, \end{array} $$

which holds for any uniformly sampled ground truth model.