1 Introduction

Annular flow situation comes across many applications such as oil well drilling, food processing, pipeline engineering, pulp and paper industries, mining industries, slurry transport processes etc. For example, in oil well drilling process, the drilling fluid flow takes place through the annulus formed between borehole and drill pipe. The transportation of rock cuttings generated during drilling, to the surface, drill bit lubrication and cooling requirements being related directly to the hydraulics of drilling fluid, behooves the flow to be turbulent [13]. Amanna and Movaghar [1] have studied the cutting transport behaviour for the directional drilling cases. Epelle and Gerogioris [7, 8] have simulated the cutting transport in the annular bends and complex shapes. This results in the emphasis that the cost of drilling operations may run into billion dollars of capital investments. Hence the prime investment of the drilling companies is in the research of the flow behaviour and properties of drilling fluids. The most difficult problem faced by the researchers is the calculation related to the prediction of the flow field within the drill pipe-wellbore annulus. In horizontal drilling operation, the drill pipe tends to sag leading to the annulus eccentricity. During drilling operation sometimes, the inner pipe is given some axial movement to avoid the bed formation & clogging.

Stability of the flow depends on many factor like fluid properties (primarily Rheology), geometry of the flow, flow boundary conditions, presence of the particles suspended, as physical property of the particle, properties of the carrier fluid, shape and size of the particle, temperature behavior of the carrier fluid, degree of solubility etc. Till date, many research (experimental, theoretical and computational) have been carried out for Newtonian fluid in the annulus emphasizing the need of the flow turbulence to enhance cuttings transport in drilling problems, Dewangan and Sinha [2]. Various authors have worked on different drilling problems and their effects on cuttings transport. Founargiotakis et al. [9] have analyzed the transition instability in the concentric annulus with view of bringing turbulence in the drilling fluid flow domain. Along this line of thought, the Energy gradient method (EGM) has been implemented for the study of flow instability. According to concept of this method, the transition takes place from laminar to turbulent at a particular value of K. Thus, different analytical expressions have been derived for the K considering the different geometrical parameters and boundary condition. The obtained value of K is then validated with the previous work of Dou [4]. The various results are obtained for the parameter K for varied radius ratio, pipe velocity and eccentricity.

2 Energy gradient method (EGM)

Dou [3, 4] outlaid and explained thoroughly the EGM in order to elucidate the phenomenon of transition for various flow boundary conditions considering wall-bounded shear stress. The basic idea of this method is that it treats the complete flow field as an energy field. Afterward, the energy gradient (EG) in the main flow direction as well as in the transverse flow direction is calculated. The EG in the transverse direction is primarily accountable for amplifying the velocity disturbances. On the other hand, the viscous friction loss basically represented by the EG in the main flow direction is accounted for resisting, damping and absorbing the initial disturbances in the stream wise direction. Hence, Dou [3, 6] considered that the transition of flow will depend on the relative values of these two types i.e., the amplification of EG and damping of the initial disturbances due to viscous friction present in the flow.

The comparative value of the gradient of total mechanical energy (TME) in the flow along the transverse direction to the main flow and the loss of the TME from viscous friction along the stream wise direction of the main flow primarily dominate the phenomena of flow instability. The magnitude of their relative values is the basis for calculating the instability for given disturbances. This relative magnitude has been presented as a new dimensionless parameter K which is defined to characterize the stability of the base flow for the case when there is no work input. K is the ratio of EG along the transverse direction to the gradient of energy dissipation along the stream wise direction.

$$K = \frac{\delta E/\delta n}{{\delta H/\delta s}}$$
(1)

where \(\delta E/\delta n\) and \(\delta H/\delta s\) are the EG along transverse direction and the EG along stream wise direction, respectively.

Here,

$$E = p + \frac{1}{2} \rho V^{ 2} + \rho gy$$
(2)

In the Eq. (2), E represents the TME available in the flow for incompressible flows with y-axis is taken as the coordinate against the gravitational field, H represents the TME loss for the fluid caused due to viscous dissipation along the stream-wise, n represents the direction normal to the stream-wise direction, s represents the stream-wise direction (i.e. axial z-direction of the flow), ρ, g, V and p represent the fluid density, the gravitational acceleration, local value of flow velocity and the hydrodynamic pressure, respectively.

After due analysis, the dimensionless parameters K is derived, and its variant is plotted in the flow domain for various parameters considered. It has been suggested that the transition in the flow appears to begin at the location of Kmax for the specified value of disturbances. This location is the most dangerous position within the domain as for as flow transition possibilities are concerned for a given set of the flow conditions and disturbances. The obtained value of Kmax is very significant in cuttings transport as the turbulent flow regime is needed for the effective cuttings transport. Eventually one can say, by following the conclusion of the EGM that, for given disturbances, the initiation & propagation of disturbances leading to the flow instability depends on the magnitude of this dimensionless parameter K. Hence the critical condition is evaluated by the maximum or peak value of the parameter K in the flow. For a given flow, the value of K can also be related to the Reynolds no. The larger the Kmax value, larger will be the ability of the disturbances to be amplified and so is true for vice-versa.

3 Derivation for dimensionless parameter K for Newtonian flow through eccentric annulus with constant velocity axial motion of the inner pipe

3.1 Conditions at the annulus boundaries

  • For the annulus inner wall, r = Ri = kR, vz = V and N = 0

  • For the annulus outer wall, r = Ro = R, vz = 0 and N = 0

  • \(k = {R}_{i}/{R}_{o}\)  = Annulus domain radius ratio

  • \(V =\) velocity given to inner pipe

  • \(dp/dz =\) pressure gradient in the z-direction

  • R = Ro

  • \(r =\) distance from the inner pipe

  • e = eccentricity of annulus

  • N = revolution speed of inner pipe

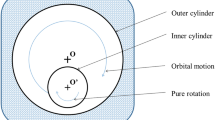
Flow velocity distribution for the considered case (as depicted in the Fig. 1 taking cylindrical coordinates has been derived by simplifying the Navier–Stokes equation as follows:

Fig. 1
figure 1

Flow domain schematic for the parallel flow within concentric annular space

Full size image

Navier–Stokes equation:

$$0 = \frac{ - dp}{{dz}} + \frac{\mu }{r}\frac{d}{dr}\left( {r\frac{{dv_{z} }}{dr}} \right)$$
(3)

After integrating we get;

$$v_{z} = \frac{1}{4\mu }\frac{dp}{{dz}}r^{2} + C_{1} \ln \left( r \right) + C_{2}$$
(4)

here \(C_{1}\) and \(C_{2}\) are integrating constant of integration. Using the boundary conditions, we may find the integrating constant \(C_{1}\) and \(C_{2}\).

$$C_{1} = \frac{V}{{{\text{ln}}\left( k \right)}} - \frac{1}{4\mu }\frac{dp}{{dz}}\frac{{R^{2} \left( {k^{2} - 1} \right)}}{{{\text{ln}}\left( k \right)}}$$
$$C_{2} = - C_{1} \ln \left( R \right) - \frac{1}{4\mu }\frac{dp}{{dz}}R^{2}$$

After substituting the value of \(C_{1}\) and \(C_{2}\) in Eq. (4) and simplifying we finally get:

$$v_{z} = \frac{ - 1}{{4\mu }}\frac{dp}{{dz}}R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + \frac{{1 - k^{2} }}{{\ln \left( \frac{1}{k} \right)}}\ln \left( \frac{r}{R} \right)} \right) + \frac{V}{ln\left( k \right)}ln\left( \frac{r}{R} \right)$$
(5)

This expression for the flow velocity distribution within the concentric annular space is to be corrected, using the correction factor i.e. pressure loss correction coefficient \(C_{i}\) for any specified value axial pressure gradient, for making it relevant in analyzing the eccentric annulus flow situations.

By utilizing the correlation proposed by the various investigators as Haciislamoglu and Langlinais [12] as well as Haciislamoglu and Cartalos [11], the coefficient \(C_{i}\) in terms of the eccentric flow parameters such as e, k as well as n, has been derived (for the power law based fluid) as follows;

$$C_{i} = 1.0 - 0.072\left( \frac{e}{n} \right)\left( {k_{1}^{0.8454} } \right) - 1.5\left( {e^{2} \surd n} \right)(k_{1} )^{0.1852} + 0.96\left( {e^{3} } \right)\surd n (k_{1} )^{0.2527}$$
(6)

Here ‘n’ is the flow behavior index. For the eccentric annulus laminar flow, \(C_{i}\) may be defined mathematically as;

$$C_{i } = \frac{{\left( {\Delta p/\Delta L} \right)_{ecc} }}{{\left( {\Delta p/\Delta L} \right)_{con} }}$$
(7)

where (Δp/ΔL)ecc and (Δp/ΔL)con are taken as the pressure loss for the eccentric annulus and concentric annulus, respectively. This can be incorporated in the predictions of the concentric annulus to convert it into predictions of the eccentric flow. By using this consideration in the present analysis, the expressive relationships evolved for the axial velocity variation for the eccentric annular space i.e. \(v_{z - e}\) taken on the form (based on the Eq. 5) as follows:

$$v_{z - e} = \frac{ - 1}{{4\mu }}\left( {\frac{dp}{{dz}}} \right)_{ecc} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + \frac{{1 - k^{2} }}{{\ln \left( \frac{1}{k} \right)}}\ln \left( \frac{r}{R} \right)} \right) + \frac{V}{{{\text{ln}}\left( k \right)}}{\text{ln}}\left( \frac{r}{R} \right)$$
(8)

or

$$v_{z - e} = \frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + \frac{{1 - k^{2} }}{{\ln \left( \frac{1}{k} \right)}}\ln \left( \frac{r}{R} \right)} \right) + \frac{V}{{{\text{ln}}\left( k \right)}}\ln \left( \frac{r}{R} \right)$$
(9)

Here Ci is obtained using Eq. (6), by placing n = 1 for the Newtonian fluid.

White [10] recommends that since the fluid has bulging tendency on the wider side of annulus while flowing through annulus, the flow velocity tends to get modified than that for the concentric annular space and can be related as follows,

$$\frac{{v_{z - ecc} }}{{v_{z - e} }} = 1 + 1.5\left( {\frac{e}{Ro - Ri}} \right)^{2}$$
(10)

Hence, by incorporating this idea, the final z-velocity distribution for the flow through eccentric annulus space, due to its eccentricity, may be modified as:

$$v_{z - ecc} = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + \frac{{1 - k^{2} }}{{\ln \left( \frac{1}{k} \right)}}\ln \left( \frac{r}{R} \right)} \right) + \frac{V}{{{\text{ln}}\left( k \right)}}\ln \left( \frac{r}{R} \right)} \right]$$
$$v_{z - ecc} = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + b \ln \left( \frac{r}{R} \right)} \right) + \frac{V}{{{\text{ln}}\left( k \right)}}\ln \left( \frac{r}{R} \right)} \right]$$
(11)

In the above Eq. (11) the \({v}_{z-e}\) and the \({v}_{z-ecc}\) both are z-velocity variation. Out of these two, the former one is velocity distribution by considering only the pressure loss correction coefficient, whereas the latter one is by considering the effect of bulging affected by the eccentricity of the flow geometry, respectively.

Further by the mathematical treatment on the axial velocity distribution we get:

$$\frac{{\partial v_{z - ecc} }}{\partial r} = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right) + \frac{V}{\ln \left( k \right)}\frac{1}{r}} \right]$$
(12)

where \(b = \frac{{1 - k^{2} }}{{ln\left( \frac{1}{k} \right)}}\)

$$\frac{{\partial^{2} v_{z - ecc} }}{{\partial r^{2} }} = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2}{{R^{2} }} - \frac{b}{{r^{2} }}} \right) - \frac{V}{\ln \left( k \right)}\frac{1}{{r^{2} }}} \right]$$
(13)

As we know that the stability parameter K, from the Dou et al. [6], is given as:

$$K = \frac{dE/dn}{{dH/ds}} = \frac{\partial E/\partial r}{{dH/dz}} = \frac{{\left[ {\rho v_{z - ecc} \frac{{dv_{z - ecc} }}{dr}} \right]}}{{\mu \left[ {\frac{1}{r}\frac{{dv_{z - ecc} }}{dr} + \frac{{d^{2} v_{z - ecc} }}{{dr^{2} }}} \right]}} = \frac{NUM}{{DEN}}$$
(14)

By proper substitutions we get;

$$\begin{aligned} NUM & = \rho \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]^{2} \left\{ {\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} } \right) + b\ln \left( \frac{r}{R} \right) + \frac{V}{\ln (k)}\ln \left( \frac{r}{R} \right)} \right]} \right. \\ & \quad *\left. {\left\{ {\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right) + \frac{V}{\ln (k)}\left( \frac{1}{r} \right)} \right]} \right.} \right\} \\ \end{aligned}$$
$$\begin{aligned} DEN & = \mu \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]*\left\{ {\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2}{{R^{2} }} + \frac{b}{{r^{2} }}} \right) + \frac{V}{\ln \left( k \right)}\frac{1}{{r^{2} }}} \right]} \right. \\ & \quad + \left. {\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2}{{R^{2} }} - \frac{b}{{r^{2} }}} \right) - \frac{V}{\ln \left( k \right)}\frac{1}{{r^{2} }}} \right]} \right\} \\ \end{aligned}$$

This may be rearranged as;

$$DEN = \mu \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]* \left\{ {\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 4}{{R^{2} }}} \right)} \right]} \right\}$$
$$DEN = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]*\left[ {C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} } \right]$$

Clubbing them in Eq. 14, we get,

$$\begin{aligned} K & = \frac{{\rho \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]^{2} }}{{\left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]*\left[ {C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} } \right]}} \\ & \quad \left[ {\left( {\left( {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} } \right) \left( { 1 - \left( \frac{r}{R} \right.} \right)^{2} + b\ln \left( \frac{r}{R} \right) - \frac{2r}{{R^{2} }} + \left. \frac{b}{r} \right)} \right)} \right. \\ & \quad + \left( {\frac{ - 1}{{4\mu }}} \right.C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + b \ln \left( \frac{r}{R} \right)} \right)\left( {\frac{V}{\ln \left( k \right)}\left. \frac{1}{r} \right)} \right) \\ & \quad \left. { + \left( {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)\frac{V}{\ln \left( k \right)}\ln \left( \frac{r}{R} \right)} \right) + \left( {\left( {\frac{V}{\ln \left( k \right)}} \right)^{2} \ln \left( \frac{r}{R} \right)\frac{1}{r}} \right)} \right] \\ \end{aligned}$$
$$\begin{aligned} K & = \frac{{ \rho \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]}}{{\left[ {C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} } \right]}} \left[ {\left( {K = \frac{{ \rho \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]}}{{\left[ {C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} } \right]}} } \right)} \right. \\ & \quad + \left( {\frac{ - 1}{{4\mu }}} \right.C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + b \ln \left( \frac{r}{R} \right)} \right)\left( {\frac{V}{\ln \left( k \right)}\left. \frac{1}{r} \right)} \right) \\ & \quad + \left( {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)\frac{V}{\ln \left( k \right)}\ln \left( \frac{r}{R} \right)} \right) \\ & \quad + \left. {\left( {\left( {\frac{V}{\ln \left( k \right)}} \right)^{2} \ln \left( \frac{r}{R} \right)\frac{1}{r}} \right)} \right] \\ \end{aligned}$$
(15)

The variation of the annular radial gap is the geometric aspect of the eccentric annulus which is absent in the concentric one. Hence there is radial as well as azimuthal dependency of the location of transition probable point. To capture this critical point, the three locations such as 12, 3, 6 and 9-O’clock hour arm position have been identified. Inner cylinder center is taken as a reference of measurement of radial coordinate of the outer peripheral curvature of the eccentric annulus space. Ri and Ro are designated as the radius of the inner border and outer border of the eccentric annular gap, taken with respect to the respective border curvature center point of the inner and outer borders. Along the location of the four various planes these inner and outer radii are presented with the corresponding suffixes P1, P2, P3 and P4 respectively. These have been given in Fig. 2 and Tables 1 and 2.

Fig. 2
figure 2

Azimuthal location of planes P1–P4 in the eccentric annulus

Full size image
Table 1 Azimuthal location and its radial coordinate for the various planes
Full size table
Table 2 Calculation of radial dimensions for the various planes for different radius ratio (k) and eccentricity ratio (ε)
Full size table

The total averaged i.e. bulk flow rate can be written as:

$$\begin{aligned} Q_{bulk} & = \mathop \int \limits_{{R_{i} }}^{{R_{o} }} v_{z} 2\pi rdr = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} } \right. \\ & \quad \left. {\left( {\frac{{\pi R^{2} }}{2}\left( {\left( {1 - k^{4} } \right) - \frac{{\left( {1 - k^{2} } \right)^{2} }}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right) + \frac{2\pi V}{{\ln \left( k \right)}}\left( {\frac{{R^{2} k^{2} \ln \left( \frac{1}{k} \right)}}{2} - \frac{{R^{2} \left( {1 - k^{2} } \right)}}{4}} \right)} \right] \\ \end{aligned}$$
(16)

The average bulk flow velocity of the annulus is obtained as:

$$\begin{aligned} V_{av} & = \frac{Q}{{\pi R^{2} \left( {1 - K^{2} } \right)}} = \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} } \right. \\ & \quad \left. {\left( {\frac{1}{2}\left( {\left( {1 + k^{2} } \right) - \frac{{\left( {1 - k^{2} } \right)}}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right) + \frac{2V}{{\ln \left( k \right)}}\left( {\frac{{k^{2} }}{{2\left( {1 - k^{2} } \right)}}\ln \left( \frac{1}{k} \right) - 0.25} \right)} \right] \\ \end{aligned}$$
(17)

And the flow Reynolds number is obtained as:

$$Re = \frac{{\rho V_{av} D_{H} }}{\mu } = \frac{{\rho V_{av} 2\left( {R_{o} - R_{i} } \right)}}{\mu }$$

Thus;

$$\begin{aligned} Re & = \frac{{\rho *2\left( {R_{o} - R_{i} } \right)\left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]}}{\mu }\left[ {\frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2} \left( {\frac{1}{2}\left( {\left( {1 + k^{2} } \right) - \frac{{\left( {1 - k^{2} } \right)}}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right)} \right. \\ & \quad \left. { + \frac{2V}{{\ln \left( k \right)}}\left( {\frac{{k^{2} }}{{2\left( {1 - k^{2} } \right)}}\ln \left( \frac{1}{k} \right) - 0.25} \right)} \right] \\ \end{aligned}$$
(18)

The axial centerline velocity of the equivalent virtual pipe for Poiseuille flow (of radius R) may be written as \(V_{max} = \frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2}\) for the eccentric annulus may be introduced in the Eq. (18). This results, the expression of the stability parameter K as follows,

$$\begin{aligned} K & = \frac{{ \rho \left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]}}{{\mu \left[ {V_{max} \left( {\frac{ - 4}{{R^{2} }}} \right)} \right]}}*\left[ {\left( {V_{max}^{2} \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)} \right)} \right. \\ & \quad + V_{max} \left( {1 - \left( \frac{r}{R} \right)^{2} + b \ln \left( \frac{r}{R} \right)} \right)\left( {\frac{V}{\ln \left( k \right)}\frac{1}{r}} \right) \\ & \quad + \left. {\left\{ {V_{max} \left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)\frac{V}{\ln \left( k \right)}\ln \left( \frac{r}{R} \right)} \right\} + \left\{ {\left( {\frac{V}{\ln \left( k \right)}} \right)^{2} \ln \left( \frac{r}{R} \right)\frac{1}{r}} \right\}} \right] \\ \end{aligned}$$
(19)

Considering that for assumed virtual pipe the Reynolds number (Reo) as;

$$Re_{o} = \frac{{\rho v_{max} R}}{\mu } = \frac{{\rho \frac{{v_{max} }}{2}2R}}{\mu }$$
(20)

Hence the expression (19) can be re-written as,

$$\begin{aligned} K & = \frac{{{\text{Re}}_{o} R\left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]}}{{\left( { - 4V_{max} } \right)}}\left[ {\left( {V_{max} \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)} \right)} \right. \\ & \quad + \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{V}{\ln \left( k \right)}\frac{1}{r}} \right) + \left( {\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)\frac{V}{\ln \left( k \right)}\ln \left( \frac{r}{R} \right)} \right) \\ & \quad \left. { + \left( {\left( {\frac{V}{\ln \left( k \right)}} \right)^{2} \ln \left( \frac{r}{R} \right)\frac{1}{{V_{max} r}}} \right)} \right] \\ \end{aligned}$$
(21)

For a limit condition of b = 0; the expression (21) takes the form of the pipe flow expression

$$K=\frac{1}{2}R{e}_{o}f(\frac{r}{R},k,\varepsilon )$$

Here, in the above expressions, e and ε are eccentricity value and eccentricity ratio, respectively.

$$\begin{aligned} f & = \frac{{R\left[ {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right]}}{{\left( { - 2V_{max} } \right)}}\left[ {\left( {V_{max} \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)} \right)} \right. \\ & \quad + \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{V}{\ln \left( k \right)}\frac{1}{r}} \right) + \left( {\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)\frac{V}{\ln \left( k \right)}\ln \left( \frac{r}{R} \right)} \right) \\ & \quad + \left. {\left( {\left( {\frac{V}{\ln \left( k \right)}} \right)^{2} \ln \left( \frac{r}{R} \right)\frac{1}{{V_{max} r}}} \right)} \right] \\ \end{aligned}$$
(22)

Hence it is obvious that the maxima or minima locations of the function f (r/R, k, ε) along various planes in its radial direction is the indicator of the location of Kmax, for the concentric case

$$f^{*} \left( {\frac{r}{R},k,\varepsilon } \right)_{max} = max\left\{ {\left| {f\left( {\frac{r}{R},k,\varepsilon } \right)} \right|_{max} ,\left| {f\left( {\frac{r}{R},k,\varepsilon } \right)} \right|_{min} } \right\}$$
(23)

Thus:

$$K_{max} = \frac{1}{2}Re_{o} f^{*} \left( {\frac{r}{R},k,\varepsilon } \right)_{max}$$
(24)

The term \(\frac{1}{2} {Re}_{o}\) is constant for the concentric annulus flow however for the flow in the eccentric annulus; it is function of the pressure gradient, eccentricity as well as of the radius ratio. In the eccentric annulus, due to its inherent geometrical property, the radius ratio shows the azimuthal dependence. The Eq. (24) reflects the peak value of stability parameter (Kmax), the deciding parameter for accessing the critical state of the transition [5], 6].

Based on the Kc as needed for the flow transition, the critical flow variables i.e. average critical velocity (vav,c), maximum critical velocity (vmax,c), the critical flow rate and Reynolds number i.e. (Qc) & (Rec) respectively, can be obtained for various \({d}_{i}/{d}_{o}\) of the eccentric annulus flow domain. When the flow in the annulus operates below these critical values, the laminar flow is sustained therein regardless of the disturbance extent. These are given below:

For this state, the Eq. (24) assumes the following form:

$$\frac{{K_{max,c} }}{{f_{max}^{*} }} = \frac{1}{2}Re_{o} = \frac{{\rho v_{max,c} R }}{2\mu }$$
(25)

Thus;

$$v_{max,c} = \frac{{2\mu K_{c} }}{{\rho Rf_{max}^{*} }}$$
(26)

Using the critical condition expression Eq. (24), the critical flow rate expression may be derived from the Eqs. (16) and (27).

$$v_{max} = \frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2}$$
(27)

Flow rate assumes the following form:

$$Q = \left( {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right)\left[ {\begin{array}{*{20}c} {v_{max} \left( {\frac{{\pi R^{2} }}{2}\left( {\left( {1 - k^{4} } \right) - \frac{{\left( {1 - k^{2} } \right)^{2} }}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right)} \\ { + \frac{2\pi V}{{\ln \left( k \right)}}\left( {\frac{{R^{2} k^{2} \ln \left( \frac{1}{k} \right)}}{2} - \frac{{R^{2} \left( {1 - k^{2} } \right)}}{4}} \right)} \\ \end{array} } \right]$$
(28)

And for critical state:

$$Q_{C} = \left( {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right)\left[ {\begin{array}{*{20}c} {v_{max,C} \left( {\frac{{\pi R^{2} }}{2}\left( {\left( {1 - k^{4} } \right) - \frac{{\left( {1 - k^{2} } \right)^{2} }}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right)} \\ { + \frac{2\pi V}{{\ln \left( k \right)}}\left( {\frac{{R^{2} k^{2} \ln \left( \frac{1}{k} \right)}}{2} - \frac{{R^{2} \left( {1 - k^{2} } \right)}}{4}} \right)} \\ \end{array} } \right]$$
(29)

After duly substituting the expression of vmax,c this is presented as:

$$\begin{aligned} Q_{c} & = \left( {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right)\left( {\frac{{2\mu K_{max} }}{{\rho Rf_{max}^{*} }}} \right)\left( {\frac{{\pi R^{2} }}{2}\left( {\left( {1 - k^{4} } \right) - \frac{{\left( {1 - k^{2} } \right)^{2} }}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right) \\ & \quad + \frac{2\pi V}{{\ln \left( k \right)}}\left( {\frac{{R^{2} k^{2} \ln \left( \frac{1}{k} \right)}}{2} - \frac{{R^{2} \left( {1 - k^{2} } \right)}}{4}} \right) \\ \end{aligned}$$
(30)

The above expression assumes the following form for pipe flow:

$$Q_{c,pipe} = \frac{{2\mu K_{max} }}{{\rho Rf_{max,pipe}^{*} }}$$

Here, f*max,pipe = 0.7698;

The normalized flow rate;

$$\begin{aligned} Q_{c,norm} & = \left( {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right)\left( {\frac{{f_{max,pipe}^{*} }}{{f_{max}^{*} }}} \right)\left( {\frac{{\pi R^{2} }}{2}\left( {\left( {1 - k^{4} } \right) - \frac{{\left( {1 - k^{2} } \right)^{2} }}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right) \\ & \quad + \frac{2\pi V}{{v_{max,c} \ln \left( k \right)}}\left( {\frac{{R^{2} k^{2} \ln \left( \frac{1}{k} \right)}}{2} - \frac{{R^{2} \left( {1 - k^{2} } \right)}}{4}} \right) \\ \end{aligned}$$
(31)

Now from the Eq. (15), the critical average velocity (\(V_{av,c}\)) is obtained as below:

$$\begin{aligned} V_{av,c} & = \frac{{Q_{c} }}{{\pi R^{2} \left( {1 - k^{2} } \right)}} = \left( {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right)v_{max,c} \left( {\left( {\frac{1}{2}\left( {\left( {1 + k^{2} } \right) - \frac{{\left( {1 - k^{2} } \right)}}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right)} \right. \\ & \quad + \left. {\frac{2V}{{v_{max,c} \ln \left( k \right)\left( {1 - k^{2} } \right)}}\left( {\frac{{k^{2} }}{2}\ln \left( \frac{1}{k} \right) - 0.25\left( {1 - k^{2} } \right)} \right)} \right) \\ \end{aligned}$$
(32)

The critical Reynolds number from Eq. (15):

$$Re_{c} = \frac{{\rho v_{av,c} D_{H} }}{\mu } = \frac{{\rho v_{av,c} 2\left( {R_{o} - R_{i} } \right)}}{\mu }$$
(33)

after putting the value of vmax,c:

$$\begin{aligned} Re_{c} & = \left( {1 + 1.5\left( {\frac{e}{Ro - Ri}} \right)^{2} } \right)\frac{{4K_{c} }}{{f_{\max }^{*} }}\left( {1 - k} \right)\left( {\left( {\frac{1}{2}\left( {\left( {1 + k^{2} } \right) - \frac{{\left( {1 - k^{2} } \right)}}{{\ln \left( \frac{1}{k} \right)}}} \right)} \right)} \right. \\ & \quad + \left. {\frac{2V}{{v_{\max ,c} \ln \left( k \right)\left( {1 - k^{2} } \right)}}\left( {\frac{{k^{2} }}{2}\ln \left( \frac{1}{k} \right) - 0.25\left( {1 - k^{2} } \right)} \right)} \right) \\ \end{aligned}$$
(34)

By duly incorporating the eccentricity effects (e.g. the radial gap variation) the modified value of Kc and f *max may be obtained and analyzed for the eccentric annulus. Further the variation of (Qc) & (Rec) may also be presented with respect to the various e and \({d}_{i}/{d}_{o}\) values for the annulus.

3.2 Validation of EGM with previous investigation

The model derived based on EGM can locate the point of the transition nucleation and hence trace its initiation. This model can give the flow condition suiting the transition as it being related with EG of any flow. For plane and Hagen Poiseuille flow, this method is consistent with experimental findings Table 3. This method is also used to explain the mechanism of instability of inflectional velocity profile for viscous flow and this inflectional instability is only valid for pressure driven flows. However, inflectional instability idea is inapt for shear driven flows like plane Couette flow since the energy loss could not be obtained directly from Navier–Stokes equations. EGM is a semi-empirical theory based on physical analysis since the critical Kc is experimental value and cannot be directly calculated from the theory so far. The resulting theoretical models based on EGM has this feature of semi-empiricism, Dou and Khoo [5].

Table 3 Comparison of the Rec and Kmax
Full size table

For a given flow geometry and fluid properties, when the maximum of K in the flow field is larger than a critical value Kc, it is expected that instability can occur for certain initial disturbance. For a given flow, K is proportional to the global Reynolds number. A large value of K has the ability to amplify the disturbance, and vice versa. The analysis has suggested that the transition to turbulence is due to the EG and the disturbance amplification, Dou [4].

Table 3 reflects the comparison of the critical Reynolds number (from experiments and other instability analysis methods) and EGM parameter Kmax for the subcritical condition of transition for plane Poiseuille flow, pipe Poiseuille flow as well as plane Couette flow.

Table 3 asserts that the subcritical condition of transition for Poiseuille flow occurs at Kc ≈ 385 while that in parallel flows takes place at a value of Kc ≈ 370 − 385. The obtained value of Kc from the analytical expression is found to be valid considering the critical Reynolds number Rec established from the experiments.

4 Results and discussion

After due analytical analysis the results are presented/discussed in the following manner:

  1. (a)

    Effect of various geometrical parameters of eccentric annulus on K, Kmax, f(r/R, k, ɛ) and to spot out the location for the transition initiation, along P1, P2, P3, and P4.

  2. (b)

    Variation in the initiation spot of the transition for a given plane P1 for different initial velocity given to the inner pipe.

  3. (c)

    Effect on the \({V}_{av,c}\), Qc and Rec.

For analyzing the flow stability, the variation of K has been plotted along P1 (P3 is also clubbed), P2, and P4 Tables 1, 2 and Fig. 2. In defining the dimensions of these planes the midpoint of the inner cylinder has been considered as reference center. Considering this, the extent of the plane P2 increases with an increase in the eccentricity, as the inner cylinder moves down, this is otherwise for rests of the planes. For non-rotation of the inner pipe of annulus the flow conditions for the planes P1 and P3 are the same. As established that EG along the transverse direction is accountable for the nucleation, growth as well as augmentation of the disturbances, while the viscous friction losses along the flow stream direction are accountable for resisting and absorbing the flow disturbances. The flow instability within domain rest on the relative rate of the exchange of these two EG values. The position of Kmax is the critical location for the onset of transition be maximum at there. The kinetic parameters for the calculation have been taken as follows.

  1. (i)

    Axial pipe forward velocity V = 0.01 m/s (For Figs.  3, 4, 5, 6 and 7 and, 0.02 m/s, 0.04 m/s, 0.06 m/s & 0.08 m/s (all for Fig. 8.

  2. (ii)

    Density of water (ρ) as 998 kg/m3

  3. (iii)

    Pressure gradient dp/dz = − 0.15

  4. (iv)

    Dimensions related formula and values are shown in the Tables 1, 2

Fig. 3
figure 3

Effect on K with variation in r, k and ɛ along plane P1

Full size image
Fig. 4
figure 4

Effect on K with variation in r, k and ɛ along plane P2

Full size image
Fig. 5
figure 5

Effect on K with variation in r, k and ɛ along plane P4

Full size image
Fig. 6
figure 6

Variation of the 2f value with respect to r, k and ɛ along plane P4

Full size image
Fig. 7
figure 7

Variation of the critical transition spot (r*) with eccentricity ratio (ε) for different radius ratio (k) for plane P4

Full size image
Fig. 8
figure 8

Variation of K along Plane P1, with eccentricity 0.2 and radius ratio 0.1 for different velocities

Full size image

Figure 3 is showing the modulation of the dimensionless stability parameter (K) along plane P1 as per its lengthwise direction. Results for K of the two planes P1 and P3 are going to be the same due to similar geometric arrangements & absence of rotation of the inner cylinder. Thus the discussions for plane P1 results will be valid to plane P3 also. These results have been presented for three radius ratio k = 0.1, 0.3 and 0.5 and for eccentricity ratio ɛ = 0.2, 0.4, 0.6 and 0.8. Thus in Fig. 3, three sets of the curve are appearing with each set consisting of 4 curves signifying four different eccentricities. The first set for radius ratio k = 0.1, second one is for k = 0.3 and the third set is for k = 0.5. Figure 3, illustrates that the \(\left|{K}_{min}\right|\) is larger than that of \(\left|{K}_{max}\right|\). The peak value in either of the cases i.e. for Kmin as well as Kmax reduces with increment in eccentricity & radius ratio. For a given value of k, the increment in the eccentricity leads to increment in the geometric gap of the annulus along plane P1. A similar observation can be made for plane P2 and P4.

4.1 Location of transition spot for the eccentric annulus along the various planes

The most susceptible radial location of each plane for the initiation of the transition is the position of peak and the absolute value of the K. Figures 3, 4 and 5 lucidly illustrates that the susceptible position tends to move outward the inner wall and gets close to the outer wall for the annular gap present along with a specified plane.

By comparing the absolute values of the parameter K for various planes from Figures 3, 4 and 5, it is obvious that the absolute peak value largest for the plane P2 which is the most susceptible plane for the initiation of the transition to take place.

Choosing the plane P4 for analyzing the alteration in the function f(r/R, k, ɛ).

$$K = \frac{1}{2}Re_{o} f\left( {\frac{r}{R},k,\varepsilon } \right)$$

where

$$\begin{aligned} f & = \frac{{R\left( {1 + 1.5\left( {\frac{e}{{R_{o} - R_{i} }}} \right)^{2} } \right)}}{{\left( { - 2V_{max} } \right)}}\left[ {\left( {V_{max} \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)} \right)} \right. \\ & \quad + \left( {1 - \left( \frac{r}{R} \right)^{2} + b\ln \left( \frac{r}{R} \right)} \right)\left( {\frac{V}{\ln \left( k \right)}\frac{1}{r}} \right) \\ & \quad \left. { + \left( {\left( {\frac{ - 2r}{{R^{2} }} + \frac{b}{r}} \right)\frac{V}{\ln \left( k \right)}\ln \left( \frac{r}{R} \right)} \right) + \left( {\left( {\frac{V}{\ln \left( k \right)}} \right)^{2} \ln \left( \frac{r}{R} \right)\frac{1}{{V_{max} r}}} \right)} \right] \\ \end{aligned}$$
$$Re_{o} = \frac{{\rho v_{max} R}}{\mu } = \frac{{\rho \frac{{v_{max} }}{2}2R}}{\mu }$$
$$v_{max} = \frac{ - 1}{{4\mu }}C_{i} \left( {\frac{dp}{{dz}}} \right)_{con} R^{2}$$

Thus for concentric annulus case, the position of max. & min. of the function f(r/R, k, ɛ) radially gives Kmax. position.

$$f^{*} \left( {\frac{r}{R},k,\varepsilon } \right)_{max} = max\left\{ {\left| {f\left( {\frac{r}{R},k,\varepsilon } \right)} \right|_{max} ,\left| {f\left( {\frac{r}{R},k,\varepsilon } \right)} \right|_{min} } \right\}$$

Thus;

$$K_{max} = \frac{1}{2}Re_{o} f^{*} \left( {\frac{r}{R},k,\varepsilon } \right)_{max}$$

Thus for a critical value of the parameter Kmax one may satisfactorily plot the variation of function f*(r/R, k, ɛ)max for analysis. This has been plotted in Fig. 6.

Table 4 outlays the procedure for f*(r/R, k, ɛ)max calculation radially for various k and various ɛ. From the expression of f*, we can observe that the lowest value of fmin lies at the inner cylindrical boundary of the annular space and the largest value of fmax lies at the outer boundary of annular space. The extent of fmin is larger than the extent of fmax for all the values of k. It is also seen that the amount of fmax as well as of fmin goes declining with the increment in the values of k and the locations of fmax and fmin shifts to the outer of the annulus boundary with the rise in k. Table 4 compiles the values of 2f*max and its locations (radially) along the plane P4 for the annulus of different radius ratio at different values of eccentricity ratio. The 2f*max value taken is all \(\left|2{f}_{min}\right|\) values as this is always larger than \(\left|2{f}_{max}\right|\) along any specified plane (which is plane P4, over here). Dimensionless radial distance (r*) has been calculated from the expression \({r}^{*} = (r - {R}_{1})/({R}_{2} - {R}_{1})\) which is used for positioning of 2f*max value. In this expression, \({R}_{2}- {R}_{1}\) is the radial range along the length of the plane P4. It is equal to equal to [R0 − e) − Ri], based on center of the inner boundary of the annulus as reference point. These calculated values of dimensionless radial distance r* corresponds to the radial locations at which the 2f*max value is occurring. Hence, this location is critical radial spot for the transition initiation for given geometrical and kinematic conditions for the annular flow. For any given radius ratio this location drifts away from the inner boundary of the annulus as the value of r* increases with the rise in the eccentricity ratio (ε), while keeping the radius ratio constant. This is true for all the radius rations. Further for a given eccentricity, the critical transition sport moves away from the inner annulus boundary as the radius ratio increases. A higher value of k refers to the lowering of the radial annulus gap in the specified plane for a given eccentricity ratio (ɛ). Thus, the higher value of k leads to the lowering of the f*max, which signifies the decrement in the commencement of the flow transition possibilities, provided other considered parameters being of a specified value. This is shown in the Fig. 7.

Table 4 Peak values of 2f, calculated for specified plane P4
Full size table

Variation on the initiation of the transition for a given plane P1 for different axial velocity given to the inner pipe.

From Fig. 8, It is observed that by increasing the initial linear i.e. axial forward velocity given to the inner pipe, the location of peak values of K i.e. of Kmin and Kmax is shifting towards the inner pipe. Absolute value of Kmin. is higher than the absolute value of the Kmax for all the cases of the axial pipe velocity. Higher the value of the initial pipe velocity the possibility of the transition is enhanced—which is asserting the well-known concept behind the transition that increased velocity will lead to more inertial disturbances within the flow due to increased velocity. The absolute value of Kmin and Kmax is also increased as the initial velocity given to the inner pipe is increased.

4.2 Effect on \({V}_{av,c}\), Q c and Re c

For the purpose of proper design, selection, and control of the various flow devices the understanding of the critical stages of the various flow variables becomes important. Basically, this is the practical utilization of the understanding gained by analyzing the transition prone zones in the flow domain. It is thus obvious that if the various operational flow parameters in the annular domain fall well below the corresponding critical parameters then the flow remains in the laminar regime irrespective of the presence of chaos level, as the chaos damp out eventually.

Equation 31 expresses the critical flow rate (Qc) variation for increasing value of eccentricity (ɛ) and radius ratio (k). Equation 34 expresses the variation of critical values Reynolds number (Rec) for various values of the ɛ or e and k of the annulus. From the equations, it is obvious that for the higher radius ratio we require a higher flow rate. If the annulus operates with a given flow rate which is higher than this critical flow rate then such annulus flow system is considered to be in an unstable zone. The Rec rises with the increment in the eccentricity for the given k. The critical Reynolds number begins to decrease as we increase the radius ration for a given eccentricity. We can also observe that the decline in Rec is sharp in lower radius ratio than in higher radius ratio.

5 Conclusions

The transition of flow through the eccentric annulus space for which the inner cylinder is in axial motion has been investigated from the point of view of its applicability for horizontal oil well drilling process. In this application, the cleaning of the borehole of the generated cutting makes it imperative that flow should be in the turbulent regime. Eccentricity ratio, radius ratio, and the inner pipe velocity had been the parameters whose effects have been observed on the location of the transition spot and on the critical flow variables. The most crucial location, where K acquires peak value, tends to shift towards the outer wall of the annular gap present in the annulus. This is depicted from the Figs. 3, 4 and 5. The annulus has a variable geometric gap. The locations of higher value gap lead the larger energy gradient transversely,the factor is primarily accountable for the nucleation and furthering of transition. The peculiar behavior of the location shifting of critical location (as pointed by the value of 2f*max for different radius ratio Figs. 6, 7 is attributed to the inner pipe movement velocity. From Fig. 8, it may be concluded that although for higher inner pipe velocity transition will be quick, the location of the maximum value of flow parameter K remains unchanged with the increase in the pipe axial velocity. These findings may be helpful in other industrial situations where turbulence becomes a necessity. The work can be extended considering the rotation of inner pipe for the different geometrical parameters.