Introduction

The flow of non-Newtonian fluids through annular area has received much attention due to its wide practical applications. This flow is studied to provide solutions for industry challenges, particularly in oil and gas wells drilling like cuttings transport in deviated wells, coiled tubing return flow and cementing. Among problems that can be caused by poor hydraulics design are the insufficient hole cleaning, stuck pipe and lost circulation which causes slow penetration rates (Prassl and Dipl 2003), and produce many costly problems.

Guckes (1975) conducted an earlier study of non-Newtonian fluid in eccentric annuli using a finite difference technique to solve the equations of motion for laminar flow in bipolar coordinate system. He determined the effects of pressure loss gradient, diameter ratio and eccentricity on the flow rate. Uner et al. (1988) presented the eccentricity as an equivalent slot of variable local annular clearance, where they plotted the flow rate versus pressure loss of power-law and Bingham plastic fluids. However, suitable results are obtained when diameter ratio is high (κ ≥ 0.5). Haciislamoglu and Langlinais (1990) developed a simple correlation to predict the pressure drop gradient for an eccentric annulus from calculated pressure drop of concentric one. They found that the reduction in the pressure drop in fully eccentric annulus is around 50% less than concentric annulus. McCann et al. (1995) carried out an experimental investigation using flow loop where they found that the pressure drop of power-law fluids decreases significantly in the narrow annuli, while the pressure drop increases with increasing the pipe rotation in turbulent regime. Among known experimental studies of non-Newtonian fluid flow in eccentric annulus with centerbody rotation is that of Nouri and Whitelaw (1994). The authors observed that rotation pipe causes a decrease in pressure drop for low values of Reynolds number; however, the pipe rotation has negligible impact when Reynolds number reaches high values. Likewise, the authors noticed the presence of a counter-rotating swirl flow (also known as secondary flow) in the power-law fluid. The pressure loss changes in non-Newtonian fluids through annulus are attributed to shear-thinning, inertial effects and formation of secondary flows (Ahmed and Miska 2008).

Mitsuishi and Aoyagi (1974) treated experimentally a secondary flow using hydrogen bubbles as tracers, and they noted that the radial velocity component of secondary flow is less than 2% of the axial velocity. However, they did not find such secondary flows for non-Newtonian fluid in a concentric annulus or for Newtonian fluid in an eccentric annulus. Cui and Liu (1995) numerically solved the continuity and momentum equations using bipolar coordinate, and they noticed that the secondary flow area was getting larger as the eccentricity increases. Also they stated that rotation of the inner pipe has not a noticeable effect on the secondary flow. Hussain and Sharif (2000) also performed a numerical study where they concluded that the stagnation in the narrow region of the eccentric annulus tends to intensify the secondary flow.

In the present study, the influence of pipe rotation, diameter ratio (κ) and flow behavior index (n) on the pressure drop for laminar and turbulent flow is evaluated. Moreover, since secondary flow is induced by the second normal stress difference due to the shear in the axial flow and non-symmetric of the cross-sectional geometry (Yue et al. 2008), the effects of eccentricity, flow behavior index and diameter ratio on the appearance and development of secondary flow were studied utilizing a CFD commercial code ANSYS Fluent 17.0. Moreover, impact of the appearance of secondary flow in the annulus on pressure drop of power-law fluid is discussed.

Mathematical description

To study the pressure drop and secondary flow of non-Newtonian fluid in annular section, the flow is assumed to be fully developed, incompressible, steady and isothermal in both laminar and turbulent regimes.

The continuity and momentum equations that govern the flow are expressed in cylindrical coordinates \(\left( {r, \theta , z} \right)\), respectively, as (Bird et al. 2002):

$$\frac{1}{r}\frac{{\partial \left( {rv_{r} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {v_{\theta } } \right)}}{\partial \theta } + \frac{{\partial \left( {v_{z} } \right)}}{\partial z} = 0$$
(1)
$$\rho \left( {\frac{{\partial v_{r} }}{\partial t} + v_{r} \frac{{\partial v_{r} }}{\partial r} + \frac{{v_{\theta } }}{r}\frac{{\partial v_{r} }}{\partial \theta } + v_{z} \frac{{\partial v_{r} }}{\partial z} - \frac{{v_{\theta }^{2} }}{r}} \right) = - \frac{\partial P}{\partial r} - \left( {\frac{1}{r}\frac{{\partial \left( {r\tau_{rr} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial (\tau_{\theta r} )}}{\partial \theta } + \frac{{\partial \left( {\tau_{zr} } \right)}}{\partial z} - \frac{{\tau_{\theta \theta } }}{r}} \right) + \rho g_{r}$$
(2)
$$\rho \left( {\frac{{\partial v_{\theta } }}{\partial t} + v_{r} \frac{{\partial v_{\theta } }}{\partial r} + \frac{{v_{\theta } }}{r}\frac{{\partial v_{\theta } }}{\partial \theta } + v_{z} \frac{{\partial v_{\theta } }}{\partial z} + \frac{{v_{r} v_{\theta } }}{r}} \right) = - \frac{1}{r}\frac{\partial P}{\partial \theta } - \left( {\frac{1}{{r^{2} }}\frac{{\partial \left( {r^{2} \tau_{r\theta } } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {\tau_{\theta \theta } } \right)}}{\partial \theta } + \frac{{\partial (\tau_{z\theta } )}}{\partial z} + \frac{{\tau_{\theta r} - \tau_{r\theta } }}{r}} \right) + \rho g_{\theta }$$
(3)
$$\rho \left( {\frac{{\partial v_{z} }}{\partial t} + v_{r} \frac{{\partial v_{z} }}{\partial r} + \frac{{v_{\theta } }}{r}\frac{{\partial v_{z} }}{\partial \theta } + v_{z} \frac{{\partial v_{z} }}{\partial z}} \right) = - \frac{\partial P}{\partial \theta } - \left( {\frac{1}{r}\frac{{\partial \left( {r\tau_{rz} } \right)}}{\partial r} + \frac{1}{r}\frac{{\partial \left( {\tau_{\theta z} } \right)}}{\partial \theta } + \frac{{\partial \left( {\tau_{zz} } \right)}}{\partial z}} \right) + \rho g_{z}$$
(4)

where \(v_{r}\), \(v_{\theta }\) and \(v_{z}\) are the velocity vector components, \(P\) is the pressure, ρ is the density and \(g\) is the gravity.

For fully developed turbulent flow, the Reynolds stress model (ANSYS FLUENT theory guide 2015) is used to study the effect of the inner pipe rotation, diameter ratio and flow behavior index on pressure drop gradient of power-law fluid in turbulent regime for different eccentricities. The Reynolds stress model is selected among other models (Realizable K-Epsilon, Standard K-Omega and SST K-Omega) based on comparison with the experimental work of McCann et al. (1995) as shown in Fig. 1. Moreover, Sultan et al. (2019) conducted a similar study about the accuracy of different turbulence models, and their results indicate that the Reynolds stress model provides accurate results for flow of power-law fluid through concentric and eccentric annulus. For that, the Reynolds stress is utilized to evaluate the influence of the inner pipe rotation, flow behavior index and diameter ratio on the pressure drop gradient of power-law fluid.

Fig. 1
figure 1

Comparison of different turbulence models with experimental data of McCann et al. (1995)

Full size image

The exact transport equation for the Reynolds stress model (RSM) is given as follows:

$$\frac{{{\text{D}}R_{ij} }}{{{\text{D}}t}} = P_{ij} + D_{ij} - \varepsilon_{ij} + \emptyset_{ij} + \theta_{ij}$$
(5)

where \(\frac{{{\text{D}}R_{ij} }}{{{\text{D}}t}}\) is the summation of the changing rate of \(R_{ij}\) and transport of \(R_{ij}\) by convection, \(P_{ij}\) is the production rate of \(R_{ij}\), \(D_{ij}\) is the diffusion transport of \(R_{ij}\), \(\varepsilon_{ij}\) is the rate of dissipation, \(\emptyset_{ij}\) is the pressure–strain correlation term and \(\theta_{ij}\) is the rotation term.

The diffusion term used in simulation is calculated as follows:

$$D_{T,ij} = \frac{\partial }{{\partial x_{k} }}\left( {\frac{{\mu_{t} }}{{\sigma_{k} }}\frac{{\partial R_{ij} }}{{\partial x_{k} }}} \right)$$
(6)

where \(\sigma_{k} = 0.82\), \(\mu_{t} = C_{\mu } \left( {\frac{{k^{2} }}{\varepsilon }} \right)\) and \(C_{\mu } = 0.09\).

Production rate \(P_{ij}\) of \(R_{ij}\) or \(\overline{{u_{i}^{'} u_{j}^{'} }}\) can be expressed as:

$$P_{ij} = - \left( {\overline{{u_{i}^{'} u_{m}^{'} }} \frac{{\partial U_{j} }}{{\partial x_{m} }} + \overline{{u_{j}^{'} u_{m}^{'} }} \frac{{\partial U_{i} }}{{\partial x_{m} }}} \right)$$
(7)

The pressure–strain term \(\emptyset_{ij}\) has \(\emptyset_{ij,1}\) or slow pressure–strain term also known as the return-to-isotropy term, \(\emptyset_{ij,2}\) or rapid pressure–strain term, and \(\emptyset_{ij,w}\) as wall reflection term. This term is modeled as:

$$\emptyset_{ij} = \emptyset_{ij,1} + \emptyset_{ij,2} + \emptyset_{ij,w}$$
(8)

where

$$\emptyset_{ij,1} = - C_{1} \frac{\varepsilon }{k}\left[ { \overline{{u_{i}^{'} u_{j}^{'} }} - \frac{2}{3}\delta_{ij} k} \right]$$
(9)
$$\emptyset_{ij,2} = - C_{2} \left[ {P_{ij} - \frac{2}{3}\delta_{ij} P} \right]$$
(10)

where \(C_{1} = 1.8\) and \(C_{2} = 0.6\).

The wall reflection term \(\emptyset_{ij,w}\) is responsible for the normal stresses distribution near the wall. This term is determined as follows:

$$\emptyset_{ij,w} \equiv C_{1}^{'} \frac{\varepsilon }{k}\left( {\overline{{u_{k}^{'} u_{m}^{'} }} n_{k} n_{m} \delta_{ij} - \frac{3}{2}\overline{{u_{i}^{'} u_{k}^{'} }} n_{j} n_{k} - \frac{3}{2}\overline{{u_{j}^{'} u_{k}^{'} }} n_{i} n_{k} } \right)\frac{{C_{l} k^{{\frac{3}{2}}} }}{\varepsilon d} + C_{2}^{'} \left( {\emptyset_{km,2} n_{k} n_{m} \delta_{ij} - \frac{3}{2}\emptyset_{ik,2} n_{j} n_{k} - \frac{3}{2}\emptyset_{jk,2} n_{i} n_{k} } \right)\frac{{C_{l} k^{{\frac{3}{2}}} }}{\varepsilon d}$$
(11)

where \(C_{1}^{'} = 0.5\), \(C_{2}^{'} = 0.3\), \(n_{k}\) is the horizontal component of the component normal to the wall, \(d\) is the shortest distance to the wall and \(C_{l} = \frac{{C_{\mu }^{3/4} }}{k}\), where \(C_{\mu } = 0.09\) and \(k\) is the von Kármán constant (= 0.4187).

The dissipation rate \(\varepsilon_{ij}\) or the destruction rate of \(R_{ij}\) is modeled as:

$$\varepsilon_{ij} = \frac{2}{3}\delta_{ij} \varepsilon$$
(12)

where

$$\varepsilon = 2v\overline{{s_{ij}^{'} \cdot s_{ij}^{'} }}$$
(13)

and \(s_{ij}^{'} =\) fluctuating deformation rate.

Rotation term is expressed as:

$$\theta_{ij} = - \omega_{k} \left( {R_{jm} e_{ikm} + R_{im} e_{jkm} } \right)$$
(14)

where \(\omega_{k}\) is the rotation vector, \(e_{ikm} =\) alternating symbol, \(+ \;1, - \;1\) or \(0\) depending on \(i, j\) and \(k\).

Simulation methodology

Physical model

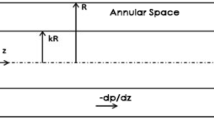
The flow of non-Newtonian fluid is bounded by two horizontal cylinders, where the outer cylinder is fixed and inner one rotates to simulate the mud pattern in horizontal borehole. In this model, the fluid flows through concentric and eccentric annulus E = 0.3, E = 0.6 and E = 0.9 in which the eccentricity is defined as:

$$E = \frac{2e}{{D_{\text{o}} - D_{\text{i}} }}$$
(15)

where e is the distance between centers.

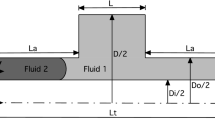
The fluid characteristics and geometry dimensions are listed in Table 1.

Table 1 Fluid and geometry characteristics
Full size table

To determine the fluid flow regime, Reynolds number is calculated using the relationship of Madlener et al. (2009)

$$Re = \frac{{\rho D_{\text{h}}^{n} u^{2 - n} }}{{K\left( {\frac{3n + 1}{4n}} \right)^{n} 8^{n - 1} }}$$
(16)

where \(u\) is the bulk flow velocity and \(D_{\text{h}}\) is the hydraulic diameter which is calculated as:

$$D_{\text{h}} = D_{\text{o}} - D_{\text{i}}$$
(17)

The length of the cylinders is selected to be longer than hydrodynamic entry length to prevent the entrance effects, where the hydrodynamic entry length is given as Yunus and Cimbala (2006)

$$L_{{{\text{h}},{\text{laminar}}}} = 0.05\left( {D_{o} - D_{i} } \right)Re$$
(18)
$$L_{{{\text{h}},{\text{turbulent}}}} = 1.359\left( {D_{o} - D_{i} } \right)Re^{1/4}$$
(19)

Table 2 summarizes the range of different parameters studied in the present numerical study.

Table 2 Range of the numerical study parameters
Full size table

CFD model

Default standard wall functions are generally applicable if the first cell center adjacent to the wall has a \(\left( {y^{ + } } \right)\) value larger than 30 (ANSYS FLUENT theory guide 2015); for that, the dimensionless wall distance \(\left( {y^{ + } } \right)\) is checked during mesh generation in consideration of the requirement of \(\left( {y^{ + } } \right)\) and maintained above the value of 40. The value of \(\left( {y^{ + } } \right)\) is calculated using the following relationship:

$$y^{ + } = \frac{y}{\mu }\sqrt {\rho \tau_{\text{w}} }$$
(20)

where \(\tau_{\text{w}}\) is the wall shear stress, \(\rho\) the fluid density, \(y\) the distance from the wall and \(\mu\) the molecular viscosity.

To attain the solution, the numerical study is performed with 1,120,000 hexahedral elements (35 radial divisions, 80 circumferential divisions and 400 axial divisions) in which the near walls are refined to obtain an accurate solution of the streamline function in these regions (Fig. 2). For that, a CFD software ANSYS Fluent 17.0 is used to solve Navier–Stokes (NS) equations based on finite volume method, as well as k − ɛ equations for turbulent regime allowing calculation of the turbulent viscosity.

Fig. 2
figure 2

Cross section of concentric and eccentric annulus

Full size image

The numerical solution of the governing equations is based on pressure–velocity coupling, in which the algorithm SIMPLE was used. For the discretization of pressure and momentum equations, PRESTO and second-order upwind are used, respectively.

Residuals of an iterative calculation are considered as convergence criteria, and the accurate results are obtained by making residuals as small as possible. For the convergence criteria of the present work, a value of 10−4 is selected.

Validation model

Figure 3 shows that the results provided by numerical calculations are independent of the mesh model used, where critical conditions were adopted (Reynolds number \(Re\) from 5070 to 10,312 and E = 0.9) in the grid independence study.

Fig. 3
figure 3

Mesh independence study

Full size image

The predicted results of pressure drop versus drill pipe rotation from 0 to 400 rpm using CFD are compared with different previous experimental works from the literature (McCann et al. 1995, Vieira Neto et al. 2014 and Ahmed and Miska 2008) as shown in Fig. 4. Moreover, the rheological parameters and geometry characteristics of the experimental studies are summarized in Table 3. In Fig. 4a, a slight deviation is stated between the experimental and simulation results where the mean error is estimated at 5.5% and 3.8% for 0.181 m/s and 0.362 m/s fluid velocity, respectively. Similarly, the calculated pressure drop slightly overpredicted the experimental results by 11.5% and 13.1% for XG 0.2% and CMC 0.2% fluids, respectively, as shown in Fig. 4b; furthermore, the simulation and experimental results are in good agreement as shown in Fig. 4c, in which the mean percentage error is 1.87% and 6.08% for 1.03 m/s and 0.44 m/s fluid bulk velocity, respectively. The comparison proves the ability of CFD model to provide accurate results.

Fig. 4
figure 4

Comparison of simulated and the experimental data: a power-law fluid through concentric annulus (McCann et al. 1995), b power-law fluid through eccentric annulus

Full size image
Table 3 Fluid and geometry characteristics
Full size table

Results and discussion

Effects of pipe rotation, flow behavior index and diameter ratio on pressure drop gradient

Figure 5 shows a reduction in the pressure drop gradient in the concentric annulus (E = 0.0) for laminar flow regime, in which the reduction is around 10% when the pipe rotation increases from 50 to 400 rpm. This reduction is due to the shear-thinning effect of power-law fluids. However, pipe rotation causes an increase of 9% of pressure drop gradient in the annulus of E = 0.6. This increase could be attributed to the beginning of the secondary flow formation where the flow in the wide region of annulus begins to form a counter-rotating swirl (Fig. 10). A negligible effect of the inner pipe rotation on pressure drop loss gradient is, however, observed for the eccentric annulus of E = 0.3 and E = 0.9.

Fig. 5
figure 5

Effect of the pipe rotation on pressure drop gradient in concentric and eccentric annulus for laminar regime (Re = 94, u = 0.2 m/s, κ = 0.5, n = 0.61)

Full size image

For turbulent regime, a negligible influence is noticed of the drill pipe rotation on pressure drop gradient for concentric and eccentric annulus, except for annulus of E = 0.6, where a slight increase was noticed with increasing the drill pipe rotation as shown in Fig. 6.

Fig. 6
figure 6

Effect of the pipe rotation on pressure drop gradient in concentric and eccentric annulus for turbulent regime (Re = 6100, u = 2 m/s, κ = 0.5, n = 0.61)

Full size image

Figures 7 and 8 depict an exponential increase in pressure drop gradient when the value of flow behavior index increases for a constant diameter ratio, where power-law fluid is less affected by shear-thinning effect as this behavior gets closer to Newtonian fluid in both laminar and turbulent regimes.

Fig. 7
figure 7

Effect of the flow behavior index on pressure drop gradient in concentric and eccentric annulus for laminar regime (Re = from 28 to 870, u = 0.2 m/s, κ = 0.5, ω = 200 rpm)

Full size image
Fig. 8
figure 8

Effect of the flow behavior index on pressure drop gradient in concentric and eccentric annulus for turbulent regime (Re = from 3200 to 701811, u = 2 m/s, κ = 0.5, ω = 200 rpm)

Full size image

As illustrated in Figs. 9 and 10, the pressure drop gradient increases gradually for low values of diameter ratio, whereas this increase becomes significant when diameter ratio reaches 0.6, particularly from κ = 0.8 to κ = 0.9 where the pressure drop increased sharply. This observed phenomenon is related to narrow annulus of oil and gas wells such as casing-while-drilling, where extra caution is required preventing formation fracture due to the occurrence of high equivalent circulating density (ECD) during drilling operation.

Fig. 9
figure 9

Effect of diameter ratio on pressure drop gradient in concentric and eccentric annulus for laminar regime (Re = from 35 to 115, u = 0.2 m/s, n = 0.61, ω = 200 rpm)

Full size image
Fig. 10
figure 10

Effect of diameter ratio on pressure drop gradient in concentric and eccentric annulus for turbulent regime (Re = from 2531 to 7428, u = 2 m/s, n = 0.61, ω = 200 rpm)

Full size image

For all parameters studied in the present study, pressure drop gradient diminishes as the eccentricity increases.

Effects of eccentricity, flow behavior index and diameter ratio on secondary flow

As shown in Fig. 12, for the eccentric annulus (E = 0.3) there was no formation of secondary flow, however, for the annulus of E = 0.6, a counter-rotating swirl begins to appear in the wide region part of the annulus for a flow behavior index from 0.4 (n ≥ 0.4) where the flow rotates in the opposite direction of the inner pipe. The appearance of secondary flow formation in this annulus could explain again the increase of pressure drop gradient of the eccentric annulus of E = 0.6 in Fig. 4.

Conversely, a fully developed counter-rotating swirl was observed for the annulus of E = 0.9 in which small difference in the second normal stress caused by low values of the flow behavior index tends to prevent the secondary flow to appear.

Figure 11 exhibits that no secondary flow occurs in the annulus of E = 0.3 for all range of diameter ratio. For the eccentric annulus of E = 0.6, the area of secondary flow decreases with increasing diameter ratio up to κ = 0.7 where the secondary flow was disappeared; however, for the eccentric annulus of E = 0.9 a developed secondary flow is observed for all diameter ratios.

Fig. 11
figure 11

Effect of flow behavior index on the streamlines and axial velocity for eccentric annulus E = 0.3, E = 0.6 and E = 0.9 (u = 0.2)

Full size image

Since cuttings are transported in the wide region of eccentric annulus which is characterized by high velocity and viscosity, the tendency of the inner pipe rotation to move the flat region of power-law velocity profile from the wide region part to the narrow region part of the annulus (E = 0.3 and E = 0.6) could improve hole cleaning efficiency by preventing cuttings bed formation. A negligible effect of the inner pipe rotation on the flat region is observed for the eccentric annulus of E = 0.9 for high values of flow behavior index and low of diameter ratios, as shown in Figs. 10 and 11, respectively.

It can be concluded from the comparison between Figs. 5 and 12 that beginning of formation of the secondary flow causes the increase in pressure drop gradient for the eccentric annulus of E = 0.6; however, the fully developed secondary flow in the eccentric annulus of E = 0.9 did not have a significant effect on pressure drop gradient.

Fig. 12
figure 12

Effect of diameter ratio on the streamlines and axial velocity for eccentric annulus E = 0.3, E = 0.6 and E = 0.9 (u = 0.2)

Full size image

For all parameters affecting formation and development of the secondary flow, the Reynolds stress of the flow has law values in which the developed secondary flow is found almost symmetric in the annulus. Same trend was stated in the work of Escudier et al. (2002)

Conclusions

The following conclusions were reported from this study:

  • For laminar flow regime, the rotation of the inner pipe causes a reduction in pressure drop gradient of power-law fluid in concentric annulus; however, a negligible effect is observed for eccentric annulus except for annulus (E = 0.6).

  • There was no a significant effect of the inner pipe cylinder rotation on the pressure drop gradient in turbulent flow regime.

  • As power-law fluid index gets closer to Newtonian behavior, the pressure drop gradient increases exponentially for a constant diameter ratio.

  • High values of diameter ratio cause a significant increase in the pressure drop gradient, particularly from κ = 0.8 to κ = 0.9 where the pressure drop gradient is increased dramatically.

  • Secondary flow of power-law fluid is mainly caused by eccentricity of the inner pipe cylinder where both high values of diameter ratio and low values of flow behavior index tend to prevent the secondary flow to appear.

  • Flat region of velocity profile of power-law fluids in the wide region of eccentric annulus is less affected by the inner pipe rotation when the eccentricity reaches high values.

  • Beginning formation of the secondary flow in the wide region of eccentric annulus of E = 0.6 induces the increase in pressure drop gradient; however, a slight effect is observed for the annulus of E = 0.9 where the secondary flow was fully developed.