1 Introduction

The reduction of earthquake-induced vibration of tall buildings is an important research topic in the areas of structural reliability. Hence, different sophisticated methods have been made to guarantee the safety and the stability of these structures. To illustrate the real interest, the outrigger system was developed. In the current context, its design is defined as the one of the most promising alternative solutions [1, 2]. It traditionally consists of a core wall, perimeter columns, and outriggers that are rigidly connected to the first-two previous elements [3,4,5,6,7]. However, one can note some cases already implemented in the world as super-tall building of 212.88 m St. Francis Shangri-La Place in Philippines [8], Shanghai Center located in Shanghai with the height of 632 m [9] and The Burj Khalifa in Dubai with the height of 828 m [10]. Although that the typical configuration of the outrigger system provides sufficient means to mitigate the undesirable vibration. It is convenient to insert the control devices into the outriggers. Since their presence provides additional energy dissipation to the whole structure [11]. Because the structures are initially not designed to withstand all possible external loads [12]. It is the main reason that the concept of damped-outriggers are widely explored in a great number of works [13, 14].

In the literature there is three kinds of the control devices [15]: One can firstly note, the passive devices. These do not need an external voltage source to operate. The second, these are active devices. Unlike to the passive case, these devices need a large external voltage source to operate. Finally, one has the semi-active devices. They need a low external voltage to operate. Despite the fact that these last exhibit the combined passive and active properties. The researchers and engineers do not cease to multiply the intensive research efforts in view of reinforcing the capacities of passive devices. All this is due to their maintenance of low cost. It is this wake that the major contribution the choice of study of High-static low dynamic stiffness (HSLDS) using in this paper also falls. This control system is defined as the one more promising device that is able to improve the vibration isolator performance. It combines the positive and negative stiffness elements at an equilibrium positive. It follows that the nonlinear stiffness of this system strongly influences its dynamic responses and vibration isolation performance [16]. In the same context, considerable research attention has been devoted to attest the isolation performance of the device within theoretical and experimental analysis [17, 18]. Wang et al.[19] explored the effects of the stiffness range parameter and static equilibrium position stiffness on the dynamic responses of the system. According to the authors, the increase of the stiffness range parameter and reduction of others improve the isolation performance of the device.

In addition to the above reports, the assumption is also considered to evaluate the behaviour dynamics of the outrigger system by neglecting the influence due to perimeter columns. Regarding the theoretical study, Pin et al. [20] investigated the effect of the damped outrigger as a general rotational spring acting on a Bernoulli-Euler beam. The authors showed that the modal damping ratio is significantly influenced by the stiffness ratio of the core to the column, and is more sensitive to damping than the position of the damped outrigger. Chen et al. [21] studied in free vibration under the assumptions of Bernoulli-Euler beam theory with two intermediate cantilever-attached viscous dampers. They obtained a transcendental equation that governs complex eigenvalues of system, whereby pseudo undamped natural frequencies, corresponding damping ratios and mode shapes are attainable. Lin et al. [22] studied the damped-outrigger, incorporating the buckling restrained brace (BRB) as an energy dissipation device. They pointed out a properly designed BRB-outrigger system can behave like a traditional elastic outrigger through BRB’s elastic responses.

Note that all aforementioned studies showed that the shear as well as the rotary deformation in the dynamic behaviour of frame core-tube are not included in the assumption of the dynamic behaviour of frame core-tube.

In the present work, The frame-core tube is considered as a continuum cantilever Timoshenko beam with a constant cross-section. This model is defined as a mathematical expansion of the Euler-Bernoulli [23].

In this present paper, the performance of the HSLDS device on the outrigger system is theoretically studied. The stochastic averaging method [24,25,26] extensively used in engineering application is developed. This analytical technique is applied to also linearize the modal equation of the structural system. Our main objective is to find the suitable values of control parameters of this passive energy dissipation leading to an acceptable level of the earthquake-induced vibration.

Known as the one more powerful of the catastrophic event influences the dynamics of a structures and building in worldwide [27]. The earthquake with two repeated sequences will be explored in work [28]. Because the structure gets damaged in the first sequence, and additional damage accumulates from secondary sequence before any repair is possible. It is thus that the efficiency of the control device will evaluate during its two intervals.

The rest of the paper is structured as follows: In Sect. 2.1, focuses on the description of the structural system. The mathematical model allowing to investigate its dynamics is developed and the linearization form of the modal equation is also illustrated. Section 3 is devoted to the numerical results and discussion. Section 4 concludes the article.

2 Description of the system

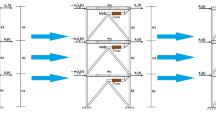
The simplified schematic of the structural system under the ground earthquake is represented in Fig. 1a. It is constituted of an uniform cantilever beam illustrating the dynamic behaviour of the core-tube and the damped-outriggers. The configuration of these ones is made so that they are forced to work as a group. It comes out from this figure that the elements such as core-tube and perimeter column are rigidly connected to work together, in order to resist lateral force.

Fig. 1
figure 1

Simple structural model with nonlinear isolator

Full size image

The damped-outriggers behave as a rigid body and are located at a point \(x_a\) along with the height of the core tube. Note that the damped-outriggers communicate to the perimeter columns through the visco-elastic devices (HSBS) vertically installed, as illustrated in Fig. 1a. Thus, the simple schematic of this mentioned devices is displayed in Fig. 1b. The design of this system is a nonlinear isolator with high static low-dynamic-stiffness of which comprising three springs of linear stiffness( two horizontals \(k_1\) and one vertical \(k_0\)) and a dashpot of the linear damping coefficient \(c_0\). Adding of these devices should enhance the dynamic performance of the structural system by providing supplementary energy dissipation [11]. By passing, it is important to point up that the outriggers and the exterior columns have commonly a high stiffness. In this context, the bending stiffness \(E_0I_0\) is assumed to be infinitely rigid.

2.1 Mathematical model

Note that the assumption well-used in the literature is to consider that the structure displayed in Fig. 1a is a cantilever uniform beam. For that, \(m_1\) defines the mass per unit length; EI is the flexural rigidity . Thus, I is the moment of inertia of the cross-section about the neutral axis, E is Young’s modulus. G is the shear modulus of elasticity; \(r_a\) is the radius of gyration of the cross-section. These defined geometrical and material properties are assumed constant.

The lateral displacement is defined by the variable \(y(x, t) = y\), which varies with the coordinate along the beam x and with time t. To remind as mentioned above the readers that the influence of the perimeter columns on the dynamics of the core is not taken into consideration. As a result, the governing equation describing the dynamics of the cantilever Timoshenko beam with damped outrigger subject to horizontal earthquake loadings can be written as follows [29]

$$\begin{aligned}&m_1\dfrac{\partial ^2 y}{\partial t^2}+EI\dfrac{\partial ^4 y}{\partial x^4}-m_1r_a^2\left( 1+\dfrac{E}{k_sG}\right) \dfrac{\partial ^4 y}{\partial x^2 \partial t^2}\nonumber \\&\quad =-m_1\ddot{y}_g(t)+\dfrac{\partial M_a}{\partial x} \end{aligned}$$
(1)

In this above formulation, the third term from the left side represents the correction for rotary inertia plus the shear deformation effect. For the convenient study, it should be noted in passing that the joint action of rotary inertia and shear deformation effects is neglected. The dimensionless quantity \(k_s\) is the shear coefficient depending on the geometric of the cross-section of the beam and depends on as well as of the Poisson’s ratio.

The random function \(\ddot{y}_g(t)\) represents the ground acceleration. It is worth pointing out that the dot denotes the derivative with respect to t. Thus, the seismic events are described through the below analytical expression [30]

$$\begin{aligned}&\ddot{y}_g(t)=\left( 2\xi _g\omega _g\dot{x}_g(t)+\omega _g^2x_g(t)\right) e(t) \end{aligned}$$
(2)
$$\begin{aligned}&\ddot{x}_g(t)+2\xi _g\omega _g\dot{x}_g(t)+\omega _g^2x_g(t)=w_a(t) \end{aligned}$$
(3)

Here, \({x}_g(t)\) is the filter response. It is important to note that \({x}_g(t)\) is numerically obtained from 3. This allows to determine the function \(\ddot{y}_g(t)\) that represents the earthquake dynamics.

\(w_a(t)\) is a stationary Gaussian white noise process with the following statistics

$$\begin{aligned}<w_a(t)>=0, \qquad <w_a(t)w_a(\tau )>=2\pi S_0\delta (t-\tau ) \end{aligned}$$

\(S_0\) is the constant power spectral intensity of the noise. The evolutionary power spectrum is described as [28]

$$\begin{aligned} S_g\left( {{\Omega },t } \right) = {\left| {e\left( t \right) } \right| ^2}S\left( {\Omega } \right) \end{aligned}$$
(4)

in which e(t) is a deterministic envelope function of time and is defined as

$$\begin{aligned} e(t)=e_{0i}te^{-\alpha _it} \end{aligned}$$
(5)

where \(e_{0i}\) and \(\alpha _i\) are positive constants that control, respectively, intensity and non-stationarity trend of the ith acceleration sequence. Note that this function in (5) is introduced to represent nonstationary into the process.

$$\begin{aligned} e(t) = \left\{ \begin{array}{l} 0 \qquad ~ \qquad ~ 0 \le t\le t_1 \\ e(t-t_1) \qquad ~ t_1 \le t\le t_2\\ 0 \qquad ~ \qquad ~ t_2 \le t\le t_3 \\ e(t-t_3) \qquad ~ t_3 \le t\le t_4\\ 0 ~\qquad ~ \qquad ~ t_4 \le t\le t_5\\ \end{array} \right. \end{aligned}$$
(6)

Expression in (6) was suggested by Abbas and Takewakib [28]. It illustrates the repeated sequences of the earthquake excitation.

Based on the study of the frequency content of a number of strong ground-motion records [31], the spectral density for the ground acceleration of the earth surface layer was suggested by Kanai and Tajimi [32]. The mathematical formulation is expressed as

$$\begin{aligned} S\left( \Omega \right) = {S_0}\frac{{\omega _g^4 + 4\xi _g^2\omega _g^2\Omega ^2}}{{{{\left( {\omega _g^2 - \Omega ^2} \right) }^2} + 4\xi _g^2\omega _g^2{\Omega ^2}}} \end{aligned}$$
(7)

where \({\omega _g}\) is the dominant frequency of the soil site, \({\xi _g}\) is the associated damping ratio of the soil layer representing the spectral characteristics of the ground excitation.

Note that the modelling earthquake excitation has received more attention. This is due to the fact that it can be defined as an analytical convenient approach showing many advantages within the assessment of the structural behaviour. Because it allows mainly characterising an accurate behaviour of the recorded models of different sites, by adjusting the intensity and frequency content or their statistical properties. It can help to also estimate the past nonstationary ground excitation having hit structures of different countries in the past for many decades.

Note that the outrigger system works by transferring global bending load from the core of the building to the outside columns [33]. Hence, the last term of Eq. (1) demonstrates that the induced-effects of outriggers on the core tube are considered as resistant moments [13]. Consequently, expression of concentrated moment generated by the control device is

$$\begin{aligned} M_a=2r\delta (x-x_a)f_H(t) \end{aligned}$$
(8)

where \(\delta (x-x_a)\) denotes the Dirac function. It shows the predefined location where the damped outrigger is installed. The point \(x_a\) indicates the distance from the bottom of the tall building. However, the mentioned function in (8) has the property as

$$\begin{aligned} \delta \left( {x - {x_a}} \right) = \left\{ \begin{array}{l} \infty \qquad ~x={x_a}\\ 0 \qquad ~x~\ne x_a \end{array} \right. \end{aligned}$$
(9)

The distance from the control devices to the centre of the core is denoted r, and is also defined as the length of each outrigger.

The number two introduces in Eq. (8), denotes the quantity of the HSLDS installed since the damped outrigger is symmetric in relation to core-tube. The force \(f_H\) of Eq. (8) is given as follows [34].

$$\begin{aligned} f_H(t)=c_0\dot{y}(x,t)+k_0y(x,t)+2k_1y(x,t) \left( 1-\dfrac{s_a}{\sqrt{s^2+y^2(x,t)}}\right) \end{aligned}$$
(10)

The obtained expression from Eq. (10) has been studied in ref. [34]. They pointed that two are additional horizontal springs, each with stiffness \(k_1\). These ones have the effects of creating a nonlinear that can be adjusted, and by automatically modifying the linear natural frequency of the structural system.

The vertical spring of linear stiffness is so-called \(k_0\). The free length of the lateral springs is so-called \(s_a\), and s is the length of each spring in the horizontal position.

Owing to reduce the mathematical difficulty of the Eq. (10) within the analytical framework, it is convenient to make Taylor’s development that consequently, lost a lot of information that is neglected. Thus, the approximated polynomial form yields [34]

$$\begin{aligned} f_H(t)=c_0\dot{y}(x,t)+k_0y(x,t)+2k_1s_1y(x,t)+k_1s_2y^3(x,t) \end{aligned}$$
(11)

It can be clearly seen that Eq. (11) is rewritten under of a third-order polynomial. Thus, one of the major steps will greatly allow to analyse the effects of different parameters of the control device.

By introducing the dimensionless variables defined as

\(X=\dfrac{x}{L}\), \(X_a=\frac{x_a}{L}\), \(Y=\dfrac{y}{L}\), \(\ddot{z}_g=\dfrac{\ddot{y}_g}{L}\), \(a_1=\dfrac{EI}{L^4m_1}\), \({a_2} = \dfrac{r_1^2}{L^2}\left( 1 + \dfrac{E}{k_sG}\right)\), \(C_0=\dfrac{c_0}{Lm_1}\), \(K_0=\dfrac{k_0}{Lm_1}\), \(K_1=\dfrac{k_1}{Lm_1}s_1\),  \(K_2=\dfrac{k_1}{Lm_1}s_2\), \(s_1=\left( \dfrac{s_a}{s}-1\right)\), \(s_2=\dfrac{s_a}{s^3}\), \(r_{ou}=\dfrac{2r}{L}\) This leads to rewrite the Eq. (1) as

$$\begin{aligned} \frac{\partial ^2Y}{\partial t^2} +a_1\frac{\partial ^4Y}{\partial X^4} - {a_2}\frac{\partial ^4Y}{\partial X^2\partial t^2} = -\ddot{z}_g(t) - r_{ou}F_H\left( t\right) \frac{\partial }{\partial X}\delta \left( X -X_a\right) \end{aligned}$$
(12)

and Eq. (11) becomes

$$\begin{aligned} F_H(t) = C_0\dot{Y}\left( X,t \right) +\left( K_0-2K_1\right) Y\left( X,t\right) +K_2Y^3\left( X,t \right) \end{aligned}$$
(13)

For the analytical purpose, it is convenient to reduce the partial differential Eq. (12) to a set of ordinary differential equations. For that, the transversal deflection of the beam \(Y\left( X,t\right)\) can be rewritten in term of product of two variables in the following form:

$$\begin{aligned} Y\left( X,t\right) = \sum \limits _{j=1}^N{\varGamma _j{\phi _j}\left( X\right) {\xi _j}\left( t\right) } \end{aligned}$$
(14)

with \(\varGamma _j\) is the modal participation factor of the ith mode of vibration; and can be determined through the following form [36]

$$\begin{aligned} \varGamma _j=\dfrac{\int \nolimits _{0}^{1}\phi _jdX}{\int \nolimits _{0}^{1}\phi _j^2dX} \end{aligned}$$
(15)

N is the total number of modes, \(\xi _j(t)\) is relative displacement response of a SDOF system, and \(\phi _j(X)\) is the amplitude of the ith mode at nondimensional height X defined as.

$$\begin{aligned} \phi _j(X)=d_1^j\sin (\delta _1^jX)+\cos (\delta _1^jX)-d_2^j\sinh (\delta _2^jX)-\cosh (\delta _2^jX) \end{aligned}$$
(16)

in which, \(\delta _1^j\) and \(\delta _2^j\) are eigenvalues defined at the j th mode of the vibration. The coefficients \(d_1^j\) and \(d_2^j\) are obtained by using the boundary conditions of the cantilever. The scheme procedure to obtain these eigenvalues and coefficients of the \(\phi _j(X)\) is detailed in ref. [32].

2.2 Modal equation

To assess the dynamic behaviour response of the structural system; it is worth reducing the partial differential equations to the modal equation. For analysis purposes, the Eq. (14) is considered and substituting into (12), performing the integration from 0 to 1 and algebraic manipulating yields

$$\begin{aligned} \ddot{z}_j\left( t\right) + \beta _j\dot{z}_j\left( t\right) + g(t,z_j,\dot{z}_j) = - \sigma _j\ddot{z} _g\left( t \right) \end{aligned}$$
(17)

z(t) is displacement of the whole system corresponding to the jth mode.

Noting that the above Eq. (17) denotes the modal equation of the structural system subjected to earthquake excitation.

With the damping coefficient gives by

$$\begin{aligned} \beta _j=2\zeta _j\omega _j+r_{ou}\varepsilon _jC_0 \end{aligned}$$
(18)

and the restoring force thus defines

$$\begin{aligned} g(t,z,\dot{z}_j)={\omega _j^2}{z_j}+ r_{ou}\varepsilon _j\left[ \left( K_0-2K_1\right) {z_j}(t) + {K_2}z_j^3(t) \right] \end{aligned}$$
(19)

where

$$\begin{aligned} \omega _j^2= & {} \frac{a_1b_3^j}{b_1^j - {a_2}b_2^j},\quad \varepsilon _j = -\frac{\phi _j^{'}\left( X_a \right) {\phi _j}\left( X_a\right) }{\varGamma _j(b_1^j - {a_2}b_2^j)},~\\ {\sigma _j}= & {} \frac{{b_4^j{\phi _j}\left( {{X_a}} \right) }}{\varGamma _j(b_1^j - {a_2}b_2^j)},~ z_j\left( t\right) = {\phi _j}\left( {X_a} \right) {\xi _j}\left( t \right) \end{aligned}$$

and

$$\begin{aligned} b_1^j= & {} \int _0^1 {{\phi _j}{{\left( X \right) }^2}dX},~ b_2^j = \int _0^1 {\phi _j^{\left( 2 \right) }\left( X \right) {\phi _j}\left( X \right) dX},\\ b_3^j= & {} \int _0^1 {\phi _j^{\left( 4 \right) }\left( X \right) {\phi _j}\left( X \right) dX},~ b_4^j = \int _0^1 {{\phi _j}\left( X \right) dX} \end{aligned}$$

\(b_i^j(i=1,2,3,4)\) can be computed once the eigenvalues \(\delta _1^j\) and \(\delta _2^j\) have been determined.

2.3 Analytical approach

Defined as a powerful approximate technique for the prediction of response of linear or non-linear under random vibration, the stochastic averaging method is widely used in literature. Its application has proved that it is a useful tool for deriving approximate solutions to problems involving the vibration response [38]

The purpose here is to develop theoretical investigation through the stochastic averaging method that will provide a good estimate of effects on the parameters of the control device such as stiffness and damping coefficient on the vibration amplitude of the whole structure.

Before starting, it is important to apply the equivalent statistic linearization method. This stochastic technique proposed by Kougioumtzoglou et al. [37] allows to approximate the non-linear system to a linear form. Thus, application to Eq. (17) leads to a suitable transform as follows.

$$\begin{aligned} \ddot{z}_j\left( t \right) + \beta _0\dot{z}_j\left( t \right) +\Omega ^2(A_j) z_j\left( t \right) = - {\sigma _1^j}{\ddot{z} _g}\left( t \right) \end{aligned}$$
(20)

The following step of this analyze is to consider that the amplitude of the structural system can be decomposed as

$$\begin{aligned} z_j(t)=&A_j(t)\cos \left[ \Omega (A_j) t+\varphi \right] \end{aligned}$$
(21)
$$\begin{aligned} \dot{z}_j(t)=&-A_j(t)\Omega \sin \left[ \Omega (A_j) t+\varphi \right] \end{aligned}$$
(22)

with natural frequency given by

$$\begin{aligned} \Omega ^2(A_j)=\omega _j^2+r_{ou}\varepsilon _j(K_0-2K_1+\dfrac{3}{4}K_2A_j^2) \end{aligned}$$
(23)

It is observed that the natural frequency from (23) should be function of the amplitude.

Combining Eqs. (21) and (22), this yields

$$\begin{aligned} A_j^2(t)=&z_j^2(t)+\left( \dfrac{\dot{z}_j(t)}{\Omega (A_j)}\right) ^2 \end{aligned}$$
(24)
$$\begin{aligned} \varphi (t)=&-\Omega t-\tan ^{-1}\left( \dfrac{\dot{z}_j(t)}{z_j(t)\Omega (A_j)}\right) \end{aligned}$$
(25)

By differentiating (22) with respect to time and combining with (21) into (20), the following averaged equations can be derived

$$\begin{aligned} \dot{A}_j( t)= & {} - \dfrac{1}{2}\beta _{j}A_j+ \sigma _j^2\dfrac{\pi S_g\left( {\Omega (A_j),t } \right) }{2A_j\left( t \right) \Omega ^2(A_j)} \nonumber \\&+ {\sigma _j}\dfrac{\left[ {\pi S_g\left( {\Omega (A_j),t } \right) } \right] ^{1/2}}{\Omega (A_j)}w_a\left( t\right) \end{aligned}$$
(26)

\(w_a(t)\) represents a stationary, zero-mean Gaussian white noise process of unit intensity [25]. It is noted that the amplitude \((A_j)\) in (26) is decoupled with the phase \((\varphi )\). The reason why these variables can be treated separately.

In what follows, the Fokker-Planck expression from (26) is governed by

$$\begin{aligned} \begin{aligned} \dfrac{\partial P\left( A_j,t\right) }{\partial t } = -\dfrac{\partial }{\partial A_j}\left\{ {\left( -{ \frac{1}{2}\beta _jA_j + \sigma _j^2\frac{{\pi S_g\left( {\Omega (A_j),t} \right) }}{{2A_j\Omega (A_j)^2}}} \right) P\left( {A_j,t } \right) } \right\} + \sigma _j^2\frac{{\pi S_g\left( {\Omega (A_j),t } \right) }}{{2\Omega (A_j)^2}}\frac{{\partial ^2 P\left( A_j,t\right) }}{{\partial {A_j^2}}} \end{aligned} \end{aligned}$$
(27)

where \(P(A_j,t)\) denotes the probability density amplitude-depending.

This above equation allows to determine the nonstationary response amplitude \(P(A_j,t)\), in which a solution of Eq. (27) can be approximated as follows [24, 39]

$$\begin{aligned} P\left( {A_j,t } \right) = \frac{A_j}{{c_j\left( t \right) }}\exp \left[ { - \frac{{{A_j^2}}}{{2c_j\left( t \right) }}} \right] \end{aligned}$$
(28)

where the function \(c_j(t)\) accounts for the time-dependent variance of the response process \(z_j\).

To determine the mentioned function defined in (28), it is readily found that by substituting the Eq. (28) into (27), and the manipulating yields

$$\begin{aligned} \dot{c}_j \left( t \right) = -\beta _jc\left( t\right) + \sigma _j^2\frac{\pi S_g\left( {\Omega _{eq}(c_j(t)),t} \right) }{\Omega _{eq}(c_j(t))^2} \end{aligned}$$
(29)

with the equivalent time-dependant stiffness \(\Omega _{eq}^2(c(t))\) given by

$$\begin{aligned} \Omega _{eq}^2(c(t))=&\int \limits _{0}^{\infty }\Omega ^2(A_j)~P(A_j,t)dA_j\nonumber \\ =&\omega _j^2+r_{ou}\varepsilon _j\left[ \left( K_0-2K_1\right) +\dfrac{3}{2}K_2c_j(t)\right] \end{aligned}$$
(30)

and the moment of the amplitude

$$\begin{aligned} <A_j^2>=\int \limits _{0}^{\infty }A_j^2~p(A_j,t)dA_j= 2c_j(t) \end{aligned}$$
(31)

Remind the reader that the subscript \((j=1,2,3..)\) represents the mode of vibration of the structural system.

Note by passing that Eq. (29) is a first-order nonlinear ordinary differential equation, which can be solved numerically.

2.4 Floor displacement

In Tall buildings combining the shear and flexural effects, the interstory drift ratio IDR can be explored. It is defined as the difference of displacements of the floors above and below the story of interest normalized by the interstory height [36]. Although, IDR seems to correlate well with the seismic damage potential of buildings [40]. It will not develop here, because the obtained results by Xie and Wen [41] indicated that Timoshenko’s theory is restricted for the evaluation of lateral drifts for shear wall structures and might not be adequate.

In our context, Floor’s displacement is defined as the displacement of each floor of the tall building. The study of this approach is a powerful tool to better observe. it also allows to analyse the effect of the control device on each floor of the tall building. Thus, Floor’s displacement can be computed through the formulated Eq. (14) of the transverse deflection. Hence, the below equation can be deduced as follows

$$\begin{aligned} \text {FD}(X,t)=\sum \limits _{j=1}^{N_m}\dfrac{\varGamma _j\phi _j(X)}{\phi _j(X_a)}z_j(t) \end{aligned}$$
(32)

\(N_m\) is the number of modes considered in this work

As the Tall building illustrated Herein, has a finite number of stories. The value of each of stories should be found within interval nondimensional height \(0<X<1\)

3 Numerical analysis and discussions

It is well-known that the tall buildings primarily consist of structural members (columns, walls, floors) with a considerable number of degrees of freedom. To reduce this complexity, the mentioned structure can approximately describe by equivalent homogeneous elastic-continuum. Deng et al. [35] were found that the results obtained from the simplified model agree well with those obtained from the finite element model. Note that the main objective is to find the threshold values of \(K_0\) and \(C_0\) that limit the seismic-induced structural vibration to a considerable level.

To investigate the dynamic response of the structure, the simplified model based on a cantilever beam leads us to define the concrete core with geometric properties \(12~m\times 12~m\), a thickness of 0.5 m, and with sixty-story a total building height of 210 m [29]. The mass per unit length is \(m_1 = 62500Kg/m\). Note that the structural system described here, have a single outrigger therefore the effect of the distance from the core to the perimeter columns on the dynamic response will be analysed.

Through the constitutive relationship existing between the coefficients, this leads to having the value of parameters as presented in Table 1. It illustrates the parameters of the shape function and frequencies of the modal equation in the three first modes of vibration.

Table 1 Parameters of the shape function and frequencies
Full size table

In this paper, the mathematical model of the earthquake acceleration sequences is governed by Eqs. (2)–(6). Hence, the simulated nonstationary ground acceleration is shown in Fig. 2. The intensities of the acceleration sequences at the first and second sequences \(S_0=0.02~m^2/s^3\) and \(S_0=0.01~m^2/s^3\), respectively. The parameters of the envelope functions are adopted as 0.30 and 0.35, and the separating time interval between the sequences is 15 s. The interval time of the envelope function are \(t_1=5s\), \(t_2=25\), \(t_3=40\) and \(t_3=60\)

Fig. 2
figure 2

The simulated acceleration sequences, \(\omega _g=3\pi \,rad/s\)

Full size image

Figure 2 explicitly displays the temporal dynamics of seismic events from Eqs. 2 and 3. It can be seen that, depending on the envelope function (see Eq.6), the dynamic exhibits two sequences with the separating time interval both of them.

The stiffness coefficient must be selected suitably so that the nonlinear stiffness is always positive. Hence, the values of different stiffness are chosen as \(K_1=K_0/4\), \(K_2=55~K_0\).

Fig. 3
figure 3

Influence of the stiffness on maximum response amplitude in Eq. (31) in First mode

Full size image

In order to quantify the effect of the stiffness coefficient \(K_0\) on response of the structural system, Fig. 3 shows the variation of the stiffness on the peak response amplitude corresponding to different values of the dimensionless damping coefficient \(C_0\). It is obviously observed that when \(C_0\) increases, the response amplitude decreases. In each of the cases shown, it can be concluded that the influence of \(K_0\) automatically reinforces the reduction of the response of the structure.

Figure 4 shows the influence of damping coefficient on response amplitude in the three first modes of vibration. It can be seen the increasing damping coefficient decreases automatically the response amplitude.

Figure 4a matches in the first vibration mode, thus, it is observed a reduction amplitude rapidly occurs when the damping coefficient \(C_0\) increases. While the attenuation of the amplitude observed in Fig. 4b and c is due to especially at the frequency values corresponding to the second and third modes of vibration, respectively. It comes out as further information that \(C_0\) considerably influences the amplitude.

Fig. 4
figure 4

Influence of the damping coefficient on response amplitude to the different modes of vibration (\(K_0=0.1)\)

Full size image
Fig. 5
figure 5

Comparison between the simulated responses with the linearization method , \(C_0=0.76\)

Full size image

The result is evaluated in the first mode of vibration. As similar information will be obtained to other modes of vibration. It is not necessary to display here because the analyse of modes is independence.

In Fig. 5, the comparison is made with results based on Monte Carlos simulations of linear and nonlinear systems. More specifically, the response amplitude obtained by the linearization approach (see (20)) is very similar qualitatively to that obtained by nonlinear simulation (see (17)). The nonlinear response amplitude is in good agreement with linear simulation estimates, with a notable discrepancy when of linear the coefficient stiffness \(K_0\) of the vertical spring increases. The response amplitude calculated by the linearization equation , with the low computed values of \(K_0\) in practice, is accurately satisfied. It is thus that the results shown in Fig. 5a also indicate in first sequence a difference of the percentage of Error=1.6% of the peak value of amplitudes, and an error 0.75% in second sequence ground excitation. While Fig. 5b exhibits a percentage Error=3.9% in the first sequence and the error in the second sequence is 1.9%. According to Fig. 5c, a percentage of error=5.4% between the different peak amplitude first sequence and the error \(2.7\%\) in the second sequence are observed.

Note that the errors are extremely small when \(K_0\) decreases, causing a softening nonlinearity. Although when \(K_0\) increases, it causes a hardening nonlinearity that an undesirable effect as mentioned in ref. [34]. They indicated that the presence of the mentioned effects in the isolator results in the resonance peak bending to higher frequencies range over there is a violation isolator.

Thus, to analyse the influence of the control device on each floor. The maximal lateral deflection versus some stories is presented in Fig. 6. It can be noticed that in Fig. 6a, the influence of the coefficient stiffness is illustrated. While in Fig. 6b rather exhibits, the influence of the damping coefficient of the control device on the control vibration of the structural system

Fig. 6
figure 6

Effect of damping and stiffness parameters of the control device on the lateral deflection

Full size image

The supplementary information from Fig. 6 allow to found the threshold values of coefficients \(K_0\) and \(C_0\). These parameters should lead the control device to provide the high capability of mitigating transversal displacements against seismic events. As a result, Table 2 illustrates the reduction percentage of the vibration of each floor of the tall building when the stiffness coefficient \(K_0\) of the control device increases as seen in Fig. 6a. It can be seen that its influence considerably affects the displacement response at the bottom than the top of the structural system.

Table 2 Reduction percentage with \(C_0=0.405\)
Full size table

Unlike the observation made in Table 2, the results of the Table 3 illustrate the reduction percentage of the vibration of each floor of the tall building when the damping coefficient \(C_0\) of the control device increases as seen in Fig. 6b. It can be seen that its variation significantly affects the transversal displacement at the top than the bottom of the tall building compared to the case displays in Table 2.

Table 3 Reduction percentage with \(K_0=0.5\)
Full size table

Thus, By combining information from both Tables 2 and 3, it can be concluded that the variation of coefficients \(K_0\) and \(C_0\) significantly reduces of the transversal response at the top and the bottom of the structural system.

As mentioned above, the outrigger without the control device is one of the structural element which is connected to the core-tube and perimeter columns. Their association forms a unit block that is able to provide a dynamic action in resisting the lateral loads. On top of that it is important to note by passing that the position of outrigger along the height of the structure is a major factor that significantly affects the dynamics of the tall building [29]. However, one of the major steps will be to evaluate the efficiency outrigger’s length on deflection transverse of the whole system.

Figure 7 displays the influence of the outrigger’s length on maximal deflection displacement of each floor. It comes out that when the increase of the outrigger’s length significantly reduces the earthquake-induced structural vibration.

Fig. 7
figure 7

Effect of the outrigger’s length on deflection transverse, \(C_0=0.96\), \(K_0=0.5\)

Full size image
Table 4 Reduction percentage in Fig. 7a
Full size table
Table 5 Reduction percentage in Fig. 7b
Full size table
Table 6 Reduction percentage Fig. 7c
Full size table

In what follows, The results show in Tables 4, 5 and 6 illustrate the data from in Fig. 7a–c, respectively. It can be seen that the variation of the outrigger’s length on the dynamic response by reducing the excessive vibration of the whole structure. Moreover, the results indicate that the distance between the control device and core-tube should not be close to each other. For a design contribution of the outrigger system, a distance must be respected to accentuate the effectiveness of the dynamic response of the structure.

Fig. 8
figure 8

Root mean square acceleration

Full size image

Figure 8 shows the temporal evolution of root mean square acceleration. The results indicate that the percentage of the peak root mean square in the first sequence is 3.5% and the second sequence is \(4.43\%\). It comes out that the variation of parameters of the control device slowly affects the acceleration amplitude. Nevertheless, they allow to rapidly reach the reduction amplitude during each sequence of the earthquake excitation.

4 Conclusion

The current paper investigated the High static low dynamic stiffness outrigger effects on the cantilever beam under earthquake loads. The Timoshenko model based on partial equations is used to describe the dynamic response of the core-tube of the structural system. However a numerical comparison is made between equivalent linearisation method and the direct simulation approach to justify the precision of the analytical averaging method used. This has allowed to determine the threshold values of stiffness as well as the damping coefficients of the nonlinear control device. Moreover, it is showed that the performance of the control devices on the structural system depends intensively on of stiffness and damping coefficients. As a matter of fact, the provided results clearly reveal that the control device has the potential to reduce the excessive lateral deflection up to 10% at the top and bottom of the structural system.

It was also possible to assess the impact of the distance of the control device vertically installed at the column to the centre of the core-tube. It is observed that the variation of this distance can greatly influence the dynamics of the outrigger system with a reduction of vibration up to 39% at the middle of the structure. This suggests that a good compromise should be found between the control devices and the centre of the core-tube to optimise the performance of structural system. Another conclusion of this work is that the analytical investigation is really necessary to estimate the threshold parameters of the nonlinear control device leading the acceptable level of the reduced amplitude of the structural system. Thus, the future work will focus on the investigation the delay-effects of HSLDS on the structural response.