1 Introduction

Our time is marked by the search for new substitute materials that meet very specific needs. In this context, materials base organic molecules have many advantages: they are most often light, transparent or colored on demand, easy to use, durable, easy to synthesize, have an ultra-fast optical response and great flexibility [1,2,3,4,5,6]. These organic molecules having all these characteristics are assimilated to organic semiconductors. Organic semiconductors have been studied intensively in recent years, due to their unique optical properties, such as: size-dependent emission wavelength, narrow emission spectrum, and high luminescent efficiency [7,8,9]. All of these attractive characteristics make organic semiconductor excellent candidates for the next-generation lighting and display, as well as optical communication technologies. Organic materials have a very low conductivity as long as they are intrinsic, therefore having the possibility of a controllable doping technology is even more desirable. Different excitations or doping can generate charges or excited states in semiconductors. We cite a few, electronic doping by charge transfer or chemical doping: it consists in doping the semiconductor, that is to say increasing the density of charge carriers (electrons and holes), by adding donor species (n-type doping) or acceptors (p-type doping) of electrons [10], doping by field effect or injection (which locally modifies the concentration of carriers): in the case of metal–semiconductor molecule contact, the charges can be injected directly from the metal to the semiconductor under the application of a voltage. This principle is used in transistors and light emitting diodes [11]. Upon doping, the charge carrier density can be significantly increased resulting in a good conductivity, ohmic injection at the contacts, and a negligible drop of voltage across these layers. Obviously, this concept is allow for new device structures, like pn-junctions, that are known from inorganic semiconductors and can be applied to the field of organic devices as well. These doping, considerably improve the optoelectronic and nonlinear optical properties of these organic compounds. Significant interest still exists in the design and development of materials exhibiting an important second order NLO response due to potential application in telecommunications, optical computing, and optical signal processing [12]. In fact, the third order response governed by the second hyperpolarizability offers a more varied and richer behavior than the second order NLO process due to the higher dimensionality of the frequency space. Recently, one can observe a huge increase in the NLO properties of conjugated and organics functionalized molecules due to their potential applications in optoelectronic devices [13, 14]. The same, materials with suitable nonlinear responses to incident light can be exploited to alter propagation characteristics such as frequency, amplitude or phase of the transmitted electromagnetic radiation [15]. A study of the optoelectronic, nonlinear optical and thermodynamic properties of the 4- [2- (2-N, N-dihydroxy amino thiophene) vinyl] benzenamine (DATVB) (See Fig. 1) molecule was carried out by F. Tchangnwa Nya et al. [16]. The results obtained show that this molecule has a gap energy \({\text{E}}_{{{\text{gap}}}}\) = 2.16 \({\text{eV}}\), a dipole moment µ = 2.88 Debye and a first order hyperpolarisability \(\beta_{mol} .10^{ - 33} = 412.27 {\text{esu}}\) which predisposes it for applications in electronics, optoelectronics and non-linear optics [16]. In order to design such high performance NLO materials, various strategies have been put forth for both organic and inorganic systems. For organic systems, NLO response is generally enhanced by increasing the degree of charge transfer [17]. In this manuscript, we report the halogen (chlorine and fluorine) doping of DATVB for designing novel materials more active for electronic and photonic devices and suggest an others fields of applications. The structural, electronic, optoelectronic and nonlinear optical properties of the doped molecules i.e. 4-[2-(2-(5-(bis (chlorooxy) amino) thiophene) vinyl] benzenamine (BCATVB) and 4-[2-(2-(5-(bis (fluorooxy) amino) thiophene) vinyl] benzenamine (BFATVB) are also studied theoretically. The enhancement in the NLO properties of BCATVB and BFATVB is investigated through first and second hyperpolarizability calculations. The results of doped structures (BCATVB and BFATVB) are also compared with each other to study the doping effect of DATVB. This investigations is carried out using the quantum method approach, in particular the density functional theory (DFT).

Fig. 1
figure 1

4-[2-(2-N, N-dihydroxy amino thiophene) vinyl] benzenamine (DATVB) molecule

Full size image

2 Computational methodology and theoretical frame work

2.1 Computational methodology

In this study, the geometrical and electronic properties of all systems in their ground state are studied by density functional theory (DFT) using B3LYP and B3PW9 exchange–correlation functional combined with 6-311G +  + (d, p) basis set for all atoms to predict the optimized structures, optical properties, and the quantum chemical properties of all studied compounds. The DFT method has proven to be one of the most accurate methods for the computation of the electronic structure of solids [15, 18, 19]. The geometries were optimized by minimizing the energies with respect to all geometrical parameters without imposing any molecular symmetry constraints. Gauss View 6.0.16 [20] has been used to draw the structures of the optimized geometries. Also, frequency calculations were performed using the same level of theory. The B3LYP and B3PW91 has been chosen for our calculation in ground state for its performance to describe the optoelectronics properties for organic materials containing especially C, H, S and halogen atoms[21,22,23,24]. These two methods have been chosen for comparison purpose and also because no theoretical and experimental study have been done on these doped molecules. Besides B3LYP and B3PW91, calculations of dipole moment, polarizability and hyperpolarizability are also perform using CAM-B3LYP with the same basis set. This functional is quite reliable for excitation by charge transfer, non-covalent interactions [25,26,27,28,29]. The localization of electron populations has been obtained through the calculated electronic populations of the HOMO (Highest Occupied Molecular Orbital) and LUMO (Lowest Unoccupied Molecular Orbital) with their energy. All calculations have been performed by Gaussian 09 package [30].

2.2 Theoretical frame work

The mathematical relations used to calculate the optoelectronic, nonlinear optical, electronic transport and chemical parameters are as follows:

For optoelectronic properties, the electric displacement field is given by

$$D = \varepsilon_{0} E + P = \varepsilon_{0} \varepsilon_{r} E = \varepsilon_{0} \left( {1 + \chi_{e} } \right)E$$
(1)

where

$$P = \varepsilon_{0} \chi_{e} E = (\varepsilon_{r} - 1)E\varepsilon_{0}$$
(2)

is the density of polarization.

The refractive index is given by the relation:

$$n = \sqrt {1 + \chi_{e} }$$
(3)

In the non-linear domain, the dipole moment is governed by the formula: where

$$\mu = \alpha E + \beta E^{2} + \gamma E^{3} + \cdots$$
$$\beta = \left[ {\left( {\beta_{xxx} + \beta_{xyy} + \beta_{xzz} } \right)^{2} + \left( {\beta_{yyy} + \beta_{yxx} + \beta_{yzz} } \right)^{2} + \left( {\beta_{zzz} + \beta_{zxx} + \beta_{zyy} } \right)^{2} } \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}$$
(4)

and

$$\gamma = \left( {1/5} \right)\left[ {\gamma_{xxxx} + \gamma_{yyyy} + \gamma_{zzzz} + 2\left( {\gamma_{xxyy} + \gamma_{xxzz} + \gamma_{yyzz} } \right)} \right]$$
(5)

are respectively the first and the second hyperpolarisability.

The anisotropy, \(\Delta \alpha\) are calculated by

$$\Delta \alpha = \frac{1}{2}\left[ {\left( {\alpha_{xx} - \alpha_{yy} } \right)^{2} + \left( {\alpha_{yy} - \alpha_{zz} } \right)^{2} + \left( {\alpha_{zz} - \alpha_{xx} } \right)^{2} + 6\left( {\alpha_{xy}^{2} + \alpha_{yz}^{2} + \alpha_{zx}^{2} } \right)} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}$$
(6)

In the linear domain, β≈0, γ≈0, the dipole moment will be given by the formula

$$\mu = \alpha E$$
(7)

We show that:

$$\alpha = \frac{1}{3}\left( {\alpha_{xx} + \alpha_{yy} + \alpha_{zz} } \right)$$
(8)
$$\mu = \sqrt {\mu_{x}^{2} + \mu_{y}^{2} + \mu_{z}^{2} }$$
(9)

These relations above are also found in the literature [15, 16, 31,32,33,34,35].

For electronic transport and quantum chemical properties: parameters such as energy gap (Egap), ionization potential (IP), electron affinity (EA), global hardness (M), flexibility (ζ), electronegativity (∅), chemical potential (μc), and electrophilicity index (ω) are given by the following formulas [31, 36, 37]:

$${\text{ E}}_{{{\text{gap}}}} = {\text{E}}_{{{\text{LUMO}}}} - {\text{E}}_{{{\text{HOMO}}}}$$
(10)
$${\text{IP}} = - {\text{E}}_{{{\text{HOMO}}}}$$
(11)
$${\text{EA}} = - {\text{E}}_{{{\text{LUMO}}}}$$
(12)
$$\mu_{c} = - \left( {\frac{{{\text{IP}} + {\text{EA}}}}{2}} \right)$$
(13)
$$\emptyset = - \mu_{c}$$
(14)
$${\text{M}} = \frac{{{\text{IP}} - {\text{EA}}}}{2}$$
(15)
$$\zeta = \frac{1}{{\text{M}}}$$
(16)
$$\omega = \frac{{\mu_{c}^{2} }}{2M}$$
(17)

Piezoelectric materials are characterized by the piezoelectric (d) and pyroelectric (p) coefficients.

[38, 39]. The set of piezoelectricity equations is given by the relation (17):

$$\left\{ {\begin{array}{*{20}c} {D = \varepsilon^{T} E + dT} \\ {S = dE + S^{E} T} \\ \end{array} } \right.$$
(18)

\(D\): The electric displacement field (C.m−1), \(\varepsilon^{T}\): permittivity (F.m−1), E: the electric field (V.m−1), SE: compliance, T: mechanical stress (N.m−2), d: piezoelectric constant (C\(.N^{ - 1}\)), S: strain (m). The piezoelectric and pyroelectric coefficients are also given by the following relations:

$$\left\{ {\begin{array}{*{20}c} {d = \frac{\delta P}{{\delta T}}} \\ {p = \frac{\delta P}{{\delta T_{e} }}} \\ \end{array} } \right.$$
(19)

where Te is the temperature [40, 41].

3 Results and discussion

3.1 optimized structure

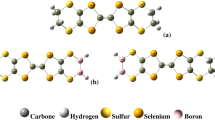
The optimized structure of the molecules doped with chlorine and fluorine are shown in Fig. 2.

Fig. 2
figure 2

Optimized structure of BCATVB and BFATVB respectively

Full size image

3.2 Geometric properties

Tables 1 and 2 respectively give us the interatomic distances and the valence angles of the various structures optimized according to the labels of the atoms. These optimized structures were obtained using the DFT (B3LYP /B3PW91) method with 6–311 +  + G (d, p) basis set. From our results, it can be seen that, the geometrical parameters of the two molecules varies slightly when we move from one method to another. Equally, no imaginary frequency was observed after optimization of our systems. This led us to the conclusion that the optimized molecular systems are stable at all the level and basis set used. Thus, when we compare these interatomic distances and valence angle with those obtained in previous work on the DATVB undoped molecule [16], the values obtained after doping are clearly higher, this is certainly due to the addition of halogens in the systems which creates load shifting and makes the system attractive. So we can conclude that doping influences the structural geometry of these compounds.

Table 1 Bond lengths (Å) in the molecules BCATVB and BFATVB obtained with B3LYP and B3PW91 using 6–311 +  + G (d, p) basis set
Full size table
Table 2 Bond angles (°) of molecules BCATVB and BFATVB obtained with B3LYP and B3PW91 using 6–311 +  + G (d, p) basis set
Full size table

3.3 Optoelectronic properties

Table 3 gives the values of the average electric field (E), the magnetic field (B), the phase celerity \(({V}_{ph}\)), the electric polarization density (P), the electrical susceptibility (χe), the relative dielectric constant ( ε), the refractive index (n), the electrical displacement vector (D), the radius (R) and the volume (V) of each molecule. These optoelectronic parameters were calculated applying the Eqs. (1, 2, 3) given above. The electric polarization density values (P) of the doped molecules are on average three times higher than that of the initial molecule studied by F. Tchangnwa Nya et al. [16]; similarly, the values of E, ε, n, D are much higher compare the results with the previous similar findings in previous works [15, 42]. These results led us to conclude that the doping of these materials with chlorine and fluorine promotes the dynamics and distribution of charges within these molecules. This makes them more likely to apply optoelectronic applications in particular in renewable energy for the production of photovoltaic cells, organic light emitting diodes and photonic devices.

Table 3 Average electric field (E), electric polarization density (P), electrical susceptibility (χe), relative dielectric constant (ε), refractive index (n), phase celerity \({(\mathrm{V}}_{\mathrm{ph}})\), magnetic field \((\mathrm{B})\), electric displacement vector (D), radius (R) and volume (V) of molecules BCATVB and BFATVB obtained with B3LYP and B3PW91 using 6–311 +  + G (d, p) basis set
Full size table

3.4 Transport properties and energy analysis

The energy difference between the HUMO-LUMO borders is called energy gap (\({E}_{gap}\)) [42]. The values of the energies \({E}_{HOMO}\) and \({E}_{LUMO}\) of these molecules, calculated are recorded in Table 4. \({E}_{gap}\) is a critical parameter for determining the electrical transport properties of a molecule. By using the values of the energies \(E_{HOMO}\) and \(E_{LUMO}\) for a molecule, the global descriptors of the chemical reactivity of the molecules such as the global hardness (M), the chemical potential (\({\mu }_{c}\)), the flexibility (ζ), the electronegativity (∅), the ionization potential (IP), the electronic affinity (EA) and the electrophilicity index (ω) were calculated using the mathematical formulas given earlier. These values are also recorded in Table 3. We observed that the gap energy (\(E_{gap}\)) of these two molecules varies between 1 eV and 1.5 eV, these energies being less than 3 eV. The calculated parameters shows that these materials are good semiconductors which further confirms the results presented above, so these materials can have applications in electronics, optoelectronics and photonics. [43,44,45,46,47]. Concerning the frontier molecular orbitals of our molecules. The highest occupied and the lowest unoccupied molecular orbitals (HOMO and LUMO respectively), are the most important parameters which permit us to know how the molecule interacts and explain the structure and reactivity of the molecules [35]. The HOMO which is nucleophilic or electron-donating, represent the capacity of a molecule to give an electron while LUMO which is electrophilic or electron-accepting, represent the capacity of a molecule to receive an electron. Figure 3 present the 3D molecular orbital diagrams. From this figure we can see that the halogen (chlorine and fluorine) atoms participates favorably in the charge-transfer to improve the electronic dynamism which reigns within these compounds. (Table 4)

Table 4 \({\text{E}}_{{{\text{LUMO}}}} ,{\text{E}}_{{{\text{HOMO}}}} , {\text{E}}_{{{\text{gap}}}}\), chemical potential (\(\mu_{c}\)), electronegativity (\(\emptyset\)), absolute hardness (M), softness (ζ), ionization potential (IP), Electronic affinity (EA) and electrophilic index (ω) of the molecules BCATVB and BFATVB obtained using B3LYP and B3PW91 with 6-311G +  + (d, p) basis set
Full size table
Fig. 3
figure 3

Diagram of the LUMO and HOMO molecular orbitals of the BCATVB and BFATVB structures obtained at the B3LYP/6–311 +  + G (d, p) level of theory

Full size image

3.5 Nonlinear optical properties

The organic compounds exhibiting a high hyperpolarisability are those which contain electron donor group and an electron attractor group interacting through a system of conjugated double bonds as observed in our studied systems. To fully understand the non-linear optical (NLO) properties, certain parameters such as dipole moment, polarizability, anisotropy, the first and second hyperpolarisability were calculated in this work. These parameters were obtained by applying the mathematical formulas (4, 5, 6, 7, 8) giving above. Table 5 presents these different calculated values. We note that the values of the dipole moments are around 13 Debye with B3LYP and B3PW91 and found around 5 Debye with CAM-B3LYP. We can therefore conclude that these different materials are polar as reported in the literature [33, 48]. Moreover when we observe the six components of the asymmetric tensor of polarizability as well as the ten components of the tensor of hyperpolarizability of the first order we note that only the components \({\alpha }_{\mathrm{xx}}\) and \({\beta }_{\mathrm{xxx}}\) have larger values, we can therefore conclude that these are parameters which give the linear and non-linear character respectively of these molecules. By comparing our values of the first order hyperpolarizabilities calculated with B3LYP, B3PW91 and CAM-B3LYP with the experimental values of para-nitroaniline (p-NA)\(\left( {\beta_{mol} \left( {esu} \right) = 9261,32.10^{ - 33} } \right)\) [49] and p-Na/CAM-B3LYP which is a reference organic molecule for the study of non-linear optical parameters of materials organic, we can see that our values are much higher than that of this referencing molecule, which suggests that our studied systems have very good NLO properties. In addition, our \(\beta_{mol}\) and \(\mu\) values are very much higher than those of other NLO compounds found in the other work [50,51,52,53,54,55] obtained with the same methods at the theoretical level and experimental. These result show us that these doped molecules (BCATVB and BFATVB) are very good materials for applications in non-linear optics namely in frequency shift, optical modulation, optical communication, optical logic, optical memories for emerging technologies in fields such as telecommunications, signal processing devices, dynamic imaging, data storage, computer devices and optical connectors [13, 14, 55].

Table 5 Dipolar moment (\(\mu \left( {{\text{Debye}}} \right)\)), average polarisability \(\left( {\left\langle {\upalpha } \right\rangle \left( {{\text{esu}}} \right) 10^{ - 24} } \right)\)), anisotropy \(\left( {\Delta {\upalpha }\left( {{\text{esu}}} \right).10^{ - 24} } \right)\), first order hyperpolarisability (\({\upbeta }_{{{\text{mol}}}} \left( {{\text{esu}}} \right)10^{ - 33}\)) and second order hyperpolarisability (\({\upgamma }\left( {{\text{esu}}} \right)10^{ - 36} )\) of the molecules BCATVB and BFATVB obtained using B3LYP and B3PW91 with 6-311G +  + (d, p) basis set
Full size table

3.6 Piezoelectric properties

Piezoelectricity is a renewable energy whose principle is to produce electricity thanks to a pressure exerted on a material. In 1880, the brothers Pierre and Jacques Curie undertook a theoretical and experimental study of the piezoelectric effect, which made it possible to establish the conditions that a material must meet to be piezoelectric. This work is considered to be the discovery of the direct piezoelectric effect [56]. So-called piezoelectric materials have the property of converting mechanical energy into electrical energy: under the effect of mechanical stress, the electrical polarization of the crystal is modified. Table 6 presents the values of the piezoelectric coefficients (d) and the average values of the pyroelectric coefficient (p) applying mathematical formulas presented previously. It should be noted that the volume obtained with the Gaussian software for a molecule, using the same method, the same basis of calculation and the same functional are not always the same. This may be due to the indefinite position of atoms in space. This same remark has been mentioned in the literature [55], this phenomenon allows the increase or decrease of the volume which causes a reorientation of the microscopic dipoles according to the literature [56] therefore the calculation of the piezoelectricity parameters is possible. From Table 6, it can be seen that the values of the piezoelectric coefficient of the fluorinated molecule are above that of the reference organic molecule polyvinylidene fluoride (PVDF), which values varies between 12 and 23 \(pC.N^{ - 1}\) [57,58,59]. We can therefore conclude that these molecules are piezoelectric materials and can be used in the manufacture of medical ultrasound or non-destructive testing equipment, components used in radio and telecommunications as a frequency reference or as a microphone or loudspeaker [56].

Table 6 Piezoelectric coefficient (d) and pyroelectric coefficient (p) of the molecules BCATVB and BFATVB obtained using B3LYP and B3PW91 with 6-311G +  + (d, p) basis set
Full size table

In this study the influence of temperature on the pyroelectric coefficient was also observed, the temperature was raised from 250 to 500 K with a step of 50 K.Table 7 presents the results obtained. We note that the pyroelectric coefficient is related to the variations of the elementary dipoles. It can be concluded that these molecules tend to lose their pyroelectric activity when the temperature increases. This result is also observed in the literature [60].

Table 7 Variation of the pyroelectric coefficient as a function of the temperature of the molecules BCTAVB and BFTAVB obtained using B3LYP and B3PW91 with 6-311G +  + (d, p) basis set
Full size table

3.7 Thermodynamic properties

Zero vibrational point energy (ZPVE), Gibbs free energy (G), thermal energy (E), entropy (S), enthalpy (H), Constant Volume Heat Capacity (Cv) were calculated at temperature Te = 298.15 K and pressure P = 1 atm. The results are recorded in Table 7. It is noted that these parameters are more important with the fluorinated molecule. This is simply due to the fact that, fluorine is more electronegative than chlorine. We also observe that the entropy of the doped materials is higher than that of the original molecule, which confirms what was said previously, the charge dynamics of the doped molecules are higher than its original molecule at the same temperature. This result further demonstrates that these doped materials have a high chemical reactivity and a high thermal resistivity, hence their application in the fields cited above. (Table 8)

Table 8 Zero Vibrational Point Energy (ZPVE), Gibbs free energy \(\left( {\text{G}} \right)\), Thermal Energy (E), Entropy (S), Enthalpy (H), Constant Volume Calorific Capacity (Cv), of the molecules BCATVB and BFATVB Obtained using B3LYP and B3PW91 with 6-311G +  + (d, p) basis set at constant temperature and pressure
Full size table

4 Conclusion

In this study, we addressed the effect of doping with halogens (chlorine and fluorine) on the 4- [2- (2-N, N-dihydroxy amino thiophene) vinyl] benzenamine (DATVB) molecule. This study were done using DFT methods at the (B3LYP, CAM-B3LYP and B3PW91) levels of the theory and with the 6–311 +  + g ** basis set. Some interesting results were found. The new materials resulting from this doping are 4-[2-(2-(5-(bis (chlorooxy) amino) thiophene) vinyl] benzenamine (BCATVB) and 4-[2-(2-(5-(bis (fluorooxy) amino) thiophene) vinyl] benzenamine (BFATVB). From this investigation, we found that, halogen doping systematically influences the structural, optoelectronic, nonlinear optical and thermodynamic properties. These properties are more interesting when compared to the undoped DATVB molecule. The value of the gap energy range between 1 and 1.5ev, value less than 3ev, shows that these doped materials are good semiconductors. In addition, these \({\text{E}}_{{{\text{gap}}}}\), for doped molecules are smaller than the theoretical values of the DATVB molecule studied in the literature. We believe that the intrinsic conductivity, optical transitions, or electronic transions of these molecules vary greatly. The piezoelectric coefficients of fluorine-doped molecule (BFATVB) calculated at the B3LYP and B3PW91 levels are greater than the experimental values of the piezoelectric reference molecule (p-Na) found in the literature. This result opens up another field of application of this molecule in piezoelectricity as in the manufacture of medical ultrasound or non-destructive testing equipment, components used in radio and telecommunications as a frequency reference or as a microphone or loudspeaker and many more. The thermodynamic properties obtained show that they have a high chemical reactivity and a high thermal resistivity. The large values of the average electric field, first molecular hyperpolarizability, total dipole moment, average polarizability, refractive index, electric susceptibility and small value of the dielectric constant of our molecule suggest the potential applications of the molecule in the development of nonlinear optical materials.