1 Introduction

The issues pertinent to the laminar, and forced convection heat transfer in a plane duct is very significant in heat exchangers design, cooling of electronic systems, etc. Most industrial fluids such as suspensions, emulsions, polymer solutions of liquid adhesives have non-Newtonian behavior. Due to the inherent complexity of their fundamental equations, it is hard to achieve an exact solution even in simple geometries. Therefore, we have to use numerical or semi-analytical methods to calculate the velocity field and temperature field in the non-Newtonian fluid flows.

Another interesting issue in new technology, which is very important in heat transfer, is the heat transfer problem of the magnetohydrodynamic (MHD) flow [1, 2]. The magnetic field can be applied as a powerful implement to control the flow by exerting the Lorentz force [3].

Hayat et al. [4] provided an analytical study of third-grade flow in a porous channel. They employed the analytical homotopy method to investigate the effects of Reynolds number and Hartmann number on the flow. The results revealed that the homotopy method is a convenient, effective, and converge method for analyzing non-Newtonian problems.

Ziabakhsh and Domairry [5] presented an analytical solution for a third-grade non-Newtonian natural convection flow between to vertical flat plate. They used the analytical homotopy analysis method (HAM) for solving the governing equations; also, validated their solution using the numerical method. The increase of Prandtl and Eckert numbers leads to the augmentation of the dimensionless velocity and temperature.

Hosseini et al. [6] solved the momentum and energy of a non-Newtonian fluid in an axisymmetric channel with a porous wall using the optimal homotopy analysis method (OHAM). The numerical method was used to validate the results. The application of the problem was the turbine cooling.

Ellahi et al. [7] studied the heat transfer of MHD third-grade non-Newtonian fluid flow with constant and variable viscosity in a pipe with constant wall temperature. They applied HAM for solving the governing equations and obtained the velocity and temperature distributions. They reported that the increase in the pressure gradient leads to the reduction of fluid velocity. Besides, as the non-Newtonian and magnetic field parameters increase, the velocity and temperature reduce.

An investigation of a steady fourth-grade non-Newtonian fluid when the slip occurred between the plate and fluid was conducted by Islam et al. [8]. They used OHAM for solving the problem and observed that the velocity reduces as the slip parameter rises. Further, the velocity reduces as the non-Newtonian and pressure parameters decline.

Abbasi et al. [9] provided an analytical analysis for fourth-grade non-Newtonian fluid flow in a channel using HAM and VIM. They showed that HAM is a suitable, simple, and more accurate method in comparison with the other analytical methods.

Ghasemi et al. [10] studied the fully developed, fourth-grade non-Newtonian fluid flow under the influence of the magnetic field in a channel considering the slip condition, analytically. They used the analytical collocation method (CM) and concluded that if the non-Newtonian parameter increases, the velocity profile becomes flattened. Besides, the Hartmann number augmentation increases the velocity, and the reduction of the slip parameter declines the velocity.

An analytical solution of third-grade non-Newtonian fluid flow and heat transfer between two parallel plates was examined by Ahmed et al. [11]. The investigation was performed in two cases. In the first case, the bottom plate is stable, and the upper wall moved with constant velocity. In the second case, both plates were considered fixed, and the pressure gradient drives the fluid flow. Besides, in both cases, the temperature of the plates was considered constant. They used an analytical method for solving the problem and validated using a numerical method.

Ebrahimi et al. [12] presented an analytical investigation on heat transfer of a third-grade non-Newtonian flow in a plane channel with the convection boundary layer on the walls. They used CM for solving the governing equations and demonstrated the dimensionless velocity and temperature profiles become more flattened when the non-Newtonian parameter increases. Hence, the convective heat transfer declines.

In the other investigation, Ebrahimi et al. [13] investigated on fourth-grade non-Newtonian fluid flow and heat transfer in a plane duct with the convection heat transfer on the walls. They solved the governing equations using the finite element method. For the validity, they applied the 4th order Runge–Kutta (RK4) method. They revealed that the increase of the non-Newtonian parameter and Biot number lead to the reduction of the dimensionless velocity, temperature, and temperature gradient; hence, the heat transfer rate decreases.

The main objective of this research is to apply the analytical least square method (LSM) for solving the momentum and full energy equations of fourth-grade non-Newtonian fluid flow in a plane duct with the convection heat transfer on the walls. The accuracy of the results is examined in comparison with the numerical 4th order Runge–Kutta (RK4) method. The other aim of the research is to obtain the velocity and temperature distribution; furthermore, the effect of physical parameters such as the magnetic field angle, non-Newtonian parameter, forced convection heat transfer boundary on the duct wall, etc.

The following sections provide the illustration and definition of the problem, the introduction of governing equations, boundary conditions, and the dimensionless parameters. Hereafter, the solution methodology is defined, the validation of the results presented, and the discussion is provided.

2 Problem statement

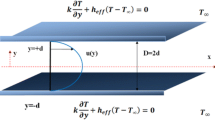
In Fig. 1, a plane duct under the influence of the angular magnetic field is depicted. A steady, laminar, incompressible, non-Newtonian fluid flows through the duct.

Fig. 1
figure 1

Problem schematic

Full size image

The forced convection heat transfer and a uniform applied magnetic field with α angle regard to the duct perpendicular axes are introduced on the duct walls. The flow is fully developed, as well all the thermophysical properties are considered constant.

The governing equations including the continuity, momentum, and energy are introduced as [13]:

$$\vec{\nabla }.\rho \vec{V} = 0$$
(1)
$$\rho \frac{{D\vec{V}}}{Dt} = - \vec{\nabla }p + \rho gh + \nabla .\tau + \vec{J} \times \vec{B}$$
(2)
$$\rho C_{p} \frac{DT}{{Dt}} = k\nabla^{2} T - \vec{V}.(\vec{J} \times \vec{B}) + \tau L$$
(3)

where τL is the viscous dissipation term. Besides, the last term in the right-hand side of Eq. (2) is the volumetric Lorentz force term and the second term in the right-hand side of Eq. (3), is the Joule heating term.

2.1 Momentum equation

By inserting Cauchy stress pertinent to fourth-grade non-Newtonian fluid in Eq. (2), and also neglecting the gravity force, the momentum equations are obtained as [13]:

x-momentum

$$\mu \left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) + 6(\beta_{2} + \beta_{3} )\left( {\frac{d}{dy}u\left( y \right)} \right)^{2} \left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) - \sigma B_{0}^{2} u\left( y \right)\cos^{2} \alpha = \frac{\partial }{\partial x}p\left( {x,y} \right)$$
(4)

y-momentum

$$\left( {2\alpha_{2} \left( {\frac{d}{dy}u\left( y \right)} \right) + 8\gamma_{6} \left( {\frac{d}{dy}u\left( y \right)} \right)^{3} } \right)\left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) + \sigma B_{0}^{2} u\left( y \right)\sin \alpha \cos \alpha = \frac{\partial }{\partial y}p\left( {x,y} \right)$$
(5)

By integrating Eq. (5) with respect to y, we have:

$$p = \int {\left( {\left( {2\alpha_{2} \left( {\frac{d}{dy}u\left( y \right)} \right) + 8\gamma_{6} \left( {\frac{d}{dy}u\left( y \right)} \right)^{3} } \right)\left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) + \sigma B_{0}^{2} u\left( y \right)\sin \alpha \cos \alpha } \right)} dy = F(y) + p^{*} (x)$$
(6)

We know that p is the function of x and y; therefore, the integral constant (p*(x)) is the function of x. Hence, by differentiating Eq. (6) with respect to x, yields:

$$\frac{\partial p}{{\partial x}} = \frac{{dp^{*} }}{dx}$$
(7)

Substituting Eq. (7) into Eq. (4) we have:

$$\mu \left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) + 6(\beta_{2} + \beta_{3} )\left( {\frac{d}{dy}u\left( y \right)} \right)^{2} \left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) - \sigma B_{0}^{2} u\left( y \right)\cos^{2} \alpha = \frac{{dp^{*} }}{dx}$$
(8)

In Eq. (8); the left side is the function of y; while, the other side is the function of x. Thus, the pressure gradient can be assumed as a determined quantity. As a result, the momentum equation is defined as follows:

$$\mu \left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) + 6(\beta_{2} + \beta_{3} )\left( {\frac{d}{dy}u\left( y \right)} \right)^{2} \left( {\frac{{d^{2} }}{{dy^{2} }}u\left( y \right)} \right) - \sigma B_{0}^{2} u\left( y \right)\cos^{2} \alpha - \frac{{dp^{*} }}{dx} = 0$$
(9)

2.2 Energy equation

According to the aforementioned assumptions, the energy equations can be obtained as follows:

$$u\frac{\partial T}{{\partial x}} = \left( {\frac{k}{{\rho c_{p} }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \left( {\frac{1}{{\rho c_{p} }}} \right)\left( {\mu \left( {\frac{\partial u}{{\partial y}}} \right)^{2} + 2(\beta_{2} + \beta_{3} )\left( {\frac{\partial u}{{\partial y}}} \right)^{4} } \right) + \frac{{\sigma \,B_{0}^{2} \cos^{2} \alpha }}{{\rho c_{p} }}u^{2}$$
(10)

The governing equations including Eq. (9) and (10) have to be solved. For obtaining the generalized solution, the governing equations are transformed into the dimensionless form. The dimensionless parameters are introduced as [13]:

$$\eta = \frac{y}{d},\,\,\,\,\,\,U(\eta ) = \frac{\mu u(y)}{{\left( {\frac{{dp^{*} }}{dx}} \right)d^{2} }},\,\,\,\,\,\theta \left( \eta \right) = \frac{{\left( {T_{\infty } - T} \right)}}{{\left( {T_{\infty } - T_{m} } \right)}}$$
(11)

where Tm is the fluid bulk temperature inside the duct and T∞ is the free flow temperature outside the duct.

By inserting Eq. (11) into Eq. (9) and Eq. (10), we obtain:

$$\frac{{d^{2} U}}{{d\eta^{2} }} + \beta \left( {\frac{dU}{{d\eta }}} \right)^{2} \frac{{d^{2} U}}{{d\eta^{2} }} - Ha\cos^{2} \alpha U - 1 = 0$$
(12)
$$u\theta \frac{{\partial T_{m} }}{\partial x} = - \left( {\frac{k}{{\rho c_{p} }}} \right)\left( {\frac{{T_{\infty } - T_{m} }}{{d^{2} }}} \right)\left( {\frac{{\partial^{2} \theta }}{{\partial \eta^{2} }}} \right) + \left( {\frac{1}{{\rho c_{p} }}} \right)\left( {\mu \left( {\frac{\partial u}{{\partial y}}} \right)^{2} + 2\left( {\beta_{2} + \beta_{3} } \right)\left( {\frac{\partial u}{{\partial y}}} \right)^{4} } \right) + \frac{{\sigma B_{0}^{2} \cos^{2} \alpha }}{{\rho c_{p} }}u^{2}$$
(13)

where Ha is the Hartmann number and β is the non-Newtonian parameter are defined as [13]:

$$Ha = \frac{{\sigma d^{2} B_{0}^{2} }}{\mu },\,\,\,\,\,\,\beta = \frac{{6\left( {\beta_{2} + \beta_{3} } \right)\left( {\frac{{dp^{*} }}{dx}} \right)^{2} d^{2} }}{{\mu^{3} }}$$
(14)

According to Fig. 2, the energy balance is applied for determining \(\frac{{\partial T_{m} }}{\partial x}\) in Eq. (13). In Fig. 2, ϕ is the viscous dissipation and heff is the effective convective heat transfer coefficient; which is defined as:

$$h_{eff} = \frac{1}{{\frac{{\delta_{w} }}{{k_{w} }} + \frac{1}{{h_{e} }}}}$$
(15)
Fig. 2
figure 2

Energy balance

Full size image

where he is the outer convective heat transfer coefficient, kw and δw are the plates thickness and the outer thermal conductive coefficient, respectively.

Using the energy balance and doing some algebraic manipulation, we have:

$$\begin{gathered} \frac{{\partial^{2} \theta }}{{\partial \eta^{2} }} + \left( {Bi + Ec\Pr \left( {\frac{\partial U}{{\partial \eta }}} \right)^{2} + \frac{1}{3}\beta Ec\Pr \left( {\frac{\partial U}{{\partial \eta }}} \right)^{4} + HaEc\Pr \cos^{2} \alpha U^{2} } \right)\frac{U}{{\int_{0}^{1} {Ud\eta } }}\theta \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - Ec\Pr \left( {\frac{\partial U}{{\partial \eta }}} \right)^{2} - \frac{1}{3}\beta Ec\Pr \left( {\frac{\partial U}{{\partial \eta }}} \right)^{4} - HaEc\Pr \cos^{2} \alpha U^{2} = 0 \hfill \\ \end{gathered}$$
(16)

where Pr denote the Prandtl number, Ec denote the Eckert number and Bi denote the Biot number and are defined as:

$$Bi = \frac{{h_{eff} d}}{k},\,\,\,\,Ec = \frac{{\left( {\frac{{dp^{*} }}{dx}} \right)^{2} d^{4} }}{{\mu^{2} c_{p} (T_{\infty } - T_{m} )}},\,\,\,\,\,\Pr = \frac{{\mu c_{p} }}{k}$$
(17)

2.3 Boundary conditions

Due to the geometric symmetry and symmetric boundary conditions of velocity and temperature on the walls, the velocity and temperature gradient in the centerline of the channel is zero; hence, the boundary conditions are introduced as follows:

$$\begin{gathered} y = 0:\,\,\,\,\frac{\partial u}{{\partial y}} = 0\,\,,\,\,\,\,\,\,\frac{\partial T}{{\partial y}} = 0\,\, \hfill \\ y = d:\,\,\,\,u = 0\,\,,\,\,\,\,k\frac{\partial T}{{\partial y}} + h_{eff} \left( {T - T_{\infty } } \right) = 0\,\,\, \hfill \\ \end{gathered}$$
(18)

Similarly, the boundary conditions are transformed into the dimensionless form are given as:

$$\begin{gathered} \eta = 0,\,\,\,\,\frac{\partial U}{{\partial \eta }} = 0,\,\,\,\frac{\partial \theta }{{\partial \eta }} = 0 \hfill \\ \eta = 1,\,\,\,\,U = 0,\,\,\,\,\,\frac{\partial \theta }{{\partial \eta }} + Bi.\theta = 0 \hfill \\ \end{gathered}$$
(19)

3 Solution procedure

For solving the nonlinear dimensionless governing equations, the analytical least square method (LSM) is applied. LSM is one of the approximation techniques for solving differential equations named the method of residual weight. The mathematical and theoretical detail of LSM is elaborated in [14, 15]. The main concept of this method is approximating a trail function in a way that the boundary conditions are satisfied. The trail function has some unknown coefficients. This method aims to determine the value of the unknown coefficients, in which the residual tends to be zero.

The trail functions for solving Eqs. (12) and (16) are approximated as follows:

$$U(\eta ) = c_{1} \left( {\eta^{2} - 1} \right) + c_{2} \left( {\eta^{3} - 1} \right) + c_{3} \left( {\eta^{4} - 1} \right) + c_{4} \left( {\eta^{5} - 1} \right)$$
(20)
$$\theta (\eta ) = \frac{1}{Bi}\left[ {b_{1} \left( {\eta^{2} - 1 - \frac{2}{Bi}} \right) + b_{2} \left( {\eta^{3} - 1 - \frac{3}{Bi}} \right) + b_{3} \left( {\eta^{4} - 1 - \frac{4}{Bi}} \right) + b_{4} \left( {\eta^{5} - 1 - \frac{5}{Bi}} \right)} \right]$$
(21)

It is obvious Eqs. (20) and (21) are satisfied with the boundary conditions (Eq. (19)).

4 Results and discussion

Primarily, the validity of the obtained results has to be checked; hence, the numerical 4th order Runge–Kutta (RK4) method is employed. In Figs. 3, 4 and 5, the comparison of LSM results with RK4 is illustrated. It can be seen that the accuracy of LSM is significant, and there is excellent agreement between LSM and RK4 results.

Fig. 3
figure 3

Comparison of LSM with RK4 for U

Full size image
Fig. 4
figure 4

Comparison of LSM with RK4 for θ

Full size image
Fig. 5
figure 5

Comparison of LSM with RK4 for \(\frac{d\theta }{{d\eta }}\)

Full size image

In the following, the impact of thermophysical parameters on the dimensionless velocity profile, dimensionless temperature profile, and dimensionless temperature gradient is discussed.

In Fig. 6, the influence of β is plotted. When β increases, U becomes flattened; thus, the average velocity inside the duct reduces. Due to the existing pressure gradient in the dimensionless velocity definition, the velocity value is negative. Moreover, the effect of β on θ and \(\frac{d\theta }{{d\eta }}\) is depicted in Figs. 7 and 8. It can be observed that the increase of this parameter leads to a reduction of θ. Generally, as β increases, θ becomes flattened, and the bulk temperature inside the duct declines. Consequently, due to the reduction f velocity inside the duct, the absolute value of the temperature gradient reduces on the duct wall. Thus, the dimensionless heat transfer rate on the duct wall decreases. The results are in agreement with refs [16] and [13].

Fig. 6
figure 6

Effect of β on U

Full size image
Fig. 7
figure 7

Effect of β on θ

Full size image
Fig. 8
figure 8

Effect of β on \(\frac{d\theta }{{d\eta }}\)

Full size image

The impact of Ha is discussed in the following. Since Ha increases, U and the θ have been reduced (Figs. 9 and 10). The Lorentz force rises, whereas the bulk temperature declines, and both U and θ become flattened. Besides, the augmentation of the Lorentz force leads to the reduction of velocity inside the duct; as a result, the increase of Ha leads to a reduction in \(\frac{d\theta }{{d\eta }}\) (Fig. 11). Therefore, the heat transfer rate decreases. A similar result was reported in refs [16] and [13].

Fig. 9
figure 9

Effect of Ha on U

Full size image
Fig. 10
figure 10

Effect of Ha on θ

Full size image
Fig. 11
figure 11

Effect of Hartmann number (Ha) on \(\frac{d\theta }{{d\eta }}\)

Full size image

The influence of the magnetic field angle (α) on U is presented in Fig. 12. The average velocity inside the duct increases as the magnetic field angle rises. The increase of α leads to the decreases of Lorentz force; so, the flow velocity increases. Further, the increase of α, augment θ and \(\frac{d\theta }{{d\eta }}\) (Figs. 13 and 14). Indeed, the bulk temperature inside the duct and the heat transfer rate on the duct wall increases.

Fig. 12
figure 12

Effect of magnetic field angle (\(\alpha\)) on U

Full size image
Fig. 13
figure 13

Effect of \(\alpha\) on θ

Full size image
Fig. 14
figure 14

Effect of α on \(\frac{d\theta }{{d\eta }}\)

Full size image

The other parameter to be discussed is Pr. Prandtl's number is defined as the ratio of momentum diffusion to thermal diffusion. According to Pr definition, θ becomes flattened when Pr reduces; hence, θ becomes more uniform (Fig. 15). Further, Fig. 15 shows when Pr increases, the dimensionless temperature inside the duct increases. Besides, the augmentation of Pr leads to an increase in heat transfer rate towards the duct walls (Fig. 16). The results can be validated according to ref.[13].

Fig. 15
figure 15

Effect of Pr on θ

Full size image
Fig. 16
figure 16

Effect of Prandtl number (Pr) on \(\frac{d\theta }{{d\eta }}\)

Full size image

The influence of Ec on θ and \(\frac{d\theta }{{d\eta }}\) are demonstrated in Fig. 17 and Fig. 18. Either due to the reduction of the temperature difference between the average bulk temperature and the duct outside temperature or the augmentation of the pressure gradient inside the duct, θ rises when Ec increases. Furthermore, the dimensionless temperature profile becomes flattened and θ becomes more uniform. Also, the absolute value of \(\frac{d\theta }{{d\eta }}\) increases inside the duct; hereupon, the dimensionless heat transfer rate rises. These results are in agreement with refs [16]. and [13].

Fig. 17
figure 17

Effect of Eckert number (Ec) on θ

Full size image
Fig. 18
figure 18

Effect of Ec on \(\frac{d\theta }{{d\eta }}\)

Full size image

The impact of the Bi on the θ and \(\frac{d\theta }{{d\eta }}\) in Figs. 19 and 20. Generally, θ has been reduced since Bi augments. Besides, the absolute value of \(\frac{d\theta }{{d\eta }}\) increases first and then decreases; therefore, the heat transfer rate on the duct wall declines. It can be expressed that the effective convective heat transfer coefficient on the duct wall increases when the Bi increases in a small value. Although, with the more increase of Bi, the heat transfer rate on the wall reduces due to the reduction of the conductive heat transfer coefficient. The results of Bi impact on the temperature can be validated by ref.[13]; however, the results of the temperature gradient are somewhat different. This can be due to the difference in the range of Bi in the present work compared to the ref.[13].

Fig. 19
figure 19

Effect of Bi on θ

Full size image
Fig. 20
figure 20

Effect of Bi on \(\frac{d\theta }{{d\eta }}\)

Full size image

5 Conclusion

In the present study, we employed the analytical least square method (LSM) to solve the full energy equation of a laminar, steady, and fully developed MHD fourth-grade non-Newtonian flow in a duct. The angular magnetic field is exerted on the duct wall; furthermore, the forced convection heat transfer is considered on the duct walls. The dimensionless velocity and temperature distributions are obtained, and the effect of various parameters is discussed. It is observed that the average velocity and the bulk temperature decline inside the duct when the non-Newtonian parameter augments. As a result, the heat transfer rate reduces. The influence of the Hartmann number is similar to the behavior of the non-Newtonian parameter. Besides, since the magnetic field increases, the average velocity and the bulk temperature on the duct wall has been augmented; hence, the heat transfer rate increase. Moreover, due to the reduction of the Prandtl number and augmentation of the Eckert number, the dimensionless temperature profile becomes more flattened. Therefore, the dimensionless temperature distribution becomes more uniform, and the heat transfer rate increases. Also, when the Biot number increases, the dimensionless temperature inside the duct reduces; however, the dimensionless temperature gradient increases first and then reduce. In the present study, we neglected the influence of electromagnetic nuisances and considered the fluid flow fully developed. Therefore, in the future study, it is recommended the influence of electromagnetic nuisances will be considered by the researcher, and the fluid flow and heat transfer are analyzed in the entrance region of the duct.