1 Introduction

Flows of immiscible materials in the channel/pipe are commonly found in nature. The study of simultaneous flow of two or more immiscible fluids is significant due to its wide applications in science, medical, geophysics, industry, petroleum engineering and hydrogeology [1,2,3,4]. Various applications include oil recovery, blood flow through capillary vessels, equipment cleaning, bio-films and mucus flow in living cells, removal of carbon dioxide from the atmosphere, groundwater management, crude oil flow through pipelines, bubble generation in microfluidics and bubble trains flow in various complex porous systems.

Several researchers have studied the stability/instability of two-layer or multi-layer immiscible fluids flow [5,6,7]. The linear stability of the viscoelastic two-layered plane Poiseuille and Couette flows have been first studied by Yih [8] with the help of long-wave approach. He observed that both density and viscosity stratification can cause interfacial Kelvin–Helmholtz instability. Herve Le Meur [9] has studied the uniqueness and the existence of the multi-layered Poiseuille/ Couette fluid flow in pipes/channel and observed that interpolated Oldroyd derivative parameter and the viscosity ratios are significant for a unique solution. Kalogirou and Blyth [10] have considered the Couette–Poiseuille flow of the two-layered superposed fluids to discuss stability. The fluid at the lower layer is populated with surfactants and these surfactants get adsorbed on the interface. It has been observed that if the thickness ratio is much higher than the fluid viscosity ratio and if the surfactant is sufficiently soluble, the flow is stable.

In [11], Kim et al. have worked on the two-layered immiscible Couette flow with the help of a hybrid method. The flow is between two parallel planes in which the upper plane is moving while the lower plane is kept stationary. It has been found that the viscosity ratio has strong effects on the fluid velocity than the surface energy. Two layer simultaneous natural convectional flow in a vertical semi-corrugated channel under the magnetic effects have been investigated by Abd Elmaboud [12]. The flow domain consists of two subdomains, the first one contains the magneto nanofluids, and the other contains a pure non-conducting viscous fluid. The results demonstrate that in the absence of heat soures nad with the rise in the nano-particle volume fraction, theremal transfer enhancement has been observed in both sub-domains. Later, Abd Elmaboud et al. [13], have studied the electro-magnetic simultaneous two layers immiscible fluids flow over an inclined plate. The flow domain comprises two parts, one of which is made of porous matrix saturated in Newtonian fluid, and the other has clear fluid. The findings demonstrate that the electrical field raises the velocity profile of both subdomains. Whereas the velocity decreases by rising the magnetic field owing to the Lorentz power. In [14], Khan et al have investigated the heat transfer and the fluid velocity of the two-layer immiscible fluid in the presence of pressure type die. The first layer is filled with the inelastic fluid, namely, power-law fluid and the second layer is filled with the viscoelastic liquid (Phan-Thien–Tanner fluids). It has been seen that the fluid velocity and the fluid temperature increase with the increase in the Deborah number.

Hisham et al. [15], for example, presented an analytical study of the two-layer flow of immiscible Maxwell fluids between two parallel moving plates in the presence of time-dependent pressure gradient. Analytical solutions for velocities and shear stresses are recovered with the help of integral transforms, Laplace and finite Fourier sine transform. It has been found that the increase in kinematic viscosity decreases the maximum value of the velocity. Later Rauf et al. [16], found the analytical and the semi-analytical solutions for the velocity fields and the temperature fields for the simultaneous flow of n-immiscible fractional Maxwell fluid in a rectangular channel bounded by the two parallel translating planes and in the presence of time-dependent pressure gradient. It has been observed that the thermal transport in the ordinary fluids is higher as compared with the fluids with the thermal memory, whereas the fractional parameters for the velocity fields act as accelerating factors of the fluids. Recently Rauf et al. [17], studied the simultaneous flow of n-immiscible fractional Maxwell fluid in a cylindrical domain. The motion is caused by the translational motion of the cylinder and in the presence of the time-dependent pressure gradient in the direction of the flow. Analytical solutions for the velocities and the shear stresses are obtained with the help of the Laplace transform coupled with the finite Weber transform of order zero and the finite Hankel transform of order zero. It has been seen that the fluid velocity decreases with the increase in the values of the fluids fractional parameters. Other interesting results relating to sigle layer fluid flow [18,19,20,21] and simultaneous flow two or more fluids can be seen in [7, 15, 22,23,24,25,26]. To the best of authors knowledge, the study of simultaneous flow of multi-layer immiscible second grade not exist in literature. In this paper, we have carried out this study.

Modeling of complex systems with the fractional order differential and integral operators have applications in many fields of science such as geophysics, biology, demography, bioengineering, physics and mathematics; see [27] and the references therein. There exist many fractional differential operators in literature such as Caputo-Fabrizio fractional derivative [27], Riemann–Liouville fractional integral/derivative [28], Caputo fractional derivative [29], and Yang-Srivastava-Machado fractional derivative [30], are some of the examples of the fractional-order differential operators used in viscoelasticity, mass and heat transport processes. Hristov [31] studied the transient space-fractional diffusion with power-law superdiffusivity modeled by the Riemann–Liouville fractional derivative. Ahmad et al.  [32] have applied the time-fractional Caputo–Fabrizio derivative to study the two-dimensional advective diffusion process with concentrated source and the short-range memory.

In this paper, we have studied the multi-layer flow of immiscible fractional second grade fluids between two parallel plates. We have considered an unsteady, incompressible, and one dimensional fully developed flow which is generated by the movement of the boundary walls and the time-dependent pressure gradient in the presence of the generalized thermal flux within the fluid layers. Moreover, we have considered the linear interfacial fluid–fluid condition between two consecutive layers. To find analytical solutions for velocities and shear stresses we have used finite Fourier sine transform in conjunction with the Laplace transformation. The main advantage of the analytic solution is that comparing an analytical solution with the numerical scheme is the best way to examine the accuracy. A semi-analytical solution for temperature fields is recovered with the help of Laplace transform and Tablot’s algorithms used for the numerical Laplace inversion.

2 Mathematical modeling

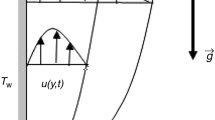
The flow domain for the simultaneous n-layer flow of the fractional second grade fluids is \(D' = \left\{ {\left( {x',y',z'} \right) ,\; { - \infty<x',z'<\infty },\;{0\le y'\le h}} \right\}\) with the boundary walls situated in planes \(y'=0\) and \(y'=h>0\). Initially at time \(t'=0\)  both boundary plates and the fluids enclosed inside them are at rest. After this moment, the boundary plate at \(y'=0\) start translating towards the \(x'\)-axis with the velocity \(u_{10}'=U_0f_1(t')\), whereas the other plate at \(y'=h\) moves parallel to the \(x'\)-axis with the velocity \(u'_{20}=U_0g_1(t')\) (Fig. 1), where \(U_0\) is the characteristic velocity. We assumes that the functions \(f_1(t')\) \(g_1(t')\) are piece-wise continuous functions with \(f_1(0)=g_1(0)=0\). We assume that the n-layer flow of fluids is immiscible, fully developed, unsteady and one dimensional. The motion of the fluids is caused by the motion of the boundary walls and the time-dependent pressure gradient in the direction of the flow. Under the given conditions, fluids velocities take the form \(\mathbf {v'}_i=(u'_i(y',t'),0,0)\). Let \(h_0=0\) and \(h_n=h\). In the region \(y'\in [h_{i-1},h_i]\),\(h_{i-1}<h_i\) flows a second grade fluid with viscosity \(\mu _{i}\), the density \(\rho _{i}\), \(G_i\), the elastic modulus, velocity \(u'_i(y',t')\) and the share stress \(\tau '_i(y',t')\)  where \(i=1,2,\ldots ,n\). We fix here the notations \(I_n^1:=\{1,2,\ldots ,n\}\), \(I_{n-1}^0:=\{0,1,\ldots ,n-1\}\). The continuity equation is identically satisfied by all velocities \(u_i(y',t')\), \(i\in I_n^1\). The governing equations of motion along with initial, boundary and the fluid–fluid interfacial conditions are

Fig. 1
figure 1

Geometry of the problem

Full size image

  • the system of linear momentum equations

    $$\begin{aligned} \rho _i\frac{\partial u'_i}{\partial t'}=\frac{\partial \tau '_i}{\partial y'}-\frac{\partial p'}{\partial x'},\qquad i\in I_n^1, \end{aligned}$$
    (1)

  • the system of constitutive equations

    $$\begin{aligned} {\tau '_i} = \bigg ({\mu _i}+\alpha _i' \frac{{\partial {{u'}_i}}}{{\partial t'}}\bigg )\frac{{\partial {{u'}_i}}}{{\partial y'}},i \in I_n^1, \end{aligned}$$
    (2)

  • the initial conditions

    $$\begin{aligned} {u'_i}\left( {y',0} \right) = 0,{\tau '_i}\left( {y',0} \right) = 0,i \in I_n^1 \end{aligned}$$
    (3)

  • the boundary conditions

    $$\begin{aligned} \text {at } y'=0,\qquad \qquad \qquad {u'_1}\left( {0,t'} \right) = {U_0}{f_1}\left( {t'} \right) , \end{aligned}$$
    $$\begin{aligned} \text {at } y' = {h_n} = h,\qquad \qquad {u'_n}\left( {h,t'} \right) = {U_0}{g_1}\left( {t'} \right) , \end{aligned}$$
    (4)

  • the fluid–fluid interface conditions

    $$\begin{aligned} {u'_i}\left( {{h_i},t'} \right) = {u'_{i + 1}}\left( {{h_i},t'} \right) ,{\tau '_i}\left( {{h_i},t'} \right) = {\tau '_{i + 1}}\left( {{h_i},t'} \right) ,i \in I_{n - 1}^1 \end{aligned}$$
    (5)

    Consider the following non-dimensional parameters into Eqs. (1)–(5),

    $$\begin{aligned} x=\, & {} \frac{{x'}}{h},y = \frac{{y'}}{h},t = \frac{{{\nu _1}t'}}{{{h^2}}},{u_i} = \frac{{{{u'}_i}}}{{{U_0}}},{\tau _i} = \frac{{h{{\tau '}_i}}}{{{\mu _1}{U_0}}},\\ {\nu _i}=\, & {} \frac{{{\mu _i}}}{{{\rho _i}}},p = \frac{{hp'}}{{{\mu _1}{U_0}}},\\ {\alpha _i}= \,& {} \frac{{{{\alpha '}_i U_0}}}{{{\rho _1 h^2}}},{a_i} = \frac{{{\rho _i}}}{{{\rho _1}}},{b_i} = \frac{{{\mu _i}}}{{{\mu _1}}},\\ f(t)=\, & {} {f_1}\left( {\frac{{{h^2}t}}{{{\nu _1}}}} \right) ,g\left( t \right) = {g_1}\left( {\frac{{{h^2}t}}{{{\nu _1}}}} \right) ,\\ {d_i}=\, & {} \frac{{{h_i}}}{h},{\sigma _i} = \frac{{{\nu _i}}}{{{\nu _1}}},i \in I_n^1, \end{aligned}$$

we get the following non-dimensional mathematical model for governing equations,

$$\begin{aligned} {a_i}\frac{{\partial {u_i}}}{{\partial t}}=\, & {} - \frac{{\partial p}}{{\partial x}} + \frac{{\partial {\tau _i}}}{{\partial y}},i \in I_n^1, \end{aligned}$$
(6)
$$\begin{aligned} {\tau _i}=\, & {} \bigg ({b_i} + {\alpha _i}\frac{{\partial {u_i}}}{{\partial t}} \bigg )\frac{{\partial {u_i}}}{{\partial y}},i \in I_n^1, \end{aligned}$$
(7)

along with the dimensionless initial conditions, the boundary conditions and the interface conditions

$$\begin{aligned} {u_i}\left( {y,0} \right)=\, & {} 0,{\tau _i}\left( {y,0} \right) = 0,i \in I_n^1, \end{aligned}$$
(8)
$$\begin{aligned} {u_1}\left( {0,t} \right)=\, & {} f\left( t \right) ,{u_n}\left( {1,t} \right) = g\left( t \right) , \end{aligned}$$
(9)

the interface conditions

$$\begin{aligned} {u_i}\left( {{d_i},t} \right) = {u_{i + 1}}\left( {{d_i},t} \right) ,{\tau _i}\left( {{d_i},t} \right) = {\tau _{i + 1}}\left( {{d_i},t} \right) , i \in I_{n - 1}^1. \end{aligned}$$
(10)

2.1 Fractional mathematical model for constitutive equations

Consider the following generalized constitutive mathematical relation,

$$\begin{aligned} {\tau _i} = {b_i}\frac{{\partial {u_i}}}{{\partial y}} + {\alpha _i}{\mathfrak {D}}_t^{{\gamma _i}}\frac{{\partial {u_i}}}{{\partial y}},\gamma _i \in \left( {0,1} \right] ,i \in I_n^1, \end{aligned}$$
(11)

where the Caputo derivative \({\mathfrak {D}}_t^\sigma\) is defined as,  [17],

$$\begin{aligned} {\mathfrak {D}}_t^\sigma {\mathfrak {F}}(y,t)=\frac{1}{\Gamma (1-\sigma )}\int _0^t(t-\varrho )^{-\sigma }\frac{\partial {\mathfrak {F}}(y,\varrho )}{\partial \varrho } d\varrho ,\; 0\le \sigma < 1\nonumber \\ \end{aligned}$$
(12)

For the special case \(\sigma =1,\) \({\mathfrak {D}}_t^1 {\mathfrak {F}}(y,t)=\frac{\partial {\mathfrak {F}}(y,t)}{\partial t}\). Let \({\mathfrak{G}}(y,\xi )\) be the Laplace transform of the \({\mathfrak {F}}(y,t)\) with \({\mathfrak {F}}(y,0)=0\), then the Laplace transform of the Caputo derivative is defined by \(L\{{\mathfrak {D}}_t^\sigma {\mathfrak {F}}(y,t)\}=\xi ^\sigma {\mathfrak {G}}(y,\xi )\), where \(0\le \sigma < 1\) [33]. The Laplace transformation of the Caputo derivative It is significant to remark that the generalized model (11) have the following equivalent formulae as

$$\begin{aligned} \frac{{\partial {u_i}\left( {y,t} \right) }}{{\partial y}}=\, & {} \psi _i(t,\gamma _i) * {\tau _i}\left( {y,t} \right) \end{aligned}$$
(13)
$$\begin{aligned}=\, & {} \int _0^t \psi _i(t-\delta ,\gamma _i) {\tau _i}\left( {y,\delta } \right) d\delta , \,\,i \in I_n^1, \end{aligned}$$
(14)

where \(\psi _i(t,\gamma _i)={\frac{1}{\alpha _i} t^{{\gamma _i} - 1}}{E_{{\gamma _i},{\gamma _i}}}\left( { - \frac{{{b_i}}}{{{\alpha _i}}}{t^{{\gamma _i}}}} \right) ,\) \(i \in I_n^1,\) is the velocity gradient non-locality kernel. Here in the flow direction the pressure gradient is the known function

$$\begin{aligned} - \frac{{\partial p}}{{\partial x}} = P\left( t \right) , \end{aligned}$$
(15)

where P(t) is the piece-wise continuous function over positive real line.

3 Solution of the problem

We have used the Laplace transform coupled with the finite sine-Fourier transform [34] for the analytical solutions of the Eqs. (6), (11) with conditions (8)–(10). With the application of the Laplace transform to Eqs. (6), (9)–(11) in the presence of the initial conditions (8), we obtain

$$\begin{aligned} {a_i}\xi {{{\bar{u}}}_i}\left( {y,\xi } \right)=\, & {} {{\bar{P}}}\left( \xi \right) + \frac{{\partial {{{{\bar{\tau }}} }_i}\left( {y,\xi } \right) }}{{\partial y}},i \in I_n^1, \end{aligned}$$
(16)
$$\begin{aligned} {\bar{\tau _{i}}}\left( {y,\xi } \right)=\, & {} \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) \frac{{\partial {{{{\bar{u}}}}_i}\left( {y,\xi } \right) }}{{\partial y}},i \in I_n^1, \end{aligned}$$
(17)
$$\begin{aligned} {{{\bar{u}}}_1}\left( {0,\xi } \right)=\, & {} {{\bar{f}}}\left( \xi \right) ,{\bar{u}_n}\left( {1,\xi } \right) = {{\bar{g}}}\left( \xi \right) \end{aligned}$$
(18)
$$\begin{aligned} {{{\bar{u}}}_j}\left( {{d_j},\xi } \right)=\, & {} {{{\bar{u}}}_{j + 1}}\left( {{d_j},\xi } \right) ,{{{\bar{\tau }}} _j}\left( {{d_j},\xi } \right) \nonumber \\=\, & {} {\bar{\tau }_{j + 1}}\left( {{d_j},\xi } \right) ,j \in I_{n - 1}^1. \end{aligned}$$
(19)

where \({{\bar{\chi }}} \left( {y,\xi } \right) = \int \limits _0^\infty {\chi \left( {y,t} \right) \exp \left( { - \xi t} \right) dt}\) is the Laplace transform of the function \(\chi \left( {y,t} \right)\) [34].

3.1 Analytical solutions for velocities and shear stresses

By using Eqs. (16) and (17) we get the Laplace transformed n-layer velocities,

$$\begin{aligned} {a_i}\xi {{{\bar{u}}}_i}\left( {y,\xi } \right) = {{\bar{P}}}\left( \xi \right) + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) \frac{{{\partial ^2}{{{{\bar{u}}}}_i}\left( {y,\xi } \right) }}{{\partial {y^2}}},i \in I_n^1, \end{aligned}$$
(20)

We will further apply the finite sine-Fourier transform to Eq. (20) for which the function \({{\bar{\chi }}} \left( {y,\xi } \right) ,y \in \left[ {a,b} \right]\), \(a<b\), is defined as [35]

$$\begin{aligned} {\widetilde{{{\overline{\chi }}} }_m}\left( \xi \right)=\, & {} \int \limits _a^b {{{\bar{\chi }}} \left( {y,\xi } \right) \sin \left( {{\vartheta _m}\left( {y - a} \right) } \right) dy,} \nonumber \\ {\vartheta _m}=\, & {} \frac{{m\pi }}{{b - a}},m = 1,2,3, \ldots , \end{aligned}$$
(21)

along with the inverse Fourier transform defined by

$$\begin{aligned} {{\overline{\chi }}} \left( {y,\xi } \right) = \frac{2}{{b - a}}\cdot \sum \limits _{m = 1}^\infty {\widetilde{{{\overline{\chi }}} }_m}\left( \xi \right) {\sin \left( {{\vartheta _m}\left( {y - a} \right) } \right) } . \end{aligned}$$
(22)

With the application of finite Fourier sine transformation (21) to Eq. (20) along with the boundary conditions (18) and interface fluid–fluid condition (19), the transformed velocities take the form

$$\begin{aligned} {\tilde{{{\bar{u}}}}_{im}}\left( \xi \right)=\, & {} \frac{{\left[ {1 - {{\left( { - 1} \right) }^m}} \right] }}{{\vartheta _m^{\left( i \right) }}}\frac{{{{\bar{P}}}\left( \xi \right) }}{{{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}}} \\&+ \frac{{\vartheta _m^{\left( i \right) }\left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) \left( {{{{{\bar{u}}}}_i}\left( {{d_{i - 1}},\xi } \right) } \right) }}{{{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}}}\\&- \frac{{\vartheta _m^{\left( i \right) }\left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( { - 1} \right) }^m}{{\bar{u}}_i}\left( {{d_i},\xi } \right) }}{{{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}}}, \end{aligned}$$
$$\begin{aligned} \vartheta _m^{\left( i \right) } = \frac{{m\pi }}{{{d_i} - {d_{i - 1}}}},m = 1,2, \ldots ,i \in I_n^1, \end{aligned}$$
(23)

where for \(i = 1,{{{\bar{u}}}_1}\left( {{d_0},\xi } \right) = {{\bar{f}}}\left( \xi \right)\) and for \(i = n,{{{\bar{u}}}_n}\left( {{d_n},\xi } \right) = {{\bar{g}}}\left( \xi \right)\). In order to apply the inverse Fourier sine transform, we rewrite the Eq. (23) in the following suitable form

$$\begin{aligned} {\tilde{{\bar{u}}}_{im}}\left( \xi \right)=\, & {} \frac{{{{\left( { - 1} \right) }^{m + 1}}{{{{\bar{u}}}}_i}\left( {{d_i},\xi } \right) }}{{\vartheta _m^{\left( i \right) }}} + \frac{{{{{{\bar{u}}}}_i}\left( {{d_{i - 1}},\xi } \right) }}{{\vartheta _m^{\left( i \right) }}} \\&+ \frac{{\left[ {1 - {{\left( { - 1} \right) }^m}} \right] }}{{\vartheta _m^{\left( i \right) }}}\frac{{{{\bar{P}}}\left( \xi \right) }}{{{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^i} \right) }^2}}}\\&- \frac{{{a_i}\xi {{{{\bar{u}}}}_i}\left( {{d_{i - 1}},\xi } \right) }}{{\vartheta _m^i\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}} \right] }} \\&+ \frac{{{a_i}\xi {{\left( { - 1} \right) }^m}{{{{\bar{u}}}}_i}\left( {{d_i},\xi } \right) }}{{\vartheta _m^{\left( i \right) }\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}} \right] }}, \end{aligned}$$
$$\begin{aligned} \vartheta _m^{\left( i \right) } = \frac{{m\pi }}{{{d_i} - {d_{i - 1}}}},m = 1,2, \ldots ,i \in I_n^1. \end{aligned}$$
(24)

Consider the auxiliary functions \({\wp _{1i}}\left( y \right)\), \({\wp _{2i}}\left( y \right)\) and their inverse Fourier sine transforms \({{{\tilde{\wp }}} _{1im}}\), \({{{\tilde{\wp }}} _{2im}}\)

$$\begin{aligned} {\wp _{1i}}\left( y \right) = \frac{{{d_i} - y}}{{{d_i} - {d_{i - 1}}}},y \in \left[ {{d_{i - 1}},{d_i}} \right] ,{{{\tilde{\wp }}} _{1im}} = \frac{1}{{\vartheta _m^{\left( i \right) }}}, \end{aligned}$$
$$\begin{aligned} {\wp _{2i}}\left( y \right) = \frac{{y - {d_{i - 1}}}}{{{d_i} - {d_{i - 1}}}},y \in \left[ {{d_{i - 1}},{d_i}} \right] ,{{{\tilde{\wp }}} _{2im}} = \frac{{{{\left( { - 1} \right) }^{m + 1}}}}{{\vartheta _m^{\left( i \right) }}} \end{aligned}$$
(25)
$$\begin{aligned} m = 1,2, \ldots ,i \in I_n^1,{d_0} = 0,{d_n} = 1. \end{aligned}$$

The inverse Fourier sine transform of Eq. (24) takes the form

$$\begin{aligned} {{{\bar{u}}}_i}\left( {y,\xi } \right)=\, & {} {\wp _{1i}}\left( y \right) {\bar{u}_i}\left( {{d_{i - 1}},\xi } \right) + {\wp _{2i}}\left( y \right) {{{\bar{u}}}_i}\left( {{d_i},\xi } \right) \\&+\frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty {\sin \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) }\\&\frac{{\left[ {1 - {{\left( { - 1} \right) }^m}} \right] }}{{\vartheta _m^{\left( i \right) }}}\frac{{{{\bar{P}}}\left( \xi \right) }}{{{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^i} \right) }^2}}} \\&-\frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty {\sin \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) } \\&\frac{{{a_i}\xi {{{{\bar{u}}}}_i}\left( {{d_{i - 1}},\xi } \right) }}{{\vartheta _m^i\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}} \right] }} \\&+\frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty {\sin \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) } \\&\frac{{{a_i}\xi {{\left( { - 1} \right) }^m}{{\bar{u}}_i}\left( {{d_i},\xi } \right) }}{{\vartheta _m^{\left( i \right) }\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}} \right] }}, \end{aligned}$$
$$\begin{aligned} \vartheta _m^{\left( i \right) } = \frac{{m\pi }}{{{d_i} - {d_{i - 1}}}},m = 1,2, \ldots ,i \in I_n^1. \end{aligned}$$
(26)

Now, from (17) and (26), we obtain

$$\begin{aligned} {{{\bar{\tau }}} _i}\left( {y,\xi } \right)=\, & {} \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) \frac{{\partial {{{{\bar{u}}}}_i}\left( {y,\xi } \right) }}{{\partial y}} = {{{\bar{T}}}_{i1}}\left( {y,\xi } \right) {{{\bar{u}}}_i}\left( {{d_i},\xi } \right) \nonumber \\&- {{{\bar{T}}}_{i2}}\left( {y,\xi } \right) {{{\bar{u}}}_i}\left( {{d_{i - 1}},\xi } \right) + {{{\bar{T}}}_{i3}}\left( {y,\xi } \right) {{\bar{P}}}\left( \xi \right) , \end{aligned}$$
(27)

where

$$\begin{aligned} {{{\bar{T}}}_{i1}}\left( {y,\xi } \right)=\, & {} \frac{{\left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) }}{{{d_i} - {d_{i - 1}}}}\nonumber \\&\left( {1 + 2\sum \limits _{m = 1}^\infty {\frac{{{a_i}{{\left( { - 1} \right) }^m}\xi \cos \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) }}{{\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^i} \right) }^2}} \right] }}} } \right) ,\nonumber \\ {{{\overline{T}}} _{i2}}\left( {y,\xi } \right)=\, & {} \frac{{\left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) }}{{{d_i} - {d_{i - 1}}}}\nonumber \\&\left( {1 + 2\sum \limits _{m = 1}^\infty {\frac{{{a_i}\xi \cos \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) }}{{\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^i} \right) }^2}} \right] }}} } \right) ,\nonumber \\ {{{\overline{T}}} _{i3}}\left( {y,\xi } \right)=\, & {} \frac{{2\left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) }}{{{d_i} - {d_{i - 1}}}}\nonumber \\&\left( {\sum \limits _{m = 1}^\infty {\frac{{\left[ {1 - {{\left( { - 1} \right) }^m}} \right] \cos \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) }}{{\left[ {{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^i} \right) }^2}} \right] }}} } \right) ,i \in I_n^1. \end{aligned}$$
(28)

With the help of the interface liquid-liquid conditions (19) in Eqs. (27) and (28), we obtained the following algebraic system for the Laplace transformed velocities on the interfaces \(y = {d_i},i = 1,2, \ldots ,n - 1,\)

$$\begin{aligned}&-\bar{{\mathfrak {e}}}_{1,1}(\xi ){\bar{u}}_1(d_1,\xi )+\bar{{\mathfrak {e}}}_{1,2}(\xi ){\bar{u}}_2(d_2,\xi )={\bar{b}}_1(\xi ),\nonumber \\&\bar{{\mathfrak {e}}}_{i,i-1}(\xi ){\bar{u}}_{i-1}(d_{i-1},\xi )-\bar{{\mathfrak {e}}}_{i,i}(\xi ){\bar{u}}_i(d_i,\xi )+\bar{{\mathfrak {e}}}_{i,i+1}(\xi ){\bar{u}}_{i+1}(d_{i+1},\xi )\nonumber \\&\qquad ={\bar{b}}_i(\xi ),\,\,i\in J_{n-2}^{(2)},\nonumber \\&\bar{{\mathfrak {e}}}_{n-1,n-2}(\xi ){\bar{u}}_{n-2}(d_{n-2},\xi )-\bar{{\mathfrak {e}}}_{n-1,n-1}(\xi ){\bar{u}}_{n-1}(d_{n-1},\xi )={\bar{b}}_{n-1}(\xi ), \end{aligned}$$
(29)

where

$$\begin{aligned} \bar{{\mathfrak {e}}}_{1,1}(\xi )=\, & {} {\bar{T}}_{1,1}(d_1,\xi )+{\bar{T}}_{1,2}(d_1,\xi ),\,\, \bar{{\mathfrak {e}}}_{1,2}={\bar{T}}_{1,2}(d_1,\xi ),\,\, \nonumber \\ \bar{{\mathfrak {e}}}_{i,i-1}(\xi )=\, & {} {\bar{T}}_{i,2}(d_i,\xi ),\,\, \bar{{\mathfrak {e}}}_{i,i}={\bar{T}}_{i,1}(d_i,\xi )+{\bar{T}}_{i+1,2}(d_i,\xi ),\nonumber \\ \bar{{\mathfrak {e}}}_{i,i+1}(\xi )=\, & {} {\bar{T}}_{i+1,1}(d_i,\xi ),\,\,i\in J_{n-1}^{(2)}, \end{aligned}$$
(30)

and

$$\begin{aligned} {\bar{b}}_j(\xi )={\bar{T}}_{j,3}(d_j,\xi )-{\bar{T}}_{j+1,3}(d_j,\xi )-\delta _{j,n-1}{\bar{g}}(\xi )-\delta _{j,1}{\bar{f}}(\xi ),\,\,\, j\in J_{n-1}^{(1)}, \end{aligned}$$
(31)

\(\delta _{j,m-1}\) is Kronecker delta. The system (29) can be written in the following equivalent form

$$\begin{aligned} {\bar{M}}(\xi ){\bar{U}}(\xi )={\bar{N}}(\xi ), \end{aligned}$$
(32)

where

$$\begin{aligned} {\bar{M}}(\xi )=\, & {} \left[ {\begin{array}{cccccc} -{\bar{f}}(\xi )&{}\bar{{\mathfrak {e}}}_{1,2}(\xi )&{}{0}&{}{0}&{}{\cdots }&{}{0}\\ {\bar{{\mathfrak {e}}}_{2,1}}(\xi )&{}-\bar{{\mathfrak {e}}}_{2,2}(\xi )&{}\bar{{\mathfrak {e}}}_{2,3}(\xi )&{}{0}&{}{\cdots }&{}{0}\\ {0}&{}{\bar{{\mathfrak {e}}}_{3,2}}(\xi )&{}-{\bar{{\mathfrak {e}}}_{3,3}}(\xi )&{}{\bar{{\mathfrak {e}}}_{3,4}}(\xi )&{}{\cdots }&{}\\ {\vdots }&{}{\vdots }&{}{\ddots }&{}{\ddots }&{}{\ddots }&{}\vdots \\ {0}&{}{0}&{}{\cdots }&{}-{\bar{{\mathfrak {e}}}_{n-3,n-3}}(\xi )&{}{\bar{{\mathfrak {e}}}_{n-3,n-2}}(\xi )&{}0\\ {0}&{}{0}&{}{\cdots }&{}{\bar{{\mathfrak {e}}}_{n-2,n-3}}(\xi )&{}-{\bar{{\mathfrak {e}}}_{n-2,n-2}}(\xi )&{}{\bar{{\mathfrak {e}}}_{n-2,n-1}}(\xi )\\ {0}&{}{0}&{}{\cdots }&{}{0}&{}{\bar{{\mathfrak {e}}}_{n-1,n-2}}(\xi )&{}-{{\bar{g}}(\xi )} \end{array}} \right] , \end{aligned}$$
(33)
$$\begin{aligned} {\bar{U}}(\xi )=\, & {} \left[ \begin{array}{l} {{\bar{u}}_1(d_1,\xi )}\\ {{\bar{u}}_2(d_2,\xi )}\\ \,\,\;\;\;{\vdots }\\ {{\bar{u}}_{n-1}(d_{n-1},\xi )}\\ \end{array}\right] , \end{aligned}$$
(34)

and

$$\begin{aligned} {\bar{N}}(\xi )= \left[ \begin{array}{l} {{\bar{b}}_1(\xi )}\\ \\ {{\bar{b}}_2(\xi )}\\ \\ \;{\vdots }\\ \\ {{\bar{b}}_{n-1}(\xi )}\\ \end{array}\right] . \end{aligned}$$
(35)

Finally, we obtain

$$\begin{aligned} {\bar{U}}(\xi )={\bar{M}}^{-1}(\xi ){\bar{N}}(\xi ). \end{aligned}$$
(36)

Now, \({\bar{u}}_i(d_i,\xi ),\) \(i\in J_{n}^{(1)}\) are known functions, therefore the velocities \({\bar{u}}_1(y,\xi ),\cdots ,{\bar{u}}_n(y,\xi )\) are known. To obtained the inverse Laplace transforms of the functions \({{{\bar{u}}}_i}\left( {y,\xi } \right) ,i \in I_n^1\)

we consider the following auxiliary functions,

$$\begin{aligned} {{{\bar{H}}}_{i0}}\left( {m,\xi } \right)=\, & {} \frac{1}{{{a_i}\xi + \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}}}\nonumber \\=\, & {} \frac{{{\xi ^{ - \gamma _i}}}}{{\left( {{a_i}} \right) \left( \xi ^{1-\gamma _i}+\frac{ \alpha _i {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}}{a_i} \right) }}\cdot \frac{1}{{1 + \frac{{{b_i}{{{\left( {\vartheta _m^{\left( i \right) }} \right) }^2 \xi ^{-\gamma _i}}}}}{{{ {{a_i}} \left( \xi ^{1-\gamma _i}+\frac{ \alpha _i {{\left( {\vartheta _m^{\left( i \right) }} \right) }^2}}{a_i} \right) }}}}} \nonumber \\=\, & {} \sum \limits _{k=0}^\infty \left( { - 1} \right) ^k \frac{b_i^k \left( \vartheta _m^{\left( i \right) } \right) ^{2k}}{a_i^{k+1}}\frac{\xi ^{-(k+1)\gamma _i}}{\left( \xi ^{1-\gamma _i}+ \frac{\alpha _i\left( {\vartheta _m^{\left( i \right) }} \right) ^2}{a_i} \right) ^{k+1} } \end{aligned}$$
(37)
$$\begin{aligned} {{{\bar{H}}}_{i3}}\left( {m,\xi } \right)=\, & {} \xi {{{\bar{H}}}_{i0}}\left( {m,\xi } \right) \nonumber \\=\, & {} \frac{{{\xi ^{ - {\gamma _i} + 1}}}}{{{a_i}\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^i} \right) }^2}}}{{{a_i}}}} \right) }}\nonumber \\&+ \sum \limits _{k = 0}^\infty \frac{{{{\left( { - 1} \right) }^{k+1}}{{\left( {{b_i}} \right) }^{k+1 }}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k+2}}}}{{a_i^{k + 2}}} \nonumber \\&\cdot \frac{{{\xi ^{ - \left( {k + 2} \right) {\gamma _i} + 1}}}}{{{{\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^{\left( i \right) }} \right) }^2}}}{{{a_i}}}} \right) }^{k + 2}}}} \end{aligned}$$
(38)
$$\begin{aligned} {{{\bar{H}}}_{i1}}\left( {m,\xi } \right)=\, & {} \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) {{{\bar{H}}}_{i0}}\left( {m,\xi } \right) \nonumber \\=\, & {} \sum \limits _{k = 0}^\infty \frac{{{{\left( { - 1} \right) }^k}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k}}}}{{a_i^{k + 1}}} \nonumber \\&\cdot \frac{{{\xi ^{ - \left( {k + 1} \right) {\gamma _i}}}}}{{{{\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^{\left( i \right) }} \right) }^2}}}{{{a_i}}}} \right) }^{k + 1}}}} \nonumber \\&+ \sum \limits _{k = 0}^\infty \frac{{{{\left( { - 1} \right) }^k}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k}}\left( {{\alpha _i}} \right) }}{{a_i^{k + 1}}} \nonumber \\&\cdot \frac{{{\xi ^{ - k{\gamma _i}}}}}{{{{\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^{\left( i \right) }} \right) }^2}}}{{{a_i}}}} \right) }^{k + 1}}}} \end{aligned}$$
(39)

and

$$\begin{aligned} {{{\bar{H}}}_{i2}}\left( {m,\xi } \right) :=\, & {} \xi {{{\bar{H}}}_{i1}}\left( {m,\xi } \right) \nonumber \\=\, & {} \frac{{{\xi ^{ - {\gamma _i} + 1}}}}{{{a_i}\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^i} \right) }^2}}}{{{a_i}}}} \right) }}\nonumber \\&+ \sum \limits _{k = 0}^\infty \frac{{{{\left( { - 1} \right) }^{k+1}}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k+2}}}}{{a_i^{k + 2}}} \nonumber \\&\cdot \frac{{{\xi ^{ - \left( {k + 2} \right) {\gamma _i} + 1}}}}{{{{\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^{\left( i \right) }} \right) }^2}}}{{{a_i}}}} \right) }^{k + 2}}}} \nonumber \\&+ \frac{{{\alpha _i}\xi }}{{{a_i}\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^i} \right) }^2}}}{{{a_i}}}} \right) }}\nonumber \\&+ \sum \limits _{k = 0}^\infty \frac{{{{\left( { - 1} \right) }^{k+1}}{{\left( {{b_i}} \right) }^{k + 2}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k+2}}\left( {{\alpha _i}} \right) }}{{a_i^{k + 2}}} \nonumber \\&\cdot \frac{{{\xi ^{ - \left( {{(k+1)}{\gamma _i} - 1} \right) }}}}{{{{\left( {{\xi ^{1 - {\gamma _i}}} + \frac{{{\alpha _i}{{\left( {\theta _m^{\left( i \right) }} \right) }^2}}}{{{a_i}}}} \right) }^{k + 2}}}} . \end{aligned}$$
(40)

We know that,

$$\begin{aligned} G_{{\sigma _1},{\sigma _2},{\sigma _3}}(t,\sigma )=\, & {} {\mathcal {L}}^{-1}\bigg [\frac{s^{\sigma _2}}{(s^{\sigma _1}-\sigma )^{\sigma _3}}\bigg ]\nonumber \\= \,& {} {\sum _{k=0}^\infty }\frac{\Gamma (k+{\sigma _3})\sigma ^kt^{(k+{\sigma _3}){\sigma _1}-{\sigma _2}-1}}{k!\Gamma ((k+{\sigma _3}){\sigma _1}-{\sigma _2})\Gamma ({\sigma _3})},\; \end{aligned}$$
(41)
$$\begin{aligned} \texttt {Re}(s)>0,\;\; \texttt {Re}({\sigma _1}{\sigma _3}-{\sigma _2})>0,\;\; |\frac{\sigma }{s^{\sigma _1}}|<1, \end{aligned}$$

and for \({\alpha _i},{\beta _i}>0,\)

$$\begin{aligned} {{\mathcal {L}}^{-1}}\bigg [\frac{s^{{\alpha _i}-{\beta _i}}}{s^{{\alpha _i}}-d}\bigg ]=t^{{\beta _i}-1}E_{{\alpha _i},{\beta _i}}(dt^{{\alpha _i}}), \end{aligned}$$
(42)

where \({E_{{\alpha _i},{\beta _i}}}\)(.) is the Mittag–Leffler function and \(G_{{\sigma _1},{\sigma _2},{\sigma _3}}(t,\sigma )\) is the generalized G-Lorenzo–Hartley function [36]. The inverse Laplace transform of \({{{\bar{H}}}_{i0}}\left( {m,\xi } \right)\), \({\bar{H}_{i1}}\left( {m,\xi } \right)\), \({{{\bar{H}}}_{i2}}\left( {m,\xi } \right)\) and \({{{\bar{H}}}_{i3}}\left( {m,\xi } \right) ,\) takes the form

$$\begin{aligned} {H_{i0}}\left( {m,t} \right)= & {} \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{{\left( {{b_i}} \right) }^k}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k}}}}{{{{\left( {{a_i}} \right) }^{k + 1}}}}} \nonumber \\&\cdot {G_{1 - {\gamma _i}, - \left( {k + 1} \right) {\gamma _i},k + 1}}\left( {t, - \alpha a_i^{ - 1}{{\left( {\theta _m^i} \right) }^2}} \right) , \end{aligned}$$
(43)
$$\begin{aligned} {H_{i3}}\left( {m,t} \right)= & {} \frac{\delta (t)}{{{a_i}}}-\frac{\alpha _i {{\left( {\theta _m^{\left( i \right) }} \right) }^{2}}}{{a_i}^2}t^{1-\gamma _i}E_{1-\gamma _i,1-\gamma _i}\left( \frac{-\alpha _i {{\left( {\theta _m^{\left( i \right) }} \right) }^{2}}}{a_i}t\right) \nonumber \\&+ \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^{k + 1}}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k + 2}}}}{{{{\left( {{a_i}} \right) }^{k + 2}}}}} \nonumber \\&\cdot {G_{1 - {\gamma _i}, - k{\gamma _i},k + 1}}\left( {t, - \alpha a_i^{ - 1}{{\left( {\theta _m^i} \right) }^2}} \right) , \end{aligned}$$
(44)
$$\begin{aligned} {H_{i1}}\left( {m,t} \right)= & {} \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k}}}}{{{{\left( {{a_i}} \right) }^{k + 1}}}}} \nonumber \\&\cdot {G_{1 - {\gamma _i}, - \left( {k + 1} \right) {\gamma _i},k + 1}}\left( {t, - \alpha a_i^{ - 1}{{\left( {\theta _m^i} \right) }^2}} \right) \nonumber \\&+ \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^k}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k}}\left( {{\alpha _i}} \right) }}{{{{\left( {{a_i}} \right) }^{k + 1}}}}} \nonumber \\&\cdot {G_{1 - {\gamma _i}, - k{\gamma _i},k + 1}}\left( {t, - \alpha a_i^{ - 1}{{\left( {\theta _m^i} \right) }^2}} \right) \end{aligned}$$
(45)

and

$$\begin{aligned} {H_{i2}}\left( {m,t} \right)= & {} \frac{\delta (t)}{{{a_i}}}-\frac{\alpha _i {{\left( {\theta _m^{\left( i \right) }} \right) }^{2}}}{{a_i}^2}t^{1-\gamma _i}E_{1-\gamma _i,1-\gamma _i}\left( \frac{-\alpha _i {{\left( {\theta _m^{\left( i \right) }} \right) }^{2}}}{a_i}t\right) \nonumber \\&+ \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^{k + 1}}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k + 2}}}}{{{{\left( {{a_i}} \right) }^{k + 2}}}}} \nonumber \\&\cdot {G_{1 - {\gamma _i}, - \left( {k + 2} \right) {\gamma _i} + 1,k + 2}}\left( {t, - \alpha a_i^{ - 1}{{\left( {\theta _m^i} \right) }^2}} \right) \nonumber \\&+ \frac{\alpha _i}{a_i}\delta '(t)*t^{1-\gamma _i}E_{1-\gamma _i,1-\gamma _i}\left( \frac{-\alpha _i {{\left( {\theta _m^{\left( i \right) }} \right) }^{2}}}{a_i}t\right) \nonumber \\&+ \sum \limits _{k = 0}^\infty {\frac{{{{\left( { - 1} \right) }^{k + 1}}{{\left( {{b_i}} \right) }^{k + 1}}{{\left( {\theta _m^{\left( i \right) }} \right) }^{2k + 2}}\left( {{\alpha _i}} \right) }}{{{{\left( {{a_i}} \right) }^{k + 2}}}}} \nonumber \\&\cdot {G_{1 - {\gamma _i}, - \left( {\left( {k + 1} \right) {\gamma _i} - 1} \right) ,k + 2}}\left( {t, - \alpha a_i^{ - 1}{{\left( {\theta _m^i} \right) }^2}} \right) \end{aligned}$$
(46)

where \({h_1}\left( t \right) * {h_2}\left( t \right) = \int _0^1 {{h_1}\left( {t - \tau } \right) {h_2}\left( \tau \right) d\tau }\) denotes the convolution product of the functions \({h_1}\left( t \right) ,{h_2}\left( t \right)\). Using Eqs. (26), (43) and (44), we obtain for velocities the following expressions:

$$\begin{aligned} {u_i}\left( {y,t} \right)= & {} {\wp _{1i}}\left( y \right) {u_i}\left( {{d_{i - 1}},t} \right) + {\wp _{2i}}\left( y \right) {u_i}\left( {{d_i},t} \right) \nonumber \\&+\frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty {\sin \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) \frac{{\left[ {1 - {{\left( { - 1} \right) }^m}} \right] }}{{\vartheta _m^{\left( i \right) }}}.{H_{i0}}\left( {m,t} \right) * P\left( t \right) } \nonumber \\&-\frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty {\sin \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) \frac{{{a_i}}}{{\vartheta _m^{\left( i \right) }}}{H_{i3}}\left( {m,t} \right) * {u_i}\left( {{d_{i - 1}},t} \right) } \nonumber \\&+\frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty \sin \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) \nonumber \\&\frac{{{a_i}{{\left( { - 1} \right) }^m}}}{{\vartheta _m^{\left( i \right) }}}{H_{i3}}\left( {m,t} \right) * {u_i}\left( {{d_{i - 1}},t} \right) ,\nonumber \\ \vartheta _m^{\left( i \right) }= & {} \frac{{m\pi }}{{{d_i} - {d_{i - 1}}}},m = 1,2,\ldots ,i \in I_n^1. \end{aligned}$$
(47)

The shear stresses system \({\tau _i}\left( {y,\xi } \right) ,i \in I_n^1,\) can be obtained by applying inverse Laplace transform to Eqs. (27), (28) and using Eqs. (45), (46), we get

$$\begin{aligned} { \tau _i}\left( {y,t } \right)= & {} { T_{i1}}\left( {y,t } \right) *{ u_i}\left( {{d_i},t } \right) -{ T_{i2}}\left( {y,t } \right) *{ u_i}\left( {{d_{i - 1}},t } \right) \nonumber \\&+ { T_{i3}}\left( {y,t } \right) * P\left( t \right) , \end{aligned}$$
(48)

where

$$\begin{aligned} {T_{i1}}\left( {y,t} \right)= & {} \left[ \frac{1}{{{d_i} - {d_{i - 1}}}}\left( {{\alpha _i}{t^{{\alpha _i} - 1}}{E_{{\alpha _i},{\alpha _i}}}\left( { - {b_i}\alpha _i^{ - 1}{t^{{\alpha _i}}}} \right) } \right) \right. \\&\left. + 2\sum \limits _{m = 1}^\infty {{a_i}{{\left( { - 1} \right) }^m}{H_{i2}}\left( {m,t} \right) \cos \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) } \right] ,\\ {T _{i2}}\left( {y,t} \right)= & {} \left[ \frac{1}{{{d_i} - {d_{i - 1}}}}\left( {{\alpha _i}{t^{{\alpha _i} - 1}}{E_{{\alpha _i},{\alpha _i}}}\left( { - {b_i}\alpha _i^{ - 1}{t^{{\alpha _i}}}} \right) } \right) \right. \\&\left. + 2\sum \limits _{m = 1}^\infty {{a_i}{H_{i2}}\left( {m,t} \right) \cos \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) } \right] , \end{aligned}$$
$$\begin{aligned} {T _{i3}}\left( {y,t} \right) = \frac{2}{{{d_i} - {d_{i - 1}}}}\sum \limits _{m = 1}^\infty {\left[ {1 - {{\left( { - 1} \right) }^m}} \right] {H_{i1}}\left( {m,t} \right) \cos \left( {\vartheta _m^{\left( i \right) }\left( {y - {d_{i - 1}}} \right) } \right) } ,i \in I_n^1. \end{aligned}$$
(49)

The considered model of multi-layer flow of second grade fluids is more general and several special cases can be deduced from it. In order to certify the correctness of results that have been here obtained, as well as to get some physical insight of them, we consider a particular case whose solution is well known in the existing literature or can be easily determined. For the special case when \(\alpha _i\rightarrow 0\) in Eqs. (47) and (48), we obtain analytical solutions of velocities for the n-immiscible Newtonian fluids. These velocities (47) of n-immiscible fluids match with the results obtained in ([16]; Eq. (72) with \(\lambda _i\rightarrow 0\)).

3.2 Semi-analytical solution for velocity and shear stress

In this subsection, we obtained a new solution for the velocities and shear stresses corresponding to the governing equations given by Eqs. (16)–(19) by applying the Laplace transform in conjunction with the classical method for the ordinary differential equations. The general solution for the Eq. (20) provides a system of the Laplace transformed velocities as

$$\begin{aligned} {{{\bar{u}}}_i}\left( {y,\xi } \right) = {A_i(\xi )}{e^{ - y\sqrt{{m_i}(\xi )} }} + {B_i(\xi )}{e^{y\sqrt{{m_i}\left( \xi \right) } }} + \frac{{{{\bar{P}}}\left( \xi \right) }}{{{a_i}\xi }}, \end{aligned}$$
(50)

where

$$\begin{aligned} {m_i}\left( \xi \right) = \frac{{{a_i} \xi }}{{\left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) }},i \in I_n^1. \end{aligned}$$

Now with Eqs. (17) and (50), the Laplace transformed form of the shear stresses \({\tau _i}\left( {y,t} \right) ,i \in I_n^1,\) can be written as

$$\begin{aligned} {{{\bar{\tau }}} _i}\left( {y,\xi } \right)= & {} \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) \frac{{\partial {{{{\bar{u}}}}_i}\left( {y,\xi } \right) }}{{\partial y}} \nonumber \\= & {} \left( {{b_i} + {\alpha _i}{\xi ^{{\gamma _i}}}} \right) \left[ - \sqrt{{m_i}\left( \xi \right) } {A_i(\xi )}{e^{ - y\sqrt{{m_i}(\xi )} }} \nonumber \right. \\&\left. + \sqrt{{m_i}\left( \xi \right) } {B_i(\xi )}{e^{y\sqrt{{m_i}\left( \xi \right) } }} \right] \end{aligned}$$
(51)

Using the boundary conditions (18) and the interface conditions (19), we have

$$\begin{aligned} {C_1}\left( \xi \right) {D_1}\left( \xi \right) = {E_1}\left( \xi \right) , \end{aligned}$$
(52)

where the \(C_1\left( \xi \right)\) is given by

$$\begin{aligned}{C_1}\left( \xi \right) = \left[ {\begin{array}{cccccccccc} 1 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 1 &{} 0 &{} 0 &{} \cdots &{} 0 \\ {{{\mathfrak {f}}_1}} &{} { - {{\mathfrak {g}}_1}} &{} 0 &{} \cdots &{} 0 &{} {\frac{1}{{{{\mathfrak {f}}_1}}}} &{} { - \frac{1}{{{{\mathfrak {g}}_1}}}} &{} 0 &{} \cdots &{} 0 \\ 0 &{} {{{\mathfrak {f}}_2}} &{} { - {{\mathfrak {g}}_2}} &{} \cdots &{} 0 &{} 0 &{} {\frac{1}{{{{\mathfrak {f}}_2}}}} &{} { - \frac{1}{{{{\mathfrak {g}}_2}}}} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \ddots &{} \vdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} {{{\mathfrak {f}}_{n - 1}}} &{} { - {{\mathfrak {g}}_{n - 1}}} &{} 0 &{} 0 &{} 0 &{} {\frac{1}{{{{\mathfrak {f}}_{n - 1}}}}} &{} { - \frac{1}{{{{\mathfrak {g}}_{n - 1}}}}} \\ {{{\mathfrak {h}}_1}} &{} { - {{\mathfrak {k}}_1}} &{} 0 &{} \cdots &{} 0 &{} {{{\mathfrak {l}}_1}} &{} { - {{\mathfrak {p}}_1}} &{} 0 &{} \cdots &{} 0 \\ 0 &{} {{{\mathfrak {h}}_2}} &{} { - {{\mathfrak {k}}_2}} &{} \cdots &{} 0 &{} 0 &{} {{{\mathfrak {l}}_2}} &{} { - {{\mathfrak {p}}_2}} &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \cdots &{} \vdots &{} \vdots &{} \vdots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} 0 &{} \cdots &{} {{{\mathfrak {h}}_{n - 1}}} &{} { - {{\mathfrak {k}}_{n - 1}}} &{} 0 &{} 0 &{} 0 &{} {{{\mathfrak {l}}_{n - 1}}} &{} { - {{\mathfrak {p}}_{n - 1}}} \\ 0 &{} 0 &{} \cdots &{} 0 &{} {{{\mathfrak {h}}_n}} &{} 0 &{} 0 &{} 0 &{} 0 &{} {{{\mathfrak {l}}_n}} \\ \end{array}} \right] \end{aligned}$$

and the columns \({D_1}\left( \xi \right)\) and \({E_1}\left( \xi \right)\) are

$$\begin{aligned} {D_1}\left( \xi \right) = \left[ {\begin{array}{c} {{A_1(\xi )}} \\ {{A_2(\xi )}} \\ \vdots \\ {{A_n(\xi )}} \\ {{B_1(\xi )}} \\ {{B_2(\xi )}} \\ \vdots \\ {{B_n(\xi )}} \\ \end{array}} \right] ,{E_1}\left( \xi \right) = \left[ {\begin{array}{*{20}{c}} {{P_0}\left( \xi \right) } \\ {{P_1}\left( \xi \right) } \\ \vdots \\ {{P_{n - 1}}\left( \xi \right) } \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{array}} \right] \end{aligned}$$

here

$$\begin{aligned} {{\mathfrak {f}}_j}= & {} {e^{ - {d_j}\sqrt{{m_j}\left( \xi \right) } }},{{\mathfrak {g}}_j} = {e^{ - {d_j}\sqrt{{m_{j + 1}}\left( \xi \right) } }},\\ {{\mathfrak {h}}_j}= & {} - \sqrt{{m_j}\left( \xi \right) } {e^{ - {d_j}\sqrt{{m_j}\left( \xi \right) } }},\\ {{\mathfrak {k}}_j}= & {} - \left( {\frac{{{b_{j + 1}} + {\alpha _{j + 1}}{\xi ^{{\gamma _{j + 1}}}}}}{{{b_j} + {\alpha _j}{\xi ^{{\gamma _j}}}}}} \right) \sqrt{{m_{j + 1}}\left( \xi \right) } {e^{ - {d_j}\sqrt{{m_{j + 1}}\left( \xi \right) } }},\\ {{\mathfrak {l}}_j}= & {} - \sqrt{{m_j}\left( \xi \right) } {e^{{d_j}\sqrt{{m_j}\left( \xi \right) } }},\\ {{\mathfrak {p}}_j}= & {} \left( {\frac{{{b_{j + 1}} + {\alpha _{j + 1}}{\xi ^{{\gamma _{j + 1}}}}}}{{{b_j} + {\alpha _j}{\xi ^{{\gamma _j}}}}}} \right) \sqrt{{m_{j + 1}}\left( \xi \right) } {e^{{d_j}\sqrt{{m_{j + 1}}\left( \xi \right) } }},\\ {P_0}\left( \xi \right)= & {} {{\bar{f}}}\left( \xi \right) - \frac{{{{\bar{P}}}\left( \xi \right) }}{{{a_1}\xi }},\\ {P_j}\left( \xi \right)= & {} \left( {\frac{1}{{{a_{j + 1}}}} - \frac{1}{{{a_j}}}} \right) \frac{{{{\bar{P}}}\left( \xi \right) }}{\xi },j = 1,2, \ldots ,n - 1 \end{aligned}$$

The system (52) can be written in equivalent form as,

$$\begin{aligned} {W_1(\xi )}A(\xi ) + {X_1(\xi )}B(\xi )= & {} {L_3(\xi )}, \nonumber \\ {Y_1(\xi )}A(\xi ) + {Z_1(\xi )}B(\xi )= & {} {L_4(\xi )}, \end{aligned}$$
(53)

Where

$$\begin{aligned}&{W_1} = {\left( {{{W'}_{ij}}} \right) _{i,j \in I_{n - 1}^0}} \vdots {X_1} = {\left( {{{X'}_{ij}}} \right) _{i,j \in I_{n - 1}^0}}\\&W_{0j}^1 = {\delta _{0,j}},j \in I_{n - 1}^0 \vdots X_{0j}^1 = {\delta _{0,j}},j \in I_{n - 1}^0\\&{W'_{ij}} = {{\mathfrak {f}}_i}{\delta _{i,j + 1}} - {{\mathfrak {g}}_i}{\delta _{i + 1,j + 1,}} \vdots X_{ij}^1 = \frac{1}{{{{\mathfrak {f}}_i}}}{\delta _{i,j + 1}} - \frac{1}{{{{\mathfrak {g}}_i}}}{\delta _{i + 1,j + 1,}}\\&i \in I_{n - 1}^1,j \in I_{n - 1}^0, \vdots i \in I_{n - 1}^1,j \in I_{n - 1}^0,\\&{Y_1} = {\left( {{{Y'}_{ij}}} \right) _{i,j \in I_{n - 1}^0}} \vdots {Z_1} = {\left( {{{Z'}_{ij}}} \right) _{i,j \in I_{n - 1}^0}}\\&{Y'_{ij}} = {{\mathfrak {h}}_{i + 1}}{\delta _{i + 1,j + 1}} - {{\mathfrak {k}}_{i + 1}}{\delta _{i + 2,j + 1,}} \vdots {Z'_{ij}} = {{\mathfrak {l}}_{i + 1}}{\delta _{i + 1,j + 1}} - {{\mathfrak {p}}_{i + 1}}{\delta _{i + 2,j + 1,}}\\&i \in I_{n - 2}^0,j \in I_{n - 1}^0, \vdots i \in I_{n - 2}^0,j \in I_{n - 1}^0,\\&{Y'_{\left( {n - 1} \right) j}} = {{\mathfrak {h}}_n}{\delta _{n - 1,j,}}j \in I_{n - 1}^0 \vdots {Z'_{\left( {n - 1} \right) j}} = {{\mathfrak {l}}}_n {\delta _{n - 1,j,}}j \in I_{n - 1}^0,\\&{L_3} = {\left( {\begin{array}{c} {{P_0}\left( \xi \right) } \\ {{P_1}\left( \xi \right) } \\ \vdots \\ {{P_{n - 1}}\left( \xi \right) } \\ \end{array}} \right) },{L_4} = {\left( {\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\ \end{array}} \right) _{n \times 1}},\\&A = {\left( {\begin{array}{c} {{A_1(\xi )}} \\ {{A_2(\xi )}} \\ \vdots \\ {{A_n(\xi )}} \\ \end{array}} \right) },B = {\left( {\begin{array}{*{20}{c}} {{B_1(\xi )}} \\ {{B_2(\xi )}} \\ \vdots \\ {{B_n(\xi )}} \\ \end{array}} \right) } \end{aligned}$$

Where \({\delta _{ij}}\) is the Kronecker tensor. Matrices \({W_1},{X_1},{Y_1},{Z_1}\) are invertible triangular matrices, therefore Eqs. (47) can be written as

$$\begin{aligned} \left( {X_1^{ - 1}{W_1} - Z_1^{ - 1}{Y_1}} \right) A= & {} X_1^{ - 1}{L_3} \nonumber \\ B= & {} - Z_1^{ - 1}{Y_1}A \end{aligned}$$
(54)

Suppose that matrix \({S_1} = X_1^{ - 1}{W_1} - Z_1^{ - 1}{Y_1}\) is invertible, we have

$$\begin{aligned} A= & {} S_1^{ - 1}X_1^{ - 1}{L_3}, \nonumber \\ B= & {} - Z_1^{ - 1}{Y_1}S_1^{ - 1}X_1^{ - 1}{L_3}, \end{aligned}$$
(55)

where

$$\begin{aligned}W_1^{ - 1} = \left( {w_{ij}^1} \right) i,j \in I_{n - 1}^0,\end{aligned}$$
$$\begin{aligned} w_{0j}^1 = {\delta _{0j,}}j \in I_{n - 1}^0,w_{i0}^1 = \prod \limits _{r = 1}^i {\frac{{{\mathfrak {f}}_r}}{{{\mathfrak {g}}_r}}} ,i \in I_{n - 1}^1, \end{aligned}$$
(56)
$$\begin{aligned} w_{ij}^1= & {} - \prod \limits _{s = 1}^i {\frac{{{{\mathfrak {f}}_s}}}{{{{\mathfrak {g}}_s}}}} \prod \limits _{r = 0}^{j - 1} {\frac{{{{\mathfrak {g}}_r}}}{{{{\mathfrak {f}}_{r + 1}}}}} \sum \limits _{k = 0}^{n - 1} {{\delta _{i,j + k,}}i,j \in I_{n - 1}^1;} \\ X_1^{ - 1}= & {} \left( {x_{ij}^1} \right) i,j \in I_{n - 1}^0,\\ x_{0j}^1= & {} {\delta _{0j,}}j \in I_{n - 1}^0,x_{i0}^1 = \prod \limits _{r = 1}^i {\frac{{{\mathfrak {f}}_r}}{{{\mathfrak {g}}_r}}} ,i \in I_{n - 1}^1,\\ x_{ij}^1= & {} - \prod \limits _{s = 1}^i {\frac{{{{\mathfrak {f}}_s}}}{{{{\mathfrak {g}}_s}}}} \prod \limits _{r = 0}^{j - 1} {\frac{{{{\mathfrak {f}}_{r + 1}}}}{{{{\mathfrak {g}}_r}}}} \sum _{k = 0}^{n - 1} {{\delta _{i,j + k,}}i,j \in I_{n - 1}^1;} \\&\begin{array}{l} Z_1^{ - 1} = {\left( {z_{ij}^1} \right) _{i,j \in I_{n - 1}^0,}} \\ \textit{with,}\\ z_{ij}^1 = {\left( {\prod \limits _{s = 0}^i {\frac{{{{\mathfrak {l}}_s}}}{{{{\mathfrak {p}}_s}}}\prod \limits _{r = 0}^{} {\frac{{{{\mathfrak {p}}_s}}}{{{{\mathfrak {l}}_{r + 1}}}}} } } \right) } \sum _{k = 0}^{n - 1}{\delta _{i - k,j}},{{\mathfrak {l}}_0} = {{\mathfrak {p}}_0} = {{\mathfrak {l}}_n} = 1,i,j \in I_{n - 1}^0. \end{array} \end{aligned}$$

And the matrix \({S_1} = {\left( {S_{ij}^1} \right) _{i,j \in I^0_{n-1}}}\) is defined by the elements

$$\begin{aligned} S_{ij}^1 = \sum \limits _{k = 0}^{n - 1} {\left( {x_{ik}^1W_{kj}^1 - z_{ik}^1Y_{kj}^1} \right) .} \end{aligned}$$

The Laplace transforms given by Eqs. (50), (51) and (55) involve intricate functions, which makes it difficult to apply analytical methods to compute the inverse Laplace transforms of these relations.

Here we have used two precision numerical procedures for the Laplace inversion of Eqs. (50),(51) and (55), specifically the fixed Talbot procedure and the improved Talbot procedure [37, 38].

Consider a function g(y, t) with the Laplace transform \(\bar{G}(y,s)\). Talbot algorithm [37] approximates the function g(y, t) from a given function \({{\bar{G}}}(y,s)\) as

$$\begin{aligned} g(y,t)\cong & {} \frac{r}{M}\left\{ \frac{{\exp (rt)}}{2}{{\bar{G}}}(y,r) \nonumber \right. \\&\left. + \sum \limits _{k = 1}^{M - 1} {{\mathop {\mathrm{Re}}\nolimits } \left[ {\exp (tz({ \Omega _k})){{\bar{G}}}(y,z({ \Omega _k}))\left( {1 + i\zeta ({ \Omega _k})} \right) } \right] } \right\} ,\nonumber \\ \end{aligned}$$
(57)

where

$$\begin{aligned} r= & {} \frac{{2M}}{{5t}},\;\;z( \Omega ) = r \Omega (\cot \Omega + i),\;\; \Omega \in ( - \pi ,\pi ),\nonumber \\ \zeta ( \Omega )= & {} \Omega + ( \Omega cot \Omega - 1)cot \Omega ,\;{ \Omega _k} = \frac{{k\pi }}{M}. \end{aligned}$$
(58)

The improved Talbot algorithm is applied to approximate the function g(y, t) as

$$\begin{aligned} g(y,t) \cong \sum \limits _{k = 1}^M {{{\bar{G}}}(y,{z_1}({\sigma _k}))\left( {\nu + i{\zeta _{\,1}}({\sigma _k})} \right) }\frac{\exp (t{z_1}({\sigma _k}))}{t} , \end{aligned}$$
(59)

where,

$$\begin{aligned} {z_1}( \Omega )= & {} \frac{M}{t}\left[ {\nu i \Omega + \mu \Omega \cot (\alpha \Omega ) - \Omega } \right] ,\;\; \Omega \in [ - \pi ,\pi ],\nonumber \\ {\zeta _1}( \Omega )= & {} \alpha \mu \Omega + \mu (\alpha \Omega cot(\alpha \Omega ) - 1)cot(\alpha \Omega ),\;{\sigma _k} = \frac{{(2k - 1)\pi }}{M} - \pi .\nonumber \\ \end{aligned}$$
(60)

Here the parameters \(M,\;\;\alpha ,\;\;\mu ,\;\;\nu ,\;\;\xi\) are quantified by the handler.

The results obtained by Luo et al. [39], are the special case \(n=2\), of our more general semi-analytical solutions (50)–(51).

4 Numerical results and discussions

The unsteady, laminar flow of multi-layer fractional n-immiscible second-grade fluids between two parallel plates have been investigated. The flow of the fluids is caused by the time-dependent pressure gradient along the axis of the flow and by the movement of the channel walls in their planes with the time-dependent velocities, and in the presence of the fluid–fluid interfacial conditions.

A generalized mathematical model based on the fractional differential constitutive equation with time-fractional Caputo derivative has been developed and studied. On the solid boundaries, the no-slip condition is considered, while at the fluid–fluid interfaces, the velocity and shear stress are considered continuous.

Semi-analytical solutions of the problem with initial, boundary and interface conditions have been determined by employing the Laplace transform coupled with the Talbot algorithms for the numerical inverse Laplace transforms. Using the Laplace transform and the finite sine-Fourier transform, the analytical solutions of the same problem have been determined.

In the present study, we considered the particular case of three layers of immiscible fluids when the velocity of the bottom plate is \({u_1}(0,t) = f(t) = 0.5H(t)\) the velocity of the upper plate is \({u_3}(0,t) = g(t) = 0.4H(t)\). \(H(t) = \left\{ \begin{array}{l} 0,t \le 0 \\ 1,t > 0 \\ \end{array} \right. = \frac{1}{2}sign(t)(1 + sign(t))\) is the unit step Heaviside function, and the pressure gradient is \(P(t) = 1 + \sin (t)\). The flows regions are determined by \({d_0}\mathrm{{ }} = \mathrm{{ }}0,\;{d_1}\mathrm{{ }} = \mathrm{{ }}0.\mathrm{{3}},\;{d_2}\mathrm{{ }} = \mathrm{{ }}0.\mathrm{{7}},\;{d_3}\mathrm{{ }} = \mathrm{{ 1}}\).

With the help of Math-cad software, numerical results have been obtained and graphically presented for the velocity of the fluids. Some aspects of the fluid motion are presented in Figs. 2, 3, 4, 5, 6, 7, 8, 9 and 10 that are sketched for the following values of the densities of fluids \({\rho _1} = 1000,{\rho _2} = 1300,\,{\rho _3} = 1500\) (other parameters are given in the figures’ labels).

Fig. 2
figure 2

Variation of the damping kernels \(\psi _i(t,\gamma _i)\), \(i=1,2,3\), with the fractional parameters \(\gamma _i\), \(i=1,2,3\)

Full size image
Fig. 3
figure 3

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.5\), \(\alpha _1=0.2, \alpha _2=0.3, \alpha _3=0.6\) and for different values of \(\gamma _1\)

Full size image
Fig. 4
figure 4

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.5\), \(\alpha _1=0.2, \alpha _2=0.3, \alpha _3=0.6\) and for different values of \(\gamma _2\)

Full size image
Fig. 5
figure 5

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.5\), \(\alpha _1=0.2, \alpha _2=0.3, \alpha _3=0.6\) and for different values of \(\gamma _3\)

Full size image
Fig. 6
figure 6

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\gamma _1=0.8, \gamma _2=0.7, \gamma _3=0.4\), \(\alpha _1=0.2, \alpha _2=0.3, \alpha _3=0.6\) and for different values of \(\mu _1\)

Full size image
Fig. 7
figure 7

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\gamma _1=0.8, \gamma _2=0.7, \gamma _3=0.4\), \(\alpha _1=0.2, \alpha _2=0.3, \alpha _3=0.6\) and for different values of \(\mu _2\)

Full size image
Fig. 8
figure 8

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\gamma _1=0.8, \gamma _2=0.7, \gamma _3=0.4\), \(\alpha _1=0.2, \alpha _2=0.3, \alpha _3=0.6\) and for different values of \(\mu _3\)

Full size image
Fig. 9
figure 9

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\gamma _1=0.8, \gamma _2=0.7, \gamma _3=0.4\), \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.5\) and for different values of \(\alpha _1\)

Full size image
Fig. 10
figure 10

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\gamma _1=0.8, \gamma _2=0.7, \gamma _3=0.4\), \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.5\) and for different values of \(\alpha _2\)

Full size image

To emphasize the influence of the memory on the fluid motion, let’s refer to the constitutive Eq. (11) that can be written in the equivalent form \(\frac{{\partial u(y,t)}}{{\partial y}} = \frac{1}{{{\alpha _i}}}\int \nolimits _0^t {{E_{{\gamma _i},{\gamma _i}}}\left( { - \frac{{{b_i}}}{{{\alpha _i}}}{{\left( {t - s} \right) }^{{\gamma _i}}}} \right) } \;{\tau _i}(y,s)ds\). This relationship shows that the shear rate is strongly influenced by the memory kernel present in the mathematical model, namely, by the weight function \({E_{{\gamma _i},{\gamma _i}}}\left( { - \frac{{{b_i}}}{{{\alpha _i}}}{t^{{\gamma _i}}}} \right)\). The profiles of kernels corresponding to three fluids considered in the present study are given in Fig. 2, for different values of the time t, \(t \in \{ 0.05,\;0.1,\;0.2,\;0.4,\;0.5,\;0.8,\;1\}\). Note that, in the case of the ordinary fluids \(({\gamma _i} = 1)\) fluids defined by the constitutive equation with the derivative of integer order, the dumping kernel is the exponential function \(\exp \left( {\frac{{ - {b_i}t}}{{{\alpha _i}}}} \right)\) has a profile different from the profiles shown in Fig. 2. It is observed from Fig. 2 that for small values of time t, the damping fractional kernel increases to a maximum value and then decreases to a minimum value. For time values t greater than or equal to 0.4, the kernel values are ascending by the fractional parameter. On the other hand, for positive values of the argument, the exponential function \(\exp \left( {\frac{{ - {b_i}t}}{{{\alpha _i}}}} \right)\) is decreasing.This discussion highlights that there are essential differences between memory effects for the fractional and ordinary fluids.The different behavior of the dumping kernel for the shear rate in the case of the fractional model, respectively for the ordinary model, it is visible to the profiles of the velocities of fluids presented in Figs. 3, 4, 5, 6, 7, 8, 9, 10 and 11.

Fig. 11
figure 11

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\gamma _1=0.8, \gamma _2=0.7, \gamma _3=0.4\), \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.5\) and for different values of \(\alpha _3\)

Full size image

Figure 2 has been plotted to study the influence of the memory of the fluid in the first layer on the fluids in layers two and three which are considered with constant fractional parameters. It is seen in Fig. 2 that for increasing the values of the fractional parameter in the first fluid layer, its velocity decreases. Obviously, the motion of the first layer influences the second and third layers through the interface interactions.

Figures 3, 4 and 5 present the influence of the variation of the fractional parameters in layers two and three. We must point out that in these cases the effect on the velocity of the fluid in the first layer is null. This was to be expected because there are no changing parameters in the first layer, so the speed on the interface between the first layer and the second layer will be the same due to the imposed continuity conditions.

The influence of the dynamic viscosity of the fluids on their velocity is analyzed in Figs. 6, 7 and 8. Taking into account the mathematical model, the influence of the dynamic viscosity occurs through the parameters \({b_i}\).

The variation of these parameters changes the kernel’s profile of the fractional/integer derivative, so the shape of the velocity field. As expected and as shown in Fig. 6, the fluid with the lowest viscosity has the highest velocity because, in this case, the viscous forces have lower values.

The influence of the material coefficients specific of the second-grade fluids, namely \({\alpha _i}\), on the fluid motion, was investigated in Figs. 9, 10 and 11. Like the dynamic viscosity, the material coefficients \({\alpha _i}\) are in the expression of the fractional derivative kernels, so they participate significantly in the memory process.

In Fig. 12 is presented the profile of velocities \({u_i}(y,t)\), i=1,2,3, for different values of the time t. It can be observed from Fig. 12 that at a very short time the profile for velocities \({u_i}(y,t), i=1,2,3,\) are similar to the initial condition, that is zero everywhere.

Fig. 12
figure 12

Profile of velocities \(u_i(y,t)\), \(i=1,2,3\), at \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.4\), \(\alpha _1=0.2, \alpha _2=0.4, \alpha _3=0.6\), \(\gamma _1=0.8\), \(\gamma _2=0.7\), \(\gamma _3=0.4\) and for different values of t

Full size image

In order to verify the accuracy of numerical results, we used the analytical solution of velocity given by Eq. (47) and the semi-analytical solution given by Eq. (50) for following values of parameters: \(\mu _1=0.05, \mu _2=0.3, \mu _3=0.95\), \(\alpha _1=0.2, \alpha _2=0.4, \alpha _3=0.6\), \(\gamma _1=0.8\), \(\gamma _2=0.7\), \(\gamma _3=0.4\) and \(t=3\). Numerical results are given in Fig. 13. There is a good agreement between the results obtained with the two formulas.

Fig. 13
figure 13

Comparison between results obtained with analytical and semi-analytical solutions for velocities \(u_i(y,t)\), \(i=1,2,3\)

Full size image

5 Conclusion

The simultaneous flow of generalized n-immiscible second grade fluids with the Caputo time-fractional derivative have been studied between two parallel plates. The unsteady, laminar simultaneous n-fluids flow is caused by the motion of the side walls with time dependent velocities, and by the time dependent pressure gradient in flow direction.

On the solid boundaries, the no-slip condition is considered, while at the fluid–fluid interface \(y = {d_i}\), the velocity and shear stress are considered continuous. Semi-analytical solutions of the problem with initial, boundary and interface conditions have been determined by employing the Laplace transform coupled with the Talbot algorithms for the numerical inverse Laplace transforms. Using the Laplace transform and the finite sine-Fourier transform, the analytical solutions of the same problem have been determined. It has been found that the memory effects are significant in the fluid motion. Furthermore, the fluid with the lowest viscosity has the highest velocity, as expected.