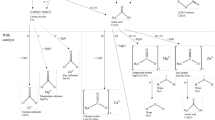
Abstract
Current study aimed to evaluate kinetic parameters and mechanisms for the thermal degradation of palm empty fruit bunch fibre (EFBF) in presence of calcium oxide (CaO), magnesium oxide (MgO), and zinc oxide (ZnO). These oxides have been proved to improve the bio-oil properties as a catalyst in pyrolysis. In order to achieve the aim, the amount of oxides (0, 5, and 10 wt%) and heating rates (10, 20, 30, and 40 °C/min) are manipulated in thermogravimetric analyses. In addition, cellulose, the most abundant component in EFBF was taken as another feed to understand the changes in kinetic mechanism due to the presence of other lignocellulosic components. The results showed that the incorporation of these oxides, the average activation energy of EFBF lowered in general, where the most significant decrement was observed for the addition of 10 wt% of MgO (274.5 to 194.8 kJ/mol). This reflected that the oxides pose catalytic activities on biomass pyrolysis. However, the oxides (CaO, MgO, and ZnO) would not affect the mechanisms other than catalysing the reactions. Mainly second order chemical reaction and three-dimensional diffusion are the most suitable mechanisms to describe the degradation of EFBF in presence of oxide catalysts. Whereas the cellulose degradation was controlled by 1.5 order chemical reaction and three-dimensional diffusion mechanisms.
Graphic abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Among renewable energy sources, lignocellulosic biomass shows high potential in terms of feed flexibility and abundance. Fast pyrolysis is a thermochemical process, where lignocellulosic biomass is converted into carbon rich liquid fuel, known as bio-oil. The bio-oil produced has properties that are comparable to those of crude oil and is a potential source of various chemicals (e.g. acetol, hydroxyacetaldehyde, and resins). However, bio-oil cannot be used directly as fuel yet, as bio-oil is generally highly acidic (pH 2–3), has low calorific value, and highly oxygenated. Hence, the quality of the bio-oil needs to be improved to reduce the amount of acids and oxygenated compounds in the bio-oil. One of the popular methods to improve the properties of bio-oil is catalytic fast pyrolysis (CFP) [1].
Many researchers have focused on the utilization of alkali and alkaline earth metals (AAEMs) and relative compounds as catalysts for CFP such as employing magnesium oxide (MgO) for pyrolysis of cotton seed and introducing calcium oxide (CaO) for pyrolysis of cotton stalk. While MgO has the ability to improve the stability of the bio-oil via deoxygenation, CaO was found to be an excellent catalyst for deacidification of bio-oil and concurrently promoting the formation of hydrocarbons [2,3,4]. Chen et al. concluded that CaO plays three distinct roles during pyrolysis: (1) CO2 absorbent, (2) reactant in decreasing acid content of the bio-oil and increasing ketone content, and (3) catalyst in promoting formation of furan and hydrocarbons [3]. Calcium carbonate (CaCO3) and sodium carbonate (Na2CO3) have been investigated for their performances as catalysts in pyrolysis of combed cotton wastes as well, where the latter provided higher liquid product efficiency than that of CaCO3 [5]. The chloride forms of AAEMs such as sodium chloride (NaCl), potassium chloride (KCl), magnesium chloride (MgCl2), and calcium chloride (CaCl2) also affect the properties of cellulose-derived bio-oil in terms of decrement in levoglucosan yield and substantial increment in lower molecular weight products (e.g. glycoaldehyde, formic acid, and acetol) [6, 7].
Aside from the oxide, carbonate, and chloride forms, AAEMs were supported onto other materials to be used as catalysts for pyrolysis. Zabeti et al. used amorphous silica alumina (ASA) containing AAEMs like sodium (Na), potassium (K), caesium (Cs), magnesium (Mg), and calcium (Ca) for pyrolysis of Canadian pinewood. All the alkali/ASA catalysts were effective in deoxygenation of pyrolysis vapours. While K/ASA and Na/ASA were most active in eliminating oxygen (O2) via decarboxylation, Cs/ASA was most active in oxygen removal via decarbonylation. Cs/ASA also selectively converted undesired phenols to hydrocarbons and maximized the amount of required furans [8].
Transition metals were also used in catalytic pyrolysis studies. Transition metals were mostly used in the form of oxides or supported on zeolites. Under carbon dioxide (CO2) atmosphere, zinc oxide (ZnO) posed catalytic effects on the pyrolysis of textile wastes and was stable throughout [9]. Ma et al. utilized the metal oxides of cobalt, molybdenum, nickel, iron, manganese, and copper, as well as those metals loaded zeolites for pyrolysis of lignin. The study concluded that by supporting cobalt and nickel onto zeolites, more aromatic hydrocarbons were obtained as compared to blank zeolite. It was also concluded that the variation of catalyst and reaction conditions has the potential for obtaining targeted compounds such as vanillin and guaiacol [10]. Besides that, nano titanium dioxide, iron(III) oxide, nickel oxide, and ZnO were used as catalysts in fast pyrolysis of poplar wood. The study concluded that the oxides have the potential to improve the bio-oil qualities in terms of stability, calorific value, and phenol content [11].
I addition to studies for the influences of the catalysts on biomass pyrolysis for production of bio-oil, studies regarding the effects of the catalysts on the thermal behaviour of biomass and on the kinetics involved are essential. Having known the kinetic triplets (apparent reaction activation energy, E, apparent frequency factor, A, and kinetic model,\(f(\alpha)\)), the degradation behaviour of the blends and their mechanisms can be further understood, which may assist in the design, optimization, and scaling up of the operation [12, 13]. Thermogravimetric analysis (TGA) is one of the most common methods to evaluate and compare the kinetics during thermal conversion of biomass [14].
The distributed activation energy model (DAEM) has been widely used to predict the kinetic parameters for the pyrolysis of lignocellulosic biomass by utilizing the data obtained from TGA. This model has been comprehensively reviewed by Cai et al. DAEM assumes that during the pyrolysis of solid fuels, multiple independent, parallel, first order or nth order reactions with distinct activation energies takes place [15]. Simplification of DAEM was carried out to facilitate the prediction of devolatilization curves and to obtain the kinetic triplets in a more straightforward manner. One of the commonly used simplified DAEM was proposed by Miura and Maki, where the reactions were assumed to be first-order reactions [16]. Besides that, model free methods such as Coats-Redfern (CR) have been broadly used to obtain the thermal kinetic triplets by applying the Arrhenius equation [17].
The current study takes interest in employing CaO, MgO, and ZnO for the catalytic pyrolysis of cellulose and palm empty fruit bunch fibre (EFBF). These oxides were selected as they are naturally available and had exhibited potential for bio-oil upgrading using other biomass. A variation in biomass feedstock may exhibit different behaviours in thermal processes as biomass is diverse in nature and may have distinct heat and mass transfer characteristics. Since Malaysia is one of the world’s largest palm oil producers, a great amount of palm waste such as empty fruit bunches (EFB) is being generated simultaneously. Therefore, palm based lignocellulosic biomass has been the focus in many biofuel studies in Malaysia due to its abundance and at the same time to solve the issue on waste disposal without contributing negatively to the environment. Thus, EFBF was used as feed in current study.
On the other hand, as cellulose is the most abundant compound in lignocellulosic biomass, current study utilized cellulose as feed to understand the influence of the oxides on the thermal behaviour of lignocellulosic biomass at its simplest form. In addition, the results may be used as a general reference to understand the effects of the oxides on lignocellulosic biomass upon catalytic pyrolysis.
To our knowledge, the kinetics study on the catalytic pyrolysis of EFBF and cellulose with CaO, MgO, and ZnO have yet to be done. Hence, the current study aims to investigate the influences of the selected oxides on the pyrolytic behaviour, kinetics, and mechanisms on catalytic pyrolysis of EFBF and cellulose. In order to achieve the aim, thermogravimetric study experiments of cellulose and EFBF in the presence these oxides at different weight percentages (0, 5, and 10 wt%) were carried out over a range of heating rates (5, 10, 20, and 30 °C/min). The effects of heating rates and amount of oxides added on pyrolytic behaviour of the biomasses were initially studied. Following that, simplified DAEM was employed to evaluate the activation energy of the samples. Then, the reaction mechanisms during non-catalytic and catalytic pyrolysis were analysed using Coats-Redfern method. In this detailed analysis, the TGA curves were divided into different stages and all possible reactions mechanisms such as simple kinetic equations of different orders, phase boundary reactions and diffusion mechanisms were evaluated to get the highest correlation coefficient.
2 Materials and methods
2.1 Feedstock characterization
Two feedstocks were utilized in this study, which are cellulose and palm empty fruit bunch fibre (EFBF). The cellulose (CAS number 9004-34-6) was in the form of microcrystalline powder, purchased from Sigma–Aldrich (M) Sdn. Bhd. (Malaysia) and used as received. On the other hand, EFBF was collected from Seri Ulu Langat Palm Oil Mill Sdn. Bhd, Dengkil, Selangor Darul Ehsan (Malaysia). The characterization methodology has been presented elsewhere [18]. Besides that, the lignocellulosic content and extractives amount of EFBF were determined with reference to the procedure described by Lee et al. [19].
2.2 Catalysts characterization and treatment
The characterization of selected oxides, namely, calcium oxide (CaO), magnesium oxide (MgO) and zinc oxide (ZnO) were obtained from R&M Chemicals (M) Sdn. Bhd. (Malaysia). To remove volatile impurities, the catalysts were calcined in a chamber furnace (Carbolite ELF 11/68, UK) for 5 h at 600 °C. The surface properties of the oxides were characterized and presented elsewhere [20]. The oxides are considered to be macroporous (pore diameter > 50 nm), with pore volumes of 0.10, 0.27, and 0.01 cm3/g for CaO, MgO, and ZnO, respectively.
2.3 Thermogravimetric analysis (TGA)
The oxides used in current study were subjected to thermogravimetric analysis (TGA) as a blank test to exclude the behaviour change in the oxides from that of biomass if any. Besides, TGA was also carried out to study the pyrolytic behaviour of both cellulose and EFBF with and without the presence of selected oxides. Oxides were added to both feedstock at various weight percentages of 0, 5, and 10 wt%. The analyses were carried out in a programmable TGA DSC 1 Mettler Toledo (M) Sdn. Bhd. (Malaysia). In each experimental run, approximately 10 mg of sample was subjected to heating from room temperature to 900 °C, and then held at that temperature for 10 min. The heating rate was varied at 10, 20, 30, and 40 °C/min and the nitrogen (N2) purge was fixed at 20 mL/min. All experiments were duplicated.
2.4 Kinetic model
Kinetics analysis of cellulose and EFBF, with and without catalysts was carried out using simplified distributed activation energy model (DAEM) and Coats-Redfern (CR) method.
2.4.1 Simplified distributed activation energy model (DAEM)
The brief derivation of simplified DAEM is presented in the current section whereas the detailed derivation can be obtained elsewhere [16].
To study the reaction kinetics of biomass at solid state, the change in extent of reaction or also known as the conversion degree, \(\alpha\) was used:
where \({m}_{o}\), \(m\), and \({m}_{f}\) are the initial, instantaneous, and final masses of the solids, respectively. On the other hand, \(V\) and \({V}^{*}\) are the total and effective volatile contents, accordingly.
Based on the DAEM model, the total conversion degree of biomass to volatiles over time for non-isothermal processes may be expressed as:
where \(A\) is the frequency factor \((1/\mathrm{s})\) and is assumed to be the same for all reactions. \(E\) is the activation energy \((\mathrm{kJ}/\mathrm{mol})\); \(R\) is the gas constant of \(8.314 \mathrm{J}/\mathrm{mol K}\); \(T\) is the absolute temperature \(\left(\mathrm{K}\right)\); \(f\left(E\right)\) is the normalized distribution curve of the activation energy.
Upon a series of approximation and simplification by Miura and Maki (1998), Eq. (3) is obtained:
where \(\beta\) is the heating rate (°C/min).
By plotting of \(\mathrm{ln}\frac{\beta }{{T}^{2}}\) against \(\frac{1}{{T}^{2}}\) at a certain conversion degree, \(E\) and \(A\) values may be calculated as follows:
where, \(m\) is the slope and \(c\) is the intercept.
2.4.2 Coats-Redfern (CR) method
The detailed mathematical background of the CR method may be obtained elsewhere whereas the current section presents a simplified version [21].
In non-isothermal experiments, the rate of solid degradation may be written as:
where k is the temperature-dependant rate constant and \(f\left(\alpha \right)\) is a function of conversion that varies according to the reaction model.
By expressing k as Arrhenius equation and considering constant heating rate of \(\beta =\frac{dT}{dt}\), the following equation is obtained
Upon integration, the logarithmic expression of Eq. (7) may be written as
where \(g\left(\alpha \right)\) is the integrated form of the conversion dependence function \(f\left(\alpha \right)\). As the value of \(\frac{2RT}{E}\) was far less than one, the term was omitted and Eq. (9) is obtained.
where, \(\mathrm{ln}(\frac{AR}{\beta E})\) is essentially a constant value.
A straight line should be obtained from the plotting of \(\mathrm{ln}\left[\frac{g\left(\alpha \right)}{{T}^{2}}\right]\) against \(\frac{1}{T}\) as they have a linear relationship. If the correct \(g\left(\alpha \right)\) is used, the straight line should have a high correlation coefficient of linear regression analysis. Then, the values of E and A can be derived from the slope \(-\frac{E}{R}\) and the intercept \(\mathrm{ln}(\frac{AR}{\beta E})\), respectively.
By identifying \(g\left(\alpha \right)\) that gives the highest correlation coefficient, the pyrolysis reaction of the samples may be associated with the appropriate mechanisms. The basic model functions \(f\left(\alpha \right)\) that were used in this kinetic study of solid-state reactions include chemical processes or mechanisms, phase boundary reactions, and diffusion mechanisms [14, 21]. The detailed models and equations are shown in supplementary file.
3 Results and discussion
3.1 Characterization of feedstock
Based on the results presented in Table 1, both cellulose and hemicellulose content in empty fruit bunch fibre (EFBF) were similar. Cellulose is the most abundant compound in lignocellulosic biomass, and was opted as the model compound in current study, which helps to find the interaction of other components on cellulose pyrolysis for a lignocellulosic biomass. For proximate analysis, EFBF exhibited lower volatile matter, higher ash content, and higher fixed carbon due to the presence of hemicellulose and lignin, as compared to those of pure cellulose. As for the ultimate analysis and higher heating values (HHV), the results were comparable, except for nitrogen (N) content.
3.2 Thermogravimetric analysis (TGA)
3.2.1 Oxides
Figure 1 presents the behaviour of the oxides (calcium oxide (CaO), magnesium oxide (MgO), and zinc oxide (ZnO)) used in the current study when subjected to thermogravimetric analyses (TGA) with heating rate of 20 °C/min. The aim of the analysis was to differentiate the changes in behaviour of oxides from biomass upon TGA. CaO showed two weight loss stages at 440 °C (10% weight loss) and 700 °C (3% weight loss), respectively. Wang et al. regarded the weight loss at 440 °C to decomposition of calcium hydroxide (Ca(OH)2) in CaO, where Ca(OH)2 was formed from the reaction of CaO with the moisture in air prior to experiments [2]. The second weight loss stage may be attributed to decomposition of calcium carbonate (CaCO3), which occurs at 700 °C [22]. Similarly, CaCO3 was possibly formed from the reaction of CaO before the experiment with carbon dioxide (CO2) from surroundings. At ambient temperature, CaO-based sorbents are able to capture CO2, even though the carbonation reaction is slower than at elevated temperatures [23].
MgO is known to be a hygroscopic material and would adsorb moisture from air, forming magnesium hydroxide (Mg(OH)2). The Mg(OH)2 formed would then decompose in the temperature range of 200 °C to 450 °C [24]. Hence, a weight loss stage (2% weight loss) may be observed in the range of 190 °C to 350 °C for MgO. On the other hand, ZnO was stable throughout the analysis.
3.2.2 Cellulose and empty fruit bunch fibre (EFBF)
Figure 2 displays the weight loss (TG) and the derivative weight loss (DTG) curves for the thermal degradation of cellulose and EFBF at various heating rates (10, 20, 30, and 40 °C/min) at fixed N2 flow of 20 mL/min. As the heating rates increased, the degradation behaviour of the biomass remained almost the same whereas the degradation temperature increased. This is because at lower heating rates, the reaction time for the sample at a certain temperature range is longer and the heating of biomass particles occurs more gradually. Therefore, degradation temperatures of biomass are lower and heat transfer between the biomass particles are more effective at lower heating rates [25]. On the other hand, the mass loss rate of biomass increased with the heating rates because at higher heating rates, biomass particles would exhibited higher activity due to stronger thermal shock [25].
For heating rate of 20 °C/min, the degradation of both cellulose and EFBF may be distinguished into three stages: (1) evaporation of moisture (50–160 °C); (2) devolatilization (160–420 °C); and (3) further decomposition to form gaseous products and residual char (and lignin for EFBF, above 420 °C). The first degradation stage may be attributed to the dehydration of biomass, which involved the drying of free and bound moistures on the raw material [26]. Stage 2 of biomass degradation showed the most significant weight loss, where the weight loss rate for cellulose and EFBF reached the maximum at approximately 350 and 325 °C, respectively. This may accredited to the fact that glyosidic bonds in cellulose become very reactive at temperatures above 300 °C and upon rupturing, depolymerization of cellulose occurs. Volatilization is an endothermic reaction and at this stage, most of the released volatiles are condensable organic compounds [27, 28]. Additionally, for EFBF, hemicellulose would devolatilize at this stage as well as cellulose. In order to justify this statement using TGA results, the weight loss of EFBF in Stage 2c was recalculated by excluding the moisture (6.8 wt%) and extractives content (18.8 wt%) in EFBF. The recalculated weight loss from TGA results is 72.3 wt%, which is close to the sum of cellulose and hemicellulose shown in Table 1 (74.4 wt%). Subsequently, Stage 3 is an exothermic reaction, accredited to secondary cracking of char formed in the first two stages [29, 30]. For EFBF, decomposition of lignin and other stronger chemical bonds occurs at this stage as well.
The pyrolytic behaviour of cellulose and EFBF was also studied under various heating rates (10, 20, 30, and 40 °C/min) with the addition of 5 wt% and 10 wt% of oxides. The sample labelled as ‘C-CaO 5%’ refers to cellulose samples with addition of 5 wt% CaO, ‘C-CaO 10%’ to cellulose sample with addition of 10 wt% CaO, and so on for other cellulose samples. Similarly, the sample labelled as ‘E-CaO 5%’ refers to EFBF sample with 5 wt% CaO added, ‘E-CaO 10%’ refers to EFBF sample with 10 wt% CaO added, and so on for the other EFBF samples.
The addition of MgO and ZnO did not alter the behaviour of both cellulose and EFBF degradation substantially and their respective curves at different heating rates are presented in Supplementary file. Alternatively, the weight losses experienced at each of the distinctive stages when heating rate was set to 20 °C/min are presented in Fig. 3. On the other hand, the residual weight and maximum weight loss rate of the samples are tabulated and presented in Table 2.
When compared to the weight loss of cellulose only, it may be interpreted as the addition of MgO and ZnO did not substantially affected the releasing of volatiles (Stages 1 and 2). Nevertheless, a slight decrement in maximum weight loss rate upon the incorporation of CaO was observed, suggesting that CaO decreased the activity of cellulose in thermal decomposition. For EFBF, both the amounts of volatiles and maximum weight loss rate decreased notably (difference of > 5 wt%) when MgO and ZnO were added. Such observation indicates that the addition of MgO and ZnO would restrain the releasing of volatiles in EFBF due to the presence of other components instead of purely cellulose. In addition, the residual weight of both biomasses increased overall. The observations may be contributed by the formation of coke on the oxides, which would block the diffusion pathways of volatiles, suggesting that these oxides would increase the char yield during pyrolysis [31]. In other works involving the catalytic pyrolysis of biomass in reactors for production of bio-oil, the coke formed not only increased char yield but also filled the interspaces in MgO, lowering the bio-oil yield [20, 32].
The incorporation of CaO showed visible change in the pyrolytic behaviour of both cellulose and EFBF, where two additional peaks were obtained, as observed from Fig. 4. For both cases, an addition stage was noticed when CaO was added: Stage 1 (50–16 °CC), 2 (160–380 °C), 3 (380–580 °C), and 4b (above 580 °C). The stages may be accredited to moisture loss, devolatilization, decomposition of Ca(OH)2, and secondary reactions together with decomposition of CaCO3, respectively. For EFBF, lignin degrades in Stage 4 as well. The formation and dissociation of Ca(OH)2 and CaCO3 have been explained earlier in Sect. 3.2.1. More weight loss may be observed for EFBF as compared to the amount of CaCO3 degraded than that in cellulose, indicating that CaCO3 were formed not only prior to TGA but also during the degradation of EFBF with CaO. Upon the pyrolysis of biomass, CO2 is one of the main gas products and is mainly formed from the cracking and reforming of carboxyl groups at relatively low temperatures [33]. One of the forms of carboxyl group is present in the form of acetic acid, which is produced mainly from the deacetylation of hemicellulose [34]. Hence, the weight loss of Ca(OH)2 and CaCO3 in EFBF is more noticeable than in cellulose due to the higher amount of CO2 released in the reaction. Besides, it may be observed from Table 2 that the residual weight of EFBF increased with the addition of CaO. The observation is consistent with Zhang et al. in the microwave pyrolysis of textile sludge with CaO, where an increase in bio-char yield was recorded. The authors regarded the observation to the formation of CaCO3 and enhancement of secondary reactions [35].
3.3 Kinetics of catalytic pyrolysis by simplified distributed activation energy model (DAEM)
Reaction kinetics for pyrolysis of biomass requires proper understanding for the efficient design, operation and modelling of equipment for production. Apart from that, the influence of oxides to the kinetics of biomass pyrolysis, if any, is important for better understanding of the interactions between the oxides and the biomass. Usually, the kinetic parameters determined are the activation energy (E) and the frequency factor (A). While the activation energy may reflect the reactivity of the biomass, the frequency factor plays a role as a scaling parameter, which determines the absolute value of the reaction rate.
In the current study, simplified distributed activation energy model (DAEM) was used for determining the kinetics of cellulose and EFBF, with and without the presence of catalysts (CaO, MgO, and ZnO). Simplified DAEM assumes that complex reactions like the pyrolysis of biomass as an infinite number of irreversible first-order parallel reactions occurring simultaneously, with their distinct rate parameters [16].
The \(\mathrm{ln}(\frac{\beta }{{T}^{2}})\) against \(\frac{1000}{T}\) graphs that were used to determine the E and A of the samples are presented in supplementary file. The correlation coefficients of the plots were high with a minimum value of 0.97 for cellulose and an average of 0.95 for EFBF.
The activation energy of cellulose has been studied, compared, and discussed by Jin et al., where the values ranged from 194 to 381 kJ/mol. The wide range of activation energy values may be attributed to the different calculation methods and to the different crystallinity of cellulose used [36]. Here, the activation energies (Eα) of cellulose, with and without oxides, against the degree of conversion, α are presented in Fig. 5. whereas the average values of E (Eavg) and range of A are presented in Table 3. The average E of 201.03 kJ/mol obtained is within the range of literature values for α in the range of 0.2–0.8, which corresponds to the temperature range of 320–380 °C. In this temperature range, cellulose was devolatilized and achieved maximum mass loss rate.
The activation energy of cellulose decreased from conversions 0.2 to 0.6, and hereafter slightly increased. The decrement and increment of Eα were observed in other studies as well and accredited the trend to the competitive pathways in cellulose pyrolysis [37, 38]. On the other hand, other studies considered the change in Eα in this conversion range as constant [39, 40].
The employment of the MgO and ZnO catalysts did not alter the trend of Eα with regards to α but did lower the average values of activation energy, Eavg. This suggests that the oxides elevated the reaction rate of cellulose. On the other hand, although the addition of CaO lowered Eavg slightly, E increased from α of 0.2 and 0.8. This may be due to the decomposition of Ca(OH)2 and CaCO3, where the formation of the compounds has been explained in Sect. 3.2.
The kinetic study of EFBF has been carried out by others and Eavg obtained ranges from 145 to 195 kJ/mol [18, 41, 42]. Based on Table 3, the Eavg obtained in the current study was 274.5 kJ/mol, which is out of the range as compared to literature. This may be attributed to the difference in source, lignocellulosic content of the EFB, and pre-treatment of the EFB used for analysis. Nevertheless, the change in E with respect to α showed similar trend (Fig. 6). The E of EFBF increased gradually from conversion 0.2 to a maximum at 0.5, where the E was 295.04 kJ/mol and later decreased. Comparable observations were in the previous work and literature [18, 41]. Nyakuma et al. accredited the conversion degree of 0.2–0.6 and > 0.6 to active pyrolysis and passive pyrolysis stages of the thermal decomposition of EFBF based on the mass loss rate.
The change of Eα with regards to α altered slightly when the oxides were employed. When MgO and ZnO were added, the activation energy reached a maximum α is 0.7 and 0.6, respectively instead of 0.5; when CaO was added, the activation energy increased from conversion 0.2 to 0.8. Since conversions above 0.6 may be regarded as the passive pyrolysis stage and as the stage where lignin, char, and heavier compounds decompose, the continuous increment in activation energies may be contributed by the formation of coke on the catalysts, as discussed in Sect. 3.2. Hence, higher activation energies would be required for higher conversions. Furthermore, the effects of CaO on the increment in activation energy, may be contributed by the decomposition of Ca(OH)2 and CaCO3, as well as the coke formed. The formation of the compounds has been explained in Sect. 3.2.
Generally, the addition of the oxides lowered the average activation energy of cellulose and EFBF, indicating that the oxides increased the reaction rate of the biomasses. Nonetheless, based on the results presented in Sect. 3.2, the incorporation of oxides did not enhance the release of volatiles. Therefore, further analysis on the reaction and diffusion mechanisms during catalytic pyrolysis of cellulose and EFBF at individual stages was studied using Coats-Redfern method.
3.4 Kinetics and mechanisms for catalytic pyrolysis at individual stages by Coats-Redfern (CR) method
The decomposition of cellulose and EFBF were divided into stages based on DTG curve at heating rate of 20 °C/min, as presented in Sect. 3.2. Using Coats and Redfern (CR) method, the mechanisms involved in the pyrolysis of cellulose and EFBF, with and without oxides may be understood. A high correlation coefficient would indicate the kinetic model that fits the data well (> 0.95). The basic model functions \(f\left(\alpha \right)\) that were used in this kinetic study of solid-state reactions include chemical processes or mechanisms (F series), phase boundary reactions (R series), and diffusion mechanisms (D series). The F series (F1/3, F3/4, F1, F3/2, F2, and F3) are order-based models and are the simplest models among all. For this mechanism, the reaction rate is proportional to the concentration of the reactant, raised to a particular power [43]. The rate-determining step is the nucleation or chemical reaction. Phase boundary-controlled reactions (R1, R2, and R3) assume that the reaction is controlled by the movement of an interface at a constant velocity and nucleation occurs almost instantly. Then, a layer of product would cover each particle [44]. Next, the diffusion kinetic models (D1, D2, D3, D4, D5, D6, D7, D8) are characterized by the mobility of components in the system, usually in solid-state reactions. In these reactions, the rate of product formation decreases proportionally with the thickness of the product barrier layer [43].
The kinetic parameters obtained for cellulose and EFBF, with and without oxides at heating rate of 20 °C/min, are presented in Fig. 7. Stage 1 mainly involves the dewatering of samples. While the second order chemical reaction model (F2) was in dominion for cellulose, the EFBF samples fitted well with the third order kinetic model (F3). Protective nature of lignin and hemicellulose in biomass caused higher order of reaction than that of cellulose alone. The addition of oxides did not affect the water evaporation rate as activation energy was almost similar even when the oxides were added.
Subsequently, the main devolatilization of cellulose occurs at Stage 2, as presented in Table 4. At this stage, the solid-state reaction was controlled by one and a half order (F3/2) and the three-dimensional diffusion mechanism of Zhuravlev, Lasokin, Tempelman equation (D5). Here, diffusion in all three directions is important. Even though there were no changes in the kinetic models when the oxides were employed, the activation energies increased in general. This indicates that the oxides did not influence the reaction mechanisms but reduced the rate of reaction. Nevertheless, this did not affect the weight loss of cellulose at this stage. An extra kinetic model showed high correlation coefficient when CaO was employed, which is the phase boundary reaction (R3). R3 is a function for a sphere reacting from the surface inward, suggesting that the presence of spherical particles may be contributed by CaO, Ca(OH)2 or CaCO3.
EFBF also experienced the highest weight loss at Stage 2, (Table 4) which may be ascribed to the devolatilization of mainly cellulose and hemicellulose. The reactions were not only controlled by second order reaction (F2) but also three-dimensional diffusion mechanism of Zhuravlev, Lasokin, Tempelman equation (D5), which is similar to that of cellulose. This further justifies the devolatilization of cellulose at this stage. The addition of MgO and ZnO did not pose any significant effect on the kinetic model nor the activation energy of EFBF. Nonetheless, the weight loss at this stage decreased when the oxides were added (Sect. 3.2). As observed, the addition of oxides caused a reduction in the frequency factor, which, by definition signifies the probability for reaction occurrence [45]. Hence, it may be hypothesized that the addition of the oxides did not affect the reaction rate of EFBF for devolatilization but rather, reduced the probability for reaction to occur. Aside from kinetic models of F1 and D5, the addition of CaO also showed high correlation coefficient with the power law in the phase boundary reaction (R3), which is again, similar to that of cellulose.
EFBF exhibited higher reaction rates in dewatering of the sample and in devolatilization of the sample. This was reflected from the higher reaction orders obtained for EFBF, indicating that the presence of metal elements in EFBF such as magnesium (Mg), calcium (Ca), potassium (K), and zinc (Zn) might have played a role in the thermal degradation of EFBF [46, 47].
Stage 3 may be attributed to the further decomposition of cellulose and additional lignin for EFBF, to form gaseous products and residual char. For all samples, the unanimous kinetic model that was most fitting is the third order kinetic model (F3) and the kinetic parameters are presented in Fig. 8. As observed for cellulose, the activation energy increased with the addition of the MgO and ZnO. This may be because the oxides promoted the formation of coke, which was reflected by the higher residual weight obtained as presented in Sect. 3.2. Hence, higher activation energy would be required for the further degradation of cellulose. On the contrary, when MgO and ZnO were added to EFBF, the activation energy decreased slightly, which explains the higher weight loss as presented in Sect. 3.2. This possibly suggests that MgO and ZnO are more effective in catalysing the decomposition of lignin and more complex components. Phenolic compounds are the products of lignin depolymerization and pyrolysis experiments did show that the utilization of MgO and ZnO would increase the amount of phenolic compounds in the bio-oil [32, 48].
When CaO was added to cellulose, Stage 3 and Stage 4 may be accredited to the decomposition of Ca(OH)2 and secondary reactions alongside with the decomposition of CaCO3, respectively. Similarly, F3 kinetic model fits well with the data, showing that aside from secondary reactions, the decomposition rate of calcium compounds was also limited by chemical reactions.
For EFBF with CaO, while Stage 3 may be accredited to the decomposition of Ca(OH)2, Stage 4 may be ascribed to the decomposition of mainly lignin together and CaCO3. The degradation of Ca(OH)2 obtained good linearity with the F3 kinetic model, which is the same as that of cellulose. However, for Stage 4, the solid-state reaction was controlled by first order kinetic model (F1), phase boundary reaction (R3), and Jander equation (D3). As both R3 and D3 are functions for reactions in a sphere, it is indicated that the CaCO3 in the current study are of spherical shape. Such observation was not made for cellulose probably due to the little amount of CaCO3 formed as explained in Sect. 3.2.
4 Conclusion
The thermal degradation of EFBF and cellulose were evaluated by different reaction mechanisms. The addition of oxides (CaO, MgO, ZnO) to both cellulose and EFBF did not affect their pyrolytic behaviour. However, these oxides decreased the average activation energies, indicating the exhibition of catalytic effects. Even though MgO and ZnO did not affect the reaction mechanisms, their presence reduced the reaction rate in cellulose and lowered the chances for reaction to occur in EFBF. The effects of the oxides on both EFBF and cellulose were mostly similar, however the effects were more noticeable in EFBF than in cellulose. Owing to its moisture and carbon dioxide (CO2) capability, an extra weight loss stage was observed in presence of CaO cases due to the decomposition of calcium hydroxide (Ca(OH)2) and calcium carbonate (CaCO3). These compounds gave an impression of being spherical in shape and may have contributed to the increase in residual weight of EFBF. On the whole, the oxides (CaO, MgO, ZnO) posed catalytic effects on the pyrolytic degradation of biomass without affecting the reaction mechanisms.
References
Liu C, Wang H, Karim AM, Sun J, Wang Y (2014) Catalytic fast pyrolysis of lignocellulosic biomass. Chem Soc Rev 43:7594–7623. https://doi.org/10.1039/C3CS60414D
Wang D, Xiao R, Zhang H, He G (2010) Comparison of catalytic pyrolysis of biomass with MCM-41 and CaO catalysts by using TGA-FTIR analysis. J Anal Appl Pyrolysis 89:171–177. https://doi.org/10.1016/j.jaap.2010.07.008
Chen X, Chen Y, Yang H, Chen W, Wang X, Chen H (2017) Fast pyrolysis of cotton stalk biomass using calcium oxide. Bioresour Technol 233:15–20. https://doi.org/10.1016/j.biortech.2017.02.070
Pütün E (2010) Catalytic pyrolysis of biomass: Effects of pyrolysis temperature, sweeping gas flow rate and MgO catalyst. Energy 35:2761–2766. https://doi.org/10.1016/j.energy.2010.02.024
Barişçi S, Öncel MS (2014) The disposal of combed cotton wastes by pyrolysis. Int J Green Energy 11:255–266. https://doi.org/10.1080/15435075.2013.772516
Patwardhan PR, Satrio JA, Brown RC, Shanks BH (2010) Influence of inorganic salts on the primary pyrolysis products of cellulose. Bioresour Technol 101:4646–4655. https://doi.org/10.1016/j.biortech.2010.01.112
Shimada N, Kawamoto H, Saka S (2008) Different action of alkali/alkaline earth metal chlorides on cellulose pyrolysis. J Anal Appl Pyrolysis 81:80–87. https://doi.org/10.1016/j.jaap.2007.09.005
Zabeti M, Nguyen TS, Lefferts L, Heeres HJ, Seshan K (2012) In situ catalytic pyrolysis of lignocellulose using alkali-modified amorphous silica alumina. Bioresour Technol 118:374–381. https://doi.org/10.1016/j.biortech.2012.05.034
Wu Y, Wen C, Chen X, Jiang G, Liu G, Liu D (2017) Catalytic pyrolysis and gasification of waste textile under carbon dioxide atmosphere with composite Zn-Fe catalyst. Fuel Process Technol 166:115–123. https://doi.org/10.1016/j.fuproc.2017.05.025
Ma Z, Custodis V, van Bokhoven JA, Martineau DR, Kwon G, Lee S, Lee B, DeBartolo JE, Seifert S, Winans RE, Si R, Ricks B, Goergen S, Rutter M, Zugic B, Flytzani-Stephanopoulos M, Wang ZW, Palmer RE, Neurock M, Vajda S (2014) Selective deoxygenation of lignin during catalytic fast pyrolysis. Catal Sci Technol 4:766. https://doi.org/10.1039/c3cy00704a
Lu Q, Zhang ZF, Dong CQ, Zhu XF (2010) Catalytic upgrading of biomass fast pyrolysis vapors with nano metal oxides: an analytical Py-GC/MS study. Energies 3:1805–1820. https://doi.org/10.3390/en3111805
Mu L, Chen J, Yao P, Zhou D, Zhao L, Yin H (2016) Evaluation of co-pyrolysis petrochemical wastewater sludge with lignite in a thermogravimetric analyzer and a packed-bed reactor: pyrolysis characteristics, kinetics, and products analysis. Bioresour Technol 221:147–156. https://doi.org/10.1016/j.biortech.2016.09.011
Qi Y, Guo C, Xu X, Gao B, Yue Q, Jiang B, Qian Z, Wang C, Zhang Y (2020) Co/Fe and Co/Al layered double oxides ozone catalyst for the deep degradation of aniline: preparation, characterization and kinetic model. Sci Total Environ 715:136982. https://doi.org/10.1016/j.scitotenv.2020.136982
Gil MV, Casal D, Pevida C, Pis JJ, Rubiera F (2010) Thermal behaviour and kinetics of coal/biomass blends during co-combustion. Bioresour Technol 101:5601–5608. https://doi.org/10.1016/j.biortech.2010.02.008
Cai J, Wu W, Liu R (2014) An overview of distributed activation energy model and its application in the pyrolysis of lignocellulosic biomass. Renew Sustain Energy Rev 36:236–246. https://doi.org/10.1016/j.rser.2014.04.052
Miura K, Maki T (1998) A simple method for estimating f(E) and k0(E) in the distrubuited activation energy model. Energy Fuels 12:864–869
Coats AW, Redfern JP (1964) Kinetic parameters from thermogravimetric data. Nature 201:68–69. https://doi.org/10.1038/201068a0
Chong YY, Thangalazhy-Gopakumar S, Gan S, Ng HK, Lee LY, Adhikari S (2017) Kinetics and Mechanisms for copyrolysis of palm empty fruit bunch fiber (EFBF) with palm oil mill effluent (POME) sludge. Energy Fuels 31:8217–8227. https://doi.org/10.1021/acs.energyfuels.7b00877
Lee XJ, Lee LY, Gan S, Thangalazhy-Gopakumar S, Ng HK (2017) Biochar potential evaluation of palm oil wastes through slow pyrolysis: Thermochemical characterization and pyrolytic kinetic studies. Bioresour Technol 236:155–163. https://doi.org/10.1016/j.biortech.2017.03.105
Chong YY, Thangalazhy-Gopakumar S, Ng HK, Lee LY, Gan S (2019) Effect of oxide catalysts on the properties of bio-oil from in-situ catalytic pyrolysis of palm empty fruit bunch fiber. J Environ Manag 247:38–45. https://doi.org/10.1016/j.jenvman.2019.06.049
Vlaev L, Nedelchev N, Gyurova K, Zagorcheva M (2008) A comparative study of non-isothermal kinetics of decomposition of calcium oxalate monohydrate. J Anal Appl Pyrolysis 81:253–262. https://doi.org/10.1016/j.jaap.2007.12.003
Kwon EE, Lee T, Sik Y, Tsang DCW, Park C, Lee J (2018) Effects of calcium carbonate on pyrolysis of sewage sludge. Energy 153:726–731. https://doi.org/10.1016/j.energy.2018.04.100
Ridha FN, Manovic V, Macchi A, Anthony EJ (2015) CO2 capture at ambient temperature in a fixed bed with CaO-based sorbents. Appl Energy 140:297–303. https://doi.org/10.1016/j.apenergy.2014.11.030
Aphane ME (2009) The hydration of magnesium oxide with different reactivities by water and magnesium acetate. Thesis
El-Sayed SA, Khairy M (2015) Effect of heating rate on the chemical kinetics of different biomass pyrolysis materials. Biofuels 6:157–170. https://doi.org/10.1080/17597269.2015.1065590
Chen D, Li M, Zhu X (2012) TG-DSC method applied to drying characteristics and heat requirement of cotton stalk during drying. Heat Mass Transf und Stoffuebertragung 48:2087–2094. https://doi.org/10.1007/s00231-012-1050-6
Collard F-X, Blin J (2014) A review on pyrolysis of biomass constituents: mechanisms and composition of the products obtained from the conversion of cellulose, hemicelluloses and lignin. Renew Sustain Energy Rev 38:594–608. https://doi.org/10.1016/j.rser.2014.06.013
Yang H, Yan R, Chen H, Lee DH, Zheng C (2007) Characteristics of hemicellulose, cellulose and lignin pyrolysis. Fuel 86:1781–1788. https://doi.org/10.1016/j.fuel.2006.12.013
Kilzer FJ, Broido A (1965) Speculations on the nature of cellulose pyrolysis. Pyrodynamics 2:151–163. https://doi.org/10.1143/JPSJ.20.457
Wang S, Liu Q, Luo Z, Wen L, Cen K (2007) Mechanism study on cellulose pyrolysis using thermogravimetric analysis coupled with infrared spectroscopy. Front Energy Power Eng China 1:413–419. https://doi.org/10.1007/s11708-007-0060-8
Balasundram V, Ibrahim N, Kasmani RM, Hamid MKA, Isha R, Hasbullah H, Ali RR (2018) Thermogravimetric catalytic pyrolysis and kinetic studies of coconut copra and rice husk for possible maximum production of pyrolysis oil. J Clean Prod 167:218–228. https://doi.org/10.1016/j.jclepro.2017.08.173
Stefanidis SD, Karakoulia SA, Kalogiannis KG, Iliopoulou E, Delimitis A, Yiannoulakis H, Zampetakis T, Lappas AA, Triantafyllidis KS (2016) Natural magnesium oxide (MgO) catalysts: a cost-effective sustainable alternative to acid zeolites for the in situ upgrading of biomass fast pyrolysis oil. Appl Catal B Environ 196:155–173. https://doi.org/10.1016/j.apcatb.2016.05.031
Fu P, Yi W, Bai X, Li Z, Hu S, Xiang J (2011) Effect of temperature on gas composition and char structural features of pyrolyzed agricultural residues. Bioresour Technol 102:8211–8219. https://doi.org/10.1016/j.biortech.2011.05.083
Shen DK, Gu S (2009) The mechanism for thermal decomposition of cellulose and its main products. Bioresour Technol 100:6496–6504. https://doi.org/10.1016/j.biortech.2009.06.095
Zhang H, Gao Z, Ao W, Li J, Liu G, Fu J, Ran C, Mao X, Kang Q, Liu Y, Dai J (2017) Microwave pyrolysis of textile dyeing sludge in a continuously operated auger reactor: char characterization and analysis. J Hazard Mater 334:112–120. https://doi.org/10.1016/j.jhazmat.2017.03.048
Jin W, Singh K, Zondlo J (2013) Pyrolysis kinetics of physical components of wood and wood-polymers using isoconversion method. Agriculture 3:12–32. https://doi.org/10.3390/agriculture3010012
Rantuch P, Balog K (2014) Thermogravimetric analysis of cellulose insulation and determination of activation energy of its thermo-oxidation using non-isothermal, model-free methods. Polym Adv Technol 25:1169–1174. https://doi.org/10.1002/pat.3373
Cooley S, Antal MJ (1988) Kinetics of cellulose pyrolysis in the presence of nitric oxide. J Anal Appl Pyrolysis 14:149–161. https://doi.org/10.1016/0165-2370(88)85005-8
Huang FY (2012) Thermal properties and thermal degradation of cellulose tri-stearate (CTs). Polymers (Basel) 4:1012–1024. https://doi.org/10.3390/polym4021012
Sonobe T, Worasuwannarak N (2008) Kinetic analyses of biomass pyrolysis using the distributed activation energy model. Fuel 87:414–421. https://doi.org/10.1016/j.fuel.2007.05.004
Nyakuma BB, Ahmad A, Johari A, Abdullah TAT (2016) Thermogravimetric and kinetic analyses of oil palm empty fruit bunch (OPEFB) Pellets using the distributed activation energy model. J Phys Sci 27:67–83. https://doi.org/10.21315/jps2016.27.3.5
Surahmanto F, Saptoadi H, Sulistyo H, Rohmat TA (2017) Investigation of the slow pyrolysis kinetics of oil palm solid waste by the distributed activation energy model. Biofuels. https://doi.org/10.1080/17597269.2017.1387750
Guida MY, Hannioui A (2016) Evaluation of reliability of coats-redfern and criado methods for kinetics analysis of olive mill solid waste and olive mill wastewater. Int J Sci Eng Res 7:193–203
Fink D (2013) Transport processes in ion-irradiated polymers
Valdés CF, Betancur Y, López D, Gómez CA, Chejne F (2018) Effects of pyrolysis atmosphere on the porous structure and reactivity of chars from middle and high rank coals. Ing e Investig 38:31–45. https://doi.org/10.15446/ing.investig.v38n1.64516
Hayawin ZN, Astimar AA, Ibrahim MH, Abdul Khalil HPS, Syirat ZB, Menon NR (2014) The growth and reproduction of Eisenia fetida and Eudrilus eugeniae in mixtures of empty fruit bunch and palm oil mill effluent. Compost Sci Util 22:40–46. https://doi.org/10.1080/1065657X.2014.882247
Mahadevan R, Adhikari S, Shakya R, Wang K, Dayton D, Lehrich M, Taylor SE (2016) Effect of alkali and alkaline earth metals on in-situ catalytic fast pyrolysis of lignocellulosic biomass: a microreactor study. Energy Fuels 30:3045–3056. https://doi.org/10.1021/acs.energyfuels.5b02984
Zhou L, Yang H, Wu H, Wang M, Cheng D (2013) Catalytic pyrolysis of rice husk by mixing with zinc oxide: characterization of bio-oil and its rheological behavior. Fuel Process Technol 106:385–391. https://doi.org/10.1016/j.fuproc.2012.09.003
Funding
The authors would like to express sincere gratitude to Ministry of Higher Education Malaysia for funding this research project under the Grant FRGS/1/2015/TK02/UNIM/02/1. However, only the authors are responsible for the opinion expressed in this paper and for any remaining errors.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Chong, Y.Y., Ng, H.K., Lee, L.Y. et al. Kinetics and mechanisms for catalytic pyrolysis of empty fruit bunch fibre and cellulose with oxides. SN Appl. Sci. 2, 1464 (2020). https://doi.org/10.1007/s42452-020-03249-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-03249-1