1 Introduction

There is a great importance of incompressible fluid flow with heat transfer in cooling systems of malls and nuclear plants. The effect of angle between two unparalleled walls on the velocity profiles of viscous fluid was first studied by Jeffery [8] and Hamel [6]. They derived a mathematical formulation to explain the behaviour of velocity profile in both divergent and convergent channels. Since then, due to its importance in industry applications, some researchers analysed the Jeffery–Hamel flow problem with nano-particle with the effect of the magnetic field and heat transfer. Rivkind and Solonnikov [21] computed the solution of the stationary problem with a finite number of “outlets” to infinity in the form of infinite sectors. Akulenko et al. [1] discussed the solution of steady viscous flow in a convergent channel by taking different values of Reynolds numbers to explain the physical phenomena of the problem. Makinde and Mhone [11] used a special type of Hermite-Padé approximation semi-numerical approach to obtain the solution of the MHD Jeffery–Hamel problem, whereas the same problem was also analyzed by Esmaili et al. [4] using Adomian Decomposition Method.

Many approaches, like Travelling Wave Transformation Method, Cole-Hopf Transformation method, Optimal Homotopy Asymptotic Method, Adomian Decomposition Method, Reproducing Kernel Hilbert Space Method [16] and Generalized Boundary Element Approach were applied by several researchers to deal with Jeffery–Hamel flow problem and other fluid mechanics problems which are inherently non-linear. Patil and Khambayat [19] used this technique for the solution of linear differential equation and later it was extended by Mirzaee [12] for finding the solution of a system of differential equation. Zhou et al. [23] applied this technique to the problems arising in electric circuit analysis. Similarly Ayaz [2] derived a solution of the system of partial differential equation using DTM whereas Chen and Ho [3] extended it to two-dimensional DTM and obtained the solution of partial differential equation. Nazari et al. [17] used it to solve a fractional order integro-differential equation with non-vocal boundary conditions. Hossein et al. [7] used Differential Transform Method and derived a solution of non-linear Gas Dynamics and Klein-Gordon equations arising in fluid flow problems. Muhmmad et al. [15] analysed the effects of magnetic fields between two parallel walls for the unsteady double phase nano-fluid flow and heat transfer using Differential Transform Method. Khudir [9] extended the Differential Transform Method to Fractional Differential Transform Method (FDTM) and solved an irrational order fractional differential equations. Kundu et al. [10] appllied DTM and investigated the thermal analysis of exponential fins under sensible and latent heat transfer. Mirzaee [13, 14] extended this method to three-dimensional fuzzy Differential Transform Method and obtained the solution of fuzzy partial differential equations. Sayed and Nour [22] extended it to Modified Fractional Differential Transform Method using the Adomain Polynomials and investigated the behaviour of the projectile motion with quadratic drag force with the local path angle, velocity and position at any time t. Patel and Meher [18] used it to compute the solution of Kolmogrove–Petrovskii–Piskunov equation and also studied the behaviour of saturation profiles in fingero-Imbibition phenomena during two-phase fluid flow through porous media.

In this paper, the MHD Jeffery–Hamel fluid flow between two non-parallel plates with heat transfer is considered to analyse the effects of Reynolds number, Hartmann number and thermal profiles on velocity profiles of fluid flow. Differential Transform Method is used to study the variation of velocity profiles during MHD Jeffery Hamel flow between two non-parallel plates and thermal profiles with different values of Reynolds number and Hartmann number in both divergent and convergent channels and also checked the accuracy and the validity of the obtained results by comparing the obtained results with the results obtained by Optimal Homotopy Perturbation Method and Runge–Kutta Method.

2 Mathematical formulation of the problem

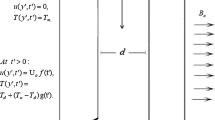
As shown in Fig. 1, consider a viscous fluid flow between two non-parallel plates with angles 2θ and (E0) electromagnetic induction. The continuity equation, the Navier–Stokes equation and the energy equation in cylindrical coordinates can be written as

$$\frac{1}{l}\frac{\partial }{\partial l}(lu_{l} ) + \frac{1}{l}\frac{\partial }{\partial l}(lu_{\alpha } ) = 0$$
(1)
$$u_{l} \frac{{\partial u_{l} }}{\partial l} + \frac{{u_{\alpha } }}{l}\frac{{\partial u_{l} }}{\partial \alpha } - \frac{{u_{\alpha }^{2} }}{l} = - \frac{1}{\rho }\frac{\partial P}{\partial l} + v\left[ {\frac{1}{l}\frac{{\partial (l\xi_{ll} )}}{\partial l} + \frac{1}{l}\frac{{\partial (l\xi_{l\alpha } )}}{\partial l} - \frac{{\xi_{l\alpha } }}{l} - \frac{{E_{0} M^{2} }}{{\rho l^{2} }}u_{l} } \right]$$
(2)
$$u_{l} \frac{{\partial u_{\alpha } }}{\partial l} + \frac{{u_{\alpha } }}{l}\frac{{\partial u_{\alpha } }}{\partial \alpha } - \frac{{u_{l} u_{\alpha } }}{l} = - \frac{1}{\rho l}\frac{\partial P}{\partial l} + v\left[ {\frac{1}{{l^{2} }}\frac{{\partial (l\xi_{l\alpha } )}}{\partial l} + \frac{1}{l}\frac{{\partial (l\xi_{\alpha \alpha } )}}{\partial \alpha } - \frac{{\xi_{l\alpha } }}{l} - \frac{{E_{0} M^{2} }}{{\rho l^{2} }}u_{\alpha } } \right]$$
(3)
$$u_{l} \frac{\partial T}{\partial l} + \frac{k}{{\rho T_{p} }}(\nabla^{2} T) + \frac{v}{{T_{p} }}\left[ {2\left\{ {\left( {\frac{{\partial u_{l} }}{\partial l}} \right)^{2} + \left( {\frac{{u_{l} }}{l}} \right)^{2} } \right\} + \left( {\frac{1}{l}\frac{{\partial u_{l} }}{\partial l}} \right)^{2} } \right] + \frac{{E_{0} M^{2} }}{{\rho l^{2} }}u_{l}^{2}$$
(4)

where ρ is the fluid density, P is the pressure, v is the kinematic viscosity, T is the temperature, k is the thermal conductivity, Tp is the specific heat at constant pressure, E0 is the electrical conductivity, M is the induced magnetic field and the stress components are defined as

Fig. 1
figure 1

3D Geometry of MHD Jeffery Hamel Flow

Full size image
$$\xi_{ll} = 2\frac{{\partial u_{l} }}{\partial l} - \frac{2}{3}div(\bar{u})$$
(5)
$$\xi_{\alpha \alpha } = \frac{2}{r}\frac{{\partial u_{\alpha } }}{\partial \alpha } + \frac{{2\partial u_{l} }}{l} - \frac{2}{3}div(\bar{u})$$
(6)
$$\xi_{l\alpha } = \frac{2}{r}\frac{{\partial u_{l} }}{\partial \alpha } + \frac{\partial }{\partial l}\left( {\frac{{2u_{\alpha } }}{l}} \right)$$
(7)

Upon considering the velocity field only along the radial direction, i.e., uα = 0 and substituting Eqs. (5)–(7) into Eqs. (2) and (3), the continuity, Navier–Stokes and energy equations become:

$$\frac{1}{l}\frac{\partial }{\partial l}(lu_{l} ) = 0$$
(8)
$$u_{l} \frac{{\partial u_{l} }}{\partial l} = - \frac{1}{\rho }\frac{\partial P}{\partial l} + v\left[ {\nabla^{2} u_{l} + \frac{{u_{l} }}{{l^{2} }} - \frac{{E_{0} M^{2} }}{{\rho l^{2} }}u_{l} } \right]$$
(9)
$$- \frac{1}{\rho l}\frac{\partial P}{\partial \alpha } + \frac{2v}{{l^{2} }}\frac{{\partial u_{\alpha } }}{\partial \alpha } = 0$$
(10)

The relevant boundary conditions, due to the symmetry assumption at the channel centreline, are as follows:

$$\frac{{\partial u_{l} }}{\partial \alpha } = \frac{\partial T}{\partial \alpha } = 0,\;u_{l} = \frac{{u_{c} }}{l}at\quad \alpha = 0$$
(11)

and at the plates making the body of the channel:

$$u_{l} = 0,T = \frac{{T_{c} }}{{l^{2} }}at\quad \alpha = \theta$$
(12)

where um and Tm are the middle line rate of movement and the constant wall temperature, respectively.


From the continuity Eq. (8), one can get,

$$lu_{l} = g(\alpha )$$
(13)
$$p(l,\alpha ) = \frac{2\rho v}{{l^{2} }}g(\alpha ) + \rho h(l)$$
(14)

in which h(l) is an arbitrary function of l only.


Upon considering the dimensionless parameters:

$$\gamma = \frac{\alpha }{\theta },\quad e(\gamma ) = \frac{g(\alpha )}{{u_{m} }},\quad h(\gamma ) = l^{2} \frac{T}{{T_{m} }}$$
(15)

into Eqs. (4)–(9) and eliminating the pressure term, it obtains

$$e^{{{\prime \prime \prime }}} + 2\theta R_{e} ee^{{\prime }} + \left( {4 - H_{a} } \right)\theta^{2} e^{{\prime }} = 0$$
(16)
$$h^{{\prime \prime }} + 2\theta^{2} h + 2\theta R_{e} P_{r} eh + \beta P_{r} \left( {H_{a} + 4\theta^{2} } \right)e^{2} + \beta P_{r} \left( {e^{{\prime }} } \right)^{2} = 0$$
(17)

Subjected to the boundary conditions

$$e(0) = 1,\quad e^{{\prime }} (0) = 0,\quad e(1) = 0.$$
(18)
$$h^{{\prime }} (0) = 0,\quad h(1) = 0.$$
(19)

where \(P_{r} = \frac{{vT_{p} }}{\rho k},\beta = \frac{{u_{m} }}{{T_{p} }},R_{e} = \frac{{\theta u_{m} }}{v}\) is the Reynolds number, \(H_{a}^{2} = \frac{{E_{0} M^{2} }}{\rho v}\) is the Hartmann number and Tm is the ambient temperature.

3 Differential transform method for ordinary differential equation

Differential Transform of function e(η) can be defined as follows:

$$E(k) = \frac{1}{k!}\left[ {\frac{{d^{k} e(\eta )}}{{d\eta^{k} }}} \right]_{\eta = 0}$$
(20)

where e()is original function and E(k) is the transformed function. The uppercase and the lowercase letters represent the transformed and the original function respectively. The inverse differential transform of E(k) is defined as:

$$e(\eta ) = \sum\limits_{0}^{\infty } {E(k)\eta^{k} }$$
(21)

Using Eq. (20) in (21), it gives,

$$e(\eta ) = \sum\limits_{0}^{\infty } {\left[ {\frac{{d^{k} e(\eta )}}{{d\eta^{k} }}} \right]_{\eta = 0} } \frac{{\eta^{k} }}{k!}$$

4 Solution through differential transform method

Upon applying the fundamental operations of differential transform method to Eq. (16)–(17), it obtains,

$$ \begin{aligned} & (k + 1)(k + 2)(k + 3)E(k + 3) - 2qR_{e} \sum\limits_{m = 0}^{k} {(m + 1)E(m + 1)E(k - m) - (4 - H_{a} )q^{2} (k + 1)E(k + 2) = 0} \\ & k + 1)(k + 2)H(k + 2) - 4q^{2} H(k) - 2qR_{e} P_{r} \sum\limits_{m = 0}^{k} {H(m)E(k - m)} \\ & \quad \quad \quad \qquad \qquad \qquad \quad - bP_{r} (H_{a} + 4q^{2} )\sum\limits_{m = 0}^{k} {E(m)E(k - m) - bP_{r} (m + 1)(k - m + 1)E(m + 1)E(k - m + 1)} = 0 \\ \end{aligned} $$

And by using the conditions (18) and (19), it becomes,

$$ \begin{aligned} e(\gamma ) = & 1 + c_{1} \gamma^{2} + \left( { - \frac{1}{6}\theta R_{e} c_{1} + \frac{1}{12}(H_{a} - 4)\theta^{2} c_{1} } \right)\gamma^{4} \\ & + \left( { - \frac{1}{60}\theta R_{e} \left( {2c_{1}^{2} - \frac{2}{3}\theta R_{e} c_{1} + \frac{1}{3}(H_{a} - 4)\theta^{2} c_{1} } \right) + \frac{1}{30}(H_{a} - 4)\theta^{2} \left( { - \frac{1}{6}\theta R_{e} c_{1} + \frac{1}{12}(H_{a} - 4)\theta^{2} c_{1} } \right)} \right)\gamma^{6} + \cdots \\ \end{aligned} $$

In particular case, for Re = 50, Pr = 1, β = 3.492161428 10−13, \(\theta = \frac{\pi }{24}\) and H = 0, we have,

$$ \begin{aligned} e(\gamma ) = & 1 - 2.31003427572800\gamma^{2} + 2.51667482980824\gamma^{4} - 2.15076187988905\gamma^{6} \\ & + 1.46378679137772\gamma^{8} - 0.651983643033483\gamma^{10} + 0.132318469962628\gamma^{12} + \cdots \\ \end{aligned} $$
(22)
$$ \begin{aligned} h(\gamma ) = & 4.566876678 \times 10^{ - 13} - 3.016631685 \times 10^{ - 12} \gamma^{2} + 3.822970788 \times 10^{ - 12} \gamma^{4} \\ & - 3.684168116 \times 10^{ - 12} \gamma^{6} + 3.125395871 \times 10^{ - 12} \gamma^{8} - 2.370112507 \times 10^{ - 12} \gamma^{10} \\ & + 1.665857981 \times 10^{ - 12} \gamma^{12} + \cdots \\ \end{aligned} $$
(23)

Equations (22) and (23) describes the velocity profile of Jeffery Hamel flow with heat transfer with fixed value of Reynolds and Hartmann numbers.

5 Convergence of solution

Theorem

Let ϕ be an operator from a Hilbert space H0 into H0 and let E be an exact solution of Eqs. (16) and (17). Then \(\sum\nolimits_{0}^{\infty } {E(k)} \gamma^{k}\) which is obtained by Eq. (21), converges to the exact solution, if there exists a Ψ, 0 ≤ Ψ<1, such that \(\left\| {E_{k + 1} } \right\| \le \varPsi \left\| {E_{k} } \right\|,\;\forall k \in N \cup \{ 0\} .\)

Proof

We have

$$ \begin{aligned} & S_{0} = 0, \hfill \\ & S_{1} = S_{0} + E_{1} = E_{1} , \hfill \\ & S_{2} = S_{1} + E_{2} = E_{1} + E_{2} , \hfill \\ & \qquad \vdots \hfill \\ & S_{n} = S_{n - 1} + E_{n} = E_{1} + E_{2} + E_{3} + \cdots + E_{n} \hfill \\ \end{aligned} $$

and we will show that \(\left\{ {S_{n} } \right\}_{n = 0}^{\infty }\) is a Cauchy sequence in a Hilbert Space H0.

Now for \(\left\| {S_{n + 1} - S_{n} } \right\| = \left\| {E_{n + 1} } \right\| \le \varPsi \left\| {E_{n} } \right\| \le \varPsi^{2} \left\| {E_{n - 1} } \right\| \le \cdots \le ,\varPsi^{n + 1} \left\| {E_{0} } \right\|\) for every \(n,m \in N,n \ge m\) we have,

$$ \begin{aligned} \left\| {S_{n} - S_{m} } \right\| & = \left\| {(S_{n} - S_{n - 1} ) + (S_{n - 1} - S_{n - 2} ) + \cdots + (S_{m - 2} - S_{m + 1} ) + (S_{m + 1} - S_{m} )} \right\| \\ & \le \left\| {S_{n} - S_{n - 1} } \right\| + \left\| {S_{n - 1} - S_{n - 2} } \right\| + \cdots + \left\| {S_{m - 2} - S_{m + 1} } \right\| + \left\| {S_{m + 1} - S_{m} } \right\| \\ & \le \varPsi^{n} \left\| {E_{0} } \right\| + \varPsi^{n - 1} \left\| {E_{0} } \right\| + \varPsi^{n - 2} \left\| {E_{0} } \right\| + \cdots + \varPsi^{m + 2} \left\| {E_{0} } \right\| + \varPsi^{m + 1} \left\| {E_{0} } \right\| \\ & \le \left( {\varPsi^{m + 1} + \varPsi^{m + 2} + \cdots } \right)\left\| {E_{0} } \right\| \\ & = \frac{{\varPsi^{m + 1} }}{1 - \varPsi }\left\| {E_{0} } \right\| \\ \end{aligned} $$

Which implies \(\mathop {\lim }\nolimits_{n,m \to \infty } \left\| {S_{n} - S_{m} } \right\|\), i.e., \(\left\{ {S_{n} } \right\}_{n = 0}^{\infty }\) is a Cauchy sequence in a Hilbert space H and it convergence to S for S ∈ H.

Definition

For every i ∈ N ∪ {0}, Ψi can be defined as

$$ \varPsi_{i} = \left\{ {\begin{array}{*{20}l} {\frac{{\left\| {E_{i + 1} } \right\|}}{{E_{i} }},} \hfill & {\left\| {E_{i} } \right\| \ne 0} \hfill \\ {0,} \hfill & {\left\| {E_{i} } \right\| = 0} \hfill \\ \end{array} } \right. $$

Corollary

If \(0 \le \varPsi_{i} < 1,\;i = 1,2,3,{ \ldots }\) , then \(\sum\nolimits_{i = 0}^{\infty } {E_{i} }\) is converges to the exact solution E.

Now by Corollary, since \(\varPsi_{0} = \frac{{\left\| {E_{1} } \right\|}}{{\left\| {E_{0} } \right\|}} = 0 < 1,\varPsi_{1} = \frac{{\left\| {E_{2} } \right\|}}{{\left\| {E_{1} } \right\|}} = 0 < 1,\varPsi_{2} = \frac{{\left\| {E_{3} } \right\|}}{{\left\| {E_{2} } \right\|}} = 0 < 1\) similarly, Ψn= 0 for all n. Therefore \(\sum\nolimits_{i = 0}^{\infty } {E(k)\gamma^{k} }\) is convergent. Similarly, \(\sum\nolimits_{0}^{\infty } {E(k)\gamma^{k} }\) is convergent.

6 Results and discussion

Figures 2, 3 and Tables 1, 2 discusses the comparison of the DTM results numerically as well as graphically with the existing OHPM and numerical results from which it can be observed that there is a good agreement between the obtained DTM results with the available results.

Fig. 2
figure 2

Comparison between DTM and numerical results for the velocity e(γ) when H = 0, θ = 7.5°

Full size image
Fig. 3
figure 3

Comparison between DTM and numerical results for the velocity h(γ) when H = 0, θ = 7.5°

Full size image
Table 1 Comparison between DTM (Differential Transform Method), OHPM and Numerical solution [5] when Ha = 0 and θ = 7.5° for e(γ)
Full size table
Table 2 Comparison between DTM (Differential Transform Method),OHPM(Optimal Homotopy Perturbation method) and Numerical solution [5] when Ha = 0 and θ = 7.5° for e(γ)
Full size table

Figures 4, 5, 6, 7, 8, 9, 10, 11 and 12 discusses the variation of velocity profiles of the MHD Jeffery Hamel flow with the effects of different parameters. Figures 4 and 5 discuss the variation of velocity profiles for different Hartmann number keeping Re fixed, which shows that the flow velocity is increased as the value of Hartmann number increases with the fixed value of Reynolds number and it is more for higher Hartmann number i.e. H = 1000 and it is lower for H = 500.

Fig. 4
figure 4

Variation of velocity profiles with different Hartmann number with θ = 7.5°

Full size image
Fig. 5
figure 5

Variation of velocity profiles with different Hartmann number with θ = 5°

Full size image
Fig. 6
figure 6

Variation of velocity profiles with different Reynolds number with θ = 5°

Full size image
Fig. 7
figure 7

Variation of velocity profiles with different Reynolds number with θ = 5°

Full size image
Fig. 8
figure 8

Variation of velocity profiles with different Reynolds number with θ = 7.5°

Full size image
Fig. 9
figure 9

Variation of velocity profiles with different Reynolds number with θ = 7.5°

Full size image
Fig. 10
figure 10

Variation of velocity profiles with different angle with H = 250

Full size image
Fig. 11
figure 11

Variation of velocity profiles with different angle with H = 250

Full size image
Fig. 12
figure 12

Variation of velocity profiles with different angle with H = 1000

Full size image

Similarly, Figs. 6, 7, 8 and 9 discusses the variation of velocity profiles for different Reynolds number keeping Ha and θ fixed which shows that the flow velocity is decreased as the value of the Reynolds number is increased with the fixed value of Hartmann number and it is more for Re = 40 while it is lower for Re = 60.

Figures 10, 11, 12 discusses the variation of velocity profiles in divergent channels with different angles for fixed Reynolds number Re = 50 and for different Hartmann number H = 200, 500 and 1000 which shows that the flow velocity decreases as the angel of inclination is increases and it is higher for high Hartmann number H = 1000 and lower for low Hartmann number H = 200 keeping Re = 50 fixed.

The effect of Hartmann number, half angle θ and Reynolds number on the thermal profile of flow is presented in Figs. 13, 14, 15, 16, 17 and 18. From Figs. 13, 14, it can be observed that the thermal temperature decreases as the value of Hartmann number increases and it is more for higher Hartman number i.e. for Ha = 1000. Similarly, Figs. 15, 16, 17 and 18 discusses the effect of the half angle θ on the thermal velocity profiles which shows that the thermal temperature of the velocity profiles decreases as the angle of inclination of the plane is increases with different Hartmann number and it is maximum for Ha = 1000.

Fig. 13
figure 13

Variation of thermal profiles with different Hartmann number

Full size image
Fig. 14
figure 14

Variation of thermal profiles with different Hartmann number

Full size image
Fig. 15
figure 15

Variation of thermal profiles with different angle for H = 0

Full size image
Fig. 16
figure 16

Variation of thermal profiles with different angle for H = 250

Full size image
Fig. 17
figure 17

Variation of thermal profiles with different angle for H = 500

Full size image
Fig. 18
figure 18

Variation of thermal profiles with different angle for H = 1000

Full size image

Tables 3 and 4 discuss the comparison of the numerical results obtained by DTM with the numerical results of Runge–Kutta method for Re = 50 and θ = 7.5° while Tables 5 and 6 discuss the comparison of the numerical results of DTM with the numerical results of Runge–Kutta method for Re = 50, θ = 5° with different Hartmann number which shows that there is a good agreement between the obtained DTM results with the available numerical results.

Table 3 Comparison of DTM with numerical solution for Re = 50
Full size table
Table 4 Comparison of DTM with numerical solution for Re = 50, θ = 7.5°
Full size table
Table 5 Comparison of DTM with numerical solution for Re = 50, θ = 5°
Full size table
Table 6 Comparison of DTM with numerical solution for Re = 50, θ = 5°
Full size table

7 Conclusion

In this article, the flow behavior of the velocity profiles in MHD Jeffery–Hamel fluid flow between two unparalleled plates with thermal profiles is discussed using Differential Transform Method at different slopes for different Reynolds number and Hartmann number in both convergent and divergent channels and derived the efficiency of the present method by comparing the obtained results with the available results obtained by the Optimal Homotopy Perturbation method and with the Numerical results. It can be concluded that Differential Transform Method is a reliable method that gives the solution in the form of a convergent series that can be easily handled in analysing the effect of Reynolds numbers, Hartmann numbers and half angle on both velocity profiles as well as on the heat transfer in MHD Jeffery–Hamel fluid flow.