1 Introduction

The field of fluid–structure interactions (FSI), especially pipes carrying fluid flows, is extensively investigated by numerous researchers. Due to their application in various fields of engineering especially in chemical plant piping systems, municipal water supply, heat exchangers, risers and marine structures, production pipelines, boiling water reactors, hydropower systems, pump discharge lines, hydroelectric power plants and etc., their dynamics is widely studied [1, 2]. The first works in this field date back to the studies conducted by Ashley [3] and Benjamin [4]. Although Ashley and Benjamin were pioneers to study the rich dynamics of pipes conveying fluid, a deep understanding of the dynamics of pipes was obtained both theoretically and experimentally by Paidoussis [5, 6].

In the last two decades, the application of micro/nanostructures in high-tech fields has been considered as a novel rich dynamical problem in the field of mechanics of vibrational systems[7]. For instance, in novel drug delivery fields, micro/nano-tubes could be applied for the drug transportation into the targeted organs and tumors which accelerate the curing process and can dramatically reduce the side effects of the traditional methods already being used [8]. Other applications include information technology, semiconductors, fluid storage, transport and biosensors, electromechanical devices, actuators and biology, among others [9,10,11,12,13,14,15]. Recent developments have accompanied to design and manufacture smaller micro/nano tubes which have made researchers to promote theoretical and molecular models enabling them to mathematically model such systems with satisfying precision, considering the micro/nano structure small effects which is not feasible utilizing classical continuum theories [16,17,18,19]. Recent research outcomes revealed that materials exhibit strong size-dependent characteristics in micron and nano sizes [20,21,22,23,24,25,26,27,28,29,30,31]. Zhang et al. [32] investigated the dynamical behavior of a Timoshenko nanobeam conveying fluid flow considering surface effects using Gurtin and Murdoch surface theorem. McFarland et al. [33] experimentally observed that size effects play a significant role on material properties and as a result on the stiffness of micro-cantilevers such that they figured out that the bending stiffness values were at least four times greater than what they predicted using classical theories. This indicates that considering the material length scale is necessary to make sure that the results are compatible with the experimental tests. Consequently, scale-free formulations disregarding the size-dependent characteristics of ultra-small systems are not reliable [34]. To capture the influence of such phenomena, a modified continuum mechanics theory was developed. The so-called couple stress theory is considered as a higher order elasticity theory that was developed by Mindlin et al. [35], in which the couple stress tensor was supposed to be symmetric. Yang et al. [36] developed a modified couple stress theory in which despite the classical couple stress theory that uses two additional material length scale parameters, considers only one additional small length scale parameter. Applying this theory, Park et al. [37] investigated an Euler–Bernoulli beam and concluded that the newly developed model predicts much higher values of bending stiffness, an outcome that was proved to be in a good agreement with the experiments [37]. Moreover, Wang [38], Ke et al. [39] and Ghayesh [40] have stated that the modified couple stress theory is powerfully capable of predicting microstructure dynamical behavior. Bhirde et al. [8], utilized the carbon nanotubes (CNTs) both in vitro and in vivo on a cancerous organ and affirmed that several challenges remain including specificity and stability of the CNT embedded in the biological soft tissues. Zhang et al. [41] analyzed the vibration of single walled CNTs on the basis of quantum effects. They concluded that utilizing such theory can more accurately predict the dynamics of nano-resonators containing fluid flow than considering conventional non-local theories. Wang et al. [42] studied the possibility of tuning the stability of a CNT with the aid of magnetic field and found out that in general the critical flow velocity for a CNT with magnetic field effect is generally higher than that for a system in the absence of such field. Other researches based on other theories are also extensive in the literature [43].

The most important issue concerning the dynamical behavior of micro/nanofluid conveying systems is their instability caused by internal fluid flow movement and has been used to be an attractive field of study to researchers. Extending the stability region of micro/nanotubes is a crucial requirement that should be considered in designing such systems. Undoubtedly, fluid conveying structures embedded in different elastic environments are much more anticipated to result in wider thresholds of stability. In macro-scales, Lottati [44] carried out a detailed study on the cantilevered and clamped pipes and figured out that although internal damping could have either stabilizing or destabilizing effects on the overall behavior of the system, application of elastic foundation far from the damping effects, stabilizes the system. Djondjorov et al. [45, 46] examined a cantilevered pipe embedded in Winkler elastic media. In their investigations, they also studied the effect of the elastic foundation length and rigidity on critical velocities and determined that the maximal stabilizing effect is achieved if one determines the true position and stiffness distribution of the foundation for each of possible boundary conditions.

Due to the interesting results of the investigations of fluid conveying pipes embedded in foundations, similarly, a limited number of researchers reported their results in micron and nano criteria. For instance, Yoon et al. [47] analyzed the flutter instability of CNTs embedded in Winkler elastic media caused by flow-induced oscillations. They figured out that CNTs embedded in stiff elastic media are less sensitive to internal fluid velocities and such foundations can suppress the flow induced unwanted flutter instabilities. Bahaadini et al. [48] employed the nonlocal elasticity theory for CNT surrounded by elastic foundations and figured out that stiffer elastic foundations lead to an increase in the fluid critical frequencies and velocities. Wang et al. [49] and also concluded that elastic foundations have a significant role in stability situations of a CNT. Ghayesh et al. [50, 51]studied the large amplitude bifurcation of microtubes surrounded by nonlinear spring media and deduced that nonlinear spring bed does not affect the amplitude of oscillation much.

Since enlarging the stability region in real time operation of the structure conveying fluid flow is a crucial requirement, in this paper aiming at simulating operational environments of micro-tubes, an exhaustive study on fluid-elastic fluid conveying micro-tubes has been carried out, and the most important aspects of vibrational characteristics of the micro-structure, i.e., natural frequencies and instability conditions are comprehensively elaborated. Since most of the studies reviewed above are not comprehensive in terms of investigating various forms of elastic beds, the objective of the current paper is to investigate the effect of different types of variable, partial and series elastic as well as Pasternak media on the dynamical behavior of cantilevered micro-tubes in order to clarify the effect of such simulated environments on the stability thresholds. By modulating the length and form of the elastic and Pasternak media, one is capable to dramatically expand stability are of the fluid conveying structure. Motivated by this, initially the equations of lateral motions, using modified couple stress theory, will be derived using the extended Hamilton’s variation method. The dynamical partial governing equation describing the vibrational motions of the microstructure and its corresponding boundary conditions are discretized utilizing the extended Galerkin’s method. Various essential diagrams such as stability maps showing the effect of material length scale, external diameter and different types of elastic foundations are plotted and their influence on stability borders have comprehensively studied and analyzed. It will be portrayed that both the material length scale coefficient and various forms of elastic and Pasternak foundations have a significant effect on the stability of the system under consideration and considering their role on dynamical behavior and response of the structure is inevitable.

2 Theoretical formulations

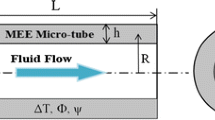
As shown schematically in Fig. 1, consider a cantilevered micro-tube of length \(L\), inner diameter d, outer diameter D, and mass per unit length of m owing a flexural rigidity of EI, in which an incompressible fluid of mass per unit length of M is flowing. A Cartesian coordinate is attached to the upstream of the micro-tube whose \(x\)-axis is coincident with the direction of the flowing fluid. Also, it is assumed that L/D ≫ 10 that the Euler–Bernoulli holds true. Moreover, all out of plane movements are supposed to be ignorable and hence the structure oscillates in x–z plane.

Fig. 1
figure 1

Schematic of a fluid conveying micro-tube embedded in elastic and Pasternak foundations

Full size image

Considering modified couple stress theory, the strain energy density is simultaneously dependent on both the curvature and strain tensors. Hence, the energy density function for a material occupying region \({\text{S}}\) could be written as follows [52,53,54,55]:

$$U = \frac{1}{2}\mathop \smallint \limits_{\text{S}}^{{}} \left( {\sigma_{ij} \varepsilon_{ij} + m_{ij} \chi_{ij} } \right)dv \left( {i, j = 1, 2, 3} \right)$$
(1)

In which \(\sigma_{\text{ij}} , \varepsilon_{\text{ij}} , m_{\text{ij}}\) and \(\chi_{\text{ij}}\) are the stress and strain tensors, deviatoric part of the couple stress and the symmetric curvature tensor, respectively. They are given by [56, 57]:

$$\sigma_{ij} = \lambda {\text{tr}}\left( { \varepsilon_{\text{ij}} } \right) \delta_{\text{ij}} + 2G\varepsilon_{\text{ij}}$$
(2)
$$\varepsilon_{\text{ij}} = \frac{1}{2}\left[ {\nabla u_{\text{i}} + \left( {\nabla u_{\text{i}} } \right)^{T} } \right]$$
(3)
$$m_{ij} = 2\ell G\chi_{\text{ij}}$$
(4)
$$\chi_{\text{ij}} = \frac{1}{2}\left[ {\nabla \theta_{\text{i}} + \left( {\nabla \theta_{i} } \right)^{T} } \right]$$
(5)

where λ, G and \(\ell \text{ }\) are the first and second (shear modulus) Lame’s constants and the material length scale parameter, respectively. Also, ui and δij are the displacement components and Kronecker delta. The rotation vector \(\theta\) may be defined as:

$$\theta = \frac{1}{2}\nabla \times \vec{u}$$
(6)

It is assumed that the walls of the micro-tube are thick enough to be assured that it maintains its circular shape while undergoing oscillatory motions. Hence, According to the Euler–Bernoulli theorem, the displacements can be considered as [38]:

$$u = - z\psi \left( {x,t} \right), v = 0, w = w\left( {x,t} \right)$$
(7)

For very small deformations the angle of rotation of the centroidal of the micro-tube can be expressed as:

$$\psi \left( {x,t} \right) \approx \frac{{\partial w\left( {x,t} \right)}}{\partial x}$$
(8)

The Cauchy stress \(\sigma_{\text{ij}}\) can be obtained using relations (3), (7) and (8):

$$\sigma_{xx} = - Ez\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }},\;\sigma_{xy} = \sigma_{xz} = \sigma_{yz} = \sigma_{zz} = \sigma_{yy} = 0$$
(9)

Considering relation (6) one may write:

$$\theta_{y} = - \frac{{\partial w\left( {x,t} \right)}}{\partial x}, \theta_{x} = \theta_{z} = 0$$
(10)

Hence, using relations (5) and (10) yields:

$$\chi_{\text{xy}} = - \frac{1}{2}\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }},\;\chi_{\text{xx}} = \chi_{\text{yy}} = \chi_{\text{zz}} = \chi_{xz} = \chi_{\text{yz}} = 0$$
(11)

Also by means of relations (4) and (11) one obtains:

$$m_{\text{xy}} = - G\ell^{2} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }},\;m_{\text{xx}} = m_{\text{yy}} = m_{\text{zz}} = m_{zx} = m_{\text{yz}} = 0$$
(12)

Referring to Eq. (1) and substituting the related relations yields:

$$U = \frac{1}{2}\mathop \smallint \limits_{0}^{L} \left( {EI + GA\ell^{2} } \right)\left( {\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}} \right)dx$$
(13)

where A is the cross-sectional area of the micro-tubes material and I is the second moment of cross-sectional area. The first term in the above equation is representative of bending strain energy while the second one stands for shear deformations. Now, the kinetic energy of the tube and the fluid flowing in it would be [48, 58,59,60,61]:

$$T_{T} = T_{P} + T_{f} = \frac{1}{2}\left\{ {m\mathop \smallint \limits_{0}^{L} \left( {\frac{{\partial w\left( {x,t} \right)}}{\partial t}} \right)^{2} dx + M\mathop \smallint \limits_{0}^{L} \left[ {\left( {\frac{{\partial w\left( {x,t} \right)}}{\partial t} + V\frac{{\partial w\left( {x,t} \right)}}{\partial x}} \right)^{2} + V^{2} } \right]dx} \right\}$$
(14)

The work done by the elastic foundation may be written as [48, 62]:

$$W_{b} = \mathop \smallint \limits_{0}^{L} k_{W} \left( x \right)w\left( {x,t} \right)^{2} dx - \mathop \smallint \limits_{0}^{L} k_{W} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }}dx$$
(15)

According to Benjamin’s formulation [4], in order to derive the partial differential equation of vibrational motion of the system, Hamilton’s statement for an axially constrained pipe may be written as [63, 64]:

$$\delta \mathop \smallint \limits_{{t_{1} }}^{{t_{2} }} Ldt = 0$$
(16)

where L = TT − U + Wb.

By substitution of expressions (13) and (14) into Eq. (15), the FSI governing equation of lateral motion may be derived as:

$$\left( {EI + GA\ell^{2} } \right)\frac{{\partial^{4} w\left( {x,t} \right)}}{{\partial x^{4} }} + MV^{2} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} + \left( {m + M} \right)\frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial t^{2} }} + 2MV\frac{{\partial^{2} w\left( {x,t} \right)}}{\partial x\partial t} + k_{w} w\left( {x,t} \right) - k_{G} \frac{{\partial^{2} w\left( {x,t} \right)}}{{\partial x^{2} }} = 0$$
(17)

The corresponding boundary conditions for a cantilevered micro-tube can be expressed as [65]:

$$w\left( {0,t} \right) = \frac{{\partial w\left( {0,t} \right)}}{\partial x} = 0, \frac{{\partial^{2} w\left( {L,t} \right)}}{{\partial x^{2} }} = \frac{{\partial^{3} w\left( {L,t} \right)}}{{\partial x^{3} }} = 0$$
(18)

For the sake of convenience, to rewrite the equation of motion in its dimensionless form, the following dimensionless quantities are introduced:

$$\begin{aligned} & \eta = \frac{w}{L}, \xi = \frac{x}{L}, \tau = \frac{t}{{L^{2} }}\sqrt {\frac{EI}{m + M}} , K_{W} \left( \xi \right) = \frac{{L^{4} }}{EI}k_{w} \left( {\frac{x}{L}} \right), \\ & K_{G} \left( \xi \right) = \frac{{L^{2} }}{EI}K_{G} \left( {\frac{x}{L}} \right), \beta = \frac{M}{m + M}, u = LV\sqrt {\frac{M}{EI}} , \vartheta = \frac{{GA\ell^{2} }}{{L^{2} }} \\ \end{aligned}$$
(19)

In which \(\alpha = d/D\) and \(\upsilon\) is the Poisson’s ratio. Using the aforementioned non-dimensional parameters, the dimensionless form of the FSI governing equations of motion may be written as:

$$\left( {1 + \vartheta } \right)\frac{{\partial^{4} \eta }}{{\partial \xi^{4} }} + u^{2} \frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} + 2\sqrt \beta u\frac{{\partial^{2} \eta }}{\partial \xi \partial \tau } + \frac{{\partial^{2} \eta }}{{\partial \tau^{2} }} + K_{W} \left( \xi \right)\eta - K_{G} \frac{{\partial^{2} \eta }}{{\partial \xi^{2} }} = 0$$
(20)

The corresponding dimensionless boundary conditions are given as:

$$\eta \left( {0,\tau } \right) = \frac{{\partial \eta \left( {0,\tau } \right)}}{\partial \xi } = 0, \frac{{\partial^{2} \eta \left( {1,\tau } \right)}}{{\partial \xi^{2} }} = \frac{{\partial^{3} \eta \left( {1,\tau } \right)}}{{\partial \xi^{3} }} = 0$$
(21)

2.1 Galerkin approach

In this section the so called extended Galerkin procedure is applied to discretize the partial differential equation of oscillatory motion of the micro-tube. The proper weighting functions η have been chosen so that they satisfy the specified essential boundary conditions. The transverse normalized displacement η is approximated as the following series [66,67,68]:

$$\eta \left( {\xi ,\tau } \right) = \mathop \sum \limits_{r = 0}^{n} \varphi_{r} \left( \xi \right)q_{r} \left( \tau \right)$$
(22)

where n, \(q_{r} \left( \tau \right)\) and \(\phi_{r} \left( \xi \right)\) are number of modes to be considered, generalized coordinates and natural modes of free transversal oscillations of the micro-tube, respectively. Finally, the discretized form of the equation of motion can be acquired to be [53]:

$$\left[ M \right]\left\{ {\ddot{q}\left( \tau \right)} \right\} + \left[ C \right]\left\{ {\dot{q}\left( \tau \right)} \right\} + \left[ K \right]\left\{ {\left( \tau \right)} \right\} = 0$$
(23)

Following the procedure presented in [5], the eigenvalues and the corresponding eigenvectors of the above mentioned micro-tube system can be obtained by solving the eigenvalue problem (23). Recalling that \(\lambda_{r} = i\omega_{r} \left( {i = \sqrt { - 1} } \right)\), the real part of ω being associated with frequency of oscillations while the imaginary part is associated with the decaying rate of amplitude.

3 Results and discussion

In order the considered linear constitutive relations to be hold, the micro-tube material is considered to be homogeneous, isotropic and linearly elastic. For the sake of comparison, the micro-tubes material and fluid properties are considered as \(:E = 1.44\;{\text{GPa}},\;\rho_{p} = \rho_{f} = 1000\;{\text{Kg}}/{\text{m}}^{3} ,\;\nu = 0.35,\;\alpha = {\raise0.7ex\hbox{$d$} \!\mathord{\left/ {\vphantom {d D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}} = 0.8,\; {\raise0.7ex\hbox{$L$} \!\mathord{\left/ {\vphantom {L D}}\right.\kern-0pt} \!\lower0.7ex\hbox{$D$}} = 20\). In this paper, the length parameter \(\ell\) is assumed to be \(17.6\) μm [38, 69].

3.1 Model validation

In this section, an ten mode approximation is applied for the sake of validation with the references available in the literature. Herein, the influence of the elastic media is neglected firstly and then the small effect coefficient \(\ell\) is ignored in non-classical manners for comparison purposes with the results obtained by Hosseini et al. [69].

In Fig. 2, the horizontal and vertical axes indicate dimensionless flow velocity and natural frequencies, respectively. As the dimensionless internal flow velocity increases, the frequencies of oscillations of the system are reduced until vanish. This is the initiation of the so-called coupled-mode flutter bifurcation [5]. It is clear that the results obtained in Fig. 2 are in a very good agreement with those represented by Hosseini et al. [69] when the modified couple stress (MCST) and classical continuum theories (CT) are applied. Moreover, the natural frequencies acquired by means of modified couple stress theory are much larger than those by the classical continuum model; hence, considering the small-scale effects for acquiring accurate results comparable with the experimental outcomes is a must [33]. In fact, considering small effects has caused the coupled-mode flutter bifurcation to occur later in comparison with the classical model. By inspection, it is understood that the effect of material length scale parameter is only significant when its value is comparable with the outside diameter of the micro-tube.

Fig. 2
figure 2

Comparison of the first mode natural frequencies based on couple stress and classical theories as a function of flow velocity; D = 10 μm, \(K_{G} = K_{w} = 0\)

Full size image

Furthermore, the stability map of the proposed model is represented in Fig. 3. The system will be stable only for values of fluid velocity that lie below the curve. Being in the stable region indicates that the system oscillations will asymptotically diminish. In other words, the vibrations of any point lying below the curve are damped and consequently the system loses its energy; else, they are amplified and as a result, the micro-system carrying fluid flow gains energy. In addition, the S-shaped segments are related to the instability-restabilization-instability sequence in which the negative slope portions are associated with thresholds of restabilization. It is obvious that the model in which the material length scale is considered, predicts much higher values of critical flow velocity in comparison with the classical continuum model; hence, by considering material small effects, one predicts a more stable system which predicts higher critical fluid velocities. On the other hand, although a clearer feature of the number of S-shaped segments is observed in the upper curve, the number of these segments remains constant in both theories. It is noteworthy to state that the stability investigation in Fig. 3 is based on a linear analysis and a nonlinear refinement is needed for the curves of this figure.

Fig. 3
figure 3

Validation of flutter instability boundaries in terms of β; D = 20 μm, \(K_{G} = K_{w} = 0\)

Full size image

3.2 The effect of length scale parameter

So far, the importance of the material length scale is illuminated. Figure 4a elaborates the effect of this parameter on stability and flutter regions of the micro-cantilever tube. In this figure, the dimensionless critical velocity and frequency diagrams are plotted in terms of dimensionless mass ratio β for three different values of the material length scale parameters, respectively. As this parameter decreases, both the critical velocity and frequency decrease. Also, as β increases, the curves show a more distinct feature of S-shaped segments with respect to each other indicating the more the value of the length scale parameter is, the more widen the range of instability-restabilization-instability sequence will be. In addition, higher values of \(\ell\) delay the appearance of flutter instability phenomenon. Hence, one can deduce that enhancement in length scale parameter results in a stiffer system. Consequently, as anticipated, in Fig. 4b, the critical frequencies undergo a significant increase as \(\text{ }\ell\) increases. Additionally, similar to the trend occurring for critical velocities, the critical frequencies experience a substantial increase as the jumps take place in specific values of β.

Fig. 4
figure 4

Flutter instability boundaries for three distinct values of \(\ell\) in terms of dimensionless mass ratio β; D = 10 μm,\(K_{G} = K_{w} = 0\)

Full size image

The following section mainly discusses the influence of various types of elastic media the micro-structure embedded in. In each section, the effect of foundation parameters on the stability is shown by stability map diagrams. Then in each part, in order to evaluate the effect of the foundation on the stability of the microstructure, a comparison is made with a state in which there are no elastic foundations attached to the system.

3.3 Variable elastic foundation

In the first step, three different probable types of variable elastic foundations is considered, namely strengthening, Winkler and weakening ones, and their effect on stabilization of the system is investigated. The foundation modulus distribution in its non-dimensional form is defined as [70]:

$$K\left( \zeta \right) = k_{0} \left[ {4\left( {1 - \gamma } \right)\left( {\xi^{2} - \xi } \right) + 1} \right]$$
(24)

In which \(k_{0}\) and γ are constants. The foundation modulus distribution is shown in Fig. 5.

Fig. 5
figure 5

The 3-D dimensionless variable foundation modulus distribution of relation (24)

Full size image

In Fig. 5 it is obvious that the case γ < 1 can be interpreted as a weakening of foundation whereas γ > 1 is equivalent to the strengthening of it. In fact, in case of γ < 1, the two ends of the foundation are the stiffest parts of the elastic environment whereas for γ > 1 the elastic media will form a concave shaped function with the maximal value at the middle of the micro-tube span while vanishing at the two ends of the micro-tube. In addition, γ = 1 represents a Winkler type foundation.

In order to investigate the effect of the micro-tubes diameter on critical flow velocities of the system under consideration, Fig. 6 is considered in which various values of the critical velocity ucr are calculated for different micro-tube diameters and for three distinct values of γ. It is apparent that both foundations with γ = 1, 3 will significantly enhance the stability of the system especially for larger values of the external diameter. On the other hand, however, the foundation with γ = − 1 results in an enhancement in stability region only for D < 5.5 μm which is an unpredicted outcome.

Fig. 6
figure 6

Flutter instability diagrams as a function of external diameter; k0 = 200

Full size image

As the diameter becomes smaller, the difference between the stability curves becomes negligible. This means that the critical velocities computed for various values of γ will eventually converge to the results obtained when the micro-tube is not embedded in the elastic foundations. It should be noted that the results of the micro-tube without any foundations are in a good agreement with [69].

In Fig. 7 the effect of the length scale parameter in a specified range for three distinct values of γ is shown. It is seen again that as the γ values increase, the stability region enlarges. A significant feature of the curves is for \(\text{ }\ell > 0.4\) μm, where the slope of the curves increase significantly, indicating a stronger dependency of the stability curves on \(\ell\), otherwise one can deduce that the effect of \(\ell\) is ignorable. Moreover, the difference in critical flow velocities between the weakening and Winkler elastic media is much more prominent than the difference between the strengthening and Winkler types.

Fig. 7
figure 7

Flutter instability velocity boundaries versus material length scale parameter \(\ell\)

Full size image

In order to figure out the dynamical behavior of the system embedded in distinctive types of variable elastic media more accurately, the Re(ω)-u and Imag(ω)-u curves are plotted. Figure 8a, b demonstrates the imaginary and real parts of the eigenvalues of the system. As mentioned before, the imaginary and real parts of the eigenvalues are associated with natural frequencies and damping of the structure. In Fig. 8a only the first mode of natural frequencies of the system is considered since it represents the principal vibration characteristics of the fluid conveying micro-tubes [38].

Fig. 8
figure 8

Variations of the first mode eigenfrequencies of the micro-tube; D = 10 μm predicted for γ = − 1, 1, 3 (a) Real part (b) Imaginary part

Full size image

As the dimensionless flow velocity increases, the damping of the system continuously increases, however, on the other hand, the natural frequencies of the system decrease monotonously until they vanish at points ai (i = 1, 2, 3) and simultaneously, the imaginary part of the frequencies of the system are divided into two distinct branches; this is the initiation of a coupled-mode flutter and implies that the system overdamps and consequently the micro-tube does not vibrate in the range from ai to bi. Increasing flow velocities after points bi, the natural frequencies of the system increase and the system undergoes oscillations. It is clear in Fig. 8a, as expected, that strengthening the foundation delays the coupled-mode flutter bifurcation occurrence. Additionally, it is noteworthy to state that variations in parameter γ does not change the range in which the system overdamps. It is also noteworthy to state that the sooner the system undergoes over damping, the sooner the vibrating motions reoccur. Continuing to increase the flow velocity will decrease the decaying rate of amplitude of the system until it loses its stability by flutter at points \(c_{i}\), and thus, the system begins to gain energy from the fluid flow.

Figure 8b also indicates that the more the value of γ is, the more dissipation in the system will exist. Moreover, this figure implies that by increasing γ the velocity at which flutter instability takes place increases. Actually, the foundation type has the capability to dramatically displace the points at which bifurcations occurs.

Figure 9 portrays the stability maps for two different values of material length scale parameter. These graphs are known as flutter instability boundary curves. For each material length scale parameter, the stability map is drawn for three values of γ, each of them makes the foundation behavior distinctive. It is anticipated that applying elastic foundations will improve the system stability areas.

Fig. 9
figure 9

The dimensionless critical flow velocity and frequency for the flutter of a cantilevered micro-tube in terms of β for varying \(\gamma\); k0 = 600; a critical velocities (b) critical frequencies

Full size image

Considering Fig. 9a, one can figure out that keeping \(k_{0}\) to be constant, enhancing the value of \(\gamma\) except that for 0 < β<0.11 when \(\text{ }\ell = 17.6\) μm, and 0 < β<0.13 when \(\text{ }\ell = 23\) μm, results in an enhancement of the stability regions. Surprisingly, for β values in the aforementioned ranges, strengthening the foundation results in a decrease in the flutter region. Furthermore, increasing the value of \(\ell\) leads to an enlargement of the stability region which affirms that increasing this parameter enhances the bending rigidity of the micro-structure. In case of corresponding critical frequencies of the system, as shown in Fig. 9b, although except in the vicinity of jumps, all curves undergo a mild decrease in critical frequencies as the fluid velocity increases, but as the values of γ are going up, the critical frequencies will monotonously increase throughout the domain of β. This is due to the fact that by taking k0 to be a constant, any increase in γ will make the foundation much stiffer. In addition, Fig. 9a, b also indicates that the \(\ell\) parameter influence on both the location of S-shaped segments and stability region is far more prominent than that the effect of γ.

Figure 10 illustrates the influence of the coefficient k0 on the stability of the system. Again, the instability-restabilization-instability sequence similar to the previously discussed stability map diagrams is observed. As the parameter \(\gamma\) increases, this sequence occurs in a more limited range of coefficients k0. For instance, by scrutinizing Fig. 10, this sequence is observed to take place in the range of 42 < k0 < 122 for γ = − 1 while for γ = 3 this will occur at 10 < k0 < 40. It is remarkable that the more the value of parameter γ is, the more widen the stability area will be.

Fig. 10
figure 10

Flutter velocities as a function of stiffness modulus \(k_{0}\) for various values of \(\gamma\); D = 20 μm

Full size image

Moreover, it is illuminated that strengthening the foundation decreases the range of curve with negative slope and consequently the system experiences instability phenomenon in a limited range of flow velocities. Hence, one can deduce that flutter velocity and frequency sets are smaller in smaller values of γ.

3.4 Partial elastic foundations

This section is devoted to figuring out whether it is possible to further develop cantilevered micro-tube stability by applying partly supported elastic foundations consisting equal surfaces of rigidity just equal to the variable elastic one when γ = 3. Herein, it is assumed that the system is embedded in an elastic environment of Winkler type i.e. γ = 1. The foundation whose length is considered to be the half of length of the flow conveying cantilevered micro-tube is attached at different positions namely at 0 ≤ ξf ≤ 0.5, 0.25 ≤ ξf ≤ 0.75, and 0.5 ≤ ξf ≤ 1.

Figure 11 displays that with respect to the equivalent Winkler type, application of the foundation in upstream of the micro-tube (at 0 ≤ ξf ≤ 0.5) decreases the stability except for 0.62 ≤ β ≤ 1, but, on the other hand, applying the foundation on the downstream span, unless for mass ratios greater than 0.75, results in a significant promotion in stability. Another possibility for partial elastic foundation location is at 0.25 ≤ ξf ≤ 0.75. Surprisingly for 0 ≤ β ≤ 0.2, this is the weakest one in point of stability for β > 0.55, this foundation acts as the most effective. Generally, Fig. 11 shows that regarding the real time value of β, in comparison with a through Winkler foundation, embedding the system with a partial elastic foundation gives the capability of enhancing the stability of the system.

Fig. 11
figure 11

Flutter instability boarders of a cantilevered-micro tube as a function of β embedded in partly supported elastic foundation; D = 10 μm

Full size image

Figure 12 shows the stability map of the cantilevered micro-tube as the foundations located at the downstream span shorten. In comparison to the cases investigated here, the foundation applied in the downstream of the micro-tube in the range of 0.75 ≤ ξf ≤ 1 for 0 ≤ β ≤ 0.15 tends to stabilize the system, otherwise, shrinking the length of the foundation reduces the stability region. Moreover, it is observed that shortening the foundation, for instance to \(\ell /64\)(0 < ξf < 0.98), will dramatically deteriorate the stability conditions of the micro-tube for larger values of β. As a result, for small values of β, one can find an appropriate length for the application of the foundation such that the stability borders are improved. Also one can figure out that shortening the foundation while keeping the rigidity surface to be constant will transfer the S-shaped segments to the higher values of βs. Also shortening the foundation length will cause the S-shaped segments to take place in wider ranges of the dimensionless mass parameter.

Fig. 12
figure 12

Flutter instability boarders of a cantilevered-micro tube as a function of \(\beta\) embedded in shortening elastic foundation; D = 10 μm

Full size image

3.5 Series foundations

Considering elastic foundations as polynomials of various orders yields the capability to simulate the elastic media of the real time operating situations with an accurate precision. In this section, the stability maps are acquired for a cantilevered micro-tube lying on symmetric and non-symmetric elastic media. The foundation modulus distribution in its non-dimensional form is defined as [70]:

$$K_{W} \left( \xi \right) = c_{0} + \mathop \sum \limits_{m = 1}^{\text{p}} c_{\text{m}} \xi^{\text{m}}$$
(25)

where p is the order of the polynomial to accurately simulate the elastic environment that the micro-tube has embedded in. Herein, three of them are shown in Fig. 13a and their corresponding stability maps are plotted and displayed in Fig. 13b. The corresponding coefficients cm (m = 1, …, p) are introduced in Table 1. Afterwards, for the sake of comparison, it is required mentioning that all graphs make surfaces with equal rigidities with the variable case in which γ = 3.

Fig. 13
figure 13

a Foundation stiffness modulus of Eq. (23): the coefficients of all polynomials are represented in Table 1. b The critical flow velocities in terms of mass ratio \(\beta\) embedded in series elastic foundations

Full size image
Table 1 Coefficients of the polynomials of Eq. (25) shown in Fig. 13a
Full size table

Considering Fig. 13a, b it is understood that various types of series elastic foundations result in an improvement in stability in comparison with other types of foundations, dependent severely on the real time operational values of β. For instance, for β < 0.11, the foundation with triangle form (curve (1)) yields higher values of critical flutter velocities whereas for 0.11 ≤ β ≤ 0.49 curve (2) is more stable. It is also interesting that for high values of β the system embedded in a symmetric foundation (curve (3)) will be the most stable one. As a result, determining the operational values of β enables one to select the most effective form of elastic foundation resulting in the maximal stability and vice versa. It is noteworthy to state that the series foundation has the capability to be defined in a way so that it will simulate any operational elastic medium.

3.6 Pasternak foundation

Dimensionless critical flow velocities versus various Pasternak foundation coefficients are plotted in Fig. 14 for various values of β and for two different values of the micro-tube external diameters. As expected, any increment in shearing modulus of Pasternak foundation, KG, enhances the stiffness of the system and as a result a significant enhancement in stability region is observed.

Fig. 14
figure 14

Dimensionless critical velocities in terms of dimensionless shearing modulus of Pasternak foundation for different external diameters and mass ratios

Full size image

Generally, the smaller the diameter of the micro-tube is, the more stable the system will be. This is due to the fact that smaller diameter results in a larger dimensionless couple stress coefficient \(\vartheta\) and as a result a stiffer system.

As is obvious, for lower values of β, the critical values of flow velocity increase gradually; however, for moderate and higher values of this parameter the critical flow velocities are not monotonously increasing with increasing β and a clearer feature of S-shaped segments is observed. For instance, in case of β = 0.64 or 0.8, in ucr − KG diagram not only the stability region enlarges significantly with respect to β = 0.2 but also the number of S-shaped segments increases in the stability boundaries indicating an enhancement in the number of transference of instability modes. In general, one can deduce that the effect of Pasternak foundations on stability is much more prominent than elastic foundations.

4 Conclusions

In this manuscript, utilizing the modified couple stress theory and by application of extended Hamilton variational principle, the governing equation of motion of a cantilevered micro-tube conveying fluid flow is obtained. The acquired equation of motion was discretized by employing extended Galerkin’s method. Numerically solving the discretized equations, the influences of some physical parameters such as material length scale, external diameter of the micro-tube and influence of various types of elastic media were investigated precisely to clarify their effect on the stability thresholds. For summary, the following main conclusions are listed:

  • The material length scale parameter plays a substantial role for the stability of cantilevered micro-tubes. In fact, enhancing \(\ell\) by choosing appropriate materials is a certain scenario of enlarging the stability region of the system.

  • Embedding the system in a variable type of elastic media can either stabilize or destabilize the fluid-conveying cantilevered micro-tube with respect to the equivalent system without foundations, depending severely on \(\beta\) values.

  • The more the value of γ is, the more dissipative the system will be, however, the system will later undergo flutter instability.

  • Varying \(k_{0}\) for variable elastic foundations, affirms that as the parameter \(\gamma\) increases, the instability-restabilization-instability sequence occurs in a more limited range. Hence, one can deduce that flutter velocity and frequency sets are smaller in smaller values of γ.

  • In case of partly supported elastic foundations, depending on the operational values of β, one can choose the location of the foundation such that to enlarge the stability region. Moreover, shortening the foundation which is highly dependent on β, would result in a more stable condition. Hence, by determining the real time operational values of β, one can select not only the appropriate length of the partial elastic foundation, but also, its true position to significantly enlarge the stability area.

  • By considering series foundations of various polynomial orders, simulation of virtually any operational environment for the micro-tubes conveying fluid flow is feasible. Furthermore, for the sake of comparison, assuming the rigidity surface to be a constant, one can define series foundations to optimally promote the system stability.

  • In general, one can conclude that the influence of Pasternak foundations on the enlargement of stability regions is much more prominent than elastic foundations. Considering a Pasternak foundation for low values of β leads to a gradual enhancement of the critical values of flow velocities. However, for moderate and higher values of this parameter, the critical flow velocities do not monotonously increase with increasing β and a clearer feature of S-shaped segments is observed indicating an enhancement in the number of transference of instability modes.

  • Determination of the operational conditions of the structure especially the true range of dimensionless mass ratio parameter enables one to enhance the stability regions of the micro-tube significantly by considering the appropriate form of the elastic foundations such as variable, partial, series or Pasternak.

It is demonstrated that a breakthrough in the performance of the micro-tube conveying fluid could be made by designating appropriate operating and structural conditions. It is hoped that the results of the current paper can hold a great promise for mechanics and biomedical engineers who try to design and optimize micron and nanoscale structures carrying fluid flows.