The Rotational Motion of a Symmetric Rigid Body Similar to Kovalevskaya’s Case

Abstract

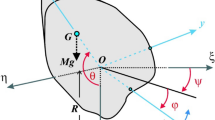
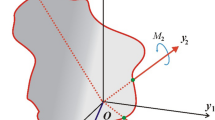
In this article, we study the three-dimensional rotational motion of a symmetric rigid body (gyro) about a fixed point under the influence of a gyrostatic moment vector about the principal axes of inertia according to Kovalevskaya’s conditions. The six nonlinear differential equations of motion beside their first integrals are reduced to two differential equations from second order composed an autonomous system with one first integral. It is taken into consideration that the gyro spins with high angular velocity about one of the orthogonal principal axes. The small parameter method is used to obtain the analytical solutions of the governing system. The attained solutions are represented graphically through several plots concerning with the different values of the gyrostatic moment vector to evaluate the performance of these values on the gyro’s motion. Euler’s angles are estimated to describe the motion at any instant. The fourth-order Runge–Kutta algorithms through Matlab packages are used to obtain the numerical solutions for the mentioned problem and to represent these solutions graphically. A comparison between the analytical and the numerical solutions shows high consistency between them which indicates the powerful of the presented analytical technique. The phase plane plots are presented in order to give a full description about the regular motion of the gyro. The considered subject has a great interest in many applications such as submarines, satellites and aircrafts.

Appendix 1

From (16) and (24), we can write

$$\begin{aligned} \varGamma_{11}^{(0)} = \varGamma_{11} (p_{2}^{(0)} ,\dot{p}_{2}^{(0)} ,\gamma_{2}^{(0)} ,\dot{\gamma }_{2}^{(0)} ), \hfill \\ \varGamma_{21}^{(0)} = \varGamma_{21} (p_{2}^{(0)} ,\dot{p}_{2}^{(0)} ,\gamma_{2}^{(0)} ,\dot{\gamma }_{2}^{(0)} ). \hfill \\ \end{aligned}$$

(i)

Since

$$\begin{aligned} p_{2}^{(0)} &= E\cos (\varOmega \tau - \eta ) \,\,\,\,\,\,\,\,\, \Rightarrow p_{20}^{(0)} = E\cos \eta \hfill \\ \dot{p}_{2}^{(0)}& = - E\varOmega \sin (\varOmega \tau - \eta ) \Rightarrow \dot{p}_{20}^{(0)} = E\varOmega \sin \eta , \hfill \\ \gamma_{2}^{(0)} &= M_{3} \cos \tau \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Rightarrow \gamma_{20}^{(0)} = M_{3} , \hfill \\ \dot{\gamma }_{2}^{(0)} &= - M_{3} \sin \tau \,\,\,\,\,\,\,\,\,\,\, \,\,\,\,\,\,\, \Rightarrow \dot{\gamma }_{20}^{(0)} = 0. \hfill \\ \end{aligned}$$

(ii)

Substituting (ii) into (16), gives

$$\varGamma_{11}^{(0)} = 2[(p_{20}^{(0)2} - p_{2}^{(0)2} ) + X^{2} (\dot{p}_{20}^{(0)2} - \dot{p}_{2}^{(0)2} ) - x^{\prime}_{0} (\gamma_{20}^{(0)} - \gamma_{2}^{(0)} ) - X^{2} y_{2} (\dot{p}_{20}^{(0)} - \dot{p}_{2}^{(0)} )].$$

Using (ii), we obtain

$$\begin{aligned} \varGamma_{11}^{(0)} & = 2\{ \,E^{2} [\,\cos^{2} \eta - \cos^{2} (\varOmega \tau - \eta )] + X^{2} E^{2} [\varOmega^{2} \sin^{2} \eta - \varOmega^{2} \sin^{2} (\varOmega \tau - \eta )] \\& \quad - x^{\prime}_{0} M_{3} (1 - \cos \tau ) - X^{2} y_{2} E\varOmega [\sin \eta + \sin (\varOmega \tau - \eta )]\} . \\ \end{aligned}$$

That is,

$$\begin{aligned} \varGamma_{11}^{(0)} & = \{ E^{2} [2\cos^{2} \eta - (1 + \cos 2(\varOmega \tau - \eta ))] + X^{2} E^{2} \varOmega^{2} [2\sin^{2} \eta - (1 - \cos 2(\varOmega \tau - \eta ))] \\& \quad - 2x^{\prime}_{0} M_{3} (1 - \cos \tau ) - 2X^{2} y_{2} E\varOmega [\sin \eta + \sin (\varOmega \tau - \eta )]\} . \\ \end{aligned}$$

Then, one obtains the first equation of systems (28). Similarly the other three equations can be obtained easily.