Exact Frequencies for Free Vibration of Exponential and Polynomial AFG Beams with Lumped End Masses and Elastic Supports

Abstract

Purpose

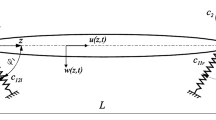
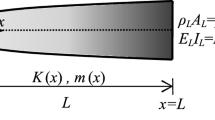
In this paper, free vibration of polynomial and exponential axially functionally graded (AFG) beam with lumped end masses and elastic supports is studied within the Euler–Bernoulli beam theory. The axial eccentricity and rotatory inertia of the end lumped masses are considered. Also, a new equation is proposed for the equivalence of the exponential AFG beams with the polynomial AFG beams.

Methods

Both the geometrical and material properties of the beam are graded along the AFG beam axis according to the polynomial (P-AFG) and exponential (E-AFG) functions. An analytical approach to derive the exact characteristic equations of two types of AFG beams with end lumped masses and elastic supports is presented. Accordingly, through numerical solving of the characteristic equations, the exact natural frequencies of AFG beams with arbitrary boundary conditions are obtained.

Results and Conclusion

The effects of end lumped mass parameters, i.e., end mass ratio, rotatory inertia ratio, axial eccentricity ratio, the AFG parameters, and the end support parameters on the first three natural frequencies of several P-AFG beams and their equivalent E-AFG beams are investigated. Results show the mentioned parameters play an important role in determining the natural frequencies for the AFG beams. Moreover, the present results can use as a benchmark for other numerical solutions and be served for purposeful design vibrating a wide range of non-uniform and composite beams.

Appendix 1

The elements of matrix F which are used in Eq. (20) for the P-AFG beam are as follows:

$$\begin{aligned} F_{11} & = - \mu (1 - R_{0} )\left( {1 + \alpha_{0} \gamma_{0} \mu^{2} } \right)J_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) \\ & \quad + \left[ {R_{0} + c_{\mathrm{p}} (n_{\mathrm{p}} + 1)(1 - R_{0} ) - \alpha_{0} \mu^{4} (\beta_{0}^{2} + \gamma_{0}^{2} )(1 - R_{0} )} \right]J_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right), \\ \end{aligned}$$

(21)

$$\begin{aligned} F_{12} & = - \mu (1 - R_{0} )\left( {1 + \alpha_{0} \gamma_{0} \mu^{2} } \right)Y_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) \\ & \quad + \left[ {R_{0} + c_{\mathrm{p}} (n_{\mathrm{p}} + 1)(1 - R_{0} ) - \alpha_{0} \mu^{4} (\beta_{0}^{2} + \gamma_{0}^{2} )(1 - R_{0} )} \right]Y_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right), \\ \end{aligned}$$

(22)

$$\begin{aligned} F_{13} & = \mu (1 - R_{0} )\left( {1 - \alpha_{0} \gamma_{0} \mu^{2} } \right)I_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) \\ & \quad - \left[ {R_{0} + c\mathrm{p}(n_{\mathrm{p}} + 1)(1 - R_{0} ) - \alpha_{0} \mu^{4} (\beta_{0}^{2} + \gamma_{0}^{2} )(1 - R_{0} )} \right]I_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right), \\ \end{aligned}$$

(23)

$$\begin{aligned} F_{14} & = \mu (1 - R_{0} )\left( {1 - \alpha_{0} \gamma_{0} \mu^{2} } \right)K_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) \\ & \quad + \left[ {R_{0} + c_{\mathrm{p}} (n_{\mathrm{p}} + 1)(1 - R_{0} ) - \alpha_{0} \mu^{4} (\beta_{0}^{2} + \gamma_{0}^{2} )(1 - R_{0} )} \right]K_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right), \\ \end{aligned}$$

(24)

$$F_{21} = \left[ {T_{0} - \alpha_{0} \mu^{4} (1 - T_{0} )} \right]J_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) + \mu^{3} (1 - T_{0} )\left( {1 - \alpha_{0} \gamma_{0} \mu^{2} } \right)J_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right),$$

(25)

$$F_{22} = \left[ {T_{0} - \alpha_{0} \mu^{4} (1 - T_{0} )} \right]Y_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) + \mu^{3} (1 - T_{0} )\left( {1 - \alpha_{0} \gamma_{0} \mu^{2} } \right)Y_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right),$$

(26)

$$F_{23} = \left[ {T_{0} - \alpha_{0} \mu^{4} (1 - T_{0} )} \right]I_{{n_{\mathrm{p}} }} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right) + \mu^{3} (1 - T_{0} )\left( {1 + \alpha_{0} \gamma_{0} \mu^{2} } \right)I_{{n_{\mathrm{p}} + 1}} \left( {\frac{2\mu }{{c_{\mathrm{p}} }}} \right),$$

(27)

$$F_{24} = \left[ {T_{0} - \alpha_{0} \mu^{4} (1 - T_{0} )} \right]K_{{n_{p} }} \left( {\frac{2\mu }{{c_{p} }}} \right) - \mu^{3} (1 - T_{0} )\left( {1 + \alpha_{0} \gamma_{0} \mu^{2} } \right)K_{{n_{p} + 1}} \left( {\frac{2\mu }{{c_{p} }}} \right),$$

(28)

$$\begin{aligned} F_{31} & = - \mu \sqrt {1 + c_{\mathrm{p}} } (1 - R_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} + \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]J_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \\ & \quad + \left[ { - R_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + c_{\mathrm{p}} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} (n_{\mathrm{p}} + 1)(1 - R_{L} ) + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )(1 - R_{L} )} \right]J_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \\ \end{aligned}$$

(29)

$$\begin{aligned} F_{32} & = - \mu \sqrt {1 + c_{\mathrm{p}} } (1 - R_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} + \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]Y_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ &\quad + \left[ { - R_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + c_{\mathrm{p}} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} (n{}_{\mathrm{p}} + 1)(1 - R_{L} ) + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )(1 - R_{L} )} \right]Y_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \hfill \\ \end{aligned}$$

(30)

$$\begin{aligned} F_{33} & = \mu \sqrt {1 + c_{\mathrm{p}} } (1 - R_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} - \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]I_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ & \quad - \left[ { - R_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + c_{\mathrm{p}} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} (n_{\mathrm{p}} + 1)(1 - R_{L} ) + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )(1 - R_{L} )} \right]I_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \hfill \\ \end{aligned}$$

(31)

$$\begin{aligned} F_{34} & = \mu \sqrt {1 + c_{\mathrm{p}} } (1 - R_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} - \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]K_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ & \quad + \left[ { - R_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + c_{\mathrm{p}} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} (n_{\mathrm{p}} + 1)(1 - R_{L} ) + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )(1 - R_{L} )} \right]K_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \hfill \\ \end{aligned}$$

(32)

$$\begin{aligned} F_{41} & = \sqrt {1 + c_{\mathrm{p}} } \left[ { - T_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + \alpha_{{L_{\mathrm{p}} }} (1 - T_{L} )\mu^{4} } \right]J_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ & \quad + \mu^{3} (1 - T_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} - \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]J_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \hfill \\ \end{aligned}$$

(33)

$$\begin{aligned} F_{42} & = \sqrt {1 + c_{\mathrm{p}} } \left[ { - T_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (1 - T_{L} )} \right]Y_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ & \quad + \mu^{3} (1 - T_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} - \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]Y_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \hfill \\ \end{aligned}$$

(34)

$$\begin{aligned} F_{43} & = \sqrt {1 + c_{\mathrm{p}} } \left[ { - T_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (1 - T_{L} )} \right]I_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ & \quad + \mu^{3} (1 - T_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} + \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]I_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right), \hfill \\ \end{aligned}$$

(35)

$$\begin{aligned} F_{44} & = \sqrt {1 + c_{\mathrm{p}} } \left[ { - T_{L} (1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 2}} + \alpha_{{L_{\mathrm{p}} }} \mu^{4} (1 - T_{L} )} \right]K_{{n_{\mathrm{p}} }} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right) \hfill \\ & \quad - \mu^{3} (1 - T_{L} )\left[ {(1 + c_{\mathrm{p}} )^{{n_{\mathrm{p}} + 1}} + \alpha_{{L_{\mathrm{p}} }} \gamma_{L} \mu^{2} } \right]K_{{n_{\mathrm{p}} + 1}} \left( {\frac{{2\mu \sqrt {1 + c_{\mathrm{p}} } }}{{c_{\mathrm{p}} }}} \right). \hfill \\ \end{aligned}$$

(36)

The elements of matrix F which are used in Eq. (20) for the E-AFG beam are as follows:

$$F_{11} = \left[ {n_{\mathrm{e}}^{2} - \delta_{1}^{2} - \alpha_{0} \mu^{4} \left( {(\beta_{0}^{2} + \gamma_{0}^{2} )n_{\mathrm{e}} + \gamma_{0} } \right)} \right](1 - R_{0} ) + R_{0} n_{\mathrm{e}} ,$$

(37)

$$F_{12} = - \delta_{1} \left( {2n_{\mathrm{e}} - \alpha_{0} \mu^{4} (\beta_{0}^{2} + \gamma_{0}^{2} )} \right)(1 - R_{0} ) - R_{0} \delta_{1} ,$$

(38)

$$F_{13} = \left[ {n_{\mathrm{e}}^{2} + \delta_{2}^{2} - \alpha_{0} \mu^{4} \left( {(\beta_{0}^{2} + \gamma_{0}^{2} )n_{\mathrm{e}} + \gamma_{0} } \right)} \right](1 - R_{0} ) + R_{0} n_{\mathrm{e}} ,$$

(39)

$$F_{14} = - \delta_{2} \left( {2n_{\mathrm{e}} - \alpha_{0} \mu^{4} (\beta_{0}^{2} + \gamma_{0}^{2} )} \right)(1 - R_{0} ) - R_{0} \delta_{2} ,$$

(40)

$$F_{21} = \left( {n_{\mathrm{e}} (n_{\mathrm{e}}^{2} + \delta \,_{1}^{2} ) - \alpha_{0} \mu^{4} (1 + \gamma_{0} n_{\mathrm{e}} )} \right)(1 - T_{0} ) + T_{0} ,$$

(41)

$$F_{22} = - \delta_{1} (n_{\mathrm{e}}^{2} + \delta \,_{1}^{2} - \alpha_{0} \gamma_{0} \mu^{4} )(1 - T_{0} ),$$

(42)

$$F_{23} = \left( {n_{\mathrm{e}} (n_{\mathrm{e}}^{2} - \delta \,_{2}^{2} ) - \alpha_{0} \mu^{4} (1 + \gamma_{0} n_{\mathrm{e}} )} \right)(1 - T_{0} ) + T_{0} ,$$

(43)

$$F_{24} = - \delta_{2} (n_{\mathrm{e}}^{2} - \delta \,_{2}^{2} - \alpha_{0} \gamma_{0} \mu^{4} )(1 - T_{0} ),$$

(44)

$$\begin{gathered} F_{31} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {\alpha_{{L_{\mathrm{e}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )\left( {n_{\mathrm{e}} \cos (\delta_{1} ) + \delta_{1} \sin (\delta_{1} )} \right) + 2n_{\mathrm{e}} \delta_{1} \sin (\delta_{1} ) + (n_{\mathrm{e}}^{2} - \delta_{1}^{2} - \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\cos (\delta_{1} )} \right]} \right.(1 - R_{L} ) - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\left( {n_{\mathrm{e}} \cos (\delta_{1} ) + \delta_{1} \sin (\delta_{1} )} \right)R_{L} } \right\}, \hfill \\ \end{gathered}$$

(45)

$$\begin{gathered} F_{32} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {\alpha_{{L_{\mathrm{e}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )\left( {n_{\mathrm{e}} \sin (\delta_{1} ) - \delta_{1} \cos (\delta_{1} )} \right) - 2n_{\mathrm{e}} \delta_{1} \cos (\delta_{1} ) + (n_{\mathrm{e}}^{2} - \delta_{1}^{2} - \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\sin (\delta_{1} )} \right](1 - R_{L} ) + } \right. \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\left( {\delta_{1} \cos (\delta_{1} ) - n_{\mathrm{e}} \sin (\delta_{1} )} \right)R_{L} } \right\}, \hfill \\ \end{gathered}$$

(46)

$$\begin{gathered} F_{33} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {\alpha_{{L_{\mathrm{e}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )\left( {n_{\mathrm{e}} \cosh (\delta_{2} ) - \delta_{2} \sinh (\delta_{2} )} \right) - 2n_{\mathrm{e}} \delta_{2} \sinh (\delta_{2} ) + (n_{\mathrm{e}}^{2} + \delta_{2}^{2} - \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\cosh (\delta_{2} )} \right]} \right.(1 - R_{L} ) + \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\left( {\delta_{2} \sinh (\delta_{2} ) - n_{\mathrm{e}} \cosh (\delta_{2} )} \right)R_{L} } \right\} \hfill \\ \end{gathered}$$

(47)

$$\begin{gathered} F_{34} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {\alpha_{{L_{\mathrm{e}} }} \mu^{4} (\beta_{L}^{2} + \gamma_{L}^{2} )\left( {n_{\mathrm{e}} \sinh (\delta_{2} ) - \delta_{2} \cosh (\delta_{2} )} \right) - 2n_{\mathrm{e}} \delta_{2} \cosh (\delta_{2} ) + (n_{\mathrm{e}}^{2} + \delta_{2}^{2} - \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\sinh (\delta_{2} )} \right](1 - R_{L} ) + } \right. \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\left( {\delta_{2} \cosh (\delta_{2} ) - n_{\mathrm{e}} \sinh (\delta_{2} )} \right)R_{L} } \right\}, \hfill \\ \end{gathered}$$

(48)

$$\begin{gathered} F_{41} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {(n_{\mathrm{e}}^{2} + \delta_{1}^{2} - \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\left( {n_{\mathrm{e}} \cos (\delta_{1} ) + \delta_{1} \sin (\delta_{1} )} \right) + \alpha_{{L_{\mathrm{e}} }} \mu^{4} \cos (\delta_{1} )} \right]} \right.(1 - T_{L} ) - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\cos (\delta_{1} )T_{L} } \right\}, \hfill \\ \end{gathered}$$

(49)

$$\begin{gathered} F_{42} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {(n_{\mathrm{e}}^{2} + \delta_{1}^{2} - \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\left( {n_{\mathrm{e}} \sin (\delta_{1} ) - \delta_{1} \cos (\delta_{1} )} \right) + \alpha_{{L_{\mathrm{e}} }} \mu^{4} \sin (\delta_{1} )} \right]} \right.(1 - T_{L} ) - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\sin (\delta_{1} )T_{L} } \right\}, \hfill \\ \end{gathered}$$

(50)

$$\begin{gathered} F_{43} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {(\delta_{2}^{2} - n_{\mathrm{e}}^{2} + \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\left( {\delta_{2} \sinh (\delta_{2} ) - n_{\mathrm{e}} \cosh (\delta_{2} )} \right) + \alpha_{{L_{\mathrm{e}} }} \mu^{4} \cosh (\delta_{2} )} \right]} \right.(1 - T_{L} ) - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\cosh (\delta_{2} )T_{L} } \right\}, \hfill \\ \end{gathered}$$

(51)

$$\begin{gathered} F_{44} = e^{{ - n_{\mathrm{e}} }} \left\{ {\left[ {(\delta_{2}^{2} - n_{\mathrm{e}}^{2} + \alpha_{{L_{\mathrm{e}} }} \gamma_{L} \mu^{4} )\left( { - n_{\mathrm{e}} \sinh (\delta_{2} ) + \delta_{2} \cosh (\delta_{2} )} \right) + \alpha_{{L_{\mathrm{e}} }} \mu^{4} \sinh (\delta_{2} )} \right]} \right.(1 - T_{L} ) - \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\sinh (\delta_{2} )T_{L} } \right\}. \hfill \\ \end{gathered}$$

(52)