Free Transverse Vibration of General Power-Law NAFG Beams with Tip Masses

Abstract

Purpose

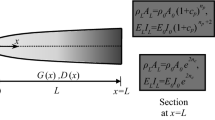
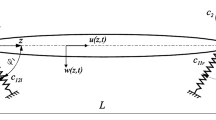
The present study aims to obtain the exact solutions of the free transverse vibration of non-uniform axially functionally graded (NAFG) beams with end point masses and general boundary conditions. Also, the effects of the attached end point masses, rotational and translational elastic supports, and NAFG parameters on the natural frequencies of the power-law NAFG beams are investigated.

Methods

Based on the Euler–Bernoulli beam theory, the governing differential equation of motion was solved accurately using the Bessel functions. Then, the constant coefficients matrices of the power-law NAFG beams with the end point masses and general elastic supports were derived by applying the boundary conditions. The general elastic boundary conditions are modeled with the linear rotational and lateral translational springs. Furthermore, the material and geometrical properties of the NAFG beams are assumed to change continuously and together in the axial direction according to the power-law forms. By taking the constant coefficients matrix determinant equal to zero and calculating the positive real roots, the natural frequencies were obtained. By comparing the responses of the numerical examples with the available solutions, the accuracy and ability of the proposed formulations are demonstrated.

Results and Conclusion

Obtained results show the natural frequencies of the power-law NAFG beam decrease with the increase of the mass ratio and increase with the increase of the stiffness ratios of the supports. Moreover, the natural frequencies of the power-law NAFG beam increase with the increase of NAFG parameters. Depending on the boundary conditions, the mass sensitivity differs from one power-law NAFG beam to another, and from one mode of vibration to another. The exact analytical solutions are listed in tabular and graphical forms and can be used as the benchmark solutions. Moreover, the results presented here can be used for the proper design of composite beams carrying end point masses with different elastic boundary conditions.

Appendices

Appendix A

For the derivation of the general solution Eq. (9), the compact form of the differential equation obtained in Eq. (8), according to Eq. (4), can be expressed as follows [67]:

$$\frac{{d^{2} }}{{\text{d}X^{2} }}\left[ {X^{p + 2} \frac{{d^{2} W_{i} \left( X \right)}}{{\text{d}X^{2} }}} \right] - \frac{{\Omega_{i}^{4} }}{{c^{4} }}X^{p} W_{i} \left( X \right) = 0.$$

(28)

Eq. (28) can be factored into:

$$\left[ {X^{ - p} \frac{d}{{\text{d}X}}\left( {X^{p + 1} \frac{d}{{\text{d}X}}} \right) + \frac{{\Omega_{i}^{2} }}{{c^{2} }}} \right]\left[ {X^{ - p} \frac{d}{{\text{d}X}}\left( {X^{p + 1} \frac{d}{{\text{d}X}}} \right) - \frac{{\Omega_{i}^{2} }}{{c^{2} }}} \right]W_{i} \left( X \right) = 0.$$

(29)

Each one of the brackets in Eq. (29) is a Bessel operator. One can find the general solution of W_i(X) as:

$$W_{i} \left( X \right) = A_{i} \left( X \right) + B_{i} \left( X \right),$$

(30)

where

$$\left[ {X^{ - p} \frac{d}{{\text{d}X}}\left( {X^{p + 1} \frac{d}{{\text{d}X}}} \right) + \frac{{\Omega_{i}^{2} }}{{c^{2} }}} \right]A_{i} \left( X \right) = 0,$$

(31)

$$\left[ {X^{ - p} \frac{d}{{\text{d}X}}\left( {X^{p + 1} \frac{d}{{\text{d}X}}} \right) - \frac{{\Omega_{i}^{2} }}{{c^{2} }}} \right]B_{i} \left( X \right) = 0.$$

(32)

The Eq. (31) is the regular Bessel differential equation, and the solution can be written as:

$$A_{i} \left( X \right) = X^{{ - \frac{p}{2}}} \left[ {C_{1} J_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + } \right.\left. {C_{2} Y_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right)} \right],$$

(33)

where C₁ and C₂ are unknown constants, and J_p and Y_p are, respectively, the Bessel functions of first and second kinds of order p. The Eq. (32) is known as the modified Bessel differential equation, and the solution can be expressed as:

$$B_{i} \left( X \right) = X^{{ - \frac{p}{2}}} \left[ {C_{3} I_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + } \right.\left. {C_{4} K_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right)} \right],$$

(34)

where C₃ and C₄ are unknown constants, and I_p and K_p are, respectively, the modified Bessel functions of first and second kinds of order p. Therefore, the general solution of W_i(X) according to Eq. (30) is:

$$W_{i} \left( X \right) = X^{{ - \frac{p}{2}}} \left[ {C_{1} J_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + } \right.C_{2} Y_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + C_{3} I_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right) + \left. {C_{4} K_{p} \left( {\frac{{2\Omega_{i} \sqrt X }}{c}} \right)} \right].$$

(35)

Appendix B

The elements of the constant coefficients matrix, A for the NAFG beams with the positive gradient coefficient (i.e., c > 0), carrying tip masses and various elastic boundary conditions are as follows:

$$A_{11} = - \Omega J_{p} \left( {\frac{2\Omega }{c}} \right) + \left[ {R_{0} + c(p + 1)} \right]J_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(36)

$$A_{12} = - \Omega Y_{p} \left( {\frac{2\Omega }{c}} \right) + \left[ {R_{0} + c(p + 1)} \right]Y_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(37)

$$A_{13} = \Omega I_{p} \left( {\frac{2\Omega }{c}} \right) - \left[ {R_{0} + c(p + 1)} \right]I_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(38)

$$A_{14} = \Omega K_{p} \left( {\frac{2\Omega }{c}} \right) + \left[ {R_{0} + c(p + 1)} \right]K_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(39)

$$A_{21} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)J_{p} \left( {\frac{2\Omega }{c}} \right) + \Omega^{3} J_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(40)

$$A_{22} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)Y_{p} \left( {\frac{2\Omega }{c}} \right) + \Omega^{3} Y_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(41)

$$A_{23} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)I_{p} \left( {\frac{2\Omega }{c}} \right) + \Omega^{3} I_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(42)

$$A_{24} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)K_{p} \left( {\frac{2\Omega }{c}} \right) - \Omega^{3} K_{p + 1} \left( {\frac{2\Omega }{c}} \right),$$

(43)

$$A_{31} = - \Omega \sqrt {1 + c} J_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \left[ {R_{L} (1 + c) - c(p + 1)} \right]J_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(44)

$$A_{32} = - \Omega \sqrt {1 + c} Y_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \left[ {R_{L} (1 + c) - c(p + 1)} \right]Y_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(45)

$$A_{33} = \Omega \sqrt {1 + c} I_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \left[ {R_{L} (1 + c) - c(p + 1)} \right]I_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(46)

$$A_{34} = \Omega \sqrt {1 + c} K_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \left[ {R_{L} (1 + c) - c(p + 1)} \right]K_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(47)

$$A_{41} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]J_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} J_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(48)

$$A_{42} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]Y_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} Y_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(49)

$$A_{43} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]I_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} I_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right),$$

(50)

$$A_{44} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]K_{p} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} K_{p + 1} \left( {\frac{{2\Omega \sqrt {1 + c} }}{c}} \right).$$

(51)

For the uniform beam, i.e., c = 0, the entries of the unknown constants' matrix, A are as below:

$$A_{11} = - R_{0}$$

(52)

$$A_{12} = - \Omega$$

(53)

$$A_{13} = - R_{0}$$

(54)

$$A_{14} = \Omega$$

(55)

$$A_{21} = - \Omega^{3}$$

(56)

$$A_{22} = T_{0} - \alpha_{0} \Omega^{4}$$

(57)

$$A_{23} = \Omega^{3}$$

(58)

$$A_{24} = T_{0} - \alpha_{0} \Omega^{4}$$

(59)

$$A_{31} = - \Omega \sin (\Omega ) + R_{L} \cos (\Omega )$$

(60)

$$A_{32} = - \Omega \cos (\Omega ) - R_{L} \sin (\Omega )$$

(61)

$$A_{33} = \Omega \sinh (\Omega ) + R_{L} \cosh (\Omega )$$

(62)

$$A_{34} = \Omega \cosh (\Omega ) + R_{L} \sinh (\Omega )$$

(63)

$$A_{41} = ( - T_{L} + \alpha_{L} \Omega^{4} )\sin (\Omega ) - \Omega^{3} \cos (\Omega )$$

(64)

$$A_{42} = ( - T_{L} + \alpha_{L} \Omega^{4} )\cos (\Omega ) + \Omega^{3} \sin (\Omega )$$

(65)

$$A_{43} = ( - T_{L} + \alpha_{L} \Omega^{4} )\sinh (\Omega ) + \Omega^{3} \cosh (\Omega )$$

(66)

$$A_{44} = ( - T_{L} + \alpha_{L} \Omega^{4} )\cosh (\Omega ) + \Omega^{3} \sinh (\Omega )$$

(67)

The elements of the constant coefficients matrix, A for the NAFG beams with the negative gradient coefficient (i.e., -1 < c < 0), carrying tip masses and general elastic boundary conditions are as follows:

$$A_{11} = - \Omega J_{p} \left( { - \frac{2\Omega }{c}} \right) - \left[ {R_{0} + c(p + 1)} \right]J_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(68)

$$A_{12} = - \Omega Y_{p} \left( { - \frac{2\Omega }{c}} \right) - \left[ {R_{0} + c(p + 1)} \right]Y_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(69)

$$A_{13} = \Omega I_{p} \left( { - \frac{2\Omega }{c}} \right) + \left[ {R_{0} + c(p + 1)} \right]I_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(70)

$$A_{14} = \Omega K_{p} \left( { - \frac{2\Omega }{c}} \right) - \left[ {R_{0} + c(p + 1)} \right]K_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(71)

$$A_{21} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)J_{p} \left( { - \frac{2\Omega }{c}} \right) - \Omega^{3} J_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(72)

$$A_{22} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)Y_{p} \left( { - \frac{2\Omega }{c}} \right) - \Omega^{3} Y_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(73)

$$A_{23} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)I_{p} \left( { - \frac{2\Omega }{c}} \right) - \Omega^{3} I_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(74)

$$A_{24} = \left( {T_{0} - \alpha_{0} \Omega^{4} } \right)K_{p} \left( { - \frac{2\Omega }{c}} \right) + \Omega^{3} K_{p + 1} \left( { - \frac{2\Omega }{c}} \right)$$

(75)

$$A_{31} = - \Omega \sqrt {1 + c} J_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \left[ {R_{L} (1 + c) - c(p + 1)} \right]J_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(76)

$$A_{32} = - \Omega \sqrt {1 + c} Y_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \left[ {R_{L} (1 + c) - c(p + 1)} \right]Y_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(77)

$$A_{33} = \Omega \sqrt {1 + c} I_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \left[ {R_{L} (1 + c) - c(p + 1)} \right]I_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(78)

$$A_{34} = \Omega \sqrt {1 + c} K_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \left[ {R_{L} (1 + c) - c(p + 1)} \right]K_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(79)

$$A_{41} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]J_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} J_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(80)

$$A_{42} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]Y_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} Y_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(81)

$$A_{43} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]I_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) - \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} I_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right)$$

(82)

$$A_{44} = \left[ { - T_{L} (1 + c)^{p + 2} + \alpha_{L} \Omega^{4} } \right]K_{p} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right) + \Omega^{3} (1 + c)^{{p + \frac{1}{2}}} K_{p + 1} \left( { - \frac{{2\Omega \sqrt {1 + c} }}{c}} \right).$$

(83)