Free vibration analysis of exponential AFGM beams with general boundary conditions and tip masses

Abstract

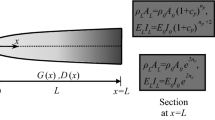
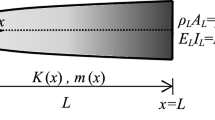
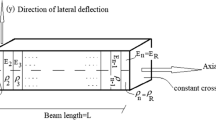
In this paper, the analytical method and design charts for finding the exact solutions to the free transverse vibration of the exponential axially functionally graded material (AFGM) beams with concentrated tip masses and general boundary conditions are presented. According to the derived formulations, the effects of the elastic supports, attached tip masses, and exponential gradient index on the natural frequencies and mode shapes of the AFGM beams with symmetric and asymmetric boundary conditions are investigated. First, by solving the differential equation governing the free vibration of the exponential AFGM Euler–Bernoulli beams, exact solutions are obtained. The material properties of beams are assumed to vary continuously in the axial direction according to the exponential functions. Second, by applying the general boundary conditions, the matrix of constant factors of the beam is derived explicitly. By setting the determinant of this matrix to zero, the natural frequencies of the exponential AFGM beam with the general boundary conditions will be available. In the following, the mode shapes and design charts of the AFGM beams can be obtained. The advantages of the proposed formulations are accuracy, generality, and simplicity in modeling the various boundary conditions. Results show that tip masses, exponential gradient index, and end supports play an influential role in the dynamic behavior of the AFGM beams. Accordingly, the results and design charts presented for the first time are helpful for the proper design and finding the identical frequency of the exponential AFGM beams, exponential non-uniform beams, and uniform beams with different boundary conditions.

Appendix

The elements of the constant coefficients matrix, A for the exponential AFGM beam with carrying tip masses and various elastic boundary conditions in the framework of the Euler–Bernoulli theory are as follows:

$$A_{11} = (\delta_1^2 - \beta^2 )(1 - R_0 ) - R_0 \beta$$

(A-1)

$$A_{12} = \delta_1 \left[ {2\beta (1 - R_0 ) + R_0 } \right]$$

(A-2)

$$A_{13} = - (\delta_2^2 + \beta^2 )(1 - R_0 ) - R_0 \beta$$

(A-3)

$$A_{14} = \delta_2 \left[ {2\beta (1 - R_0 ) + R_0 } \right]$$

(A-4)

$$A_{21} = \left[ { - \beta (\delta \,_1^2 + \beta \,^2 ) + \Omega^2 \alpha_0 } \right](1 - T_0 ) - T_0$$

(A-5)

$$A_{22} = \delta_1 \left( {\delta \,_1^2 + \beta \,^2 } \right)(1 - T_0 )$$

(A-6)

$$A_{23} = \left[ {\beta \,(\delta \,_1^2 - \beta \,^2 ) + \Omega^2 \alpha_0 } \right](1 - T_0 ) - T_0$$

(A-7)

$$A_{24} = \delta_2 \left( {\beta \,^2 - \delta \,_1^2 } \right)(1 - T_0 )$$

(A-8)

$$A_{31} = e^{ - \beta } \left\{ {\left[ {(\delta_1^2 - \beta^2 )\cos (\delta_1 ) - 2\beta \delta_1 \sin (\delta_1 )} \right](1 - R_L ) + \left( {\beta \cos (\delta_1 ) + \delta_1 \sin (\delta_1 )} \right)R_L } \right\}$$

(A-9)

$$A_{32} = e^{ - \beta } \left\{ {\left[ {(\delta_1^2 - \beta^2 )\sin (\delta_1 ) + 2\beta \delta_1 \cos (\delta_1 )} \right](1 - R_L ) + \left( {\beta \sin (\delta_1 ) - \delta_1 \cos (\delta_1 )} \right)R_L } \right\}$$

(A-10)

$$A_{33} = e^{ - \beta } \left\{ {\left[ { - (\delta_2^2 + \beta^2 ){\rm cosh}(\delta_2 ) + 2\beta \delta_2 \sinh (\delta_2 )} \right](1 - R_L ) + \left( {\beta \cosh (\delta_2 ) - \delta_2 \sinh (\delta_2 )} \right)R_L } \right\}$$

(A-11)

$$A_{34} = e^{ - \beta } \left\{ {\left[ { - (\delta_2^2 + \beta^2 )\sinh (\delta_2 ) + 2\beta \delta_2 \cosh (\delta_2 )} \right](1 - R_L ) + \left( {\beta {\rm sinh}(\delta_2 ) - \delta_2 \cosh (\delta_2 )} \right)R_L } \right\}$$

(A-12)

$$A_{41} = e^{ - \beta } \left\{ {\left[ {(\delta \,_1^2 + \beta^2 )\left( {\delta_1 \sin \,(\delta_1 ) + \beta \cos \,(\delta_1 )} \right) + \Omega^2 \alpha_L \cos \,(\delta_1 )} \right](1 - T_L ) - \cos \,(\delta_1 )T_L } \right\}$$

(A-13)

$$A_{42} = e^{ - \beta } \left\{ {\left[ {(\delta \,_1^2 + \beta \,^2 )\left( {\delta_1 \cos\,(\delta_1 ) - \beta \sin \,(\delta_1 )} \right) - \Omega^2 \alpha_L \sin\,(\delta_1 )} \right](1 - T_L ) + \sin \,(\delta_1 )T_L } \right\}$$

(A-14)

$$A_{43} = e^{ - \beta } \left\{ {\left[ {(\delta \,_2^2 - \beta \,^2 )\left( {\beta \,\cosh (\delta_2 ) - \delta_2 \sinh \,(\delta_2 )} \right) - \Omega^2 \alpha_L \cosh \,(\delta_2 )} \right](1 - T_L ) + \cosh \,(\delta_2 )T_L } \right\}$$

(A-15)

$$A_{44} = e^{ - \beta } \left\{ {\left[ {(\delta \,_2^2 - \beta \,^2 )\left( {\beta \sinh \,(\delta_2 ) - \delta_2 {\rm cosh}\,(\delta_2 )} \right) - \Omega^2 \alpha_L {\rm sinh}\,(\delta_2 )} \right](1 - T_L ) + \sinh \,(\delta_2 )T_L } \right\}$$

(A-16)