Skip to main content
SpringerLink
Log in

Out-of-plane equilibrium points and invariant manifolds about an asteroid with gravitational orbit—attitude coupling perturbation

  • Research Article
  • Published:
Astrodynamics Aims and scope Submit manuscript

Abstract

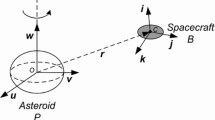
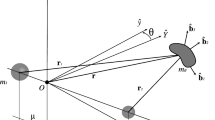
By considering the spacecraft as an extended, rigid body with a prior known attitude instead of a point mass, the attitude-restricted orbital dynamics can improve the precision of the classical point-mass orbital dynamics in close proximity to an asteroid, because it includes the perturbation caused by the gravitational orbit–attitude coupling of the spacecraft (GOACP). The GOACP is defined as the difference between the gravity acting on a non-spherical, extended body (the real case of a spacecraft) and the gravity acting on a point mass (the approximation of a spacecraft in classical orbital dynamics). In-plane equilibrium points that are within the principal planes of the asteroid have been investigated for the attitude-restricted orbital dynamics in previous studies, including equatorial and in-plane non-equatorial equilibrium points. In this study, out-of-plane equilibrium points outside the principal planes of the asteroid were examined. Out-of-plane equilibrium points cannot exist in the classical point-mass orbital dynamics but do exist in the attitude-restricted orbital dynamics owing to the effects of the GOACP. The previously investigated in-plane equilibrium points and the out-of-plane ones examined in this study provide a complete map of the equilibrium points in close proximity to an asteroid with the GOACP. Equatorial and in-plane non-equatorial equilibrium points have extended the longitude and latitude ranges of the classical equilibrium points without the GOACP, respectively, while the out-of-plane ones examined in the present study extend both the longitude and latitude ranges. Additionally, the invariant manifolds of out-of-plane equilibrium points were calculated, and the results indicated that the attitude of spacecraft significantly affects the invariant manifolds. In practice, these equilibrium points can provide natural hovering positions for operations in proximity to asteroids, and their invariant manifolds can be used for transfers to or from the equilibrium points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Wang, Y., Xu, S. J. Orbital dynamics and equilibrium points around an asteroid with gravitational orbit-attitude coupling perturbation. Celestial Mechanics and Dynamical Astronomy, 2016, 125(3): 265–285.

    Article  MathSciNet  Google Scholar 

  2. Wang, Y., Xu, S. J. Non-equatorial equilibrium points around an asteroid with gravitational orbit-attitude coupling perturbation. Astrodynamics, 2020, 4(1): 1–16.

    Article  Google Scholar 

  3. Russell, R. P. Survey of spacecraft trajectory design in strongly perturbed environments. Journal of Guidance, Control, and Dynamics, 2012, 35(3), 705–720.

    Article  Google Scholar 

  4. Scheeres, D. J. Orbit mechanics about asteroids and comets. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 987–997.

    Article  Google Scholar 

  5. Scheeres, D. J. Orbit mechanics about small bodies. Acta Astronautica, 2012, 72: 1–14.

    Article  Google Scholar 

  6. Scheeres, D. J. Orbital Motion in Strongly Perturbed Environments. Springer, Berlin, Heidelberg, 2012.

    Book  Google Scholar 

  7. Scheeres, D. J. Close proximity dynamics and control about asteroids. In: Proceedings of the 2014 American Control Conference, 2014: 1584–1598.

  8. Riverin, J. L., Misra, A. K. Attitude dynamics of satellites orbiting small bodies. In: Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, 2002: AIAA 2002–4520.

  9. Misra, A. K., Panchenko, Y. Attitude dynamics of satellites orbiting an asteroid. The Journal of the Astronautical Sciences, 2006, 54(3–4): 369–381.

    Article  MathSciNet  Google Scholar 

  10. Kumar, K. D. Attitude dynamics and control of satellites orbiting rotating asteroids. Acta Mechanica, 2008, 198(1–2): 99–118.

    Article  Google Scholar 

  11. Wang, Y., Xu, S. J. Attitude stability of a spacecraft on a stationary orbit around an asteroid subjected to gravity gradient torque. Celestial Mechanics and Dynamical Astronomy, 2013, 115(4): 333–352.

    Article  MathSciNet  Google Scholar 

  12. Wang, Y., Xu, S. Equilibrium attitude and nonlinear stability of a spacecraft on a stationary orbit around an asteroid. Advances in Space Research, 2013, 52(8): 1497–1510.

    Article  Google Scholar 

  13. Wang, Y., Xu, S. Analysis of the attitude dynamics of a spacecraft on a stationary orbit around an asteroid via Poincaré section. Aerospace Science and Technology, 2014, 39: 538–545.

    Article  Google Scholar 

  14. Zhang, M. J., Zhao, C. Y. Attitude stability of a spacecraft with two flexible solar arrays on a stationary orbit around an asteroid subjected to gravity gradient torque. Astrophysics and Space Science, 2014, 351(2): 507–524.

    Article  Google Scholar 

  15. Zhang, M. J., Zhao, C. Y. Attitude stability of a dualspin spacecraft on a stationary orbit around an asteroid subjected to gravity gradient torque. Astrophysics and Space Science, 2015, 355(2): 203–212.

    Article  Google Scholar 

  16. Scheeres, D. J. Spacecraft at small NEO. 2006: arXiv: physics/0608158v1. Available at https://arxiv.org/abs/physics/0608158.

  17. Wang, Y., Xu, S. Gravitational orbit-rotation coupling of a rigid satellite around a spheroid planet. Journal of Aerospace Engineering, 2014, 27(1): 140–150.

    Article  Google Scholar 

  18. Sincarsin, G. B., Hughes, P. C. Gravitational orbit-attitude coupling for very large spacecraft. Celestial Mechanics, 1983, 31(2): 143–161.

    Article  Google Scholar 

  19. Wang, L. S., Krishnaprasad, P. S., Maddocks, J. H. Hamiltonian dynamics of a rigid body in a central gravitational field. Celestial Mechanics and Dynamical Astronomy, 1990, 50(4): 349–386.

    Article  MathSciNet  Google Scholar 

  20. Wang, L.-S., Maddocks, J. H., Krishnaprasad, P. S. Steady rigid-body motions in a central gravitational field. Journal of Astronautical Sciences, 1992, 40: 449–478.

    MathSciNet  Google Scholar 

  21. Sanyal, A. K. Dynamics and control of multibody systems in central gravity. Ph.D. Dissertation. Ann Harbor, MI: Department of Aerospace Engineering, The University of Michigan, 2004.

    Google Scholar 

  22. Teixidó Román, M. Hamiltonian methods in stability and bifurcations problems for artificial satellite dynamics. Master Thesis. Facultat de Matemàtiques i Estadística, Universitat Politècnica de Catalunya, 2010: 51–72.

  23. Wang, Y., Xu, S. Symmetry, reduction and relative equilibria of a rigid body in the J2 problem. Advances in Space Research, 2013, 51(7): 1096–1109.

    Article  Google Scholar 

  24. Wang, Y., Xu, S. J. Stability of the classical type of relative equilibria of a rigid body in the J2 problem. Astrophysics and Space Science, 2013, 346(2): 443–461.

    Article  Google Scholar 

  25. Wang, Y., Xu, S. J. Relative equilibria of full dynamics of a rigid body with gravitational orbit-attitude coupling in a uniformly rotating second degree and order gravity field. Astrophysics and Space Science, 2014, 354(2): 339–353.

    Article  Google Scholar 

  26. Wang, Y., Xu, S. J., Tang, L. On the existence of the relative equilibria of a rigid body in the J2 problem. Astrophysics and Space Science, 2014, 353(2): 425–440.

    Article  Google Scholar 

  27. Wang, Y., Xu, S. J. On the nonlinear stability of relative equilibria of the full spacecraft dynamics around an asteroid. Nonlinear Dynamics, 2014, 78(1): 1–13.

    Article  MathSciNet  Google Scholar 

  28. Hu, W., Yin, T., Zheng, W., Deng, Z. Symplectic analysis on orbit-attitude coupling dynamic problem of spatial rigid rod. Journal of Vibration and Control, 2020, 26(17–18): 1614–1624.

    Article  MathSciNet  Google Scholar 

  29. Kikuchi, S., Howell, K. C., Tsuda, Y., Kawaguchi, J. Orbit-attitude coupled motion around small bodies: Sun-synchronous orbits with Sun-tracking attitude motion, Acta Astronautica, 2017, 140: 34–48.

    Article  Google Scholar 

  30. Jean, I., Misra, A. K., Ng, A. Orbital and attitude coupled dynamics of a spacecraft around an asteroid. In: Proceedings of the 3rd IAA Conference on Dynamics and Control of Space Systems, 2017.

  31. Lee, D., Sanyal, A. K., Butcher, E. A., Scheeres, D. J. Almost global asymptotic tracking control for spacecraft body-fixed hovering over an asteroid. Aerospace Science and Technology, 2014, 38: 105–115.

    Article  Google Scholar 

  32. Lee, D., Sanyal, A. K., Butcher, E. A., Scheeres, D. J. Finite-time control for spacecraft body-fixed hovering over an asteroid. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(1): 506–520.

    Article  Google Scholar 

  33. Misra, G., Izadi, M., Sanyal, A., Scheeres, D. J. Coupled orbit-attitude dynamics and pose estimation of spacecraft near small solar system bodies. Advances in Space Research, 2016, 57(8), 1747–1761.

    Article  Google Scholar 

  34. Li, X., Warier, R. R., Sanyal, A. K., Qiao, D. Trajectory tracking near small bodies using only attitude control. Journal of Guidance, Control, and Dynamics, 2019, 42(1): 109–122.

    Article  Google Scholar 

  35. Hu, W., Yu, L., Deng, Z. Minimum control energy of spatial beam with assumed attitude adjustment target. Acta Mechanica Solida Sinica, 2020, 33: 51–60.

    Article  Google Scholar 

  36. Howard, J. E. Spectral stability of relative equilibria. Celestial Mechanics and Dynamical Astronomy, 1990, 48(3): 267–288.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant Nos. 11602009, 11432001, and 11872007, as well as the Fundamental Research Funds for the Central Universities.

Author information

Authors and Affiliations

  1. School of Astronautics, Beihang University, Beijing, 102206, China

    Yue Wang & Ruikang Zhang

Authors
  1. Yue Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ruikang Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yue Wang.

Ethics declarations

The authors have no competing interests to declare that are relevant to the content of this article.

Additional information

Yue Wang received his B.Eng. and Ph.D. degrees in aerospace engineering from Beihang University (formerly known as Beijing University of Aeronautics and Astronautics), Beijing, China, in 2009 and 2014, respectively. From 2014 to 2015, he worked as a postdoctoral fellow in the Distributed Space Systems Lab in the Faculty of Aerospace Engineering at Technion-Israel Institute of Technology, Haifa, Israel. In 2016, he joined the School of Astronautics at Beihang University as an associate professor of the “Zhuoyue” Recruitment Program. He was rewarded the Young Elite Scientist Sponsorship Program by China Association for Science and Technology. His current research interests center on orbital dynamics and control about asteroids and the Earth-Moon system, orbital evolution and reentry prediction of space debris, and NEO impact hazard assessment.

Ruikang Zhang received his B.Eng. degree in aerospace engineering from Beihang University (formerly known as Beijing University of Aeronautics and Astronautics), Beijing, China, in 2017. At present, he is a Ph.D. candidate in aerospace engineering at Beihang University. His research interests include orbital dynamics and control about asteroids and the Earth-Moon system.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Y., Zhang, R. Out-of-plane equilibrium points and invariant manifolds about an asteroid with gravitational orbit—attitude coupling perturbation. Astrodyn 6, 269–283 (2022). https://doi.org/10.1007/s42064-021-0106-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42064-021-0106-0

Keywords

Search

Navigation